a neural representation of sketch drawings

Introduction

In this paper, The authors present a recurrent neural network: sketch-rnn to construct stroke-based drawings. Besides new robust training methods, they also outline a framework for conditional and unconditional sketch generation.

Neural networks have been heavily used as image generation tools, for example, Generative Adversarial Networks, Variational Inference and Autoregressive models. Most of those models are focusing on modelling pixels of the images. However, people learn to draw using sequences of strokes since very young ages. The authors decide to use this character to create a new model that utilize strokes of the images as a new approach to vector images generations and abstract concept generalization.

The model is trained with hand-drawn sketches as input sequences. The model is able to produce sketches in vector format. In the conditional generation model, they also explore the latent space representation for vector images and discuss a few future application of this model. The model and dataset are now available as an open source project.

Related Work

There are some works in the history that used a similar approach to generate images such as Portrait Drawing by Paul the Robot and some reinforcement learning approaches. They work more like a mimic of digitized photographs. There are some Neural network based approaches too, but those are mostly dealing with pixel images. Little work is done on vector images generation. There are models that use Hidden Markov Models or Mixture Density Networks to generate human sketches, continuous data points or vectorized Kanji characters.

The model also allows us to explore the latent space representation of vector images. There are previous works that achieved similar functions as well, such as combining Sequence-to-Sequence models with Variational Autoencoder to model sentences into latent space and using probabilistic program induction to model Omniglot dataset.

The dataset they use contains 50 million vector sketches. Before this paper, there is a Sketch data with 20k vector sketches, a Sketchy dataset with 70k vector sketches along with pixel images, and a ShadowDraw system that used 30k raster images along with extracted vectorized features. They are all comparatively small.

Methodology

Dataset

QuickDraw is a dataset with 50 million vector drawings collected by a game Quick Draw!. It contains hundreds of classes, each class has 70k training samples, 2.5k validation samples and 2.5k test samples.

The data format of each sample is a representation of a pen stroke action event. The Origin is the initial coordinate of the drawing. The sketches are points in a list. Each point consists of 5 elements ###( x, y, p 1 , p 2 , p 3 )### where x and y are the offset distance in x and y directions from the previous point. ### p1, p2 and p3### are three possible states in binary one-hot representation where ### p1 ### indicates the pen is touching the paper, ### p2 ### indicates the pen will be lifted from here, and ###p3### represents the drawing has ended.

Sketch-RNN

1. 1. 1. image###

The model is a Sequence-to-Sequence Variational Autoencoder(VAE). The encoder is a bidirectional RNN, the input is a sketch sequence and a reversed sketch sequence, so there will be two final hidden states. The output is a size ###N_z### latent vector.

1. 1. 1. eq1 ###

Then the authors project h into to ###mu and sigma###, convert ###mu### into non-negative and use them with ###N(0,I)### to construct a random vector ###z###.

1. 1. 1. eq2###

Note that ###z### is not deterministic but a conditioned random vector.

The decoder is an autoregressive RNN. The initial hidden states are generated using ### [ h 0 ; c 0 ] = tanh(W z z + b z ) ###. ###s_0### is ###(0,0,1,0,0)### For each step i in the decoder, the input ###x_i### is the concatenation of previous point ###S_i-1### and latent vector z. The output are probability distribution parameters for the next data point ###S_i###. The authors model ###(deltax, delta y)### as a Gaussian mixture model (GMM) with M normal distributions and model ###(p1 p2 p3)### as categorical distribution where they sum up to 1. The generated sequence is conditioned from the latent vector ###z### that sampled from the encoder, which is end-to-end trained together with the decoder.

1. 1. 1. eq3###

Here the ###N(x,y| .....)### i the probability distribution function for ###x,y###, ###ro_xy### is the correlation parameter for this bivariate normal distribution. The ### ### is a lenth M categorical distribution vector are the mixture weights of the Gaussian mixture model.

The output vector ###y_i### is generated using a fully-connected forward propagation in the hidden state of the RNN.

1. 1. 1. eq4###

The output consists the probability distribution of the next data point.

1. 1. 1. eq5###

1. 1. 1. exp### and ###tanh### operations will be applied to standard deviations to ensure they are non-negative and between -1 and 1.

1. 1. 1. eq6###

Categorical distribution probabilities for ###(p1,p2,p3)### using ###(q1,q2,q3)### can be obtained as :

1. 1. 1. eq7###

It is hard do decide when to stop drawing because ###(p1,p2,p3)### is very unbalanced. scholars in the past used different weights for each pen event probability, but the authors have a better idea. They define a hyperparameter representing the max length of the longest sketch in the training set ###N_max###, and set the ### Si to be (0, 0, 0, 0, 1) for i > Ns.#

The outcome sample ###S_i'### can be generated in each time step during sample process and fed as input for the next time step. The process will stop when ###p3 = 1### or ###i = N_max###. The output is not deterministic but conditioned random sequences. The level of randomness can be controlled using a temperature parameter ###tao###.

1. 1. 1. eq8###

References

1. Bahdanau, Dzmitry, Kyunghyun Cho, and Yoshua Bengio. "Neural machine translation by jointly learning to align and translate." arXiv preprint arXiv:1409.0473 (2014).

fonts and examples

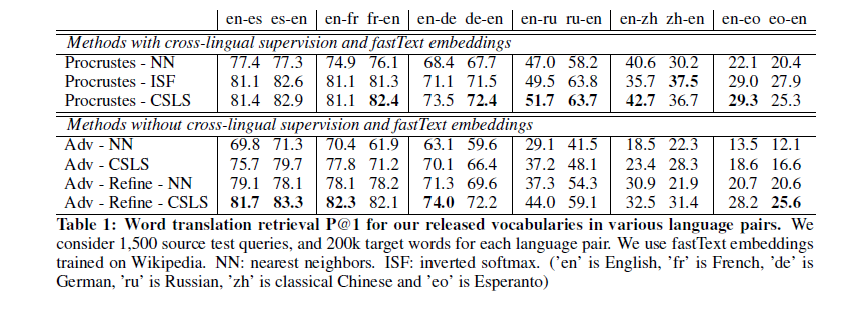
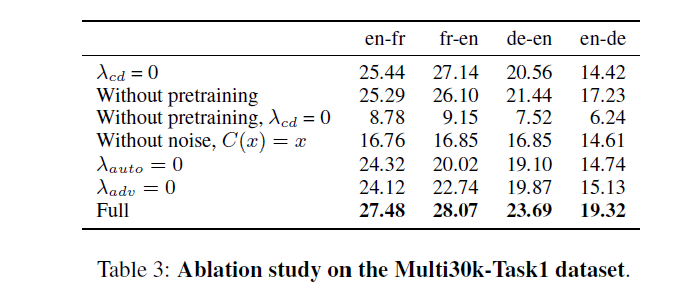
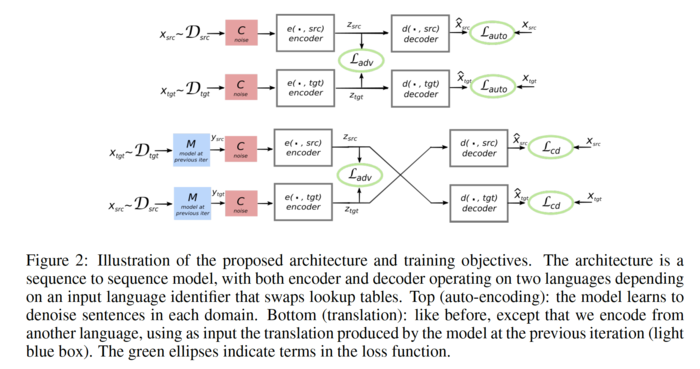
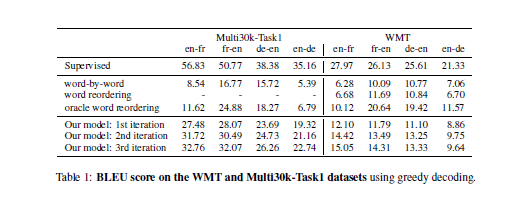
The unsupervised translation scheme has the following outline:

• The word-vector embeddings of the source and target languages are aligned in an unsupervised manner.
• Sentences from the source and target language are mapped to a common latent vector space by an encoder, and then mapped to probability distributions over

The objective function is the sum of:

1. The de-noising auto-encoder loss,

I shall describe these in the following sections.

From Conneau et al. (2017). The final row shows the performance of alignment method used in the present paper. Note the degradation in performance for more distant languages.

From the present paper. Results of an ablation study. Of note are the first, third, and forth rows, which demonstrate that while the translation component of the loss is relatively unimportant, the word vector alignment scheme and de-noising auto-encoder matter a great deal.