Co-Teaching

Introduction

Title of Paper

Co-teaching: Robust Training Deep Neural Networks with Extremely Noisy Labels

Contributions

The paper proposes a novel approach to training deep neural networks on data with noisy labels. The proposed architecture, named ‘co-teaching’, maintains two networks simultaneously.

Terminology

Ground-Truth Labels: The proper objective labels (i.e. the real, or ‘true’, labels) of the data.

Noisy Labels: Labels that are corrupted (either manually or through the data collection process) from ground-truth labels.

Motivation

The paper draws motivation from two key facts:

    •	That many data collection processes yield noisy labels. 
    •	That deep neural networks have a high capacity to overfit to noisy labels. 

Because of these facts, it is challenging to train deep networks to be robust with noisy labels.

Current Approaches

Learning with noisy labels is typically done by estimating the noise transition matrix (i.e.; integrating the effects of noise into the model), but this matrix is hard to estimate especially when the number of classes is large.

Another type of approach currently uses selected samples (sifting cleaner data out of the original noisy set, and using this data to update the network). However this type of model suffers from sample-selection bias.

Established models that take either of these approaches are used as baseline comparisons to co-teaching in the experiment.

Summary of Experiment

Proposed Method

The proposed co-teaching method maintains two networks simultaneously, and samples instances with small loss at each mini batch. The sample of small-loss instances is then taught to the peer network.

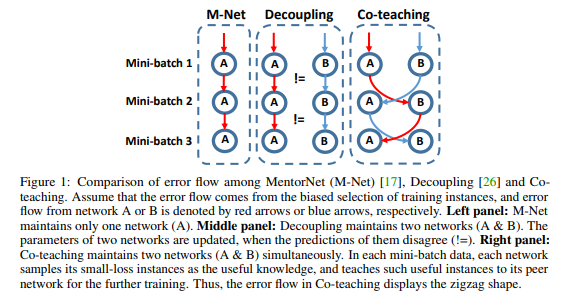
The co-teaching method relies on research that suggests deep networks learn clean and easy patterns in initial epochs, but are susceptible to overfitting noisy labels as the number of epochs grows. To counteract this, the co-teaching method reduces the mini-batch size by gradually increasing a drop rate (i.e., noisy instances with higher loss will be dropped at an increasing rate). The mini-batches are swapped between peer networks due to the underlying intuition that different classifiers will generate different decision boundaries. Swapping the mini-batches constitutes a sort of ‘peer-reviewing’ that promotes noise reduction, since the error from a network is not directly transferred back to itself.

Dataset Corruption

To simulate learning with noisy labels, the datasets (which are clean by default) are manually corrupted by applying a noise transformation matrix. Two methods are used for generating such noise transformation matrices: pair flipping and symmetry.

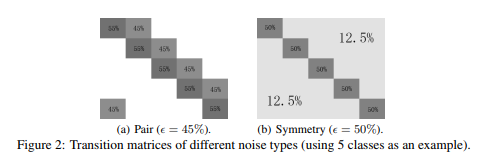
Three noise conditions are simulated for comparing co-teaching with baseline methods.

Method	Noise Rate	Rationale
Pair Flipping	45%	Almost half of instances have noisy labels. Simulates erroneous labels which are similar to true labels.
Symmetry	50%	Half of instances have noisy labels. Further rationale can be found at [1].
Symmetry	20%	Verify the robustness of co-teaching in a low-level noise scenario.

Baseline Comparisons

The co-teaching method is compared with several baseline approaches, which have varying:

    •	proficiency at dealing with a large number of classes,
    •	ability to resist heavy noise,
    •	need to combine with specific network architectures, and
    •	need to be pre-trained.   

Bootstrap

A method that deems a weighted combination of predicted and original labels as correct, and then solves kernels by backpropagation [2].

S-Model

Using an additional softmax layer to model the noise transition matrix [3].

F-Correction

Correcting the prediction by using a noise transition matrix which is estimated by a standard network [4].

Decoupling

Two separate classifiers are used in this technique. Parameters are updated using only the samples that are classified differently between the two models [5].

MentorNet

A teacher network is trained to identify and discard noisy instances in order to train the student network on cleaner instances [6].

Implementation Details

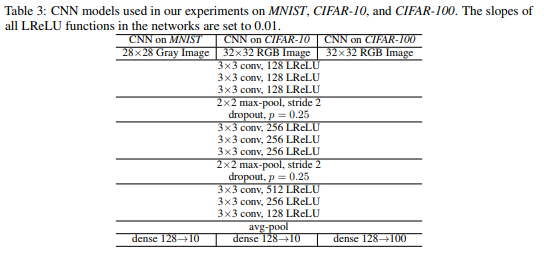
Two CNN models using the same architecture (shown below) are used as the peer networks for the co-teaching method. They are initialized with different parameters in order to be significantly different from one another (different initial parameters can lead to different local minima). An Adam optimizer (momentum=0.9), a learning rate of 0.001, a batch size of 128, and 200 epochs are used for each dataset.

Results and Discussion

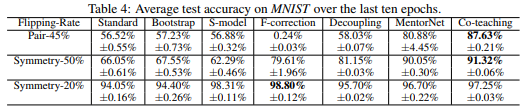
The co-teaching algorithm is compared to the baseline approaches under the noise conditions previously described. The results are as follows.

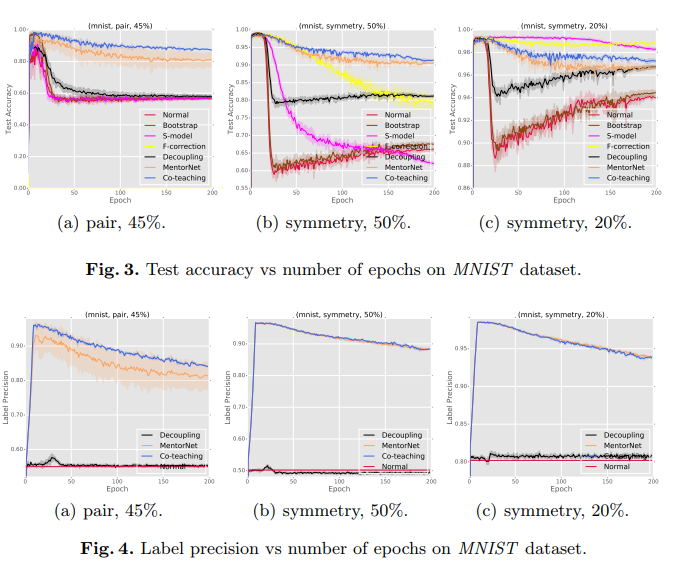
MNIST

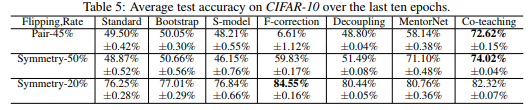
CIFAR10

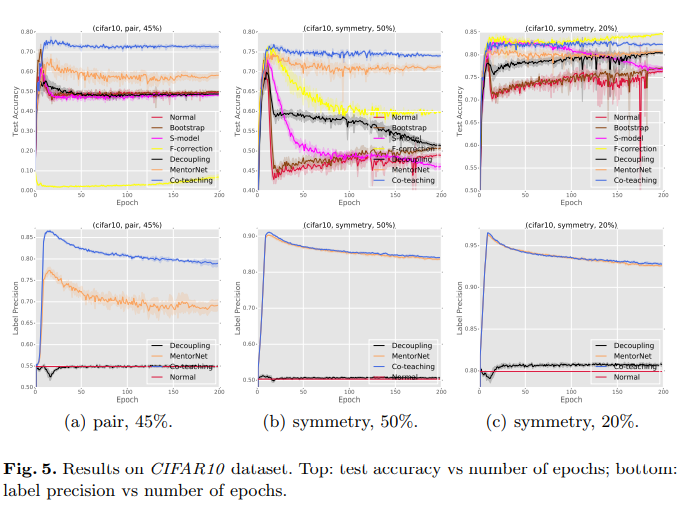
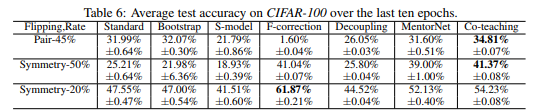
CIFAR100

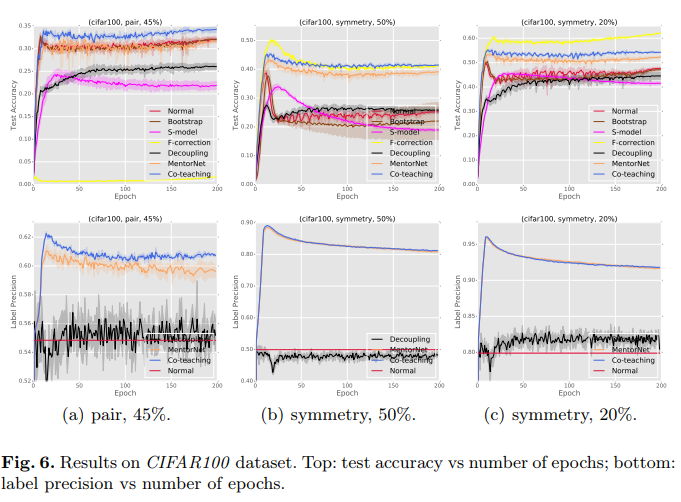
Conclusions

In the simulated ‘extreme noise’ scenarios (pair-45% and symmetry-50%), the co-teaching methods outperforms baseline methods in terms of accuracy. This suggests that the co-teaching method is superior to the baseline methods in scenarios of extreme noise. The co-teaching method also performs competitively in the low-noise scenario (symmetry-20%).

Critique

Lack of Task Diversity

The datasets used in this experiment are all image classification tasks – these results may not generalize to other deep learning applications, such as classifications from data with lower or higher dimensionality.

Needs to be expanded to other weak supervisions (Mentioned in conclusion)

Adaptation of the co-teaching method to train under other weak supervision (e.g. positive and unlabeled data) could expand the applicability of the paradigm.

Lack of Theoretical Development (Mentioned in conclusion)

This paper lacks any theoretical guarantees for co-teaching. Proving that the results shown in this study are generalizable would bolster the findings significantly.

References

[1] A. Gramfort, M. Luessi, E. Larson, D. A. Engemann, D. Strohmeier, C. Brodbeck, L. Parkkonen, and M. S. Hämäläinen. MNE software for processing MEG and EEG data. Neuroimage, 86:446–460, 2014.

[2] P. Richtárik and M. Takáč. Iteration complexity of randomized block-coordinate descent methods for minimizing a composite function. Mathematical Programming, 144(1-2):1–38, 2014.

[3] M. Jas, T. Dupré La Tour, U. Şimşekli, and A. Gramfort. Learning the morphology of brain signals using alpha-stable convolutional sparse coding. In Advances in Neural Information Processing Systems (NIPS), pages 1–15, 2017.

[4] J. Friedman, T. Hastie, H. Höfling, and R. Tibshirani. Pathwise coordinate optimization. The Annals of Applied Statistics, 1(2):302–332, 2007.

[5] R. Chalasani, J. C. Principe, and N. Ramakrishnan. A fast proximal method for convolutional sparse coding. In International Joint Conference on Neural Networks (IJCNN), pages 1–5, 2013. ISBN 9781467361293.

[6] F. Heide, W. Heidrich, and G. Wetzstein. Fast and flexible convolutional sparse coding. In Computer Vision and Pattern Recognition (CVPR), pages 5135–5143. IEEE, 2015.