Dynamic Routing Between Capsules STAT946

Presented by

Yang, Tong(Richard)

Hinton's Critiques on CNN

Four arguments against pooling

• It is a bad fit to the psychology of shape perception: It does not explain why we assign intrinsic coordinate frames to objects and why they have such huge effects.

• It solves the wrong problem: We want equivariance, not invariance. Disentangling rather than discarding.

• It fails to use the underlying linear structure: It does not make use of the natural linear manifold that perfectly handles the largest source of variance in images.

• Pooling is a poor way to do dynamic routing: We need to route each part of the input to the neurons that know how to deal with it. Finding the best routing is equivalent to parsing the image.

Equivariance

• Without the sub-sampling, convolutional neural nets give "place-coded" equivariance for discrete translations.

Two types of equivariance

Place-coded equivariance

If a low-level part moves to a very different position it will be represented by a different capsule.

Rate-coded equivariance

If a part only moves a small distance it will be represented by the same capsule but the pose outputs of the capsule will change.

Higher-level capsules have bigger domains so low-level place-coded equivariance gets converted into high-level rate-coded equivariance.

== Extrapolating shape recognition to very different viewpoints

• Current neural net wisdom:
  • Learn different models for different viewpoints.
  • This requires a lot of training data.
• A much better approach:
  • The manifold of images of the same rigid shape is highly non-linear in the space of pixel intensities.
  • Transform to a space in which the manifold is globally linear

Dynamic Routing

In the second section of this paper, authors give a mathematical representations for two key features in routing algorithm in capsule network, which are squashing and agreement.

The general setting for this algorithm is between two arbitrary capsules i and j.

Capsule

\begin{align} s_j = \sum_{i}c_{ij}\hat{u}_{j|i} \end{align}

where

\begin{align} \hat{u}_{j|i} = W_{ij}u_i \end{align}

Squashing

\begin{align} v_j = \frac{||s_j||^2}{1+||s_j||^2}\frac{s_j}{||s_j||} \end{align}

Routing By Agreement

\begin{align} c_{ij} = \frac{exp(b_ij)}{\sum_{k}exp(b_ik)} \end{align}

Routing Algorithm

Source: Sabour, Frosst, Hinton, 2017

CapsNet Architecture

Source: Sabour, Frosst, Hinton, 2017

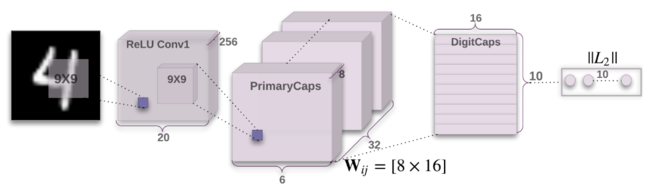
How many routing iteration to use?

In appendix A of this paper, the authors have shown the empirical results from 500 epochs of training at different choice of routing iterations. According to their observation, more routing iterations increases the capacity of CapsNet but tends to bring additional risk of overfitting. Moreover, CapsNet with routing iterations less than three are not effective in general. As result, they suggest 3 iterations of routing for all experiments.

Decoder

Source: Sabour, Frosst, Hinton, 2017

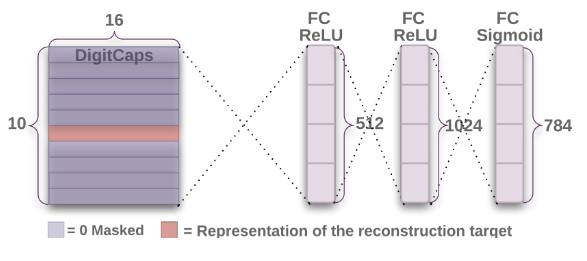
Regularization Method: Reconstruction

Source: Sabour, Frosst, Hinton, 2017

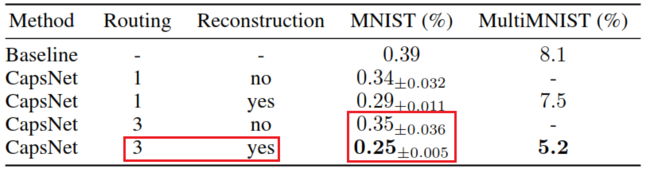
MINST

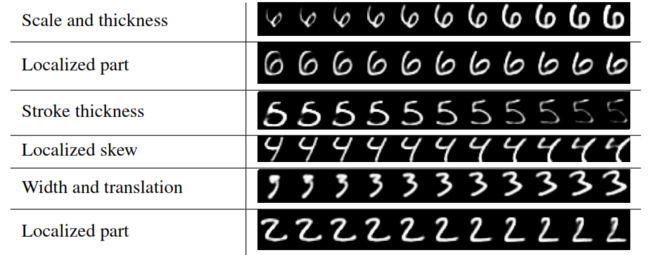
Interpretation of Each Capsule

Source: Sabour, Frosst, Hinton, 2017