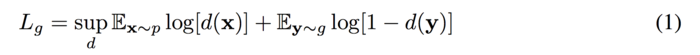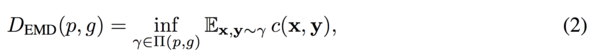stat946w18/IMPROVING GANS USING OPTIMAL TRANSPORT: Difference between revisions

From statwiki
Jump to navigation Jump to search
Line 1: Line 1:
== Introduction ==
== Introduction ==
Generative Adversarial Networks (GANs) are powerful generative models. A GAN model consists of a generator and a discriminator or critic. The generator is a neural network which is trained to generate data having a distribution matched with the one of real data. The critic is also a neural network, which is trained to separate the generated data from the real data. A loss function is important in the critic that measures the distribution distance between the generated data and the real one. The generator and the critic are trained in turn based on the loss function and the critic is trained by real data at first.
Generative Adversarial Networks (GANs) are powerful generative models. A GAN model consists of a generator and a discriminator or critic. The generator is a neural network which is trained to generate data having a distribution matched with the distribution of the real data. The critic is also a neural network, which is trained to separate the generated data from the real data. A loss function that measures the distribution distance between the generated data and the real one is important to train the generator.


Optimal transport theory is a similar approach to measure the distance between the generated data and the training data distribution. The idea of this theory is by optimally transporting the data points between the training data and the generated data, the two data distribution will be approximately the same. This method produces a closed form solution instead of the approximated solution which is the advantage of this method. However, the primal form optimal transport could give biased gradients when mini-batches are applied.  
Optimal transport theory evaluates the distribution distance based on metric, which provides another method for generator training. The main advantage of optimal transport theory over the distance measurement in GAN is its closed form solution for having a tractable training process. But the theory might also result in inconsistency in statistical estimation due to the given biased gradients if the mini-batches method is applied.


This paper presents a variant GANs named OT-GAN, which incorporates a MIni-batch Energy Distance into its critic. This newly defined metric is unbiased when min-batch is applied.
This paper presents a variant GANs named OT-GAN, which incorporates a discriminative metric called 'MIni-batch Energy Distance' into its critic in order to overcome the issue of biased gradients.


== GANs AND OPTIMAL TRANSPORT ==
== GANs AND OPTIMAL TRANSPORT ==

Revision as of 00:41, 13 March 2018

Introduction

Generative Adversarial Networks (GANs) are powerful generative models. A GAN model consists of a generator and a discriminator or critic. The generator is a neural network which is trained to generate data having a distribution matched with the distribution of the real data. The critic is also a neural network, which is trained to separate the generated data from the real data. A loss function that measures the distribution distance between the generated data and the real one is important to train the generator.

Optimal transport theory evaluates the distribution distance based on metric, which provides another method for generator training. The main advantage of optimal transport theory over the distance measurement in GAN is its closed form solution for having a tractable training process. But the theory might also result in inconsistency in statistical estimation due to the given biased gradients if the mini-batches method is applied.

This paper presents a variant GANs named OT-GAN, which incorporates a discriminative metric called 'MIni-batch Energy Distance' into its critic in order to overcome the issue of biased gradients.

GANs AND OPTIMAL TRANSPORT

Generative Adversarial Nets

The objective function of the GAN:

The goal of GANs is to train the generator g and the discriminator d and find a pair of (g,d) which the game reaches a Nash equilibrium. However, it could cause failure to converge since the generator and the discriminator is trained using gradient descent techniques which are not used to find a Nash equilibrium of a game.

In order to solve this problem, Arjovsky et al (2017) suggested a new GAN with the optimal transport theory.

Earth-Mover Distance

Retrieved from "http://wiki.math.uwaterloo.ca/statwiki/index.php?title=stat946w18/IMPROVING_GANS_USING_OPTIMAL_TRANSPORT&oldid=33663"