stat441w18/mastering-chess-and-shogi-self-play: Difference between revisions
| Line 36: | Line 36: | ||
=== Theory of Alpha-Beta Search === | === Theory of Alpha-Beta Search === | ||
[[File:abs.jpeg | frame | center |Fig 1. ]] | |||
=== Theory of Monte Carlo Search Trees === | === Theory of Monte Carlo Search Trees === | ||
Revision as of 11:03, 8 March 2018
Presented by
1. Bhalla, Amar
2. Florian, Alex
3. Iaboni, Alessandra
4. Lu, Thomas
5. Morjaria, Deep
6. Poole, Zach
7. Stoev, Victor
8. Zhang, Wendy
Introduction
History of Algorithms in Chess-like Games
With challenging games such as Chess, there has long been a fascination with determining the optimal playing method. The challenge, until this point, has been creating a system to achieve “superhuman” performance with minimal training from human expertise or experience. Deep Blue, an IBM supercomputer, defeated a world champion in 1997 marking a huge step forward in artificial intelligence that would continue to be built upon for the coming decades. The methods in Deep Blue, as well as other methods around the same time, still utilized knowledge from chess grandmasters. It was through such methods that Stockfish was also developed. This program is the 2016 Top Chess Engine Championship world-champion and used as the gold standard against which any new algorithms are evaluated.
The Japanese game Shogi is even more complex than chess from a computational standpoint. It’s gold standard, is the Computer Shogi Association world champion, Elmo. Constructed in much the same way as the chess programs, Elmo is also highly dependent real human input and modifications compared to solely computation learning methods.
The game Go is more easily predicted without the use human expertise to beat human player. Such models are well suited to being built with neural networks. The rules of Go are translationally invariant and reflectionally symmetric. These qualities are not present in Chess and Shogi as the rules of these differ based on position on the board or piece and are asymmetric as the left and right side of the board allow for different moves. Go also has simplistic properties such as allowing stones to be placed at all locations on the board and terminating in a win or loss. Chess and Shogi have a more complex field of playable locations for each piece on a given turn, captured pieces may be returned to the field of play in certain scenarios, and the game is designed to allow for draws (stalemates). All of these are indicative of the properties that make neural networks more easily applicable to the game Go.
Purpose of the AlphaZero Algorithm
This paper primarily focuses on the general reinforcement algorithm implemented in the AlphaZero program. This program was developed as a generalization of AlphaGo (a program designed to be the best at Go) for the purpose of winning at other games such as Chess and Shogi. This paper will compare the training and performance of AlphaZero against other programs that, at the time of the development of AlphaZero, were considered to be the best “players” in the world: human or otherwise.
Model
Theory of Reinforcement Learning
Theory of Alpha-Beta Search

Theory of Monte Carlo Search Trees
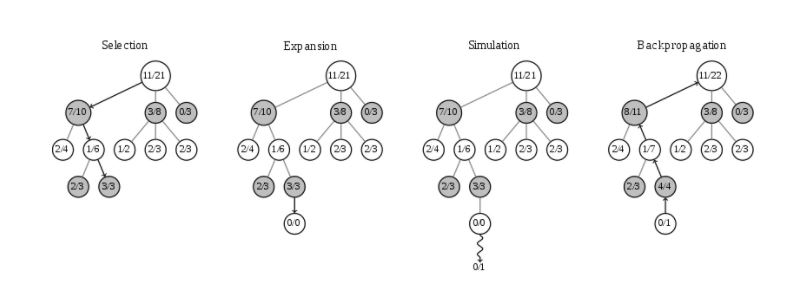
Neural Networks with the Interaction of MCST
Differences Between Game Algorithms
AlphaGo vs. AlphaGo Zero
| AlphaGo | AlphaGo Zero |
|---|---|
| Included knowledge from game experts to improve model performance | Trained solely from self-play experience using tabula rasa reinforcement |
| Utilized Multiple neural networks | Combined previous version's networks into a single neural network |
AlphaGo Zero vs. Alpha Zero
| AlphaGo Zero | AlphaZero |
|---|---|
| Estimates and optimises probability of winning assuming binary win/loss | Estimates and optimises expected outcome, including draws |
| Augments training data with rotations and reflections since Go is invariant to these changes | Does not augment training data since other games (like chess) are asymmetric |
| The model is updated after completed iteration; if new player wins against “best” player by a margin of 55%, they are replaced | The model is continually updated (not waiting for iteration to complete); it does not include the evaluation or best player selection |
| Hyper-parameter of the search is tuned with Bayesian optimisation | Same hyper-parameters are reused for all games without tuning (except for adding noise) |
| No access to opening books or endgame tables |
Training and Results
Training the Model
Scoring and Evaluation
Criticisms
Sources
Ha, Karel. “Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm.” AI Seminar. AI Seminar, 19 Dec. 2017, Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm.
Silver, David, et al. "Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm." arXiv preprint arXiv:1712.01815 (2017).
Silver, David, et al. "Mastering the game of Go with deep neural networks and tree search." nature 529.7587 (2016): 484-489.
Silver, David, et al. "Mastering the game of go without human knowledge." Nature 550.7676 (2017): 354.