stat441w18/Convolutional Neural Networks for Sentence Classification: Difference between revisions
| Line 25: | Line 25: | ||
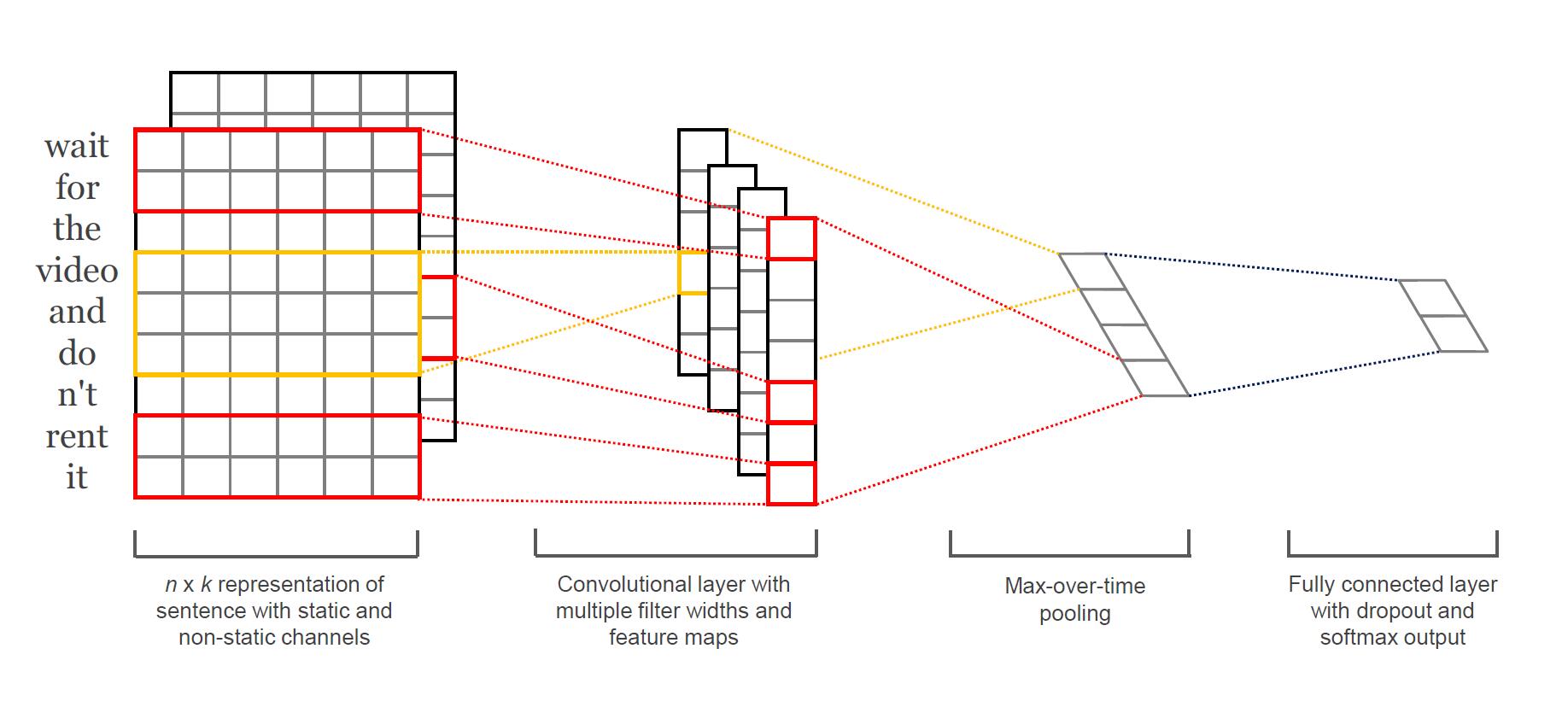
A Convolutional Neural Network (CNN) is a nonlinear function <math> f: \mathbb{R}^{hk} \to \mathbb{R} </math> that computes a series of outputs <math> c_i = f \left( \boldsymbol{w} \cdot \boldsymbol{x}_{i:i+h-1} + b \right) </math> from windows of <math> h </math> words <math> \boldsymbol{x}_{i:i+h-1} </math> in the sentence, where <math> \boldsymbol{w} \in \mathbb{R}^{hk} </math> is call a ''filter'' and <math> i \in \{ 1, \dots, n-h+1 \} </math>. The outputs form a <math> (n-h+1) </math>-dimensional vector <math> \boldsymbol{c} = \left[ c_1, c_2, \dots, c_{n-h+1} \right] </math> called a ''feature map''. | A Convolutional Neural Network (CNN) is a nonlinear function <math> f: \mathbb{R}^{hk} \to \mathbb{R} </math> that computes a series of outputs <math> c_i = f \left( \boldsymbol{w} \cdot \boldsymbol{x}_{i:i+h-1} + b \right) </math> from windows of <math> h </math> words <math> \boldsymbol{x}_{i:i+h-1} </math> in the sentence, where <math> \boldsymbol{w} \in \mathbb{R}^{hk} </math> is call a ''filter'' and <math> i \in \{ 1, \dots, n-h+1 \} </math>. The outputs form a <math> (n-h+1) </math>-dimensional vector <math> \boldsymbol{c} = \left[ c_1, c_2, \dots, c_{n-h+1} \right] </math> called a ''feature map''. | ||
To capture the most important feature from a ''feature map'', we take the maximum value <math> \hat{c} = max \{ \boldsymbol{c} \} </math>. Since each ''filter'' corresponds to one feature, we obtain several features from multiple ''filters'' the model uses which form a penultimate layer. The penultimate layer gets passed | To capture the most important feature from a ''feature map'', we take the maximum value <math> \hat{c} = max \{ \boldsymbol{c} \} </math>. Since each ''filter'' corresponds to one feature, we obtain several features from multiple ''filters'' the model uses which form a penultimate layer. The penultimate layer then gets passed into a fully connected softmax layer which produces the probability distribution over labels. | ||
Below is a slight variant of CNN with two "channels" of word vectors: static vectors and fine-tuned vectors via backpropagaton. We calculate <math> c_i </math> by applying each filter to both channels and adding them together. The rest of the model is equivalent to a single channel CNN architecture. | Below is a slight variant of CNN with two "channels" of word vectors: static vectors and fine-tuned vectors via backpropagaton. We calculate <math> c_i </math> by applying each filter to both channels and then adding them together. The rest of the model is equivalent to a single channel CNN architecture. | ||
[[File:CNN_for_Sentence_Classification_1.jpg]] | [[File:CNN_for_Sentence_Classification_1.jpg]] | ||
Revision as of 22:39, 4 March 2018
Presented by
1. Ben Schwarz
2. Cameron Miller
3. Hamza Mirza
4. Pavle Mihajlovic
5. Terry Shi
6. Yitian Wu
7. Zekai Shao
Introduction
Model
Theory of Convolutional Neural Networks
Let [math]\displaystyle{ \boldsymbol{x}_{i:i+j} }[/math] be the concatenation of words [math]\displaystyle{ \boldsymbol{x}_i, \boldsymbol{x}_{i+1}, \dots, \boldsymbol{x}_{i+j} }[/math] with the concatenation operation [math]\displaystyle{ \oplus }[/math]. Then, [math]\displaystyle{ \boldsymbol{x}_{i:i+j} = \boldsymbol{x}_i \oplus \boldsymbol{x}_{i+1} \oplus \dots \oplus \boldsymbol{x}_{i+j} }[/math]. Thus, a sentence of length [math]\displaystyle{ n }[/math] is a concatenation of [math]\displaystyle{ n }[/math] words, denoted as [math]\displaystyle{ \boldsymbol{x}_{1:n} }[/math], [math]\displaystyle{ \boldsymbol{x}_{1:n} = \boldsymbol{x}_1 \oplus \boldsymbol{x}_2 \oplus \dots \oplus \boldsymbol{x}_n }[/math]. Let [math]\displaystyle{ \boldsymbol{x}_i \in \mathbb{R}^k }[/math] denote the [math]\displaystyle{ i }[/math]-th word in the sentence, [math]\displaystyle{ i \in \{ 1, \dots, n \} }[/math].
A Convolutional Neural Network (CNN) is a nonlinear function [math]\displaystyle{ f: \mathbb{R}^{hk} \to \mathbb{R} }[/math] that computes a series of outputs [math]\displaystyle{ c_i = f \left( \boldsymbol{w} \cdot \boldsymbol{x}_{i:i+h-1} + b \right) }[/math] from windows of [math]\displaystyle{ h }[/math] words [math]\displaystyle{ \boldsymbol{x}_{i:i+h-1} }[/math] in the sentence, where [math]\displaystyle{ \boldsymbol{w} \in \mathbb{R}^{hk} }[/math] is call a filter and [math]\displaystyle{ i \in \{ 1, \dots, n-h+1 \} }[/math]. The outputs form a [math]\displaystyle{ (n-h+1) }[/math]-dimensional vector [math]\displaystyle{ \boldsymbol{c} = \left[ c_1, c_2, \dots, c_{n-h+1} \right] }[/math] called a feature map.
To capture the most important feature from a feature map, we take the maximum value [math]\displaystyle{ \hat{c} = max \{ \boldsymbol{c} \} }[/math]. Since each filter corresponds to one feature, we obtain several features from multiple filters the model uses which form a penultimate layer. The penultimate layer then gets passed into a fully connected softmax layer which produces the probability distribution over labels.
Below is a slight variant of CNN with two "channels" of word vectors: static vectors and fine-tuned vectors via backpropagaton. We calculate [math]\displaystyle{ c_i }[/math] by applying each filter to both channels and then adding them together. The rest of the model is equivalent to a single channel CNN architecture.
Model Regularization
Datasets and Experimental Setup
Hyperparameters and Training
MR:
SST-1:
SST-2:
Subj:
TREC:
CR:
MPQA:
Pre-trained Word Vectors
Model Variations
CNN-rand:
CNN-static:
CNN-static:
CNN-non-static:
CNN-multichannel: