Learning What and Where to Draw

Introduction

Generative Adversarial Networks (GANs) have been successfully used to synthesize compelling real-world images. In what follows we outline an enhanced GAN called the Generative Adversarial What- Where Network (GAWWN). In addition to accepting as input a noise vector, this network also accepts as input instructions describing what content to draw and in which location to draw the content. Traditionally, these models use simply conditioning variables such as a class label or a non-localized caption. The authors of 'Learning What and Where to Draw' believe that image synthesis will be drastically enhanced by incorporating a notion of localized objects.

The main goal in constructing the GAWWN network is to seperate the questions of 'what' and 'where' to modify the image at each step of the computational process. Prior to elaborating on the experimental results of the GAWWN the authors cite that this model benefits from greater parameter efficiency and produces more interpratable sample images. The proposed model learns to perform location and content-controllable image synthesis on the Caltech-USCD (CUB) bird data set and the MPII Human Pose (HBU) data set.

A highlight of this work is that the authors demonstrate two ways to encode spatial constraints into the GAN. First, the authors provide an implementation showing how to condition on the coarse location of a bird by incorporating spatial masking and cropping modules into a text-conditional General Adversarial Network. This technique is implemented using spatial transformers. Second, the authors demonstrate how they are able to condition on part locations of birds and humans in the form of a set of normalized (x,y) coordinates.

Related Work

This is not that first paper to show how Deep convolutional networks can be used to generate synthetic images. Other notable works include:

• Dosovitsky et al. (2015) trained a deconvolutional network to generate 3D chair renderings conditioned on a set of graphics codes indicating shape, position and lighting
• Yang et al. (2015) followed with a recurrent convolutional encoder-decoder that learned to apply incremental 3D rotations to generate sequences of rotated chair and face images
• Reed et al. (2015) trained a network to generate images that solved visual analogy problems

The authors cite how the above models are all deterministic and discuss how other recent work attempts to learn a probabilistic model with variational autoencoders (Kingma and Welling, 2014, Rezende et al., 2014). In discussing current work in this area it is stated how all of the above formulations could benefit from the principle of seperating what and where conditioning variables.

Background Knowledge

Generative Adversarial Networks

Before outlining the GAWWN we briefly review GANs. A GAN consists of a generator G that generates a synthetic image given a noise vector drawn from typically either a Gaussian or Uniform distribution. The discriminators objective is tasked with classifying images generated by the generator as either real or synthetic. The two networks compete in the following minimax game:

$\displaystyle \min_{G}$ $\max\limits_{G} V(D,G) = \mathop{\mathbb{E}}_{x \sim p_{data}(x)}[log[D(x)] + \mathop{\mathbb{E}}_{x \sim p_{x}(x)}[log(1-D(G(z)))] $

where z is the noise vector previously discussed. In this context when considering GAWWN networks we are now playing the above minimax game with G(z,c) and D(z,c), where c is the additional what and where information supplied to the network.

Structured Joint Embedding of Visual Descriptions and Images

In order to encode visual content from text descriptions the authors use a convolutional and recurrent text encoder to establish a correspondence function between images and text features. This approach is not new, the authors rely on the previous work of Reed et al. (2016) to implement this procedure. To learn sentence embeddings the following function is optimized:

$\frac{1}{N}\sum_{n=1}^{N} \Delta (y_{n}, f_{v}(n)) + \Delta (y_{n}, f_{t}(t_{n}) $

where ${(v_{n}, t_{n}, , n=1,...N}$ is the training data, $\Delta$ is the 0-1 loss, $v_{n}$ are the images, $t_{n}$ are the text descriptions of class y. The functions $f_{v}$ and $f_{t}$ are defined as folows:

$ f_{v}(v)$ = $\displaystyle \max_{y \in Y}$ $\mathop{\mathbb{E}}_{t \sim T(y)}[\phi(v)^{T}\varphi(t)], \space f_{t}(t) = \displaystyle \max_{y \in Y}$ $\mathop{\mathbb{E}}_{v \sim V(y)}[\phi(v)^{T}\varphi(t)]$

where $\phi$ is the image encoder and $\varphi$ is the text encoder.

GAWWN Visualization and Description

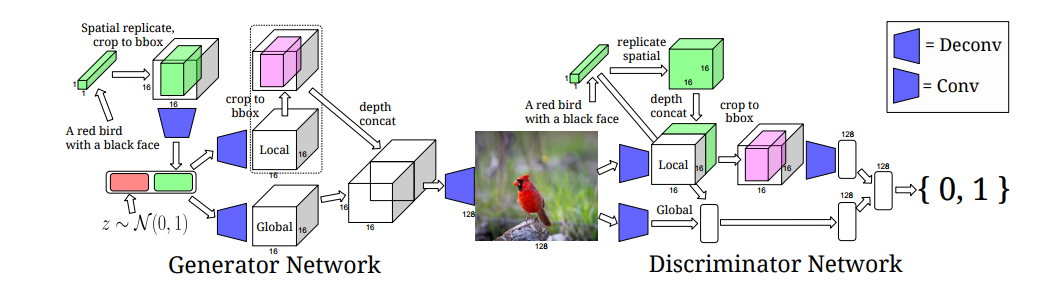
Bounding-box-conditional text-to-image model

Generator Network

The major steps:

• Step 1: Start with input noise and text embedding
• Step 2: Replicate text embedding to form a $MxMxT$ feature map then wrap spatially to fit into unit interval bounding box coordinates
• Step 3: Apply convolution, pooling to reduce spatial dimension to $1x1$
• Step 4: Concatenate feature vector with the noise vector z
• Step 5: Generator branching into local and global processing stages
• Step 6: Global pathway stride-2 deconvolutions, local pathway appy masking operation applied to set regions outside the object bounding box to 0
• Step 7: Merge local and global pathways
• Step 8: Apply a series of deconvolutional layers and in the final layer apply tanh activation to restrict oupt to [-1,1]

Discriminator Network

• Step 1: Replicate text as in Step 2 above
• Step 2: Process image in local and global pathways
• Step 3: In local pathway stride2-deconvolutional layers, in global pathway convolutions down to a vector
• Step 4: Local and global pathway output vectors are merged
• Step 5: Produce discriminator score

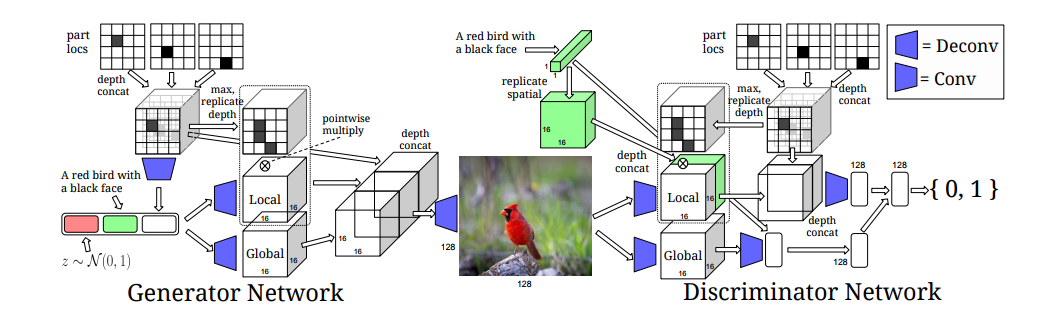
Keypoint-conditional text-to-image

Generator Network

• Step 1: Keypoint locations are encoded into a $MxMxK$ spatial feature map
• Step 2: Keypoint tensor progresses through several stages of the network
• Step 3: Concatenate keypoint vector with noise vector
• Step 4: Keypoint tensor is flattened into a binary matrix, then replicated into a tensor
• Step 5: Noise-text-keypoint vector is fed to global and local pathways
• Step 6: Orginal keypoint tensor is is concatenated with local and global tensors with additional deconvolutions
• Step 7: Apply tanh activation function

Discriminator Network

• Step 1: Feed text-embedding into discriminator in two stages
• Step 2: Combine text embedding additively with global pathway for convolutional image processing
• Step 3: Spatially replicated text-embedding and concatenate with feature map
• Step 4: Local pathway produces into stride-2 deconvolutions producing an output vector
• Step 5: Combine local and global pathways and produce discriminator score

Conditional keypoint generation model

In creating this application the researchers discuss how it is not feasible to ask the user to input all of the keypoints for a given image. In order to remedy this issue a method is developed to access the conditional distributions of unobserved keypoints given a subset of observed keypoints and the image caption. In order to solve this problem a generic GAN is used.

The authors formulate the generator network $G_{k}$ for keypoints s,k as follows:

$G_{k}(z,t,k,s) := s \odot k + (1-s) \odot f(z,t,k)$

where $\odot$ denotes pointwise multiplication and $f: \Re^(Z+T+3K) \mapsto \Re^(3k)$ is an MLP. As usual, the discriminator learn to distinguish real key points from synthetic keypoints

Experiments

In this section of the wiki we examine the synthetic images generated by the GAWWN conditioning on different model inputs. The experiments are conducted with Caltech-USCD Birds (CUB) and MPII Human Pose (MHP) data sets. CUB has 11,788 images of birds, each belonging to one of 200 different species. The authors also include an additional data set from Reed et al. [2016]. Each image contains bird location via bounding box and keypoint coordinates for 15 bird parts. MHP contains 25K images with individuals participating in 410 different common activities. Mechanical Turk was used to collect three single sentence descriptions for each image. For HBU each image contains multiple sets of keypoints. Caption information was encoded using a pre-trained char-CNN-GRU. The solver used to train the GAWWN was Adam with a batch size of 16 and learning rate of 0.0002.

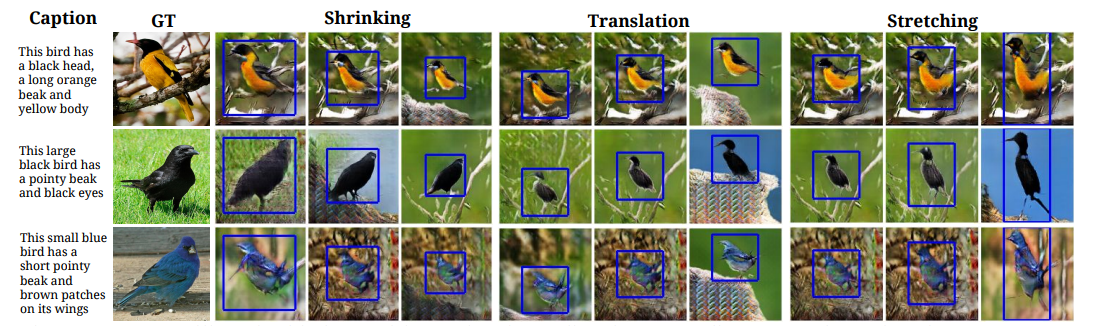
Controlling via Bounded Boxes

Controlling individual part locations via keypoints

Beyond birds: generating images of humans

Summary of Contributions

• Novel architecture for text- and location-controllable image synthesis, which yields more realistic and high-resolution Caltech-USCD bird samples
• A text-conditional object part completion model enabling a streamlined user interface for specifying part locations
• Exploratory results and a new dataset for pose-conditional text to human image synthesis