Revision as of 01:41, 13 October 2011

STAT 441/841 / CM 463/763 - Tuesday, 2011/09/20

Wiki Course Notes

Students will need to contribute to the wiki for 20% of their grade. Access via wikicoursenote.com Go to editor sign-up, and use your UW userid for your account name, and use your UW email.

primary (10%) Post a draft of lecture notes within 48 hours. You will need to do this 1 or 2 times, depending on class size.

secondary (10%) Make improvements to the notes for at least 60% of the lectures. More than half of your contributions should be technical rather than editorial. There will be a spreadsheet where students can indicate what they've done and when. The instructor will conduct random spot checks to ensure that students have contributed what they claim.

Classification (Lecture: Sep. 20, 2011)

Definitions

classification: Predict a discrete random variable [math]\displaystyle{ Y }[/math] (a label) by using another random variable [math]\displaystyle{ X }[/math] (new data point) picked iid from a distribution

[math]\displaystyle{ X_i = (X_{i1}, X_{i2}, ... X_{id}) \in \mathcal{X} \subset \mathbb{R}^d }[/math] ([math]\displaystyle{ d }[/math]-dimensional vector) [math]\displaystyle{ Y_i }[/math] in some finite set [math]\displaystyle{ \mathcal{Y} }[/math]

classification rule: [math]\displaystyle{ h : \mathcal{X} \rightarrow \mathcal{Y} }[/math] Take new observation [math]\displaystyle{ X }[/math] and use a classification function [math]\displaystyle{ h(x) }[/math] to generate a label [math]\displaystyle{ Y }[/math]. In other words, If we fit the function [math]\displaystyle{ h(x) }[/math] with a random variable [math]\displaystyle{ X }[/math], it generates the label [math]\displaystyle{ Y }[/math] which is the class to which we predict [math]\displaystyle{ X }[/math] belongs.

Example: Let [math]\displaystyle{ \mathcal{X} }[/math] be a set of 2D images and [math]\displaystyle{ \mathcal{Y} }[/math] be a finite set of people. We want to learn a classification rule [math]\displaystyle{ h:\mathcal{X}\rightarrow\mathcal{Y} }[/math] that with small true error predicts the person who appears in the image.

true error rate for classifier [math]\displaystyle{ h }[/math] is the error with respect to the underlying distribution (that we do not know).

[math]\displaystyle{ L(h) = P(h(X) \neq Y ) }[/math]

empirical error rate (or training error rate) is the amount of error that our classification function [math]\displaystyle{ h(x) }[/math] makes on the training data.

[math]\displaystyle{ \hat{L}_n(h) = (1/n) \sum_{i=1}^{n} \mathbf{I}(h(X_i) \neq Y_i) }[/math]

where [math]\displaystyle{ \mathbf{I}() }[/math] is an indicator function. Indicator function is defined by

[math]\displaystyle{ \mathbf{I}(x) = \begin{cases} 1 & \text{if } x \text{ is true} \\ 0 & \text{if } x \text{ is false} \end{cases} }[/math]

So in this case, [math]\displaystyle{ \mathbf{I}(h(X_i)\neq Y_i) = \begin{cases} 1 & \text{if } h(X_i)\neq Y_i \text{ (i.e. when misclassification happens)} \\ 0 & \text{if } h(X_i)=Y_i \text{ (i.e. classified properly)} \end{cases} }[/math]

e.g., 100 new data points with known (true) labels

[math]\displaystyle{ y_1 = h(x_1) }[/math]

...

[math]\displaystyle{ y_{100} = h(x_{100}) }[/math]

To calculate the empirical error we count how many labels our function [math]\displaystyle{ h(x) }[/math] assigned incorrectly and divide by n=100

Bayes Classifier

The principle of Bayes Classifier is to calculate the posterior probability of a given object from its prior probability via Bayes formula, and then place the object in the class with the largest posterior probability<ref> http://www.wikicoursenote.com/wiki/Stat841#Bayes_Classifier </ref>.

First recall Bayes' Rule, in the format [math]\displaystyle{ P(Y|X) = \frac{P(X|Y) P(Y)} {P(X)} }[/math]

P(Y|X) : posterior , probability of [math]\displaystyle{ Y }[/math] given [math]\displaystyle{ X }[/math]

P(X|Y) : likelihood, probability of [math]\displaystyle{ X }[/math] being generated by [math]\displaystyle{ Y }[/math]

P(Y) : prior, probability of [math]\displaystyle{ Y }[/math] being selected

P(X) : marginal, probability of obtaining [math]\displaystyle{ X }[/math]

We will start with the simplest case: [math]\displaystyle{ \mathcal{Y} = \{0,1\} }[/math]

[math]\displaystyle{ r(x) = P(Y=1|X=x) = \frac{P(X=x|Y=1) P(Y=1)} {P(X=x)} = \frac{P(X=x|Y=1) P(Y=1)} {P(X=x|Y=1) P(Y=1) + P(X=x|Y=0) P(Y=0)} }[/math]

Bayes' rule can be approached by computing either:

1) The posterior: [math]\displaystyle{ \ P(Y=1|X=x) }[/math] and [math]\displaystyle{ \ P(Y=0|X=x) }[/math] or

2) The likelihood: [math]\displaystyle{ \ P(X=x|Y=1) }[/math] and [math]\displaystyle{ \ P(X=x|Y=0) }[/math]

The former reflects a Bayesian approach. The Bayesian approach uses previous beliefs and observed data (e.g., the random variable [math]\displaystyle{ \ X }[/math]) to determine the probability distribution of the parameter of interest (e.g., the random variable [math]\displaystyle{ \ Y }[/math]). The probability, according to Bayesians, is a degree of belief in the parameter of interest taking on a particular value (e.g., [math]\displaystyle{ \ Y=1 }[/math]), given a particular observation (e.g., [math]\displaystyle{ \ X=x }[/math]). Historically, the difficulty in this approach lies with determining the posterior distribution, however, more recent methods such as Markov Chain Monte Carlo (MCMC) allow the Bayesian approach to be implemented <ref name="PCAustin">P. C. Austin, C. D. Naylor, and J. V. Tu, "A comparison of a Bayesian vs. a frequentist method for profiling hospital performance," Journal of Evaluation in Clinical Practice, 2001</ref>.

The latter reflects a Frequentist approach. The Frequentist approach assumes that the probability distribution, including the mean, variance, etc., is fixed for the parameter of interest (e.g., the variable [math]\displaystyle{ \ Y }[/math], which is not random). The observed data (e.g., the random variable [math]\displaystyle{ \ X }[/math]) is simply a sampling of a far larger population of possible observations. Thus, a certain repeatability or frequency is expected in the observed data. If it were possible to make an infinite number of observations, then the true probability distribution of the parameter of interest can be found. In general, frequentists use a technique called hypothesis testing to compare a null hypothesis (e.g. an assumption that the mean of the probability distribution is [math]\displaystyle{ \ \mu_0 }[/math]) to an alternative hypothesis (e.g. assuming that the mean of the probability distribution is larger than [math]\displaystyle{ \ \mu_0 }[/math]) <ref name="PCAustin"/>. For more information on hypothesis testing see <ref>R. Levy, "Frequency hypothesis testing, and contingency tables" class notes for LING251, Department of Linguistics, University of California, 2007. Available: http://idiom.ucsd.edu/~rlevy/lign251/fall2007/lecture_8.pdf </ref>.

There was some class discussion on which approach should be used. Both the ease of computation and the validity of both approaches were discussed. A main point that was brought up in class is that Frequentists consider X to be a random variable, but they do not consider Y to be a random variable because it has to take on one of the values from a fixed set (in the above case it would be either 0 or 1 and there is only one correct label for a given value X=x). Thus, from a Frequentist's perspective it does not make sense to talk about the probability of Y. This is actually a grey area and sometimes Bayesians and Frequentists use each others' approaches. So using Bayes' rule doesn't necessarily mean you're a Bayesian. Overall, the question remains unresolved.

The Bayes Classifier uses [math]\displaystyle{ \ P(Y=1|X=x) }[/math]

[math]\displaystyle{ P(Y=1|X=x) = \frac{P(X=x|Y=1) P(Y=1)} {P(X=x|Y=1) P(Y=1) + P(X=x|Y=0) P(Y=0)} }[/math]

P(Y=1) : the prior, based on belief/evidence beforehand

denominator : marginalized by summation

[math]\displaystyle{ h(x) = \begin{cases} 1 \ \ \hat{r}(x) \gt 1/2 \\ 0 \ \ otherwise \end{cases} }[/math]

The set [math]\displaystyle{ \mathcal{D}(h) = \{ x : P(Y=1|X=x) = P(Y=0|X=x)... \} }[/math]

which defines a decision boundary.

[math]\displaystyle{ h^*(x) = \begin{cases} 1 \ \ if \ \ P(Y=1|X=x) \gt P(Y=0|X=x) \\ 0 \ \ \ \ \ \ otherwise \end{cases} }[/math]

Theorem: Bayes rule is optimal. I.e., if h is any other classification rule, then [math]\displaystyle{ L(h^*) \lt = L(h) }[/math] (This is to be proved in homework.)

Why then do we need other classfication methods? A: Because X densities are often/typically unknown. I.e., [math]\displaystyle{ f_k(x) }[/math] and/or [math]\displaystyle{ \pi_k }[/math] unknown.

[math]\displaystyle{ P(Y=k|X=x) = \frac{P(X=x|Y=k)P(Y=k)} {P(X=x)} = \frac{f_k(x) \pi_k} {\sum_k f_k(x) \pi_k} }[/math] f_k(x) is referred to as the class conditional distribution (~likelihood).

Therefore, we rely on some data to estimate quantities.

Three Main Approaches

1. Empirical Risk Minimization: Choose a set of classifiers H (e.g., line, neural network) and find [math]\displaystyle{ h^* \in H }[/math] that minimizes (some estimate of) L(h).

2. Regression: Find an estimate ([math]\displaystyle{ \hat{r} }[/math]) of function [math]\displaystyle{ r }[/math] and define [math]\displaystyle{ h(x) = \begin{cases} 1 \ \ \hat{r}(x) \gt 1/2 \\ 0 \ \ otherwise \end{cases} }[/math]

The [math]\displaystyle{ 1/2 }[/math] in the expression above is a threshold set for the regression prediction output.

In general regression refers to finding a continuous, real valued y. The problem here is more difficult, because of the restricted domain (y is a set of discrete label values).

3. Density Estimation: Estimate [math]\displaystyle{ P(X=x|Y=0) }[/math] from [math]\displaystyle{ X_i }[/math]'s for which [math]\displaystyle{ Y_i = 0 }[/math] Estimate [math]\displaystyle{ P(X=x|Y=1) }[/math] from [math]\displaystyle{ X_i }[/math]'s for which [math]\displaystyle{ Y_i = 1 }[/math] and let [math]\displaystyle{ P(Y=?) = (1/n) \sum_{i=1}^{n} Y_i }[/math]

Define [math]\displaystyle{ \hat{r}(x) = \hat{P}(Y=1|X=x) }[/math] and [math]\displaystyle{ h(x) = \begin{cases} 1 \ \ \hat{r}(x) \gt 1/2 \\ 0 \ \ otherwise \end{cases} }[/math]

It is possible that there may not be enough data to estimate from for density estimation. But the main problem lies with high dimensional spaces, as the estimation results may not be good (high error rate) and sometimes even infeasible. The term curse of dimensionality was coined by Bellman <ref>R. E. Bellman, Dynamic Programming. Princeton University Press, 1957</ref> to describe this problem.

As the dimension of the space goes up, the learning requirements go up exponentially.

To Learn more about methods for handling high-dimensional data <ref> https://docs.google.com/viewer?url=http%3A%2F%2Fwww.bios.unc.edu%2F~dzeng%2FBIOS740%2Flecture_notes.pdf</ref>

Multi-Class Classification

Generalize to case Y takes on k>2 values.

Theorem: [math]\displaystyle{ Y \in \mathcal{Y} = \{1,2,..., k\} }[/math] optimal rule

[math]\displaystyle{ \ h^{*}(x) = argmax_k P(Y=k|X=x) }[/math]

where [math]\displaystyle{ P(Y=k|X=x) = \frac{f_k(x) \pi_k} {\sum_r f_r \pi_r} }[/math]

Examples of Classification

Face detection in images.
Medical diagnosis.
Detecting credit card fraud (fraudulent or legitimate).
Speech recognition.
Handwriting recognition.

LDA and QDA

Discriminant function analysis finds features that best allow discrimination between two or more classes. The approach is similar to analysis of Variance (ANOVA) in that discriminant function analysis looks at the mean values to determine if two or more classes are very different and should be separated. Once the discriminant functions (that separate two or more classes) have been determined, new data points can be classified (i.e. placed in one of the classes) based on the discriminant functions <ref> StatSoft, Inc. (2011). Electronic Statistics Textbook. [Online]. Available: http://www.statsoft.com/textbook/discriminant-function-analysis/. </ref>. Linear discriminant analysis (LDA) and Quadratic discriminant analysis (QDA) are methods of discriminant analysis that are best applied to linearly and quadradically separable classes, respectively. Fisher discriminant analysis (FDA) another method of discriminant analysis that is different from linear discriminant analysis, but oftentimes both terms are used interchangeably.

LDA

The simplest method is to use approach 3 (above) and assume a parametric model for densities. Assume class conditional is Gaussian.

[math]\displaystyle{ \mathcal{Y} = \{ 0,1 \} }[/math] assumed (i.e., 2 labels)

[math]\displaystyle{ h(x) = \begin{cases} 1 \ \ P(Y=1|X=x) \gt P(Y=0|X=x) \\ 0 \ \ otherwise \end{cases} }[/math]

[math]\displaystyle{ P(Y=1|X=x) = \frac{f_1(x) \pi_1} {\sum_k f_k \pi_k} \ \ }[/math] (denom = P(x))

1) Assume Gaussian distributions

[math]\displaystyle{ f_k(x) = \frac{1}{(2\pi)^{d/2} |\Sigma_k|^{1/2}} exp(-(1/2)(\mathbf{x} - \mathbf{\mu_k}) \Sigma_k^{-1}(\mathbf{x}-\mathbf{\mu_k}) ) }[/math]

must compare [math]\displaystyle{ \frac{f_1(x) \pi_1} {p(x)} }[/math] with [math]\displaystyle{ \frac{f_0(x) \pi_0} {p(x)} }[/math] Note that the p(x) denom can be ignored: [math]\displaystyle{ f_1(x) \pi_1 }[/math] with [math]\displaystyle{ f_0(x) \pi_0 }[/math]

To find the decision boundary, set [math]\displaystyle{ f_1(x) \pi_1 = f_0(x) \pi_0 }[/math]

2) Assume [math]\displaystyle{ \Sigma_1 = \Sigma_0 }[/math], we can use [math]\displaystyle{ \Sigma = \Sigma_0 = \Sigma_1 }[/math].

Cancel [math]\displaystyle{ (2\pi)^{-d/2} |\Sigma_k|^{-1/2} }[/math] from both sides.

Take log of both sides.

Subtract one side from both sides, leaving zero on one side.

[math]\displaystyle{ -(1/2)(\mathbf{x} - \mathbf{\mu_1})^T \Sigma^{-1} (\mathbf{x}-\mathbf{\mu_1}) + log(\pi_1) - [-(1/2)(\mathbf{x} - \mathbf{\mu_0})^T \Sigma^{-1} (\mathbf{x}-\mathbf{\mu_0}) + log(\pi_0)] = 0 }[/math]

[math]\displaystyle{ (1/2)[-\mathbf{x}^T \Sigma^{-1}\mathbf{x} - \mathbf{\mu_1}^T \Sigma^{-1} \mathbf{\mu_1} + 2\mathbf{\mu_1}^T \Sigma^{-1} \mathbf{x} + \mathbf{x}^T \Sigma^{-1}\mathbf{x} + \mathbf{\mu_0}^T \Sigma^{-1} \mathbf{\mu_0} - 2\mathbf{\mu_0}^T \Sigma^{-1} \mathbf{x} ] + log(\pi_1/\pi_0) = 0 }[/math]

Cancelling out the terms quadratic in [math]\displaystyle{ \mathbf{x} }[/math] and rearranging results in

[math]\displaystyle{ (1/2)[-\mathbf{\mu_1}^T \Sigma^{-1} \mathbf{\mu_1} + \mathbf{\mu_0}^T \Sigma^{-1} \mathbf{\mu_0} + (2\mathbf{\mu_1}^T \Sigma^{-1} - 2\mathbf{\mu_0}^T \Sigma^{-1}) \mathbf{x}] + log(\pi_1/\pi_0) = 0 }[/math]

We can see that the first pair of terms is constant, and the second pair is linear in x. Therefore, we end up with something of the form [math]\displaystyle{ ax + b = 0 }[/math]. For more about LDA <ref>http://sites.stat.psu.edu/~jiali/course/stat597e/notes2/lda.pdf</ref>

LDA and QDA Continued (Lecture: Sep. 22, 2011)

If we relax assumption 2 (i.e. [math]\displaystyle{ \Sigma_1 \neq \Sigma_0 }[/math]) then we get a quadratic equation that can be written as [math]\displaystyle{ {x}^Ta{x}+b{x} + c = 0 }[/math]

Generalizing LDA and QDA

Theorem:

Suppose that [math]\displaystyle{ \,Y \in \{1,\dots,K\} }[/math], if [math]\displaystyle{ \,f_k(x) = Pr(X=x|Y=k) }[/math] is Gaussian, the Bayes Classifier rule is

[math]\displaystyle{ \,h^*(x) = \arg\max_{k} \delta_k(x) }[/math]

Where

[math]\displaystyle{ \,\delta_k(x) = - \frac{1}{2}log(|\Sigma_k|) - \frac{1}{2}(x-\mu_k)^\top\Sigma_k^{-1}(x-\mu_k) + log (\pi_k) }[/math]

When the Gaussian variances are equal [math]\displaystyle{ \Sigma_1 = \Sigma_0 }[/math] (e.g. LDA), then

[math]\displaystyle{ \,\delta_k(x) = x^\top\Sigma^{-1}\mu_k - \frac{1}{2}\mu_k^\top\Sigma^{-1}\mu_k + log (\pi_k) }[/math]

(To compute this, we need to calculate the value of [math]\displaystyle{ \,\delta }[/math] for each class, and then take the one with the max. value).

In practice

We estimate the prior to be the chance that a random item from the collection belongs to class k, e.g.

[math]\displaystyle{ \,\hat{\pi_k} = \hat{Pr}(y=k) = \frac{n_k}{n} }[/math]

The mean to be the average item in set k, e.g.

[math]\displaystyle{ \,\hat{\mu_k} = \frac{1}{n_k}\sum_{i:y_i=k}x_i }[/math]

and calculate the covariance of each class e.g.

[math]\displaystyle{ \,\hat{\Sigma_k} = \frac{1}{n_k}\sum_{i:y_i=k}(x_i-\hat{\mu_k})(x_i-\hat{\mu_k})^\top }[/math]

If we wish to use LDA we must calculate a common covariance, so we average all the covariances e.g.

[math]\displaystyle{ \,\Sigma=\frac{\sum_{r=1}^{k}(n_r\Sigma_r)}{\sum_{r=1}^{k}n_r} }[/math]

Where: [math]\displaystyle{ \,n_r }[/math] is the number of data points in class [math]\displaystyle{ \,r }[/math], [math]\displaystyle{ \,\Sigma_r }[/math] is the covariance of class [math]\displaystyle{ \,r }[/math], [math]\displaystyle{ \,n }[/math] is the total number of data points, and [math]\displaystyle{ \,k }[/math] is the number of classes.

Computation

For QDA we need to calculate: [math]\displaystyle{ \,\delta_k(x) = - \frac{1}{2}log(|\Sigma_k|) - \frac{1}{2}(x-\mu_k)^\top\Sigma_k^{-1}(x-\mu_k) + log (\pi_k) }[/math]

Lets first consider when [math]\displaystyle{ \, \Sigma_k = I, \forall k }[/math]. This is the case where each distribution is spherical, around the mean point.

Case 1

When [math]\displaystyle{ \, \Sigma_k = I }[/math]

We have:

[math]\displaystyle{ \,\delta_k = - \frac{1}{2}log(|I|) - \frac{1}{2}(x-\mu_k)^\top I(x-\mu_k) + log (\pi_k) }[/math]

but [math]\displaystyle{ \ \log(|I|)=\log(1)=0 }[/math]

and [math]\displaystyle{ \, (x-\mu_k)^\top I(x-\mu_k) = (x-\mu_k)^\top(x-\mu_k) }[/math] is the squared Euclidean distance between two points [math]\displaystyle{ \,x }[/math] and [math]\displaystyle{ \,\mu_k }[/math]

Thus in this condition, a new point can be classified by its distance away from the center of a class, adjusted by some prior.

Further, for two-class problem with equal prior, the discriminating function would be the bisector of the 2-class's means.

Case 2

When [math]\displaystyle{ \, \Sigma_k \neq I }[/math]

Using the Singular Value Decomposition (SVD) of [math]\displaystyle{ \, \Sigma_k }[/math] we get [math]\displaystyle{ \, \Sigma_k = U_kS_kV_k^\top }[/math]. In particular, [math]\displaystyle{ \, U_k }[/math] is a collection of eigenvectors of [math]\displaystyle{ \, \Sigma_k\Sigma_k^* }[/math], and [math]\displaystyle{ \, V_k }[/math] is a collection of eigenvectors of [math]\displaystyle{ \,\Sigma_k^*\Sigma_k }[/math]. Since [math]\displaystyle{ \, \Sigma_k }[/math] is a symmetric matrix<ref> http://en.wikipedia.org/wiki/Covariance_matrix#Properties </ref>, [math]\displaystyle{ \, \Sigma_k = \Sigma_k^* }[/math], so we have [math]\displaystyle{ \, \Sigma_k = U_kS_kU_k^\top }[/math].

For [math]\displaystyle{ \,\delta_k }[/math], the second term becomes what is also known as the Mahalanobis distance <ref>P. C. Mahalanobis, "On The Generalised Distance in Statistics," Proceedings of the National Institute of Sciences of India, 1936</ref> :

[math]\displaystyle{ \begin{align} (x-\mu_k)^\top\Sigma_k^{-1}(x-\mu_k)&= (x-\mu_k)^\top U_kS_k^{-1}U_k^T(x-\mu_k)\\ & = (U_k^\top x-U_k^\top\mu_k)^\top S_k^{-1}(U_k^\top x-U_k^\top \mu_k)\\ & = (U_k^\top x-U_k^\top\mu_k)^\top S_k^{-\frac{1}{2}}S_k^{-\frac{1}{2}}(U_k^\top x-U_k^\top\mu_k) \\ & = (S_k^{-\frac{1}{2}}U_k^\top x-S_k^{-\frac{1}{2}}U_k^\top\mu_k)^\top I(S_k^{-\frac{1}{2}}U_k^\top x-S_k^{-\frac{1}{2}}U_k^\top \mu_k) \\ & = (S_k^{-\frac{1}{2}}U_k^\top x-S_k^{-\frac{1}{2}}U_k^\top\mu_k)^\top(S_k^{-\frac{1}{2}}U_k^\top x-S_k^{-\frac{1}{2}}U_k^\top \mu_k) \\ \end{align} }[/math]

If we think of [math]\displaystyle{ \, S_k^{-\frac{1}{2}}U_k^\top }[/math] as a linear transformation that takes points in class [math]\displaystyle{ \,k }[/math] and distributes them spherically around a point, like in case 1. Thus when we are given a new point, we can apply the modified [math]\displaystyle{ \,\delta_k }[/math] values to calculate [math]\displaystyle{ \ h^*(\,x) }[/math]. After applying the singular value decomposition, [math]\displaystyle{ \,\Sigma_k^{-1} }[/math] is considered to be an identity matrix such that

[math]\displaystyle{ \,\delta_k = - \frac{1}{2}log(|I|) - \frac{1}{2}[(S_k^{-\frac{1}{2}}U_k^\top x-S_k^{-\frac{1}{2}}U_k^\top\mu_k)^\top(S_k^{-\frac{1}{2}}U_k^\top x-S_k^{-\frac{1}{2}}U_k^\top \mu_k)] + log (\pi_k) }[/math]

and,

[math]\displaystyle{ \ \log(|I|)=\log(1)=0 }[/math]

For applying the above method with classes that have different covariance matrices (for example the covariance matrices [math]\displaystyle{ \ \Sigma_0 }[/math] and [math]\displaystyle{ \ \Sigma_1 }[/math] for the two class case), each of the covariance matrices has to be decomposed using SVD to find the according transformation. Then, each new data point has to be transformed using each transformation to compare its distance to the mean of each class (for example for the two class case, the new data point would have to be transformed by the class 1 transformation and then compared to [math]\displaystyle{ \ \mu_0 }[/math] and the new data point would also have to be transformed by the class 2 transformation and then compared to [math]\displaystyle{ \ \mu_1 }[/math]).

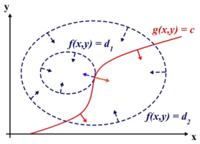
The difference between Case 1 and Case 2 (i.e. the difference between using the Euclidean and Mahalanobis distance) can be seen in the illustration below.

Illustration of Euclidean distance (a) and Mahalanobis distance (b) where the contours represent equidistant points from the center using each distance metric. Source: <ref>R. De Maesschalck, D. Jouan-Rimbaud and D. L. Massart, "Tutorial - The Mahalanobis distance," *Chemometrics and Intelligent Laboratory Systems*, 2000 </ref>

As can be seen from the illustration above, the Mahalanobis distance takes into account the distribution of the data points, whereas the Euclidean distance would treat the data as though it has a spherical distribution. Thus, the Mahalanobis distance applies for the more general classification in Case 2, whereas the Euclidean distance applies to the special case in Case 1 where the data distribution is assumed to be spherical.

Generally, we can conclude that QDA provides a better classifier for the data then LDA because LDA assumes that the covariance matrix is identical for each class, but QDA does not. QDA still uses Gaussian distribution as a class conditional distribution. In our real life, this distribution can not be happened each time, so we have to use other distribution as a complement.

Principal Component Analysis (PCA) (Lecture: Sep. 27, 2011)

Principal Component Analysis (PCA) is a method of dimensionality reduction/feature extraction that transforms the data from a D dimensional space into a new coordinate system of dimension d, where d <= D ( the worst case would be to have d=D). The goal is to preserve as much of the variance in the original data as possible when switching the coordinate systems. Give data on D variables, the hope is that the data points will lie mainly in a linear subspace of dimension lower than D. In practice, the data will usually not lie precisely in some lower dimensional subspace.

The new variables that form a new coordinate system are called principal components (PCs). PCs are denoted by [math]\displaystyle{ \ u_1, u_2, ... , u_D }[/math]. The principal components form a basis for the data. Since PCs are orthogonal linear transformations of the original variables there is at most D PCs. Normally, not all of the D PCs are used but rather a subset of d PCs, [math]\displaystyle{ \ u_1, u_2, ... , u_d }[/math], to approximate the space spanned by the original data points [math]\displaystyle{ \ x_1, x_2, ... , x_D }[/math]. We can choose d based on what percentage of the original data we would like to maintain.

Let [math]\displaystyle{ \ PC_j }[/math] be a linear combination of [math]\displaystyle{ \ x_1, x_2, ... , x_D }[/math] defined by the coefficients [math]\displaystyle{ \ w^{(j)} }[/math] = [math]\displaystyle{ ( {w_1}^{(j)}, {w_2}^{(j)},...,{w_D}^{(j)} )^T }[/math]

Thus, [math]\displaystyle{ u_j = {w_1}^{(j)} x_1 + {w_2}^{(j)} x_2 + ... + {w_D}^{(j)} x_D = w^{(j)^T} X }[/math]

This is a unique configuration since it sets up the PCs in order from maximum to minimum variances. The first PC, [math]\displaystyle{ \ u_1 }[/math] is called first principal component and has the maximum variance, thus it accounts for the most significant variance in the data [math]\displaystyle{ \ x_1, x_2, ... , x_D }[/math]. The second PC, [math]\displaystyle{ \ u_2 }[/math] is called second principal component and has the second highest variance and so on until PC, [math]\displaystyle{ \ u_D }[/math] which has the minimum variance.

To get the first principal component, we would like to use the following equation:

[math]\displaystyle{ \ max (Var(w^T X)) = max (w^T S w) }[/math]

Where [math]\displaystyle{ \ S }[/math] is the covariance matrix. And we solve for [math]\displaystyle{ \ w }[/math].

Note: we require the constraint [math]\displaystyle{ \ w^T w = 1 }[/math] because if there is no constraint on the length of [math]\displaystyle{ \ w }[/math] then there is no upper bound. With the constraint, the direction and not the length that maximizes the variance can be found.

Lagrange Multiplier

Before we proceed, we should review Lagrange multipliers.

"The red line shows the constraint g(x,y) = c. The blue lines are contours of f(x,y). The point where the red line tangentially touches a blue contour is our solution." [Lagrange Multipliers, Wikipedia]

Lagrange multipliers are used to find the maximum or minimum of a function [math]\displaystyle{ \displaystyle f(x,y) }[/math] subject to constraint [math]\displaystyle{ \displaystyle g(x,y)=0 }[/math]

we define a new constant [math]\displaystyle{ \lambda }[/math] called a Lagrange Multiplier and we form the Lagrangian,

[math]\displaystyle{ \displaystyle L(x,y,\lambda) = f(x,y) - \lambda g(x,y) }[/math]

If [math]\displaystyle{ \displaystyle f(x^*,y^*) }[/math] is the max of [math]\displaystyle{ \displaystyle f(x,y) }[/math], there exists [math]\displaystyle{ \displaystyle \lambda^* }[/math] such that [math]\displaystyle{ \displaystyle (x^*,y^*,\lambda^*) }[/math] is a stationary point of [math]\displaystyle{ \displaystyle L }[/math] (partial derivatives are 0).
In addition [math]\displaystyle{ \displaystyle (x^*,y^*) }[/math] is a point in which functions [math]\displaystyle{ \displaystyle f }[/math] and [math]\displaystyle{ \displaystyle g }[/math] touch but do not cross. At this point, the tangents of [math]\displaystyle{ \displaystyle f }[/math] and [math]\displaystyle{ \displaystyle g }[/math] are parallel or gradients of [math]\displaystyle{ \displaystyle f }[/math] and [math]\displaystyle{ \displaystyle g }[/math] are parallel, such that:

[math]\displaystyle{ \displaystyle \nabla_{x,y } f = \lambda \nabla_{x,y } g }[/math]

where,
[math]\displaystyle{ \displaystyle \nabla_{x,y} f = (\frac{\partial f}{\partial x},\frac{\partial f}{\partial{y}}) \leftarrow }[/math] the gradient of [math]\displaystyle{ \, f }[/math]
[math]\displaystyle{ \displaystyle \nabla_{x,y} g = (\frac{\partial g}{\partial{x}},\frac{\partial{g}}{\partial{y}}) \leftarrow }[/math] the gradient of [math]\displaystyle{ \, g }[/math]

Example :

Suppose we want to maximize the function [math]\displaystyle{ \displaystyle f(x,y)=x-y }[/math] subject to the constraint [math]\displaystyle{ \displaystyle x^{2}+y^{2}=1 }[/math]. We can apply the Lagrange multiplier method to find the maximum value for the function [math]\displaystyle{ \displaystyle f }[/math]; the Lagrangian is:

[math]\displaystyle{ \displaystyle L(x,y,\lambda) = x-y - \lambda (x^{2}+y^{2}-1) }[/math]

We want the partial derivatives equal to zero:

[math]\displaystyle{ \displaystyle \frac{\partial L}{\partial x}=1+2 \lambda x=0 }[/math]

[math]\displaystyle{ \displaystyle \frac{\partial L}{\partial y}=-1+2\lambda y=0 }[/math]

[math]\displaystyle{ \displaystyle \frac{\partial L}{\partial \lambda}=x^2+y^2-1 }[/math]

Solving the system we obtain two stationary points: [math]\displaystyle{ \displaystyle (\sqrt{2}/2,-\sqrt{2}/2) }[/math] and [math]\displaystyle{ \displaystyle (-\sqrt{2}/2,\sqrt{2}/2) }[/math]. In order to understand which one is the maximum, we just need to substitute it in [math]\displaystyle{ \displaystyle f(x,y) }[/math] and see which one as the biggest value. In this case the maximum is [math]\displaystyle{ \displaystyle (\sqrt{2}/2,-\sqrt{2}/2) }[/math].

Determining w :

Use the Lagrange multiplier conversion to obtain: [math]\displaystyle{ \displaystyle L(w, \lambda) = w^T Sw - \lambda (w^T w - 1) }[/math] where [math]\displaystyle{ \displaystyle \lambda }[/math] is a constant

Take the derivative and set it to zero: [math]\displaystyle{ \displaystyle{\partial L \over{\partial w}} = 0 }[/math]

To obtain: [math]\displaystyle{ \displaystyle 2Sw - 2 \lambda w = 0 }[/math]

Rearrange to obtain: [math]\displaystyle{ \displaystyle Sw = \lambda w }[/math]

where [math]\displaystyle{ \displaystyle w }[/math] is eigenvector of [math]\displaystyle{ \displaystyle S }[/math] and [math]\displaystyle{ \ \lambda }[/math] is the eigenvalue of [math]\displaystyle{ \displaystyle S }[/math] as [math]\displaystyle{ \displaystyle Sw= \lambda w }[/math] , and [math]\displaystyle{ \displaystyle w^T w=1 }[/math] , then we can write

[math]\displaystyle{ \displaystyle w^T Sw= w^T\lambda w= \lambda w^T w =\lambda }[/math]

Note that the PCs decompose the total variance in the data in the following way :

[math]\displaystyle{ \sum_{i=1}^{D} Var(u_i) }[/math]

[math]\displaystyle{ = \sum_{i=1}^{D} (\lambda_i) }[/math]

[math]\displaystyle{ \ = Tr(S) }[/math]

[math]\displaystyle{ = \sum_{i=1}^{D} Var(x_i) }[/math]

Principal Component Analysis (PCA) Continued (Lecture: Sep. 29, 2011)

As can be seen from the above expressions, [math]\displaystyle{ \ Var(W^\top X) = W^\top S W= \lambda }[/math] where lambda is an eigenvalue of the sample covariance matrix [math]\displaystyle{ \ S }[/math] and [math]\displaystyle{ \ W }[/math] is its corresponding eigenvector. So [math]\displaystyle{ \ Var(u_i) }[/math] is maximized if [math]\displaystyle{ \ \lambda_i }[/math] is the maximum eigenvalue of [math]\displaystyle{ \ S }[/math] and the first principal component (PC) is the corresponding eigenvector. Each successive PC can be generated in the above manner by taking the eigenvectors of [math]\displaystyle{ \ S }[/math]<ref>www.wikipedia.org/wiki/Eigenvalues_and_eigenvectors</ref> that correspond to the eigenvalues:

[math]\displaystyle{ \ \lambda_1 \geq ... \geq \lambda_D }[/math]

such that

[math]\displaystyle{ \ Var(u_1) \geq ... \geq Var(u_D) }[/math]

Alternative Derivation

Another way of looking at PCA is to consider PCA as a projection from a higher D-dimension space to a lower d-dimensional subspace that minimizes the squared reconstruction error. The squared reconstruction error is the difference between the original data set [math]\displaystyle{ \ X }[/math] and the new data set [math]\displaystyle{ \hat{X} }[/math] obtained by first projecting the original data set into a lower d-dimensional subspace and then projecting it back into the the original higher D-dimension space. Since information is (normally) lost by compressing the the original data into a lower d-dimensional subspace, the new data set will (normally) differ from the original data even though both are part of the higher D-dimension space. The reconstruction error is computed as shown below.

Reconstruction Error

[math]\displaystyle{ e = \sum_{i=1}^{n} || x_i - \hat{x}_i ||^2 }[/math]

Minimize Reconstruction Error

Suppose [math]\displaystyle{ \bar{x} = 0 }[/math] where [math]\displaystyle{ \hat{x}_i = x_i - \bar{x} }[/math]

Let [math]\displaystyle{ \ f(y) = U_d y }[/math] where [math]\displaystyle{ \ U_d }[/math] is a D by d matrix with d orthogonal unit vectors as columns.

Fit the model to the data and minimize the reconstruction error:

[math]\displaystyle{ \ min_{U_d, y_i} \sum_{i=1}^n || x_i - U_d y_i ||^2 }[/math]

Differentiate with respect to [math]\displaystyle{ \ y_i }[/math]:

[math]\displaystyle{ \frac{\partial e}{\partial y_i} = 0 }[/math]

we can rewrite reconstruction-error as : [math]\displaystyle{ \ e = \sum_{i=1}^n(x_i - U_d y_i)^T(x_i - U_d y_i) }[/math]

[math]\displaystyle{ \ \frac{\partial e}{\partial y_i} = 2(-U_d)(x_i - U_d y_i) = 0 }[/math]

since [math]\displaystyle{ \ U_d(x_i - U_d y_i) }[/math] is a linear combination of the columns of [math]\displaystyle{ \ U_d }[/math],

which are independent (orthogonal to each other) we can conclude that:

[math]\displaystyle{ \ x_i - U_d y_i = 0 }[/math] or equivalently,

[math]\displaystyle{ \ x_i = U_d y_i }[/math]

[math]\displaystyle{ \ y_i = U_d^T x_i }[/math]

Find the orthogonal matrix [math]\displaystyle{ \ U_d }[/math]:

[math]\displaystyle{ \ min_{U_d} \sum_{i=1}^n || x_i - U_d U_d^T x_i||^2 }[/math]

Using SVD

A unique solution can be obtained by finding the Singular Value Decomposition (SVD) of [math]\displaystyle{ \ X }[/math]:

[math]\displaystyle{ \ X = U S V^T }[/math]

For each rank d, [math]\displaystyle{ \ U_d }[/math] consists of the first d columns of [math]\displaystyle{ \ U }[/math]. Also, the covariance matrix can be expressed as follows [math]\displaystyle{ \ S = \frac{1}{n-1}\sum_{i=1}^n (x_i - \mu)(x_i - \mu)^T }[/math].

Simply put, by subtracting the mean of each of the data point features and then applying SVD, one can find the principal components:

[math]\displaystyle{ \tilde{X} = X - \mu }[/math]

[math]\displaystyle{ \ \tilde{X} = U S V^T }[/math]

Where [math]\displaystyle{ \ X }[/math] is a d by n matrix of data points and the features of each data point form a column in [math]\displaystyle{ \ X }[/math]. Also, [math]\displaystyle{ \ \mu }[/math] is a d by n matrix with identical columns each equal to the mean of the [math]\displaystyle{ \ x_i }[/math]'s, ie [math]\displaystyle{ \mu_{:,j}=\frac{1}{n}\sum_{i=1}^n x_i }[/math]. Note that the arrangement of data points is a convention and indeed in Matlab or conventional statistics, the transpose of the matrices in the above formulae is used.

As the [math]\displaystyle{ \ S }[/math] matrix from the SVD has the eigenvalues arranged from largest to smallest, the corresponding eigenvectors in the [math]\displaystyle{ \ U }[/math] matrix from the SVD will be such that the first column of [math]\displaystyle{ \ U }[/math] is the first principal component and the second column is the second principal component and so on.

Examples

Note that in the Matlab code in the examples below, the mean was not subtracted from the datapoints before performing SVD. This is what was shown in class. However, to properly perform PCA, the mean should be subtracted from the datapoints.

Example 1

Consider a matrix of data points [math]\displaystyle{ \ X }[/math] with the dimensions 560 by 1965. 560 is the number of elements in each column. Each column is a vector representation of a 20x28 grayscale pixel image of a face (see image below) and there is a total of 1965 different images of faces. Each of the images are corrupted by noise, but the noise can be removed by projecting the data back to the original space taking as many dimensions as one likes (e.g, 2, 3 4 0r 5). The corresponding Matlab commands are shown below:

 >> % start with a 560 by 1965 matrix X that contains the data points
 >> load(noisy.mat);
 >>  
 >> % set the colors to grayscale 
 >> colormap gray
 >> 
 >> % show image in column 10 by reshaping column 10 into a 20 by 28 matrix
 >> imagesc(reshape(X(:,10),20,28)')
 >> 
 >> % perform SVD, if X matrix if full rank, will obtain 560 PCs
 >> [S U V] = svd(X);
 >> 
 >> % reconstruct X ( project X onto the original space) using only the first ten principal components
 >> Y_pca = U(:, 1:10)'*X;
 >> 
 >> % show image in column 10 of X_hat which is now a 560 by 1965 matrix
 >> imagesc(reshape(X_hat(:,10),20,28)')

The reason why the noise is removed in the reconstructed image is because the noise does not create a major variation in a single direction in the original data. Hence, the first ten PCs taken from [math]\displaystyle{ \ U }[/math] matrix are not in the direction of the noise. Thus, reconstructing the image using the first ten PCs, will remove the noise.

Example 2

Consider a matrix of data points [math]\displaystyle{ \ X }[/math] with the dimensions 64 by 400. 64 is the number of elements in each column. Each column is a vector representation of a 8x8 grayscale pixel image of either a handwritten number 2 or a handwritten number 3 (see image below) and there are a total of 400 different images, where the first 200 images show a handwritten number 2 and the last 200 images show a handwritten number 3.

The corresponding Matlab commands for performing PCA on the data points are shown below:

 >> % start with a 64 by 400 matrix X that contains the data points
 >> load 2_3.mat;
 >> 
 >> % set the colors to grayscale 
 >> colormap gray
 >> 
 >> % show image in column 2 by reshaping column 2 into a 8 by 8 matrix
 >> imagesc(reshape(X(:,2),8,8))
 >> 
 >> % perform SVD, if X matrix if full rank, will obtain 64 PCs
 >> [U S V] = svd(X);
 >> 
 >> % project data down onto the first two PCs
 >> Y = U(:,1:2)'*X;
 >> 
 >> % show Y as an image (can see the change in the first PC at column 200,
 >> % when the handwritten number changes from 2 to 3)
 >> imagesc(Y)
 >> 
 >> % perform PCA using Matlab build-in function (do not use for assignment)
 >> % also note that due to the Matlab convention, the transpose of X is used
 >> [COEFF, Y] = princomp(X');
 >> 
 >> % again, use the first two PCs
 >> Y = Y(:,1:2);
 >> 
 >> % use plot digits to show the distribution of images on the first two PCs
 >> images = reshape(X, 8, 8, 400);
 >> plotdigits(images, Y, .1, 1);

Using the plotdigits function in Matlab, clearly illustrates that the first PC captured the differences between the numbers 2 and 3 as they are projected onto different regions of the axis for the first PC. Also, the second PC captured the tilt of the handwritten numbers as numbers tilted to the left or right were projected onto different regions of the axis for the second PC.

Example 3

(Not discussed in class) In the news recently was a story that captures some of the ideas behind PCA. Over the past two years, Scott Golder and Michael Macy, researchers from Cornell University, collected 509 million Twitter messages from 2.4 million users in 84 different countries. The data they used were words collected at various times of day and they classified the data into two different categories: positive emotion words and negative emotion words. Then, they were able to study this new data to evaluate subjects' moods at different times of day, while the subjects were in different parts of the world. They found that the subjects generally exhibited positive emotions in the mornings and late evenings, and negative emotions mid-day. They were able to "project their data onto a smaller dimensional space" using PCS. Their paper, "Diurnal and Seasonal Mood Vary with Work, Sleep, and Daylength Across Diverse Cultures," is available in the journal Science.<ref>http://www.pcworld.com/article/240831/twitter_analysis_reveals_global_human_moodiness.html</ref>.

Assumptions Underlying Principal Component Analysis can be found here<ref>http://support.sas.com/publishing/pubcat/chaps/55129.pdf</ref>

Example 4

(Not discussed in class) A somewhat well known learning rule in the field of neural networks called Oja's rule can be used to train networks of neurons to compute the principal component directions of data sets. <ref>A Simplified Neuron Model as a Principal Component Analyzer. Erkki Oja. 1982. Journal of Mathematical Biology. 15: 267-273</ref> This rule is formulated as follows

[math]\displaystyle{ \,\Delta w = \eta yx -\eta y^2w }[/math]

where [math]\displaystyle{ \,\Delta w }[/math] is the neuron weight change, [math]\displaystyle{ \,\eta }[/math] is the learning rate, [math]\displaystyle{ \,y }[/math] is the neuron output given the current input, [math]\displaystyle{ \,x }[/math] is the current input and [math]\displaystyle{ \,w }[/math] is the current neuron weight. This learning rule shares some similarities with another method for calculating principal components: power iteration. The basic algorithm for power iteration (taken from wikipedia: <ref>Wikipedia. http://en.wikipedia.org/wiki/Principal_component_analysis#Computing_principal_components_iteratively</ref>) is shown below

[math]\displaystyle{ \mathbf{p} = }[/math] a random vector
do c times:
      [math]\displaystyle{ \mathbf{t} = 0 }[/math] (a vector of length m)
      for each row [math]\displaystyle{ \mathbf{x} \in \mathbf{X^T} }[/math]
            [math]\displaystyle{ \mathbf{t} = \mathbf{t} + (\mathbf{x} \cdot \mathbf{p})\mathbf{x} }[/math]
      [math]\displaystyle{ \mathbf{p} = \frac{\mathbf{t}}{|\mathbf{t}|} }[/math]
return [math]\displaystyle{ \mathbf{p} }[/math]

Comparing this with the neuron learning rule we can see that the term [math]\displaystyle{ \, \eta y x }[/math] is very similar to the [math]\displaystyle{ \,\mathbf{t} }[/math] update equation in the power iteration method, and identical if the neuron model is assumed to be linear ([math]\displaystyle{ \,y(x)=x\mathbf{p} }[/math]) and the learning rate is set to 1. Additionally, the [math]\displaystyle{ \, -\eta y^2w }[/math] term performs the normalization, the same function as the [math]\displaystyle{ \,\mathbf{p} }[/math] update equation in the power iteration method.

Observations

Some observations about the PCA were brought up in class:

PCA assumes that data is on a linear subspace or close to a linear subspace. For non-linear dimensionality reduction, other techniques are used. Amongst the first proposed techniques for non-linear dimensionality reduction are Locally Linear Embedding (LLE) and Isomap. More recent techniques include Maximum Variance Unfolding (MVU) and t-Distributed Stochastic Neighbor Embedding (t-SNE). Kernel PCAs may also be used, but they depend on the type of kernel used and generally do not work well in practice. (Kernels will be covered in more detail later in the course.)

Finding the number of PCs to use is not straightforward. It requires knowledge about the instrinsic dimentionality of data. In practice, oftentimes a heuristic approach is adopted by looking at the eigenvalues ordered from largest to smallest. If there is a "dip" in the magnitude of the eigenvalues, the "dip" is used as a cut off point and only the large eigenvalues before the "dip" are used. Otherwise, it is possible to add up the eigenvalues from largest to smallest until a certain percentage value is reached. This percentage value represents the percentage of variance that is preserved when projecting onto the PCs corresponding to the eigenvalues that have been added together to achieve the percentage.

It is a good idea to normalize the variance of the data before applying PCA. This will avoid PCA finding PCs in certain directions due to the scaling of the data, rather than the real variance of the data.

PCA can be considered as an unsupervised approach, since the main direction of variation is not known beforehand, i.e. it is not completely certain which dimension the first PC will capture. The PCs found may not correspond to the desired labels for the data set. There are, however, alternate methods for performing supervised dimensionality reduction.

(Not in class) Even though the traditional PCA method does not work well on data set that lies on a non-linear manifold. A revised PCA method, called c-PCA, has been introduced to improve the stability and convergence of intrinsic dimension estimation. The approach first finds a minimal cover (a cover of a set X is a collection of sets whose union contains X as a subset<ref>http://en.wikipedia.org/wiki/Cover_(topology)</ref>) of the data set. Since set covering is an NP-hard problem, the approach only finds an approximation of minimal cover to reduce the complexity of the run time. In each subset of the minimal cover, it applies PCA and filters out the noise in the data. Finally the global intrinsic dimension can be determined from the variance results from all the subsets. The algorithm produces robust results.<ref>Mingyu Fan, Nannan Gu, Hong Qiao, Bo Zhang, Intrinsic dimension estimation of data by principal component analysis, 2010. Available: http://arxiv.org/abs/1002.2050</ref>

(Not in class) While PCA finds the mathematically optimal method (as in minimizing the squared error), it is sensitive to outliers in the data that produce large errors PCA tries to avoid. It therefore is common practice to remove outliers before computing PCA. However, in some contexts, outliers can be difficult to identify. For example in data mining algorithms like correlation clustering, the assignment of points to clusters and outliers is not known beforehand. A recently proposed generalization of PCA based on a Weighted PCA increases robustness by assigning different weights to data objects based on their estimated relevancy.<ref>http://en.wikipedia.org/wiki/Principal_component_analysis</ref>

(Not in class) Comparison between PCA and LDA: Principal Component Analysis (PCA)and Linear Discriminant Analysis (LDA) are two commonly used techniques for data classification and dimensionality reduction. Linear Discriminant Analysis easily handles the case where the within-class frequencies are unequal and their performances has been examined on randomly generated test data. This method maximizes the ratio of between-class variance to the within-class variance in any particular data set thereby guaranteeing maximal separability. ... The prime difference between LDA and PCA is that PCA does more of feature classification and LDA does data classification. In PCA, the shape and location of the original data sets changes when transformed to a different space whereas LDA doesn’t change the location but only tries to provide more class separability and draw a decision region between the given classes. This method also helps to better understand the distribution of the feature data." [24] [[1]]

Summary

The PCA algorithm can be summarized into the following steps:

Recover basis
[math]\displaystyle{ \ \text{ Calculate } XX^T=\Sigma_{i=1}^{t}x_ix_{i}^{T} \text{ and let } U=\text{ eigenvectors of } XX^T \text{ corresponding to the largest } d \text{ eigenvalues.} }[/math]
Encode training data
[math]\displaystyle{ \ \text{Let } Y=U^TX \text{, where } Y \text{ is a } d \times t \text{ matrix of encodings of the original data.} }[/math]
Reconstruct training data
[math]\displaystyle{ \hat{X}=UY=UU^TX }[/math].
Encode test example
[math]\displaystyle{ \ y = U^Tx \text{ where } y \text{ is a } d\text{-dimensional encoding of } x }[/math].
Reconstruct test example
[math]\displaystyle{ \hat{x}=Uy=UU^Tx }[/math].

Fisher Discriminant Analysis (FDA) (Lecture: Sep. 29, 2011)

Fisher Discriminant Analysis (FDA) is sometimes called Fisher Linear Discriminant Analysis (FLDA) or just Linear Discriminant Analysis (LDA). This causes confusion with the Linear Discriminant Analysis (LDA) technique covered earlier in the course. The LDA technique covered earlier in the course has a normality assumption and is a boundary finding technique. The FDA technique outlined here is a supervised feature extraction technique. FDA differs from PCA as well because PCA does not use the class labels, [math]\displaystyle{ \ y_i }[/math], of the data [math]\displaystyle{ \ (x_i,y_i) }[/math] while FDA organizes data into their classes by finding the direction of maximum separation between classes.

Fisher Discriminant Analysis (FDA) Continued (Lecture: Oct. 04, 2011)

One main drawback of the PCA technique is that the direction of greatest variation may not be the classification we desire. For example, imagine if the data set above had a lightening filter applied to a random subset of the images. Then the greatest variation would be the brightness and not the more important variations we wish to classify. FDA circumvents this problem by using the labels, [math]\displaystyle{ \ y_i }[/math], of the data [math]\displaystyle{ \ (x_i,y_i) }[/math] i.e. the FDA uses supervised learning. An elementary way to see the algorithm is to imagine two classes of data projected onto a suitably chosen line that minimizes the within class variance, and maximizes the distance between the two classes i.e. group similar data together and spread different data apart. This way, new data acquired can be compared, after a transformation, to where these projections, using some well-chosen metric.

We first consider the cases of two-classes. Denote the mean and covariance matrix of class [math]\displaystyle{ i=0,1 }[/math] by [math]\displaystyle{ \mathbf{\mu}_i }[/math] and [math]\displaystyle{ \mathbf{\Sigma}_i }[/math] respectively. We transform the data so that it is projected into 1 dimension i.e. a scalar value. To do this, we compute the inner product of our [math]\displaystyle{ dx1 }[/math]-dimensional data, [math]\displaystyle{ \mathbf{x} }[/math], by a to-be-determined [math]\displaystyle{ dx1 }[/math]-dimensional vector [math]\displaystyle{ \mathbf{w} }[/math]. The new means and covariances of the transformed data:

[math]\displaystyle{ \mu'_i:\rightarrow \mathbf{w}^{T}\mathbf{\mu}_i }[/math]

[math]\displaystyle{ \Sigma'_i :\rightarrow \mathbf{w}^{T}\mathbf{\sigma}_i \mathbf{w} }[/math]

The new means and variances are actually scalar values now, but we will use vector and matrix notation and arguments throughout the following derivation as the multi-class case is then just a simpler extension.

Goals of FDA

As will be shown in the objective function, the goal of FDA is to maximize the separation of the classes (between class variance) and minimize the scatter within each class (within class variance). That is, our ideal situation is that the individual classes are as far away from each other as possible and at the same time the data within each class are as close to each other as possible (collapsed to a single point in the most extreme case). An interesting note is that R. A. Fisher who FDA is named after, used the FDA technique for purposes of taxonomy, in particular for categorizing different species of iris flowers. <ref name="RAFisher">R. A. Fisher, "The Use of Multiple measurements in Taxonomic Problems," Annals of Eugenics, 1936</ref>. It is very easy to visualize what is meant by within class variance (i.e. differences between the iris flowers of the same species) and between class variance (i.e. the differences between the iris flowers of different species) in that case.

1) Our first goal is to minimize the individual classes' covariance. This will help to collapse the data together. We have two minimization problems

[math]\displaystyle{ \min_{\mathbf{w}} \mathbf{w} \mathbf{\Sigma}_0 \mathbf{w}^{T} }[/math]

and

[math]\displaystyle{ \min_{\mathbf{w}} \mathbf{w} \mathbf{\Sigma}_1 \mathbf{w}^{T} }[/math].

But these can be combined:

[math]\displaystyle{ \min_{\mathbf{w}} \mathbf{w} \mathbf{\Sigma}_0 \mathbf{w}^{T} + \mathbf{w} \mathbf{\Sigma}_1 \mathbf{w}^{T} }[/math]

[math]\displaystyle{ = \min_{\mathbf{w}} \mathbf{w} ( \mathbf{\Sigma_0} + \mathbf{\Sigma_1} ) \mathbf{w}^{T} }[/math]

Define [math]\displaystyle{ \mathbf{S}_W =\mathbf{\Sigma_0} + \mathbf{\Sigma_1} }[/math], called the within class variance matrix.

2) Our second goal is to move the minimized classes as far away from each other as possible. One way to accomplish this is to maximize the distances between the means of the transformed data i.e.

[math]\displaystyle{ \max_{\mathbf{w}} |\mathbf{w}^{T}\mathbf{\mu}_0 - \mathbf{w}^{T}\mathbf{\mu}_1|^2 }[/math]

Simplifying:

[math]\displaystyle{ \max_{\mathbf{w}} \,(\mathbf{w}^{T}\mathbf{\mu}_0 - \mathbf{w}^{T}\mathbf{\mu}_1)^T (\mathbf{w}^{T}\mathbf{\mu}_0 - \mathbf{w}^{T}\mathbf{mu}_1) }[/math]

[math]\displaystyle{ = \max_{\mathbf{w}}\, (\mathbf{\mu}_0-\mathbf{\mu}_1)^{T}\mathbf{w}^{T} \mathbf{w} (\mathbf{\mu}_0-\mathbf{\mu}_1) }[/math]

[math]\displaystyle{ = \max_{\mathbf{w}} \,\mathbf{w}^{T}(\mathbf{\mu}_0-\mathbf{\mu}_1)(\mathbf{\mu}_0-\mathbf{\mu}_1)^{T}\mathbf{w} }[/math]

Recall that [math]\displaystyle{ \mathbf{\mu}_i }[/math] are known. Denote

[math]\displaystyle{ \mathbf{S}_B = (\mathbf{\mu}_0-\mathbf{\mu}_1)(\mathbf{\mu}_0-\mathbf{\mu}_1)^{T} }[/math]

This matrix, called the between class variance matrix, is a rank 1 matrix, so an inverse does not exist. Altogether, we have two optimization problems we must solve simultaneously:

1) [math]\displaystyle{ \min_{\mathbf{w}} \mathbf{w} \mathbf{S_W} \mathbf{w}^{T} }[/math]

2) [math]\displaystyle{ \max_{\mathbf{w}} \mathbf{w} \mathbf{S_B} \mathbf{w}^{T} }[/math]

There are other metrics one can use to both minimize the data's variance and maximizes the distance between classes, and other goals we can try to accomplish (see metric learning, below...one day), but Fisher used this elegant method, hence his recognition in the name, and we will follow his method.

We can combine the two optimization problems into one after noting that the negative of max is min:

[math]\displaystyle{ \max_{\mathbf{w}} \mathbf{w} \mathbf{S_W} \mathbf{w}^{T} - \alpha \mathbf{w} \mathbf{S_B} \mathbf{w}^{T} }[/math]

The [math]\displaystyle{ \alpha }[/math] coefficient is a necessary scaling factor: if the scale of one of the terms is much larger than the other, the optimization problem will be dominated by the larger term. This means we have another unknown, [math]\displaystyle{ \alpha }[/math], to solve for. Instead, we can circumvent the scaling problem by looking at the ratio of the quantities, the original solution Fisher proposed:

[math]\displaystyle{ \max_{\mathbf{w}} \frac{\mathbf{w} \mathbf{S_B} \mathbf{w}^{T}}{\mathbf{w} \mathbf{S_W} \mathbf{w}^{T}} }[/math]

This optimization problem can be shown<ref> http://www.socher.org/uploads/Main/optimizationTutorial01.pdf </ref> to be equivalent to the following optimization problem:

[math]\displaystyle{ \max_{\mathbf{w}} \mathbf{w} \mathbf{S_B} \mathbf{w}^{T} }[/math]

subject to:

[math]\displaystyle{ \mathbf{w} \mathbf{S_W} \mathbf{w}^{T} = 1 }[/math]

A heuristic understanding of this equivalence is that we have two degrees of freedom: direction and scalar. The scalar value is irrelevant to our discussion. Thus, we can set one of the values to be a constant. We can use Lagrange multipliers to solve this optimization problem:

[math]\displaystyle{ L( \mathbf{w}, \lambda) = \mathbf{w} \mathbf{S_B} \mathbf{w}^{T} - \lambda(\mathbf{w} \mathbf{S_W} \mathbf{w}^{T}-1) }[/math]

[math]\displaystyle{ \Rightarrow \frac{\partial L}{\partial \mathbf{w}} = 2 \mathbf{S}_B \mathbf{w} - 2\lambda \mathbf{S}_W\mathbf{w} }[/math]

Setting the partial derivative to 0 gives us a generalized eigenvalue problem:

[math]\displaystyle{ \mathbf{S}_B \mathbf{w} = \lambda \mathbf{S}_W \mathbf{w} }[/math]

[math]\displaystyle{ \Rightarrow \mathbf{S}_W^{-1} \mathbf{S}_B \mathbf{w} = \lambda \mathbf{w} }[/math]

This is a generalized eigenvalue problem and [math]\displaystyle{ \ W }[/math] can be computed as the eigenvector corresponds to the largest eigenvalue of

[math]\displaystyle{ \mathbf{S}_W^{-1} \mathbf{S}_B }[/math]

It is very likely that [math]\displaystyle{ \mathbf{S}_W }[/math] has an inverse. If not, the pseudo-inverse<ref> http://en.wikipedia.org/wiki/Generalized_inverse </ref><ref> http://www.mathworks.com/help/techdoc/ref/pinv.html </ref> can be used. In Matlab the pseudo-inverse function is named pinv. Thus, we should choose [math]\displaystyle{ \mathbf{w} }[/math] to equal the eigenvector of the largest eigenvalue as our projection vector.

In fact we can simplify the above expression further in the of two classes. Recall the definition of [math]\displaystyle{ \mathbf{S}_B = (\mathbf{\mu}_0-\mathbf{\mu}_1)(\mathbf{\mu}_0-\mathbf{\mu}_1)^{T} }[/math]. Substituting this into our expression:

[math]\displaystyle{ \mathbf{S}_W^{-1}(\mathbf{\mu}_0-\mathbf{\mu}_1)(\mathbf{\mu}_0-\mathbf{\mu}_1)^{T} \mathbf{w} = \lambda \mathbf{w} }[/math]

[math]\displaystyle{ (\mathbf{S}_W^{-1}(\mathbf{\mu}_0-\mathbf{\mu}_1) ) ((\mathbf{\mu}_0-\mathbf{\mu}_1)^{T} \mathbf{w}) = \lambda \mathbf{w} }[/math]

This second term is a scalar value, let's denote it [math]\displaystyle{ \beta }[/math]. Then

[math]\displaystyle{ \mathbf{S}_W^{-1}(\mathbf{\mu}_0-\mathbf{\mu}_1) = \frac{\lambda}{\beta} \mathbf{w} }[/math]

[math]\displaystyle{ \Rightarrow \, \mathbf{S}_W^{-1}(\mathbf{\mu}_0-\mathbf{\mu}_1) \propto \mathbf{w} }[/math]

All we are interested in the direction of [math]\displaystyle{ \mathbf{w} }[/math], so to compute this is sufficient to finding our projection vector. Though this will not work in higher dimensions, as [math]\displaystyle{ \mathbf{w} }[/math] would be a matrix and not a vector in higher dimensions.

Extensions to Multiclass Case

If we have [math]\displaystyle{ \ k }[/math] classes, we need [math]\displaystyle{ \ k-1 }[/math] directions i.e. we need to project [math]\displaystyle{ \ k }[/math] 'points' onto a [math]\displaystyle{ \ k-1 }[/math] dimensional hyperplane. What does this change in our above derivation? The most significant difference is that our projection vector,[math]\displaystyle{ \mathbf{w} }[/math], is no longer a vector but instead is a matrix [math]\displaystyle{ \mathbf{W} }[/math]. We transform the data as:

[math]\displaystyle{ \mathbf{x}' :\rightarrow \mathbf{W}^{T} \mathbf{x} }[/math]

so our new mean and covariances for class k are:

[math]\displaystyle{ \mathbf{\mu_k}' :\rightarrow \mathbf{W}^{T} \mathbf{\mu_k} }[/math]

[math]\displaystyle{ \mathbf{\Sigma_k}' :\rightarrow \mathbf{W}^{T} \mathbf{\Sigma_k} \mathbf{W} }[/math]

What are our new optimization sub-problems? As before, we wish to minimize the within class variance. This can be formulated as:

[math]\displaystyle{ \min_{\mathbf{W}} \mathbf{W}^{T} \mathbf{\Sigma_1} \mathbf{W} + \dots + \mathbf{W}^{T} \mathbf{\Sigma_k} \mathbf{W} }[/math]

Again, denoting [math]\displaystyle{ \mathbf{S}_W = \mathbf{\Sigma_1} + \dots + \mathbf{\Sigma_k} }[/math], we can simplify above expression:

[math]\displaystyle{ \min_{\mathbf{W}} \mathbf{W}^{T} \mathbf{S}_W \mathbf{W} }[/math]

Similarly, the second optimization problem is:

[math]\displaystyle{ \max_{\mathbf{W}} \mathbf{W}^{T} \mathbf{S}_B \mathbf{W} }[/math]

What is [math]\displaystyle{ \mathbf{S}_B }[/math] in this case? It can be shown that [math]\displaystyle{ \mathbf{S}_T = \mathbf{S}_B + \mathbf{S}_W }[/math] where [math]\displaystyle{ \mathbf{S}_T }[/math] is the covariance matrix of all the data. From this we can compute [math]\displaystyle{ \mathbf{S}_B }[/math].

Next, if we express [math]\displaystyle{ \mathbf{W} = ( \mathbf{w}_1 , \mathbf{w}_2 , \dots ,\mathbf{w}_k ) }[/math] observe that, for [math]\displaystyle{ \mathbf{A} = \mathbf{S}_B , \mathbf{S}_W }[/math]:

[math]\displaystyle{ Tr(\mathbf{W}^{T} \mathbf{A} \mathbf{W}) = \mathbf{w}_1^{T} \mathbf{A} \mathbf{w}_1^{T} + \dots + \mathbf{w}_k \mathbf{A} \mathbf{w}_k }[/math]

where [math]\displaystyle{ \ Tr() }[/math] is the trace of a matrix. Thus, following the same steps as in the two-class case, we have the new optimization problem:

[math]\displaystyle{ \max_{\mathbf{W}} \frac{ Tr(\mathbf{W}^{T} \mathbf{S}_B \mathbf{W}) }{Tr(\mathbf{W}^{T} \mathbf{S}_W \mathbf{W})} }[/math]

subject to:

[math]\displaystyle{ Tr( \mathbf{W} \mathbf{S_W} \mathbf{W}^{T}) = \mathbf{I} }[/math]

Again, in order to solve the above optimization problem, we can use the Lagrange multiplier <ref> http://en.wikipedia.org/wiki/Lagrange_multiplier </ref>:

[math]\displaystyle{ \begin{align}L(\mathbf{W},\Lambda) = Tr[\mathbf{W}^{T}\mathbf{S}_{B}\mathbf{W}] - \Lambda\left\{ Tr[\mathbf{W}^{T}\mathbf{S}_{W}\mathbf{W}] - I \right\}\end{align} }[/math].

where [math]\displaystyle{ \ \Lambda }[/math] is a d by d diagonal matrix.

Then, we differentiating with respect to [math]\displaystyle{ \mathbf{W} }[/math]:

[math]\displaystyle{ \begin{align}\frac{\partial L}{\partial \mathbf{W}} = (\mathbf{S}_{B} + \mathbf{S}_{B}^{T})\mathbf{W} - \Lambda (\mathbf{S}_{W} + \mathbf{S}_{W}^{T})\mathbf{W}\end{align} = 0 }[/math].

Thus:

[math]\displaystyle{ \begin{align}\mathbf{S}_{B}\mathbf{W} = \Lambda\mathbf{S}_{W}\mathbf{W}\end{align} }[/math]

[math]\displaystyle{ \begin{align}\mathbf{S}_{W}^{-1}\mathbf{S}_{B}\mathbf{W} = \Lambda\mathbf{W}\end{align} }[/math]

where, [math]\displaystyle{ \mathbf{\Lambda} =\begin{pmatrix}\lambda_{1} & & 0\\&\ddots&\\0 & &\lambda_{d}\end{pmatrix} }[/math]

The above equation is of the form of an eigenvalue problem. Thus, for the solution the k-1 eigenvectors corresponding to the k-1 largest eigenvalues should be chosen as the projection matrix, [math]\displaystyle{ \mathbf{W} }[/math]. In fact, there should only by k-1 eigenvectors corresponding to k-1 non-zero eigenvalues using the above equation.

Summary

FDA has two optimization problems:

1) [math]\displaystyle{ \min_{\mathbf{w}} \mathbf{w} \mathbf{S_W} \mathbf{w}^{T} }[/math]

2) [math]\displaystyle{ \max_{\mathbf{w}} \mathbf{w} \mathbf{S_B} \mathbf{w}^{T} }[/math]

where [math]\displaystyle{ \ S_W = \Sigma_0 + \Sigma_1 }[/math] is called the within class variance and [math]\displaystyle{ \ S_B = (\mu_0 - \mu_1)(\mu_0 - \mu_1)^T }[/math] is called the between class variance.

The two optimization problems are combined as follows:

[math]\displaystyle{ \max_{\mathbf{w}} \frac{\mathbf{w} \mathbf{S_B} \mathbf{w}^{T}}{\mathbf{w} \mathbf{S_W} \mathbf{w}^{T}} }[/math]

By adding a constraint as shown:

[math]\displaystyle{ \max_{\mathbf{w}} \mathbf{w} \mathbf{S_B} \mathbf{w}^{T} }[/math]

subject to:

[math]\displaystyle{ \mathbf{w} \mathbf{S_W} \mathbf{w}^{T} = 1 }[/math]

Lagrange multipliers can be used and essentially the problem becomes an eigenvalue problem:

[math]\displaystyle{ \begin{align}\mathbf{S}_{W}^{-1}\mathbf{S}_{B}\mathbf{w} = \lambda\mathbf{w}\end{align} }[/math]

And [math]\displaystyle{ \ w }[/math] can be computed as the k-1 eigenvectors corresponding to the largest k-1 eigenvalues of [math]\displaystyle{ \mathbf{S}_W^{-1} \mathbf{S}_B }[/math].

Variations

Some adaptations and extensions exist for the FDA technique (Source: <ref>R. Gutierrez-Osuna, "Linear Discriminant Analysis" class notes for Intro to Pattern Analysis, Texas A&M University. Available: [2]</ref>):

1) Non-Parametric LDA (NPLDA) by Fukunaga

This method does not assume that the Gaussian distribution is unimodal and it is actually possible to extract more than k-1 features (where k is the number of classes).

2) Orthonormal LDA (OLDA) by Okada and Tomita

This method finds projections that are orthonormal in addition to maximizing the FDA objective function. This method can also extract more than k-1 features (where k is the number of classes).

3) Generalized LDA (GLDA) by Lowe

This method incorporates additional cost functions into the FDA objective function. This causes classes with a higher cost to be placed further apart in the lower dimensional representation.

Linear and Logistic Regression (Lecture: Oct. 06, 2011)

Linear Regression

In regression, [math]\displaystyle{ \ y }[/math] is a continuous variable. In classification, [math]\displaystyle{ \ y }[/math] is a discrete variable. Regression problems are easier to formulate into functions (since [math]\displaystyle{ \ y }[/math] is continuous) and it is possible to solve classification problems by treating them like regression problems. In order to do so, the requirement in classification that [math]\displaystyle{ \ y }[/math] is discrete must first be relaxed. Once [math]\displaystyle{ \ y }[/math] has been found using regression techniques, it is possible to determine the discrete class corresponding to the [math]\displaystyle{ \ y }[/math] that has been found to solve the original classification problem. The discrete class is obtained by defining a threshold where [math]\displaystyle{ \ y }[/math] values below the threshold belong to one class and [math]\displaystyle{ \ y }[/math] values above the threshold belong to another class.

More formally: a more direct approach to classification is to estimate the regression function [math]\displaystyle{ \ r(\mathbf{x}) = E[Y | X] }[/math] without bothering to estimate [math]\displaystyle{ \ f_k(\mathbf{x}) }[/math].

In two-class problems, if [math]\displaystyle{ \ Y = \{0,1\} }[/math], then [math]\displaystyle{ \, h^*(\mathbf{x})= \left\{\begin{matrix} 1 &\text{,if } \hat r(\mathbf{x})\gt \frac{1}{2} \\ 0 &\mathrm{,otherwise.} \end{matrix}\right. }[/math]

Basically, we can use a linear function [math]\displaystyle{ \ f(x, \beta) = \mathbf{\beta\,}^T \mathbf{x_{i}} + \mathbf{\beta\,_0} }[/math] and use the least squares approach to fit the function to the given data. This is done by minimizing the following expression:

[math]\displaystyle{ \min_{\mathbf{\beta}} \sum_{i=1}^n (y_i - \mathbf{\beta}^T \mathbf{x_{i}} - \mathbf{\beta_0})^2 }[/math]

where

[math]\displaystyle{ \tilde{\mathbf{\beta}} = \left( \begin{array}{c}\mathbf{\beta_{1}} \\ \\ \dots \\ \\ \mathbf{\beta}_{d} \\ \\ \mathbf{\beta}_{0} \end{array} \right) }[/math].

For convenience, [math]\displaystyle{ \mathbf{\beta} }[/math] and [math]\displaystyle{ \mathbf{\beta}_0 }[/math] have been combined into a d+1 dimensional vector. And an extra term 1 is appended to to [math]\displaystyle{ \ x }[/math]. Thus, the function to be minimized can now be expressed as:

[math]\displaystyle{ \ min_{\tilde{\beta}} \sum_{i=1}^{n} (y_i - \tilde{\beta} \tilde{x_i} )^2 }[/math]

[math]\displaystyle{ \ = min_{\tilde{\beta}} | y - X \tilde{\beta}^T |^2 }[/math]

where [math]\displaystyle{ \ y }[/math] and [math]\displaystyle{ \tilde{\beta} }[/math] are vectors and [math]\displaystyle{ \ X }[/math] is a matrix.

The solution for [math]\displaystyle{ \ \tilde{\beta} }[/math] is

[math]\displaystyle{ \ {\tilde{\beta}} = (XX^T)^{-1}Xy }[/math]

Using regression to solve classification problems is not mathematically correct, if we want to be true to classification. However, this method works well in practice, if the problem is not complicated. When we have only two classes (encoded as [math]\displaystyle{ \ \frac{-n}{n_1} }[/math] and [math]\displaystyle{ \ \frac{n}{n_2}) }[/math], this method is identical to LDA.

Matlab Example

The following is the code and the explanation for each step.

Again, we use the data in 2_3.m.

 >>load 2_3;
 >>[U, sample] = princomp(X');
 >>sample = sample(:,1:2);

We carry out Principal Component Analysis (PCA) to reduce the dimensionality from 64 to 2.

 >>y = zeros(400,1);
 >>y(201:400) = 1;

We let y represent the set of labels coded as 0 and 1.

 >>x=[sample;ones(1,400)];

Construct x by adding a row of vector 1 to data.

 >>b=inv(x*x')*x*y;

Calculate b, which represents [math]\displaystyle{ \beta }[/math] in the linear regression model.

 >>x1=x';
 >>for i=1:400
   if x1(i,:)*b>0.5
        plot(x1(i,1),x1(i,2),'.')
        hold on
   elseif x1(i,:)*b < 0.5
       plot(x1(i,1),x1(i,2),'r.')
   end 
 end

Plot the fitted y values.

File:linearregression.png

the figure shows that the classification of the data points in 2_3.m by the linear regression model

Logistic Regression

Logistic regression is a more advanced method for classification, and is more commonly used.

We can define a function
[math]\displaystyle{ f_1(x)= P(Y=1| X=x) = (\frac{e^{\mathbf{\beta\,}^T \mathbf{x}}}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}}) }[/math]

[math]\displaystyle{ P(Y=1 | X=x) }[/math]

This is a valid density function. It looks similar to a step function, but we have relaxed it so that we have a smooth curve, and can therefore take the derivative.

The range of this function is (0,1) since
[math]\displaystyle{ \lim_{x \to -\infty}f_1(\mathbf{x}) = 0 }[/math] and [math]\displaystyle{ \lim_{x \to \infty}f_1(\mathbf{x}) = 1 }[/math].

As shown on this graph:
http://www.wolframalpha.com/input/?i=Plot[E^x/%281+%2B+E^x%29,+{x,+-10,+10}]%29

Then we compute the complement of f1(x), and get

[math]\displaystyle{ f_2(x)= P(Y=0| X=x) = 1-f_1(x) = (\frac{1}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}}) }[/math], denoted f2.

[math]\displaystyle{ P(Y=0 | X=x) }[/math]

Function f2 is commonlly called Logistic function, and it behaves like
[math]\displaystyle{ \lim_{x \to -\infty}f_2(\mathbf{x}) = 1 }[/math] and
[math]\displaystyle{ \lim_{x \to \infty}f_2(\mathbf{x}) = 0 }[/math].

As shown on this graph:
http://www.wolframalpha.com/input/?i=Plot[1/%281+%2B+E^x%29,+{x,+-10,+10}]%29

From here, we can form the conditional density function. To do this, we must combine
[math]\displaystyle{ f_1 }[/math] and [math]\displaystyle{ f_2 }[/math]
such that
[math]\displaystyle{ f_1=1 }[/math] and[math]\displaystyle{ f_2=0 }[/math] if y=1 ( which means it’s in class 1),
and [math]\displaystyle{ f_1=0 }[/math] and [math]\displaystyle{ f_2=1 }[/math] if y=2 (which means it’s in class 2).

Eventually, we have our conditional density function formula
[math]\displaystyle{ f(y|\mathbf{x})= (\frac{e^{\mathbf{\beta\,}^T \mathbf{x}}}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}})^{y} (\frac{1}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}})^{1-y} }[/math]

To way to use this formula is, with given the training data (x(i), y(i)),to fit the data with [math]\displaystyle{ f(Y : X) }[/math].

In general, we can think of the problem as having a box with some knobs. Inside the box is our objective function which gives the form to classify our input (xi) to our output (yi). The knobs in the box are functioning like the parameters of the objective function. Our job is to find the proper parameters that can minimize the error between our output and the true value. So we have turned our machine learning problem intoan optimization problem.

Since we need to find the parameters that maximize the chance of having our observed data coming from the distribution of f(x|parameter), we need to introduce Maximum Likelihood Estimation.

Maximum Likelihood Estimation

Given iid data points [math]\displaystyle{ ({\mathbf{x}_i})_{i=1}^n }[/math] and density function [math]\displaystyle{ f(\mathbf{x}|\mathbf{\theta}) }[/math], where the form of f is known but the parameters [math]\displaystyle{ \theta }[/math] are our unknown. The maximum likelihood estimation of [math]\displaystyle{ \theta\,_{ML} }[/math] is a set of parameters that maximize the probability of observing [math]\displaystyle{ ({\mathbf{x}_i})_{i=1}^n }[/math] given [math]\displaystyle{ \theta\,_{ML} }[/math].

[math]\displaystyle{ \theta_\mathrm{ML} = \underset{\theta}{\operatorname{arg\,max}}\ f(\mathbf{x}|\theta) }[/math].

There was some discussion in class regarding the notation. In literature, Bayesians use [math]\displaystyle{ f(\mathbf{x}|\mu) }[/math] while Frequentists use [math]\displaystyle{ f(\mathbf{x};\mu) }[/math]. In practice, these two are equivalent.

Our goal is to find theta to maximize [math]\displaystyle{ \mathcal{L}(\theta\,) = f({\mathbf{x}_i})_{i=1}^n|\;\theta) = \prod_{i=1}^n f(\mathbf{x_i}|\theta) }[/math]. (The second equality holds because data points are iid.)

In many cases, it’s more convenient to work with the natural logarithm of the likelihood. (Recall that the logarithm preserves minumums and maximums.) [math]\displaystyle{ \ell(\theta|x\mathbf)=\ln\mathcal{L}(\theta\,) }[/math]

[math]\displaystyle{ \ell(\theta\,)=\sum_{i=1}^n \ln f(\mathbf{x_i}|\theta) }[/math]

Applying Maximum Likelihood Estimation to [math]\displaystyle{ f(y|\mathbf{x})= (\frac{e^{\mathbf{\beta\,}^T \mathbf{x}}}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}})^{y} (\frac{1}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}})^{1-y} }[/math], gives

[math]\displaystyle{ \mathcal{L}(\mathbf{\beta\,})=\prod_{i=1}^n (\frac{e^{\mathbf{\beta\,}^T \mathbf{x}}}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}})^{y_i} (\frac{1}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}})^{1-y_i} }[/math]

[math]\displaystyle{ \begin{align} {\ell(\mathbf{\beta\,})} & {} = \sum_{i=1}^n \left(y_i ({\mathbf{\beta\,}^T \mathbf{x_i}} - \ln({1+e^{\mathbf{\beta\,}^T \mathbf{x_i}}})) + (1-y_i) (\ln{1} - \ln({1+e^{\mathbf{\beta\,}^T \mathbf{x_i}}}))\right) \\[10pt]&{} = \sum_{i=1}^n \left(y_i ({\mathbf{\beta\,}^T \mathbf{x_i}} - \ln({1+e^{\mathbf{\beta\,}^T \mathbf{x_i}}})) - (1-y_i) \ln({1+e^{\mathbf{\beta\,}^T \mathbf{x_i}}})\right) \\[10pt] &{} = \sum_{i=1}^n \left(y_i ({\mathbf{\beta\,}^T \mathbf{x_i}} - \ln({1+e^{\mathbf{\beta\,}^T \mathbf{x_i}}})) - \ln({1+e^{\mathbf{\beta\,}^T \mathbf{x_i}}}) + y_i \ln({1+e^{\mathbf{\beta\,}^T \mathbf{x_i}}})\right) \\[10pt] &{} = \sum_{i=1}^n \left(y_i {\mathbf{\beta\,}^T \mathbf{x_i}} - \ln({1+e^{\mathbf{\beta\,}^T \mathbf{x_i}}})\right) \end{align} }[/math]

[math]\displaystyle{ \begin{align} {\frac{\partial \ell}{\partial \mathbf{\beta\,}}}&{} = \sum_{i=1}^n \left(y_i \mathbf{x_i} - \frac{e^{\mathbf{\beta\,}^T \mathbf{x}}}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}} \mathbf{x_i} \right) \\[8pt] & {}= \sum_{i=1}^n \left(y_i \mathbf{x_i} - P(\mathbf{x_i} | \mathbf{\beta\,}) \mathbf{x_i}\right) \end{align} }[/math]

[math]\displaystyle{ \frac{\partial \ell}{\partial \mathbf{\beta\,}} }[/math] can be numerically solved by Newton’s Method.

Newton's Method

Newton's Method (or Newton-Ralphson method) is a numerical method to find better approximations to the solutions of real-valued function. The function usually does not have an analytical form.

The goal is to find [math]\displaystyle{ \mathbf{x} }[/math] such that [math]\displaystyle{ f(\mathbf{x}) = 0 }[/math]. The recursion can be implemented by [math]\displaystyle{ \mathbf{x_1} = \mathbf{x_0} - \frac{f(\mathbf{x_0})}{f'(\mathbf{x_0})}.\,\! }[/math].

It takes an initial guess [math]\displaystyle{ \mathbf{x_0} }[/math] and the direction "[math]\displaystyle{ \mathbf{f(x_{0}) / f' (x_{0})} }[/math]" that moves toward a better approximation. It then finds a newer and better [math]\displaystyle{ \mathbf{x_1} }[/math]. Taking this [math]\displaystyle{ \mathbf{x_1} }[/math] as [math]\displaystyle{ \mathbf{x_0} }[/math] in the second run, it finds a newer and better [math]\displaystyle{ \mathbf{x_1} }[/math] than the previous [math]\displaystyle{ \mathbf{x_1} }[/math]. Repeating the same process, the [math]\displaystyle{ \mathbf{x_1} }[/math] will be sufficiently accurate to the actual solutions.

Advantages of Logistic Regression

Logistic regression has several advantages over discriminant analysis:

it is more robust: the independent variables don't have to be normally distributed, or have equal variance in each group
It does not assume a linear relationship between the IV and DV
It may handle nonlinear effects
You can add explicit interaction and power terms
The DV need not be normally distributed.
There is no homogeneity of variance assumption.
Normally distributed error terms are not assumed.
It does not require that the independents be interval.
It does not require that the independents be unbounded.

Newton-Raphson Method (Lecture: Oct 11, 2011)

Previously we had derivated the log likelihood function for the logistic function.

[math]\displaystyle{ \begin{align} L(\beta\,) = \prod_{i=1}^n \left( (\frac{e^{\mathbf{\beta\,}^T \mathbf{x}}}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}})^{y_i}(\frac{1}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}})^{1-y_i} \right) \end{align} }[/math]

After taking log, we can have

[math]\displaystyle{ \begin{align} \ell(\beta\,) = \sum_{i=1}^n \left( y_i \log{\frac{e^{\mathbf{\beta\,}^T \mathbf{x}}}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}}} + (1 - y_i) \log{\frac{1}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}}} \right) \end{align} }[/math]

which implies that

[math]\displaystyle{ \begin{align} {\ell(\mathbf{\beta\,})} & {} = \sum_{i=1}^n \left(y_i {\mathbf{\beta\,}^T \mathbf{x_i}} - \ln({1+e^{\mathbf{\beta\,}^T \mathbf{x_i}}})\right) \end{align} }[/math]

Our goal is to find the [math]\displaystyle{ \beta\, }[/math] that maximizes [math]\displaystyle{ {\ell(\mathbf{\beta\,})} }[/math]. We use calculus to do this ie solve [math]\displaystyle{ {\frac{\partial \ell}{\partial \mathbf{\beta\,}}}=0 }[/math]. To do this we use the famous numerical method of Newton-Raphson. This is an iterative method were we calculate the first & second derivative at each iteration.

The first derivative is typically called the score vector.

[math]\displaystyle{ \begin{align} S(\beta\,) {}= {\frac{\partial \ell}{ \partial \mathbf{\beta\,}}}&{} = \sum_{i=1}^n \left(y_i \mathbf{x_i} - \frac{e^{\mathbf{\beta\,}^T \mathbf{x}}}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}} \mathbf{x_i} \right) \\[8pt] \end{align} }[/math]

The negative of the second derivative is typically called the information matrix.

[math]\displaystyle{ \begin{align} I(\beta\,) {}= -{\frac{\partial \ell}{\partial \mathbf {\beta\,} \partial \mathbf{\beta\,}^T}}&{} = \sum_{i=1}^n \left(\mathbf{x_i}\mathbf{x_i}^T (\frac{e^{\mathbf{\beta\,}^T \mathbf{x}}}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}})(\frac{1}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}}) \right) \\[8pt] \end{align} }[/math]

We then use the following update formula to calcalute continually better estimates of the optimal [math]\displaystyle{ \beta\, }[/math]. It is not typically important what you use as your initial estimate [math]\displaystyle{ \beta\,^{(1)} }[/math] is.

[math]\displaystyle{ \beta\,^{(r+1)} {}= \beta\,^{(r)} + I^{-1}(\beta\,^{(r)} )S(\beta\,^{(r)} ) }[/math]

Matrix Notation

let [math]\displaystyle{ \mathbf{y} }[/math] be a (n x 1) vector of all class labels. This is called the response in other contexts.

let [math]\displaystyle{ \mathbb{X} }[/math] be a (n x (d+1)) matrix of all your features. Each row represents a data point. Each column represents a feature/covariate.

let [math]\displaystyle{ \mathbf{p}^{(r)} }[/math] be a (n x 1) vector with values [math]\displaystyle{ P(\mathbf{x_i} |\beta\,^{(r)} ) }[/math]

let [math]\displaystyle{ \mathbb{W}^{(r)} }[/math] be a (n x n) diagonal matrix with [math]\displaystyle{ \mathbb{W}_{ii}^{(r)} {}= P(\mathbf{x_i} |\beta\,^{(r)} )(1 - P(\mathbf{x_i} |\beta\,^{(r)} )) }[/math]

we can rewrite our score vector, information matrix & update equation in terms of this new matrix notation, so the first derivitive is

[math]\displaystyle{ \begin{align} S(\beta\,^{(r)}) {}= {\frac{\partial \ell}{ \partial \mathbf{\beta\,}}}&{} = \mathbb{X}^T(\mathbf{y} - \mathbf{p}^{(r)})\end{align} }[/math]

and the second derivitive is

[math]\displaystyle{ \begin{align} I(\beta\,^{(r)}) {}= -{\frac{\partial \ell}{\partial \mathbf {\beta\,} \partial \mathbf{\beta\,}^T}}&{} = \mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X} \end{align} }[/math]

Therfore, we can fit a regression problem as follows

[math]\displaystyle{ \beta\,^{(r+1)} {}= \beta\,^{(r)} + I^{-1}(\beta\,^{(r)} )S(\beta\,^{(r)} ) {}= \beta\,^{(r)} + (\mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X})^{-1}\mathbb{X}^T(\mathbf{y} - \mathbf{p}^{(r)}) }[/math]

Iteratively Re-weighted Least Squares

If we reorganize this updating formula we can see it is really a iteratively solving a least squares problem each time with a new weighting.

[math]\displaystyle{ \beta\,^{(r+1)} {}= \beta\,^{(r)} + (\mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X})^{-1}(\mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X}\beta\,^{(r)} + \mathbb{X}^T(\mathbf{y} - \mathbf{p}^{(r)})) }[/math]

[math]\displaystyle{ \beta\,^{(r+1)} {}= \beta\,^{(r)} + (\mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X})^{-1}\mathbb{X}^T\mathbb{W}^{(r)}\mathbf(z)^{(r)} }[/math]

where [math]\displaystyle{ \mathbf{z}^{(r)} = \mathbb{X}\beta\,^{(r)} + (\mathbb{W}^{(r)})^{-1}(\mathbf{y}-\mathbf{p}^{(r)}) }[/math]

Fisher Scoring Method

Fisher Scoring is a method very similiar to Newton-Raphson. It uses the expected Information Matrix as opposed to the observed information matrix. This distinction simplifies the problem and in perticular the computational complexity. To learn more about this method & logistic regression in general you can take Stat431/831 at the University of Waterloo.

Multi-class Logistic Regression

In a multi-class logistic regression we have K classes. For 2 classes k and l

[math]\displaystyle{ \frac{P(Y=l|X=x)}{P(Y=k|X=x)} = e^{\beta_l^T x} }[/math]

We call [math]\displaystyle{ log(\frac{P(Y=l|X=x)}{P(Y=k|X=x)}) = \beta_l^T x }[/math] as the logit transformation. The decision boundary between the 2 classes is the set of points where the logit transformation is 0.

For each class from 1 to K-1 we then have:

[math]\displaystyle{ log(\frac{P(Y=1|X=x)}{P(Y=K|X=x)}) = e^{\beta_1^T x} }[/math]

[math]\displaystyle{ log(\frac{P(Y=2|X=x)}{P(Y=K|X=x)}) = e^{\beta_2^T x} }[/math]

[math]\displaystyle{ log(\frac{P(Y=K-1|X=x)}{P(Y=K|X=x)}) = e^{\beta_{K-1}^T x} }[/math]

Note that choosing Y=K is arbitrary and any other choice is equally valid.

Based on the above the posterior probabilities are given by: [math]\displaystyle{ P(Y=k|X=x) = \frac{e^{\beta_k^T x}}{1 + \sum_{i=1}^{K-1}{e^{\beta_i^T x}}} }[/math]

Comparison Between Logistic Regression And Linear Discriminant Analysis (LDA)

Logistic Regression Model and Linear Discriminant Analysis are widely used to analyze data which has categorical outcome variables. Both of the models are to build linear boundaries to classify different groups. Also, the categorical outcome variables (i.e. the dependent variables) must be mutually exclusive.

However, these two models differ in their basic idea. While Logistic Regression is more relaxed and flexible in its assumptions, Linear Discriminant Analysis has the requirement that its explanatory variables must be normally distributed, linearly related and have equal covariance matrix within each class. Therefore, it can be expected that linear Discriminant Analysis should be more appropriate if the normality assumptions and equal covariance assumption are fulfilled in its explanatory variables. But in all other situations Logistic Regression should be appropriate. Besides, the total number of estimates to compute between these models is different. If the explanatory variables have d dimensions, we need to estimate [math]\displaystyle{ d+1 }[/math] parameters in Logistic Regression and the number of parameters grows linearly w.r.t. dimension, while we need to estimate [math]\displaystyle{ 2d+\frac{d*(d+1)}{2}+2 }[/math] parameters in Linear Discriminant Analysis and the number of parameters grows quadratically w.r.t. dimension.

Perceptron (Lecture: Oct. 11, 2011)

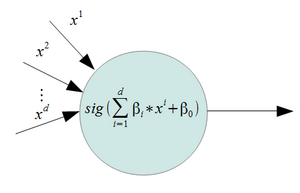
Simple perceptron where [math]\displaystyle{ \beta_0 }[/math] is defined as 1

The perceptron is the building block for neural networks. It was invented by Rosenblatt in 1957 at Cornell Labs, and first mentioned in the paper "The Perceptron - a perceiving and recognizing automaton". The perceptron is used on linearly separable data sets.

For a 2 class problem, and a set of inputs with d features, a perceptron will use a weighted sum and it will classify the information using the sign of the result. The figures on the right give an example of a perceptron. In these examples, [math]\displaystyle{ x^i }[/math] is the i-th feature of a sample and [math]\displaystyle{ \beta_i }[/math] is the i-th weight. [math]\displaystyle{ \beta_0 }[/math] is defined as the bias. The bias alters the position of the decision boundary between the 2 classes.

Perceptrons are generally trained using gradient descent. This type of learning can have 2 side effects:

If the data sets are well separated, the training of the perceptron can lead to multiple valid solutions,
If the data sets are not linearly separable, the learning algorithm will never finish.

Perceptrons are the simplest kind of a feedforward neural network. A perceptron is the building block for other neural networks such as:

Multi-layer perceptron
ADALINE
MADALINE

References

24. Balakrishnama, S., Ganapathiraju, A. LINEAR DISCRIMINANT ANALYSIS - A BRIEF TUTORIAL. http://www.isip.piconepress.com/publications/reports/isip_internal/1998/linear_discrim_analysis/lda_theory.pdf [[3]]

@@ Line 1,058: / Line 1,058: @@
 <math>\begin{align} I(\beta\,^{(r)}) {}= -{\frac{\partial \ell}{\partial \mathbf {\beta\,} \partial \mathbf{\beta\,}^T}}&{} = \mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X} \end{align}</math>
+Therfore, we can fit a regression problem as follows
 <math> \beta\,^{(r+1)} {}= \beta\,^{(r)} + I^{-1}(\beta\,^{(r)} )S(\beta\,^{(r)} ) {}= \beta\,^{(r)} + (\mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X})^{-1}\mathbb{X}^T(\mathbf{y} - \mathbf{p}^{(r)})</math>

stat841f11: Difference between revisions

Revision as of 01:41, 13 October 2011

Proposal for Final Project

Editor Sign Up

STAT 441/841 / CM 463/763 - Tuesday, 2011/09/20

Wiki Course Notes

Classification (Lecture: Sep. 20, 2011)

Definitions

Bayes Classifier

Three Main Approaches

Multi-Class Classification

Examples of Classification

LDA and QDA

LDA

LDA and QDA Continued (Lecture: Sep. 22, 2011)

Generalizing LDA and QDA

In practice

Computation

Case 1

Case 2

Principal Component Analysis (PCA) (Lecture: Sep. 27, 2011)

Lagrange Multiplier

Example :

Determining w :

Principal Component Analysis (PCA) Continued (Lecture: Sep. 29, 2011)

Alternative Derivation

Reconstruction Error

Minimize Reconstruction Error

Using SVD

Examples

Example 1

Example 2

Example 3

Example 4

Observations

Summary

Fisher Discriminant Analysis (FDA) (Lecture: Sep. 29, 2011)

Fisher Discriminant Analysis (FDA) Continued (Lecture: Oct. 04, 2011)

Goals of FDA

Extensions to Multiclass Case

Summary

Variations

Linear and Logistic Regression (Lecture: Oct. 06, 2011)

Linear Regression

Matlab Example

Logistic Regression

Maximum Likelihood Estimation

Newton's Method

Advantages of Logistic Regression

Newton-Raphson Method (Lecture: Oct 11, 2011)

Matrix Notation

Iteratively Re-weighted Least Squares

Fisher Scoring Method

Multi-class Logistic Regression

Comparison Between Logistic Regression And Linear Discriminant Analysis (LDA)

Perceptron (Lecture: Oct. 11, 2011)

References

Navigation menu

Search