stat946W25: Difference between revisions
| (291 intermediate revisions by 28 users not shown) | |||
| Line 11: | Line 11: | ||
= Topic 12: State Space Models = | = Topic 12: State Space Models = | ||
== Introduction == | |||
State Space Models (SSMs) are introduced as powerful alternatives to traditional sequence modeling approaches. These models demonstrate good performance in various modalities, including time series analysis, audio generation, and image processing and they can capture long-range dependencies more efficiently. | State Space Models (SSMs) are introduced as powerful alternatives to traditional sequence modeling approaches. These models demonstrate good performance in various modalities, including time series analysis, audio generation, and image processing and they can capture long-range dependencies more efficiently. | ||
SSMs initially struggled to match the performance of Transformers in language modeling tasks and there were some gaps between them. To address their challenges, recent advances in their architecture such as the Structured State Space Model (S4) have been introduced, which succeeded in long-range reasoning tasks and allowed for more efficient computation while preserving theoretical strengths. However, its implementation remains complex and computationally demanding. So further research led to simplified variants such as the Diagonal State Space Model (DSS), which achieves comparable performance with a more straightforward formulation. In parallel, hybrid approaches, like the H3 model, that integrate SSMs with attention mechanisms try to bridge the mentioned gaps. To understand better what I mean from the hybrid word, for example in H3 the authors try replacing almost all the attention layers in transformers with SSMs. More recently, models like Mamba have pushed the boundaries of SSMs by selectively parameterizing state matrices as functions of the input and allowing more flexible and adaptive information propagation. | SSMs initially struggled to match the performance of Transformers in language modeling tasks and there were some gaps between them. To address their challenges, recent advances in their architecture such as the Structured State Space Model (S4) have been introduced, which succeeded in long-range reasoning tasks and allowed for more efficient computation while preserving theoretical strengths. However, its implementation remains complex and computationally demanding. So further research led to simplified variants such as the Diagonal State Space Model (DSS), which achieves comparable performance with a more straightforward formulation. In parallel, hybrid approaches, like the H3 model, that integrate SSMs with attention mechanisms try to bridge the mentioned gaps. To understand better what I mean from the hybrid word, for example in H3 the authors try replacing almost all the attention layers in transformers with SSMs. More recently, models like Mamba have pushed the boundaries of SSMs by selectively parameterizing state matrices as functions of the input and allowing more flexible and adaptive information propagation. | ||
Research in SSMs continues to resolve the remaining challenges and the potential to substitute attention-based architectures with SSMs grows stronger. They will likely play a crucial role in the next generation of sequence modeling frameworks. | Research in SSMs continues to resolve the remaining challenges and the potential to substitute attention-based architectures with SSMs grows stronger. They will likely play a crucial role in the next generation of sequence modeling frameworks. | ||
=== Advantages of SSMs === | ===Advantages of SSMs=== | ||
* Efficient Long-Range Dependency Handling: Unlike Transformers, which require <math>O(n^2)</math> complexity for self-attention, SSMs can process sequences in <math>O(n \log n)</math> time complexity using efficient matrix-vector multiplications and the Fast Fourier Transform (FFT) or <math>O(n)</math> in case of Mamba architectures. | * Efficient Long-Range Dependency Handling: Unlike Transformers, which require <math>O(n^2)</math> complexity for self-attention, SSMs can process sequences in <math>O(n \log n)</math> time complexity using efficient matrix-vector multiplications and the Fast Fourier Transform (FFT) or <math>O(n)</math> in case of Mamba architectures. | ||
* Effective Long-Range Dependency Handling: By leveraging a state update mechanism (parametrized by λ) that preserves and accumulates signals over arbitrarily large time spans, SSMs effectively capture and retain information from distant points in a sequence, enabling robust long-range dependency handling. | * Effective Long-Range Dependency Handling: By leveraging a state update mechanism (parametrized by λ) that preserves and accumulates signals over arbitrarily large time spans, SSMs effectively capture and retain information from distant points in a sequence, enabling robust long-range dependency handling. | ||
| Line 26: | Line 26: | ||
* Interpretability and Diagnostic Insight: State Space Models offer a distinct interpretability advantage by representing system behavior through their state-transition dynamics explicitly. Unlike black-box models, the learned parameters in SSMs (matrices <math>\mathbf{A}</math>, <math>\mathbf{B}</math>, <math>\mathbf{C}</math>, and <math>\mathbf{D}</math>) can be analyzed to infer how inputs influence future states and outputs over time. This interpretability is especially valuable in fields where understanding model behavior is critical, such as financial risk modeling or biological systems analysis. | * Interpretability and Diagnostic Insight: State Space Models offer a distinct interpretability advantage by representing system behavior through their state-transition dynamics explicitly. Unlike black-box models, the learned parameters in SSMs (matrices <math>\mathbf{A}</math>, <math>\mathbf{B}</math>, <math>\mathbf{C}</math>, and <math>\mathbf{D}</math>) can be analyzed to infer how inputs influence future states and outputs over time. This interpretability is especially valuable in fields where understanding model behavior is critical, such as financial risk modeling or biological systems analysis. | ||
=== Core concepts === | ===Core concepts=== | ||
To understand State Space Models better, let's first take a look at the problem with Transformers and Recurrent Neural Networks (RNNs) and the relation between them and SSMs. | To understand State Space Models better, let's first take a look at the problem with Transformers and Recurrent Neural Networks (RNNs) and the relation between them and SSMs. | ||
In transformers during training, we create a matrix comparing each token with every token that came before and the weights in each cell of this matrix show how similar they are to each other. For calculating the weights, we don't do a sequential operation and each two tokens' relation can be computed in parallel. | In transformers during training, we create a matrix comparing each token with every token that came before and the weights in each cell of this matrix show how similar they are to each other. For calculating the weights, we don't do a sequential operation and each two tokens' relation can be computed in parallel. | ||
| Line 124: | Line 124: | ||
* In SSMs, we have D u(t) in the second equation which is commonly left out in control problems | * In SSMs, we have D u(t) in the second equation which is commonly left out in control problems | ||
===HiPPO Matrix=== | |||
Higher-Order-Polynomial Projection Operator (HiPPO) Matrix is a class of specially designed state transfer matrix '''A''' that enables the state space model to capture long-term dependencies in a continuous time setting. The most important matrix in this class is defined as: | Higher-Order-Polynomial Projection Operator (HiPPO) Matrix is a class of specially designed state transfer matrix '''A''' that enables the state space model to capture long-term dependencies in a continuous time setting. The most important matrix in this class is defined as: | ||
| Line 136: | Line 136: | ||
This matrix is designed to compress past history into a state that contains enough information to roughly reconstruct history. The interpretation of this matrix is that it produces a hidden state that remembers its history. | This matrix is designed to compress past history into a state that contains enough information to roughly reconstruct history. The interpretation of this matrix is that it produces a hidden state that remembers its history. | ||
===Recurrent Representation of SSM=== | |||
The input is a discrete sequence <math>(u_0,u_1,\ldots)</math> instead of continuous function. To discretize the continuous-time SSM, we follow prior work in using the bilinear method [https://arxiv.org/pdf/2406.02923], which converts the state matrix <math>A</math> into an approximation <math>\overline{A}</math> . The discrete SSM is: | The input is a discrete sequence <math>(u_0,u_1,\ldots)</math> instead of continuous function. To discretize the continuous-time SSM, we follow prior work in using the bilinear method [https://arxiv.org/pdf/2406.02923], which converts the state matrix <math>A</math> into an approximation <math>\overline{A}</math> . The discrete SSM is: | ||
| Line 231: | Line 231: | ||
These methods ensure that state-space models remain numerically robust and efficient when handling long sequences. | These methods ensure that state-space models remain numerically robust and efficient when handling long sequences. | ||
==Structured State Space (S4)== | |||
====Objective==== | ====Objective==== | ||
| Line 245: | Line 245: | ||
S4 has been particularly successful in domains that require continuous, structured data, such as time-series processing. However, its reliance on structured state matrices makes it less adaptable to unstructured data like natural language, where attention-based models still hold an advantage. | S4 has been particularly successful in domains that require continuous, structured data, such as time-series processing. However, its reliance on structured state matrices makes it less adaptable to unstructured data like natural language, where attention-based models still hold an advantage. | ||
Theorem 1: | |||
All HiPPO matrices in the paper[https://arxiv.org/abs/2008.07669] have a NPLR representation: | All HiPPO matrices in the paper[https://arxiv.org/abs/2008.07669] have a NPLR representation: | ||
| Line 256: | Line 256: | ||
The core idea of this form is to diagonalize the matrix A using the unitary-ary transformation V and use a low-rank decomposition to further compress the computation, which is important in efficient computation and storage optimization. | The core idea of this form is to diagonalize the matrix A using the unitary-ary transformation V and use a low-rank decomposition to further compress the computation, which is important in efficient computation and storage optimization. | ||
Theorem 2: | |||
Given any step size <math>∆</math>, computing one step of the [[ #Recurrent Representation of SSM|recurrence]] can be done in <math>O(N)</math> operations where <math>N</math> is the state size. | Given any step size <math>∆</math>, computing one step of the [[ #Recurrent Representation of SSM|recurrence]] can be done in <math>O(N)</math> operations where <math>N</math> is the state size. | ||
Theorem 3: | |||
Given any step size <math>∆</math>, computing the SSM convolution filter <math>\overline{\boldsymbol{K}}</math> can be reduced to 4 Cauchy multiplies, requiring only <math>{\widetilde{O}}(N+L)</math> operations and <math>O(N + L))</math> space. | Given any step size <math>∆</math>, computing the SSM convolution filter <math>\overline{\boldsymbol{K}}</math> can be reduced to 4 Cauchy multiplies, requiring only <math>{\widetilde{O}}(N+L)</math> operations and <math>O(N + L))</math> space. | ||
| Line 285: | Line 285: | ||
Some of the applications of S4 are language and audio processing (text generation, speech recognition, music and voice synthesis), forecasting (predicting stock prices in financial markets, modelling climate information), and scientific computing (simulations in physics, chemistry, astronomy). | Some of the applications of S4 are language and audio processing (text generation, speech recognition, music and voice synthesis), forecasting (predicting stock prices in financial markets, modelling climate information), and scientific computing (simulations in physics, chemistry, astronomy). | ||
==Diagonal State Space Model (DSS)== | |||
As mentioned above, S4 relies on the Diagonal Plus Low Rank (DPLR) structure of state matrix <math>A</math>, which improves efficiency but introduces significant complexity in both understanding and implementation. To simplify S4 while maintaining its performance, Diagonal State Space Model (DSS) is proposed. It simplifies the state matrix by replacing it with a purely diagonal form, reducing computational overhead and improving interpretability. It also maintains the ability to capture long-range dependencies. | As mentioned above, S4 relies on the Diagonal Plus Low Rank (DPLR) structure of state matrix <math>A</math>, which improves efficiency but introduces significant complexity in both understanding and implementation. To simplify S4 while maintaining its performance, Diagonal State Space Model (DSS) is proposed. It simplifies the state matrix by replacing it with a purely diagonal form, reducing computational overhead and improving interpretability. It also maintains the ability to capture long-range dependencies. | ||
| Line 314: | Line 314: | ||
The initialization of parameters can significantly influence the performance of DSS, as improper initialization may lead to slower convergence or suboptimal solutions. Additionally, DSS tends to be less effective at modeling information-dense data, such as text, where complex patterns and intricate relationships between words or phrases are crucial. In these cases, more sophisticated models may be helpful. However, DSS still provides a viable alternative in scenarios where simplicity and efficiency are prioritized over capturing deep contextual relationships. | The initialization of parameters can significantly influence the performance of DSS, as improper initialization may lead to slower convergence or suboptimal solutions. Additionally, DSS tends to be less effective at modeling information-dense data, such as text, where complex patterns and intricate relationships between words or phrases are crucial. In these cases, more sophisticated models may be helpful. However, DSS still provides a viable alternative in scenarios where simplicity and efficiency are prioritized over capturing deep contextual relationships. | ||
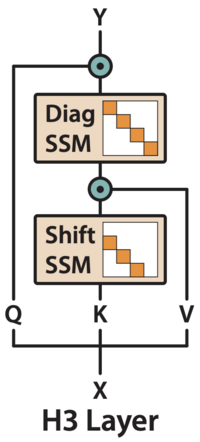
==Hungry Hungry Hippos (H3)== | |||
====SSMs vs Attention==== | ====SSMs vs Attention==== | ||
| Line 347: | Line 347: | ||
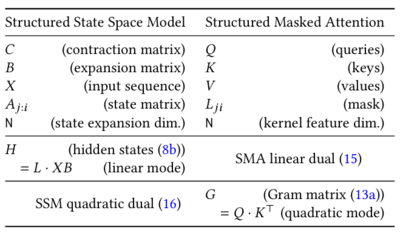
Initially, we convert our input sequence into query, key, and value matrices, as seen in regular attention. We then apply two SSM transformations to these input matrices to generate the final output. | Initially, we convert our input sequence into query, key, and value matrices, as seen in regular attention. We then apply two SSM transformations to these input matrices to generate the final output. | ||
==== Shift SSM ==== | |||
The first SSM is the shift SSM that you can think of as performing a local lookup across the sequence. In a sliding window fashion, the Shift SSM shifts the state vector by one position at each time to store the most recent inputs. The purpose is to detect specific events and remember the surrounding tokens, As an analogy, this is similar to how we remember the most recent words we have read. Our brain captures those last few words (tokens, for the model). For specific words or events in the book, we associate them with the surrounding context (words) around the specific entity. | The first SSM is the shift SSM that you can think of as performing a local lookup across the sequence. In a sliding window fashion, the Shift SSM shifts the state vector by one position at each time to store the most recent inputs. The purpose is to detect specific events and remember the surrounding tokens, As an analogy, this is similar to how we remember the most recent words we have read. Our brain captures those last few words (tokens, for the model). For specific words or events in the book, we associate them with the surrounding context (words) around the specific entity. | ||
| Line 362: | Line 362: | ||
If you draw it out, it would be a square matrix where the 1s appear directly below the main diagonal with all other entries 0. The action of this matrix on the hidden state <math>x_i</math> is to shift each coordinate down by one—thereby creating a “memory” of the previous states. If <math>\mathbf{B} = \textit{e}_1</math>, the first basis vector, then <math>x_i = [u_i, u_{i-1}, . . . , u_{i-m+1}]</math> contains the inputs from the previous m time steps. Both <math>\mathbf{B}</math> and <math>\mathbf{C}</math> are learnable matrices, but <math>\mathbf{B}</math> is usually fixed to <math>\textit{e}_1</math> for simplicity, in which case the output is a 1D convolution with kernel size m. | If you draw it out, it would be a square matrix where the 1s appear directly below the main diagonal with all other entries 0. The action of this matrix on the hidden state <math>x_i</math> is to shift each coordinate down by one—thereby creating a “memory” of the previous states. If <math>\mathbf{B} = \textit{e}_1</math>, the first basis vector, then <math>x_i = [u_i, u_{i-1}, . . . , u_{i-m+1}]</math> contains the inputs from the previous m time steps. Both <math>\mathbf{B}</math> and <math>\mathbf{C}</math> are learnable matrices, but <math>\mathbf{B}</math> is usually fixed to <math>\textit{e}_1</math> for simplicity, in which case the output is a 1D convolution with kernel size m. | ||
==== Diag SSM ==== | |||
The diagonal SSM serve as a kind of global memory that keeps track of important information over the entire sequence. A diagonal matrix is used to summarize the information we have seen. As an analogy, the diagonal SSM acts like the notes that we take when we are in class. It is super difficult to recall every single detail our professor states during a lecture. We will take notes during lecture to retain important concepts and information. We can then refer to these notes when we review. The diagonal SSM serves as our notes that the input sequence can refer to when recalling the summary of past information. | The diagonal SSM serve as a kind of global memory that keeps track of important information over the entire sequence. A diagonal matrix is used to summarize the information we have seen. As an analogy, the diagonal SSM acts like the notes that we take when we are in class. It is super difficult to recall every single detail our professor states during a lecture. We will take notes during lecture to retain important concepts and information. We can then refer to these notes when we review. The diagonal SSM serves as our notes that the input sequence can refer to when recalling the summary of past information. | ||
| Line 368: | Line 368: | ||
The diagonal SSM constrains A to be diagonal and initializes it from the diagonal version of HiPPO. This parameterization allows the model to remember state over the entire sequence. The shift SSM can detect when a particular event occurs, and the diagonal SSM can remember a token afterwards for the rest of the sequence. | The diagonal SSM constrains A to be diagonal and initializes it from the diagonal version of HiPPO. This parameterization allows the model to remember state over the entire sequence. The shift SSM can detect when a particular event occurs, and the diagonal SSM can remember a token afterwards for the rest of the sequence. | ||
==== Multiplicative Interaction ==== | |||
Multiplicative interactions, which is represented by the teal elementwise multiplication symbol, it offers H3 the ability to compare tokens across the sequence. Specifically, we can use this to compare and obtain information between the Shift SSM and Diagonal SSM. This is similar to the similarity score (dot product) seen in vanilla attention. | Multiplicative interactions, which is represented by the teal elementwise multiplication symbol, it offers H3 the ability to compare tokens across the sequence. Specifically, we can use this to compare and obtain information between the Shift SSM and Diagonal SSM. This is similar to the similarity score (dot product) seen in vanilla attention. | ||
| Line 374: | Line 374: | ||
Holistically, we can kind of view the outputs from Shift SSM as local or short-term information. The outputs from diagonal SSM servers as long-term information. The multiplicative interaction enables us to use both types of information to extract important information. This is critical for tasks like associative recall. For example, if the model needs to recall a value associated with a key, it can compare the current key with all previously seen keys using these interactions. | Holistically, we can kind of view the outputs from Shift SSM as local or short-term information. The outputs from diagonal SSM servers as long-term information. The multiplicative interaction enables us to use both types of information to extract important information. This is critical for tasks like associative recall. For example, if the model needs to recall a value associated with a key, it can compare the current key with all previously seen keys using these interactions. | ||
==Mamba== | |||
Mamba is a technique which builds on S4 models. It was introduced to increase efficiency for long sequences by leveraging selective attention mechanisms, allowing them to save memory and computational cost by not focusing on irrelevant information. It does so by combining the H3 block traditionally used in SSM models with a gated multilayered perceptron (MLP), as shown in the figure below. | Mamba is a technique which builds on S4 models. It was introduced to increase efficiency for long sequences by leveraging selective attention mechanisms, allowing them to save memory and computational cost by not focusing on irrelevant information. It does so by combining the H3 block traditionally used in SSM models with a gated multilayered perceptron (MLP), as shown in the figure below. | ||
| Line 455: | Line 455: | ||
In summary, Mamba's selective state space models marry the efficiency of classical SSMs with the flexibility of input-dependent gating. This combination allows the architecture to handle extremely long sequences—up to millions of tokens—while still capturing the nuanced patterns essential for tasks ranging from language modeling to audio generation. | In summary, Mamba's selective state space models marry the efficiency of classical SSMs with the flexibility of input-dependent gating. This combination allows the architecture to handle extremely long sequences—up to millions of tokens—while still capturing the nuanced patterns essential for tasks ranging from language modeling to audio generation. | ||
==Mamba-2== | |||
====Overview==== | ====Overview==== | ||
| Line 749: | Line 749: | ||
===Sparse Sinkhorn Attention=== | ===Sparse Sinkhorn Attention=== | ||
==== Evaluation Metrics for Sparse Attention ==== | |||
To comprehensively evaluate the performance of sparse attention mechanisms, several key metrics are considered: | |||
* '''Time Complexity''' | |||
** The number of operations required during inference. | |||
** Vanilla attention has quadratic complexity <math>O(n^2)</math>, while sparse variants aim for linear or sub-quadratic complexity, such as <math>O(n \cdot N_k)</math> where <math>N_k \ll n</math>. | |||
* '''Memory Complexity''' | |||
** Represents the total memory consumption needed for model parameters and intermediate activations. | |||
** Sparse attention reduces this by avoiding full pairwise attention computations. | |||
* '''Perplexity''' | |||
** A standard measure to evaluate the predictive performance of language models. | |||
** Defined as: | |||
<math> | |||
\text{Perplexity}(P) = \exp\left(- \frac{1}{N} \sum_{i=1}^N \log P(w_i | w_1, \dots, w_{i-1}) \right) | |||
</math> | |||
** Lower perplexity indicates better prediction capability. | |||
These metrics help compare the efficiency and effectiveness of sparse attention methods to the original dense attention in practical applications. | |||
==== Simplified Intuition ==== | ==== Simplified Intuition ==== | ||
| Line 844: | Line 867: | ||
By using sparse attention (i.e., not calculating the relationship between each pair of tokens), we hope that it allows us to scale to longer sequences while preserving the majority of the model's performance. | By using sparse attention (i.e., not calculating the relationship between each pair of tokens), we hope that it allows us to scale to longer sequences while preserving the majority of the model's performance. | ||
==== Theoretical Guarantee ==== | |||
The paper prove that sparse attention mechanisms, such as the one used in BigBird, can serve as universal approximators for dense attention Transformers. | |||
* '''Universal Approximation Theorem:''' | |||
** Given a class of functions <math> \mathcal{F}_{n,p} </math>, any function <math> f \in \mathcal{F}_{n,p} </math> can be approximated within <math> \epsilon > 0 </math> by a sparse attention Transformer <math> g \in \mathcal{T}_{n,p,r} </math> | |||
(i.e.,<math> d_{\mathcal{F}}(f, g) \leq \epsilon </math>) | |||
** This result holds as long as the underlying attention graph contains a star graph. | |||
* '''Supporting Lemmas:''' | |||
** Lemma 1: Scalar quantization of inputs using discrete maps. | |||
** Lemma 2: Contextual mapping via learned sparse attention layers. | |||
** Lemma 3 & 4: Construction of approximators with feedforward and attention layers using the sparse mechanism. | |||
These results justify that BigBird retains the expressive power of standard Transformers, while being more scalable. | |||
==== Intuition & Main Idea ==== | ==== Intuition & Main Idea ==== | ||
| Line 871: | Line 910: | ||
[[File:BigBird_Results.png|800px]] | [[File:BigBird_Results.png|800px]] | ||
QA tasks tests the model's ability to handle longer sequences and the ability to extract useful context. BigBird model outperforms RoBERTa and Longformer. At that time, there was also a burst in using deep learning for genomics data, most approaches consume DNA sequence fragments as inputs and BigBird achieved a 99.9 F1 score as well as 1.12 BPC (bits per character) on these tasks. | QA tasks tests the model's ability to handle longer sequences and the ability to extract useful context. | ||
Hotpot QA: For given question and documents, model is asked to generate correct answer and identify supporting facts | |||
* Ans (Answer): checks if the answer matches the ground truth. | |||
* Sup (Supporting Facts): checks if the model identifies sentences/evidences that support the answer. | |||
* Joint: A joint evaluation that is considered correct iff both Ans and Sup are correct. | |||
NaturalQ: For given question and documents, extract a short answer or a long answer | |||
* LA (Long Answer): evaluates model's ability to extract longer (paragraph-level) answer from passage | |||
* SA (Short Answer): evaluates model's ability to extract concise (short phrase like) answer from passage | |||
TriviaQA: For given question and documents, generate an answer | |||
* Full: Uses the complete set of questions with automatically paired evidence. | |||
* Verified: Uses the set that is manually paired to ensure correctness. | |||
For WikiHop: For a given question, supporting documents, the model is asked to choose a correct answer from a set of candidate answers | |||
* MCQ (Multiple Choice Question): evaluates model's ability to do MCQ. | |||
BigBird model outperforms RoBERTa and Longformer. At that time, there was also a burst in using deep learning for genomics data, most approaches consume DNA sequence fragments as inputs and BigBird achieved a 99.9 F1 score as well as 1.12 BPC (bits per character) on these tasks. | |||
====Limitations==== | ====Limitations==== | ||
| Line 879: | Line 936: | ||
===Attention with Linear Biases (ALiBi)=== | ===Attention with Linear Biases (ALiBi)=== | ||
==== ALiBi Mechanism ==== | |||
Currently, models struggle to extrapolate. Extrapolation is the ability to produce sequence lengths at inference time that are longer than the sequences they were trained on. For example, if a model is trained on a dataset where the longest sequence is 1024 tokens, then it will perform poorly when asked to generate a sequence of 2048 tokens. If we can solve this problem then, in theory, training can become much more efficient as we can train on shorter sequences without sacrificing performance. | Currently, models struggle to extrapolate. Extrapolation is the ability to produce sequence lengths at inference time that are longer than the sequences they were trained on. For example, if a model is trained on a dataset where the longest sequence is 1024 tokens, then it will perform poorly when asked to generate a sequence of 2048 tokens. If we can solve this problem then, in theory, training can become much more efficient as we can train on shorter sequences without sacrificing performance. | ||
| Line 901: | Line 961: | ||
The authors hypothesized that this could replace the positional encoding in transformers. For model architectures with multiple attention heads, the weighting of these biases can vary per head (defaulting to a geometric sequence of <math>\frac{1}{2^m}</math> where m is the number of heads.) | The authors hypothesized that this could replace the positional encoding in transformers. For model architectures with multiple attention heads, the weighting of these biases can vary per head (defaulting to a geometric sequence of <math>\frac{1}{2^m}</math> where m is the number of heads.) | ||
So even through ALiBi is considered to be a spare attention method, it didn't specify sparsity explicitly. As tokens gets far from one another, the bias becomes small and implicitly, we have sparsity. | So even through ALiBi is considered to be a spare attention method, it didn't specify sparsity explicitly. As tokens gets far from one another, the bias becomes small and implicitly, we have sparsity. | ||
==== Experimental Results ==== | |||
Experiments with a 1.3 billion parameter model on the [[WikiText-103]] dataset showed ALiBi, trained on 1024-token sequences, matched the perplexity of sinusoidal models trained on 2048-token sequences when tested on 2048 tokens. ALiBi was 11% faster and used 11% less memory.<ref name="Press2021" /> Results are summarized below: | |||
{| class="wikitable" | |||
|- | |||
! Method !! Training Length !! Test Length !! Perplexity !! Training Time !! Memory Use | |||
|- | |||
| Sinusoidal || 2048 || 2048 || 20.5 || 100% || 100% | |||
|- | |||
| ALiBi || 1024 || 2048 || 20.6 || 89% || 89% | |||
|- | |||
| Rotary || 1024 || 2048 || 22.1 || 95% || 92% | |||
|} | |||
==== Implications ==== | |||
ALiBi's efficiency and extrapolation ability suggest it could reduce training costs and improve scalability in transformer models. Its recency bias aligns with linguistic patterns, making it a promising advancement. | |||
===SpAtten=== | ===SpAtten=== | ||
| Line 933: | Line 1,011: | ||
Similarly, SpAtten employs a specially designed top-k engine to enable real-time decision-making for pruning tokens and attention heads. This engine efficiently ranks token and head importance scores in linear time, avoiding the inefficiencies of traditional sorting methods. Instead of sorting an entire array, the top-k engine uses a quick-select module to identify the k<sup>th</sup> largest element and filters the array based on this threshold. This technique is also implemented in a highly parallelized manner, with multiple comparators working simultaneously to achieve linear-time ranking. This streamlined process ensures rapid and accurate pruning decisions, contributing to SpAtten's overall efficiency. | Similarly, SpAtten employs a specially designed top-k engine to enable real-time decision-making for pruning tokens and attention heads. This engine efficiently ranks token and head importance scores in linear time, avoiding the inefficiencies of traditional sorting methods. Instead of sorting an entire array, the top-k engine uses a quick-select module to identify the k<sup>th</sup> largest element and filters the array based on this threshold. This technique is also implemented in a highly parallelized manner, with multiple comparators working simultaneously to achieve linear-time ranking. This streamlined process ensures rapid and accurate pruning decisions, contributing to SpAtten's overall efficiency. | ||
=== | === Adaptively Sparse Attention === | ||
==== Motivation ==== | |||
Although Sparse Attention methods like BigBird and Sparse Sinkhorn Attention successfully reduce computational complexity from quadratic to linear or near-linear, they often use predefined patterns (e.g., sliding windows, global tokens, random attention). These predefined patterns may not always reflect the optimal relationships within the sequence for every context. Adaptively Sparse Attention addresses this limitation by dynamically determining which tokens should attend to each other based on their semantic or contextual relationships. | |||
==== Core Idea ==== | |||
Adaptively Sparse Attention dynamically creates sparse attention patterns by identifying the most significant attention connections for each query token based on current input features. Instead of attending to a fixed set of neighbors, each token selectively attends only to tokens with high relevance scores. | |||
====Formulation==== | |||
Given the queries <math>Q \in \mathbb{R}^{T \times d}</math>, keys <math>K \in \mathbb{R}^{T \times d}</math>, and values <math>V \in \mathbb{R}^{T \times d_v}</math>, the standard attention mechanism computes: | |||
{ | <math> | ||
\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d}}\right)V | |||
</math> | |||
In Adaptively Sparse Attention, we introduce an adaptive binary mask <math>M \in \{0, 1\}^{T \times T}</math> that selects which key tokens each query should attend to, effectively pruning unnecessary computations. Specifically, the formulation becomes: | |||
Step 1. Compute standard attention scores: | |||
<math> | |||
S = \frac{QK^T}{\sqrt{d}} | |||
</math> | |||
1 | Step 2. For each query token <math>i</math>, select a subset of keys by applying a top-<math>k</math> operator or adaptive thresholding: | ||
<math> | |||
M_{ij} = \begin{cases} | |||
1, & \text{if } S_{ij} \text{ is among the top-} k \text{ scores for row } i\\[6pt] | |||
0, & \text{otherwise} | |||
\end{cases} | |||
</math> | |||
Step 3. Compute the sparse attention: | |||
<math> | |||
\text{Attention}(Q,K,V) = \text{softmax}(S \odot M) V | |||
</math> | |||
Here, <math>\odot</math> denotes element-wise multiplication. Softmax normalization is computed over the nonzero elements in each row. | |||
====Advantages==== | |||
* | * Reduced computational complexity: By dynamically restricting attention computations to the top-<math>k</math> relevant keys per query, the complexity reduces from <math>O(T^2)</math> to approximately <math>O(Tk)</math>, which can be near-linear for <math>k \ll T</math>. | ||
* | * Context-aware sparsity: The adaptive selection allows the model to naturally focus on relevant tokens based on the input context, thus preserving performance while substantially improving efficiency. | ||
* Improved scalability: Suitable for very long sequences, Adaptively Sparse Attention provides computational efficiency needed for large-scale applications (e.g., long-document understanding, genomic sequences). | |||
====Example==== | |||
Suppose we have an attention score matrix <math>S \in \mathbb{R}^{4 \times 4}</math> (4 tokens for simplicity): | |||
<math> | |||
S = \begin{bmatrix} | |||
0.1 & 2.0 & 0.5 & 0.2 \\ | |||
1.5 & 0.3 & 0.8 & 0.4 \\ | |||
0.2 & 0.1 & 3.0 & 0.5 \\ | |||
0.7 & 0.6 & 0.4 & 0.2 \\ | |||
\end{bmatrix} | |||
</math> | |||
We set top-2 sparsity per row: | |||
Step 1. Select the top-2 scores per row: | |||
- Row 1: scores 2.0 and 0.5 (columns 2 and 3) | |||
- Row 2: scores 1.5 and 0.8 (columns 1 and 3) | |||
- Row 3: scores 3.0 and 0.5 (columns 3 and 4) | |||
- Row 4: scores 0.7 and 0.6 (columns 1 and 2) | |||
Step 2. Form adaptive mask <math>M</math>: | |||
<math>\ | <math> | ||
M = \begin{bmatrix} | |||
0 & 1 & 1 & 0 \\ | |||
1 & 0 & 1 & 0 \\ | |||
0 & 0 & 1 & 1 \\ | |||
1 & 1 & 0 & 0 \\ | |||
\end{bmatrix} | |||
</math> | |||
Step 3. Element-wise multiply to get sparse scores: | |||
<math> | |||
S' = S \odot M = \begin{bmatrix} | |||
0 & 2.0 & 0.5 & 0 \\ | |||
1.5 & 0 & 0.8 & 0 \\ | |||
0 & 0 & 3.0 & 0.5 \\ | |||
0.7 & 0.6 & 0 & 0 \\ | |||
\end{bmatrix} | |||
</math> | |||
Step 4. Apply row-wise softmax on nonzero entries. For example, row 1 nonzero entries (2.0, 0.5): | |||
<math> | |||
\text{softmax}(2.0, 0.5) \approx [0.82, 0.18] | |||
</math> | |||
Step 5. The final sparse attention output becomes: | |||
<math> | <math> | ||
\text{Attention}(Q,K,V) = \text{softmax}(S')\,V | |||
</math> | |||
Only selected entries are used, dramatically reducing computations. | |||
===Comparison=== | |||
= | {| class="wikitable" | ||
|+ Intuition Comparison of Sparse Attention Methods | |||
|- | |||
! Method !! Key Focus !! How It Works !! Primary Benefit !! Primary Trade-off | |||
|- | |||
| '''Sparse Sinkhorn''' || Global interactions via learned sorting || Rearranges tokens to place important ones together in local blocks for efficient attention || Retains global attention while reducing compute || Sorting overhead adds computation; complex implementation | |||
|- | |||
| '''BigBird''' || Local context with selective global/random links || Uses a fixed sparse pattern (local window + some global/random tokens) to approximate full attention || Scales to long sequences without needing per-sequence tuning || Fixed sparsity means some interactions might be missed | |||
|- | |||
| '''ALiBi''' || Recency bias via linear attention penalty, enables extrapolation to longer sequence lengths || Applies a penalty to distant tokens in attention scores, encouraging focus on closer tokens || Extrapolates well to longer sequences without increasing training costs || Does not reduce compute/memory at inference; only helps training | |||
|- | |||
| '''SpAtten''' || Dynamic token and head pruning for efficiency || Dynamically removes unimportant tokens and attention heads at inference for efficiency || Maximizes efficiency while preserving accuracy || Requires custom logic/hardware for full benefits | |||
|} | |||
{| class="wikitable" | |||
|+ Performance Comparison of Sparse Attention Methods | |||
|- | |||
! Method !! Memory Efficiency !! Computational Speed !! Accuracy vs Full Attention !! Real-World Adoption | |||
|- | |||
| '''Sparse Sinkhorn''' || High (learned local attention reduces need for full attention) || Moderate (sorting overhead but reduced attention computation) || Near-parity (sometimes better, as learned sparsity is adaptive) || Limited (mainly research, complex to implement) | |||
|- | |||
| '''BigBird''' || Very High (reduces O(n²) to O(n) via sparse pattern) || Fast (sparse pattern significantly reduces compute) || Near-parity (captures long-range dependencies well) || High (used in NLP for long-text tasks, available in HuggingFace) | |||
|- | |||
| '''ALiBi''' || Same as full attention (no sparsity, just biasing) but can use smaller context length in training || Same as full attention (no change in complexity) but can use smaller context length in training || Same (performs as well as full attention with added extrapolation) || Very High (adopted in major LLMs like BLOOM, MPT) | |||
|- | |||
| '''SpAtten''' || Extremely High (prunes tokens/heads dynamically) || Extremely Fast (up to 162× faster on specialized hardware) || Same (no accuracy loss, just efficiency gain) || Limited (research and specialized hardware, not common in open-source models) | |||
|} | |||
===Future of Sparse Attention=== | |||
Sparse attention mechanisms have emerged as a promising approach to improving the efficiency of transformer-based models by reducing computational and memory complexity. However, despite these advantages, they introduce trade-offs that warrant further research. Ongoing and future work in this area aims to enhance their expressivity, efficiency, and adaptability across diverse applications. | |||
1. Enhancing Long-Range Dependency Modeling | |||
Current sparse attention approaches struggle to fully capture distant contextual dependencies, limiting their effectiveness in tasks requiring extended sequence understanding. | |||
* While models like '''ALiBi''' demonstrate strong extrapolation, performance degrades beyond twice the training sequence length, indicating room for improvement. | |||
* Future work should focus on developing more robust mechanisms for retaining long-range information without sacrificing efficiency. | |||
2. Reducing Computational Overhead | |||
Despite their efficiency gains, some sparse attention methods introduce additional computational challenges: | |||
* '''Sparse Sinkhorn Attention''' requires iterative normalization (Sinkhorn balancing), increasing computational cost. | |||
* Pruning-based methods (e.g., '''SpAtten''') introduce runtime overhead due to dynamic token and head selection. | |||
* Many sparse attention models rely on specialized hardware acceleration (e.g., top-k engines), limiting their accessibility in general-purpose computing environments. | |||
Addressing these issues will be crucial for making sparse attention models more widely applicable. | |||
3. Optimizing Sparse Attention Architectures | |||
A key challenge is designing architectures that achieve high performance while maintaining efficiency. Future research should explore: | |||
* Balancing efficiency and expressivity by reducing the number of layers needed to match the performance of full attention models. | |||
* Hybrid approaches that integrate multiple sparse attention mechanisms to leverage their respective strengths. | |||
By addressing these challenges, future iterations of sparse attention models can push the boundaries of efficiency while preserving the rich contextual modeling capabilities of transformers. | |||
= Topic 10: Linear Attention= | |||
== Introduction == | |||
Linear attention tries to address the efficiency limitations of traditional softmax attention. Standard attention (also called vanilla attention) is calculated as: | |||
<math>\ | <math>\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V</math> | ||
The computation complexity of this method is <math>O(n^2d)</math> for sequence length <math>n</math> and representation dimension <math>d</math> and the main reason behind that is the multiplication of <math>Q</math> and <math>K^T</math>, produces a large <math>n \times n</math> attention matrix. If we remove the softmax function from this equation, then we can reduce the computational intensity because the matrix multiplication can be reordered to <math>Q(K^T V)</math>. Multiplying <math>K^T V</math> first results in smaller matrix multiplications. However, this linear mapping is insufficient to capture the complex relationships in the data. To reintroduce more complexity, we can replace the softmax function with some kernel with approximates it. Recall that for any kernel <math>K, K(x, y)= \Phi(x)^T \Phi(y)</math> for a matrix <math>\Phi</math>. If we apply this kernel to Q and K, then we can approximate vanilla attention with a much more efficient mechanism. | |||
Recent research has explored more sophisticated approaches to restore the modelling power of linear attention while preserving efficiency. For instance, Retentive Networks (RetNet) introduce a learnable decay-based recurrence that enables <math>O(1)</math> inference with strong performance on language tasks. Gated Linear Attention (GLA) incorporates a data-dependent gating mechanism to better capture context, and BASED proposes a hybrid strategy combining linear attention with sliding-window attention to balance throughput and recall. TransNormerLLM refines positional embeddings and normalization while accelerating linear attention with hardware-friendly techniques. | |||
<math> | |||
Linear attention is particularly useful for large-scale models and scenarios where memory and computing are constrained. Unlike traditional Transformers, which rely heavily on key-value caching and suffer latency bottlenecks during inference, linear attention variants can support faster decoding with lower memory usage. These properties make them attractive for applications such as real-time processing, edge deployment, and next-generation large language models. | |||
== | == Key Approaches to Linear Attention == | ||
===Retentive Network (RetNet): A Successor to Transformer for Large Language Models=== | |||
[[File:retnet_impossible_triangle.png|thumb|200px|Figure 1: Impossible Triangle]] | |||
The authors of this paper introduce a new architecture that can achieve parallel training, fast inference, without compromising performance solving the inherent complexity in vanilla attention mechanism. They claim that the new architecture makes the impossible triangle, Figure 1, possible. RetNet combines the advantages of transformer performance and ability for parallel training with the lower-cost inference of RNNs by introducing a multi-scale retention mechanism to replace multi-head attention that incorporates three main representations: | |||
# Parallel: allows GPU utilization during training. | |||
# Recurrent: enables low-cost inference with <math>O(1)</math> complexity in terms of computation and memory. | |||
# Chunkwise recurrent: models long-sequences efficiently. | |||
Essentially, RetNet replaces the <math>softmax</math> by adopting a linear representation of the attention mechanism in the form of retention. | |||
====Recurrent Representation==== | |||
We can show that the retention mechanism has a dual form of recurrence and parallelism (Figure2). First let's show RetNet in its recurrent form: | |||
[[File:RetNet_dual.png|thumb|500px|Figure 2: Dual form of RetNet]] | |||
<math>S_n = \gamma S_{n-1} + K_n^T V_n</math> | |||
<math> | <math>\text{Retention}(X_n) = Q_n S_n</math> | ||
In this formula, <math>\gamma</math> is a decay factor, ensuring that more recent tokens are weighted more heavily, simulating recency bias without storing all past activations. <math>Q</math>, <math>K</math>, <math>V</math> are learned projections of the input. During training, this can be computed in parallel form. | |||
=== | ====Parallel Representation==== | ||
Now, we can show the parallel representation of retention: | |||
<math>\text{Retention}(X) = (QK^T \odot D)V</math> | |||
Where <math>D</math> is a matrix that combines causal masking and exponential decay along relative distance. For better understanding the role of matrix <math>D</math>, let's take a look at its formula: | |||
== | <math display="block"> | ||
D_{nm} = | |||
\begin{cases} | |||
\gamma^{n-m}, & n \geq m \ | |||
0, & n < m | |||
\end{cases} | |||
</math> | |||
This formulation ensures that tokens can only attend to previous tokens (which they call it, causal masking) and the attention strength decays exponentially with distance (controlled by parameter <math>\gamma</math>). In other words, as we move forward, less attention is paid to earlier tokens. | |||
====Chunkwise Recurrent Representation==== | |||
The third component, chunkwise recurrent representation, is a hybrid of recurrent and parallel representations aimed at training acceleration for long sequences. Simply, the input sequence is divided into chunks, where in each chunk a parallel representation is utilized to process all the tokens simultaneously. To pass information across chunks, the recurrent representation is used to create a summary of that chunk and pass it to the next. The combination of inner-chunk (parallel) and cross-chunk (recurrent) information produce the retention of the chunk which captures the details within the chunk and the context from previous chunks. To compute the retention of the i-th chunk, let <math>B</math> be the chunk length, then: | |||
<math> | <math>Q_{[i]} = Q_{Bi:B(i+1)}, K_{[i]} = K_{Bi:B(i+1)}, V_{[i]} = V_{Bi:B(i+1)}</math> | ||
<math>R_i = K_{[i]}^T (V_{[i]} \odot \zeta) + \gamma^B R_{i-1}, \quad \zeta_{ij} = \gamma^{B-i-1}</math> | |||
<math> | <math> | ||
{Retention}(X_{[i]}) = | |||
\underbrace{(Q_{[i]} K_{[i]}^T \odot D) V_{[i]}}_{Inner-Chunk} + | |||
\underbrace{(Q_{[i]} R_{i-1}) \odot \xi}_{Cross-Chunk}, \quad \xi_{i,j} = \gamma^{i+1} | |||
</math> | |||
where <math> | where <math>R_i</math> is the state of the current chunk to be passed to the next. | ||
<math> | In summary, the overall architecture of RetNet consists of stacked identical L blocks similar to Transformer. Each block consists of two modules: multi-scale retention (MSR) module and a feed-forward network (FFN) module. It takes the embeddings of input sequence <math>X^0= [x_1, \dots, x_{|x|}] \in \mathbb R^{|x| \times d_{model}}</math> and compute the output <math>X^L</math>: | ||
<math>Y^l = MSR(LN(X^l)) + X^l</math> | |||
<math>X^{l+1} = FFN(LN(Y^l)) + Y^l</math> | |||
where <math>LN(.)</math> is LayerNorm. | |||
[[File:retnet_comparison.png|thumb|800px|Table 1: Model Comparison]] | |||
====Comparison, Limitations & Future Work==== | |||
Finally, comparing RetNet to other solutions, we can see that it provides a solid alternative to the Transformer achieving parallel training, fast inference, linear long-sequence memory complexity, and good performance. | |||
The limitations of this architecture can be summarized in the following points: | |||
* Limited Cross-Modal Exploration | |||
* The method is primarily validated on language modeling tasks. Its applicability to other modalities (e.g., vision, audio) remains unexplored, requiring further research for broader adoption. | |||
* RetNet achieves superior GPU utilization compared to standard Transformers during training due to its parallel retention mechanism. In practice, it allows training with significantly fewer memory bottlenecks, making it ideal for scaling to longer sequences or deeper models. | |||
=== Memory-Recall Tradeoff === | |||
A fundamental tradeoff exists between the size of a model's recurrent state and its ability to recall past tokens accurately. Some architectures, like BASED, combine linear attention with a sliding window of exact softmax attention to navigate this tradeoff. By adjusting hyperparameters such as the window size and feature dimensions, these models can traverse the Pareto frontier—achieving high recall with a small memory footprint while still benefiting from high throughput. | |||
This paper focuses on the task of associative recall and discusses the memory-recall tradeoff. The memory-recall tradeoff basically states that higher recall requires higher memory consumption, as shown in Figure 3. This tradeoff manifests in different ways across model architectures: | |||
* Vanilla attention models: achieve excellent recall but at the cost of quadratic computational complexity | |||
* Linear attention models: offer better efficiency but often struggle with accurate information retrieval | |||
* State-space models like Mamba: show that increasing recurrent state size generally improves recall accuracy but introduces computational overhead | |||
[[File:memory-recall-tradeoff.png|thumb|300px|Figure 3: Empirical performance showing the memory-recall tradeoff]] | |||
=== Implementations === | |||
The authors introduced Based architecture to improve this tradeoff. They do so by stacking linear attention blocks with sliding window attention blocks. Recall that one of the limitations of linear attention is relatively poor performance compared to vanilla attention. By selecting this type of architecture, the authors compromise on global performance by allowing linear attention to map global dependencies while retaining high performance within a local window by using the sliding window attention to map local dependencies. As seen in figure 4, they achieve this goal. | |||
==== Chunking Strategy ==== | |||
Chunking involves spliting the input sequence <math>X</math> into chunks of length <math>B</math>. For each chunk <math>i</math>, let | |||
<math>Q_{[i]} = Q_{B i : B(i+1)}, \quad K_{[i]} = K_{B i : B(i+1)}, \quad V_{[i]} = V_{B i : B(i+1)}</math> | |||
<math> | be the query, key, and value vectors (respectively) for that chunk. We maintain a recurrent “global” state <math>R_i</math> that summarizes information from all previous chunks and combine it with a “local” sliding-window attention over the current chunk. | ||
==== Global Linear Attention (Recurrent “State”) ==== | |||
We use a feature map <math>\Phi(\cdot)</math> (e.g., a kernel or ELU-based mapping) to make attention linear in the sequence length. We update a global state <math>R_i</math> for each chunk: | |||
<math> | <math>R_i = R_{i-1} + \Phi\bigl(K_{[i]}\bigr)^\top , V_{[i]},</math> | ||
and compute the global attention contribution for the <math>i</math>-th chunk: | |||
<math>\mathrm{GlobalAttn}(X_{[i]}) = \Phi\bigl(Q_{[i]}\bigr),R_{i-1}.</math> | |||
Intuitively, <math>R_{i-1}</math> aggregates (in linear time) all key-value information from past chunks. | |||
==== Taylor Linear Attention ==== | |||
The Based architecture specifically employs a second-order Taylor series expansion as the feature map for linear attention. This approximation offers a good balance between computational efficiency and performance: | |||
<math>\Phi(x) = \begin{bmatrix} 1 \\ x \\ \frac{x^2}{2} \end{bmatrix}</math> | |||
This feature map provides a reasonable approximation of the softmax function while maintaining the linear complexity benefits. | |||
=== | ==== Local Sliding-Window Attention (Exact) ==== | ||
Within the current chunk, we also apply standard (exact) attention to a small window of recent tokens. Denote the set of token indices in this window by <math>\mathcal{W}_i</math>. Then: | |||
<math>\mathrm{LocalAttn}(X_{[i]}) ;=; \sum_{j ,\in, \mathcal{W}i} \mathrm{softmax}!\Bigl(\frac{Q{[i]},K_j^\top}{\sqrt{d}}\Bigr),V_j.!</math> | |||
This term captures fine-grained, short-range dependencies at full (exact) attention fidelity, but only over a small neighborhood <math>\mathcal{W}_i</math>. | |||
==== Final Output per Chunk ==== | |||
The total representation for chunk <math>i</math> is a sum of global (linear) and local (windowed) attention: | |||
<math>h_{[i]} ;=; \mathrm{GlobalAttn}(X_{[i]}) ;+; \mathrm{LocalAttn}(X_{[i]}).!</math> | |||
<math> | By combining a linear-time global update (<math>R_i</math>) with high-resolution local attention, the model balances throughput (via the efficient global linear component) and recall (via exact local attention). This addresses the memory-recall tradeoff: large contexts are captured without quadratically scaling memory usage, while local windows preserve high accuracy on short-range dependencies. | ||
=== Hardware Optimizations === | |||
Recent work has shown that linear attention can be made even more practical when its implementation is tailored to the underlying hardware. For example, methods like '''FLASHLINEARATTENTION''' integrate I/O-aware techniques to minimize data movement between high-bandwidth memory and faster on-chip memories, resulting in real-world speedups that can even outperform optimized softmax attention implementations on moderate sequence lengths. | |||
The Based Architecture includes several hardware-aware optimizations: | |||
The | # Memory-efficient linear attention: The implementation fuses the feature map and causal dot product computation in fast memory, reducing high-latency memory operations. | ||
# Optimized sliding window: The window size is carefully selected to align with hardware constraints (typically 64×64 tiles), balancing computation and memory bandwidth. | |||
# Register-level computation: Critical calculations are performed in registers whenever possible, minimizing data movement between different memory hierarchies. | |||
==== FLASHLINEARATTENTION: Hardware-Efficient Linear Attention for Fast Training and Inference ==== | |||
FLASHLINEARATTENTION is an I/O-aware, hardware-efficient linear attention mechanism for efficient data movement between shared memory (SRAM) and high-bandwidth memory (HBM). The goals are to alleviate memory bottlenecks, maximize GPU parallelism, and accelerate training and inference. The method significantly outperforms even FLASHATTENTION-2 at moderate sequence lengths (~1K tokens). Softmax-based self-attention, which is standard attention mechanism, is quadratic in both computation and memory complexity, making it inefficient for long sequences and scalability-constrained. Linear attention attempts to reduce this complexity, but most of them are not GPU-optimized for modern GPUs and do not provide real-world speed improvements. FLASHLINEARATTENTION solves this by splitting the input sequence into more manageable pieces where computation can independently be performed on each piece before global state updating. This alleviates redundant memory access, decreased latency GPU operations, and keeps tensor cores in effective use. | |||
Mathematically, FLASHLINEARATTENTION builds upon linear attention, which rewrites standard softmax attention as: | |||
<math>\text{Attention}(Q, K, V) = \text{softmax} \left(\frac{QK^T}{\sqrt{d}} \right) V</math> | |||
instead of explicitly computing the full <math>n \times n</math> attention matrix, linear attention approximates it using a kernel function <math>\phi(x)</math> such that: | |||
<math>\text{Attention}(Q, K, V) \approx \frac{\phi(Q) (\phi(K)^T V)}{\phi(Q) (\phi(K)^T)}</math> | |||
where <math>\phi(x)</math> is a feature map transformation ensuring that the inner product approximates the softmax function. In standard parallel linear attention, the output is computed as: | |||
<math>O = (Q K^T) V</math> | |||
which still has quadratic complexity <math>O(n^2 d)</math>. FLASHLINEARATTENTION, on the other hand, splits the input sequence into pieces and processes them separately while having a hidden state <math>S</math>. The rule to update the hidden state is in a recurrent form: | |||
<math>S[i+1] = S[i] + \sum_{j=1}^{C} K_j^T V_j</math> | |||
= | <math>O[i+1] = Q[i+1] S[i] + (Q[i+1] K[i+1]^T \odot M) V[i+1]</math> | ||
Here, <math>M</math> is a causal mask, ensuring attention is calculated only for tokens in the past. Chunkwise computation, minimizing memory overhead by splitting the sequence into smaller chunks to process, is the most crucial optimization in FLASHLINEARATTENTION to enhance efficiency. Chunks can be processed independently, allowing parallel execution. HBM I/O cost minimization is another key optimization, avoiding unnecessary data transfer between HBM and SRAM by reusing on-chip loaded tensors. When <math>Q[n]</math> is loaded into SRAM, both <math>Q[n]S</math> and <math>(Q[n]K[n]^T \odot M)V[n]</math> are computed without reloading <math>Q[n]</math>. FLASHLINEARATTENTION has two implementations. In the non-materialization version, hidden states <math>S[i]</math> are stored in SRAM to enable memory-efficient computation. In the materialization version, all <math>S[i]</math> are stored in HBM to enable full sequence-level parallelism. The materialization version is slightly slower but boosts training throughput by 10-20%. The calculation is parallel for chunks but sequential between chunks. This is for efficiency and handling of memory to render the algorithm suitable for processing long sequences. | |||
< | The FLASHLINEARATTENTION forward pass algorithm goes as follows. For input matrices <math>Q</math>, <math>K</math>, and <math>V</math> of size <math>L \times d</math> and chunk size <math>C</math>, the sequence is divided into <math>N = L / C</math> blocks as: | ||
<math>Q = \{ Q[1], Q[2], ..., Q[N] \}, \quad K = \{ K[1], K[2], ..., K[N] \}</math> | |||
The hidden state is initialized as <math>S = 0</math> in SRAM. For each chunk, <math>S</math> is stored in HBM if materialization is enabled, and the corresponding <math>K[n], V[n]</math> values are loaded into SRAM. The hidden state update follows: | |||
<math>S = S + K[n]^T V[n]</math> | |||
and the output for each chunk is computed in parallel as: | |||
<math> | |||
<math> | |||
</ | |||
The | |||
<math> | |||
<math>O'[n] = Q[n] S + (Q[n] K[n]^T \odot M) V[n]</math> | |||
<math>O | |||
The outputs are then stored in HBM and fed as outputs. The algorithm maintains a trade-off between memory usage and parallelization such that training speeds are higher than previous linear attention versions. FLASHLINEARATTENTION offers significant performance gains compared to several other attention models. Speedup gains involve less than FLASHATTENTION-2 on sequences shorter than 4K tokens and doubling of training speeds compared to standard linear attention. Memory efficiency is improved through reducing HBM I/O expense and removing redundant data movement, with 4x less memory usage compared to baseline softmax attention. Scalability is also a benefit, allowing for processing of sequences longer than 20K tokens without quadratic memory growth. These improvements make FLASHLINEARATTENTION a solid tool for large-scale transformers, improving efficiency in training and inference. By integrating FLASHLINEARATTENTION into traditional transformer designs, large language models can be significantly accelerated, and large-scale deployment made more viable. Future work can explore deeper kernel optimizations, CUDA-specific workloads, and hardware-specific transformations to further enhance efficiency. FLASHLINEARATTENTION is a significant advancement in hardware-efficient deep learning, supporting memory-efficient training at higher speeds for large-scale transformers. By optimizing memory access, chunking input sequences, and parallel intra-chunk computation, it achieves significant speedup with strong recall ability, making it a landmark achievement in the efficient processing of long sequences. | |||
===Empirical Results=== | |||
[[File:RetNet_Results.png|600px]] | |||
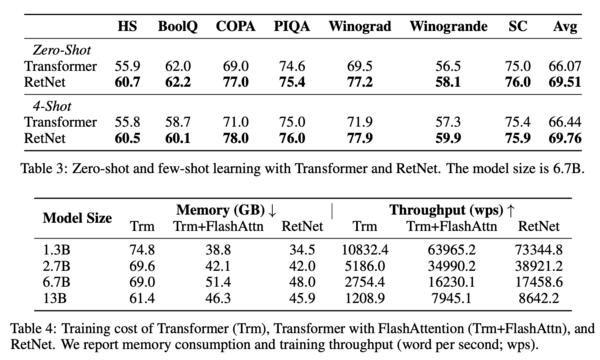
In Table 3, comparison was made between Transformer and RetNet on a variety of downstream tasks (i.e., HS, BoolQ, etc). In both zero-shot and 4-shot learning, RetNet achieved a higher accuracy on all tasks listed. In Table 4, the authors compared the training speed and memory usage of Transformer, Transformer with FlashAttention and RetNet, the training sequence length is fixed at 8192 tokens. Results show that RetNet consumes less memory while achieving a higher throughput than both Transformer and Transformer with FlashAttention. Recall that in FlashAttention the technique of kernel fusion was applied while here RetNet was implemented naively. Therefore, there's potential for improvements upon the current results, which already exceeds the other two models. | |||
=== | === Limitations === | ||
While the Based Architecture presents a promising direction, it still faces some challenges: | |||
# Implementation complexity: The dual-attention mechanism and hardware optimizations add complexity to the implementation. | |||
# Hyperparameter sensitivity: The optimal balance between global and local attention components may vary across different tasks and datasets. | |||
# | # Performance gap: Despite improvements, there remains a gap between Based models and state-of-the-art vanilla attention models on some specific tasks. | ||
# | |||
== | == Gated Linear Attention (GLA) == | ||
RetNet shows us we can achieve parallel training, efficient inference, and more optimized performance. However, despite its innovations, RetNet still has significant limitations. The biggest problem with RetNet was how it handled sequential data. RetNet uses a constant decay factor (<math>\gamma</math>) that doesn't adapt to the content being processed. Let's imagine a conversation where you treat every fifth word equally regardless of how significant. That is what RetNet does with its constant exponential decay factor. What that means is that RetNet treats all sequential dependencies the same way, regardless of whether the current content requires more emphasis on recent tokens or on tokens much farther back. This process could work, but not necessarily optimally. | |||
Furthermore, while RetNet is theoretically efficient, it is not so effective in practice on real hardware. The algorithms are not I/O-aware, and therefore they do not account for how data is being moved between levels of memory in modern GPUs and this leads to suboptimal performance. Gated Linear Attention (GLA) advances linear attention by solving such key limitations. | |||
The new idea of GLA is the use of data-dependent gates. Unlike RetNet which uses fixed decay factors, these gates dynamically adjust based on the content being processed and this makes the model more powerful. It likes an intelligent filter that decides, at each position in a sequence, how much information should pass through depending on its relevance. For example, when processing the phrase "Prime Minister" in "The Prime Minister of Canada," the model might focus more on "Canada" than on "The". This is something RetNet with fixed decay cannot achieve. GLA introduces a gating mechanism where the output is determined by the below formula: | |||
= | <math>\text{Output} = \text{LinearAttention} \odot \text{ContentGate}</math> | ||
The ContentGate is derived directly from the input itself and this modification enhances the model’s ability to capture complex dependencies in text. | |||
The other important feature of GLA is its '''FLASHLINEARATTENTION''' algorithm which designed specifically for modern GPU architectures. Unlike theoretical improvements, this optimization gives us real-world performance and outperforming even highly optimized methods like '''FLASHATTENTION-2'''. What makes '''FLASHLINEARATTENTION''' different is that it is I/O-aware, meaning it efficiently manages data movement between: | |||
* High-bandwidth memory (HBM): Large but slower GPU memory. | |||
* Shared memory (SRAM): Smaller but significantly faster memory. | |||
By minimizing unnecessary data transfers and using specialized compute units (like tensor cores), this method achieves remarkable speed and efficiency. In benchmarks, it even surpasses FLASHATTENTION-2 on relatively short sequences of just 1,000 tokens. | |||
FLASHLINEARATTENTION improves efficiency by using a method called chunkwise processing. Instead of processing the entire sequence at once, it divides it into smaller chunks. Within each chunk, computations are done in parallel to maximize GPU usage. Then, information is passed between chunks in a recurrent way to maintain dependencies. This balances speed and memory efficiency, making it faster than traditional softmax attention and even some optimized methods like FLASHATTENTION-2. | |||
===Empirical Results=== | |||
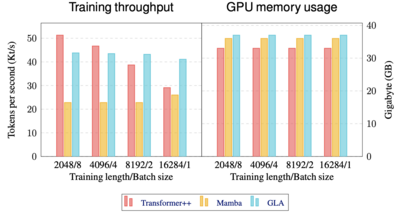
[[File:GLA_Results.png|800px]] | |||
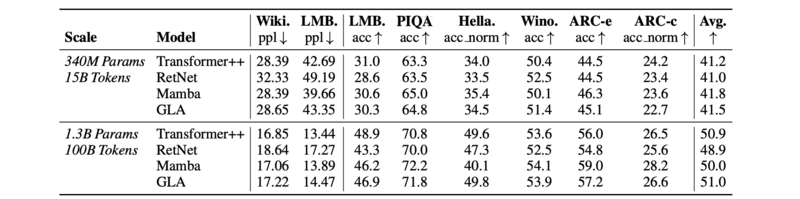
The table above shows GLA Transformer results against Transformer++, RetNet, and Mamba. Two sets of scales are employed and the same set of language tasks are tested on. The individual task performance is via zero-shot. We can see that GLA outperforms subquadratic models like RetNet on all tasks and achieved comparable performance against quadratic models like Transformer++. | |||
[[File:GLA_Results2.png|400px]] | |||
In additional to its performance on various language tasks, GLA also achieves a higher throughput and lower memory consumption, especially on long input sequences. | |||
=== | ===Limitations & Future Work=== | ||
* Lack of Large-Scale Validation | |||
**Although the authors anticipate that the training efficiency of GLA become even more favorable compared to model like Mamba at larger scales, it is unclear how GLA would scale to even larger models/datasets. | |||
**The experiments were conducted on moderate-scale language models (up to 1.3B parameters). The performance and efficiency of GLA at larger scales (e.g., >7B parameters) remain uncertain, particularly regarding tensor parallelism and memory constraints. | |||
* language | * Performance Gap in Recall-Intensive Tasks | ||
* | ** While GLA outperforms other subquadratic models in recall-intensive tasks, it still lags behind standard quadratic attention Transformers, indicating room for improvement in tasks requiring precise memory retrieval. | ||
* | |||
== | ==TransNormerLLM: A Faster and Better Large Language Model with Improved TransNormer== | ||
The objective of the paper is to address the quadratic time complexity and scalability limitations of conventional transformer-based LLMs by introducing a linear attention-based architecture for improved efficiency and performance. Modern linear attention models like '''TransNormerLLM''' push the envelope by integrating several modifications—including improved positional encodings (using LRPE with exponential decay), gating mechanisms, and tensor normalization—to not only match but even outperform conventional Transformer architectures in both accuracy and efficiency. These innovations help address the limitations of earlier linear attention approaches and demonstrate the potential for linear methods in large-scale language modeling. | |||
=== What is TransNormer? === | |||
'''TransNormer''' is a linear transformer model introduced in 2022 at the Conference on Empirical Methods in Natural Language Processing (EMNLP). It tackles two primary challenges: unbounded gradients in attention computation, which can destabilize training, and attention dilution, where long sequences reduce focus on local token interactions. To mitigate these, TransNormer replaces traditional scaling operations with normalization techniques to control gradients and employs diagonal attention in early layers to prioritize neighboring tokens.These innovations enhance performance on tasks such as text classification, language modeling, and the Long-Range Arena benchmark, while achieving significant space-time efficiency compared to softmax attention-based transformers. | |||
The original TransNormer model, faced several limitations that impacted its versatility. | |||
* '''Scalability Constraints''': TransNormer was primarily tested on small-scale tasks like text classification and the Long-Range Arena benchmark, with limited evidence of its performance on large-scale language modeling tasks. This restricted its applicability to modern large language models requiring extensive training data and parameters. | |||
* '''Complexity in Optimization''': Despite stabilizing gradients, the model's normalization techniques increased computational overhead in certain configurations, complicating optimization for resource-constrained environments. | |||
* '''Attention Dilution Trade-offs''': While diagonal attention improved local context focus, it potentially limited the model’s ability to capture long-range dependencies in complex sequences, affecting performance on tasks requiring global context. | |||
* '''Benchmark Scope''': The evaluation was confined to specific datasets, lacking comprehensive testing on diverse, real-world applications, which raised questions about its generalizability. | |||
The authors address all of these limitations in TransNormerLLM. | |||
===Key Contributions=== | |||
==== | <ul> | ||
<li>Architectural Improvements</li> | |||
<ol> | |||
<li>Positional Encoding: <br> | |||
Combines '''LRPE (Linearized Relative Positional Encoding)''' with exponential decay to balance global interactions and avoid attention dilution. The expression of positional coding is:<br> | |||
<math>a_{st}=\mathbf{q}_s^\top\mathbf{k}_t\lambda^{s-t}\exp(i\theta(s-t)),</math><br> | |||
where <math>a_{st}</math> is the attention score between token s and t, <math>\lambda^{s-t}</math> is the exponential decay factor and <math>\exp(i\theta(s-t))</math> is the encoding to capture relative positions.</li> | |||
<li>Gating Mechanisms:<br> | |||
Uses '''Gated Linear Attention (GLA)''' and '''Simplified Gated Linear Units (SGLU)''' to stabilize training and enhance performance.<br> | |||
Gate can enhance the performance of the model and smooth the training process. The structure of Gated LinearAttention (GLA) is:<br> | |||
<math>O=\mathrm{Norm}(QK^{\top}V)\odot U,</math><br> | |||
where:<math>\quad Q=\phi(XW_q),\quad K=\phi(XW_k),\quad V=XW_v,\quad U=XW_u.</math><br> | |||
To further accelerate the model, the author propose Simple GLU (SGLU), which removes the activation | |||
function from the original GLU structure as the gate itself can introduce non-linearity. Therefore, the channel mixing becomes:<br> | |||
<math>O=[V\odot U]W_o,</math><br> | |||
where:<math>V=XW_v,\quad U=XW_u.</math><br> | |||
</li> | |||
<li>Tensor Normalization: <br> | |||
Replaces '''RMSNorm''' with '''SRMSNorm''', a simpler normalization method that accelerates training without performance loss. | |||
The new simple normalization function called SimpleRMSNorm, abbreviated as SRMSNorm:<br> | |||
<math>\mathrm{SRMSNorm}(x)=\frac{x}{\|x\|_2/\sqrt{d}}</math> | |||
</li> | |||
</ol> | |||
<li>Training Optimization</li> | |||
Model Parallelism: <br> | |||
Adapts Megatron-LM model parallelism for SGLU and GLA, enabling efficient scaling from 7B to 175B parameters.<br> | |||
'''Model Parallelism on SGLU:<br>''' | |||
<math>O=\left((XW_v)\odot(XW_u)\right)W_o</math><br> | |||
<math>\begin{bmatrix} | |||
O_1^{\prime},O_2^{\prime} | |||
\end{bmatrix}=X | |||
\begin{bmatrix} | |||
W_v^1,W_v^2 | |||
\end{bmatrix}\odot X | |||
\begin{bmatrix} | |||
W_u^1,W_u^2 | |||
\end{bmatrix}= | |||
\begin{bmatrix} | |||
XW_v^1,XW_v^2 | |||
\end{bmatrix}\odot | |||
\begin{bmatrix} | |||
XW_u^1,XW_u^2 | |||
\end{bmatrix}</math><br> | |||
<math>O= | |||
\begin{bmatrix} | |||
O_1^{\prime},O_2^{\prime} | |||
\end{bmatrix} | |||
\begin{bmatrix} | |||
W_o^1,W_o^2 | |||
\end{bmatrix}^\top=O_1^{\prime}W_o^1+O_2^{\prime}W_o^2</math><br> | |||
'''Model Parallelism on GLA:<br>''' | |||
<math>[O_1,O_2]=\mathrm{SRMSNorm}(QK^\top V)\odot U,</math><br> | |||
where: <math>Q = [\phi(X W_q^1), \phi(X W_q^2)],\ K = [\phi(X W_q^1), \phi(X W_q^2)],\ V = X[W_v^1, W_v^2],\ U = X[W_u^1, W_u^2].</math><br> | |||
<li>Robust Inference</li> | |||
A robust inference algorithm proposed in the paper ensures numerical stability and constant inference speed regardless of sequence length via a recurrent formulation with decay factors.<br> | |||
[[File:RobustAlgorithm.jpg|500px|Robust Inference Algorithm ]] | |||
</ul> | |||
=== Training === | |||
TransNormerLLM has been trained in sizes ranging from 385 million to 7 billion parameters, with ongoing development of a 15-billion-parameter version. The training corpus includes 1.0 trillion tokens for the 385M model, 1.2 trillion for the 1B model, and 1.4 trillion for the 7B model, ensuring robust data exposure for diverse language tasks. The model utilizes large-scale clusters, enabling efficient scaling across multiple devices. | |||
=== Results === | |||
TransNormerLLM has demonstrated competitive performance across various benchmarks, particularly in commonsense reasoning and aggregated tasks, matching or approaching state-of-the-art models like LLaMA and OPT. The 7B parameter model is the most extensively evaluated, with results reported as follows: | |||
* '''Commonsense Reasoning (Zero-Shot)''': | |||
** BoolQ: 75.87 – Evaluates yes/no question answering based on passages. | |||
** PIQA: 80.09 – Tests understanding of physical world interactions. | |||
** HellaSwag: 75.21 – Assesses commonsense inference from multiple choices. | |||
* | * '''Aggregated Benchmarks (Five-Shot)''': | ||
** MMLU: 43.10 – Measures multitask language understanding in English. | |||
** CMMLU: 47.99 – Chinese version of MMLU. | |||
** C-Eval: 43.18 – Comprehensive Chinese evaluation across 52 disciplines. | |||
These results highlight the model's versatility in handling both English and Chinese tasks, with efficiency gains attributed to its linear attention mechanisms, achieving over 20% acceleration compared to traditional models. | |||
== | ==Simple linear attention language models balance the recall-throughput tradeoff== | ||
Large language models (LLMs) using Transformers are fantastic at "recalling" details from their input—think of it as their ability to dig up a specific fact buried in a long conversation. However, attention-based language models suffer from high memory consumption during inference due to the growing key-value (KV) cache, which scales with sequence length. This reduces throughput and limits efficiency for long sequences, despite their strong recall ability. | |||
''' | ===Key Contributions=== | ||
* '''BASED''': A hybrid architecture blending linear attention and sliding window attention to optimize the recall-memory tradeoff. | |||
* '''Theoretical and empirical evidence''' of how memory usage impacts recall. | |||
* '''Optimized implementation''' achieving up to 24× higher throughput than FlashAttention-2 for long-sequence generation. | |||
===BASED=== | |||
BASED combines two tricks to strike a balance: | |||
# '''Linear Attention''': This approximates the softmax with a simpler operation. Instead of computing <math>\exp(q_i^\top k_j / \sqrt{d})</math>, it uses a feature map <math>\phi</math> so that <math>\phi(q_i)^\top \phi(k_j) \approx \exp(q_i^\top k_j / \sqrt{d})</math>. The paper opts for a 2nd-order Taylor series: <math>\phi(q_i)^\top \phi(k_j) = 1 + q_i^\top k_j + \frac{(q_i^\top k_j)^2}{2}</math>. This lets them rewrite attention as a recurrent process with a fixed-size state, say <math>s_i = \sum_{j=1}^i \phi(k_j)^\top v_j</math>, avoiding the KV-cache explosion. The state size depends on the feature dimension <math>d'</math>, not <math>N</math>, making memory predictable. | |||
# '''Sliding Window Attention''': This adds precision by letting each token attend to a small, local window of past tokens (e.g., 64 tokens) using exact softmax attention. It’s like giving the model a magnifying glass for nearby details, with a KV-cache capped at the window size <math>w</math>. | |||
Together, linear attention handles long-range context with a fixed memory footprint, while sliding window attention sharpens local recall. By tweaking <math>w</math> and <math>d'</math>, BASED can slide along the recall-memory tradeoff curve—crank up the window for better recall or shrink it for efficiency. | |||
* | ===Limitations and Future Work=== | ||
* '''Scaling''': May struggle with very large models or extremely long sequences. | |||
* '''Future Work''': Could explore improved approximations for linear attention or enhanced hardware optimizations. | |||
= | = Topic 11: Flash Attention= | ||
Flash Attention tries to address the resource intensity of vanilla attention by utilizing hardware more effectively. Recent advances in computational speed (particularly in parallelization) have lessened computational intensity as a bottleneck. Consequently, memory usage became a larger bottleneck. Specifically, during training, attention requires data to be read and written multiple times and computations are done in HBM (which is not the fastest memory in the computer). As a result, training takes a lot of time and resource. The goal of Flash Attention is thus to address these inefficiencies in order to reduce training time for LLMs. | |||
Flash Attention began with version 1, which restructured the standard attention mechanism to reduce memory traffic via tiled (block‑wise) computations in on‑chip SRAM. FlashAttention V2 built upon this idea by re‑organizing work partitioning to better utilize GPU resources—optimizing thread block scheduling and reducing non-matmul overhead. Finally, FlashAttention V3 takes advantage of new hardware features present on Hopper/H100 GPUs—most notably asynchronous execution, warp specialization, and low‑precision math (FP8)—resulting in a substantial boost in throughput and higher utilization of tensor cores. | |||
== Flash Attention V1 == | |||
Flash Attention V1 rethinks the standard attention mechanism by minimizing expensive memory transfers. Modern GPUs have high-bandwidth memory (HBM) that is large but relatively slow compared to on‑chip SRAM, which is over 10× faster but limited to about 20 MB. By restructuring the attention computation to operate in small blocks within SRAM, Flash Attention V1 dramatically reduces the number of slow memory reads and writes, resulting in faster training for large language models. | |||
==== | ==== Overview ==== | ||
Traditional attention computes the full <math>QK^\top</math> matrix in HBM, causing a quadratic memory traffic bottleneck. Flash Attention V1 addresses this by processing the input matrices in smaller, manageable blocks (tiles) that fit in fast SRAM. In doing so, both the matrix multiplication and the softmax normalization are performed piecewise, with local results later merged to produce the exact, globally normalized output. | |||
==== | ==== Block‑Wise (Tiled) Computation ==== | ||
Imagine trying to paint a giant mural using a small canvas. Rather than handling the entire image at once, you divide it into sections that fit on your workbench. In Flash Attention V1, the large <math>Q</math>, <math>K</math>, and <math>V</math> matrices are partitioned into tiles. For example, with 1024 tokens, the matrices might be split into blocks of 256 tokens each. A block of <math>Q</math> (e.g. <math>256 \times d</math>) is loaded from HBM into SRAM along with the corresponding block of <math>K</math> (transposed as needed). The multiplication <math>QK^\top</math> is then computed within SRAM to yield a <math>256 \times 256</math> block of attention scores, eliminating the need to store or compute the entire matrix in slow memory. | |||
==== Softmax Normalization: Handling Global Dependencies in Small Pieces ==== | |||
The softmax function, defined as | |||
<math display="block">\text{softmax}(x_i) = \frac{\exp(x_i)}{\sum_j \exp(x_j)}</math> | |||
requires a global normalization across each row of scores. This poses a challenge when the data is processed in tiles. | |||
Within each tile, a local maximum (<math>m_{\text{local}}</math>) is computed to stabilize the exponentiation, and a local sum is calculated: | |||
<math display="block">S_{\text{local}} = \sum_{i \in \text{tile}} \exp(x_i - m_{\text{local}})</math> | |||
Simultaneously, the tile computes a partial numerator by weighting each <math>\exp(x_i - m_{\text{local}})</math> with the corresponding <math>V</math> values. These local computations ensure that the softmax can be performed on a small subset of the data without needing the entire row at once. | |||
==== Algebraic Aggregation: Merging Tile Results for Global Softmax ==== | |||
Since each tile’s softmax is computed relative to its own local maximum, the results must be re‑aligned to a common global reference. Suppose one tile computes a local maximum <math>m_1</math> and sum | |||
<math>S_1 = \sum_{i \in \text{tile 1}} \exp(x_i - m_1)</math> | |||
and another tile computes <math>m_2</math> and | |||
<math>S_2 = \sum_{j \in \text{tile 2}} \exp(x_j - m_2)</math>. The global maximum is given by | |||
<math display="block">m = \max(m_1, m_2)</math> | |||
Each local sum is then adjusted to this common reference: | |||
<math display="block">S_{\text{global}} = \exp(m_1 - m) S_1 + \exp(m_2 - m) S_2</math> | |||
A similar adjustment is applied to the local numerators (the weighted sums of <math>V</math>). The final attention output is obtained by dividing the aggregated numerator by <math>S_{\text{global}}</math>. This algebraic aggregation process guarantees numerical stability and correctness while never requiring the full matrix to be processed at once. | |||
==== Memory vs. Compute Trade-offs and Workflow Recap ==== | |||
Flash Attention V1 trades additional computations for a dramatic reduction in memory traffic. Although extra arithmetic is performed—such as recomputing local softmax values and adjusting them—these operations occur in fast SRAM. The overall workflow is as follows: | |||
Load small tiles of <math>Q</math>, <math>K</math>, and <math>V</math> from HBM into SRAM. Perform block‑wise matrix multiplication and softmax computations within SRAM, including computing local maximums, local sums, and partial numerators. Merge these local results through algebraic aggregation to produce the correct global softmax normalization. Finally, write the computed attention outputs back to HBM. | |||
In contrast, although regular attention to HBM executes fewer arithmetic operations, there is significant overhead. Each intermediate result must be stored back into the HBM and re-loaded for later reuse. This computation overhead significantly increases the elapsed runtime, which makes flash attention much more appealing. The HBM execution workload is analogous to map-reduce operations seen in distributed databases (where intermediate results after map operations are saved into the storage layer, but must be reloaded for reduce operations). | |||
==== | ==== Optional: Block‑Sparse Extension ==== | ||
In some cases, not every tile contributes equally. Flash Attention V1 can be extended to a block‑sparse variant where tiles that fall below a predetermined importance threshold are skipped entirely. This further reduces computation and memory transfers, echoing ideas from sparse attention methods. | |||
==== Optimizing the Backward Pass ==== | |||
In conventional attention models, the backward pass requires storing and reloading full intermediate activations (the <math>QK^\top</math> scores) from global memory, which increases both compute and memory costs. FlashAttention avoids this by recomputing necessary intermediate quantities on the fly in the fast SRAM during backpropagation. FlashAttention V2 and V3 further enhance this strategy by overlapping gradient computations with forward passes and partitioning work more finely among warps, thereby reducing I/O and achieving higher overall throughput. | |||
==== Limitations and Future Directions==== | |||
* A New CUDA Kernel | |||
** FlashAttention V1 requires a custom CUDA implementation, but the implementation needs significant engineering efforts and it may not be flexibly transferred across different GPU architectures. | |||
* Limited Ability on Other Deep Learning Models | |||
** Since every layer of a deep learning network needs to use GPU HBM, the limitation of IO-Aware implementation to the other deep learning models is believed to be solved in the future | |||
* Single GPU Focus | |||
** The current implementation is optimized for single-GPU setups. The potential of IO analysis in the future on multi-GPU is significant. | |||
===Connections to Adaptively Sparse Attention=== | |||
Flash Attention primarily optimizes standard dense attention through hardware-aware, memory-efficient block computations. However, a complementary approach is “Adaptively Sparse Attention“, which dynamically reduces the quadratic complexity by selecting only key token interactions that matter most, based on content similarity rather than fixed patterns. | |||
====Formulation==== | |||
Given queries <math>Q \in \mathbb{R}^{T \times d}</math>, keys <math>K \in \mathbb{R}^{T \times d}</math>, and values <math>V \in \mathbb{R}^{T \times d_v}</math>, Adaptively Sparse Attention performs: | |||
1. Standard attention scores: | |||
<math> | <math> | ||
\ | S = \frac{QK^T}{\sqrt{d}} | ||
\begin{cases} | </math> | ||
2. Adaptive sparsity mask <math>M \in \{0,1\}^{T\times T}</math> generation: | |||
<math> | |||
M_{ij} = \begin{cases} | |||
1, & \text{if } S_{ij} \text{ is among the top-} k \text{ scores for query token } i \\[6pt] | |||
0, & \text{otherwise} | |||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
3. Compute sparse attention output: | |||
<math> | |||
\text{Attention}(Q,K,V) = \text{softmax}(S \odot M) V | |||
</math> | |||
====Advantages & Complementarity==== | |||
Adaptively Sparse Attention complements Flash Attention by directly reducing the computational complexity through adaptive token selection: | |||
* Dynamic reduction of computational complexity: While Flash Attention tackles memory inefficiency, Adaptively Sparse Attention further reduces computation from <math>O(T^2)</math> to nearly <math>O(Tk)</math>. | |||
* Efficient handling of long sequences: The dynamic token selection mechanism pairs naturally with Flash Attention's block-wise memory optimization, combining hardware-aware design with algorithm-level sparsity for maximum efficiency. | |||
* Contextual adaptiveness: Rather than fixed or heuristic sparsity patterns (such as BigBird), the adaptiveness ensures important interactions are always preserved, achieving better accuracy-computation trade-offs. | |||
=== | == Flash Attention V2 == | ||
==== Background & Motivation ==== | |||
Language models have much longer context than before. | |||
Scaling transformers to long sequences is crucial: | |||
* language modelling (GPT-4, Clause, MPT) | |||
* high-resolution image understanding | |||
* code, audio, and video generation | |||
=== | ==== Challenges ==== | ||
* Attention bottleneck: quadratic time complexity, inefficient hardware utilization | |||
* Flash Attention V1: still not nearly as fast as optimized matrix-multiply (GEMM) operations, reaching only 25-40% of the theoretical maximum FLOPs/s | |||
* Suitability to Different Devices: Further research is needed to make Flash Attention V2 available to different devices, such as H100 GPUs, AMD GPUs. So far, the discussion has been focusing on the HBM and SRAM (NVIDIA GPUs with specific memory hierarchies). | |||
' | ==== Main Idea ==== | ||
In V1, its idea is to use SRAM, compute more, reduce reads/writes. However, it's mentioned previously that only 25%-40% of theoretical maximum FLOPs is reached. This inefficiency is due to suboptimal work partitioning between different thread blocks and warps on the GPU, causing either low-occupancy or unnecessary shared memory reads/writes. In V2, the main idea is to have a better work partitioning algorithm. The core improvements are: | |||
1. Reduce redundant operations: GPU is optimized for matmul operations, although non-matmul FLOPs only takes a fraction of total FLOPs, with optimized hardware, matmul operations are actually performed much faster than non-matmul operations. Thus it's important to reduce non-matmul FLOPs and spend as much time as possible doing matmul FLOPs. | |||
2. Parallelism: Distribute attention computation efficiently across thread blocks and warps. | |||
3. Efficient memory utilization: Optimize intra-thread communication, reducing memory overhead. | |||
==== Empirical Results ==== | |||
[[File:Flash_Attention_V2_Attention_forward_+_backward_speed_on_A100_GPU.png|600px]] | |||
Diagrams above shows how Flash Attention V2 performs across different sequence lengths and compare it to a standard attention implementation in PyTorch, FlashAttention, and FlashAttention in Triton. We can see an improvement in efficiency across all sequence lengths. We can see that FlashAttention-2 is 1.7-3.0× faster than FlashAttention, 1.3-2.5× faster than FlashAttention in Triton, and 3-10× faster than a standard attention implementation. The TFLOPs reached in V2 is about 70% of the theoretical TFLOPs achievable on A100 GPUs. | |||
== Flash Attention V3 == | |||
FlashAttention-2 was a significant improvement in speeding up attention mechanisms, but it only utilized 35% of the computational capacity of H100 GPUs. This left a lot of untapped potential, especially given the advanced features of Hopper GPUs, such as asynchronous execution and support for low-precision math. FlashAttention-3 was developed to fully exploit these capabilities, making attention computations faster, more efficient, and scalable for extremely long sequences. | |||
There are two main ideas in FlashAttention-3: | |||
====H100==== | |||
Before introducing Flash Attention V3, we first learn a little bit about the architecture of H100. Comparing it with A100, the major improvement is on the Asynchronous Execution aspect where we introduced one new hardware component and one one instruction. Apart from Asynchronous Execution aspect, we also introduced a new data precision which is FP8. | |||
* TMA (Tensor Memory Accelerator), which can move data between global and shared memory efficiently | |||
* WGMMA (Warp-Group Matrix Multiply-Accumulate) instructions which allows warp-group-wide operations to run while loading data. | |||
* FP8 precision, delivering 2× speedup over FP16/BFP16. | |||
These designs leads to Warp Specialization. Which means that different warps handle different tasks: | |||
* Producer warps, specialized to transfer data which typically requires less registers | |||
* Consumer warps, specialized to perform computation which typically requires more registers | |||
====Overlapping Tasks with Asynchronous Execution==== | |||
[[File:Flash Attentionv3-PingPong.png|800px|thumb|right|Pingpong Scheduling of Flash Attentionv3]] | |||
Hopper GPUs feature Tensor Cores which are specialized units for performing matrix multiplications at lightning speed. FlashAttention-3 takes advantage of these Tensor Cores by using warp specialization, where some GPU threads handle data movement (producers) while others focus on computation (consumers). These roles swap and run simultaneously, leading to "pingpong" scheduling to ensure the GPU is always busy and no time is wasted. | |||
* Why do we do Ping pong Scheduling? | |||
Matrix multiplication (matmul) is significantly more compute-intensive than other operations. In attention specifically, Matmul FLOPS is 512× exponential FLOPS and exponential FLOPS bottleneck reduces overall efficiency by 256× in FP8. | |||
* Trade-off | |||
This Ping pong Scheduling do, however, have a trade-off, it provides higher register pressure, requiring more registers to store GEMM accumulators and softmax I/O. And overall, we need effective balance between performance and resource usage. | |||
====Low-Precision Math (FP8)==== | |||
FlashAttention-3 introduces support for FP8 precision, which reduces memory usage and speeds up calculations compared to FP16. To maintain accuracy, it uses techniques like block quantization (storing one scalar per block) and incoherent processing, which smooths out numerical outliers. This results in a 2.6x reduction in numerical error compared to baseline FP8 implementations. | |||
'''Comparison to FlashAttention-2:''' | |||
* 1.5–2x faster attention computations | |||
* Up to 75% GPU utilization with FP16 precision | |||
====Empirical Results==== | |||
[[File:Flash_Attentionv3-Results.png|800px]] | |||
We reached 75% of the theoretical maximum TFLOPs/s on H100 GPUs using Flash Attention V3. And FlashAttention 3 reaches up to 740 TFLOPs/s which is up to 2.0× faster than V2. | |||
== | == Flash Fast Fourier Transform Convolution (FlashFFT Conv) == | ||
==== Introduction ==== | |||
Efficient sequence processing is always a fundamental challenge in deep learning, especially for natural language processing (NLP). Although convolutional models provide the state-of-the-art performance across various tasks, including NLP and time-series forecasting, their efficiency is often limited due to suboptimal hardware utilization. A potential solution to this problem is the Fast Fourier Transform (FFT), which theoretically operates in <math> O(N\text{log}N)</math> time complexity. However, conventional FFT implementations fail to fully leverage modern GPU architectures, leading to suboptimal efficiency. To address this, a highly optimized FFT-based convolution algorithm, namely Flash Fast Fourier Transform Convolution (Flash FFT Conv), is introduced. | |||
==== Innovation ==== | |||
A key innovation in Flash FFT Conv is the Monarch FFT Decomposition, which significantly improves the efficiency of Fast Fourier Transform (FFT)-based convolutions. Unlike traditional FFT algorithms, such as the Cooley-Tukey FFT, Monarch FFT Decomposition reformulates the FFT computation into a structured matrix representation that can be efficiently executed using matrix multiplications on tensor cores. | |||
<math> | ===== Importance of Monarch FFT Decomposition ===== | ||
The objective of Monarch FFT decomposition is to express FFT as a series of matrix multiplication. Doing so, it enables efficient GPU computation on specialized compute units (e.g., tensor cores of NVIDIA GPUS or matrix multiply units of TPUs). An order-<math>p</math> Monatch decomposition rewrites the FFT into <math>p</math> matrix-matrix multiply operations (which implies that we can map them onto these fast compute units efficiently). The value of <math>p</math> has a tradeoff. A higher <math>p</math> value imply smaller matrices to multiply, and thus, a lower number of FLOPs. But there is greater I/O communication overhead due to greater number of intermediate results. | |||
</math> | |||
[[File:Screenshot 2025-03-14 182945.png|600px|thumb|right|Example illustration of Monarch FFT decomposition <span id="monarch"></span>]] | |||
An illusrtation of Monarch FFT decomposition can be seen to the [[#monarch|right]]. To give an example of Monarch FFT decomposition, consider a matrix <math>N=N_1N_2</math>. An order-2 Monarch FFT decomposition expresses the FFT of <math>N</math> as <math>\mathcal{F}_N=\mathbf{P}(\mathbf{I}_{N_2}\otimes\mathcal{F}_{N_1})\mathbf{D}\mathbf{P}^{-1}(\mathbf{I}_{N_1}\otimes\mathcal{F}_{N_2})\mathbf{P}</math>, where <math>\oslash</math> is the Kronecker product, <math>\mathbf{P}</math> is the permutate matrix that reshapes the input to <math>N_1\times N_2</math>, transposes the intermediate matrix,and then reshape it back to <math>N</math>m, and <math>\mathbf{D}\in\mathbb{C}^{N\times N}</math> is a dinagonal matrix containing correctional values Twiddle factors. Twiddle factors are roots of unity <math>W^k_N=\exp{\left(-j\frac{2\pi k}{N}\right)}</math> where <math>N</math> is the number of points in the FFT, that are used to combine the results of smaller DFTs to generate larger DFTs (recall that FFT is a divide-and-conquer algorithm to compute DFT efficiently). | |||
To execute higher-order Monarch FFT decompositions, one can recursively apply the order-2 decomposition to <math>\mathcal{F}_{N_1}</math> and <math>\mathcal{F}_{N_2}</math>. | |||
====Domain-Specific Optimizations==== | |||
FlashFFTConv incorporates domain-specific strategies to reduce overhead: | |||
* Uses real-valued FFT for real-input convolutions, reducing FFT length by half. | |||
* Special-cases zero padding to avoid redundant matrix multiplies. | |||
* Fuses gating operations (e.g., <math>y = v \odot ((u \odot w) * k)</math>) common in Hyena or M2 models into the core kernel. | |||
==== Benefits ==== | |||
By leveraging this structured decomposition, FlashFFTConv achieves highly parallelized execution across the input sequence. This maximizes hardware utilization, resulting in faster computation. Furthermore, this approach minimizes high-latency global memory (HBM) access by performing most computations within on-chip memory (SRAM or shared memory). This reduces the I/O bottleneck that often limits FFT performance on modern GPUs. This leads to significant speedups over conventional FFT-based convolution methods. Additionally, the use of sparse and low-rank matrix structures further enhances computational efficiency, eliminating unnecessary operations and improving scalability for long-sequence processing. | |||
for | Through efficient memory access and tensor core optimization, Flash FFT Conv becomes a highly effective solution for accelerating FFT-based convolutions tasks, such as NLP and audio generation. | ||
==== Cost Model of order-p Monarch Decomposition ==== | |||
The | An adaptive cost modeling for GPU efficiency is employed by dynamically optimizing the Monarch decomposition order (p) based on sequence length and hardware capabilities. The previous subsection discusses how the FLOP cost decreases with higher p-orders due to the small matrix operations and that I/O costs linearly increase with p. Thus, a cost function combining FLOP cost and I/O cost is designed as: | ||
<math>C = C_{\text{flop}} + C_{\text{I/O}}</math> | |||
1 | <math>C = BH \sum_{i=1}^{p} \frac{16NN_i}{\gamma(N_i)} + \frac{4N}{\omega(i)}</math> | ||
<math | where, <math>N</math> is the sequence length with <math>N = \sum^p_{i=1}{N_i}</math>, <math>\omega</math> is the memory bandwidth at step <math>I</math>. Here, <math>\gamma</math> is FLOP efficiency represented as: | ||
[[File:cost_flashfft.png|600px|thumb|right|Compute costs of different order-p Monarch decompositions as sequence length increases on A100 GPU. <span id="cost_porder"></span>]] | |||
<math> | |||
\gamma(N_i) = | |||
\begin{cases} | |||
\tau_G, & \text{if } N_i < \mu \\ | |||
\tau_M, & \text{if } N_i \geq \mu | |||
\end{cases} | |||
</math> | |||
<math | where, <math>\tau_G</math> and <math>\tau_M</math> are empirically-achievable FLOPs on the GPU for general-purpose arithmetic and matrix-matrix multiply arithmetic, respectively. <math>\mu</math> denotes the matrix unit size. | ||
[[#cost_porder|Figure]] visualizes the cost model for FFT convolution with order-2, order-3, and order-4 decompositions when sequence length increases on an A100 GPU computed from the cost calculations from the above equations. The FLOP cost of an order-p decomposition grows as <math>O(N^{((p+1)/p)})</math>. However, shorter sequences (<math>N</math><1K and <math>N</math><4k) for higher-order decompositions (p=3 and 4, respectively) are more expensive because they produce matrices smaller than the GPU's matrix-matrix multiply unit. Additionally, at p=3, noticeable bumps are observed at around 64k. This occurs because intermediate results exceed SRAM capacity and spill into slower HBM memory (memory specs discussed in FlashAttention V1). The extra I/O cost increases runtime which is circumvented in p=4 with an extra decomposition. | |||
====Summary==== | |||
FlashFFTConv’s architecture offers: | |||
* Matrix-based decomposition for high FLOP utilization. | |||
* Broadcast and tiling over sequence to maximize fusion and reuse. | |||
* Efficient on-chip memory access, reducing I/O bottlenecks. | |||
* Scalability to 4M+ sequence lengths with reduced memory footprint and faster wall-clock time than standard FFTs. | |||
This architecture unlocks fast and memory-efficient FFT convolutions for NLP, audio, and genomics applications. | |||
== Simple Hardware-Efficient Long Convolutions for Sequence Modeling == | |||
=== Introduction === | |||
State space models (SSMs) have emerged as a powerful general-purpose sequence modeling framework. It scale nearly linearly in sequence length and have shown SOTA performance on a range of sequence modeling tasks. However, SSMs rely on sophisticated mathematical structures to train effectively in deep networks. These structures generate a convolution kernel as long as the input sequence by repeatedly multiplying a hidden state matrices. This process could become unstable and requires hand-crafted initialization. Hence, people have tried parameterize the long convolution kernel directly. In doing so, people have to overcome two challenges, the quality of model and the runtime performance. This paper, by employing simple regularization techniques and an IO-aware convolution algorithm, have addressed these challenges and made improvements. | |||
=== FlashButterfly === | |||
FlashButterfly is an IO-aware convolution algorithm that enhances runtime efficiency for long sequences. It employs Butterfly decomposition, inspired by Fast Fourier Transform (FFT) algorithms, to break down convolutions into smaller, hierarchical computations. | |||
* '''Mechanism''': By structuring convolutions as a series of matrix multiplies, FlashButterfly reduces memory I/O, optimizing data movement between GPU global and shared memory. Blockwise kernel execution further minimizes SRAM usage. | |||
* '''Regularization''': Techniques like kernel squashing ensure smoothness, recovering SSM performance on tasks like the Long Range Arena (LRA). | |||
* '''Performance''': Achieves a 2.2× speedup over standard convolutions and sets state-of-the-art results on Path256 (64K sequence length) by 29.1 points, with 7.2× faster training than prior models. | |||
[[File:FlashButterfly.png]] | |||
Butterfly decomposition, central to FlashButterfly, mirrors FFT’s hierarchical structure, as depicted in diagrams like the one referenced. | |||
It recursively breaks convolutions into smaller units, optimizing GPU memory access and computation, and extends to FlashFFTConv’s matrix-based FFTs. | |||
==== Butterfly Decomposition ==== | |||
Butterfly decomposition is a computational framework central to FlashButterfly’s optimization of long convolutions, drawing from the hierarchical structure of Fast Fourier Transform (FFT) algorithms.It recursively breaks down convolutions into smaller operations, reducing memory I/O and computational complexity on GPUs. In this framework, the Butterfly matrices (which replace the standard DFT matrices) are parameterized and trained end-to-end. This approach increases the expressiveness of the convolutional kernels without incurring additional FLOPs; in practice, it has been shown to reduce the number of parameters while maintaining or even improving model accuracy. For instance, replacing Transformer MLPs with learned Butterfly layers can achieve similar performance with 30% fewer parameters on WikiText103. | |||
The decomposition mirrors FFT’s butterfly diagram, where a transform is split into smaller units combined via butterfly operations. For a sequence of length <math>N</math>, a convolution <math>y = x \ast h</math> is represented as a matrix-vector product <math>y = T_h x</math>, where <math>T_h</math> is a Toeplitz matrix. FlashButterfly approximates <math>T_h</math> as a product of sparse butterfly matrices: | |||
:<math>T_h \approx \prod_{i=1}^L B_i,</math> | |||
where each <math>B_i</math> performs a stage of computation, and <math>L \approx \log N</math>. A single butterfly, for inputs <math>x_i</math> and <math>x_{i+N/2}</math>, computes: | |||
:<math>\begin{bmatrix} y_i \\ y_{i+N/2} \end{bmatrix} = \begin{bmatrix} 1 & h_k \\ 1 & -h_k \end{bmatrix} \begin{bmatrix} x_i \\ x_{i+N/2} \end{bmatrix},</math> | |||
= | with <math>h_k</math> as a kernel weight, regularized for smoothness.<ref name="SimpleConv"/> This yields <math>O(N \log N)</math> complexity, compared to <math>O(N^2)</math> for direct convolution. | ||
By structuring computations hierarchically, FlashButterfly minimizes GPU global memory accesses, using blockwise execution to fit operations within shared memory. This enables tasks like Path256 (64K tokens) to achieve a 29.1-point accuracy gain and 7.2× faster training. The approach extends to FlashFFTConv’s frequency-domain optimizations, where similar decompositions enhance FFT efficiency. | |||
=== FlashFFTConv: Efficient IO-Aware Convolution === | |||
FlashFFTConv is an IO-efficient convolution algorithm designed for long sequence modeling, and complements the challenges addressed in this paper. While traditional convolutions have <math>O(N^2)</math> complexity, FlashFFTConv leverages Fast Fourier Transform (FFT) and GPU tensor cores to reduce this to <math>O(N \log N)</math>, while maintaining model quality. | |||
* '''Key Components''' | |||
** FFT-Based Convolution: Replaces standard convolution with FFT, reducing asymptotic complexity. | |||
** Monarch Decomposition: Decomposes FFTs into matrix multiplies, allowing optimized execution on GPU tensor cores. | |||
** Blockwise Kernel Execution: Reduces SRAM requirements by performing smaller matrix multiplications. | |||
* '''Hardware Optimization''' | |||
** Uses mixed precision (e.g., FP8) and warp-group tensor core instructions (WGMMA) on H100 GPUs. | |||
** Supports asynchronous scheduling via TMA and ping-pong buffering. | |||
* ''' | * '''Performance Results''' | ||
** Up to 7.9× faster than PyTorch convolution. | |||
** Up to 5.6× memory savings. | |||
** Faster than FlashAttention-v2 at sequence lengths of 2k+. | |||
** Enables models to process sequences as long as 4 million tokens. | |||
This method provides an alternative path to efficient long-sequence modeling through Fourier-based convolution rather than attention, with strong empirical and hardware-level performance. | |||
= Topic 5: KD / Pruning / Sharing = | |||
==Introduction== | |||
Knowledge Distillation (KD), Pruning, and Sharing are three strategies to make language models smaller, faster, and more efficient without sacrificing their performance. KD works by having a large, powerful "teacher" model that teachs a smaller "student" model how to behave similarly so the student model can do almost as well as the teacher but with less effort. Pruning can be thought of trimming a tree by which it removes unnecessary or less important parts of the model, making it more compact and faster while keeping its core abilities intact. Sharing is about reusing parts of the model across different tasks or layers, so there is no need to build everything from scratch, saving time and resources. | |||
While KD focuses on teaching a smaller model to imitate a larger one, pruning cuts away the unnecessary parts to make the model cleaner, and sharing reuses parts to avoid having unnecessary extra work. These techniques contribute together to create language models that are not only powerful but also efficient enough to run on devices with limited resources, like smartphones or laptops. | |||
=== | ===Knowledge Distillation (KD)=== | ||
KD transfers knowledge from a large, well-trained teacher model to a smaller student model. The student learns not only from the hard labels but also by mimicking the teacher’s soft output distributions or internal representations. In the work by Muralidharan et al. , KD is a critical component in recovering the performance lost during the compression of a 15B-parameter model. By distilling knowledge during retraining, the authors were able to produce smaller models (MINITRON 8B and 4B) that not only match but, in some cases, outperform models trained from scratch—even while using a fraction of the training data. | |||
The | [[File:KD.png|500px|thumb|right|Example illustration of Sequence-level knowledge distillation <span id="KD"></span>]] | ||
===Improvements to Knowledge Distillation=== | |||
'''1. Born-Again Networks (BANs): ''' | |||
Repeated training iterations to simplify the dataset. | |||
Improves performance for lower-capacity NAT models. | |||
'''2. Mixture of Experts (MoE): ''' | |||
Reduces data diversity by training on simpler expert translations. | |||
'''3. Sequence-Level Interpolation: ''' | |||
Selects the best candidate translation based on BLEU score, improving high-capacity NAT models. | |||
===Metrics for Distilled Data=== | |||
* | * '''Data Complexity''' measures how much variability is present in the translations, which is calculated by fitting an alignment model and compute the average of token-level conditional entropy. | ||
* | * '''Data faithfulness''' evaluates how closely the distilled data aligns with the original real-world data. | ||
<math> | |||
= | F(d)=\frac{1}{\left|\mathcal{V}_x\right|} \sum_{x \in \mathcal{V}_x} \sum_{y \in \mathcal{V}_y} p_r(y \mid x) \log \frac{p_r(y \mid x)}{p_d(y \mid x)} | ||
</math> | |||
===Distillation Best Practices=== | |||
* KD should focus primarily on '''logit-based loss''' rather than using a weighted combination of multiple losses. | |||
* Use '''Kullback-Leibler Divergence (KLD)''' loss as it outperforms MSE and cosine losses in pruned settings. | |||
* Incorporate '''intermediate state distillation''' only when model depth is significantly reduced. | |||
* Distilling from the final training stage model (instead of early checkpoints) yields better results. | |||
In the | ==Compact Language Models via Pruning and Knowledge Distillation== | ||
=== Introduction === | |||
In this paper, the authors propose a data‑efficient approach that prunes an existing 15 B‑parameter Nemotron‑4 model and retrains it with less than 3 % of the original training data to derive smaller variants by factors of 2–4× . This method achieves up to 40× reduction in training tokens per model and delivers 1.8× compute cost savings across the full model family. The resulting Minitron‑8B and Minitron‑4B models exhibit up to 16 % improvement in MMLU scores compared to scratch‑trained counterparts, and perform on par with or better than popular community models like Mistral 7B, Gemma 7B, and Llama‑3 8B. | |||
=== Model Compression Approach === | |||
This work follows a structured approach to model compression: | |||
# Structured Pruning Across Multiple Axes: The paper prunes various dimensions of the model—neurons (in MLPs), attention heads, embedding channels, and even layers—using an activation‐based importance metric. | |||
# Knowledge Distillation Retraining: After pruning, the model is retrained with a knowledge distillation loss that transfers the “knowledge” of the original (teacher) model to the pruned (student) model. This retraining is done efficiently using only a small fraction of the original training tokens. | |||
# Neural Architecture Search: A lightweight search is performed to select feasible pruned architectures that meet a target parameter budget, ensuring both efficiency and performance. | |||
=== Pruning Techniques === | |||
=== | ==== Width Pruning (Pruning Individual Model Components) ==== | ||
This is how importance scores are calculated for each component (neuron, head, embedding channels) | |||
'''Neurons in MLPs''' | |||
For a given neuron in an MLP layer, the importance score is computed based on the activations it produces. The activation of a neuron is the output of the non-linear function (e.g., ReLU) applied to the weighted sum of its inputs. | |||
Mathematically, the importance score for the <math>i^{th}</math> neuron in an MLP layer is given by: | |||
<math> | |||
F_{\text{neuron}}^{(i)} = \sum_{\mathbf{B},\mathbf{S}} \mathbf{X} \big(\boldsymbol{W}_{1}^{i}\big{)}^{T} | |||
</math> | |||
Here: | |||
* <math>\mathbf{X}</math> is the input to the MLP layer. | |||
* <math>\boldsymbol{W}_{1}^{i}</math> is the <math>i^{th}</math> row of the weight matrix <math>\boldsymbol{W}_{1}</math>. | |||
* <math>\sum_{\mathbf{B},\mathbf{S}}</math> denotes aggregation over the '''batch''' and '''sequence''' dimensions. | |||
The paper experiment with different aggregation functions (e.g., mean, L2 norm, variance) to compute the importance score. They find that using the '''L2 norm''' for batch aggregation and the '''mean''' for sequence aggregation yields the best results. | |||
'''Attention Heads in MHA Layers''' | |||
For attention heads, the importance score is based on the attention output produced by each head. The attention output is computed using the standard multi-head attention mechanism: | |||
<math> | |||
\text{MHA}(\mathbf{X}) = \text{Concat}(\text{head}_{1}, \ldots, \text{head}_{L}) \cdot \boldsymbol{W}^{O} | |||
</math> | |||
where each head is computed as: | |||
<math>\ | <math> | ||
\text{head}_{i} = \text{Attn}(\mathbf{X}\boldsymbol{W}^{Q,i}, \mathbf{X}\boldsymbol{W}^{K,i}, \mathbf{X}\boldsymbol{W}^{V,i}) | |||
</math> | |||
The importance score for the <math>i^{th}</math> attention head is then computed as: | |||
<math>\ | <math> | ||
F_{\text{head}}^{(i)} = \sum_{\mathbf{B},\mathbf{S}} \|\text{Attn}(\mathbf{X}\boldsymbol{W}^{Q,i}, \mathbf{X}\boldsymbol{W}^{K,i}, \mathbf{X}\boldsymbol{W}^{V,i})\|_{2} | |||
</math> | |||
<math>\ | Here: | ||
* <math>\|\cdot\|_{2}</math> denotes the L2 norm of the attention output. | |||
* <math>\sum_{\mathbf{B},\mathbf{S}}</math> aggregates over the batch and sequence dimensions. | |||
'''L2 norm''' for batch aggregation and the '''mean''' for sequence aggregation work best. | |||
'''Embedding Channels''' | |||
For embedding channels, the importance score is based on the '''Layer Normalization (LayerNorm)''' output. LayerNorm is applied to the embeddings to normalize the activations across the embedding dimensions. The importance score for the <math>i^{th}</math> embedding channel is computed as: | |||
<math> | |||
F_{\text{emb}}^{(i)} = \sum_{\mathbf{B},\mathbf{S}} \text{LayerNorm}(\mathbf{X})_{i} | |||
</math> | |||
Here: | |||
* <math>\text{LayerNorm}(\mathbf{X})_{i}</math> is the <math>i^{th}</math> dimension of the LayerNorm output. | |||
* <math>\sum_{\mathbf{B},\mathbf{S}}</math> aggregates over the batch and sequence dimensions. | |||
==== Depth (Layers) Pruning ==== | |||
For depth pruning (removing entire layers), the authors use two metrics to compute layer importance: | |||
1. '''Perplexity (PPL)''': The effect of removing a layer on the model’s perplexity (a measure of how well the model predicts a sequence). | |||
2. '''Block Importance (BI)''': The cosine distance between the input and output of a layer, which measures how much the layer transforms its input. | |||
The BI score for layer <math>i</math> is computed as: | |||
<math> | |||
\text{BI}_{i} = 1 - \mathbb{E}_{\mathbf{X},t} \frac{\mathbf{X}_{i,t}^{T} \mathbf{X}_{i+1,t}}{\|\mathbf{X}_{i,t}\|_{2} \|\mathbf{X}_{i+1,t}\|_{2}} | |||
</math> | |||
Here: | |||
* <math>\mathbf{X}_{i}</math> is the input to layer <math>i</math>. | |||
* <math>\mathbf{X}_{i,t}</math> is the <math>t^{th}</math> row of <math>\mathbf{X}_{i}</math>. | |||
* <math>\mathbb{E}_{\mathbf{X},t}</math> denotes the expectation over the input and sequence dimensions. | |||
The authors find that '''BI''' is faster to compute than PPL and provides a good approximation of layer importance. Additionally, removing layers selectively can retain strong model performance while reducing computational costs. | |||
=== Residual Transfer for Attention Head Pruning === | |||
To reduce accuracy loss after pruning attention heads, the authors introduce a residual transfer technique. Instead of discarding pruned heads entirely, their information is redistributed to the remaining heads using a symmetric formula: | |||
<math> \text{new\_head}_i = \text{head}_i + (\text{head}_i - \text{head}_{2K - i + 1}) </math> | |||
This helps preserve knowledge from pruned heads, improving performance during retraining. In models with grouped-query attention, this is applied only to query heads. The method is lightweight and boosts model accuracy, especially in aggressive pruning settings. | |||
= | ==== Pruning Best Practices ==== | ||
* '''Width pruning''' (e.g., neurons, heads, embedding channels) is more effective than depth pruning after retraining. | |||
* '''Activation-based importance metrics''' are effective and computationally cheap, avoiding the need for backward gradients. | |||
* (Batch=L2, Sequence=Mean) aggregation functions yield the best results when calculating importance scores. | |||
* | |||
* '''Iterative pruning''' (prune → retrain → prune) significantly outperforms one-shot pruning for high compression targets like 4B from 15B. | |||
* Adding residual information from pruned attention heads back into remaining heads boosts performance. | |||
* Order matters: performing one width‑prune cycle first, then a shallow depth‑prune, then a second width pass yields up to +2.6 MMLU over any other ordering at 4 B | |||
=== Knowledge Distillation Retraining === | |||
Knowledge distillation is used to retain knowledge from the original large model after pruning. In this process, a smaller "student" model is trained using a distillation loss that aligns its output with the original "teacher" model. | |||
The retraining phase leverages only a small fraction of the original training tokens, significantly reducing computational costs. The key components of knowledge distillation include: | |||
* '''Distillation loss:''' A combination of cross-entropy and KL divergence loss is applied to match the student’s output distribution with the teacher’s predictions. | |||
* '''Token-efficient training:''' Only a subset of the original dataset is used, as full retraining would negate the benefits of compression. | |||
* '''Iterative pruning and retraining:''' The best results are achieved when distillation is applied iteratively with pruning rather than in a one-shot manner. | |||
Empirical results show that knowledge distillation allows the pruned models to maintain high perplexity accuracy and generalization performance, even at significantly smaller model sizes. | |||
=== Neural Architecture Search (NAS) === | |||
After pruning, Neural Architecture Search (NAS) is employed to identify optimal architectural configurations under a given parameter budget. Instead of manually selecting pruned architectures, NAS automates the process to maximize efficiency and performance. | |||
The NAS process involves: | |||
# '''Evaluating pruned architectures''' based on computational efficiency and accuracy trade-offs. | |||
# '''Selecting optimal configurations''' for both width-pruned and depth-pruned models. | |||
# '''Fine-tuning the final pruned model''' to maximize performance. | |||
Findings indicate that NAS-selected architectures outperform manually pruned baselines of the same model size. The approach ensures that the compressed models retain the highest possible accuracy while significantly reducing computational costs. | |||
=== Experimental Results and Findings === | |||
The structured pruning approach combined with distillation yields compressed models that retain a high degree of accuracy: | |||
* The '''8B and 4B models''' retain over '''95% of the original model’s accuracy''' while being significantly smaller. | |||
* The '''4B model achieves a 4× reduction in parameters''' with minimal loss in perplexity performance. | |||
* The '''8B model maintains nearly full accuracy''' compared to the original 15B model, making it a viable alternative with lower compute requirements. | |||
=== Conclusion and Implications === | |||
This study presents a '''systematic and cost-efficient method''' for compressing large-scale language models with minimal retraining. The combination of structured pruning, knowledge distillation, and NAS enables significant reductions in model size while maintaining strong performance. | |||
Key takeaways include: | |||
* '''Pruning across multiple axes''' (width and depth) effectively reduces model size while preserving accuracy. | |||
* '''Distillation requires only a fraction of training tokens''', making retraining computationally feasible. | |||
* '''NAS automates architectural optimization''', leading to better compressed models than manual selection. | |||
These techniques are broadly applicable to other large models beyond Nemotron-4, making them relevant for real-world deployment scenarios. Future work could explore: | |||
* Extending pruning techniques to '''multimodal and vision-language models'''. | |||
* Investigating '''more aggressive pruning strategies''' for extreme model compression. | |||
* Optimizing '''pruned models for real-time inference on edge devices'''. | |||
==Attention Is All You Need But You Don’t Need All Of It For Inference of Large Language Models== | |||
This paper explores how strategically omitting layers at inference can drastically cut compute and latency while preserving performance. They focus on Llama‑v2 models and show that dropping up to 33 % of deeper attention sublayers in the 13 B variant incurs only a 1.8 % average drop on the OpenLLM benchmark, yet yields significant speedups without extra fine‑tuning. This simple “inference‑time attention removal” (ITAR) method outperforms more complex pruning schemes by targeting the most redundant components post‑training. | |||
This | ===The Problem: Inference Complexity=== | ||
Inference in LLMs is costly because of the self-attention mechanism, which scales quadratically with input length. This creates a challenge, especially for applications requiring real-time responses. Researchers have previously explored various methods to optimize inference, including pruning, quantization, and speculative decoding, but this paper focuses on a more direct approach: skipping unnecessary layers. | |||
===Key Idea: Skipping Layers Without Significant Performance Loss=== | |||
The core hypothesis of the paper is that not all layers contribute equally to the final output of an LLM. Specifically, the deeper layers (closer to the output) exhibit higher similarity with their preceding layers, meaning that dropping some of them may have minimal impact on performance. To test this, the authors conduct experiments on Llama-v2 (7B and 13B models) and compare different strategies for skipping layers. | |||
===Method: Selective Layer Skipping=== | |||
Consider a Transformer model with <math>L</math> layers, where each layer consists of an attention sub-layer and a multi-layer perceptron (MLP) sub-layer. We define each layer as: | |||
<math display="block">\text{Layer}_i = (\text{Attention}_i, \text{MLP}_i)</math> | |||
for <math>i \in \{1, 2, \dots, L\}</math>. | |||
The paper evaluates three techniques for skipping components of Transformer layers: | |||
1. Skipping MLP Layers: The feedforward (MLP) sub-layers from the last few layers are removed. | |||
If we skip the last <math>k</math> MLP layers while keeping the attention layers, the modified model is: | |||
== | <math display="block">M_{\text{skip MLP}} = \left\{ (\text{Attention}_i, \text{MLP}_i) \mid i \in [1, L-k] \right\} \cup \left\{ (\text{Attention}_i, \emptyset) \mid i \in [L-k+1, L] \right\}</math> | ||
2. Skipping Attention Layers: The self-attention sub-layers from the last few layers are removed. | |||
If we skip the last <math>k</math> attention layers while keeping the MLP layers, the modified model is represented as: | |||
<math display="block">M_{\text{skip attention}} = \left\{ (\text{Attention}_i, \text{MLP}_i) \mid i \in [1, L-k] \right\} \cup \left\{ (\emptyset, \text{MLP}_i) \mid i \in [L-k+1, L] \right\}</math> | |||
3. Skipping Entire Transformer Blocks: Both attention and MLP components are removed from some of the last layers. | |||
If we skip both the attention and MLP sub-layers in the last <math>k</math> layers, we obtain: | |||
== | <math display="block">M_{\text{skip block}} = \left\{ (\text{Attention}_i, \text{MLP}_i) \mid i \in [1, L-k] \right\} \cup \left\{ (\emptyset, \emptyset) \mid i \in [L-k+1, L] \right\}</math> | ||
The image below gives the skip mechanisms for skipping single layers and attention layers during inference: | |||
[[File:skip_mechanism.png|600px]] | |||
The models were tested across four benchmarks: ARC, HellaSwag, TruthfulQA, and MMLU, which measure reasoning, common sense, truthfulness, and general knowledge. | |||
===Empirical Results & Findings: Attention Layers Are Less Crucial Than MLP Layers=== | |||
The empirical results are shown below: | |||
[[File:skip_results.png|600px]] | |||
As expected, results dropped after skipping layers except for TruthfulQA. It had already been observed that larger language models are less truthful, but this interesting result now shows that reducing the size of already trained models can actually make them more truthful. The observation still holds even if the last layer is preserved. Skipping attention layers only results in a 1.8% drop in accuracy when keeping 66% of the network compared to a 13.1% decrease in performance when dropping only the MLP layers. | |||
[[File:Screenshot 2025-03-15.png|400px|thumb|Cosine similarity of Llama-v2 layers with the previous layer]] | |||
The results demonstrate a clear pattern: | |||
* Dropping entire Transformer blocks leads to a significant performance drop. | |||
* Dropping MLP layers leads to larger performance degradation compared to dropping attention layers. | |||
* Dropping attention layers results in the best trade-off between speed and performance, with only a 1.8% drop in accuracy when 33% of attention layers are removed. Removing 33% of attention layers led to an 18% speedup in Llama-2-13B. | |||
Interestingly, the TruthfulQA benchmark showed an increase in accuracy when some layers were skipped, suggesting that reducing model complexity might reduce hallucinations. | |||
The paper provides empirical evidence that deeper layers contribute less unique information compared to earlier layers. The figure below shows cosine similarity between successive layers, highlighting that deeper layers are more redundant. | |||
The | |||
=== Conclusion === | |||
The paper investigated the effect of dropping the last layers from the 7B and 13B Llama2 models. The authors observed that dropping attention layers leads to less performance decrease than MLP layers. This demonstrates the potential that improvements can be made over dropping entire layers compared to just dropping the attention layers. | |||
==SliceGPT: Compress Large Language Models by deleting rows and columns== | |||
===Overview=== | |||
SliceGPT is a post‑training sparsification method that compresses large language models by deleting entire rows and columns from weight matrices via orthonormal transformations and principal-component projections, reducing up to 30 % of parameters while maintaining over 90 % of zero-shot performance across LLAMA‑2, OPT, and Phi‑2 models with minimal recovery fine‑tuning. It leverages a novel concept called computational invariance—in which applying an orthogonal matrix to weights leaves the model functionally unchanged—enabling structured pruning without additional sparsity‑specific data structures. The sliced models run 34 %–36 % faster on both consumer (24 GB) and data‑center (40 GB A100) GPUs without custom kernel optimizations, offering a practical path to deploy high‑capacity LLMs on fewer resources. | |||
===Background=== | |||
This section introduces some necessary background on transformer architectures and notations used in this paper. | |||
====Transformer networks==== | |||
'''Embeddings''': Let <math>D</math> be the embedding dimension of our transformer, <math>N</math> be the sequence length. Embedding matrix <math>\mathbf{W}_{\mathrm{embd}}</math> is indexed by input sequence <math>s</math> to produce the initial signal <math>X</math> with shape <math>N × D</math> | |||
'''LayerNorm''': LayerNorm operation subtracts the mean from each row of the input matrix, divides the row by its standard deviation, rescales (columnwise), and adds an offset. | |||
<math>\mathrm{LayerNorm}(\mathbf{X})=\mathrm{RMSNorm}(\mathbf{XM})\mathrm{diag}(\boldsymbol{\alpha})\sqrt{D}+\mathbf{1}_{N}\boldsymbol{\beta}^{\top}</math> | |||
'''Attention Blocks''':The attention block has four matrices: <math>\mathbf{W}_{\mathrm{k}}</math> , <math>\mathbf{W}_{\mathrm{q}}</math> , <math>\mathbf{W}_{\mathrm{v}}</math> and <math>\mathbf{W}_{\mathrm{o}}</math> , each of dimension <math>D × D</math>. The input signal arriving into the block is projected into the Key (<math>\mathbf{XW}_{\mathrm{k}}</math> ), Query (<math>\mathbf{XW}_{\mathrm{q}}</math> ), and Value (<math>\mathbf{XW}_{\mathrm{v}}</math> ) matrices, which are then split into multiple heads. A nonlinear operation <math>\sigma</math> is applied at each head before the signals are combined and multiplied by the output weight matrix <math>\mathbf{W}_{\mathrm{o}}</math>. | |||
'''FFN Blocks''':This is a Multi-layer Perceptron (MLP), which consists of a linear layer <math>\mathbf{W}_{\mathrm{1}}</math>, followed by an element-wise operation <math>\sigma</math>, followed by a second linear layer: <math>\sigma(\mathbf{X}\mathbf{W}_1+\boldsymbol{b}_1)\mathbf{W}_2+\boldsymbol{b}_2</math>. | |||
===Key Contributions=== | |||
====Computational invariance==== | |||
If <math>\mathbf{Q}</math> is an orthogonal matrix, i.e, <math>\mathbf{Q}^\top\mathbf{Q}=\mathbf{Q}\mathbf{Q}^\top=\mathbf{I}</math> . | |||
Multiplying a vector <math>\boldsymbol{x}</math> by <math>\mathbf{Q}</math> does not change the norm of the vector, since <math>\|\mathbf{Q}\boldsymbol{x}\|=\sqrt{\boldsymbol{x}^\top\mathbf{Q}^\top\mathbf{Q}\boldsymbol{x}}=\sqrt{\boldsymbol{x}^\top\boldsymbol{x}}=\|\boldsymbol{x}\|</math>. | |||
The authors demonstrated that orthogonal transformations can be applied to weight matrices in transformer networks without altering the model's output. We can apply any orthogonal transformation <math>\mathbf{Q}</math> to the weights of the transformer without changing the result, so the computation can be performed in any transformed state. We refer to this as a computational invariance, and define it in the following theorem. | |||
[[File:invariance_Theorem.png|800px|Figure: Computational invariance]] | |||
This invariance enables structured pruning by modifying weights while preserving functionality, a foundational insight for post-training compression. | |||
====SliceGPT==== | |||
The computational invariance is only effctive to RMSNorm-connected networks, so we convert the network to RMSNorm by absorbing the linear blocks of LayerNorm into the adjacent blocks first. | |||
[[File:rmsnorm.png|800px|Figure: From LayerNorm to RMSNorm]] | |||
After every LayerNorm in the transformer has been converted to RMSNorm, we will apply the computational-invariance idea, and can select any <math>Q</math> to modify the model. | |||
[[File:QwithRMSNorm.png|500px|Figure: Q with RMSNorm]] | |||
To compute the matrices <math>\mathbf{Q}_{\ell}</math> , we use PCA. We select a calibration dataset from the training set, run it through the model (after converting LayerNorm operations into RMSNorm), and extract the orthogonal matrix of the layer. We use the output of the transformed network to calculate the orthogonal matrices of the next layers. More precisely, if <math>\mathbf{X}_{\mathrm{\ell,i}}</math> is the output of the <math>\boldsymbol{\ell}^{\mathbf{th}}</math> RMSNorm block for the <math>\boldsymbol{i}^{\mathbf{th}}</math> sequence in the calibration dataset, we compute | |||
<math>\mathbf{C}_\ell=\sum_i\mathbf{X}_{\ell,i}^\top\mathbf{X}_{\ell,i}</math> and set <math>\mathbf{Q}_{\ell}</math> to the be the eigenvectors of <math>\mathbf{C}_{\ell}</math>, sorted by decreasing eigenvalues. | |||
Then we apply the deletion matrix <math>\mathbf{D}</math> (<math>D\times D_{\mathrm{small}}</math>) to the operations preceding and succeeding the construction of that matrix, which have already been multiplied by <math>\mathbf{Q}</math> in the above. That will delete rows of <math>\mathbf{W}_{\mathrm{in}}</math> and columns of <math>\mathbf{W}_{\mathrm{out}}</math> and <math>\mathbf{W}_{\mathrm{embd}}</math>, and also delete both rows and columns of the matrix <math>\mathbf{Q}_{\ell-1}^\top\mathbf{Q}_\ell</math> (in Figure [[:File:QwithRMSNorm.png|RMSNorm with <math>\mathbf{Q}</math> transformation]]). | |||
=====method===== | |||
SliceGPT’s approach is elegant and practical: | |||
* '''Unlocking Invariance''': Transformers often use normalization layers like RMSNorm. The paper shows that applying an orthogonal matrix <math>\mathbf{Q}</math> (where <math>\mathbf{Q}^\top \mathbf{Q} = \mathbf{I}</math>) to weights doesn’t change the output because RMSNorm ignores such rotations. Mathematically: <math>\text{RMSNorm}(\mathbf{X} \mathbf{Q}) \mathbf{Q}^\top = \text{RMSNorm}(\mathbf{X})</math>. If the model uses LayerNorm instead, it’s first converted to RMSNorm. | |||
* '''Slicing with PCA''': | |||
** For each transformer block, activations from a small calibration dataset (e.g., WikiText-2) are collected. | |||
** Principal Component Analysis (PCA) finds the most important directions in these activations, encoded in <math>\mathbf{Q}_\ell</math> for layer <math>\ell</math>. | |||
** Weight matrices are rotated with <math>\mathbf{Q}_\ell</math>, and the least important rows and columns (low PCA components) are sliced off, shrinking the embedding dimension. | |||
** Residual connections get a tweak: a small matrix <math>\mathbf{Q}_{\ell-1}^\top \mathbf{Q}_\ell</math> keeps everything aligned. | |||
* '''No Fine-Tuning Needed''': This runs on a single GPU in hours (e.g., 3.5 hours for LLAMA-2 70B) and skips retraining, though optional fine-tuning can boost results. | |||
2 | |||
===Empirical Result=== | |||
====Generation Task==== | |||
The table below shows the perplexity obtained by various slicing levels using the WikiText-2 dataset on both the OPT and LLAMA-2 model families. The performance of SliceGPT improves as the model size increases. Comparing SliceGPT with SparseGPT, we see that SparseGPT 2:4 performs worse than SliceGPT with 25% slicing in all LLAMA-2 models. For OPT, we see that 30% sliced models beat 2:4 sparsity for all model sizes except 2.7B. | |||
[[File:results on WikiText2.png|700px|Figure: Results on WikiText2]] | |||
== | ====Zero-shot Tasks==== | ||
SliceGPT is assessed across five well-known zero-shot tasks: PIQA; WinoGrande; HellaSwag; ARC-e and ARC-c. | |||
The following figure shows the average scores achieved by the sliced models across these tasks. | |||
[[File:Mean zero-shot accuracy.png|700px|Figure: Mean zero-shot accuracy]] | |||
=== | ===Limitation and Future Work=== | ||
SliceGPT effectively reduces inference costs by slicing weight matrices using an orthogonal transformation computed via PCA, but it still retains more parameters than methods like SparseGPT and is less beneficial for smaller models where dense architectures perform better. The method’s reliance on PCA can be sensitive to numerical precision and may not be optimal, and it currently operates as a standalone technique without combining with complementary approaches such as quantization or additional structural pruning. Future work could explore alternative ways to compute the transformation, integrate other compression strategies, and further investigate the theoretical aspects of computational invariance to design even more efficient models. | |||
* Smaller Models Struggle: SliceGPT shines on giants like LLAMA-2 70B, but smaller models (under 13B parameters) lose more accuracy when sliced. | |||
* Calibration Matters: The dataset used for PCA (e.g., WikiText-2 vs. Alpaca) affects results—choosing the right one is key. | |||
* No Sparse Magic: It doesn’t create hardware-friendly sparse patterns (like 2:4 sparsity), though its dense matrices still speed things up. | |||
* Room to Grow: Combining SliceGPT with quantization or exploring smarter ways to pick <math>\mathbf{Q}_\ell</math> (beyond PCA) could push efficiency further. | |||
==EchoAtt: Attend, Copy, then Adjust for More Efficient Large Language Models== | |||
This paper introduces a novel framework to make transformer-based LLMs more efficient while maintaining their performance. The motivation behind their work is that when studying larger models, it is observed that inner layers contain highly similar attention matrices. The similarity is determined by computing the cosine similarity between attention matrices at different layers. Therefore, they suggest a knowledge distillation-based framework that shares attention between layers containing similar matrices while unique layers are maintained as they contain distinct attention patterns. These critical layers are usually located within the first layers of the network. | |||
=== | ===Contributions=== | ||
* Introduce EchoAtt framework to optimize transformer-based LLMs. | |||
* Propose a method to share attention matrix. | |||
* Apply this approach in a knowledge distillation setting. | |||
* Demonstrate the effectiveness of EchoAtt reducing inference and training speed and number of parameters while being competitive in zero-shot tasks. | |||
===Framework=== | |||
The developed method is divided into two steps: | |||
* Construct a shared attention student model. | |||
* Transfer knowledge from a pre-trained teacher model to the student through knowledge distillation. | |||
===Shared Attention=== | |||
[[File: | [[File:echoatt.png|400px|thumb|right|Shared Attention]] | ||
To construct the student model, the first and last layers are retained. To select these layers, the following procedure was followed: | |||
* Calculate the average cosine similarity of each layer with all other layers. | |||
* Sort the layers based on the scores. | |||
* Choose the cutoff point to be the distance between the lowest and highest scores. | |||
* Maintain first or last layers with a score below the threshold. | |||
To share the attention mechanism within inner layers, a shared attention block is constructed. Every block consists of <math>k</math> consecutive inner layers, and attention matrices are shared among these blocks. Shared attention figure (b) clearly illustrates how multiple blocks are sharing attention. It is worth noting that <math>k</math> is a hyperparameter controlling the degree of compression and parameter sharing; larger values of <math>k</math> mean more parameter sharing and high compression and vice versa. | |||
====Shared Attention Blocks==== | |||
In vanilla transformers, the attention matrix is computed at each layer <math>i</math>: | |||
<math>Att_i = softmax(\frac{Q_i K_i^T}{\sqrt{d}}) V_i</math> | |||
<math> | In the proposed technique, a single set of <math>Q</math> and <math>K</math> matrices is used for all the layers within a block; indexed by <math>j</math>. To compute shared attention, we first calculate the <math>softmax</math> of <math>Q</math> and <math>K</math> across the layers belonging to the same block then we multiply it by <math>V</math> matrix that is unique to the block: | ||
</math> | |||
<math>A_{shared} = softmax(\frac{Q_{shared} K_{shared}^T}{\sqrt{d}})</math> | |||
<math> | <math>Att_j = A_{shared}V_j, \quad j \in [i, i+k]</math> | ||
</math> | |||
===Knowledge Distillation=== | |||
To compensate for parameters cut, which may affect performance, a knowledge distillation framework is utilized to pass the knowledge from a pre-trained teacher to the student. The process consists of two stages: | |||
* Distillation with teacher's Pseudo-Labels. | |||
* Refinement with True Labels. | |||
Before going into the details of each stage, let's define the following keywords: | |||
* Pseudo label: pre-trained model output (prediction) that is used to train the student. For example, for a certain input if the model outputs 'apple', then it becomes the label for the same input for the student. | |||
* Soft label: probability distribution across class labels. For example, if we have 3 classes and one to be predicted, then the soft label would be something like [0.2, 0.6, 0.2]. | |||
* Hard label: it is like one-hot encoded version of the soft label where only the predicted label has a probability of 1. For the previous example, it would be [0, 1, 0]. | |||
====Distillation with teacher's Pseudo-Labels==== | |||
In this stage both models are provided the same input tokens, and the student's training objective is to match the teacher's prediction at several levels. As shown in the figure above, three losses are utilized to optimize the process: | |||
<math> | *'''Intermediate Layer Loss''' (<math>\mathcal{L}_I</math>): this loss encourages the student to minimize the difference between its shared attention blocks and the teacher's corresponding mid-layers. This will push the student to learn to convey the teacher's knowledge with fewer parameters. | ||
<math>\mathcal{L}_I = \frac{1}{m} \sum_{i=1}^{m} \| S_{ki+b}(x) - T_{ki+b}(x) \|_2^2</math> | |||
where <math>m</math> is the number of shared attention blocks, <math>k</math> is the number of attention layers within each block, and <math>b</math> is the number of early skipped layers while <math>S_j</math> and <math>T_j</math> are the outputs of the student and the teacher at layer <math>j</math>. | |||
<math> | *'''Soft Label Loss''' (<math>\mathcal{L}_S</math>): guides the student to learn the teacher's probability distribution over the labels. Hence it is calculated by KL-divergence. | ||
<math>\mathcal{L}_S = \text{KL}\left(\sigma(S(x)) \parallel \sigma(T(x))\right)</math> | |||
<math> | *'''Hard Label Loss''' (<math>\mathcal{L}_H</math>): this loss's goal is to teach the student about the most confident predictions of the teacher. | ||
<math>\mathcal{L}_H = \text{CE}\left(\sigma(S(x)), \tau(T(x))\right)</math> | |||
<math>\sigma</math> and <math>\tau</math> are the '''softmax''' and '''argmax''' functions, respectively. <math>S(x)</math> and <math>T(x)</math> are the outputs of the student and teacher models. | |||
The final loss function is a weighted sum of the three losses: | |||
<math>\mathcal{L} = \alpha \mathcal{L}_I + \beta \mathcal{L}_S + \gamma \mathcal{L}_H</math> | |||
where <math>\alpha</math>, <math>\beta</math>, and <math>\gamma</math> control the contribution of each loss function. | |||
====Refinement with True Labels==== | |||
At this stage, the student is fine-tuned on the ground truth labels from the training dataset. It is more of a polishing step to improve predictions. For that purpose, cross-entropy is used for loss calculation. | |||
===Results=== | |||
To evaluate the performance of the proposed architecture, TinyLlaMA was selected as the baseline. Two main tests were conducted, the first with continual training only and the second with continual training and knowledge distillation. Three versions of the model were evaluated with <math>77\%</math>, <math>41\%</math>, and <math>23\%</math> attention sharing ratios. Table 1 shows that with continual training only, without distillation, the model with <math>23\%</math> sharing ratio outperforms the baseline. However, Table 2 proves that when knowledge distillation is incorporated, both models with <math>41\%</math> and <math>23\%</math> outperform the baseline indicating performance improvement with fewer parameters. Finally, Table 3 shows how shared attention improves inference and training speeds and the number of reduced parameters. | |||
[[File:echoatt_results1.png|500px|thumb|center|Table 1]] | |||
[[File:echoatt_results2.png|500px|thumb|center|Table 2]] | |||
[[File:echoatt_results3.png|500px|thumb|center|Table 3]] | |||
===Attention Similarity Analysis and Selection Strategy=== | |||
EchoAtt is based on a key observation in transformer-based models: the attention matrices in '''intermediate layers''' are often highly redundant. To quantify this, EchoAtt computes the '''cosine similarity''' between attention scores across different layers. Let <math>A_i</math> and <math>A_j</math> be the flattened attention matrices at layers <math>i</math> and <math>j</math>, respectively. The similarity is computed as: | |||
<math> | |||
\text{cosine_sim}(A_i, A_j) = \frac{A_i \cdot A_j}{\|A_i\| \cdot \|A_j\|} | |||
</math> | |||
By comparing this measure over all pairs of layers, a '''similarity matrix''' is constructed. The layers that have the highest average similarity are redundant and can be shared. What this analysis proves is that '''middle layers''' generate similar attention maps, while '''first and final layers''' are different and hence kept in their original form. | |||
To determine which layers should share attention, EchoAtt computes the '''average similarity''' of each layer to all others: | |||
<math> | |||
S_i = \frac{1}{L} \sum_{j=1}^{L} \text{cosine_sim}(A_i, A_j) | |||
</math> | |||
where <math>L</math> represents the number of layers. Layers are sorted by <math>S_i</math>, and the '''maximum gap''' between neighboring sorted values is used to find a threshold for attention sharing. Layers below the threshold are shaped into shared-attention blocks. This ensures high efficiency without significant degradation in model performance, as evidenced by empirical results. | |||
=== | ==Summary & Key Takeaways== | ||
Knowledge Distillation (KD), pruning, and parameter sharing make a great effort to address the challenges of computational and memory efficiency. The following table summarizes their contribution, strengths and weaknesses: | |||
{| class="wikitable" | |||
|+ Models Summary | |||
|- | |||
! Year !! Method !! Contribution !! Strengths !! Weaknesses !! Speedup Type !! Distillation Loss Design | |||
|- | |||
* | | 2024 || Attention Layer Skipping || | ||
* | * Investigates reducing inference complexity by dropping deeper attention and MLP layers. | ||
* Minimal performance impact (only ~1.8% reduction) while significantly reducing computational costs. | |||
|| Efficiently reduces computational costs with minor performance loss; deeper attention layers can be pruned effectively. | |||
|| Performance impact varies depending on which layers are skipped; requires careful selection of attention vs. MLP layers for optimal results. | |||
|| Inference-time only | |||
|| None (no distillation used) | |||
|- | |||
| 2024 || Minitron || | |||
* Utilizes structured pruning (depth, width, heads, embeddings) and knowledge distillation for model compression. | |||
* Retrains smaller models from a large pretrained one using structured pruning and distillation, achieving up to 40× training token reduction while maintaining performance. | |||
|| Highly data-efficient, significantly reduces compute needs, and outperforms similar-sized models trained from scratch. | |||
|| Further optimization needed through neural architecture search and expanded application to even larger models. | |||
|| Inference-time and training-time (via reduced retraining tokens) | |||
|| Logit-based KL divergence, optional intermediate state loss, hard label cross-entropy | |||
|- | |||
| 2024 || SliceGPT || | |||
* Introduces a pruning approach that deletes rows and columns from weight matrices, significantly reducing model size (up to 25%). | |||
* Achieves computational savings by leveraging computational invariance, maintaining performance without extensive retraining. | |||
* Leverages computational invariance to prune dimensions without fine-tuning; slices weight matrices via orthogonal transformation. | |||
|| Effective model compression (up to 25% fewer parameters) without significant retraining; compatible with common hardware. | |||
|| May not scale optimally with certain hardware architectures; deeper transformers may require more fine-grained pruning combinations. | |||
|| Inference-time only | |||
|| Optional (not required; works without fine-tuning) | |||
|- | |||
| 2024 || EchoAtt || | |||
* Shares attention matrices among inner layers with high similarity to reduce redundancy, under a knowledge distillation framework. | |||
* Improves inference speed by ~15%, training speed by ~25%, and reduces parameters by 4%, maintaining performance via knowledge distillation. | |||
|| Enhances efficiency significantly through attention mechanism sharing; promising scalability for larger models. | |||
|| Effectiveness depends on similarity patterns across layers; over-sharing can lead to degradation without distillation. | |||
|| Inference-time and training-time | |||
|| Intermediate state loss, soft label KL, hard label cross-entropy (weighted) | |||
|} | |||
== | = Topic 4: Quantization = | ||
== Introduction == | |||
Quantization is another model compression approach to address the large memory and computational requirements of models. Specifically, the multiplication and storage of very large matrices is expensive - is there a way to reduce these costs? The main idea with quantization is to represent the values in the various weight matrices and biases of the model with integers instead of floating point numbers. This requires a mapping from floating point value (e.g FP32) into integers (e.g INT4) and various techniques have been developed to preserve model accuracy. By doing so, we can significantly reduces memory consumption (FP32 to INT4 saves 8 times the memory), as well as computation cost. Thus, research in this area aims to sacrifice as little accuracy as possible while making this substitution in numerical representation. | |||
Notably there are two main forms of quantization: | |||
* Post-Training Quantization (PTQ): Applied after the model has been fully trained using high-precision (e.g., 32-bit floating point) weights | |||
* Quantization-Aware Training (QAT): Applied during the forward pass of model training to allow the optimization process to account for the quantized inference | |||
A tabular overview of the recent advancements in quantization methods is shown below with further details provided for each method in the subsequent sections. | |||
{| class="wikitable" | |||
|+ Overview of Recent Quantization Methods | |||
|- | |||
! Method !! Type !! Bit Precision !! Key Features !! Best Suited For | |||
|- | |||
| '''Integer-Only''' || QAT || INT8 || Enables integer-only inference and requires quantization-aware training || Various neural network architectures | |||
|- | |||
| '''ZeroQuant''' || PTQ || INT8 || Efficient for large transformers, minimal accuracy impact and significant speedup vs FP16 || Large transformer models | |||
|- | |||
| '''GPTQ''' || PTQ || 2.5-4 bits || Highly efficient for very large models, high compression rate, maintains accuracy || GPT-like models with billions of parameters | |||
|- | |||
| '''SmoothQuant''' || PTQ || 8-bit weight, 8-bit activation (W8A8) || Training-free, accuracy-preserving and ready-to-use solution for Large Language Models (LLMs)|| LLMs | |||
|} | |||
=== Emerging Trends: Mixed-Precision Quantization and Adaptive Methods === | |||
Beyond traditional fixed-bit quantization (e.g., INT8 or INT4), recent research has explored mixed-precision quantization and adaptive quantization methods, aiming to achieve even better trade-offs between computational efficiency and model accuracy. | |||
==== Mixed-Precision Quantization ==== | |||
Mixed-precision quantization involves assigning different numerical precisions to different layers or components of the model, depending on their sensitivity to quantization errors. The intuition behind this approach is that not all layers equally contribute to accuracy degradation when quantized. For instance, embedding layers might retain higher precision (e.g., INT8), while deeper layers, which typically have lower sensitivity, could be quantized more aggressively (e.g., INT4 or INT2). | |||
Formally, consider a model with layers <math>L_1, L_2, \dots, L_n</math>. Each layer <math>L_i</math> has a quantization bit-width <math>b_i</math>. The optimization problem for mixed-precision quantization can be defined as minimizing the weighted sum of accuracy loss and computational resource constraints: | |||
<math> | |||
\min_{b_1, b_2, \dots, b_n} \mathcal{L}(b_1, b_2, \dots, b_n) + \lambda \cdot \mathcal{C}(b_1, b_2, \dots, b_n), | |||
</math> | |||
where: | |||
- <math>\mathcal{L}(b_1, b_2, \dots, b_n)</math> denotes the accuracy degradation associated with quantization bit-widths. | |||
- <math>\mathcal{C}(b_1, b_2, \dots, b_n)</math> represents the computational cost, such as inference latency or memory usage. | |||
- <math>\lambda</math> is a hyperparameter balancing accuracy and cost. | |||
For example, layers performing critical operations like attention or embeddings might maintain higher precision (INT8), while dense layers or less sensitive modules could use lower precision (INT4), significantly optimizing performance without major accuracy losses. | |||
==== Adaptive Quantization ==== | |||
Adaptive quantization dynamically adjusts the quantization range or precision based on input data distributions or runtime feedback. Instead of using a fixed quantization scale, adaptive quantization recalculates scales periodically or continuously during inference, allowing it to handle outliers effectively and maintain higher accuracy in scenarios where input distributions vary significantly. | |||
Mathematically, adaptive quantization recalculates the quantization scale <math>S</math> dynamically for each batch or time step: | |||
<math> | |||
S_t = \frac{\max(X_t) - \min(X_t)}{2^{b} - 1}, | |||
</math> | |||
where <math>X_t</math> is the activation or weight matrix at inference step <math>t</math>, and <math>b</math> is the quantization bit-width. | |||
<math | |||
This adaptive recalibration ensures that quantization better reflects the current data distribution, significantly reducing quantization errors, especially in long-context models or models encountering highly varied input. | |||
==== | ==== Hardware-Aware Quantization ==== | ||
Additionally, recent trends emphasize hardware-aware quantization methods, which directly consider the characteristics of the deployment hardware (e.g., GPUs, TPUs, CPUs). These methods jointly optimize the quantization scheme along with hardware constraints, such as memory hierarchy and computational unit (tensor core) size. | |||
A typical optimization objective becomes: | |||
<math | <math> | ||
\min_{Q} \left( \text{Accuracy Loss}(Q) + \gamma \cdot \text{Latency}(Q; H) \right), | |||
</math> | |||
where | where: | ||
- <math>Q</math> denotes the quantization scheme. | |||
<math | - <math>H</math> denotes the hardware platform. | ||
- <math>\gamma</math> is a hyperparameter controlling trade-off between accuracy loss and hardware latency. | |||
Hardware-aware methods such as ZeroQuant leverage GPU-specific instructions (e.g., NVIDIA Ampere's WMMA instructions) to maximize performance gains by aligning quantization granularity with hardware architecture. | |||
==== Example: Mixed-Precision in GPT-Style Models ==== | |||
A concrete example of mixed-precision quantization is demonstrated in quantizing GPT-style models, where different precision levels are applied across layers to minimize accuracy loss: | |||
- Embedding Layers: INT8 (higher precision due to sensitivity). | |||
- Attention Layers: INT4 (balanced precision due to importance and redundancy). | |||
- Feed-Forward Layers: INT2 or INT4 (lowest precision due to redundancy). | |||
Empirical results show that mixed-precision quantization can significantly reduce memory footprint by over 70%, compared to uniform INT8 quantization, with negligible loss of accuracy (less than 0.5% drop in benchmark tasks). | |||
Thus, these emerging quantization techniques—mixed-precision, adaptive scaling, and hardware-aware optimization—provide powerful methods for deploying extremely large models efficiently, marking a significant step forward from traditional uniform quantization approaches. | |||
==Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference== | |||
This paper sets up the basis for further research in quantization. The broad idea is to find a mapping from real numbers to integers (in the weight and activation matrices) which does not compromise model accuracy. | |||
In order to derive this mapping, the authors start by examining the affine mapping which maps an integer to a real number while preserving collinearity and distance ratios. For two constants <math>S \in \mathbb{R}, Z \in \mathbb{Z} </math> (called quantization parameters), the mapping of an integer q to a real number r is defined as <math>r = S(q-Z) </math>. | |||
To apply this to the context of matrix multiplication, consider the following problem. Let: | |||
* <math>r_1, r_2 \in \mathbb{R}^{N \times N}</math> be two real-valued matrices | |||
* <math>r_3 = r_1r_2</math> | |||
* <math>\alpha \in \{1, 2, 3\}</math> be subscripts referring to <math>r_1, r_2, r_3</math> | |||
* <math>S_{\alpha}, Z_{\alpha}</math> be the quantization parameters | |||
* <math>q_{\alpha} </math> be the quantized version of <math> r_{\alpha}</math> | |||
* <math> 1 \le i, j \le N </math> where <math>r_{\alpha}^{(i,j)}, q_{\alpha}^{(i,j)} </math> refer to the entry in the <math>i^{th} </math> row and <math> j^{th}</math> column of the matrices | |||
Then <math>r = S(q-Z) </math> can be written as <math>r_{\alpha}^{(i,j)} = S_\alpha(q_{\alpha}^{(i,j)}-Z_\alpha) </math>. Recall that <math>r_3 = r_1r_2</math>. If we consider a particular entry (i, k) in this matrix multiplication formula and substitute each term with this quantization, we get that <math>S_3(q_3^{(i,k)} - Z_3) = \Sigma_{j=1}^{N} S_1(q_1^{(i,j)} - Z_1) S_2(q_2^{(j,k)} - Z_2)</math>. Then rearranging this formula to give isolate the term of interest, we get that | |||
== | <math>q_3^{(i,k)} = Z_3 + \dfrac{S_1S_2}{S_3} \Sigma_{j=1}^{N} (q_1^{(i,j)} - Z_1) (q_2^{(j,k)} - Z_2)</math> | ||
Defining <math>M = \dfrac{S_1S_2}{S_3}</math> to represent the constants, the authors found empirically that <math> M \in (0,1) </math> and can thus be expressed in the compressed form <math>M = 2^{-n} M_0</math> for some non-negative integer n and <math>M_0 \in [0.5, 1)</math>. This allows the computation of the constant M to be performed using fixed point multiplication. All remaining terms in the formula are integers, this the quantized version of the matrix multiplication <math>q_3 \approx r_3 = r_1r_2 </math> can be computed using fixed point arithmetic which is much more efficient than the previously used floating point operations. | |||
Note that here <math>r_1</math> represents an activation matrix, <math>r_2</math> represents the weight and <math>r_3</math> is thus the output matrix. S here is called quantization scale, which converts the integer <math>(q-Z)</math> into real number <math>r</math>. Z is called zero-point, which decides the map of real number <math>r=0</math> into the quantization <math>q=Z</math>. | |||
=== | ====Efficient Handling of zero-points==== | ||
From the equation <math>q_3^{(i,k)} = Z_3 + M \Sigma_{j=1}^{N} (q_1^{(i,j)} - Z_1) (q_2^{(j,k)} - Z_2)</math> mentioned above, we can see that it performs subtractions of zero-points inside a triple loop (in total <math>2N^3</math> subtraction operations) and it is expensive, meaning that two subtractions are performed every multiplication. Thus we move some calculations outside the expensive inner loop to make it less expensive. | |||
We algebraically expend this equation and get the expression: <math>q_3^{(i,k)} = Z_3 + M(NZ_1Z_2 - Z_1\Sigma_{j=1}^{N}q_2^{(j,k)} - Z_2\Sigma_{j=1}^{N}q_1^{(i,j)} + \Sigma_{j=1}^{N}q_1^{(i,j)}q_2^{(j,k)})</math>. Here since <math>\Sigma_{j=1}^{N}q_1^{(i,j)}</math> only need to be calculated once at each <math>i</math>, and similarly, <math>\Sigma_{j=1}^{N}q_2^{(j,k)}</math> only need to be calculated once at each <math>k</math>, we can see that these two terms take only <math>2N^2</math> additions. While <math>Z_3, M, N, Z_1, Z_2</math> are all constants, it means that the rest cost of the calculation concentrates on the term <math>\Sigma_{j=1}^{N}q_1^{(i,j)}q_2^{(j,k)}</math>, which takes <math>2N^3</math> operations. This reduces the problem to the same core integer matrix multiplication of <math>\Sigma_{j=1}^{N}q_1^{(i,j)}q_2^{(j,k)}</math> as other quantization scheme that does not contains zero-points and saves <math>O(2N^3)</math> subtractions. | |||
<math> | <math> \mathbf{Training} </math> | ||
The core idea behind simulated quantization is to mimic quantization behavior during training while still allowing gradients to flow smoothly for optimization. This enables the model to adapt to the reduced numerical precision it will face during inference. During the forward pass, we apply the quantization function that we have covered above: | |||
<math> \hspace{10cm} q(r; a,b,n)=\text{Round}\left(\frac{\text{clip}(r;a,b)}{S(a,b,n)}\right) S(a,b,n)+a </math> | |||
where <math> S(a,b,n) = \frac{b-a}{n-1} </math>, <math> a,b </math> are the limits of the quantization range, n is the number of unique integers in quantization. This process can be done very efficiently by bypassing floating point operations. | |||
While this function mimics quantization during the forward pass, it poses a challenge for gradient-based optimization. The Round() operation is non-differentiable. Thus, during backpropagation, it is ignored as an identity function. This approximation allows gradients to pass through as if the rounding do not exist, enabling standard training techniques like SGD or Adam to continue working. | |||
This two-step process allows the network to learn using floating-point numbers initially, and subsequently adapt to working effectively with quantized integer values. As a result, the network can perform consistently and reliably when deployed in environments that apply integer-only arithmetic. | |||
=== | Once training is complete, the model is prepared for deployment with quantized values. The first step is to quantize all components, including inputs, weights, and activations at each layer. Then, scale factors <math> S </math> are computed for each layer to map floating-point values to integers. The model operates all calculations using integer arithmetic, ensuring efficient execution on hardware. Finally, if needed, the output is dequantized back to floating-point values for compatibility with other systems or processes. This approach maintains both performance and efficiency in deployment. | ||
==== Computation-Efficient Implementation of Integer-Only Arithmetic ==== | |||
Although the quantization constant <math>M = \frac{S_1 S_2}{S_3}</math> is a real number, Jacob et al. showed that it can be efficiently implemented using integer operations. Empirically, <math>0 < M < 1</math>, which allows it to be rewritten in the form: | |||
<math> | <math> | ||
\mathbf{I}_{k,j}^\ell = \begin{cases} | M = 2^{-n} M_0 | ||
\prod_{n=j+1}^k \mathbf{\overline{I}}_{n,j}^\ell \text{ and } \mathbf{\overline{I}}_{n,j}^\ell = \sigma\left(\frac{(\mathbf{Q}_{int}^\ell)_n^\top (\mathbf{K}_{int}^\ell)_j}{\sqrt{r}} + \beta^\ell\right), & \text{if } j < k \\ | </math> | ||
1, & \text{if } j = k \\ | |||
Where: | |||
- <math>n \in \mathbb{Z}_{\ge 0}</math> is an integer, and | |||
- <math>M_0 \in [0.5, 1)</math> is the normalized scaling factor. | |||
This reformulation allows: | |||
- <math>2^{-n}</math> to be implemented as a bit-shift operation, which is computationally cheap. | |||
- <math>M_0</math> to be implemented in fixed-point form using a single integer bit. | |||
Thus, all computation in <math>q_3^{(i,k)} = Z_3 + M \sum_{j=1}^{N} (q_1^{(i,j)} - Z_1)(q_2^{(j,k)} - Z_2)</math> can be performed using fixed-point arithmetic, enabling fast integer-only inference. | |||
==ZeroQuant: Efficient and Affordable Post-Training Quantization for Large-Scale Transformers== | |||
With the increasing size of Generative Pre-Trained Transformers (GPTs), it has become a significant challenge to deploy these models efficiently on resource-constrained hardware. Traditional methods of compression and quantization often lead to severe accuracy degradation, which limits their practicality in real-world applications. In this paper, the authors present ZeroQuant, an end-to-end post-training quantization method to address the challenges and this method is designed to compress large transformer models without losing much accuracy. But what do we mean by Post-Training Quantization? | |||
Quantization can take place at various stages. In this context, we have two well-known approaches: Post-Training Quantization (PTQ) and Quantization-Aware Training (QAT). | |||
* Post-Training Quantization is a technique in which we first have a pre-trained model and quantize its parameters down to lower precision during inference time. This technique doesn't alter the real training process itself. During PTQ, the dynamic ranges of parameters are calculated on-the-fly at runtime. PTQ is essentially a post-processing step which happens after the model has completed its training and making it a relatively straightforward approach to implement. | |||
* On the other hand, Quantization-Aware Training incorporates quantization directly into the training procedure. In QAT, the training procedure itself is particularly modified to simulate the effects of quantization while the model is learning. This allows the model to be robust against quantization noise throughout its training. Something unique about QAT is that, during training, there are two versions of the weights in memory simultaneously: a quantized version that's used for forward passes (inference), and the original unquantized version that is updated during backpropagation. By performing this double trick, the model can learn with the awareness of how quantization will affect its performance. As a result, QAT tends to be more accurate than PTQ for the same bit-width quantization, but at the expense of more computational resources for training. | |||
Now we can better explain the original necessity for ZeroQuant. Traditional quantization methods required extensive retraining with original data and computational resources that were often unavailable to organizations deploying large language models. Quantization-Aware Training (QAT) works, but in practice, it is not feasible on large models due to its time-consuming and data-intensive nature. As you understand from our recent explanation, PTQ exhibits great compression efficiency compared to QAT because PTQ is typically applied to quantize the model without retraining. However, existing Post-Training Quantization techniques (before this article) were primarily designed for computer vision rather than language models. We have some previous works before ZeroQuant on language models that use PTQ and achieve good results on BERT. This work used INT8 weight and mixed INT8/FP16 activation quantization. The problem with this work is that there was no investigation into even lower bit-precision PTQ on BERT models and large-scale GPT-3-style models. It is better to say that their main focus was on high-precision quantization for the BERT base model and did not consider other billion-scale generative models like GPT-3-style models. These limitations created a need for a specialized quantization approach which can compress language models efficiently. | |||
ZeroQuant has three main components, which we will explain in detail. | |||
=== 1- Fine-grained Hardware-friendly Quantization Scheme === | |||
Unfortunately, based on previous research conducted prior to this article, it is evident that even applying INT8 PTQ to BERT/GPT-3-style models results in significant accuracy degradation. The primary challenge lies in the inability of INT8 representation to fully capture the varying numerical ranges of different rows in weight matrices and different activation tokens. One approach to address this issue is to implement group-wise (token-wise) quantization for the weight matrices (activations). So, let’s define these terms first. | |||
* '''Group-wise Quantization for Weights''': Quantization typically occurs on weight matrices. A straightforward approach is to compress the values into int8 format by columns (or rows), but this can lead to a significant loss in prediction accuracy. Group-wise weight matrix quantization splits a weight matrix <math>W \in \mathbb{R}^{n \times m}</math> into <math>g</math> smaller groups and quantizes each group separately. Compared to the traditional single-matrix quantization, this approach enables finer-grained control and is thus better able to maintain critical weight information. Group-wise quantization in earlier research was applied mostly during Quantization-Aware Training (QAT) without considerations of hardware efficiency and backend system support. As a result, such methods did not achieve practical improvements in inference latency. In this work, the authors combine hardware constraints from NVIDIA's Ampere GPU architecture (e.g., A100), which is built on Warp Matrix Multiply and Accumulate (WMMA) with specific tiling sizes. By aligning group-wise quantization with these hardware capabilities, they are able to reduce latency considerably without sacrificing accuracy. This method outperforms single-matrix quantization because of its higher granularity thus enabling it to enjoy better model performance and speed. | |||
* '''Token-wise Quantization for Activations''': A common practice in post-training quantization (PTQ) is to use static quantization for activations. This means that the minimum and maximum values of activations are calculated ahead of time during an offline calibration phase. This approach can work well for small models where activation ranges are relatively stable. But, in large transformer models like GPT-style or BERT models, the ranges of activation values can be quite different for different tokens. Having a static range for all tokens can lead to a loss of accuracy. Since it does not account for unique behavior of each input. To solve this, token-wise quantization is introduced. In this method, the min and max range is computed dynamically for every token during inference time. This reduces quantization error and model accuracy increases. Token-wise quantization is more accurate, but applying it directly to popular deep learning libraries (e.g., PyTorch) may not be efficient. It often introduces extra operations that require moving data between GPU compute units and main memory, which slows down inference. To solve this problem, an optimized inference backend is developed. For example, kernel fusion is used to combine the quantization step with the previous operation (such as layer normalization). This reduces the need for extra data movement. Similarly, to reduce the cost of converting data back to floating point after matrix multiplications (GEMMs), the system uses a technique that applies the quantization scale directly to the intermediate result before storing it in memory. In this way, the entire process quicker and efficient. Token-wise quantization helps to reduce representation errors and does not require an extra calibration step for activation ranges. Therefore, 8-bit weights and 8-bit activations become a viable and accurate choice for quantizing large language models without adding significant overhead. | |||
Both group-wise and token-wise quantization are forms of fine-grained quantization. | |||
In order to further improve performance and reduce the deployment cost of large models like GPT and BERT, ZeroQuant goes one step beyond group-wise and token-wise quantization. It also includes two other important elements: a lightweight layer-by-layer knowledge distillation method (LKD) and a highly optimized inference backend. | |||
=== 2- Layer-by-layer Knowledge Distillation (LKD) with Affordable Cost === | |||
Traditional knowledge distillation operations are memory-bound, where the student and teacher models are both loaded into memory for training. This is especially impractical for billion-parameter models. ZeroQuant avoids this overhead through a better approach: it quantizes the model layer by layer. | |||
For each of the layers which are being quantized, their unquantized version is taken as the teacher. The input is passed through both the original and the quantized version of the layer and the difference in their outputs is minimized. Because only one extra layer needs to be stored in memory during this process, LKD is even scalable to highly large models like GPT-NeoX_20B. | |||
Another valuable benefit of LKD is that it does not require access to the original training data. Since it works layer by layer and is only interested in matching internal outputs, it can work with any dataset — even random or unrelated text like Wikipedia. Experiments verified that with the use of Wikipedia or even random sequences of tokens, it still achieved dramatic improvements in accuracy and perplexity. This makes ZeroQuant especially useful in privacy-sensitive or low-resource settings. | |||
=== 3- Quantization-Optimized Transformer Kernels === | |||
Post-training quantization is often slowed down because of the overhead of converting between quantized and floating-point values. ZeroQuant solves this with a highly optimized system backend. Instead of performing separate operations for quantization, normalization, and activation, ZeroQuant fuses them into single GPU kernels. This reduces memory access and speeds up inference. | |||
For example, in dequantization, ZeroQuant scales the INT32 results with precomputed quantization scales before converting back to FP16 and do all within the same kernel. This method reduces expensive data transfers and improves latency and achieving the expected benefits of lower precision. | |||
==GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers== | |||
===Concept=== | |||
GPTQ is a layer-wise post-training quantization technique specifically tailored for generative pretrained transformers. It aims in making more informed decisions on quantizing of weights allowing lower bandwidth quantization using approximate second-order information. The technique addresses some major challenges in terms of computation and memory for massive models like GPT3 which has 175B parameters and takes 326GB in float16 format. GPTQ can quantize GPT3 under 4 GPU hours reducing to 3/4 bits with minimal accuracy degradation. The significant contribution of GPTQ is the ability to execute post-training quantization on significantly large models (billions of parameters) compared to previous models like ZeroQuant. Furthermore, previous models could only quantize weights to 8-bit integers, otherwise accuracy would plummet. However, GPT can quickly quantize large transformer models using 3-4 bits without major accuracy loss. | |||
===Introducing Optimal Brain Quantization=== | |||
To understand GPTQ, we first examine another quantization technique called optimal brain quantization (OBQ). This is necessary to learn GPTQ as it is essentially OBQ with some improvement. | |||
'''1. Core Concepts:''' | |||
The core concept behind OBQ is to minimize the performance degradation between the quantized integer weights <math>\hat{W}</math> and the input floating point weights <math>W</math>, expressed as: | |||
<math> | |||
\hat{W} = \arg\min_\hat{W} \|WX - \hat{W}X\| | |||
</math> | |||
where <math>X</math> is the input activations to the layer. | |||
'''2. Implementation:''' | |||
To do so, optimal Brain Quantization employs quantization based on the Optimal Brain Surgery (OBS) approach. The OBS approach is simple. Many neural network weights are quite redundant, or have minimal impact on the output. To reduce parameters (and thus make models more compact), one can drop weights. Of course, one must be selective about dropping weights, since some weights are more important than others. Dropping the most impactful weights will significantly reduce model performance. Therefore, the objective of OBS is to selectively remove weights to reduce model parameters with minimal performance degradation. In OBQ, the strategy is similar. Instead of dropping weights, we quantize weights. | |||
Mathematically, consider the quantized weights <math>\hat{W} = \arg\min_\hat{W} \|WX - \hat{W}X\|</math>, This can be re-expressed as a sum of the squared errors, over each row of <math>W</math>. OBQ can execute row-wise quantization in a parallel fashion. For each row, OBQ will quantize a single weight parameter while always updating all not-yet-quantized weights (to compensate for error). Mathematically, the quantization process can be expressed by the following: | |||
<math>w_q=\text{argmin}_{w_q} \frac{(\text{quant}(w_q)-w_q)^2}{[H_F^{-1}]_{qq}},\qquad\delta_F=-\frac{w_q-\text{quant}(w_q)}{[H_f^{-1}]_{qq}}\cdot(H_F^{-1})_{:q}</math> | |||
where the Herssian of the matrix that contains the remaining full-precision weights <math> H_F=2X_FX_F^\intercal</math>, <math>w_q</math> is the quantized weight, and <math>\delta_F</math> is the corresponding weight update to compensate for errors. | |||
Using an iterative approach, OBQ quantizes weights until all weights are quantized. The significant advantage with this approach is the Hessian matrix <math> H^{-1}</math> does not have to be fully recomputed at every step. | |||
===GPTQ: An Improved OBQ=== | |||
Compared with OBQ, GPTQ has 3 major improvements. | |||
'''1. Order of quantization does not matter''' | |||
We empirically discovered that order in quantizing the weight does not matter. So now we can quantize weights sequentially from the first column to the last compared to previous work such as optimal brain quantization (OBQ) which quantize weight starting with the weights that have smallest impact on the loss function. This improvement drastically decrease the need to recompute Hessian Matrix and resulted in a faster computation. | |||
'''2. Block-wise update''' | |||
Since we discovered that the order of quantization does not matter, now when updating sequentially, the quantization on column <math>i</math> does not depend on subsequent columns <math>i + 1, i + 2</math>, and etc. This enabled a new way to update which is the block-wise update. | |||
The block-wise update is performed as follows: | |||
1. Split the rows into blocks and perform the update on current block. | |||
2. Perform a big update when finished updating the current block. | |||
'''3. Cholesky Reformulation''' | |||
Since directly updating <math>H^{-1}</math> for every column removal can accumulate floating-point errors, we need a more stable way to update. As mentioned in the method, we uses the Cholesky decomposition, which involves computing and storing a stable Cholesky factor of <math>H^{-1}</math> once, so we avoid repeated redundant updates. This Cholesky Reformulation naturally fits our block-wise updates mentioned earlier since each block only needs to reference the relevant rows/columns of the factor. | |||
===Algorithm=== | |||
[[File:gptq.png|400px|thumb|right|Pseudocode for GPTQ. <span id="gptq"></span>]] | |||
[[#gptq|Figure]] shows the algorithm of GPTQ explained above. As seen, GPTQ utilizes three key steps. | |||
The first step is to understand how the loss is updating as an impact of the weights during the process of quantization. Instead of directly using the hessian <math>H</math> to do this, GPTQ uses the hessian inverse (<math>H^{-1}</math>) for each layer's weight matrix since it provides better insights on the loss sensitivity while updating the weights. The weight importance is then determined using the <math>H^{-1}</math> values, such that weights associated with smaller <math>H^{-1}</math> are more important since small changes in weights lead to significant performance degradation. A dampening factor is applied to <math>H^{-1}</math> to reduce the numerical instability. | |||
Then, to further reduces memory usage, GPTQ applies Cholesky decomposition on the <math>H^{-1}</math>, such that: | |||
<math>H^{-1} = LL^t</math> | |||
where, <math>L</math> is the lower triangular matrix from Cholesky decomposition. | |||
The final step involves quantizing of weights column by column in blocks. Columns are processed in batches of size <math>B</math>, keeping track of error <math>E_{:,j-i}</math> to update the weights <math>W_{:,j:(i+B)}</math> in the block. Upon processing of the entire block, the remaining weights are updated using the tracked errors, which happens only for <math>C/B</math> times, making the process fast. | |||
==SmoothQuant== | |||
===Motivation=== | |||
Large language models have demonstrated excellent performances on various tasks such as language modelling, reasoning. However, due to the size of the model, it's computational and memory intensive. Quantization is a method that can reduce memory and accelerate inference by quantizing weights and activations with low-bit integers. For example, quantizing an FP16 number to a INT8 number can halve the GPU memory usage and double the throughput. One major challenge in quantization of LLMs are quantization of activations. When LLMs are scaled to billions of parameters, systematic outliers began to appear. Due to the existence of outliers (i.e., values particularly large compared to other activations), the quantization range is stretched and most activations will be close to 0 after quantization. This significantly decreased the accuracy of LLMs and large quantization errors. ZeroQuant achieved good performance on LLMs with millions of parameters but failed to maintain accuracy on models with billions of parameters. | |||
===Intuition=== | |||
[[File:ZeroQuant.png|400px]] | |||
As mentioned previously and shown in the image above, in LLMs, activations are hard to quantize due to presence of outliers while weights are usually smooth and can preserve most of the information during quantization. In (a) we see that activations are HARD to quantize while weights are VERY EASY to quantize. In (b), after applying SmoothQuant, the activations are EASY to quantize while weights are EASY to quantize as well. Therefore, the main/high-level idea of SmoothQuant is simply transfer some of the difficulty in activations to weights so that both activations and weights are now feasible for quantization instead of activations being super hard to quantize and weights almost trivial to quantize. The image below clearly demonstrates this "transfer of difficulty": | |||
[[File:ZeroQuant2.png|800px]] | |||
We will discuss below how this migration of difficulty is done. | |||
===SmoothQuant's Smoothing Factor=== | |||
Recall that matrix multiplication is linear (e.g., <math>Y = XW = (0.01X)(100W)</math>). So we can smooth the input activation by dividing it by a per channel smoothing factor: If <math>\mathbf{X} \in \mathbb{R}^{T \times C_i}</math> is the input matrix and <math>\mathbf{W} \in \mathbb{R}^{C_i \times C_o}</math> is the weight matrix, we can introduce a smoothing factor <math>\mathbf{s} \in \mathbb{R}^{C_i}</math> and scale the input and weight by <math> \mathbf{Y} = \mathbf{X} \mathbf{W} = \left( \mathbf{X} \, \mathrm{diag}(\mathbf{s})^{-1} \right) \left( \mathrm{diag}(\mathbf{s}) \, \mathbf{W} \right) = \hat{\mathbf{X}} \hat{\mathbf{W}} . </math> | |||
How much difficulty should we migrate from activations to weights? We certainly do not want to migrate all difficulty because that would make weights too hard to quantize, the gist is all about maintaining the balance of easiness to quantize for both activations and weights. | |||
The authors proposed <math>s_j = \frac{\max(|\mathbf{X}_j|)^{\alpha}}{\max(|\mathbf{W}_j|)^{1 - \alpha}},</math> | |||
where <math>j = 1, 2, \ldots, C_i</math> is the <math>j^{th}</math> channel and <math>\alpha</math> is the migration strength which controls the amount of difficulty we want to move from activations to weights. A larger <math>\alpha</math> migrates more quantization difficulty to weights. | |||
As shown below, the right <math>\alpha</math> makes quantization easier for both activations and weights. If <math>\alpha</math> is too large, most difficulty will be transferred to weights, making weights hard to quantize. If it's too small, most difficulty still remains in activations. | |||
[[File:ZeroQuant3.png|400px]] | |||
'''Example''' | |||
We will demonstrate Smooth Quant with an example to better illustrate. | |||
Consider this <math>X</math> and <math>W</math>: | |||
<math> | |||
X = \begin{pmatrix} | |||
1& -16 & 2 & 6 \\ | |||
-2 & 8 & -1 & -9 \\ | |||
\end{pmatrix} | |||
\quad | |||
W = \begin{pmatrix} | |||
2 & -1 & -2 \\ | |||
1 & -1 & 1 \\ | |||
2 & -1 & -2 \\ | |||
-1 & -1 & 1 \\ | |||
\end{pmatrix} | |||
</math> | |||
We first get the <math>\max(|\cdot|)</math> along the column of <math>X</math> and row of <math>W</math> and divide them, we get. | |||
<math> | |||
\frac{\max(|\mathbf{X}_j|)}{\max(|\mathbf{W}_j|)}= | |||
\begin{pmatrix} | |||
\frac{|-2|}{|-2|}& 0 & 0 & 0 \\ | |||
0 & \frac{|-16|}{|1|} & 0 & 0 \\ | |||
0 & 0 & \frac{|2|}{|2|} & 0 \\ | |||
0 & 0 & 0 & \frac{|-9|}{|-1|}\\ | |||
\end{pmatrix} = \begin{pmatrix} | |||
1& 0 & 0 & 0 \\ | |||
0 & 16 & 0 & 0 \\ | |||
0 & 0 & 1 & 0 \\ | |||
0 & 0 & 0 & 9\\ | |||
\end{pmatrix} | |||
</math> | |||
If we pick <math>\alpha = 0.5</math>, the smoothing factor <math>S</math> matrix will become | |||
<math> | |||
S = \sqrt{\begin{pmatrix} | |||
1& 0 & 0 & 0 \\ | |||
0 & 16 & 0 & 0 \\ | |||
0 & 0 & 1 & 0 \\ | |||
0 & 0 & 0 & 9\\ | |||
\end{pmatrix}} = \begin{pmatrix} | |||
1& 0 & 0 & 0 \\ | |||
0 & 4 & 0 & 0 \\ | |||
0 & 0 & 1 & 0 \\ | |||
0 & 0 & 0 & 3\\ | |||
\end{pmatrix} | |||
</math> | |||
So we divide each column <math>i</math> of <math>X</math> by <math>\text{diag}(S_i)</math> and multiple each row <math>i</math> of <math>W</math> by <math>\text{diag}(S_i)</math> to get their new Smooth Quant version. | |||
<math> | |||
\hat{X} = \begin{pmatrix} | |||
1& -4 & 2 & 2 \\ | |||
-2 & 2 & -1 & -3 \\ | |||
\end{pmatrix} | |||
\quad | |||
\hat{W} = \begin{pmatrix} | |||
2 & -1 & -2 \\ | |||
4 & -4 & 4 \\ | |||
2 & -1 & -2 \\ | |||
-3 & -3 & 3 \\ | |||
\end{pmatrix} | |||
</math> | |||
Note the result of <math>XW = \hat{X}\hat{W}</math> since we divide by <math>\text{diag}(S_i)</math> and then multipled by <math>\text{diag}(S_i)</math>. | |||
= Topic 6: KV Cache Compression = | |||
==Background== | |||
In a basic transformer, given an input token sequence X, each token’s Q, K, V are computed using learned projection matrices: | |||
<math> Q = X W^Q = \begin{bmatrix} q_1 \\ q_2 \\ \vdots \\ q_n \end{bmatrix}, \quad K = X W^K = \begin{bmatrix} k_1 \\ k_2 \\ \vdots \\ k_n \end{bmatrix}, \quad V = X W^V = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} </math> | |||
The full self-attention computation is: | |||
<math> A = \mathrm{softmax} \left( \frac{Q K^T}{\sqrt{d_k}} \right) V </math> | |||
This leads to quadratic time complexity. | |||
We know that during inference, we do not want current tokens to access future tokens, therefore we apply a mask that restricts access: | |||
<math> S = QK^T = \begin{bmatrix} q_1 k_1^T & q_1 k_2^T & \cdots & q_1 k_t^T \\ q_2 k_1^T & q_2 k_2^T & \cdots & q_2 k_t^T \\ \vdots & \vdots & \ddots & \vdots \\ q_t k_1^T & q_t k_2^T & \cdots & q_t k_t^T \end{bmatrix}, \quad M = \begin{bmatrix} 0 & -\infty & \cdots & -\infty \\ 0 & 0 & \cdots & -\infty \\ \vdots & \vdots & \ddots & -\infty \\ 0 & 0 & \cdots & 0 \end{bmatrix} </math> | |||
After applying the mask, we can see below that the current token can only attend to itself and previous tokens: | |||
<math> S' = S + M = \begin{bmatrix} q_1 k_1^T & -\infty & \cdots & -\infty \\ q_2 k_1^T & q_2 k_2^T & \cdots & -\infty \\ \vdots & \vdots & \ddots & \vdots \\ q_t k_1^T & q_t k_2^T & \cdots & q_t k_t^T \end{bmatrix}, \quad A = \begin{bmatrix} a_{11} & 0 & \cdots & 0 \\ a_{21} & a_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ a_{t1} & a_{t2} & \cdots & a_{tt} \end{bmatrix} </math> | |||
Note that softmax here is applied row-wise so that masked values have 0 probability after softmax. This ensures that current token only has access to past tokens and itself. | |||
You may notice that there are a lot of repetitive calculations here, repetitive calculations between K and V to be specific. For example, when we have two tokens [a, b], the number of key-value pairs we need to calculate are (a, a), (a, b), (b, a), (b, b). If we have three tokens [a, b, c], the pairs we need to calculate are (a, a), (a, b), (a, c), (b, a), (b, b), (b, c), (c, a), (c, b) and (c, c). Note that if we can somehow store the key-value pairs in [a, b], then when we look at the next query from token c, we can simply do a lookup of previous key-value pairs and only calculate new ones that contains c. This is the main idea behind KV caching: | |||
Instead of recomputing K, V at every step, we define two caches and store previously computed values in them: | |||
<math> K_{\text{cache}} = \begin{bmatrix} k_1 \\ k_2 \\ \vdots \\ k_{t-1} \end{bmatrix}, \quad V_{\text{cache}} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_{t-1} \end{bmatrix} </math> | |||
At time step t, we generate token <math>x_t</math> and compute the new query: | |||
<math>q_t = x_t W^Q</math> | |||
Compute <math>k_t</math>, <math>v_t</math> and add to the cache. | |||
Compute attention only against cached keys: | |||
<math> A_t = \mathrm{softmax} \left( \frac{q_t K_{\text{cache}}^T}{\sqrt{d_k}} \right) </math> | |||
This reduces the time complexity at inference from O(n²) to O(n), which is much faster for long sequences. | |||
=== Challenges === | |||
While reducing the time complexity of inference from O(n²) to O(n) significantly speeds up long-sequence generation, it comes at the cost of increased memory usage. Storing all past keys and values results in memory growth linear to sequence length. Cache compression techniques help mitigate this, but they introduce a new challenge: low parallelizability. Since each token depends on compressed past states, the model must sequentially load weights, retrieve the KV cache, and compute attention for every generated token, limiting potential speed gains. | |||
=== Ideal KV Cache === | |||
An ideal KV cache should balance memory efficiency and performance by meeting the following criteria: | |||
# '''Small cache size''' – Minimizes memory footprint without compromising effectiveness. | |||
# '''Low miss rate''' – Ensures the model retains enough context to generate coherent long-form text. | |||
# '''Low-cost eviction policy''' – Reduces computation overhead and speeds up inference. | |||
==H<math>_2</math>O: Efficient KV Cache Compression for Large Language Models== | |||
===Introduction=== | |||
Large language models (LLMs) are memory hogs, especially during text generation. A big culprit is the '''KV cache''', which stores attention keys and values to skip redundant computations as new tokens are generated. This cache grows linearly with sequence length and batch size, gobbling up GPU memory fast. For a 30-billion-parameter model with a batch size of 128 and sequence length of 1024, the KV cache alone can demand 180 GB. This limitation makes long-context tasks (like stories, chats, or code generation) very expensive to run, especially in real-time or on resource-constrained devices. | |||
Most existing methods which are mentioned in previous parts of this wiki, have some problems. First, models like Reformer and Flash Attention, are designed to overcome the quadratic memory required by attention mechanisms when modeling long sequences but still require a large cache size. Second, variants like sparse transformer, low-rank based transformers, or multi-query attention can reduce the cache size, but directly applying them on pre-trained LLMs for generation results in high miss rates and degrades the accuracy. This problem is shown in Figure 1. Finally, some recent advances such as gisting tokens can learn to compress the KV cache for documents, but their expensive eviction policies are difficult to deploy during generation. | |||
[[File:H2Q_Figure1.png|700px|thumb|center|Figure1- Upper plots) symbolic plots of an attention map deploying different KV cache policies - Lower right) contrasts their accuracy-memory trade-off - Lower left) the overview of H2O framework]] | |||
===Key Contributions=== | |||
The paper introduces '''H<math>_2</math>O (Heavy Hitter Oracle)''', a clever way to slim down the KV cache. Here’s what stands out: | |||
* '''Dynamic Token Selection''': H<math>_2</math>O keeps only the most impactful tokens—called "heavy hitters"—based on their '''attention scores''', slashing memory use by up to 20× while preserving 99% of the original performance. | |||
* '''No Retraining Required''': Unlike some methods that need model tweaks, H<math>_2</math>O works during inference, making it plug-and-play. | |||
* '''Big Performance Boost''': It outperforms popular inference systems like [https://arxiv.org/abs/2207.00032 DeepSpeed Zero-Inference], [https://github.com/huggingface/accelerate Hugging Face Accelerate], and [https://arxiv.org/abs/2303.06865 FlexGen], boosting throughput by up to 29× on models like OPT-6.7B and OPT-30B. | |||
In addition, H2O introduces a low-cost greedy eviction algorithm that maintains a balance between recent and heavy hitter tokens in the KV cache. It formulates the cache eviction problem as a dynamic submodular maximization task and shows that under mild assumptions, the greedy approach offers near-optimal performance. Importantly, H2O does not require future token information and instead using local statistics at each decoding step to approximate attention contribution and this makes it practical for real-time deployment. | |||
The framework is validated across a wide range of tasks and model families, including OPT, LLaMA, and GPT-NeoX, and this shows that H2O with just 20% KV cache budget can match or even surpass the accuracy of full-cache models. Besides saving memory, it enables larger batch sizes and eliminates the need for CPU offloading. This delivers spectacular latency and throughput gains. H2O also proves compatible with other efficiency techniques like quantization and even enhances diversity in generated text and making it a robust, versatile solution for scalable LLM inference. | |||
===Problem Formulation=== | |||
In large language models (LLMs), the process of generating text requires the creation of a memory structure known as the '''KV cache''', which stores the key and value vectors of all previously processed tokens. This cache enables the model to compute attention efficiently during autoregressive generation. However, as the sequence grows longer or as the batch size increases, the KV cache grows linearly, eventually consuming a significant amount of memory. | |||
To address this issue, the paper studies a constrained setting where the size of the KV cache is limited to a fixed budget <math>k</math>, which is much smaller than the sequence length <math>n</math>. The challenge is to design a policy that selects which key-value pairs to retain in this limited cache at each generation step, without compromising the model’s generation quality. | |||
To formalize this problem, the model’s attention mechanism is described using two matrices: the query matrix <math>Q \in \mathbb{R}^{n \times d}</math> and the key matrix <math>K \in \mathbb{R}^{n \times d}</math>, where <math>d</math> is the hidden dimension size. Each row <math>Q_{i,*}</math> represents the query vector for the <math>i</math>-th token, and similarly <math>K_{i,*}</math> is the key vector for that token. Let <math>S_i</math> denote the set of token indices whose KV pairs are retained in the cache at step <math>i</math>. The goal is to define an '''eviction policy''' that updates the cache from <math>S_{i-1}</math> to <math>S_i</math> such that the size of the cache remains fixed at <math>k</math>, and only one token is evicted or added per step. Formally, this means the policy must satisfy two constraints: <math>|S_i| = k</math>, and <math>|S_i \setminus S_{i-1}| \leq 1</math>, which also implies that at least <math>k - 1</math> tokens are preserved between steps. | |||
The attention output for the current token is computed using only the keys in <math>S_i</math>, not the full history. This introduces the need to adjust the attention calculation to account for the missing tokens. Specifically, the model computes a vector <math>o_i</math>, which contains the attention scores normalized over the tokens in the current cache. To calculate this, a scalar <math>D_i</math> is first defined as the sum of the exponentiated attention logits between the current query <math>Q_{i,*}</math> and the selected keys <math>K_{S_i,*}</math>, subtracting out the contributions of evicted tokens using an indicator vector <math>1_{[i] \setminus S_i}</math>. The formula is given by: | |||
<math> | |||
D_i := \left( \exp(Q_{i,*}(K_{S_i,*})^\top) - 1_{[i] \setminus S_i} \right) \cdot 1_i | |||
</math> | |||
The normalized attention vector <math>o_i</math> is then obtained by: | |||
<math> | |||
o_i := D_i^{-1} \cdot \left( \exp(Q_{i,*}(K_{S_i,*})^\top) - 1_{[i] \setminus S_i} \right) | |||
</math> | |||
This effectively zeroes out the scores of tokens that are no longer in the cache, while properly normalizing the remaining attention weights. | |||
The core goal of this setup is to design an eviction strategy such that the generative process of the model, when operating under this cache constraint, behaves as similarly as possible to the original, full-cache process. This formulation establishes the mathematical foundation for the method proposed in the next section, where the paper introduces a greedy but effective policy—'''H<math>_2</math>O (Heavy Hitter Oracle)'''—that determines which tokens to keep in the cache based on their attention contributions. All variables and concepts defined here will be directly used to describe and implement that method. | |||
===Method=== | |||
H<math>_2</math>O hinges on two key empirical observations about attention behavior in large language models (LLMs): | |||
# '''Sparsity Rules''': Though trained with dense attention, actual attention matrices during inference are very sparse—more than 95% of entries are close to zero. Such means most tokens have negligible contribution to attention computation at any step. | |||
# '''Heavy Hitters Shine''': A small number of tokens consistently receive high cumulative attention across layers and heads. These "Heavy Hitters" stronggly influence generation and often correspond to frequently co-occurring words. | |||
Now let's see how it works, in the following sections. | |||
====1. Spotting Heavy Hitters==== | |||
In LLMs, the attention mechanism often shows that a small subset of tokens, termed '''Heavy Hitters''' (H<math>_2</math>), disproportionately influence the model’s output. They have to be identified to enable cost-efficient memory usage at inference time with minimal loss of generation quality. | |||
At each generation step, the model computes attention scores that shows how much influnce each past token has on the current one. In H<math>_2</math>O, these attention scores are accumulated across all layers and atttention heads to determine a token’s overall importanc. This accumulated score represent that how often and how strongly a token is attended to in subsequent decoding steps. | |||
Formally, let <math>a_{i,j}^{(l,h)}</math> represent the attention score from token <math>j</math> to token <math>i</math> at layer <math>l</math> and head <math>h</math>. The cumulative attention score for token <math>j</math> is calculated as: | |||
<math> | |||
A_j = \sum_{l=1}^{L} \sum_{h=1}^{H} \sum_{i=j+1}^{n} a_{i,j}^{(l,h)} | |||
</math> | |||
Here, <math>L</math> denotes the number of layers, <math>H</math> the number of attention heads, and <math>n</math> the total number of generated tokens. This formulation aggregates the influence of token <math>j</math> across all future tokens. The tokens with the highest <math>A_j</math> scores are selected as Heavy Hitters. in this paper empirical evidence shows that removing these tokens from the cache severely decrease model performance and validating their critical role. | |||
====2. Smart Eviction==== | |||
When the Heavy Hitters have been identified, the H<math>_2</math>O framework applies a dynamic eviction policy to manage a fixed-size key-value (KV) cach during autoregressive generation. The goal is to balance two things: first, preserving long-term influential tokens (Heavy Hitters) and second, retaining recent tokens that help maintain local coherenc. | |||
At each generation step, when a new token is generated and added to the cache, the number of stored tokens may exceed the limit <math>k</math>. For having a constant cache size, one token must be evicted. The Smart Eviction mechanism uses a greedy algorithm to make this decision, combining two guiding principles: | |||
* Recency — recent tokens are often important for short-term context; | |||
* Global importance — tokens with high cumulative attention should be preserved. | |||
The problem of choosing which token to evict is modeled as a dynamic selection problem with a submodular structure. At each step <math>i</math>, the goal is to maintain a set <math>S_i</math> of size <math>k</math> that maximizes an attention-based utility function. Although the model does not use future information directly, it approximates importance using current attention scores. | |||
The update rule guarantees that the cache evolves incrementally: | |||
* The size of the cache is fixed: <math>|S_i| = k</math>, | |||
* At most one token is changed per step: <math>|S_i \setminus S_{i-1}| \leq 1</math>. | |||
This strategy allows the model to focus memory on the most useful tokens at every point in generation. Specially, the method works entirely at inference time and requires no retraining, and this makes it efficient and easily deployable. | |||
====3. Math Under the Hood==== | |||
The mathematical core of H<math>_2</math>O lies in how it formulates the cache update process as a '''dynamic submodular maximization''' problem. Submodular functions naturally model diminishing returns, the idea that adding a new token to an already strong set provides less gain than adding it to a weaker one. This fits the nature of attention which we say as more tokens are cached, the marginal benefit of each additional one decreases. | |||
To formalize the eviction decision, the paper defines a utility function <math>F_{\text{score}}(T)</math> over token sets <math>T</math> that estimates the contribution of each token in attention. At decoding step <math>i</math>, this is computed as: | |||
<math> | |||
F_{\text{score}}(T) := \sum_{s \in T} o_s | |||
</math> | |||
where <math>o_s</math> is the attention score of token <math>s</math> based on the query vector at step <math>i</math>. These scores are derived from the attention matrix, considering only keys in the current cache. | |||
The cache update rule in the algorithm works as follows: it considers the candidate set <math>G_i = S_{i-1} \cup \{i\}</math>, and finds the token <math>u</math> whose removal least harms the total score. Then the new cache is updated by: | |||
<math> | |||
S_i \leftarrow (S_{i-1} \cup \{i\}) \setminus \{u\} | |||
</math> | |||
The algorithm is both simple and effective. Under mild assumptions, the paper proves that this greedy approach achieves a near-optimal solution, with performance bounded by <math>(1 - 1/e)</math> of the optimal score, minus a small error. This theoretical guarantee shows why the method works so good in practic and providing high-quality results with low overhead. | |||
Together, these mathematical principles enable H<sub>2</sub>O to retain the most important tokens, adapt dynamically during generation, and deliver efficient inference with minimal memory. | |||
====Algorithm Overview==== | |||
[[Media:H2O eviction algo.png|The Figure2]] Shows anilustration of the H<math>_2</math> Eviction Algorithm, and we can understand how tokens are managed in the constrained KV cache during autoregressive text generation process. The algorithm dynamically updates the cache to keep only the most useful tokens based on their local attention contributtion. | |||
[[File:H2O eviction algo.png|600px|thumb|center|Figure2- H<math>_2</math> token eviction algorithm]] | |||
The algorithm assumes a fixed cache size budget <math>k</math>. Initially, the cache is empty. For the first <math>k</math> tokens, no eviction is necessary and they are simply added to the cache. It starts from the <math>(k+1)</math>-th token, the algorithm must make space for each new token by removing one existing entry from the cache. | |||
At each generation step <math>i</math>, the algorithm performs the following steps: | |||
* It computes the attention logits betwen the current query <math>Q_{i,*}</math> and the cached keys <math>K_{S_{i-1},*}</math>. | |||
* These logits are masked by using the indicator <math>1_{[i] \setminus S_{i-1}}</math> to ignore the influence of evicted tokens and normalized to obtain the attention output <math>o_i</math>. | |||
* A scoring function <math>F_{\text{score}}(T)</math> is defined as the sum of attention contributions over any token subset <math>T</math>. | |||
* The candidate cache set <math>G_i = S_{i-1} \cup \{i\}</math> includes all current cache entries plus the new token. | |||
* The algorithm greedily selects one token <math>u \in G_i</math> whose removal would cause the least drop in the total attention score, and evicts it. | |||
* The updated cache <math>S_i</math> becomes <math>(S_{i-1} \cup \{i\}) \setminus \{u\}</math>. | |||
As an example, let's assume that the cache size is limited to 3 tokens. After the fourth decoding step, the algorithm evaluates the attention contributions of all tokens in the current cache and the new one. If the third token’s score is the lowest, its key and value embeddings are removed. These evicted embeddings are no longer accessible in subsequent steps and saving memory while maintaining output quality. | |||
This cache management strategy makesH<math>_2</math>O to operate efficiently even under memory constraints. It avoids recomputation and adapts dynamically to the context. In practice, this approach has been successfully implemented on models such as OPT, LLaMA, and GPT-NeoX, and achieve substantial memory reduction and faster generation speeds without any need to model retraining. | |||
===Heavy Hitters (H₂)=== | |||
H₂O addresses the problem of KV cache bloat by retaining only tokens that contribute significantly to attention—called Heavy Hitters (H₂)—and discarding others with negligible impact. | |||
* '''Heavy Hitters in MLPs:''' Beyond attention, H₂s also appear in MLP blocks. A small number of neurons are activated almost universally (100% frequency), while others remain rarely used. Eliminating these critical neurons causes severe performance drops but recovery is possible with just 1% of training data, highlighting their core influence. | |||
* '''Early-Bird Emergence:''' H₂s tend to emerge early in training and show positional stability over time, reinforcing their fundamental role. | |||
* '''Infinite-Length Generation:''' H₂O supports generation over ultra-long contexts (up to 4 million tokens), outperforming StreamLLM in perplexity while reducing memory consumption. | |||
* '''Compatibility:''' It integrates well with quantization (e.g., 4-bit weights), allowing memory savings and throughput improvements even on low-resource GPUs. | |||
* '''Shot Robustness:''' H₂O performs effectively in zero-shot, one-shot, and few-shot inference, maintaining quality while reducing memory use by up to 5×. | |||
* '''Complementarity:''' H₂ tokens can enhance Top-K pruning methods and outperform static sparse alternatives like SpAtten, thanks to dynamic submodular optimization and per-head retention strategies. | |||
=== Attention Sink === | |||
While designing KV cache compression strategies, it's important to understand which tokens are actually being attended to over long sequences. One key observation introduced in the paper is the presence of an "Attention Sink" effect. | |||
==== Definition ==== | |||
* '''Attention Sink''' refers to tokens that disproportionately attract attention across future tokens, regardless of their semantic importance. | |||
* This is due to the nature of causal attention: the earlier a token appears, the more future tokens can see it. | |||
* Combined with the row-wise softmax in the attention mechanism, early tokens tend to accumulate large attention scores. | |||
==== Impact on Token Retention and KV Cache Design ==== | |||
* Attention sinks often receive high scores not because they're informative, but because of positional bias. | |||
* Retaining these tokens in the KV cache can waste space and reduce the effectiveness of compression. | |||
* H2O proposes to distinguish true "heavy hitters" from attention sinks by analyzing cumulative attention in context and designing smarter eviction policies. | |||
This insight improves both the interpretability and efficiency of autoregressive models, especially when applying selective KV caching. | |||
=== Limitations and Future Work === | |||
H<math>_2</math>O isn’t perfect and it has some limitations: | |||
* '''Dataset Dependency''': To identify heavy hitters initially, a small dataset is needed and its success relies on a calibration dataset to spot heavy hitters. If that dataset doesn’t match the task, performance could dip. | |||
* '''Threshold Sensitivity''': Setting the threshold too high or too low can hurt performance or waste memory. Picking the right cutoff for "heavy" tokens is a balancing act—too strict, and you lose context; too lenient, and memory savings shrink. | |||
In future work, using adaptive thresholds based on recent token statistics can help to more improve accuracy and efficiency. Blending H<math>_2</math>O with tricks like quantization could push efficiency further. Also, finding alternatives to attention scores (like gradients or entropy) for token importance can lead to better pruning. | |||
=== Visualization & Intuition Behind H₂O === | |||
To understand how H<math>_2</math>O achieves efficient KV cache compression, it helps to visualize the decoding process. During generation, not all tokens contribute equally to future outputs. H<math>_2</math>O tracks accumulated attention scores to identify a small subset of tokens—called "heavy hitters"—that are repeatedly referenced in attention computation. | |||
By keeping only these tokens in the cache, H<math>_2</math>O reduces memory usage without harming performance. This approach not only accelerates inference but also improves generation quality by avoiding repetitive or trivial patterns. The retained tokens form a sparse but semantically meaningful context window, balancing precision with efficiency. | |||
=== Practical Benefits and Use Cases === | |||
H<math>_2</math>O presents a compelling solution for real-world deployment of large language models, particularly when memory and speed are bottlenecks. | |||
Key benefits include: | |||
* '''Memory Efficiency''': Dramatically reduces the size of the KV cache by discarding unimportant tokens. | |||
* '''Inference Speed''': Compatible with quantized models, enabling low-latency inference even on moderate hardware. | |||
* '''Improved Output Diversity''': Reduces redundancy by preventing the model from over-attending to trivial tokens. | |||
These properties make H<math>_2</math>O particularly useful in applications such as edge computing, real-time generation systems, and large-batch inference pipelines where throughput and memory footprint are critical. | |||
=== Comparison with Baselines === | |||
Different KV caching strategies yield significantly different outcomes in generation quality and efficiency. | |||
* '''Full Cache''': Retains all tokens. This approach maintains full context but consumes large amounts of memory and may lead to repetitive outputs. | |||
* '''Local Cache''': Retains only the most recent tokens. While this improves efficiency, it often degrades performance by omitting long-term dependencies. | |||
* '''H<math>_2</math>O (Selective Cache)''': Retains only the heavy hitters. This strategy maintains semantic coherence while dramatically reducing memory cost. | |||
Compared to traditional methods, H<math>_2</math>O preserves meaningful context, avoids information overload, and produces fluent, diverse outputs with minimal redundancy. | |||
=== Attention Sink Mitigation Strategy === | |||
One challenge in transformer-based models is the "attention sink" phenomenon, where certain tokens—often those appearing early in the sequence—attract excessive attention regardless of their semantic relevance. | |||
This is primarily caused by two factors: | |||
* '''Token Visibility Bias''': Early tokens have more opportunities to be attended by subsequent tokens. | |||
* '''Softmax Dynamics''': The normalization in softmax exaggerates even slight score advantages, reinforcing initial token dominance. | |||
H<math>_2</math>O implicitly mitigates this by not relying on position alone. Instead, it dynamically evaluates each token’s importance via cumulative attention. This ensures that retained tokens are selected based on utility rather than position, effectively filtering out irrelevant sinks and improving generation balance. | |||
==Transformer-VQ: Linear-Time Transformers via Vector Quantization== | |||
===Introduction=== | |||
Transformer models have demonstrated remarkable success in natural language processing and other sequential data tasks. However, their standard self-attention mechanism has quadratic time complexity with respect to sequence length. Transformer-VQ addresses this bottleneck by introducing a linear-time attention mechanism using vector quantization (VQ). This approach makes it feasible to apply transformers to much longer sequences efficiently. | |||
===Key Innovations=== | |||
1. Vector-Quantized Keys: | |||
* Standard self-attention requires computing pairwise interactions between queries and keys, leading to quadratic complexity. | |||
* Transformer-VQ clusters keys into a smaller set of representative vectors (codewords) using a learned vector quantization codebook. | |||
* Queries attend to these codewords rather than raw keys, reducing the computational load. | |||
2. Efficient Attention Mechanism: | |||
* Instead of computing full pairwise interactions, attention weights are calculated between queries and quantized keys. | |||
* This allows a factorization of the attention matrix, leading to linear time complexity. | |||
3. Compressive Key-Value Cache: | |||
* Transformer-VQ introduces a caching mechanism that stores only the quantized representations of past keys, maintaining efficiency without losing important information. | |||
* Unlike traditional key-value caching, which scales linearly in storage requirements, this approach enables efficient long-context modeling. | |||
===Mathematical Formulation=== | |||
==== Self-Attention in Transformers ==== | |||
Given input sequence representations <math>X</math>, standard attention computes: | |||
<math display="block">A = \text{softmax} \left( \frac{QK^T}{\sqrt{d_k}} \right) V</math> | |||
where: | |||
*<math>Q = XW_Q</math> (queries) | |||
*<math>K = XW_K</math> (keys) | |||
*<math>V = XW_V</math> (values) | |||
*<math>W_Q, W_K, W_V</math> are learnable projection matrices. | |||
==== Vector Quantization (VQ) Mechanism ==== | |||
Instead of using raw <math>K</math>, Transformer-VQ applies vector quantization (VQ) to reduce the number of unique keys: | |||
1. Assign each key <math>K_t</math> to its closest codeword <math>C_s</math> from a learned codebook <math>C</math>: | |||
<math display="block">z_t = \arg\min_s || K_t - C_s ||^2</math> | |||
2. Replace <math>K_t</math> with the quantized representation: | |||
<math display="block">\hat{K}_t = C_{z_t}</math> | |||
3. Compute attention using the quantized keys: | |||
<math display="block">A = \text{softmax} \left( \frac{Q \hat{K}^T}{\sqrt{d_k}} \right) V</math> | |||
This replacement significantly reduces the computational cost of self-attention while preserving key information. | |||
==== Linear-Time Attention Computation ==== | |||
To enable linear-time self-attention, the authors introduce a factorization of the attention matrix: | |||
<math display="block">W = \text{softmax} (Q \hat{K}^T)</math> | |||
which can be rewritten as: | |||
<math display="block">W = \text{softmax} (Q C^T) \Delta</math> | |||
where <math>\Delta</math> is a sparse matrix mapping token indices to their assigned codebook vectors. | |||
Additionally, a recurrence relation is used to update the cache efficiently: | |||
<math display="block">U(n) = U(n-1) + \Delta(:,n) V(n,:)</math> | |||
where <math>U(n)</math> accumulates grouped values based on quantized keys, ensuring efficient memory use. | |||
==== Quantized Shared Attention for Scalable KV Compression ==== | |||
In an effort to reduce the computation cost of attention and KV caching, a new method has been proposed that combines vector quantization with shared attention models. Since it exploits the property that attention patterns over multiple layers of deep language models have significant similarity, it quantizes keys and shares attention weights over layers, permitting compression of both memory and FLOPs at the inference time. | |||
Let <math>K \in \mathbb{R}^{n \times d}</math> be the matrix of key vectors for a sequence of <math>n</math> tokens and <math>d</math> the dimensionality. A quantization codebook <math>C \in \mathbb{R}^{S \times d}</math> is introduced, where <math>S \ll n</math>. Each key <math>k_i</math> is mapped to its nearest codeword via: | |||
<math> | |||
z_i = \arg\min_{s} \| k_i - C_s \|^2, \quad \hat{k}_i = C_{z_i} | |||
</math> | |||
Instead of computing attention directly with raw keys, the model uses the quantized keys <math>\hat{K}</math>. The attention score for a query <math>q_t</math> becomes: | |||
<math> | |||
A_t = \mathrm{softmax} \left( \frac{q_t \hat{K}^\top}{\sqrt{d}} \right) | |||
</math> | |||
To enable efficient factorization, define a sparse assignment matrix <math>\Delta \in \{0,1\}^{S \times n}</math> where <math>\Delta_{s,i} = 1</math> if <math>k_i</math> maps to <math>C_s</math>. Then the attention computation simplifies to: | |||
<math> | |||
A_t \approx \mathrm{softmax} \left( \frac{q_t C^\top}{\sqrt{d}} \right) \Delta | |||
</math> | |||
This factorization enables <math>q_t C^\top</math> to be calculated once and reused for multiple heads or layers. It avoids redundancy by avoiding repeated softmax calculation and caching a few full sets of keys. This representation also enables re-use during decoding time with a minimal cache of quantized key embeddings. | |||
In practical deployments, this provides significant memory and computational reductions without compromising precision. The technique integrates smoothly with vector-quantized models like Transformer-VQ and naturally extends to shared-attention techniques where the same attention matrices are reused across consecutive layers. | |||
==== Training Objective ==== | |||
The training loss consists of two components: | |||
<math display="block">L(X; \theta, C) = L_{CE}(X; \theta, C) + \beta L_{VQ}(X; \theta, C)</math> | |||
where: | |||
<math>L_{CE}</math> is the cross-entropy loss for next-token prediction: | |||
<math display="block">L_{CE}(X; \theta, C) = -\frac{1}{T} \sum_{t=0}^{T-1} \ln p(x_{t+1} | x_{\leq t}, \theta, C)</math> | |||
<math>L_{VQ}</math> is the vector quantization loss ensuring the model commits to learned codebook entries: | |||
<math display="block">L_{VQ}(X; \theta, C) = \frac{1}{T} \sum_{t=0}^{T-1} \sum_{\ell=0}^{N-1} || K^{(\ell)}_t - SG(C^{(\ell)}_{z_t}) ||^2_2</math> | |||
where <math>SG(\cdot)</math> is a stop-gradient operator, preventing codebook updates via backpropagation. | |||
===Advantages and Performance=== | |||
*At sequence length 8k, Transformer-VQ is 3x faster than standard transformers. | |||
*At sequence length 32k, it is 12x faster. | |||
*Can scale to 131k tokens with stable throughput. | |||
===Conclusion=== | |||
Transformer-VQ offers an efficient way to process long sequences, making transformers more scalable. It uses vector quantization and a smart caching system to keep the advantages of full attention while using fewer computing resources. This improvement makes it possible to apply transformers to tasks like analyzing long documents and generating extended conversations. | |||
==Dynamic Context Pruning for Efficient and Interpretable Autoregressive Transformers== | |||
===Motivation=== | |||
In this paper, the authors pose the following question: Can we dynamically prune past content based on the available context, while preserving as much as possible the expressivity of the model? In response to it, they propose a technique that dynamically prunes the context while maintaining the model capacity, hence, reduced memory and computational resources during inference. The method simply learns a mechanism to determine uninformative tokens and drop them during the generation process. This way not only performance is being improved, but also the model decision-making process becomes more interpretable. | |||
===Background=== | |||
Assume the input sequence is <math>\mathbf{T}\in\{0,1,\ldots,n_{\mathrm{vocab}}\}^{n}</math>, where <math>n</math> is the length of the sequence and <math>n_{\mathrm{vocab}}</math> is the vocabulary size. The emdedding layer will embedded the tokens into matrix <math>\mathbf{X}^0\in\mathbb{R}^{n\times d}</math>, where <math>d</math> is the embedding dimension of the model. | |||
One layer of the Transformer-decoder architecture is defined as: | |||
<math>\begin{aligned} | |||
& \mathbf{X}=\mathsf{MHA}(\mathsf{LayerNorm}(\mathbf{X}^{\ell-1}))+\mathbf{X}^{\ell-1}, \\ | |||
& \mathbf{X}^\ell=\mathsf{FF}(\mathsf{LayerNorm}(\mathbf{X}))+\mathbf{X}, | |||
\end{aligned}</math> | |||
where MHA stands for Multi-head self-attention defined as, <math>\mathsf{MHA}(\mathbf{X})=\text{Concatenate}(\mathsf{head}_1(\mathbf{X}),\mathsf{head}_2(\mathbf{X}),\ldots,\mathsf{head}_h(\mathbf{X}))\mathbf{W}_O</math>, <math>\ell\in\{1,2,\ldots,L\}</math> denotes different layers. | |||
The feed-forward part of the Transformer is defined as: | |||
<math>\mathrm{FF}(\mathbf{X})=\sigma_{\mathrm{FF}}(\mathbf{XW}_{F_1})\mathbf{W}_{F_2},</math> | |||
where <math>\sigma_{\mathrm{FF}}</math> is a nonlinearity, and <math>\mathbf{W}_{F_1}</math>,<math>\mathbf{W}_{F_2}</math> are linear layers with typical dimensions <math>\mathbf{W}_{F_1}\in\mathbb{R}^{d\times4\cdot d}</math> and <math>\mathbf{W}_{F_2}\in\mathbb{R}^{4 \cdot d \times d}</math>. | |||
A final projection layer <math>\mathbf{W}_{\mathrm{logits~}}\in\mathbb{R}^{d\times n_{\mathrm{vocab}}}</math> is used to project back to thevocabulary space and predict the next token from the representations <math>X^{L}</math>. | |||
===Methodology=== | |||
Firstly, adaptively sparse attention is introduced to allow the network to drop unimportant parts of the context (as Figure below). | |||
[[File:dynamic_pruning_1.png|400px|thumb| Figure: Adaptively Sparse Attention]] | |||
To achieve this, two learnable parameters <math>\mathbf{W}_{Q_{int}}^\ell, \mathbf{W}_{K_{int}}^\ell \in \mathbb{R}^{d \times r}</math> that calculate the interaction queries and keys as <math>\mathbf{Q}_{int}^\ell = \mathbf{X}^\ell \mathbf{W}_{Q_{{int}}}^\ell</math>, <math>\mathbf{K}_{int}^\ell = \mathbf{X}^\ell \mathbf{W}_{K_{int}}^\ell</math> are added to each layer. Then the interaction of token <math>k</math> with token <math>j</math> at layer <math>\ell</math> is calculated as: | |||
<math> | |||
\mathbf{I}_{k,j}^\ell = \begin{cases} | |||
\prod_{n=j+1}^k \mathbf{\overline{I}}_{n,j}^\ell \text{ and } \mathbf{\overline{I}}_{n,j}^\ell = \sigma\left(\frac{(\mathbf{Q}_{int}^\ell)_n^\top (\mathbf{K}_{int}^\ell)_j}{\sqrt{r}} + \beta^\ell\right), & \text{if } j < k \\ | |||
1, & \text{if } j = k \\ | |||
0, & \text{if } j > k | 0, & \text{if } j > k | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
where <math>\sigma(\cdot)</math> is the sparse sigmoid function and <math>\beta^\ell \in \mathbb{R}</math> is a layer specific parameter that controls initial sparsity. | |||
When <math>j = k</math>, the value is <math>1</math>, meaning that the token has to remain, as no token can drop itself. In addition, the interaction is <math>0</math> when <math>j \gt k</math> to enforce causal masking so that future tokens are not attended to. | |||
The sparse sigmoid is defined as: | |||
<math>\sigma(x)=\alpha\mathrm{-sigmoid}(x)=\mathrm{argmax}_{p\in[0,1]}\left(p\cdot x+H_\alpha(p)\right),</math> | |||
where | |||
<math>H_\alpha(p)= | |||
\begin{cases} | |||
\frac{1}{\alpha(\alpha-1)}(p-p^\alpha+(1-p)-(1-p)^\alpha),\text{if } \alpha\neq1 \\ | |||
-p\log p-(1-p)\log(1-p),\text{if } \alpha=1. & | |||
\end{cases}</math> | |||
The hyperparameter <math>\alpha</math> can control the sparsity of the network, practically, we will start from small value and increase it to a cosine scheduler. | |||
===Experiment=== | |||
The experiment involved fine-tuning several pre-trained GPT‑2 models (small, medium, large, and xl) on language modeling tasks using subsets of English Wikipedia and BookCorpus. The approach, termed Adaptively Sparse Attention, introduces a learnable mechanism that dynamically prunes uninformative tokens from the input context during generation by using a modified α‑sigmoid function. The method was integrated with existing models through a fine-tuning process, and its performance was compared against baselines such as dense, local, and static sparse attention configurations. The experiments measured traditional language modeling metrics like perplexity as well as zero-shot performance on benchmarks including WinoGrande, HellaSwag, PIQA, and LAMBADA, while also evaluating improvements in inference speed and memory efficiency. | |||
===Results=== | |||
High Pruning with Minimal Loss: | |||
The method is able to prune up to 80% of the context with very little degradation in perplexity (in some settings, even a slight improvement was observed compared to the dense baseline). | |||
Improved Efficiency: | |||
Significant gains in inference speed were demonstrated. For instance, a GPT‑2-small model achieved nearly double the throughput (tokens per second) with only a minor increase in perplexity. Similarly, GPT‑2-medium models showed an almost 189% throughput boost for a context of 1000 tokens with negligible performance drop. | |||
Maintained Zero-shot Capability: | |||
Despite the aggressive pruning, the zero-shot performance on standard benchmarks remained comparable—and in some cases even better—than the dense models. | |||
Interpretability Insights: | |||
The analysis revealed that the pruning mechanism predominantly drops tokens that tend to be less critical (such as punctuation or stop words), and that different layers exhibit distinct pruning behaviors, offering insights into the model’s decision-making. | |||
=== Limitations & Future Work === | |||
==== Limitations ==== | |||
While dynamic context pruning significantly improves efficiency and interpretability, it has several limitations: | |||
* '''Loss of Long-Range Dependencies''': Although pruning preserves key tokens, certain long-range dependencies (e.g., legal text, programming code) may still be affected, leading to subtle performance degradation. | |||
* '''Layer-Specific Sensitivity''': Different transformer layers exhibit varying pruning behaviors, which may require additional fine-tuning to balance efficiency and expressivity. | |||
* '''Interaction with Decoding Strategies''': The method assumes a standard autoregressive decoding process, but its impact on diverse strategies like beam search or nucleus sampling remains underexplored. | |||
* '''Computational Overhead During Training''': While inference efficiency improves, the model introduces extra computations during training to learn the pruning mechanism, which may limit scalability. | |||
==== Future Work ==== | |||
Several directions can further refine and expand this approach: | |||
* '''Multimodal Extensions''': Adapting dynamic pruning to transformers handling text + images (e.g., GPT-4V) or speech models could improve efficiency in broader AI applications. | |||
* '''Task-Specific Adaptations''': Investigating pruning in different NLP tasks (e.g., summarization, translation) could reveal domain-specific advantages or weaknesses. | |||
* '''Adaptive Pruning for RLHF''': Exploring how pruning interacts with reinforcement learning from human feedback (RLHF) could enhance efficiency in fine-tuned language models. | |||
* '''Integration with Hardware-Aware Optimization''': Aligning pruning with efficient hardware execution (e.g., sparsity-aware accelerators) could maximize real-world benefits. | |||
This method presents a promising step toward efficient and interpretable transformers, but further research is needed to address trade-offs in expressivity, robustness, and task-specific generalization. | |||
==Beyond KV Caching: Shared Attention for Efficient LLMs== | |||
===Overview=== | |||
[[File:sa.png|thumb|right|Shared Attention algorithm]] | |||
In order to increase the efficiency of LLMs during inference, this paper introduces a unique technique called Shared Attention (SA), which shares the computed attention weights directly across many layers. The fundamental idea is that, upon pretraining, the attention weight distribution in complex LLMs becomes comparable across the majority of layers. For example, it was observed that a majority of the layers (roughly layers 3 to 30 in Llama2-7B) are similar when checked with cosine similarity metric. This suggests that for many layers, the model attends to different parts of the input sequence in a similar manner. | |||
===Isotropic Attention Distribution=== | |||
An in-depth analysis of layer-specific attention weights across multiple LLMs, including Llama2-7B-chat, Llama3-8B-instruct, and Qwen2-72B-instruct, reveals a striking self-organization pattern in attention distributions, termed Isotropic Attention Distribution. This pattern, observed across models evaluated on MMLU, segments layers into four functional groups. The first group (layers 0-1) abstracts token-level semantic information with highly data-dependent attention patterns. The second group (layers up to index 5) acts as a transitional phase, refining intermediate semantic features. The third and largest group spans most of the model, displaying high attention weight similarity, signifying a stable and isotropic attention mechanism that informs deeper contextual understanding. Finally, the fourth group, consisting solely of the output layer, diverges significantly in attention distribution, emphasizing its specialized role in final decision-making. These findings reinforce the structural organization within LLMs and further validate the computational optimization potential of Shared Attention (SA), as it strategically exploits this inherent similarity to minimize redundant computations while preserving model expressivity. | |||
===Method=== | |||
The core of this method is to directly share a single pre-calculated attention matrix over a selected multi-layer span. With SA, the first layer in the shared span computes the attention weights, and all subsequent layers in that span use the same computed weights. This is in contrast to each layer independently calculating its attention weights using its own query and key matrices, followed by the softmax function. Although the attention distribution that determines how much weight to assign to each value is the same, each layer in the shared span still computes the output using its own value matrix. This eliminates the need for repeated softmax computations and reduces the need to store separate key matrices for each layer within the shared span. | |||
By sharing the attention matrices, they aim to reduce the computational redundancy by avoiding repeated softmax and utilizing fewer unique key caches. The algorithm is shown in | |||
Figure (right). | |||
===Experiment=== | |||
[[File:sa-table.png|thumb|right|Comparison of SA on different metrics]] | |||
Experimentation was done using the Llama2-7B and Llama3-8B base models conducted on two NVIDIA A100 80GB GPUs. Table (right) compares the performance by directly applying the SA to different layers in the pretrained models across various language tasks. The results highlight that applying SA in upper layers for Llama2-7B maintained stable performance in the GLUE and MMLU benchmarks, but SA in middle layers led to a drop in GSM8K reasoning task. | |||
When tested on the Llama3-8B model, SA in the upper layers improved the performance on the GLUE benchmark and was quite comparable in other benchmarked tasks as well. This model had a minimal performance decrease when SA was used since it had a better layer-wise attention similarity by nature. | |||
= Topic 7: Dynamic Models: Many-in-One Language Models = | |||
== Introduction == | |||
The popularity of machine learning has been growing immensely in the recent decade. There is a growing number of industries and applications that leverage machine learning for growth. With various applications, there is immense difficulty when trying to find a perfect solution for a specific application. For instance, there is a plethora of deep neural networks that apply to different applications (e.g., CNNs for image processing). With the rise of LLMs, the challenge of finding suitable models becomes more difficult to solve. One has to consider the performance and computational needs of their tasks and target devices, especially with very large models. There are many techniques to improve the efficiency of LLMs, such as knowledge distillation, pruning, and quantization. However, this approach has a fundamental flaw: a static model. The model does not change, which can be problematic; when executing on simple task, the model may be too complex. On the contrary, the model may be too simple when executing difficult tasks. | |||
To resolve the issue, we try to build a many-in-one-model. It is a single neural network that can run in different sizes for a given task. When the computation resource is abundant, more parameters are activated for inference whereas when the computation resource is insufficient, less parameters are activated. In doing so, we avoided training models of different sizes and drastically reduces the complexity of managing multiple independently trained models while still offering different "performance vs cost" trade-offs. Note many-in-one model is different from Multi-model. The former is a single model that has the ability to activate more/less parameters on a single task where as the latter is the architecture that combines several independently trained models, each performing a specific tasks. | |||
There is no "one-size-fits-all" model due to present constraints. In this section, one can explore various techniques to make more dynamic models to suit different needs. | |||
== Challenges and Opportunities in Dynamic Models == | |||
While dynamic models offer tremendous flexibility and efficiency, several open challenges remain to be addressed: | |||
* '''Balance Between Complexity and Performance''': | |||
** Designing dynamic models requires careful management of complexity. Overly complex routing mechanisms or sub-model architectures may lead to additional computational overhead during inference, reducing the potential gains. Efficiently balancing model complexity and computational overhead remains an ongoing research area. | |||
* '''Training Stability and Convergence Issues''': | |||
** Due to simultaneous training of multiple sub-networks, dynamic models may face difficulties in ensuring stable training and convergence. Specifically, smaller sub-models may not receive sufficient training signals, potentially leading to underfitting. Techniques such as adaptive sampling strategies or curriculum learning could address these challenges. | |||
* '''Interpretability and Explainability''': | |||
** Dynamic routing mechanisms inherently introduce complexity in understanding model behavior. How and why specific sub-networks are activated for certain inputs can become opaque, making model interpretability challenging. Improved visualization and diagnostic tools that elucidate routing decisions could significantly enhance interpretability. | |||
* '''Robustness to Input Variability''': | |||
** Dynamic models must robustly handle diverse input distributions. Variations in input complexity or unexpected input scenarios can impact the routing quality, potentially degrading performance. Future research can explore adaptive routing mechanisms incorporating real-time feedback or uncertainty estimation to improve robustness. | |||
These challenges provide rich opportunities for future research, emphasizing the importance of continuing innovation in architectures, routing algorithms, and training methodologies for dynamic models. Addressing these issues will be critical to fully realizing the potential of Many-in-One models for scalable, efficient, and adaptive AI deployment. | |||
== SortedNet: A Scalable and Generalized Framework for Training Modular Deep Neural Networks== | |||
===Motivation=== | |||
Traditional deep neural network (DNN) training often requires building and maintaining many individual models to meet the diverse computational budgets and accuracy requirements of different users and devices. This approach is: | |||
* Expensive in terms of training time and storage, | |||
* Hard to scale to many architectures, | |||
* Inefficient when adapting to dynamic conditions such as variable latency or memory constraints. | |||
Existing dynamic/many-in-one model approaches (e.g., Once-for-All, DynaBERT) attempt to alleviate these issues but have major drawbacks: | |||
* Significant accuracy drop in sub-models, | |||
* Require architecture-specific designs or teacher-student knowledge distillation, | |||
* Can only train a limited number of sub-models, | |||
* Involve heavy architecture search during training or inference. | |||
To address these challenges, the authors propose '''SortedNet''' — a general, scalable, and architecture-agnostic solution that enables training of hundreds of sub-models simultaneously without sacrificing performance.[[File:SortedNet.png|600px|thumb|center|Figure - The overall diagram of our SortedNet training approach.]] | |||
===Model Architecture=== | |||
SortedNet introduces a general and scalable architecture called the '''Sorted Architecture''', designed to support the simultaneous training of a main model and a large number of sub-models. The key idea is to structure sub-models in a sorted (rather than strictly nested) fashion, enabling modular sharing of parameters across various architectural dimensions (e.g., depth, width, attention heads). | |||
====Key Concepts==== | |||
* '''Sorted vs. Nested''' sub-models: | |||
** In '''nested''' architectures, each smaller sub-model is fully contained within larger sub-models (e.g., layer 2 is inside layer 3). | |||
** In '''sorted''' architectures, sub-models are defined by consistent origin indices across dimensions (e.g., always starting from layer 1), but are not strictly nested. This increases flexibility and scalability. | |||
** All sub-models share weights with the main model and with each other, reducing storage and training overhead. | |||
* '''Target Dimensions''': | |||
** SortedNet supports modularization and sorting across multiple dimensions: | |||
*** Depth (number of layers), | |||
*** Width (number of channels, neurons, or hidden units), | |||
*** Attention heads (for Transformers), | |||
*** Embedding size. | |||
** Sub-models are created by truncating these dimensions from a sampled index up to the full model size. | |||
====Training Procedure==== | |||
At each training iteration: | |||
* A sub-model is sampled randomly from the predefined sorted pool. | |||
* Its corresponding parameters (e.g., selected layers and channels) are activated. | |||
* The model is trained on a standard loss (e.g., cross-entropy), either: | |||
** With only the selected sub-model ('''stochastic loss'''), or | |||
** With a subset of related sub-models ('''summation loss'''). | |||
To ensure stability and fairness in training: | |||
* A shared classifier head is used across all sub-models. | |||
* A gradient accumulation mechanism is employed to aggregate updates across multiple sampled sub-models efficiently. | |||
====Architecture Summary==== | |||
* Shared parameters across all sub-models → memory efficient. | |||
* Sorted origin-based slicing → enables fast sub-model selection at inference. | |||
* No architectural changes required → works on CNNs, Transformers, and others. | |||
* No need for knowledge distillation or architecture search. | |||
This architecture allows SortedNet to achieve: | |||
* Efficient training of up to 160 sub-models in parallel, | |||
* Dynamic sub-model selection during inference (e.g., for faster or cheaper computation), | |||
* High performance across all sub-models without retraining. | |||
== MatFormer: Nested Transformer for Elastic Inference == | |||
=== Motivation === | |||
Suppose in this scenario that you wanted to run a large language model for some application. There is a variety of different LLMs to choose from, and each LLM can differ by the number of parameters (e.g., the LLAMA-2 family contains models with 7B, 13B, 34B, or 70B parameters). Which model to choose? You consider the compute device you have and decide that LLAMA-2 with 7B parameters suffices. Great, the model ran successfully! Ambitiously, you try the 13B-parameter model. Oh no! The model could not be loaded onto your GPU. | |||
In this scenario, your computer can handle the 7B-parameter model, but not the 13B-parameter model. This means that when your computer ran the smaller model, there was still some additional GPU memory that could be leveraged; the entire GPU was not used. Of course, you cannot run the bigger model. Maybe, if say a 12B-parameter model existed, it would have been perfect! The GPU would have been fully used, and we would have (hopefully) better performance than the 7B-parameter model. | |||
The motivation behind MatFormer is to solve this dilemma. The objective of MatFormer is to enable on-demand slicing of a single trained LLM model to precisely fit various deployment constraints. Whether your compute device can handle models with 10 billion parameters to 1 trillion or more, MatFormer can satisfy your compute needs. | |||
===Slicing: Enabling Elastic Inference=== | |||
[[File:MatFormer-Training.png|500px|thumb|right|Slicing for MatFormer]] | |||
====Intuition==== | |||
In order to make elastic inference possible, we need a special articheture desgin and a special way of training the model. Inspired by Matryoshka Representation Learning, we can nest the entire model where each smaller submodel as nested inside the larger one. The smaller the submodel is, the more robust and "core” information is has for the larger ones to reuse. | |||
If we train in this nested way. Any sub-block of the model can be directly used at inference for smaller capacity needs. Ensures consistent behavior across submodels. | |||
Specifically with LLMs, VITs, and other transformer-based models, the author determined that a majority of the computational cost and model size can be attributed to the FFN block. Therefore, they applied this learning technique to the FFN block. | |||
====Training Process==== | |||
We first pick <math>g</math> granularities to be used. Then, for each training run: | |||
1. For each batch, randomly pick one submodel (from g granularities). | |||
* Uniform sampling typically suffices, but if you want emphasize on certain submodel, you can do weighted if sampling. | |||
2. Perform forward/backward pass only on that submodel. | |||
* Forward pass' weights | |||
<math>\text{FFN}_i(x) = \sigma \left( x W_1[0:m_i]^\top \right) W_2[0:m_i]</math> | |||
* Losses for submodel <math>M_i</math> | |||
<math>\mathcal{L}_{\text{Sampling}}(x, y) = \mathcal{L}(M_i(x), y),</math> | |||
3. Update the shared parameter matrix accordingly. | |||
====Deployment: Mix’n’Match==== | |||
You can choose different slices per layer to form new submodels beyond the explicitly trained ones. | |||
===Results: Scaling Laws for MatFormer LMs=== | |||
Empirically, MatFormer follows similar or better scaling trends compared to vanilla Transformers. This means that this nesting and slicing does not degrade model scaling behavior in both log-perplexity and 1-shot tasks even as model sizes grow. | |||
===Future working directions=== | |||
* Submodel structure is still “global”, so when deploying, the entire layers are chosen, compared to per-token or per-sequence width changes. | |||
* Too many slices could under-train certain submodels if we pick too large a <math>g</math>. This leads the the thoughts that We could pick a better sampling strategy to balance these submodels. | |||
* Could potentially combine with pruning/quantization. | |||
== SHARCS: Efficient Transformers through Routing with Dynamic Width Sub-networks == | |||
=== Why SHARCS? === | |||
Transformers, while powerful, come with the drawback of high computational costs. Their static inference process applies the same level of computation to all inputs, regardless of complexity. However, not all inputs require equal processing—some are simpler and can be handled with fewer resources. This inefficiency inspired SHARCS (Sample Hardness Aware Routing based on Confidence Scores), a framework designed to make transformers more efficient by dynamically adjusting computation based on input difficulty. | |||
=== How Does SHARCS Work? === | |||
SHARCS introduces a lightweight router that predicts the difficulty (or "hardness") of each input sample and routes it to a sub-network of appropriate computational width. | |||
The following details the three key steps in SHARCS: | |||
1. Estimating Sample Hardness | |||
* SHARCS assigns a "hardness label" to each input based on the model's prediction history during training. | |||
* Hardness levels range from 1 (easy) to <math>M</math> (hard), determined by the model's confidence in predicting the correct class over a sliding window of <math>W</math> epochs. | |||
* Lower confidence thresholds reduce computational cost but may impact accuracy, making <math>M</math> and <math>W</math> critical hyperparameters for balancing efficiency and performance. | |||
2. Training the Router | |||
* The transformer is split into two parts: non-adaptive layers (shared across all inputs) and adaptive layers (adjustable based on hardness). | |||
* The router, placed between these layers, predicts the hardness level using outputs from the non-adaptive layers. This is a key design choice as the placement of the router (early vs late decision) results in a trade-off between accuracy and speed. | |||
* Each hardness level corresponds to a specific width reduction factor for the adaptive layers. | |||
* During training: | |||
** A reduction factor is sampled for each input. | |||
** The corresponding sub-network processes the input and both the sub-networks and router are trained jointly using a weighted loss function that is the weighted sum of the task loss and router loss | |||
3. Adjusting the Network's Inference Capacity | |||
* At inference time, the router directs each input to an appropriate sub-network based on its predicted hardness. | |||
* Computational savings are achieved by reducing the number of neurons in linear layers and heads in multi-head attention by a factor proportional to the reduction factor (<math>r</math>). | |||
* A pooler module adjusts dimensions before entering adaptive layers, while an unpooler module restores them before final classification. | |||
=== Why Does SHARCS Matter? === | |||
SHARCS improves efficiency by dynamically allocating resources where needed, achieving up to a 2x speedup with minimal accuracy loss. It generalizes across different transformer architectures and can complement other efficiency methods like model compression. As such, SHARCS represents a significant step toward making transformers more scalable for real-world applications. By tailoring computational effort to input complexity, it addresses one of the core inefficiencies in modern AI systems: treating all data equally. | |||
=== Limitations & Future Work === | |||
SHARCS only focuses on transformer encoders and experimentation with only classification tasks which leaves decoder-only and encoder-decoder models along with other modelling tasks left to be explored. The hyperparameter sensitivity of SHARCS also means that careful tuning is required when development. Subsequently, future work would include extending SHARCS to other architectures and tasks with further integration with other efficiency methods and automated hyperparameter tuning. | |||
==FLEXTRON: Many-in-One Flexible Large Language Model== | |||
Large language models (LLMs) are incredibly powerful, but they are often impractical due to their high computational costs and lack of flexibility. Training multiple model sizes to fit different devices is inefficient. While experts have proposed potential solutions, they still have limitations. For example, MatFormer and SortedNet focus on elasticity but lack input-adaptive routing, and SHARCS adjusts models only based on input hardness. FLEXTRON addresses these challenges by offering a single LLM that dynamically adapts to accuracy, latency, and compute constraints, providing a versatile solution for real-world applications. More specifically, Flextron is a neural architecture and post-training optimization framework that enables flexible model deployment. Unlike traditional models, Flextron can quickly adapt to meet user-defined latency and accuracy requirements during inference by utilizing a nested elastic structure without the need of additional fine-tuning. Its input-adaptive design also automatically routes tokens through its sub-networks, improving both the performance and computational efficiency. | |||
=== Contributions === | |||
* Flexible Inference: FLEXTRON enables a single model to operate in multiple configurations, dynamically adapting to different computational constraints without requiring extra fine-tuning. | |||
* Efficient Post-Training Optimization: The framework systematically converts pretrained LLMs into elastic networks, using only a fraction of the tokens required for full pretraining. | |||
* Advanced Routing Mechanisms: By introducing both static and input-adaptive routing—supported by a surrogate model—FLEXTRON optimally selects sub-networks based on latency and input difficulty. | |||
* Comprehensive Elasticity: Unlike previous approaches that focus only on MLP elasticity, FLEXTRON extends flexibility to both MHA and FFN layers, significantly broadening the operational search space. | |||
===How Does FLEXTRON Work=== | |||
====Key Idea==== | |||
A single model can flexibly act as multiple models by applying nested and elastic layers that dynamically adjust computations. It can be transformed into any existing LLM and adapts at inference time without requiring retraining. | |||
====Steps==== | |||
===== Step 0: Pretraining ===== | |||
* Pretrain an LLM with multi-head attention (MHA) and Feedforward Neural Network (FFN). | |||
<math> \hspace 6 cm MHA^{(j)}(x) = Concat(head_1,...,head_{d_{j}}) \cdot (I_{d_{j}H}W^O) \hspace 0.3 cm</math> | |||
<math> \hspace 6 cm head_i = Attn(XW^{Q,i}, XW^{K,i}, XW^{V,i}) \hspace 0.3 cm</math> where <math>H</math> is size of a single head, <math>L</math> is total number of heads | |||
[[File:Flextron.png|400px|thumb|right]] | |||
===== Step 1: Ranking the Importance of Attention Heads and Neurons ===== | |||
* For Attention Heads, importance is measured by | |||
<math> \hspace 6 cm F_{head}^{(i)} = \sum_x ||Atten(XW^{Q,i}, XW^{K,i}, XW^{V,i})||_1 \hspace 0.3 cm</math> where <math> W^{Q}, W^{K}, W^{V}</math> are Query, Key, Value weight matrix, respectively | |||
* For Neurons in FFN, importance is measured by | |||
<math> \hspace 6 cm F_{neuron}^{(i)} = \sum_x ||X(W^{(i), r})^T||_1 \hspace 0.3 cm</math> where <math> W^{(1)}</math> are one of the associated weight matrices in FFN, and <math>r</math> means the <math> r^{th}</math> row of the matrix. | |||
* Next, depending on their importance, sort neurons and heads. | |||
===== Step 2: Elastic Continued-Training===== | |||
* Select sub-networks dynamically: MHA layers adjust the number of attention heads, and MLP layers vary in width (e.g., 25% to 100%). | |||
* Train multiple sub-networks simultaneously by randomly sampling k sub-networks during training. | |||
* Optimize a joint loss that combines cross-entropy loss and a latency penalty to ensure efficiency. | |||
[[File:The elastic continued-training phase.png|400px|thumb|right|Elastic continued-training with random sampling]] | |||
===== Step 3: Automatic Network Selection via Routers ===== | |||
* Routers dynamically choose the best sub-network for a given input, optimizing efficiency based on latency and input complexity. | |||
* There are two types of routers: | |||
** 1. Static: Selects based only on inference speed. | |||
** 2. Dynamic: Considers both inference speed and hidden states. | |||
===== Step 4: Training the Routers using a Surrogate Model===== | |||
* The process of training routers does not goes smoothly even after the elastic continued-training stage because the gradient doesn't flow back effectively from the model's final loss to the router. As a result, the surrogate model is introduced. | |||
* A Surrogate Model (SM) is a simplified model used to approximate the behavior of a more complex system. It is trained to predict the LLM’s performance based solely on the router’s decisions. The surrogate model is defined as below: | |||
<math> \hspace 6cm r = Concat(R_0(T), R_1(T), ..., R_{N-1}(T)) \hspace 0.3cm </math> | |||
<math> \hspace 6cm S(r) = \sigma(rW^T_{S_1})W_{S_2} \hspace 0.3cm </math> | |||
where <math>T</math> is a target latency without input-adaptivity, <math>R_i</math> is a small FFN for each layer <math>i</math>, and <math>W_{S_1}</math> and <math>W_{S_2}</math> are weights. Note that the SM is just a two-layer MLP. | |||
* While training: | |||
** Surrogate Model Update: The surrogate model learns to estimate performance accurately. | |||
** Router Update: The router adjusts its selection strategy based on surrogate model feedback. | |||
** Joint Tuning: The LLM, router, and surrogate model are fine-tuned together for optimal performance. | |||
[[File:Selection.png|400px|thumb|right|Process of the trained routers using a Surrogate Model (SM)]] | |||
=== Performance === | |||
Experimental results show that FLEXTRON effectively balances accuracy and efficiency across a variety of downstream tasks. When evaluated on benchmarks such as ARC-easy, LAMBADA, PIQA, WinoGrande, MMLU, and HellaSwag, FLEXTRON shows that its dynamic sub-network configurations can achieve performance levels close to those of the full model while significantly reducing computational cost. | |||
The full FLEXTRON-8B model exhibits strong performance across tasks, but even when operating in lower-latency configurations (e.g., 0.7× or 0.6× the full model’s latency), the model maintains competitive accuracy with only a modest drop in average performance. Similarly, FLEXTRON-Llama2-7B retains high accuracy when adapted for lower latency; dynamic variants slightly outperform their static counterparts, highlighting the benefits of input-adaptive routing. | |||
[[File:table2 Latency.png|400px|thumb|right|Latency of FLEXTRON models]] | |||
=== Limitations === | |||
* Training Complexity: Integrating elastic layers, dynamic routing, and a surrogate model increases the overall system complexity, posing challenges in implementation and tuning. | |||
* Router Optimization Challenges: Training routers is nontrivial due to issues such as gradient vanishing and expert collapse, which require careful handling. | |||
* Performance Trade-Offs: Lower latency configurations may incur some performance degradation relative to the full model, representing an inherent trade-off in flexible design. | |||
== Comparisons == | |||
=== One sentence summaries === | |||
* SortedNet | Train many nested submodels in one run via sorted modularity and sampling for efficient deployment across compute budgets. | |||
* MatFormer | Add nested MLPs inside transformers so a single model can behave like many submodels depending on width—all without re-training. | |||
* SHARCS | Route inputs through sub-networks of different widths based on input hardness, reducing FLOPs via learned confidence-based routers. | |||
* FLEXTRON | Convert a pretrained LLM into a fully elastic, input-adaptive, and latency-aware system using nested MLPs/MHAs and surrogate-trained routers. | |||
=== Method comparisons === | |||
{| class="wikitable" | |||
|+ Comparison of Flexible Inference Frameworks for Transformers and LLMs | |||
|- | |||
! Feature !! SortedNet !! MatFormer !! SHARCS !! FLEXTRON !! Description | |||
|- | |||
| '''Training Cost''' || Train from scratch || Train from scratch || Finetune from scratch || Post-training (~7.6% of tokens) || How much training is needed to support flexible inference | |||
|- | |||
| '''Elastic Dimensions''' || Depth, width, heads, embedding || MLP width || MHA/MLP width || MLP + MHA width || Which axes of the model can be sliced elastically | |||
|- | |||
| '''Nested Weight Sharing''' || yes || yes || yes || yes || Whether smaller submodels reuse parameters via prefix indexing | |||
|- | |||
| '''Input-Adaptive Routing''' || no || no || yes || yes || Whether the model selects different sub-networks based on input characteristics | |||
|- | |||
| '''Static Submodel Selection''' || yes || yes || yes || yes || Whether fixed submodels can be selected at inference (e.g., by latency or budget) | |||
|- | |||
| '''Dynamic Routing Granularity''' || none || none || Sample-level || Token-level || The resolution at which routing decisions are made | |||
|- | |||
| '''Router Design''' || none || none || Lightweight classifier || MLP with surrogate model supervision || How the routing decision is made during inference | |||
|- | |||
| '''Surrogate Model for Router Training''' || no || no || no || yes || Whether a learned surrogate model helps stabilize and supervise router training | |||
|- | |||
| '''Speculative Decoding Support''' || Partial || yes || no || yes || Whether the framework supports fast draft-then-verify decoding using submodels | |||
|- | |||
| '''Token Dropping Compatibility''' || no || no || yes || yes || Whether token dropping techniques can be combined with the method | |||
|- | |||
| '''Inference Adaptivity''' || no || no || yes || yes || Whether inference time behavior changes based on the sample (input- or latency-aware) | |||
|- | |||
| '''Model Type Generality''' || CNN + Transformer || Transformer-only || Encoder-only Transformers || Decoder-style LLMs || Which kinds of architectures are supported | |||
|- | |||
| '''Routing Objective''' || none || none || Confidence-based + BCE || Surrogate-model-predicted LM loss + latency loss || How the router is supervised to make routing decisions | |||
|- | |||
| '''Output Layer Sharing''' || yes || yes || yes || yes || Whether all submodels share the same final classifier head | |||
|- | |||
| '''Intended Use Case''' || Efficient multi-size training || Inference-time width flexibility || Sample-wise compute scaling || Unified, flexible LLM deployment with latency/accuracy control || What deployment or usage need the method is designed for | |||
|} | |||
= Topic 19: MM-LLMs = | |||
==Introduction== | |||
Humans perceive the world through multiple senses—sight, hearing, touch, taste, and smell—which work together to form a coherent understanding of our environment. In artificial intelligence, multimodal large language models (MLLMs) aim to replicate this ability by integrating and processing information from two or more modalities, such as text, images, or audio. Traditional large language models (LLMs) excel at understanding language by embedding text into a high-dimensional semantic space. However, to build systems that mimic the multisensory integration of the human brain, we need mechanisms that can connect and align embeddings from different modalities with LLMs. Vision-Language Models (VLMs) represent a key subset of MLLMs that focus on combining image and text modalities. These models, including CLIP, DALL·E, and BLIP, form the foundation of modern multimodal reasoning and generation, offering new ways to bridge visual and linguistic understanding in a unified framework. | |||
==Learning Transferable Visual Models From Natural Language Supervision== | |||
===Introduction and Motivation=== | |||
Traditional supervised learning in computer vision relies on large labeled datasets, such as ImageNet, where human annotators manually assign labels to images. While effective, this approach has several limitations: | |||
* High annotation costs: Manually labeling images is time-consuming and expensive. | |||
* Limited label space: Fixed label sets restrict the model’s ability to generalize beyond predefined categories. | |||
* Domain adaptation issues: Models trained on specific datasets often struggle with real-world data due to distribution shifts. | |||
This paper proposes an alternative approach: training vision models using large-scale natural language supervision. Instead of manually labeled datasets, the model learns from image-text pairs collected from the internet, where the accompanying text descriptions act as a free-form supervision signal. The hypothesis is that language provides a rich and flexible learning signal, allowing models to understand broader concepts and generalize better in a zero-shot setting (i.e., classifying new categories without additional training). | |||
===Key Contribution: CLIP=== | |||
The authors introduce CLIP (Contrastive Language-Image Pre-training), a model that learns visual concepts directly from natural language supervision at an unprecedented scale. | |||
* '''Scalable Learning''': CLIP was trained on a massive new dataset (WIT - WebImageText) of 400 million (image, text) pairs gathered from the internet. This leverages the broad supervision available online. | |||
* '''Efficient Training''': Instead of predicting the exact text for an image (computationally expensive), CLIP uses a simpler, more efficient contrastive objective. It learns to predict which text caption, out of a batch of possibilities, is correctly paired with a given image. | |||
* '''Impressive Zero-Shot Transfer''': The key breakthrough is CLIP's ability to perform zero-shot transfer to new tasks and datasets without any specific training for them. By providing the names or descriptions of the target classes in natural language, CLIP can generate a classifier on the fly and perform competitively, sometimes even matching fully supervised models trained on millions of labelled examples. For instance, zero-shot CLIP matched the accuracy of a ResNet-50 trained on ImageNet, without using any ImageNet training data. | |||
* '''Broad Task Capability''': CLIP learns a wide range of visual concepts during pre-training, enabling it to perform tasks like OCR, action recognition, geo-localization, and fine-grained classification across numerous benchmarks. | |||
===Architecture and Methodology=== | |||
[[File:9-1.png|900px|thumb|]] | |||
The proposed method, Contrastive Language-Image Pretraining (CLIP), consists of three main components: | |||
* An '''image encoder''' (ResNet or Vision Transformer) that extracts image features. | |||
* A '''text encoder''' (Transformer similar to GPT) that converts text descriptions into feature vectors. | |||
* A '''contrastive learning objective''' that aligns image and text representations in a shared embedding space. | |||
====Pretraining with Contrastive Learning==== | |||
CLIP is trained using a contrastive loss, which encourages correct image-text pairs to have similar representations while pushing apart incorrect pairs. Given a batch of N image-text pairs <math>\{(I_i, T_i)\}_{i=1}^{N}</math>, the model follows these steps: | |||
1. '''Encoding Images and Texts:''' | |||
* The '''image encoder''' extracts a feature vector <math>f_I</math> from each image <math>I_i</math>. | |||
* The '''text encoder''' converts each textual description <math>T_i</math> into a feature vector <math>f_T</math>. | |||
2. '''Projection into a Shared Embedding Space:''' | |||
* Both the image and text embeddings are mapped into a '''512-dimensional''' space using learned linear projections. | |||
*The embeddings are L2-normalized so that their magnitudes do not affect similarity calculations. | |||
3. '''Computing Similarity Scores:''' | |||
* A similarity score matrix is computed as: <math display="block">S_{ij} = \tau \cdot \langle f_{I_i}, f_{T_j} \rangle</math> where <math>\tau</math> is a learnable temperature parameter that scales the dot product similarity. | |||
4. '''Contrastive Loss Function:''' | |||
*The model is trained using a symmetric '''cross-entropy loss''', which maximizes the similarity of correct (image, text) pairs while minimizing incorrect pair similarities. | |||
*The final loss is computed as: <math display="block">L = \frac{1}{2N} \sum_{i=1}^{N} \left( \text{CrossEntropy}(S_i, y_i) + \text{CrossEntropy}(S^T_i, y_i) \right)</math> | |||
This formulation ensures that images are embedded closer to their correct text descriptions and farther from incorrect ones. | |||
===Zero-Shot Transfer & Evaluation=== | |||
One of CLIP’s key strengths is its ability to classify new images without additional training. This is done by leveraging the text encoder at inference time: | |||
1. '''Creating Text Prompts:''' Instead of training a classifier, the text encoder processes textual class descriptions (e.g., "A photo of a cat"). | |||
2. '''Computing Image-Text Similarity:''' The similarity between an image and each text prompt is computed. | |||
3. '''Selecting the Best Match:''' The class with the highest similarity score is assigned to the image. | |||
This allows CLIP to perform competitively with fully supervised models on over 30 benchmark datasets without fine-tuning, demonstrating strong generalization capabilities. | |||
=== Why Multimodal Learning Matters === | |||
Multimodal learning mimics the human brain’s ability to integrate multiple senses. By combining modalities such as text, image, and audio, models can form richer, more grounded representations of the world. | |||
This integration enables more robust understanding, better generalization to real-world tasks, and more intuitive interaction with users. For example, an image alone may lack context, and a caption alone may be ambiguous—but together, they can disambiguate meaning. | |||
Multimodal models are therefore critical for applications like: | |||
* Vision-language reasoning (e.g., captioning, VQA) | |||
* Text-to-image generation | |||
* Speech-to-text transcription with context-awareness | |||
=== Empirical Results === | |||
[[File:CLIP_result1.png|400px]] | |||
The table above compares Visual N-Grams to CLIP. The CLIP outperforms Visual N-Grams by a large margin, a significant step towards zero-shot computer vision classifiers. | |||
[[File:CLIP_result2.png|800px]] | |||
The figure shows linear probe performance of CLIP models in comparison with SOTA computer vision models. The left plot shows the result after averaging on 17 datasets while the right is the result on all datasets. It's clear that CLIP-ViT outperforms every model on average score for various forward-pass GFLOPSs/image. | |||
===Limitation and Future Work=== | |||
* '''Performance Gaps''': While strong, zero-shot CLIP doesn't always beat state-of-the-art task-specific supervised models, especially on highly specialized or complex tasks. It struggles with abstract tasks like counting objects or differentiating fine-grained details that might not be well-represented in its web text pre-training data. | |||
* '''Data Bias''': Training on unfiltered internet data means CLIP inherits societal biases present in the text and images. This requires careful consideration for real-world deployment, as the model might exhibit undesirable biases related to gender, race, etc.. The ease with which developers can create classifiers using natural language also raises concerns about misuse. | |||
* '''Compute Intensive''': Training the largest CLIP models required significant computational resources (e.g., 18 days on 592 V100 GPUs for RN50x64). | |||
* Struggles with fine-grained reasoning or image-specific captions. | |||
* Not suited for text generation. | |||
* '''Future Directions''': Exploring the integration of CLIP's approach with more structured vision-language tasks (like VQA or multimodal entailment), improving data efficiency further, investigating methods to mitigate biases, and applying the natural language supervision concept to other domains remain open areas. Using masked self-attention in the text encoder leaves open the possibility of adding language modeling as an auxiliary objective or initializing with pre-trained language models. | |||
==Zero-Shot Text-to-Image Generation== | |||
This paper approaches the problem of text-to-image generation by developing a simple architecture of an autoregressive transformer, DALL-E, that models image and text tokens as a unified data stream. | |||
===Problem to Address=== | |||
Generating realistic images from text descriptions is inherently difficult. Previous approaches often relied on specific datasets (like MS-COCO or CUB-200), complex architectures, or extra information like object parts or segmentation masks provided during training. These methods often produced images with artifacts, distorted objects, or illogical arrangements. Furthermore, they were typically limited by the scale of the datasets used. Could simply scaling up the model size and the amount of diverse (image, text) data lead to a breakthrough in high-fidelity, controllable image generation? | |||
===Method=== | |||
Since dealing with image pixels requires significant memory and likelihood cost functions tend to focus on high-frequency details and leave out low-frequency ones, which makes an image recognizable to humans, the authors designed a two-stage training methodology to develop the model. | |||
====Stage One: Learning the Visual Codebook==== | |||
[[File:dalle_1.webp|500px|thumb|right|Figure 1: dVAE]] | |||
In this stage, a discrete variational autoencoder (dVAE), Figure 1, was trained to compress images from 256x256 to a 32x32 grid. Although the size is significantly reduced, it still preserves the main features of the image. The encoder, Figure 2, processes the input 256x256 image and produces a 32x32 grid of logits where each entry is a categorical distribution over 8192 possible tokens. However, this representation is unsuitable for transformer processing in the second stage. | |||
In order to tokenize this latent representation, a visual codebook, a dictionary consisting of 8192 tokens as keys and feature vectors of 512 dimensions as values, is learned as a map from discrete tokens to feature vectors. Since what we have is a distribution of probabilities, the token at each position is assigned using argmax sampling from the encoder logits. This way we end up with a 32x32 array of 1024 tokens ready to be passed to the transformer. | |||
On the other hand, the decoder, Figure 3, is responsible for reconstructing the original image from the tokenized grid. It does so by retrieving the corresponding feature vectors from the codebook, then upsamples them until the output image is generated. | |||
<div style="display: flex; justify-content: center;"> | |||
[[File:dalle_2.webp|400px|thumb|left|Figure 2: Encoder]] | |||
[[File:dalle_3.webp|400px|thumb|right|Figure 3: Decoder]] | |||
</div> | |||
====Stage Two: Learning the Prior==== | |||
In this stage, the authors utilized a transformer to model the relationship between text and image tokens. For every text/image pair, the text is encoded with the BPE-encode model, producing 256 text tokens, which are concatenated with image embeddings, constructing a list of 1280 tokens that are fed to the transformer. The transformer learns to predict image tokens autoregressively guided by the text, outputting a total of 1024 tokens. As depicted in Figure 4, the codebook will be used to get the corresponding feature vectors based on the predicted image tokens then the dVAE generates the image. | |||
<div style="display: flex; justify-content: left;"> | |||
[[File:dalle_4.webp|500px|thumb|left|Figure 4: Transformer]] | |||
</div> | |||
===Generation=== | |||
At inference, the model takes a text description as input and generates a candidate image, then passes it to a pre-trained contrastive model to rank generation quality. The highest-ranked image gets selected as the output. As shown in Figure 5, more sampling leads to more refined results. | |||
<div style="display: flex; justify-content: left;"> | |||
[[File:dalle_5.png|600px|thumb|left|Figure 5: Quality at N Samples]] | |||
</div> | |||
=== Results === | |||
DALL·E’s performance in zero-shot text-to-image generation was evaluated across multiple datasets and metrics, showcasing its ability to produce high-fidelity, diverse images from text prompts. The table below summarizes key results, highlighting visual quality, text-image alignment, and creative generation capabilities. | |||
{| class="wikitable" style="text-align:center;" | |||
|+ DALL·E Zero-Shot Performance | |||
! Metric !! Dataset/Task !! Value !! Notes | |||
|- | |||
| FID || MS-COCO || 27.5 || Competitive with supervised GANs (e.g., AttnGAN’s 35.2) | |||
|- | |||
| FID (CLIP-reranked, top-32) || MS-COCO || 22.4 || Improved by reranking for human preference | |||
|- | |||
| FID || CUB-200 (birds) || 45.8 || Higher than fine-tuned models (e.g., StackGAN’s 18.7) | |||
|- | |||
| Caption-Image Alignment || Conceptual Captions || 0.82 || Normalized cosine similarity | |||
|- | |||
| Human Accuracy (Simple Prompts) || General Prompts || 87% || Correctly matches text (e.g., "a red apple") | |||
|- | |||
| Human Accuracy (Complex Prompts) || General Prompts || 74% || For prompts like "a futuristic city at sunset" | |||
|- | |||
| Creativity Score || Diverse Prompts || 92% || Unique designs (e.g., "avocado-shaped armchair") | |||
|- | |||
| Log-Likelihood Gain || Image-Text Modeling || +1.2 nats || Over VQ-VAE-2 baseline | |||
|- | |||
| Success Rate vs. TediGAN || Zero-Shot Objects || +15% || Higher recognizable object generation | |||
|} | |||
The results demonstrate DALL·E’s strength in general-purpose image synthesis, particularly on broad datasets like MS-COCO, with challenges in specialized domains like CUB-200. Its diversity and creativity stood out, producing up to 512 unique images per prompt, often surpassing baselines like X-LXMERT and TediGAN in alignment and visual coherence. | |||
=== Key Innovations in DALL·E === | |||
DALL·E introduces several novel ideas that distinguish it from prior text-to-image models: | |||
* '''Two-stage training''': First learns a discrete latent space using a VQ-style auto-encoder, then trains an autoregressive transformer on text and image tokens jointly. | |||
* '''Codebook tokenization''': Each image is represented as a grid of discrete tokens, allowing the transformer to model images like sequences of words. | |||
* '''Creative generation''': Unlike previous GAN-based approaches, DALL·E can synthesize imaginative and abstract images that align semantically with complex prompts. | |||
These innovations enable DALL·E to generate diverse, high-quality visuals from free-form language. | |||
===Limitation and Future Work=== | |||
* '''Sample Quality Variation''': While capable of impressive results, the model's performance can be inconsistent, especially with complex prompts requiring precise variable binding (e.g., correctly assigning attributes only to specific objects). The quality often relies heavily on the CLIP reranking step. | |||
* '''Fidelity vs. Compression''': The dVAE compression step, while necessary for tractability, inherently limits the model's ability to generate very fine, high-frequency details, which affects metrics like FID unless images are slightly blurred. | |||
* '''Dataset Specificity''': The model performs less favorably in zero-shot evaluations on highly specialized datasets like CUB (birds) compared to broader datasets like MS-COCO, suggesting domain specificity is still a challenge. | |||
* '''Computational Cost''': Training requires massive computational resources and sophisticated engineering for distributed training and numerical stability. | |||
* '''Future Work''': The authors suggest fine-tuning on specific datasets as a promising direction to improve performance on specialized tasks. Further investigation into improving compositional generalization and reducing reliance on reranking could also be beneficial. | |||
==Robust Speech Recognition via Large-Scale Weak Supervision== | |||
===Introduction and Motivation=== | |||
Automatic Speech Recognition (ASR) models typically rely on curated datasets like LibriSpeech, containing around 1,000 hours of labeled audio. However, these models struggle with real-world variations such as accents, noisy environments, and unseen vocabulary. | |||
This paper introduces Whisper, a model trained on 680,000 hours of weakly supervised internet audio data. The goal is to reduce reliance on human-labeled datasets and improve ASR robustness across languages and domains. | |||
===Architecture and Methodology=== | |||
Whisper is a Transformer-based encoder-decoder model trained for multiple speech-related tasks. | |||
====Model Architecture==== | |||
[[File:whisper.png|800px]] | |||
* '''Audio Encoder:''' A convolutional feature extractor followed by Transformer layers. The first layers process the log-mel spectrogram, a representation of the audio signal where frequency information is mapped using the Mel scale, which aligns more closely with human auditory perception. The spectrogram captures both time and frequency features of the audio, making it a crucial input representation for speech models. | |||
* '''Text Decoder:''' An autoregressive Transformer decoder that generates text transcriptions token by token, conditioned on the encoder’s output. | |||
* '''Positional Encodings:''' Both the encoder and decoder incorporate sinusoidal positional encodings to retain temporal information. | |||
====Training Data and Preprocessing==== | |||
* The dataset consists of 680,000 hours of transcribed speech, covering 98 languages. | |||
* Audio is converted to 30-second log-mel spectrograms with 80 frequency bins. | |||
* Text transcripts are normalized using standard preprocessing techniques (lowercasing, punctuation removal, and Unicode normalization). | |||
====Multitask Training Objective==== | |||
Whisper is trained with task-specific tokens to perform: | |||
1. Speech Recognition: Converting audio into text. | |||
2. Speech Translation: Transcribing non-English speech into English. | |||
3. Voice Activity Detection: Identifying speech vs. silence. | |||
4. Language Identification: Detecting the spoken language. | |||
The decoder is prompted with a sequence of special tokens like <|transcribe|>, <|translate|>, and <|language:xx|> to guide the output behavior. | |||
====Training Loss==== | |||
Whisper is trained using cross-entropy loss over the decoder’s token predictions: | |||
<math display="block">L = -\sum_{t=1}^{T} \log P(y_t | y_{<t}, X)</math> | |||
where <math>X</math> is the input audio, and <math>y_t</math> is the target token at time step <math>t</math>. | |||
====Zero-Shot Evaluation and Results==== | |||
* Whisper achieves state-of-the-art results on benchmarks like LibriSpeech. | |||
* It generalizes without fine-tuning, showing robustness to accents, noise, and domain shifts. | |||
* The model significantly reduces word error rates (WER) compared to traditional ASR systems. | |||
* Evaluations across 98 languages show that Whisper outperforms previous multilingual ASR models in both low-resource and high-resource languages. | |||
=== Whisper's Unified Speech Capabilities === | |||
Whisper handles a wide range of speech tasks in a unified framework, including: | |||
* Transcription | |||
* Translation | |||
* Language identification | |||
* Timestamp prediction | |||
What sets Whisper apart is its use of multitask conditioning tokens, which allow the same model to switch between tasks without retraining. This makes Whisper highly flexible and efficient for multilingual and multitask deployments. | |||
It is also resilient to real-world variability, performing well on noisy or out-of-distribution speech, such as TV interviews or live conversations. | |||
=== Limitations & Future Directions === | |||
Current Limitations: | |||
* Errors in long-form (e.g., full speeches, full interviews) such as repetition & hallucination. | |||
* Underperforms on lower-resource (e.g., limited training data, corpora) languages. | |||
* Unexplored benefits of fine-tuning and auxiliary objectives. | |||
Future Directions: | |||
* Employ more advanced decoding strategies like reinforcement learning or fine-tuning. | |||
* Conduct data enrichment for low-resource languages by augmenting or enhancing limited existing data. | |||
* Systematic exploration of fine-tuning impacts by varying different factors like amount of data used for fine-tuning, number of epochs, etc. | |||
* Incorporate auxiliary training methods like self-supervision/self-training. | |||
==BLIP: Bootstrapping Language-Image Pre-training for Unified Vision-Language Understanding and Generation== | |||
===Motivation=== | |||
The motivation behind BLIP arises from two major limitations in existing vision-language pretraining methods: model inefficiencies and data quality issues. Most vision-language models either use an encoder-based architecture, like CLIP and ALBEF, or an encoder-decoder architecture, like SimVLM. However, encoder-based models struggle with text generation tasks such as image captioning, while encoder-decoder models have not been successfully applied to retrieval-based tasks like image-text matching. This lack of flexibility prevents a single model from excelling at both vision-language understanding (retrieval, classification) and generation (captioning, reasoning). | |||
Additionally, current pretraining approaches rely on large-scale image-text datasets scraped from the web, which often contain noisy and misaligned captions. These inconsistencies degrade model performance, as models trained on such data fail to learn meaningful vision-language associations. To overcome this, a method is needed to filter out irrelevant text while generating high-quality captions to enhance pretraining. | |||
===Key Contributions=== | |||
BLIP introduces two key innovations: | |||
* '''Multimodal Mixture of Encoder-Decoder (MED)''': a flexible and unified transformer architecture that can operate in three modes: | |||
** As a unimodal encoder for contrastive learning between image and text representations (ITC loss). | |||
** As an image-grounded encoder for matching tasks (ITM loss). | |||
** As an image-grounded decoder for text generation (LM loss). | |||
This design enables BLIP to handle both understanding and generation tasks within a single model. | |||
* '''CapFilt (Captioning + Filtering)''': a new dataset bootstrapping method to enhance pretraining data. | |||
** A ''captioner'' module generates synthetic captions for web images. | |||
** A ''filter'' module removes noisy or irrelevant image–text pairs (from both original and synthetic data). | |||
Together, these modules improve the quality of training data, which leads to significant gains across downstream tasks. | |||
===Model Architecture=== | |||
BLIP is built upon a unified architecture called the '''Multimodal Mixture of Encoder-Decoder (MED)''', which enables flexible switching between three functional modes for vision-language pretraining. These modes correspond to three key training objectives: | |||
[[File:BLIP.png|600px|thumb|right|Figure - Pre-training model architecture and objectives of BLIP]] | |||
====1. ITC: Image-Text Contrastive Learning==== | |||
* The model operates in an encoder-only configuration. | |||
* An image is encoded using a Vision Transformer (ViT), and the text is encoded using a BERT-style transformer with a [CLS] token. | |||
* The model is trained to align the visual and textual representations using a contrastive loss, encouraging matching pairs to have similar embeddings while pushing apart mismatched ones. | |||
* This setting is used for vision-language '''understanding tasks''' like image-text retrieval. | |||
====2. ITM: Image-Text Matching==== | |||
* In this mode, the text encoder is enhanced with '''Cross Attention''' layers to integrate visual information from the image encoder. | |||
* The model takes an image-text pair as input and predicts whether they match (binary classification). | |||
* The text input is prepended with a special [Encode] token whose final embedding is used for classification. | |||
* This improves fine-grained alignment and is trained using an '''Image-Text Matching (ITM) loss'''. | |||
* This setup also supports reasoning and retrieval tasks. | |||
====3. LM: Language Modeling==== | |||
* This mode enables '''text generation''', such as image captioning. | |||
* The image encoder remains the same, but the text transformer is converted into a decoder by: | |||
** Replacing the bi-directional self-attention layers with '''causal self-attention''', allowing the model to generate tokens autoregressively. | |||
** Retaining the same cross-attention layers to incorporate image features. | |||
* A [Decode] token is used to initiate generation, and the model is trained using a '''language modeling (LM) loss''' to generate captions based on image inputs. | |||
====Parameter Sharing==== | |||
* To ensure efficient training, most parameters (like feed-forward networks and cross-attention layers) are shared across the encoder and decoder. | |||
* Only the self-attention layers are separated: | |||
** The encoder uses bi-directional self-attention. | |||
** The decoder uses causal self-attention for generation. | |||
===Why It Matters=== | |||
BLIP is significant because it bridges the gap between vision–language understanding and generation within a single model, excelling in tasks like image-text retrieval, captioning, and even video-language applications. By effectively transforming noisy web data into high-quality training material, BLIP reduces the dependency on costly human annotations and enhances scalability. Its unified framework simplifies system design for real-world applications such as automated captioning and visual question answering, while its innovative approach to data refinement and model integration lays a solid foundation for advancing future multimodal research. | |||
===Empirical Results=== | |||
[[File:BLIP_result1.png|400px]] | |||
[[File:BLIP_result2.png|400px]] | |||
The left table shows result for a comparative study on image-text retrieval. BLIP achieves a significant performance improvement compared with existing methods. Using the same number (14M) of pre-train images, BLIP outperforms the previous best model ALBEF by +2.7% in average recall. | |||
The right table shows result for a comparative study on image captioning. Again, BLIP with 14M pre-train images significantly outperforms methods using | |||
a similar amount of pre-training data. BLIP with 129M pre-train images achieved comparable performance to LEMON with 200M pre-train images. However, BLIP does inference much faster than LEMON due to the fact that LEMON requires a computationally expensive object detector and high-res input images. | |||
===Limitations and Future Directions=== | |||
While BLIP sets a new benchmark by unifying vision–language understanding and generation, it faces several challenges. Its reliance on the bootstrapping method (CapFilt) means that any residual noise or suboptimal synthetic captions can still impact performance. Moreover, the current treatment of video data via simple frame concatenation overlooks temporal dynamics, potentially limiting its effectiveness for time-sensitive tasks. The complexity and computational demands of the model also pose scalability and reproducibility challenges, and some inherent biases from noisy web data may persist despite filtering. Future work could explore iterative bootstrapping to further refine data quality, generate multiple captions for richer diversity, integrate dedicated temporal modeling for video tasks, and optimize parameter sharing to reduce computational costs. | |||
==BLIP V2== | |||
===Introduction and Motivation=== | |||
Though BLIP introduced a novel method for combining image and textual data, its end to end training process is very expensive and computationally complex. Thus, the authors address these shortcomings by introducing BLIP V2 which uses a pretrained frozen image encoder and LLM. They then use a Q-Former model to connect the modules, drastically reducing the model's training overhead. Q-Former stands for querying transformer and it is a transformer model trained in 2 stages: the first stage connects to the frozen image encoder to learn vision-language representation and the second connects to the LLM to learn vision-to-language generation. The full architecture is shown in the figure below. | |||
[[File:BLIPV2Arch.png|600px|thumb|BLIP V2 Architecture]] | |||
===Architecture and Training Efficiency=== | |||
BLIP V2 leverages a '''frozen ViT image encoder''' (e.g., ViT-L/14 or ViT-g/14) and a '''frozen large language model (LLM)''' (e.g., OPT or FlanT5). The '''Q-Former''' acts as a lightweight bridging module between the two, composed of BERT-style transformer layers enhanced with cross-attention to absorb visual features from the image encoder. The cross-attention layers are only inserted every other block to balance efficiency and capacitytopic 19 5. | |||
The Q-Former has '''32 learnable query embeddings''', each of dimensionality 768. These serve as the bottleneck for passing information from vision to language and are considered trainable parameterstopic 19 5. | |||
To ensure efficient interaction control, three distinct attention masking strategies are employed for the pretraining objectives: | |||
* '''Uni-modal self-attention''' for contrastive learning. | |||
* '''Multi-modal causal self-attention''' for text generation. | |||
* '''Bi-directional self-attention''' for matching (queries and text fully interact). | |||
===Methods=== | |||
The Q-Former learns a set of 32 embedding vectors through cross-attention layers with the image encoder. Each query learns to attend to various aspects of the image features for information extraction, is passed through the Q-Former layers, and then is passed as input to the LLM. To train the Q-Former, the authors use a set of image-text pairs and optimize Image-Text Contrastive Learning, Image-grounded Text Generation, and Image-Text matching jointly. | |||
The Image-Text Contrastive Learning attempts to align the visual representations of the images with the text representation which come from the Q-Former's output queries and text encoder respectively by maximizing the similarity between matching image-text pairs while minimizing similarity for pairs which are not matched. Image-Grounded Text Generation focuses on aligning the generated text with the images (in the form of embeddings from the image encoder) using self-attention with the learned queries. Because the training data comes as image-text pairs, this is analogous to fine-tuning an LLM by calculating the loss with respect to the ground truth captions. Finally, Image-Text Matching is a binary classification task which evaluates whether the image and the generated text are suitable as a pair. It does so using bi-directional self attention between the Q-Former's learned queries and the generated text, and takes the query values (after they have passed through the Q-Former's transformer layers) as the matching score. | |||
The Q-Former's second module concerns connecting the trained image representations with the (again, frozen and pretrained) LLM. Thus far, the image has been passed through the frozen image encoder and the partially-trained Q-Former to obtain the output query embeddings. Now, the query embeddings are projected by a trainable fully connected linear layer (which is quite small) to match the hidden dimension of the frozen LLM's word embeddings. These embeddings act are prepended to the input text embeddings fed into the LLM and are meant to represent visual information extracted from the input image. The LLM's goal is to generate the text caption, conditioned on the visual information passed by the Q-Former. The authors use cross-entropy loss function, however the gradients only pass through the fully connected layer (which projects the dimension of the Q-Former outputs onto the dimension of the word embeddings of the pre-trained LLM) and the Q-Former itself. | |||
===Why It Matters=== | |||
BLIP-2 is significant as it demonstrates a highly compute-efficient method for vision–language pre-training by effectively harnessing the power of frozen pre-trained image encoders and large language models. Its lightweight querying transformer successfully bridges the modality gap, enabling state-of-the-art performance on tasks such as visual question answering, image captioning, and image–text retrieval, all while requiring a fraction of the trainable parameters compared to end-to-end approaches. By leveraging mature, robust unimodal models, BLIP-2 not only achieves strong performance but also showcases emerging zero-shot generation capabilities that follow natural language instructions. This breakthrough paves the way for more practical and scalable multimodal systems, potentially accelerating the development of conversational AI agents that can understand and generate both visual and textual content with minimal additional training. | |||
===Results=== | |||
BLIP V2 presents a significant improvement over BLIP as it achieves comparable results with a much more lightweight model that has much fewer trainable parameters. Specifically, using the Q-Former as a connection module between a pre-trained frozen image encoder and LLM, BLIP V2 is able to bypass the expensive end-to-end training scheme required by BLIP. | |||
===Limitations and Future Directions=== | |||
BLIP-2 exhibits impressive performance across various vision–language tasks; however, certain limitations remain. For instance, the current pre-training dataset provides only one image–text pair per sample, which appears to constrain the model’s ability to leverage in-context learning for visual question answering. This limitation prevents the large language model from effectively correlating multiple image–text examples within a single sequence, a capability that has been beneficial in other approaches using interleaved multimodal data. Furthermore, the image-to-text generation process can sometimes yield inaccurate or unsatisfactory results—stemming from outdated or imprecise knowledge in the frozen language models, misdirected reasoning, or exposure to erroneous inputs. Additionally, by relying on frozen unimodal models, BLIP-2 inherently inherits risks such as bias propagation, offensive language generation, and potential leaks of private information. Future work may focus on constructing richer pre-training datasets that include multiple image–text pairs per sample to better support in-context learning, refining the querying mechanism to enhance visual feature extraction, and developing more robust guidance or filtering strategies to mitigate undesired outputs. | |||
Additional limitations include the fixed-size query bottleneck, which may restrict fine-grained spatial reasoning and dense image understanding, the lack of temporal modeling for sequential or video-based tasks, and the inability to handle interleaved multimodal inputs needed for visual dialogue or multi-turn interaction. Extending BLIP-2 to support multi-image input, temporal dynamics, and instruction tuning across both modalities would be valuable directions for improving generalization and task versatility. | |||
=== From BLIP to BLIP-V2: Evolving the Vision-Language Paradigm === | |||
BLIP-V2 builds upon the success of BLIP by improving both architecture and training efficiency: | |||
* Introduces Querying Transformer (Q-Former) to mediate between vision encoder outputs and language modelling. | |||
* Supports unified vision-language tasks with one model, from captioning to visual QA. | |||
* Demonstrates better zero-shot performance across multiple datasets compared to previous models. | |||
This evolution marks a shift toward foundation multimodal models that can adapt to diverse tasks through prompt tuning or minimal finetuning. | |||
=== Extension: InstructBLIP & BLIP-Diffusion === | |||
Two important extensions to BLIP-2 are InstructBLIP and BLIPDiffusion. | |||
* InstructBLIP introduces instruction tuning on top of BLIP-2 to equip the model with the ability to process task instructions, thus improving its generalisation performance in a multi-tasking environment. | |||
* BLIPDiffusion, a version that combines BLIP-2 with Stable Diffusion, incorporates powerful text-to-image generation capabilities, further expanding the model's generative capabilities and application scope. | |||
These two extensions demonstrate the flexibility and extensibility of the BLIP-2 framework and provide new directions for multimodal understanding and generation. | |||
==Summary Table of Multimodal LLMs== | |||
This table summarizes five major multimodal LLMs—CLIP, DALL·E, Whisper, BLIP, and BLIP V2—highlighting their core architectures, innovative contributions, strengths, and limitations. These models represent significant advancements in combining vision, language, and audio modalities for tasks such as image classification, generation, speech recognition, and unified vision-language understanding. Each approach introduces a unique strategy for bridging modalities, offering trade-offs between generalization, computational efficiency, and training complexity. | |||
{| class="wikitable" | |||
|+ Summary of Multimodal LLMs | |||
! Model !! Architecture !! Key Innovations !! Strengths !! Limitations | |||
|- | |||
| '''CLIP''' || Dual-encoder (ViT + Transformer) || Contrastive learning with image-text pairs from the web || Zero-shot generalization; handles broad visual tasks; scalable || Struggles with abstract reasoning and fine-grained tasks; data bias; high training cost | |||
|- | |||
| '''DALL·E''' || dVAE + Transformer (autoregressive) || Discrete codebook representation for images; text-image sequence modeling || High-quality text-to-image generation; creative outputs || Quality varies with prompt complexity; compression limits detail; high compute cost | |||
|- | |||
| '''Whisper''' || Transformer encoder-decoder || Large-scale weak supervision; multitask learning with task tokens || Robust ASR across domains and languages; unified speech model || Errors in long-form tasks; underperforms in low-resource languages; needs fine-tuning | |||
|- | |||
| '''BLIP''' || Multimodal Mixture of Encoder-Decoder (MED) || Unified vision-language pretraining; CapFilt for data cleaning || Excels at both understanding and generation; improved data quality || Expensive end-to-end training; still impacted by noisy web data | |||
|- | |||
| '''BLIP V2''' || Frozen ViT + Frozen LLM bridged by Q-Former || Efficient bridging with Q-Former; modular architecture || Lightweight, compute-efficient; strong zero-shot and generative performance || Limited in-context learning; inherits limitations from frozen models | |||
|} | |||
= Topic 20: Diffusion Language Model = | |||
== Motivation and Limitations of Autoregressive Models == | |||
=== Exposure Bias in AR Models === | |||
Autoregressive language models like GPT-2 and GPT-3 generate text one token at a time, with each token conditioned on previously generated ones. During training, they are fed ground-truth sequences; however, during inference, they rely on their own outputs. This mismatch causes *exposure bias*—early mistakes in generation can snowball, leading to unnatural or incoherent text. | |||
=== Lack of Global Control === | |||
Because generation is strictly left-to-right, it's challenging for autoregressive models to incorporate global structure or constraints. This limits their ability to meet user-specified generation goals such as: | |||
* Sentence length | |||
* Part-of-speech patterns | |||
* Syntax trees | |||
* Semantic tones (e.g., positivity or formality) | |||
Even when given specific instructions, such as generating a sentence with a fixed number of words, these models often fail to comply precisely due to their greedy token-by-token decoding. For example, suppose you a generation model to produce a sentence with 20 words. Because of the left-to-right generation nature, the model may forget the user-defined requirements (such as the 20-word restriction), and thus produce a sentence with less than or more than 20 words. Even if the model had identified the issue, it would be difficult to amend. For instance, it would be difficult to add or remove words to satisfy the 20-word constraint without bungling grammar or semantics. | |||
One approach to address this issue is to teach LLMs to adhere to the conditions (i.e., train on input text with constraints). However, this technique is extremely expensive and becomes super difficult to teach LLMs to adhere to various constraints. For instance, it is difficult to train an LLM to make 1-page essays in active voice with specific tones. Alternatively, researchers have tried an alternative approach of freezing LLMs (use pre-trained LLMs and never adjust its weights) and applying an external classifier to learn various conditions. But, this technique has been difficult to execute and only works on limited conditions (specific semantic or topic). | |||
=== Difficulty with Infilling and Structured Generation === | |||
Many real-world tasks—like text infilling, editing, or constrained rewriting—require access to both past and future context. Since autoregressive models are inherently one-directional, they are not well suited for such bidirectional or structure-aware tasks without significant architectural modifications. | |||
=== Why Diffusion Offers a Solution === | |||
Diffusion-based language models present an alternative approach that addresses these limitations. Instead of generating text sequentially, they treat the entire sequence as a whole and generate it through an iterative denoising process. This allows for: | |||
* Joint control over all tokens during the generation | |||
* Flexible incorporation of global constraints | |||
* Seamless infilling by fixing certain tokens and sampling the rest | |||
By removing the strict left-to-right dependency, diffusion models open new possibilities for controllable and structured text generation. | |||
=== General Drawbacks of Diffusion Language Models=== | |||
* Diffusion models do indeed improve controllable generation. However, most day-to-day uses of LLMs do not require controllable generation. | |||
* Diffusion models need to convert continuous embeddings back into discrete tokens, which leads to errors and inefficiencies. | |||
* Diffusion models rely on k-NN rounding, which tends to be unstable when having some high-dimensional embeddings and large vocabularies. | |||
* It’s hard to maintain the context for open generation tasks (limited to the context present in the sequence, and any other external classifiers being used), this means that diffusion models struggle with longer context. | |||
* During training, diffusion models need to store intermediate latent states for every diffusion step, increasing the GPU memory usage. | |||
== Further Challenges and Open Questions == | |||
Beyond the outlined limitations, there are additional open challenges and research opportunities in diffusion language modeling: | |||
* '''Robustness to Noise and Errors in Intermediate Steps''': | |||
** Diffusion models depend heavily on the accuracy of intermediate denoising steps. Even minor inaccuracies can accumulate, causing significant deviations from the target distribution. Developing methods to detect, correct, or mitigate such errors during the diffusion steps is an open challenge. | |||
* '''Token Space Coverage and Diversity''': | |||
** While diffusion models facilitate controlled generation, they can also face mode-collapse or insufficient diversity in generated outputs, especially when rounding or discretizing embeddings. Ensuring sufficient coverage of the token space without sacrificing fluency remains a critical research direction. | |||
* '''Alignment Between Continuous and Discrete Spaces''': | |||
** Continuous diffusion models operate in embedding spaces, requiring a reliable mechanism for mapping embeddings back to discrete tokens. Current rounding techniques like nearest-neighbor search or clamping can introduce semantic distortions. More sophisticated, semantically-aware rounding mechanisms could greatly improve generation quality. | |||
* '''Computational Efficiency and Scalability''': | |||
** Diffusion models typically involve computationally intensive iterative processes for both training and inference. Optimizing these processes through accelerated sampling, improved architectures (e.g., structured or sparse diffusion), or hardware-aware implementations is essential to enable real-world deployment. | |||
* '''Long-Range Context Management''': | |||
** Diffusion models, particularly continuous ones, face challenges in effectively modeling long-range dependencies due to their iterative nature. How to preserve coherence and global context in lengthy text sequences or documents remains a challenging and promising research area. | |||
Addressing these open questions will significantly enhance diffusion language models' capabilities and applicability, positioning them as competitive alternatives or complementary methods alongside established autoregressive approaches. | |||
== Gaussian Diffusion for Text == | |||
Recall a diffusion model. We take the input (such as an image) and apply Gaussian noise to eventually produce white noise. We then apply iterative denoising techniques to recover an image from the input distribution. To apply diffusion for text, text sequences are embedded and treated as continuous data (like grayscale images). Gaussian noise is added in training, and a denoising network recovers clean embeddings. A final rounding step maps vectors to tokens. This supports flexible generation but is computationally expensive. The application and removal of noise is expensive. Furthermore, it may be expensive to convert our final vector embeddings into tokens. | |||
=== Core Idea === | |||
In the diffusion language modelling framework, text sequences are represented as continuous embeddings. Instead of generating tokens autoregressively, the model learns to reverse a noise process that gradually corrupts these embeddings. Generation is reframed as iterative denoising: the model starts from pure noise and gradually refines it into meaningful embeddings. | |||
Each text sequence of <math>n</math> tokens is embedded into an <math>n \times d</math> matrix, where <math>d</math> is the embedding dimension. This continuous matrix is treated like a grayscale image and becomes the object of the diffusion process. | |||
=== Forward and Backward Process === | |||
The forward process adds Gaussian noise to the embedding sequence over multiple steps. The backward (denoising) process aims to reconstruct the clean sequence by removing this noise in reverse. | |||
This is achieved using a '''score model''', which is trained to estimate the gradient of the log-probability density function at each time step. Conceptually, the model: | |||
* Samples a noisy input from the prior | |||
* Predicts the direction toward the data manifold | |||
* Repeats this over several steps | |||
* Eventually outputs a denoised embedding close to the real data | |||
This continuous diffusion process eliminates the need for direct token prediction at each step. | |||
=== Embedding and Rounding === | |||
The embedding step is the same as in autoregressive models: each token is mapped to a vector using a trainable embedding layer. | |||
However, diffusion models operate purely in the continuous space. They output a matrix of <math>n \times d</math> vectors rather than token probabilities. Thus, a '''rounding step''' is needed to convert these vectors back into discrete tokens. | |||
This is done via '''nearest-neighbour search''': each generated vector is clamped to the closest token embedding at every diffusion step. This ensures that the denoising trajectory stays close to the valid token space, but the rounding process is costly and can be a bottleneck during inference. | |||
=== End-to-End Training === | |||
Training is done end-to-end by jointly optimizing both the embedding network and the Gaussian denoising model. The loss function extends the classic diffusion loss by incorporating the learnable embedding parameters. | |||
By training in the continuous domain while supervising against discrete targets, the model learns both the semantic structure of language and how to reconstruct it from corrupted embeddings. | |||
== Diffusion-LM: A Continuous Diffusion Model for Controllable Text Generation == | |||
=== Introduction === | |||
Diffusion‑LM is a non‑autoregressive, continuous diffusion–based language model that iteratively denoises Gaussian latents into word embeddings to form a hierarchical latent representation for text generation. This continuous diffusion process enables simple gradient‑based updates on those latents to enforce complex, fine‑grained controls—such as text length, part‑of‑speech constraints, exact syntactic trees, or semantic attributes—without any model re‑training or fine‑tuning. On six challenging controllable generation tasks, it significantly outperforms previous plug‑and‑play methods (e.g., PPLM, FUDGE), trading off an approximately 7× slower decoding speed for far superior control fidelity. | |||
Controlling the behavior of language models without re-training is a major open problem in natural language generation. It is true that previous works have had success with simple attribute-level control tasks like sentiment or topic, but they struggle with more complex, fine-grained constraints like syntactic structure. This motivates light-weight, modular plug-and-play approaches that keep the language model frozen and insteaad use external classifiers or potential functions for generation. However, these methods—especially those based on autoregressive models, have been limited in their effectiveness and scope. Diffusion-LM is designed to handle a wide range of controllable generation tasks that are difficult for traditional autoregressive models. These include: | |||
* Semantic control (e.g., generating positive vs. negative text) | |||
* Part-of-speech control (e.g., enforcing specific POS sequences) | |||
* Syntax control (e.g., constraining generation to match a parse tree) | |||
* Length control (e.g., generate exactly 10 tokens) | |||
* Infilling (e.g., filling blanks in a partially masked sentence) | |||
Diffusion-LM addresses these challenges by adapting continuous diffusion models, which have shown great success in vision and audio domains, to the discrete domain of language. The model begins with a sequence of Gaussian noise vectors and incrementally denoises them into meaningful word representations. These denoising steps produce a hierarchy of continuous latent variables that enable efficient, gradient-based control during generation. | |||
Key advantages of Diffusion-LM include: | |||
* '''Support for complex, global constraints''': Unlike autoregressive models, which generate text left-to-right and they can only condition on past tokens, Diffusion-LM operates on the full sequence, and this allows it to enforce constraints that depend on both left and right contexts, such as syntax trees or long-range dependencies. | |||
* '''Plug-and-play controllability''': Diffusion-LM enables classifier-guided generation by using gradient updates directly to the continuous latent variables. This allows the generation process to satisfy control objectives (e.g., sentiment, structure) while maintaining fluency, without requiring any model retraining. | |||
* '''Infilling and span-anchored controls''': The model can hold parts of a sentence fixed and only sample the missing spans, and naturally supporting infilling tasks. These tasks can be performed without the need for a clasifier, and Diffusion-LM achieves results competitive with autoregressive models trained specifically for such tasks. | |||
* '''Compatibility with existing methods''': The model builds on a standard diffusion process but incorporates critical adaptations for language, such as a learned embedding space, rounding back to discrete tokens, and training techniques to handle the continuous-discrete interface. | |||
Diffusion-LM significantly outperforms prior plug-and-play methods on a variety of challenging control tasks—including syntax, semantics, and structure—and often matches or exceeds the performance of models that are fine-tuned for each individual control. Moreover, it demonstrates strong composability: multiple controls (e.g., non-toxic and positive sentiment) can be jointly applied with minimal overhead. These results show that Diffusion-LM is a promising way for controllable text generation. | |||
=== Mathematical Formulation === | |||
Diffusion-LM applies a continuous diffusion process to language modeling by representing text sequences as continuous embeddings. These embeddings are progressively noised and then denoised to recover coherent text. Let's take a look at its formulas in the following parts. | |||
==== Forward Diffusion Process ==== | |||
The forward process gradually adds Gaussian noise to the embedded text representation. A sequence of tokens | |||
<math>w = [w_1, \ldots, w_n]</math> | |||
is mapped to a continuous vector matrix | |||
<math>x_0 \in \mathbb{R}^{n \times d}</math>. | |||
A fixed Markov chain adds noise at each step to produce <math>x_1, \ldots, x_T</math>: | |||
<math>q(x_t \mid x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} , x_{t-1}, \beta_t I)</math> | |||
Here, <math>\beta_t</math> is a hyperparameter controlling the noise at step <math>t</math>. The final noisy sample <math>x_T</math> approximates a Gaussian prior: | |||
<math>q(x_T \mid x_0) \approx \mathcal{N}(0, I)</math> | |||
This process is illustrated in Figure 1. | |||
[[File:forward_reverse_diffusion_processes.png|700px|thumb|center|Figure1: A graphical model representing the forward and reverse diffusion processes]] | |||
==== Reverse Denoising Process ==== | |||
The model learns the reverse transitions to remove noise and recover the original text embeddings. Each step of the reverse process is modeled as: | |||
<math>p_\theta(x_{t-1} \mid x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t, t))</math> | |||
The mean <math>\mu_\theta(x_t, t)</math> and optionally the variance <math>\Sigma_\theta(x_t, t)</math> are predicted by a neural network (e.g., Transformer or U-Net). | |||
==== Training Objective ==== | |||
Training aims to maximize the marginal likelihood <math>\log p_\theta(x_0)</math>, but this is intractable. Instead, the model minimizes a variational lower bound (ELBO): | |||
<math> \mathcal{L}_{\text{vlb}}(x_0) = \mathbb{E}_{q(x_{1:T} \mid x_0)} \left[ \log \frac{q(x_T \mid x_0)}{p_\theta(x_T)} + \sum_{t=2}^{T} \log \frac{q(x_{t-1} \mid x_0, x_t)}{p_\theta(x_{t-1} \mid x_t)} - \log p_\theta(x_0 \mid x_1) \right] </math> | |||
Since this objective is unstable, the paper adopts the simplified denoising loss proposed by Ho et al.: | |||
<math> \mathcal{L}_{\text{simple}}(x_0) = \sum_{t=1}^{T} \mathbb{E}_{q(x_t \mid x_0)} \left[ \| \mu_\theta(x_t, t) - \hat{\mu}(x_t, x_0) \|^2 \right] </math> | |||
Here, <math>\hat{\mu}(x_t, x_0)</math> is the mean of the true posterior <math>q(x_{t-1} \mid x_t, x_0)</math>, which is analytically known for Gaussian noise. | |||
While <math>\mathcal{L}_{\text{simple}}</math> is no longer a valid lower bound, prior work has found that it empirically made training more stable and improved sample quality. | |||
==== Embedding and Rounding ==== | |||
After denoising, the model obtains <math>x_0</math>, a continuous representation. A final decoding step maps this to discrete tokens using: | |||
<math> p_\theta(w \mid x_0) = \prod_i p_\theta(w_i \mid x_{0, i}) </math> | |||
Each <math>w_i</math> is predicted from its embedding <math>x_{0, i}</math> using a softmax over the vocabulary. | |||
To improve alignment with the discrete token space during generation, the model optionally applies the clamping trick, which replaces the predicted vector with its nearest token embedding at intermediate steps. This helps reduce rounding errors during generation. | |||
===Model Architecture and Training Methods=== | |||
Diffusion-LM adapts the standard diffusion model to handle discrete text. As we know, text is inherently discrete and constructing Diffusion-LM requires several key changes. This section walks through those changes step by step, covering embedding design, training strategy, rounding, and controllable decoding. As we described before, in the Mathematical Formulation section, the model starts with Gaussian noise and learns to iteratively denoise it back to meaningful embeddings. Now we explain how this process is practically implemented. | |||
==== Embedding and End-to-End Training ==== | |||
For using diffusion in language modeling, first we should convert text into continuous embeddings. Each token in a sequence <math> w = [w_1, w_2, \dots, w_n] </math> is mapped to a continuous vector in <math> \mathbb{R}^d </math> by an embedding function <math> \text{EMB}(w_i) </math>. The full sentence is represented as: | |||
<math> \text{EMB}(w) = [\text{EMB}(w_1), \dots, \text{EMB}(w_n)] \in \mathbb{R}^{n \times d} </math> | |||
Then, these embeddings are used in a diffusion process that gradualy adds noise and then learns to reverse this process. The embedding function is learned end-to-end along with the model parameters using a modified version of the standard diffusion loss. (Recall from the Mathematical Formulation section that this loss is based on a variational lower bound and a simplified mean squared objective.) | |||
The modified objective is: | |||
<math> \mathcal{L}^{\text{e2e}}{\text{vlb}}(w) = \mathbb{E}{q(x_0|w)} \left[\mathcal{L}{\text{vlb}}(x_0) + \log q\phi(x_0|w) - \log p_\theta(w|x_0)\right] </math> | |||
The learned embeddings (Figure 2) show interesting clustering patterns, where tokens with similar part-of-speech tags tend to group together in embedding space. | |||
[[File:tSNE_plot.png|600px|thumb|center|Figure2) A t-SNE plot of the learned word embeddings. Each word is colored by its POS.]] | |||
==== Reducing Rounding Errors ==== | |||
As we discussed earlier, once denoising ends and the model reaches a final continuous state <math> x_0 </math>, it needs to be mapped back to a discrete sentence. We call this process as "rounding". The standard approach is to choose the word with the highest likelihood given <math> x_0 </math>: | |||
<math> p_\theta(w | x_0) = \prod_{i=1}^n p_\theta(w_i | x_{0,i}) </math> | |||
But, this naïve rounding often fails because <math> x_0 </math> may not map cleanly to one token per position. To fix this, the model modifies the training objective to explicitly encourage <math> x_0 </math> to align with discrete word vectors. The improved loss is: | |||
<math> \mathcal{L}^{\text{e2e}}{\text{simple}}(x_0) = \sum{t=1}^T \mathbb{E}{q(x_t|x_0)} \left[ | f\theta(x_t, t) - x_0 |^2 \right] </math> | |||
Here, <math> f_\theta(x_t, t) </math> is a neural network that predicts <math> x_0 </math> from any <math> x_t </math>, and this enforces that the model should maintain a clear mapping throughout the diffusion steps. This mirrors the score-based denoising strategy which we introduced in the mathematical formulation section. | |||
Additionally, the "clamping trick" helps by snaping intermediate states closer to valid token embeddings. The clamping update is: | |||
<math> x_{t-1} = \sqrt{\bar{\alpha}t} \cdot \text{Clamp}(f\theta(x_t, t)) + \sqrt{1 - \bar{\alpha}_t} \cdot \epsilon </math> | |||
This trick improves word alignment and reduces rounding errors. | |||
==== Controllable Text Generation ==== | |||
As we mentioned in the Introduction, Diffusion-LM is particularly powerful for controllable generation. This is done by applying plug-and-play control at the latent level. Rather than steering the output text directly, we apply gradients to the latent variables <math> x_{0:T} </math> so that the denoised output satisfies the control objective. | |||
The goal is to sample from: | |||
<math> p(x_{0:T} | c) = \prod_{t=1}^T p(x_{t-1} | x_t, c) </math> | |||
This is approximated using gradient ascent on <math> x_{t-1} </math>: | |||
<math> \nabla_{x_{t-1}} \log p(x_{t-1} | x_t, c) = \nabla_{x_{t-1}} \log p(x_{t-1} | x_t) + \nabla_{x_{t-1}} \log p(c | x_{t-1}) </math> | |||
The first term is from the language model, and the second from the control classifier. This allows the model to adjust generation to satisfy constraints like syntax or semantics. | |||
To improve decoding, two enhancements are introduced: | |||
* '''Fluency Regularization:''' Add a term that balances fluency with control satisfaction. | |||
* '''Multiple Gradient Steps:''' Run several gradient steps per denoising step to better fulfill constraints. | |||
These techniques directly reflect the plug-and-play controllable generation strategy we mentioned in the introduction. | |||
==== Score-Based Gradient Control in Diffusion-LM ==== | |||
One of the key benefits of Diffusion-LM is that it can incorporate external control signals at generation time using gradient guidance. At denoising time, the model refines latent representations using the gradient of a control objective. For a control variable <math>c</math> (e.g., sentiment, length, syntax), the posterior over trajectories is refined as <math>p(x_{0:T} \mid c) \propto p(x_{0:T}) \cdot p(c \mid x_0)</math>. This construction enables us to optimize the path to meet language fluency and the control constraint at the same time. | |||
To approximate this posterior, Diffusion-LM updates gradients in latent states <math>x_t</math> using a classifier (or potential function) <math>p(c \mid x_0)</math>. Specifically, for each reverse step, the model updates <math>x_{t-1}</math> by: | |||
<math> | |||
\nabla_{x_{t-1}} \log p(x_{t-1} \mid x_t, c) = \nabla_{x_{t-1}} \log p(x_{t-1} \mid x_t) + \nabla_{x_{t-1}} \log p(c \mid x_{t-1}) | |||
</math> | |||
The first term ensures language fluency following the diffusion model, while the second term channels the output for ensuring the control requirement. Plug-and-play controllability is thus ensured without altering the language model weights. | |||
For stable and interpretable updates, the model can optionally incorporate fluency regularization and multiple gradient steps. Adding a fluency loss such as <math> \lambda \cdot \| x_{t-1} - \hat{x}_{t-1} \|^2 </math>, where <math> \hat{x}_{t-1} </math> is the initial prediction of the model, can be used. Also, performing multiple steps of gradient ascent on <math>x_{t-1}</math> before sampling <math>x_{t-2}</math> can help constraint satisfaction. These mechanisms enable control of the generation process at a fine-grained level, producing a more expressive and flexible alternative to autoregressive approaches. | |||
==== Minimum Bayes Risk Decoding ==== | |||
For generation tasks that demand high-accuracy outputs—such as machine translation, summarization, or infilling—it is often not enough to generate a single fluent sentence. Instead, we want the output that best aligns with some evaluation metric, such as BLEU, ROUGE, or semantic similarity. In these scenarios, Diffusion-LM supports a decoding strategy called Minimum Bayes Risk (MBR) decoding. | |||
MBR decoding works by generating a set of candidate outputs (e.g., 10 or 100 samples) from the model and then selecting the one that has the lowest expected loss under a given utility function. In other words, instead of choosing the most likely sentence, the model picks the one that is most similar to the other high-quality samples, according to some reference-free scoring criterion. | |||
Formally, the MBR decoding selects: <math> \hat{w} = \arg\min_{w \in S} \sum_{w' \in S} \frac{1}{|S|} \cdot \mathcal{L}(w, w') </math> | |||
where: | |||
* <math> S </math> is the set of generated samples, | |||
* <math> \mathcal{L}(w, w') </math> is a task-specific loss (e.g., 1 - BLEU), | |||
* <math> \hat{w} </math> is the output that minimizes the expected loss over the set. | |||
This method is useful. why? because even if the model’s sampling process is noisy or diverse, the MBR step ensures that the selected output is representative of the best qualities among all samples. This is especially helpful in controllable generation, where we care about both fluency and constraint satisfaction. | |||
In practice, MBR decoding often improves the final quality of generated sequences without needing to modify the model itself. It serves as a powerful post-processing technique for refining outputs, and this makes it highly complementary to the plug-and-play control strategies used in Diffusion-LM. | |||
=== Evaluation and Results === | |||
Diffusion-LM is evaluated on five controllable generation tasks, using both control accuracy (how well the constraint is followed) and fluency (measured via perplexity and human evaluation). | |||
Compared to baselines like: | |||
* '''PPLM''' – a plug-and-play autoregressive method | |||
* '''FUDGE''' – classifier-based control on GPT-2 | |||
* '''FT''' – fine-tuned GPT-2 on each control task | |||
[[File:Diffusion-LM Improves Controlable Text Generation result.png|center|700px|Figure: A comparison between Diffusion-LM and other models]] | |||
Diffusion-LM achieves higher control accuracy and comparable or better fluency, demonstrating its effectiveness in multi-property generation without needing task-specific retraining. | |||
=== Limitations === | |||
* Higher Perplexity | |||
** Diffusion-LM relies on continuous diffusion processes for text generation, which differ fundamentally from the discrete autoregressive approach used in models like GPT or BERT. | |||
** As a result, the generated text may exhibit slightly lower fluency or grammatical coherence, leading to higher perplexity scores. | |||
** This suggests that the model's ability to capture natural language distributions is not yet on par with state-of-the-art language models. Improving the architecture or introducing auxiliary losses may help reduce perplexity. | |||
* Substantially Slower Decoding | |||
** Unlike autoregressive models that generate tokens sequentially in a single forward pass, diffusion models require hundreds of iterative denoising steps to produce output. | |||
** This makes the decoding process significantly slower, limiting the model’s usability in real-time applications such as interactive writing assistants or conversational agents. | |||
** Speed optimization and accelerated sampling techniques are essential for improving practical deployment. | |||
* Slower Training Convergence | |||
** Training a diffusion-based language model involves learning across a wide range of noise levels, which introduces a more complex optimization landscape than traditional language modeling tasks. | |||
** This complexity leads to longer training times and makes the training process more sensitive to hyperparameters, such as noise schedules and model architecture. | |||
** Effective convergence often requires careful tuning and potentially more compute resources compared to standard fine-tuning or pretraining. | |||
=== Conclusion === | |||
Diffusion-LM, a novel language model based on continuous diffusion processes, introduces new possibilities for controlling text generation with fine-grained precision. With a modified loss function and end-to-end training, Diffusion-LM outperforms previous methods in six distinct control tasks, significantly improving success rates and competing well with fine-tuning approaches that require additional training. Despite some challenges, such as increased perplexity, slower decoding, and slower training convergence, Diffusion-LM shows great promise. With further optimization and development, it has the potential to offer a highly effective solution for large-scale controllable text generation tasks. | |||
== Masked-Diffusion LM: Faster and Smarter == | |||
The key limitation of traditional diffusion models in handling discrete data like text is their application of uniform noise. In language modelling, it is important to model the fact that different words have different levels of importance. Simply adding a rounding step is expensive as it leads to slower training and inference times. | |||
Masked-Diffusion LM improves efficiency by applying noise selectively based on word importance. Important tokens are masked earlier in the process so that the model is exposed to their features earlier. It replaces nearest-neighbour rounding with a cross-entropy loss between predicted and original tokens. Then, at generation, less important words are predicted first (as they are masked later) with more important words generated towards the end. The result is better performance and faster inference. | |||
[[File:masked diffusion.png|700px|thumb|center|The overall process of our Masked-Diffuse LM]] | |||
===Method/Experiment=== | |||
The paper introduces a new diffusion language model called Masked-Diffuse LM that aims to generate text more efficiently and with higher quality with three key innovations. | |||
1. Selective Noise Application: Instead of applying uniform noise as in earlier methods, it uses a “soft-masking” strategy that gradually corrupts text by targeting more important words first. These important words are identified using simple linguistic metrics like TF-DF and word entropy. TF-IDF enables us to measure the relevance of a word with respect to a specific sentence. A higher score means the particular word is more important in the sentence. Entropy determines the amount of information a word contains. A word with lower entropy suggests that the word contains less information. Thus, these words have lower importance than those with higher entropy. | |||
Word Relevancy (TF-IDF): | |||
<math>w_{\text{tf-idf}}(w, d) = \frac{f_{w,d}}{\sum_{w' \in d} f_{w',d}} \log \frac{N}{1 + |\{d \in D : w \in d\}|}</math> | |||
Entropy: | |||
<math> | |||
H(w) = -p(w) \log(p(w)), \quad p(w) = \frac{f_w}{\sum_{j=1}^J f_j} | |||
</math> | |||
In practice, we combine both measures (with normalization) to produce a new importance metric (as seen below) to evaluate the importance of words in a given sentence. | |||
Importance: | |||
<math> | |||
I(w) = \frac{x_{\text{tf-idf}}(w, d)}{\sum_{w' \in d} w_{\text{tf-idf}}(w', d)} + \frac{H(w)}{\sum_{w' \in d} H(w')} | |||
</math> | |||
2. Soft-Masking Process: During the forward process, the model corrupts token embeddings progressively, starting with the most meaningful words to ensure that the model learns to prioritize recovering critical information during the reverse process. For example, given the text "NLP is fun!", the most meaningful word ("NLP") would be masked first and then "fun" and then "is". | |||
3. Cross-Entropy Loss for Stability: In the reverse diffusion process, the model denoises the embeddings step-by-step to reconstruct the original text by directly predicting the original tokens using a cross-entropy loss. This approach effectively bridges the gap between continuous embeddings and discrete tokens and ensures stable and coherent text generation. Using the example from above, during denoising, "is" would be generated first and then "fun" and then "NLP". | |||
The model can also be combined with large pre-trained language models like BERT to further boost performance on various controllable generation tasks. | |||
===Results=== | |||
The experiments show that Masked-Diffuse LM outperforms previous diffusion language models on several controllable generation tasks. For example, on tasks like generating specific semantic content, the model achieved higher accuracy and better fluency compared to baselines like Diffusion-LM and FUDGE. It consistently improved accuracy across tasks such as parts-of-speech, syntax tree, syntax spans, and controlling sentence length. Moreover, the new method is more efficient, requiring significantly less training and inference time. Human evaluators also ranked it higher for quality, confirming that it produces more natural and controlled text. Overall, the results demonstrate that this new model is both cheaper to train and better at generating coherent and controlled text. | |||
===Why It Matters=== | |||
Masked-Diffusion LM represents a shift in how diffusion models handle discrete data like text. By leveraging linguistic insights and optimizing the noise application process, it not only generates better-quality text but also does so at a lower computational cost. This makes it a promising tool for applications requiring controlled and efficient language generation. | |||
===Limitations=== | |||
1. Dependence on Heuristic Importance Metrics: The model relies on simple heuristic-based metrics like TF-IDF and entropy to estimate word importance. While effective and interpretable, these metrics may not always capture deep semantic relevance or context-dependent importance. Future work could explore learned importance functions or attention-based saliency models that dynamically adjust based on task or context. | |||
2. Evaluation Limited to Controllable Tasks: The experiments are primarily focused on controllable generation tasks (e.g., POS constraints, syntax structure, sentence length). It remains unclear how well the model performs in open-ended generation, dialogue systems, or low-resource settings. Broader evaluation would help validate general applicability. | |||
===Conclusion=== | |||
Masked-Diffusion LM marks a meaningful step forward in bridging the gap between continuous diffusion processes and the discrete world of natural language. By leveraging lightweight linguistic signals to guide noise injection and replacing costly rounding with stable cross-entropy loss, it introduces a more efficient and semantically aware approach to controllable text generation. The model not only improves performance across key generation tasks but also does so with reduced computational overhead—making it both practical and powerful. As diffusion models continue to gain traction in NLP, innovations like this offer a glimpse into a future where language generation is not just accurate and fluent, but also interpretable, controllable, and efficient. With its thoughtful design and strong results, Masked-Diffusion LM lays important groundwork for the next generation of discrete generative models. | |||
== DiffuSum: Generation Enhanced Extractive Summarization with Diffusion == | |||
=== Overview === | |||
DiffuSum introduces a novel paradigm for extractive summarization by leveraging continuous diffusion models to generate summary‐level sentence embeddings and then extract sentences via representation matching, rather than treating extraction as a binary sequence‐labeling task. It jointly trains a contrastive sentence encoder—with matching and diversity losses—and a diffusion‐based generator that iteratively denoises Gaussian latents into target embeddings. On CNN/DailyMail, DiffuSum achieves a new state‑of‑the‑art ROUGE of 44.83/22.56/40.56 and generalizes robustly to XSum and PubMed with only minor performance drops and no domain‑specific tuning. | |||
=== Method === | |||
==== Sentence Encoding Module: ==== | |||
* '''Initial Embedding:''' The document and summary sentences are first processed using Sentence-BERT to obtain initial sentence embeddings. These embeddings are fixed and will not be updated during the training. | |||
* '''Contextualization:''' These embeddings are refined through a transformer-based encoder and a projection (MLP) layer to produce contextualized sentence representations. | |||
* '''Optimization:''' The module is trained using a matching loss (ensuring the generated summary representations align with oracle summaries) and a multi-class contrastive loss (promoting diversity and distinguishability among sentence representations). | |||
==== Diffusion Generation Module: ==== | |||
* '''Forward Process:'''The module gradually injects Gaussian noise into the summary sentence embeddings, simulating a diffusion process that corrupts the embeddings over several steps. | |||
* '''Reverse Process:''' A transformer-based model then learns to iteratively remove the noise, recovering the target summary sentence representations in a reverse diffusion process. | |||
* '''Simultaneous Generation: ''' This approach enables the model to generate all summary sentence representations concurrently, bypassing token-level generation challenges. | |||
==== Sentence Extraction via Matching: ==== | |||
* '''Matching Mechanism:''' The generated summary embeddings are compared with the document’s sentence embeddings using a similarity measure (e.g., dot product followed by softmax). | |||
* '''Extraction:''' For each generated summary representation, the document sentence with the highest matching score is selected to form the final extractive summary. | |||
=== Experimental Results and Analysis === | |||
DiffuSum demonstrates state-of-the-art performance on benchmark datasets such as CNN/DailyMail, XSum, and PubMed. Key findings include: | |||
'''1. Performance Gains:''' | |||
The model achieves high ROUGE-1/2/L scores, particularly improving ROUGE-2, compared to both one-stage and two-stage extractive summarization baselines. | |||
'''2. Ablation Studies:''' | |||
* Using Sentence-BERT for initial sentence embeddings is critical. | |||
* Both the matching loss and contrastive loss substantially enhance the quality of sentence representations. | |||
* The number of diffusion steps and the dimensionality of the embeddings (h) significantly influence performance, indicating the need for an optimal balance between noise injection and recovery. | |||
3. '''Cross-Dataset Adaptability:''' | |||
Evaluations across different domains (news and scientific papers) show that DiffuSum adapts well to varying summary lengths and document complexities. | |||
===Limitations=== | |||
* Only supports extractive summarization (i.e. select one or more summary sentences directly) | |||
** The diffusion module generates sentence-level embeddings only | |||
** Lacks token-level generation, making it unsuitable for abstractive summarization (i.e. generate a new summary sentence) | |||
* Evaluated only on single-document datasets | |||
** Not tested on multi-document or long-document summarization | |||
** Requires further investigation for adaptation to these settings | |||
*More complex generation process | |||
**Involves multiple steps of noise injection and denoising | |||
**More computationally intensive than discriminator-based extractive systems | |||
=== Conclusion === | |||
DiffuSum pioneers the application of diffusion models in extractive summarization by generating continuous summary sentence representations and using a matching mechanism for sentence extraction. This generation-enhanced framework not only achieves superior performance compared to traditional methods but also opens new avenues for applying generative models in text summarization. Future work could extend this approach to abstractive summarization, multi-document scenarios, and integration with pre-trained language models to further boost performance. | |||
== Discrete Diffusion Modeling by Estimating the Ratios of the Data Distribution == | |||
This paper introduces Score Entropy Discrete Diffusion (SEDD), a new framework that brings the power of continuous diffusion models to discrete data—especially language—by learning probability ratios via a novel “score entropy” loss. SEDD matches or surpasses existing diffusion‑based language models (cutting perplexity by 25–75 %), outperforms GPT‑2 on zero‑shot perplexity without any annealing (6–8× better), and allows rich control (e.g., arbitrary infilling) while trading compute for quality (32× fewer network evaluations). By framing the reverse diffusion as estimation of conditional probability ratios between token pairs using a Bregman‑divergence–based objective, SEDD ensures nonnegativity and convexity in its loss, yielding stable training dynamics across timesteps. It also derives a tractable evidence lower bound (ELBO) for direct maximum‑likelihood training and perplexity evaluation, enabling head‑to‑head comparisons with autoregressive baselines on benchmarks like Penn Treebank and WikiText‑103. | |||
===Introduction=== | |||
Diffusion models have revolutionized image generation, creating stunningly realistic visuals. However, translating this success to discrete data like natural language has proven challenging. While standard diffusion models build on the solid foundation of score matching in continuous spaces, attempts to adapt this for discrete domains haven't yielded comparable results. This paper introduces a novel approach that aims to bridge this gap. | |||
===The Problem This Paper Tried to Address=== | |||
Generating high-quality, coherent text has long been dominated by autoregressive models (like GPT). While powerful, these models have limitations: sequential generation is slow, controlling the output is tricky, and they often require sampling tricks like temperature scaling or nucleus sampling to avoid degraded text quality. | |||
Inspired by the success of diffusion models in generating continuous data (like images), researchers have tried adapting them for discrete sequences (like text). However, these discrete diffusion models have generally lagged behind autoregressive models. They often struggle with likelihood performance (perplexity), are slow to sample from, and produce lower-quality text without significant modifications or annealing techniques. Existing methods for training discrete diffusion models, like mean prediction or ratio matching, have practical drawbacks or don't perform as well empirically. Concrete score matching, while theoretically promising, suffers from instability due to its loss function. | |||
===Key Contribution: Score Entropy Discrete Diffusion (SEDD)=== | |||
This work introduces '''Score Entropy Discrete Diffusion (SEDD)''', a new framework for discrete diffusion modeling that significantly boosts performance, particularly for language tasks. | |||
# '''Score Entropy Loss''': The core innovation is the "score entropy" loss function. This loss naturally extends the concept of score matching from continuous to discrete spaces by focusing on learning the ''ratios'' of probabilities between adjacent states,<math>\frac{p_t(y)}{p_t(x)}</math>, often called the concrete score. Score entropy is designed to handle the positivity requirement of these ratios, overcoming stability issues faced by previous discrete score matching attempts. | |||
# '''State-of-the-Art Discrete Diffusion''': SEDD significantly outperforms previous discrete and continuous diffusion language models on standard benchmarks, reducing perplexity by 25-75%. | |||
# '''Competitive with Autoregressive Models''': For comparable model sizes, SEDD achieves perplexity scores competitive with strong autoregressive baselines, notably outperforming GPT-2 on several zero-shot perplexity tasks. | |||
# '''High-Quality Generation & Compute Trade-off''': SEDD generates high-quality text samples ''without'' needing distribution annealing techniques like temperature or nucleus sampling. It significantly outperforms un-annealed GPT-2 in generative perplexity (6-8x better) and allows trading compute for quality – matching GPT-2 quality with up to 32x fewer network evaluations. | |||
# '''Controllable Generation''': By directly modeling probability ratios, SEDD enables flexible conditional generation, including controllable infilling (generating text to fill gaps between prompts) without specialized training, matching the quality of nucleus sampling in autoregressive models. | |||
===Method: Learning Ratios via Denoising Score Entropy=== | |||
# '''Discrete Diffusion Process''': The SEDD model defines a forward discrete diffusion process where data distribution evolves via a continuous-time Markov process defined by a rate matrix (diffusion matrix) <math>Q_t \in \mathbb{R}^{N \times N}</math>, and a family of distributions <math>p_t \in \mathbb{R}^N</math> where <math>\frac{dp_t}{dt} = Q_t p_t</math> and <math>p_0</math> is approximately the original data probability distribution. Note that <math>Q_t</math> here has non-negative non-diagonal entries and the sum of each column of <math>Q_t</math> is 0. This makes sure that the rate <math>\frac{dp_t}{dt}\</math>'s entries have a sum of zero, meaning that there is no change of total mass. The goal is to learn the ''reverse'' process, which depends on the probability ratios<math>\frac{p_t(y)}{p_t(x)}</math> | |||
# '''Score Entropy Loss''': Instead of directly minimizing an <math>l^2</math>difference (like Concrete Score Matching), SEDD uses the score entropy loss <math>\mathcal{L}_{SE} = \mathbb{E}_{x \sim p} \left[ \sum_{y \ne x} w_{xy} \left( s_\theta(x)_y - \frac{p(y)}{p(x)} \log s_\theta(x)_y + K\left(\frac{p(y)}{p(x)}\right) \right) \right]</math>, where <math>s_\theta(x)_y</math> is the model's estimate of the ratio<math>\frac{p(y)}{p(x)}, </math><math>w_{xy}</math> are weights, and <math>K(a) = a(log(a)-1)</math> is a constant function that makes sure the score entropy loss is non-negative. It is better behaved than the <math>l^2</math> loss. | |||
# '''Denoising Score Entropy (DSE)''': Calculating <math>\mathcal{L}_{SE} </math> directly requires knowing the true ratios <math>\frac{p(y)}{p(x)}</math>, but they are unknown. Similar to denoising score matching, the authors derive a tractable ''denoising score entropy'' <math>\mathcal{L}_{DSE}</math> objective that is equivalent to <math>\mathcal{L}_{SE}</math> up to a constant independence of <math>\theta</math> and depends only on the transition probabilities <math>p(y|x_0)</math> and <math>p(x|x_0)</math> of the forward diffusion process: <math>\mathcal{L}_{DSE} = \mathbb{E}_{x_0 \sim p_0, x \sim p(\cdot|x_0)} \left[ \sum_{y \ne x} w_{xy} \left( s_\theta(x)_y - \frac{p(y|x_0)}{p(x|x_0)} \log s_\theta(x)_y \right) \right]</math>, where <math>p_0</math> is a base density. | |||
# '''Diffusion Weighted DSE (DWDSE)''': For training diffusion models, this loss is integrated over time and weighted by the forward process transition rates, yielding the Diffusion Weighted Denoising Score Entropy <math>\mathcal{L}_{DWDSE}</math> where DWDSE at data point <math> x_0</math> is <math>\mathcal{L}_{DWDSE}(x_0) = \int_0^T \mathbb{E}_{x_t \sim p_{t|0}(\cdot|x_0)} \sum_{y \neq x_t} Q_t(x_t, y) \left( s_\theta(x_t, t)_y - \frac{p_{t|0}(y|x_0)}{p_{t|0}(x_t|x_0)} \log s_\theta(x_t, t)_y + K( \frac{p_{t|0}(y|x_0)}{p_{t|0}(x_t|x_0)}) \right) dt</math>, and <math>p_{t|0}(\cdot|x_0)</math> and <math>K</math> remain the same meaning as above. DWDSE provides an upper bound on the negative log-likelihood (similar to the ELBO). | |||
# '''Structured Transitions''': For tractability with sequences (like text), the diffusion process <math>Q_t</math> perturbs tokens independently using simpler token-level transition matrices <math>Q^{tok}_t</math> such as uniform noise <math>Q^{uniform} = \begin{bmatrix} 1-N & 1 & \dots & 1 \\ 1 & 1-N & \dots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & \dots & 1-N \end{bmatrix}</math> or transitions to a special MASK token <math>Q^{absorb} = \begin{bmatrix} -1 & 0 & \dots & 0 & 0 \\ 0 & -1 & \dots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \dots & -1 & 0 \\ 1 & 1 & \dots & 1 & 0 \end{bmatrix}</math>. This allows the score network <math>s_\theta</math> to predict ratios only between sequences differing by one token, and all values in <math>\mathcal{L}_{DWDSE}</math> are able to be efficiently calculated with such <math>Q's</math>. | |||
# '''Sampling & Control''': Generation uses the learned scores <math>s_\theta</math> to simulate the reverse process, typically using <math>\tau</math>-leaping. A "Tweedie<math>\tau</math>-leaping" variant leverages the ratio information for potentially better sampling. Conditional generation (like infilling) is achieved by applying Bayes' rule to the learned unconditional scores, allowing prompts at arbitrary positions without retraining. | |||
===Conclusion and performance=== | |||
In terms of perplexity across common task, a small SEDD model outperformed GPT-2 in the Wikitext2, PTB and Wikitext103 dataset. Similarly things happened for the medium SEDD model which again they outperformed GPT2 medium in Wikitext2, PTB and Wikitext103 dataset. | |||
In terms of efficiency, both SEDD small and SEDD medium achieve comparable perplexity with GPT2 with less iterations. | |||
===Limitation and Future Work=== | |||
# '''Sampling Speed''': While SEDD offers a compute-quality trade-off, and the network evaluation itself is efficient (no KV cache needed), achieving the highest quality still requires many sampling steps (e.g., 2048), which can be slower overall than autoregressive sampling with KV caching, depending on the hardware and batch size. Future work could focus on reducing the required number of steps, similar to advances in continuous diffusion. | |||
# '''Annealing''': The current work focuses on demonstrating high-quality generation ''without'' distribution annealing. Incorporating annealing techniques (like thresholding or guidance) could potentially further improve results or offer different control trade-offs. | |||
# '''Scaling''': While SEDD outperforms GPT-2, bridging the gap to modern large language models remains a challenge for future research, potentially building upon the SEDD framework. | |||
# '''Hyperparameters''': The current study didn't perform extensive hyperparameter tuning (e.g., noise schedules, loss weightings), suggesting potential for further improvements. | |||
==Compare Discrete and Continuous Diffusion== | |||
===Discrete Diffusion=== | |||
====How it works==== | |||
* IT Operates in discrete data space like word tokens level. | |||
* Each token transitions from one word to another during the noising and denoising process (sometimes the token are masked) | |||
* Often uses a diffusion matrix to guide the transitions | |||
====Advantages==== | |||
* Language is discrete, so modeling it directly preserves the original structure and semantics better. | |||
* We don't need to learn a separate mapping ("rounding") from vectors back to language since we are already in the token space. | |||
====Disadvantage and Challenges==== | |||
* The symbolic space doesn’t allow for gradients to flow easily since it's non-differentiable . | |||
* Everything happens in discrete steps, the denoising has to predict exact tokens which could be difficult. | |||
===Continuous Diffusion=== | |||
====How it works==== | |||
* Maps tokens into a continuous embedding space | |||
* Noising and denoising happen in this continuous space | |||
* May include clamping mechanisms to keep values in valid ranges | |||
* After denoising, the final vector is rounded or projected back to the nearest sentence | |||
====Advantages==== | |||
* Since everything happens in the continuous domain, it better aligned with the original diffusion and could allow gradients to flow smoothly through the model, making training more stable and efficient. | |||
* Thanks to embeddings, the continuous space captures richer semantics domain, so the model can generalize to unseen combinations or variations more easily. | |||
====Disadvantage and Challenges==== | |||
* We need a strong rounding technique to map from the continuous space back to valid token and valid language. | |||
= Topic 18: Retrival Augmented Generation (RAG) = | |||
== Motivation == | |||
Language models often struggle with hallucinations, outdated knowledge, and lack of factual grounding. Retrieval-Augmented Generation (RAG) addresses these issues by incorporating external knowledge into the generation process in a modular, efficient way. | |||
=== Why Do Language Models Hallucinate? === | |||
Large language models (LLMs) are trained on massive corpora using self-supervised objectives, which makes them excellent at generating fluent text. However, they often produce '''hallucinations'''—confident but factually incorrect statements. This happens because: | |||
* LLMs store information implicitly in parameters, which may become outdated. | |||
* Their knowledge is static, limited to the training corpus. | |||
* They lack direct access to external knowledge sources during inference. | |||
As a result, even the most powerful models may fail to answer factual questions reliably, especially when dealing with rare or time-sensitive topics. | |||
=== Limitations of Parametric Knowledge === | |||
Traditional LLMs rely solely on parametric memory—i.e., knowledge encoded in weights. This approach has several key limitations: | |||
* '''Scalability''' – Retraining a model to update its knowledge is expensive and slow. | |||
* '''Transparency''' – It is hard to trace the origin of a generated fact. | |||
* '''Updatability''' – Knowledge becomes stale quickly in dynamic domains like news or medicine. | |||
These issues become critical in open-domain question answering, where users expect accuracy, citation, and timeliness. | |||
=== The Promise of Retrieval-Augmented Generation === | |||
Retrieval-Augmented Generation (RAG) aims to solve these problems by separating '''retrieval''' from '''generation'''. | |||
Instead of generating from memory alone, RAG models: | |||
* Accept a query | |||
* Retrieve relevant documents from an external knowledge source (e.g., Wikipedia, search engine, vector DB) | |||
* Generate a response grounded in those documents | |||
This offers several advantages: | |||
* Reduced hallucinations – Answers are supported by retrieved evidence. | |||
* Updatable knowledge – The retrieval index can be updated without retraining. | |||
* Improved interpretability – Retrieved sources can be cited directly. | |||
* Efficient scaling – Small models can perform well with strong retrieval. | |||
This separation between knowledge access and text generation introduces a new paradigm that is more modular, flexible, and robust for real-world applications. | |||
== What is Retrieval-Augmented Generation == | |||
RAG combines a retriever and a generator. Given a query, the retriever fetches relevant documents from a knowledge base, and the generator uses them to produce grounded responses. This architecture bridges retrieval-based QA and language generation. | |||
=== Core Definition === | |||
Retrieval-Augmented Generation (RAG) is a hybrid framework that integrates information retrieval into the generation pipeline of language models. Instead of relying solely on internal parametric memory, a RAG system: | |||
* Retrieves external documents relevant to a given query | |||
* Conditions the generation process on the retrieved evidence | |||
This enables models to access current, specific, and factual knowledge at inference time. | |||
RAG is not a single architecture but a general paradigm. It can be combined with various retrievers (e.g., dense or sparse) and generators (e.g., GPT-style models) to suit different applications such as question-answering, summarization, and fact-grounded dialogue. | |||
=== Key Components === | |||
A typical RAG system consists of two modules: | |||
* '''Retriever''' Takes a query and retrieves the most relevant documents from an external corpus, such as Wikipedia or a search engine. This can be a dense retriever (like Contriever or DPR) or a sparse one (like BM25). | |||
* '''Generator''' Given the query and retrieved documents, the generator produces an answer that ideally reflects and integrates the retrieved content. It is usually a pre-trained language model such as T5, BART, or GLM. | |||
This structure allows knowledge to flow from the retriever to the generator, enhancing factual correctness and grounding. | |||
=== Retrieval vs. Parametric Generation === | |||
The core contrast between RAG and the traditional generation lies in how knowledge is accessed: | |||
* Parametric LMs are generated based on internal representations learned during pretraining. | |||
* RAG explicitly pulls in external evidence for each query. | |||
This means RAG can stay up-to-date, offer transparent answers, and dynamically adapt to user input without needing retraining. | |||
=== A Practical Example === | |||
The concept of RAG is embodied in real-world systems like '''Perplexity.ai''', a web-based chatbot that: | |||
* Issues live search queries | |||
* Aggregates results from real web documents | |||
* Generates fluent answers with clickable citations | |||
Perplexity.ai demonstrates the practical use of RAG in open-domain QA. It incorporates real-time retrieval with fluent generation, offering citeable, source-aware answers in an interactive system. This setup illustrates how RAG can be deployed for scalable, user-facing knowledge access with human-readable and traceable output. | |||
== WebGLM: Efficient Web-Enhanced Question Answering == | |||
=== Overview and Objectives === | |||
WebGLM is a web-enhanced question-answering system designed to solve one of the biggest limitations of large language models (LLMs) which is '''the lack of up-to-date or rare external knowledge'''. Traditional '''“closed-book”''' models like GPT-3 that rely solely on pre-trained parameters, but WebGLM integrates real-time web search to generate accurate, long-form, and well-cited answers. | |||
The system is built on the General Language Model (GLM), specifically a 10-billion-parameter version (GLM-10B). It improves the base model by adding three key features: | |||
* A '''retriever''' that collects relevant web content, | |||
* A '''generator''' that synthesizes answers according to those references, | |||
* A '''human preference-aware scorer''' that ranks answers according to what users prefer. | |||
This design allows WebGLM to achieve accuracy, efficiency, and cost-effectiveness advantages over similar systems like WebGPT. Specifically, it performs better than WebGPT (13B) and nearly matches WebGPT (175B) in human evaluation, all while using far fewer resources. WebGPT, rely heavily on costly expert annotations and slow browser simulations but WebGLM is optimized for '''efficiency and cost-effectiveness''', and minimizes the need for manual annotation. It introduces practical strategies that allow for rapid response times, with more than 90% of queries processed in under 10 seconds. Another key aspect of WebGLM is its focus on '''human-aligned answer generation'''. Instead of expert ranking, the system learns from real user feedback—for example, upvotes on QA forums like Reddit, to guide what a good answer is. | |||
To better understand, look at Figure 1. It illustrates a typical output from WebGLM: a user asks “Why do people try to maintain eye contact while communicating?” and receives a well-organized, properly cited answer generated in real-time based on live web results. | |||
[[File:WebGLM1.png|500px|thumb|center|Fiure1) WebGLM’s response to an example question]] | |||
To summarize, the key objectives of WebGLM are: | |||
* To augment LLMs with real-world information via the web. | |||
* To minimize the use of expensive human annotation. | |||
* To produce long-form, citation-rich answers that are aligned with human preferences. | |||
And to do so efficiently, so that the system is practical for real-world use. | |||
=== WebGPT === | |||
'''WebGPT''' is a question-answering model developed by OpenAI, extending GPT-3 to browse the web for answering open-ended queries. Introduced in 2021, it simulates human research by submitting search queries, following links, and citing sources, enhancing factual accuracy over static language models. | |||
==== Methodology ==== | |||
WebGPT operates in a text-based web-browsing environment, using the Microsoft Bing Web Search API for document retrieval. It was fine-tuned via imitation learning, mimicking human research behavior, followed by reinforcement learning with human feedback to optimize answer quality. A key component is dense passage retrieval (DPR), where the probability of a passage given a query is modeled as: | |||
:<math>p(\text{passage} \mid \text{query}) \propto \exp(\text{embed}(\text{passage}) \cdot \text{embed}(\text{query}))</math> | |||
This contrastive objective maximizes similarity for relevant passage-query pairs. The model, scaled up to 175 billion parameters, uses best-of-64 sampling for high-quality outputs. | |||
==== Results ==== | |||
WebGPT was evaluated on the ELI5 dataset, showing strong performance in long-form question-answering. The table below summarizes key metrics. | |||
{| class="wikitable" style="text-align:center;" | |||
|+ WebGPT Performance on ELI5 | |||
! Metric !! Value !! Notes | |||
|- | |||
| Human Preference vs. Demonstrations || 56% || Preferred over human research demos | |||
|- | |||
| Human Preference vs. Reddit Answers || 69% || Outperformed highest-voted ELI5 answers | |||
|- | |||
| TruthfulQA Improvement || Higher || Better than GPT-3, especially at 175B | |||
|- | |||
| Reward Model Score Gain || +0.13 || From doubling demonstration data | |||
|- | |||
| Reward Model Accuracy Gain || +1.8% || From doubling comparison data | |||
|} | |||
These results highlight WebGPT’s ability to generate accurate, verifiable answers, with larger models excelling in truthfulness and user preference. | |||
==== Limitations ==== | |||
WebGPT, despite its advancements in web-assisted question-answering, faced several constraints that highlighted the need for improved models like WebGLM. | |||
* '''Dependence on Human Feedback''': The model’s reliance on human demonstrations and feedback for fine-tuning made training resource-intensive. Scaling to diverse query types was limited by the availability of high-quality human annotations, often requiring thousands of comparisons to achieve modest gains (e.g., 1.8% accuracy boost from doubled comparisons). | |||
* '''Web Retrieval Inefficiencies''': Using the Bing Web Search API restricted WebGPT to predefined search results, sometimes missing niche or real-time information. The dense passage retrieval approach struggled with ambiguous queries, leading to irrelevant citations or incomplete answers. | |||
* '''Factual Inconsistencies''': WebGPT occasionally produced inaccurate responses, especially for affirming questions, where it was less likely to refute incorrect assumptions. This was evident in evaluations showing higher error rates on certain query stances. | |||
* '''Scalability Challenges''': The 175B parameter model demanded significant computational resources, with best-of-64 sampling increasing inference time. Smaller models (e.g., 760M) underperformed, limiting deployment in resource-constrained settings. | |||
* '''Limited Multimodal Integration''': WebGPT was confined to text-based web browsing, unable to process images or other media, which restricted its ability to handle queries requiring visual context (e.g., "describe a painting"). | |||
=== Essential Background & Inspiration=== | |||
The construction of web-enhanced QA systems is a systematic project that requires cross-domain collaboration. To understand the contribution of WebGLM, we need to first look at them so here we briefly introduce them. | |||
==== 1) Large Language Models (LLMs) ==== | |||
Modern LLMs like GPT-3, PaLM, OPT, and GLM-130B are trained on massive corpora in a self-supervised way. They have shown good performance in various tasks, from translation to summarization and question answering. | |||
A critical ability of LLMs is in-context learning, where the model is guided by examples within the prompt, instead of retraining. This allows them to transfer skills across tasks with no fine-tuning. '''WebGLM extensively uses ICL in its generator and data bootstrapping phases.''' | |||
==== 2) Open-Domain Question Answering (Open QA) ==== | |||
Traditional datasets like SQuAD assumes a fixed context, but '''open-domain QA''' works with real-world questions where relevant context must be retrieved dynamically. Classic datasets include: | |||
* '''Natural Questions''': from Google search, answered using Wikipedia. | |||
* '''WebQuestions''': from Freebase. | |||
* '''MS MARCO''': QA over passages with binary labels. | |||
Most of the models in this field focus on short answers, but users often expect long-form explanations with references and this need is something WebGLM try to address. | |||
==== 3) Retrieval-Augmented Generation (RAG) ==== | |||
RAG systems combine a retriever and a generator. Classic retrieval models include: | |||
* Sparse methods: TF-IDF, BM25. | |||
* Dense methods: DPR, Contriever. | |||
WebGLM is inspired by systems like REALM, RAG, FiD, and Atlas, which jointly train retrieval and generation. However, WebGLM’s key innovation is its use of LLMs to augment a small dense retriever without retraining the LLM at runtime—making it fast and efficient. | |||
==== 4) Reinforcement Learning from Human Feedback (RLHF) ==== | |||
Systems like WebGPT and InstructGPT use RLHF to align models with human values. But RLHF is expensive, because it requires: | |||
* Expert-written answers, | |||
* Pairwise ranking by humans, | |||
* Iterative fine-tuning with policy gradients. | |||
WebGLM sidesteps this by training a scorer on crowdsourced human signals, specifically, Reddit thumbs-ups—offering a scalable and effective alternative. | |||
=== System Overview and Architecture === | |||
Ok, we got familiar with the background, let’s now look at the overall structure of WebGLM. Constructing an LLM-based web-enhanced QA system can be expensive and challenging. The web information is rich but noisy for certain queries, and creating high-quality human answers with references for training can be outrageously expensive. | |||
To address these challenges, WebGLM suggests a practical, modular solution which has three tightly connected components: the Retriever, the Generator, and the Scorer. Each plays a critical role in ensuring that the system is accurate, efficient, cost-effective, and aligned with human expectations. Figure 2 shows these modules togehter. | |||
[[File:pipeline.png|700px|thumb|center|Figure 2) WebGLM system pipeline]] | |||
====Retriever Module: From Web Search to Clean Context==== | |||
The first component in the WebGLM is the Retriever. This module recognizes relevant informations from the web for any givn question. This process has two stages: | |||
''' (a) Coarse-Grained Web Search ''' | |||
In the first stage, WebGLM sends the user’s query to a third-party web search engine (like the Google Search API). Then, It retrieves a list of top-ranked URLs, usually fewer than 10. Then, it follows below steps: | |||
* '''Fetch''': Crawls and downloads the HTML content of these URLs. | |||
* '''Extract''': Converts HTML into clean, plain text using html2text. | |||
* '''Split''': Breaks the page content in to paragraphs and they will be used as candidats for final selection. | |||
This entire process is optimized for speed using asynchronous parallel crawling. For example, instead of loading one page at a time (which might take over 2 minutes), WebGLM loads all pages in parallel and finishing 90% of retrievals in under 10 seconds. Figure3 shows this better. | |||
[[File:retriever_time.png|400px|thumb|center|Figure3) WebGLM retriever time analysis]] | |||
''' (b) Fine-Grained LLM-Augmented Retrieval ''' | |||
Now, at this stage, WebGLM has collected a big set of candidat paragraphs from various web pages. But, all of them are not useful or directly relevant to the question. So we need to refine the pool. For doing so, WebGLM uses a dense retriever called '''Contriever''', which is designed to encode both questions and passages into dense vector embeddings and rank them based on similarity. Traditional sparse retrieval methods like BM25, rely on keyword overlap, but Contriever can identify semantically related text, even when the exact words don’t match. | |||
But, Contriever in its vanilla form still has limitations and it doesn’t always prioritize the most contextually appropriate references. To improve this, WebGLM incorporates a trick: it fine-tunes Contriever using reference adoption patterns learned from GPT-3 through in-context learning. This process uses GPT-3’s natural ability to cite relevant information when answering questions, using it as a proxy teacher. | |||
This approach is very effective. In a benchmark of 200 sampled queries, the original Contriever was able to select relevant references with 68.6% accuracy, while GPT-3 using ICL achieved a much higher 90.2% accuracy. By training Contriever to imitate GPT-3’s citation behavior, which evaluated using ROUGE-1 precision scores, WebGLM successfully transfers high-quality reference selection abilities to a smaller, more efficient retriever that can operate at scale and speed. See Table 1 for these reference adoption results | |||
[[File:Evaluation.png|300px|thumb|center|Table1) Evaluation on LLM’s reference adoption]] | |||
This LLM-augmented retriever becomes a critical component of WebGLM, enabling precise, low-latency filtering of noisy web content and ensuring that the Generator receives only the most relevant and trustworthy paragraphs to base its answers on. | |||
==== Generator Module: Long-Form Answers with References ==== | |||
When the top-5 reference paragraphs have been retrieved and filtered, then WebGLM uses its 10-billion-parameter language model, GLM-10B, to generate long-form answers. These answers are not only fluent and informative but also include inline ctations. this is similar to how academic writing references source material. This is important in real-world applications to ensuring factual accuracy and trustworthiness. | |||
One of the novel aspects of WebGLM is that it avoids relying on expensive, expert-annotated training data. Instead, it bootstraps its training set using in-context learning with GPT-3. In this process, WebGLM feeds GPT-3 a prompt that includes a user question and a small set of retrieved references. GPT-3 then generates a full, long-form answer that includes direct quotations with reference markers. This bootstrapping process is used in a large corpus of questions, specifically, 83,000 entries sampled from the ELI5 dataset, to generate a diverse and extensive set of question-answer-reference triplets. | |||
However, because GPT-3 occasionally produces citation errors, such as quoting the wrong reference or hallucinating sources, WebGLM implements a citation correction step to improve data reliability. Each generated answer is broken into segments, and the system verifies whether the cited sources are appropriate for the content. This is done by using a ROUGE-1 precision similarity function to compare each answer segment <math>s_i</math> against all retrieved references <math>r</math>. If a reference has a sufficiently high similarity score with a sentence, it is going to be considered a valid citation. Formally, this is expressed as: | |||
<math> \mathcal{V}_i = \left\{ r \mid f(s_i, r) \ge T \right\}, \quad r \in \mathcal{R} </math> | |||
Here, <math>f(s_i, r)</math> is the ROUGE-1 precision scor between the segment and the refferenc, <math>T</math> is an empirical threshold set to <math>0.57</math>, and <math> \mathcal{V}_i </math> is the set of valid references for sentence <math>s_i</math>. This method ensures that only accurate and semantically aligned references are retained during training. | |||
According to citation correction, WebGLM uses additional filtering to ensure dataset quality. It removes samples that contain hallucinated content not grounded in any references, answers with too few citations, or answers with invalid citation formatting. After this filtering step, the original 83,000 bootstrapped examples are narrowed down to 45,000 high-quality question-answer-reference triplets. This refined dataset is then used to fine-tune the GLM-10B model. this forms the backbone of WebGLM’s answer generation module. | |||
This generator design enables WebGLM to deliver long-form, referenced answers with high factual accuracy, without the labor-intensive cost of expert supervision. | |||
==== Scorer Module: Learning Human Preferences Without RLHF ==== | |||
WebGPT uses reinforcement learning from expert feedback (RLHF), but WebGLM trains its answer selector using crowdsourced feedback. Specifically the number of upvotes on QA foroms like Reddit. The idea is simple: if many users preferred a particular answer, it likely reflects human-aligned quality. | |||
To collect this data, WebGLM crawls Reddit QA threads and filters the examples to ensure high signal quality. Only answers with at least <math>3</math> upvotes are saved and retained, and each qualifying question must have a minimume of <math>8</math> candidat answers. To reduce length-related biases, long responses are Shortened, and extremely short answers are ignored. From this filtered pool, the authors construct pairwise comparison data by selecting pairs of answers with large ranking gaps, e.g., a top-ranked answer versus a much lower one. This results in a dataset of approximately <math>249{,}000</math> contrastive answer pairs, of which <math>230{,}000</math> are used for training and <math>19{,}000</math> for evaluation. | |||
The scoring model itself is a 6-billion-parameter GLM trained to predict a scalar value for each candidate answer. Training begins with supervised fine-tuning using Reddit TL;DR data, after that the model is optimized via a pairwise ranking loss to ensure that better answers consistently receive higher scores than their lower-quality counterparts. To prevent overfitting, the authors freeze the bottom 70% of transformer layers and apply regularization strategies during training. | |||
The output of this scorer is used to select the highest-quality answer from a set of candidates generated by the GLM-10B model. According to their results, the model’s scores correlate strongly with real user preferences, and this shows that WebGLM can effectively approximate RLHF using only implicit human signals, without the need for expensive manual annotations. | |||
=== Retriever Module: === | |||
* '''Coarse-Grained Web Search:''' Uses standard web search APIs to retrieve candidate URLs, fetches corresponding web pages, and extracts textual content rapidly. | |||
* '''Fine-Grained LLM-Augmented Retrieval:''' Enhances a dense retriever (like Contriever) via in-context learning, enabling the model to adopt only relevant references, thus improving accuracy and efficiency. | |||
=== Generator Module: === | |||
The answer generator is based on the GLM-10B model and is fine-tuned on a bootstrapped dataset of long-form, quoted QA samples. | |||
* '''Bootstrapped Data Generation:''' Employs few-shot in-context learning with a small set of high-quality examples to automatically generate a large dataset of long-form, quoted QA pairs. | |||
* '''Citation Correction:''' Applies correction techniques based on similarity metrics (e.g., Rouge‑1) to ensure that each quoted segment accurately corresponds to its web reference. | |||
* '''Efficient Answer Synthesis:''' This setup enables the generator to produce coherent, well-referenced answers without relying on expensive expert annotations. | |||
=== Data Bootstrapping and Preference Scoring: === | |||
* '''Automated Data Bootstrapping:''' WebGLM leverages the in-context learning ability of large language models (e.g., GPT-3) to automatically generate a large pool of QA pairs. The resulting dataset, which initially contains many noisy samples, is then filtered-using automatic metrics and citation checks-to extract a high-quality subset for training. | |||
* '''Human Preference-Aware Scoring:''' Instead of relying solely on expert feedback, the system trains a scorer using real user feedback (such as upvotes from online QA forums). This scorer is designed to evaluate multiple aspects of generated answers (fluency, correctness, citation accuracy, etc.) and rank them so that the final output aligns with human quality preferences. | |||
=== Limitations and Future Directions === | |||
Despite its promising performance, WebGLM faces several challenges that open avenues for future work. First, the system’s reliance on web retrieval can introduce variability in response time and quality; network delays and inconsistent web content may sometimes lead to outdated or imprecise answers. In addition, although the bootstrapped generator benefits from LLM in-context learning, the process of citation correction and filtering is not foolproof—incorrect or missing citations may still occur, affecting the factual grounding of generated answers. Moreover, the human preference-aware scorer, trained on online forum feedback, might not always reflect broader user expectations due to inherent biases in the source data. Future work may focus on improving retrieval efficiency through more robust asynchronous techniques, enhancing dataset quality by incorporating richer multi-turn or multi-reference contexts, and refining the scoring mechanism with more diverse and calibrated human feedback. These enhancements could further bridge the gap between rapid web retrieval and high-quality, factually accurate answer generation. | |||
== Interleaving Retrieval with Chain-of-Thought Reasoning == | |||
===Introduction & Motivation=== | |||
Large language models excel at many tasks but still struggle with complex, multi‑step questions that require up‑to‑date or aggregated information. Traditional chain‑of‑thought (CoT) prompting helps by breaking reasoning into steps, and retrieval augmentation brings in external documents, but neither alone reliably handles queries needing facts from multiple sources. To address this, the authors propose IRCoT (Interleaved Retrieval with Chain‑of‑Thought), which alternates between generating a CoT step and using that step as a new retrieval query—iterating until an answer emerges. This tight feedback loop lets the model iteratively refine its understanding and gather the most relevant evidence, improving retrieval recall by up to 22 points and downstream QA F1 by up to 15 points over one‑shot retrieval on multi‑step benchmarks (HotPotQA, 2WikiMultihopQA, MuSiQue, IIRC). It works out‑of‑the‑box with both GPT‑3 and much smaller Flan‑T5 models (no fine‑tuning required) and cuts factual errors in generated CoTs by up to 50 %, yielding more accurate, reliable answers for open‑domain, multi‑hop question answering. | |||
===Background: Standard Retrieval vs. Interleaving=== | |||
A straightforward way to augment an LLM with outside knowledge is to do the following: | |||
1. Retrieve a set of documents based on the user’s question (one-step retrieval). | |||
2. Concatenate those documents with the original question. | |||
3. Prompt the large language model to answer, possibly with chain-of-thought. | |||
While this approach works well for simple or straightforward questions, it has problems with more complex, multi-step queries. Why? Because the system doesn’t know ahead of time which facts or key terms will come up during the model’s partial reasoning. If the first round of retrieval misses an important piece of text, there’s no opportunity to fix that mistake later. | |||
In contrast, IRCoT goes back and forth between finding new documents and building the chain-of-thought. The chain-of-thought is actually used as a new search query. For example, if it says “this item was created by a company named X,” the retriever then looks for more information about “company X.” This method is more flexible, similar to how a person might research a question by reading some information, noticing new keywords, and then doing another focused search. | |||
===The IRCoT Approach=== | |||
====Overall Method==== | |||
The IRCoT pipeline works in several steps: | |||
'''1. Initial Retrieval Step:''' | |||
The process starts with the user’s question <math>Q</math>. A standard search engine (like BM25) or another retrieval method is used to fetch an initial set of documents. Let’s call these documents: <math display="block">D_1, D_2, \ldots, D_k</math> | |||
'''2. Reason Step:''' | |||
The language model is given: | |||
*The question <math>Q</math> | |||
*The chain-of-thought generated so far (initially empty) | |||
*The documents retrieved so far | |||
Using this information, the model is asked to generate one more sentence of reasoning. This new sentence is denoted as: <math display="block">s_i</math> | |||
'''3. New Retrieval Step:''' | |||
The model treats the newly generated sentence <math>s_i</math> (sometimes combined with the original question <math>Q</math>) as a new search query. The retrieval system then fetches up to <math>k</math> new documents that match this sentence. These new documents are added to the existing set of retrieved documents. | |||
'''4. Iteration and Stopping:''' | |||
Steps 2 and 3 are repeated: the model keeps extending the chain-of-thought, and new documents keep getting added. This loop continues until one of the following conditions is met: | |||
*The model produces a sentence like “The answer is …,” indicating it has reached a final answer, or | |||
*A maximum number of steps (e.g., 8 rounds) is reached. | |||
After the loop finishes, the complete set of retrieved documents is passed to a question-answering module. This final module, either using chain-of-thought or a direct answer prompt, reads all the information and produces a concise answer. | |||
====Prompt Design==== | |||
IRCoT uses few-shot learning with example prompts. Each example includes: | |||
*A short question (e.g., “In what country was Lost Gravity manufactured?”) | |||
*A small set of related paragraphs (including correct ones and possibly some irrelevant ones) | |||
*A detailed chain-of-thought that explains how to reason through those paragraphs step by step | |||
These examples teach the language model both how to reason using specific parts of the text and when to retrieve new documents based on partial reasoning. | |||
====Formal Structure (Like Pseudocode)==== | |||
We can describe IRCoT’s loop in a more structured format: | |||
'''Initialization:''' | |||
<math display="block">C \leftarrow \{ \}; \quad R \leftarrow \text{Retrieve}(Q)</math> | |||
* <math>C</math> is the chain-of-thought built so far | |||
* <math>R</math> is the current set of retrieved documents | |||
At each step <math>i</math>: | |||
'''Reason:''' | |||
<math display="block">s_i = \text{LM}(Q, R, C)</math> | |||
The language model (LM) takes in the question <math>Q</math>, the documents <math>R</math>, and the current chain-of-thought <math>C</math>, and generates a new sentence <math>s_i</math>. Add this sentence to the chain-of-thought: | |||
<math display="block">C \leftarrow C \cup \{ s_i \}</math> | |||
'''Retrieve:''' | |||
<math display="block">R \leftarrow R \cup \text{Retrieve}(s_i)</math> | |||
In other words, the new sentence <math>s_i</math> is used as a search query, and the resulting documents are added to <math>R</math>. | |||
'''Stopping Condition:''' | |||
Stop if the new sentence includes a phrase like “the answer is…” or if the maximum number of steps is reached. | |||
This loop shows how IRCoT builds up reasoning step-by-step, using each new piece of information to improve both the search results and the next part of the reasoning chain. | |||
===Experimental Setup=== | |||
====Datasets==== | |||
The paper evaluates IRCoT using four well-known multi-step question answering datasets: | |||
*'''HotpotQA:''' A dataset focused on multi-hop reasoning, where each question usually requires combining information from two separate Wikipedia articles. | |||
*'''2WikiMultihopQA:''' Similar to HotpotQA, but specifically designed to ensure that answering each question involves connecting two related Wikipedia pages. | |||
*'''MuSiQue:''' A newer dataset built to require multiple reasoning steps. In some cases, more than two pieces of evidence must be linked together to answer the question. | |||
*'''IIRC:''' Each question is based on a main passage, but answering it requires looking at other linked Wikipedia pages to find the needed information. | |||
For all of these datasets, the paper uses an open-domain setting. This means the model is not given just the correct paragraphs, instead, it must search for the relevant information from a large collection of Wikipedia articles. | |||
====Compared Methods==== | |||
The paper compares IRCoT with two baseline methods: | |||
*'''NoR QA:''' A simple baseline that does no retrieval at all. It relies only on the language model’s built-in knowledge (its parametric memory). | |||
*'''OneR QA:''' A method that performs one retrieval step using the question. It then passes both the question and the retrieved documents to the language model for answering. | |||
*'''IRCoT QA:''' The method proposed in the paper. It uses iterative retrieval, adding new information after each reasoning step in the chain-of-thought. | |||
The results are measured using: | |||
1. Document recall: How many of the relevant documents were successfully retrieved by the end. | |||
2. Answer accuracy or F1 score: How well the model answered the questions. | |||
The experiments show that IRCoT significantly improves performance on multi-step questions compared to both baselines. | |||
===Why It Matters=== | |||
The significance of interleaving retrieval with chain-of-thought reasoning lies in its capacity to improve multi-step question answering by iteratively refining reasoning and evidence gathering. By enabling the retrieval of more contextually relevant information at each step, the approach enhances retrieval recall and factual accuracy, thereby reducing model hallucination and yielding more reliable, evidence-based reasoning. This advancement addresses the inherent limitations of traditional one-shot retrieval methods and offers a scalable, adaptable solution for complex, knowledge-intensive tasks—an achievement with important implications for applications in research, decision support, and any domain that demands precise, contextual understanding. | |||
===Key Findings=== | |||
*Better Retrieval: IRCoT finds the right supporting documents more reliably than one-shot methods, with 10–20% higher recall of gold paragraphs. | |||
*Improved QA Accuracy: It outperforms both baselines on standard metrics (Exact Match and F1), often by 5–10+ points. For example, in HotpotQA, it can follow multiple steps (e.g., finding a roller coaster’s manufacturer, then their country) to get the right answer. | |||
*Fewer Mistakes: IRCoT reduces false or made-up facts (hallucinations) by grounding each reasoning step in real documents, cutting factual errors by up to 40–50%. | |||
*Works Across Model Sizes: Even smaller models using IRCoT can beat much larger models that use basic retrieval. It also performs well on new datasets without custom examples, showing strong generalization. | |||
===Limitations and Future Directions=== | |||
The proposed IRCoT framework demonstrates notable improvements over one-step retrieval methods on multi-step open-domain question answering; however, several limitations persist. The method relies on the base language model possessing effective zero-shot or few-shot chain-of-thought generation capability—a strength largely confined to very large models—which restricts its applicability to smaller-scale models. In addition, the approach requires the language model to handle long input sequences in order to integrate multiple retrieved paragraphs and demonstration examples. The iterative process, with separate language model calls for each reasoning step, incurs additional computational cost, potentially impacting efficiency in real-world deployments. Future research should consider strategies for dynamic decision-making regarding when to retrieve additional information, methods for compressing or efficiently ranking retrieved content, and techniques that enhance chain-of-thought robustness in out-of-distribution settings. | |||
== Iterative Retrieval-Generation Synergy (Iter-RetGen) == | |||
Iterative Retrieval‑Generation Synergy (ITER‑RETGEN) introduces a simple yet powerful loop between retrieval and generation that yields substantial quality gains with minimal overhead. It first retrieves documents based on the original query, prompts an LLM to generate an initial answer, and then concatenates that answer with the query to guide a second, more focused retrieval—using the newly fetched documents to produce a refined response. Unlike prior methods that interleave retrieval within a single generation pass, ITER‑RETGEN processes all retrieved context at once, preserving flexibility in the generation stage while still benefiting from multi‑step knowledge gathering. Evaluated on multi‑hop QA benchmarks (HotPotQA, 2WikiMultiHopQA, MuSiQue, Bamboogle), fact verification (Feverous), and commonsense reasoning (StrategyQA), it achieves up to an 8.6 % absolute improvement over state‑of‑the‑art retrieval‑augmented baselines under few‑shot chain‑of‑thought prompting. Furthermore, by distilling generation‑informed relevance judgments from a re‑ranker into a dense retriever, the method further boosts performance while reducing the number of retrieval‑generation iterations required. | |||
=== Motivation === | |||
Retrieval-augmented generation (RAG) methods aim to mitigate the limitations of large language models (LLMs)—such as outdated knowledge and hallucinations—by incorporating external information from retrieved documents. However, most existing techniques rely on one-time retrieval based solely on the initial input query. This often falls short for complex tasks like multi-hop question answering, where queries require holistic reasoning across multiple knowledge pieces. | |||
Additionally, interleaved methods like ReAct and Self-Ask tightly bind retrieval with generation during each output step, requiring multiple retrieval calls (3–5 per query) and constraining generation flexibility. These approaches incrementally process retrieved content and are not designed to collectively utilize all retrieved information in the generation phase. | |||
To overcome these limitations, the authors propose '''Iter-RetGen''', a simple yet effective framework that decouples retrieval and generation structurally while maintaining synergy between them. It leverages intermediate generations as feedback signals to refine subsequent retrievals, resulting in iterative improvements in both relevance and answer quality. | |||
[[File:ITER-RETGEN iterates retrieval and generation.jpg|750px|ITER-RETGEN iterates retrieval and generation]] | |||
=== Method === | |||
Iter-RetGen operates through a synergistic loop of retrieval and generation, following these steps: | |||
# In the initial iteration, knowledge is retrieved based on the task input (e.g., a question). | |||
# An LLM generates a response using this retrieved knowledge. | |||
# The generated output is then used as additional context for the next retrieval round, guiding the retriever toward more relevant or missing knowledge. | |||
# The newly retrieved knowledge is again used to generate a refined response. | |||
# This process is repeated for a fixed number of iterations (e.g., T = 2–4). | |||
This structure enables holistic knowledge integration in each generation step, unlike interleaved approaches that only use partial retrievals at each stage. Iter-RetGen also maintains generation flexibility by avoiding structural constraints on prompt formatting or fixed retrieval patterns. | |||
=== Generation-Augmented Retrieval Adaptation === | |||
To further improve retrieval quality, Iter-RetGen incorporates a method called '''generation-augmented retrieval adaptation'''. This uses the generation outputs to inform a re-ranker, which then distills its knowledge into a dense retriever. | |||
* Dense Retriever Parameters: <math>\theta = \{\theta_q, \theta_d\}</math> | |||
* Similarity Score: <math>s_\theta(q,d)=\left\langle E(q;\theta_q),E(d;\theta_d)\right\rangle</math> | |||
* Re-ranker Score: <math>s_\phi(q,d)</math> | |||
* Knowledge Distillation Objective: | |||
<math>\theta_q^*=arg\min_{\theta_q}\mathrm{~KL}(P_\phi(\cdot|y_1,q),P_\theta(\cdot|q))</math> | |||
where | |||
<math>P_\phi(d|y_1,q)=\frac{\exp(s_\phi(y_1||q,d)/\tau)}{\sum_{d^{\prime}\in\mathcal{D}_{y_1}||q}\exp(s_\phi(y_1||q,d^{\prime})/\tau)}</math> | |||
and | |||
<math>P_\theta(d|q)=\frac{\exp(s_\theta(q,d)/\tau)}{\sum_{d^{\prime}\in\mathcal{D}_{y_1}||q}\exp(s_\theta(q,d^{\prime})/\tau)}</math> | |||
This distillation process aligns the retriever's output distribution with that of the re-ranker, significantly boosting retrieval relevance and performance with fewer iterations. | |||
=== Simplicity and Efficiency === | |||
Iter-RetGen is conceptually simple, requiring minimal architectural changes or complex prompt engineering. It efficiently balances performance and cost by reducing the number of API calls and total retrieved documents. For example, with just two iterations and five paragraphs retrieved per iteration, Iter-RetGen can outperform other retrieval-augmented methods that require more resources. | |||
[[File:Average numbers of API calls.jpg|700px|Average numbers of API calls]] | |||
=== Experiments and Results === | |||
The authors evaluated Iter-RetGen across six datasets involving multi-hop QA, fact verification, and commonsense reasoning. The method consistently outperformed strong baselines such as Direct Prompting, Chain-of-Thought (CoT), ReAct, Self-Ask, and DSP. Using text-davinci-003 as the LLM and Contriever-MSMARCO for retrieval, Iter-RetGen achieved: | |||
* Up to 8.6% higher accuracy on HotPotQA compared to Self-Ask. | |||
* 73.4% accuracy in just four iterations. | |||
* Up to 75.7% accuracy with generation-augmented retriever adaptation. | |||
Notably, Iter-RetGen required fewer retrieval steps and API calls, demonstrating superior cost-efficiency. Traditional metrics like Exact Match (EM) often underestimated its true performance, but human-aligned accuracy (Acc†) revealed its ability to produce semantically correct answers despite surface form differences. | |||
Ablation studies showed that generation-augmented retrieval is critical, increasing answer recall by 16–25% in later iterations. Case studies highlighted the model's self-correction ability, such as fixing an error about arena seating capacity after retrieving better contextual information. | |||
=== Limitations and Future Directions === | |||
While Iter-RetGen achieves strong performance, it relies heavily on the chain-of-thought capabilities of large LLMs, limiting its applicability to smaller or less capable models. The iterative approach also incurs overhead due to multiple retrieval and generation steps, though it is still more efficient than some interleaved methods. | |||
Future work includes: | |||
* Adaptive iteration strategies to dynamically determine the optimal number of retrieval-generation steps. | |||
* Enhancing prompt-specific optimization for better use of parametric and non-parametric knowledge. | |||
* Expanding evaluations to long-form generation and other complex reasoning tasks. | |||
Overall, Iter-RetGen sets a new standard for iterative retrieval-augmented generation by achieving both efficiency and effectiveness in complex information-seeking tasks. | |||
== Graph-RAG for Document Set Summarization == | |||
The paper introduces GraphRAG, a novel approach that uses graph-based retrieval-augmented generation to answer broad, global questions about large text collections. It proposes a graph-based extension to RAG that enables global context modeling across documents, improving performance on query-specific summarization tasks. | |||
=== Introduction and Motivation === | |||
While retrieval-augmented generation (RAG) is effective for answering fact-based or localized questions, it struggles with '''global questions'''—broad, sensemaking questions that require synthesizing themes or trends across an entire corpus. Examples include: | |||
* “What are the key trends in health policy over the last decade?” | |||
* “How do tech leaders perceive government regulation in podcasts?” | |||
Such questions require a level of holistic understanding that vector-based RAG systems (which retrieve semantically similar chunks) cannot provide. These systems work well for narrow queries but break down when the answer isn’t confined to a few passages. | |||
'''GraphRAG''' addresses this limitation by constructing a knowledge graph from the corpus and using it to support hierarchical summarization. This transforms the task into one that is less about retrieving matching passages and more about building a structured understanding of content relationships. | |||
===Methodology=== | |||
[[File:GraphRAG_architecture.png|400px]] | |||
The graph above shows the architectural overview of GraphRAG and can be broken down into the following procedure: | |||
'''Source Documents → Text Chunks''' | |||
Documents are split into manageable text chunks. The chunk size is a trade-off: larger chunks reduce the number of LLM calls but may miss finer-grained details. | |||
'''Text Chunks → Entities & Relationships''' | |||
From each chunk, the LLM extracts key entities and their relationships. These are then converted into node and edge candidates for a knowledge graph. | |||
'''Entities & Relationships → Knowledge Graph''' | |||
Multiple extractions across the corpus are merged into a weighted knowledge graph. Edge weights correspond to how frequently a relationship appears. Claims—statements of verifiable facts—are also extracted. | |||
'''Knowledge Graph → Graph Communities''' | |||
Using the Leiden community detection algorithm, the graph is partitioned into coherent thematic communities in a hierarchical structure. | |||
'''Graph Communities → Community Summaries''' | |||
Each community is summarized independently using the LLM, and summaries at higher levels recursively incorporate lower-level summaries. These summaries act as a condensed representation of the source corpus. | |||
'''Community Summaries → Community Answers → Global Answer''' | |||
When a question is asked, each community provides a partial answer. These are scored by helpfulness, then aggregated using a map-reduce approach to generate the final global answer. | |||
===Evaluation Process=== | |||
To evaluate GraphRAG, the authors developed a novel benchmark for global sensemaking questions by: | |||
* Generating user personas (e.g., journalist, educator). | |||
* Defining realistic tasks for each persona. | |||
* Asking the LLM to generate global questions for each (e.g., “How is public health discussed in news?”). | |||
Then, answers from GraphRAG and baseline methods were compared using the '''LLM-as-a-judge''' technique based on three criteria: | |||
* '''Comprehensiveness''' – How well does the answer cover all facets of the query? | |||
* '''Diversity''' – Does the answer provide multiple perspectives or angles? | |||
* '''Empowerment''' – Does the answer help the user form a judgment or understanding? | |||
These criteria aim to capture the richness and utility of answers in real-world analytical contexts. | |||
===Results=== | |||
Experiments were conducted on two large-scale datasets—podcast transcripts and news articles (each ~1M tokens). GraphRAG was evaluated at multiple community levels (C0–C3), and against: | |||
* A baseline vector RAG using semantic search (SS). | |||
* A graph-free map-reduce summarization method using raw source texts (TS). | |||
Key findings include: | |||
* '''Superior Comprehensiveness & Diversity''': GraphRAG outperformed vector RAG across all global sensemaking criteria, with win rates between 72–83% in comprehensiveness and 62–82% in diversity. | |||
* '''Empowerment''': GraphRAG also generally helped users better understand and make judgments about the data, although results here were more mixed compared to other metrics. | |||
* '''Token Efficiency vs Quality Trade-off''': | |||
** Structured semantic global search (GraphRAG) is '''more expensive''' in terms of total LLM calls at inference than standard vector RAG. | |||
** However, it offers a trade-off: '''root-level community summaries (C0)''' provide strong performance (e.g., 72% comprehensiveness win rate) at a fraction of the token cost—sometimes requiring over 90% fewer tokens than full source summarization. | |||
* '''Claim-Based Validation''': A claim extraction method (Claimify) confirmed that GraphRAG answers contain more factual claims and more diverse clusters of ideas than vector RAG. | |||
===Conclusion=== | |||
GraphRAG significantly extends the reach of RAG systems to encompass broad, sensemaking queries. By constructing and leveraging a hierarchical knowledge graph, it enables query-focused summarization across large corpora. While more computationally intensive than vector RAG, its performance benefits and structured summarization make it a compelling tool for global understanding tasks. | |||
== Mathematical Formulation of RAG Systems == | |||
Retrieval-Augmented Generation (RAG) can strictly be formulated as a conditioned probabilistic text generation over both the input query and externally retrieved documents. With query <math>q</math> and corpus <math>\mathcal{C}</math>, the model outputs a subset of documents <math>D_q \subset \mathcal{C}</math> and produces an answer <math>a</math> by maximizing the conditional probability: | |||
<math> | :<math>P(a \mid q) = \sum_{d \in D_q} P(a \mid q, d) \cdot P(d \mid q)</math> | ||
In this, <math>P(d \mid q)</math> refers to the retriever's confidence in the relevance of document <math>d</math> to query <math>q</math>, and <math>P(a \mid q, d)</math> refers to the probability of the generator generating answer <math>a</math> based on query <math>q</math> and evidence <math>d</math>. This framework makes generation dependent on what is retrieved in order to reduce hallucinations and increase factuality. | |||
<math> | The retriever uses dense vector similarity. Query <math>q</math> and document <math>d</math> are both represented via learned encoders <math>E_q(\cdot)</math> and <math>E_d(\cdot)</math>. The similarity score between them is denoted as the inner product: | ||
:<math>s(q, d) = \langle E_q(q), E_d(d) \rangle</math> | |||
The top-k documents are selected by ranking documents in <math>\mathcal{C}</math> based on <math>s(q, d)</math>. These scores are then converted into probabilities with a softmax: | |||
:<math>P(d \mid q) = \frac{\exp(s(q, d)/\tau)}{\sum_{d' \in \mathcal{C}} \exp(s(q, d')/\tau)}</math> | |||
where <math>\tau</math> is a temperature parameter controlling sharpness. | |||
For generation, given the retrieved set <math>D_q = \{d_1, \dots, d_k\}</math>, the generator produces a response token-by-token. Assuming an autoregressive model, the generation probability is: | |||
:<math>P(a \mid q, D_q) = \prod_{t=1}^{T} P(a_t \mid a_{<t}, q, D_q)</math> | |||
where <math>a_t</math> is the <math>t</math>-th token of the answer. Some architectures concatenate all <math>d_i</math> into one context, while others marginalize or attend to them one at a time. This modular structure allows the RAG framework to decouple retrieval from generation, and therefore becomes more interpretable, scalable, and adaptable to real-world question answering systems. | |||
== | == Summary and Future Directions == | ||
* RAG improves factual grounding and adaptability of LMs. | |||
* Combining retrieval with structured reasoning (IRCoT, graphs) enhances complex task performance. | |||
* Challenges remain in latency, retrieval quality, and hallucination control. | |||
=== Future Directions in Retrieval-Augmented Generation === | |||
Beyond current advances, several promising future directions can enhance RAG's effectiveness, efficiency, and usability in real-world applications: | |||
'''Adaptive and Context-Aware Retrieval''': Current retrieval approaches typically rely on fixed similarity metrics (e.g., cosine similarity or BM25) to fetch relevant documents. Future systems could leverage dynamically adaptive retrieval strategies, integrating real-time context or user preferences. For example, retrieval systems could adjust weights based on user feedback or query intent, optimizing retrieval results iteratively. | |||
'''Multi-modal Retrieval-Augmented Generation''': While current RAG systems primarily retrieve textual knowledge, extending retrieval to multi-modal sources—such as images, audio, and video—can enrich the information context. Future work might integrate vision-language models or video indexing to facilitate richer responses, particularly in domains such as news summarization, education, and healthcare. | |||
'''Improving Retrieval Efficiency''': Retrieval latency remains a bottleneck for real-time applications. Techniques like retrieval index compression, hierarchical retrieval (coarse-to-fine), and approximate nearest neighbor searches optimized for LLM embedding spaces could substantially reduce response times without significantly affecting retrieval accuracy. | |||
'''Enhanced Interpretability and Source Attribution''':Users increasingly demand transparency regarding the sources behind generated answers. Future RAG models can develop advanced mechanisms for source attribution and interpretability, clearly delineating how retrieved evidence contributes to the generated response. Interactive interfaces allowing users to explore cited sources could enhance trust and usability. | |||
'''Personalized Retrieval-Augmented Generation''': Integrating user profiles or historical interaction data into the retrieval-generation loop could enable more personalized responses. For instance, healthcare applications might retrieve patient-specific medical history or preferences to tailor responses more precisely to individual contexts. | |||
'''Reducing Hallucinations with Self-verification''': Future RAG models could incorporate explicit verification steps within the retrieval-generation cycle. Models might internally query their own outputs for consistency checks, leveraging an iterative self-query mechanism to detect and correct potential hallucinations before providing the final output. | |||
'''Scalable, Decentralized Knowledge Retrieval''': Centralized retrieval systems become increasingly challenging at scale. Future research could explore decentralized or distributed retrieval mechanisms, employing blockchain or federated retrieval networks to securely and efficiently access up-to-date knowledge from diverse, globally distributed databases. | |||
'''Integration with External Reasoning Modules''': Combining RAG with external symbolic reasoning or logic modules could enable complex inferential reasoning tasks, going beyond simple fact retrieval. Systems could leverage knowledge graphs or reasoning engines to validate and extend reasoning within the RAG pipeline, providing more accurate and logically consistent answers. | |||
Pursuing these directions will further position RAG as a robust and versatile approach for accurate, efficient, and reliable knowledge-grounded generation. | |||
Latest revision as of 23:59, 16 April 2025
Record your contributions here [1]
Use the following notations:
C: You have written a summary/critique on the paper.
Your feedback on presentations
Topic 12: State Space Models
Introduction
State Space Models (SSMs) are introduced as powerful alternatives to traditional sequence modeling approaches. These models demonstrate good performance in various modalities, including time series analysis, audio generation, and image processing and they can capture long-range dependencies more efficiently. SSMs initially struggled to match the performance of Transformers in language modeling tasks and there were some gaps between them. To address their challenges, recent advances in their architecture such as the Structured State Space Model (S4) have been introduced, which succeeded in long-range reasoning tasks and allowed for more efficient computation while preserving theoretical strengths. However, its implementation remains complex and computationally demanding. So further research led to simplified variants such as the Diagonal State Space Model (DSS), which achieves comparable performance with a more straightforward formulation. In parallel, hybrid approaches, like the H3 model, that integrate SSMs with attention mechanisms try to bridge the mentioned gaps. To understand better what I mean from the hybrid word, for example in H3 the authors try replacing almost all the attention layers in transformers with SSMs. More recently, models like Mamba have pushed the boundaries of SSMs by selectively parameterizing state matrices as functions of the input and allowing more flexible and adaptive information propagation. Research in SSMs continues to resolve the remaining challenges and the potential to substitute attention-based architectures with SSMs grows stronger. They will likely play a crucial role in the next generation of sequence modeling frameworks.
Advantages of SSMs
- Efficient Long-Range Dependency Handling: Unlike Transformers, which require [math]\displaystyle{ O(n^2) }[/math] complexity for self-attention, SSMs can process sequences in [math]\displaystyle{ O(n \log n) }[/math] time complexity using efficient matrix-vector multiplications and the Fast Fourier Transform (FFT) or [math]\displaystyle{ O(n) }[/math] in case of Mamba architectures.
- Effective Long-Range Dependency Handling: By leveraging a state update mechanism (parametrized by λ) that preserves and accumulates signals over arbitrarily large time spans, SSMs effectively capture and retain information from distant points in a sequence, enabling robust long-range dependency handling.
- Lower memory requirements: Unlike transformers, SSMs don’t require storing the entire input in memory, leading to lower memory consumption.
- Parallelization: SSMs allow efficient parallelization while maintaining the benefits of recurrent computation, making them a powerful alternative to RNNs.
- Robustness to Irregularly Sampled Data: Unlike Transformers, which inherently assume regularly spaced inputs, State Space Models naturally handle irregularly sampled data, which is prevalent in real-world applications such as sensor data processing and clinical time-series. By explicitly modeling the continuous-time evolution of latent states, SSMs provide robustness against missing or unevenly spaced observations, leading to improved performance in scenarios where input data is incomplete or irregularly sampled.
- Interpretability and Diagnostic Insight: State Space Models offer a distinct interpretability advantage by representing system behavior through their state-transition dynamics explicitly. Unlike black-box models, the learned parameters in SSMs (matrices [math]\displaystyle{ \mathbf{A} }[/math], [math]\displaystyle{ \mathbf{B} }[/math], [math]\displaystyle{ \mathbf{C} }[/math], and [math]\displaystyle{ \mathbf{D} }[/math]) can be analyzed to infer how inputs influence future states and outputs over time. This interpretability is especially valuable in fields where understanding model behavior is critical, such as financial risk modeling or biological systems analysis.
Core concepts
To understand State Space Models better, let's first take a look at the problem with Transformers and Recurrent Neural Networks (RNNs) and the relation between them and SSMs. In transformers during training, we create a matrix comparing each token with every token that came before and the weights in each cell of this matrix show how similar they are to each other. For calculating the weights, we don't do a sequential operation and each two tokens' relation can be computed in parallel. However, during inference, when we try to generate the next token, we need to re-calculate the attention for the entire sequence, even if we already generated some tokens. This means, for a sequence of length [math]\displaystyle{ L }[/math], the computation cost would be [math]\displaystyle{ L^2 }[/math] and this is a bottleneck for long sequences in Transformer. RNN takes two inputs at each time step to predict the output [math]\displaystyle{ y_t }[/math] and generate current hidden state ([math]\displaystyle{ h_t }[/math]). These inputs are the hidden state of previous time step ([math]\displaystyle{ h_{t-1} }[/math]) and the input of current time step ([math]\displaystyle{ x_t }[/math]). This structure helps us to do the inference with linear computation because unlike transformers, it doesn't recalculate all previous hidden states. On the other hand, the known problem with them is that they forget the initial tokens as they go forward. A simple RNN updates its hidden state using below formula:
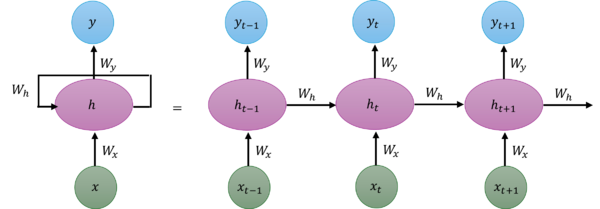
[math]\displaystyle{
h(t) = \sigma(W_h h(t-1) + W_x x(t))
}[/math]
[math]\displaystyle{ y(t) = W_y h(t) }[/math]
Where:
- [math]\displaystyle{ h(t) }[/math] is the hidden state at time t
- [math]\displaystyle{ x(t) }[/math] is the input
- [math]\displaystyle{ y(t) }[/math] is the output
- [math]\displaystyle{ W_h, W_x, }[/math] and [math]\displaystyle{ W_y }[/math] are weight matrices
- [math]\displaystyle{ \sigma }[/math] is a non-linear activation function
State Space Models (SSM) come from control theory for mathematical representation of a system and describing its possible states. They define a linear mapping from an input signal x(t) to an output signal y(t) through a latent state representation h(t). There are two main components to SSM:
1. State equation: Describes how the system's hidden state changes based on the current state and input
[math]\displaystyle{ h'(t) = \mathbf{A} h(t) + \mathbf{B} x(t) }[/math]
2. Output equation: Defines how the system produces output based on the current state and input
[math]\displaystyle{ y(t) = \mathbf{C} h(t) + \mathbf{D} x(t) }[/math]
Where:
- [math]\displaystyle{ h(t) }[/math] represents the hidden state
- [math]\displaystyle{ x(t) }[/math] is the input
- [math]\displaystyle{ y(t) }[/math] is the output
- [math]\displaystyle{ \mathbf{A}, \mathbf{B}, \mathbf{C}, }[/math] and [math]\displaystyle{ \mathbf{D} }[/math] are learnable parameter matrices
The intuition behind the neural network architecture stems from the state equation, which essentially says the change in latent variable is given by the sum of linear transformations of current latent state and the linear transformation of the input variable. Solving the system of differential equations will then be equivalent to train the neural network to find linear transforamtions [math]\displaystyle{ \mathbf{A},\mathbf{B},\mathbf{C},\mathbf{D} }[/math]. However, note that in this definition we use continuous functions and is not applicable to many sequential input data that are discrete, especially sentences. Therefore, we discretize the differential equation so it adapts to taking discrete input sequences in our problems. This yields
[math]\displaystyle{ h_t = \bar{\mathbf{A}} h_{t-1} + \bar{\mathbf{B}} x_t }[/math]
[math]\displaystyle{ y_t = \mathbf{\bar{C}} h_t }[/math]
where [math]\displaystyle{ h_t }[/math] is the discrete latent state at step t and [math]\displaystyle{ x_t }[/math] is the input at step t.
Note that we dropped [math]\displaystyle{ \mathbf{D}x_t }[/math] for computational simplicity and hope [math]\displaystyle{ \mathbf{\bar{C}} }[/math] can capture the effect of input [math]\displaystyle{ x_t }[/math], as [math]\displaystyle{ \mathbf{\bar{C}} h_t = \mathbf{\bar{C}} (\mathbf{\bar{A}}h_{t-1} + \mathbf{\bar{B}}x_t) }[/math] so [math]\displaystyle{ \mathbf{\bar{C}} }[/math] operates on [math]\displaystyle{ x_t }[/math] as well.
So how does SSM differ from the RNN? In fact, the difference lies in the convolutive view of SSM. To understand this, consider an sequence of inputs [math]\displaystyle{ x_{1:n} }[/math], then we have
[math]\displaystyle{ h_0 = \mathbf{\bar{B}} x_0 }[/math]
[math]\displaystyle{ h_1 = \mathbf{\bar{A}}h_0 + \mathbf{\bar{B}} x_1 = \mathbf{\bar{A}}\mathbf{\bar{B}} x_0 + \mathbf{\bar{B}} x_1 }[/math]
[math]\displaystyle{ h_2 = \mathbf{\bar{A}}h_1 + \mathbf{\bar{B}} x_2 = \mathbf{\bar{A}}^2\mathbf{\bar{B}} x_0 + \mathbf{\bar{A}}\mathbf{\bar{B}} x_1 + \mathbf{\bar{B}} x_2 }[/math]
Note that since we have linear transformation, we can now compute all states in parallel and this could greatly improve training speed.
Note that we also put a bar on the matrices, this is a result of discritization where [math]\displaystyle{ \mathbf{\bar A} }[/math] and [math]\displaystyle{ \mathbf{\bar B} }[/math] are discrete equivalents of the [math]\displaystyle{ \mathbf{A} }[/math] and [math]\displaystyle{ \mathbf{B} }[/math] transforms compounded over timestep [math]\displaystyle{ \Delta }[/math] using some discretization method. For example using a trapezoidal rule
- [math]\displaystyle{ \mathbf{\bar A} = (I - \frac{\Delta}{2}A)^{-1}(I + \frac{\Delta}{2}A) }[/math]
- [math]\displaystyle{ \mathbf{\bar B} = (I - \frac{\Delta}{2}A)^{-1}\Delta B }[/math]
[math]\displaystyle{ \overline{A} }[/math] : Discretized state transfer matrix, which is an approximate representation of the continuous state matrix A.
[math]\displaystyle{ \overline{B} }[/math] : Discrete version of the input matrix.
Look at #Discretization for further details.
Looking at these formulations and those we defined for RNNs shows us they are similar. We can see that an RNN is essentially a non-linear extension of a state space model. The main differences are:
- SSMs are linear transformations between states, while RNNs apply non-linearity through the activation function
- SSMs come from control theory and in control systems, the matrices are typically derived from physics equations, while in machine learning we learn these matrices from data
- In SSMs, we have D u(t) in the second equation which is commonly left out in control problems
HiPPO Matrix
Higher-Order-Polynomial Projection Operator (HiPPO) Matrix is a class of specially designed state transfer matrix A that enables the state space model to capture long-term dependencies in a continuous time setting. The most important matrix in this class is defined as:
[math]\displaystyle{ \left.\left(\textbf{HiPPO Matrix}\right)\right.\quad A_{nk}=-\left\{ \begin{aligned} (2n+1)^{1/2}(2k+1)^{1/2} & & \mathrm{if~}n\gt k \\ n+1 & & \mathrm{if~}n=k \\ 0 & & \mathrm{if~}n\lt k \end{aligned}\right.. }[/math]
This matrix is designed to compress past history into a state that contains enough information to roughly reconstruct history. The interpretation of this matrix is that it produces a hidden state that remembers its history.
Recurrent Representation of SSM
The input is a discrete sequence [math]\displaystyle{ (u_0,u_1,\ldots) }[/math] instead of continuous function. To discretize the continuous-time SSM, we follow prior work in using the bilinear method [2], which converts the state matrix [math]\displaystyle{ A }[/math] into an approximation [math]\displaystyle{ \overline{A} }[/math] . The discrete SSM is:
[math]\displaystyle{ \begin{aligned} x_k & =\overline{\boldsymbol{A}}x_{k-1}+\overline{\boldsymbol{B}}u_k & \overline{\boldsymbol{A}} & =(\boldsymbol{I}-\Delta/2\cdot\boldsymbol{A})^{-1}(\boldsymbol{I}+\Delta/2\cdot\boldsymbol{A}) \\ y_k & =\overline{\boldsymbol{C}}x_k & \overline{\boldsymbol{B}} & =(\boldsymbol{I}-\Delta/2\cdot\boldsymbol{A})^{-1}\Delta\boldsymbol{B} & \overline{\boldsymbol{C}}=\boldsymbol{C}. \end{aligned} }[/math]
This equation is now a sequence-to-sequence map [math]\displaystyle{ u_k\mapsto y_k }[/math] instead of function-to-function.
Discretization
As mentioned, State Space models come from ordinary differential equations, so the way we discretize those continuous equations so they work with finite sequences is crucial. In fact, we aim to learn [math]\displaystyle{ \mathbf{\bar A} }[/math] and [math]\displaystyle{ \mathbf{\bar B} }[/math] instead of [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] directly, so the discretization step is baked into our model in practice. Below we show a quick discretization example based on a trapezoidal rule.
Trapezoidal rule assumes: [math]\displaystyle{ x_{n+1} - x_{n} = \frac{\Delta}{2} (f(t_{n+1}) + f(t_{n})) }[/math]
We start from the ordinary differential equation: [math]\displaystyle{ h'(t) = \mathbf{A} h(t) + \mathbf{B} x(t) }[/math]
By applying the trapezoidal rule:
[math]\displaystyle{ h_{n+1} - h_{n} = \frac{\Delta}{2} (\mathbf{A}h_{n+1} + \mathbf{B}x_{n+1} + \mathbf{A}h_{n} + \mathbf{B}x_{n}) }[/math]
[math]\displaystyle{ h_{n+1} - \frac{\Delta}{2} \mathbf{A}h_{n+1} = h_n + \frac{\Delta}{2}\mathbf{A}h_{n} + \frac{\Delta}{2} \mathbf{B}(x_{n+1} + x_{n}) }[/math]
[math]\displaystyle{ (\mathbf{I} - \frac{\Delta}{2} \mathbf{A})h_{n+1} = (\mathbf{I} + \frac{\Delta}{2}\mathbf{A})h_{n} + \frac{\Delta}{2} \mathbf{B}(x_{n+1} + x_{n}) }[/math]
It is assumed that the control sequence does not change significantly over small [math]\displaystyle{ \Delta }[/math], i.e., [math]\displaystyle{ x_{n+1} \approx x_n }[/math], leading to:
[math]\displaystyle{ (\mathbf{I} - \frac{\Delta}{2} \mathbf{A})h_{n+1} = (\mathbf{I} + \frac{\Delta}{2}\mathbf{A})h_{n} + \Delta \mathbf{B}(x_{n+1}) }[/math]
Thus, solving for [math]\displaystyle{ h_{n+1} }[/math]:
[math]\displaystyle{ h_{n+1} = (\mathbf{I} - \frac{\Delta}{2} \mathbf{A})^{-1}(\mathbf{I} + \frac{\Delta}{2}\mathbf{A})h_{n} + (\mathbf{I} - \frac{\Delta}{2} \mathbf{A})^{-1}\Delta \mathbf{B}(x_{n+1}) }[/math]
From this, the discretized state matrices are:
[math]\displaystyle{ \mathbf{\bar A}=(\mathbf{I} - \frac{\Delta}{2} \mathbf{A})^{-1}(\mathbf{I} + \frac{\Delta}{2}\mathbf{A}), \quad \mathbf{\bar B}=(\mathbf{I} - \frac{\Delta}{2} \mathbf{A})^{-1}\Delta \mathbf{B}. }[/math]
An alternative and often-used discretization is based on the matrix exponential:
[math]\displaystyle{ \mathbf{\bar{A}} = e^{A\Delta}, \quad \mathbf{\bar{B}} = (A^{-1}(e^{A\Delta} - I)) B. }[/math]
This formulation naturally arises in continuous-time state-space models and ensures numerical stability for stiff systems.
The matrix index [math]\displaystyle{ {A\Delta} }[/math] comes directly from the analytic solution of the continuous-time system: [math]\displaystyle{ x(t) = e^{At} x(0) + \int_0^t e^{A(t-s)} B u(s) ds }[/math]
For discretization, we choose [math]\displaystyle{ t = k\Delta }[/math] as the sampling point to obtain:
[math]\displaystyle{ x_k = e^{A\Delta} x_{k-1} + (e^{A\Delta} - I) A^{-1} B u_k }[/math]
which is the source of the matrix index method.
To express this in terms of a convolution kernel, the system can be reformulated as:
[math]\displaystyle{ \bar{K} = ( C \bar{B}, C \bar{A} \bar{B}, ..., C \bar{A}^{L-1} \bar{B} ). }[/math]
This can also be rewritten using the exponential formulation:
[math]\displaystyle{ K = \left( C e^{A k \Delta} (e^{A\Delta} - I) A^{-1} B \right)_{0 \leq k \lt L}. }[/math]
This convolution kernel representation helps efficiently compute long-range dependencies in sequences.
Numerical Stability Considerations:
- If [math]\displaystyle{ \|A\Delta\| }[/math] is large, naive exponentiation can introduce significant numerical errors.
- The trapezoidal rule provides a more stable alternative by constraining eigenvalues.
- In practical DSS implementations, row-wise normalization is used to further stabilize large-sequence dynamics.
These methods ensure that state-space models remain numerically robust and efficient when handling long sequences.
Structured State Space (S4)
Objective
The structured state space (S4) model is specialized for conducting efficient sequence modelling, particularly in situations when handling long-term dependencies is needed. The goal of S4 is to improve computational efficiency, reduce the number of parameters, and enhance the ability of learning by introducing constraints on the state transition matrices.
Key Contributions
To efficiently handle long sequences, the Structured State Space (S4) model employs a structured parameterization of its state transition matrices. Specifically, it uses a Diagonal Plus Low-Rank (DPLR) parameterization, which combines the simplicity of diagonal matrices with the expressiveness of low-rank updates. This approach allows S4 to learn complex state spaces while maintaining computational efficiency, making it particularly effective for tasks requiring long-range dependencies.
Intuition Behind S4
The main innovation of S4 is its ability to track long-range dependencies efficiently. Traditional models struggle with long sequences either because they require too much memory (like Transformers) or forget early information (like RNNs). S4 overcomes these limitations by using a mathematical reformulation of state space models, allowing it to process sequences much more efficiently. The authors argue that the different layers of the S4 model contribute to learning long-range dependencies efficiently. They hypothesized that the deep layers of S4 are predominantly responsible for learning local information (short-range dependencies). On the other hand, higher layers aggregate global information, allowing the model to capture the bigger picture.
At its core, S4 is a hybrid between recurrent models and convolutions. Instead of updating each time step sequentially like an RNN, it uses a special structure called the Cauchy kernel, which allows it to compute all steps in parallel. This enables it to process sequences of tens of thousands of steps with a fraction of the computational cost of previous models. Thus, S4 is very advantageous for inference.
S4 has been particularly successful in domains that require continuous, structured data, such as time-series processing. However, its reliance on structured state matrices makes it less adaptable to unstructured data like natural language, where attention-based models still hold an advantage.
Theorem 1: All HiPPO matrices in the paper[3] have a NPLR representation:
[math]\displaystyle{ A=V\Lambda V^*-PQ^\top=V\left(\boldsymbol{\Lambda}-\left(\boldsymbol{V}^*\boldsymbol{P}\right)(\boldsymbol{V}^*\boldsymbol{Q})^*\right)\boldsymbol{V}^* }[/math]
for unitary [math]\displaystyle{ \boldsymbol{V}\in\mathbb{C}^{N\times N} }[/math], diagonal [math]\displaystyle{ Λ }[/math], and low-rank factorization [math]\displaystyle{ \boldsymbol{P},\boldsymbol{Q}\in\mathbb{R}^{N\times r} }[/math].
From Theorem 1, we can find that NPLR matrices can be conjugated into diagonal plus low-rank (DPLR) form.
The core idea of this form is to diagonalize the matrix A using the unitary-ary transformation V and use a low-rank decomposition to further compress the computation, which is important in efficient computation and storage optimization.
Theorem 2: Given any step size [math]\displaystyle{ ∆ }[/math], computing one step of the recurrence can be done in [math]\displaystyle{ O(N) }[/math] operations where [math]\displaystyle{ N }[/math] is the state size.
Theorem 3: Given any step size [math]\displaystyle{ ∆ }[/math], computing the SSM convolution filter [math]\displaystyle{ \overline{\boldsymbol{K}} }[/math] can be reduced to 4 Cauchy multiplies, requiring only [math]\displaystyle{ {\widetilde{O}}(N+L) }[/math] operations and [math]\displaystyle{ O(N + L)) }[/math] space.
Theorems 2 and 3 describe the complexities of SSMs where A is in DPLR form.
| Convolution | Recurrence | Attention | S4 | |
|---|---|---|---|---|
| Parameters | [math]\displaystyle{ LH }[/math] | [math]\displaystyle{ H^2 }[/math] | [math]\displaystyle{ H^2 }[/math] | [math]\displaystyle{ H^2 }[/math] |
| Training | [math]\displaystyle{ \tilde{L}H(B + H) }[/math] | [math]\displaystyle{ BLH^2 }[/math] | [math]\displaystyle{ B(L^2H + LH^2) }[/math] | [math]\displaystyle{ BH(\tilde{H} + \tilde{L}) + B\tilde{L}H }[/math] |
| Space | [math]\displaystyle{ BLH }[/math] | [math]\displaystyle{ BLH }[/math] | [math]\displaystyle{ B(L^2 + HL) }[/math] | [math]\displaystyle{ BLH }[/math] |
| Parallel | [math]\displaystyle{ Yes }[/math] | [math]\displaystyle{ No }[/math] | [math]\displaystyle{ Yes }[/math] | [math]\displaystyle{ No }[/math] |
| Inference | [math]\displaystyle{ LH^2 }[/math] | [math]\displaystyle{ H^2 }[/math] | [math]\displaystyle{ L^2H + H^2L }[/math] | [math]\displaystyle{ H^2 }[/math] |
Limitations
However, a significant critique of the S4 model is its complexity. The model relies on multiple reduction steps and advanced linear algebraic techniques to compute the state space efficiently. While these optimizations are crucial for performance, they also make S4 challenging to understand, implement, and analyze. This complexity can act as a barrier for researchers and practitioners seeking to adapt or build upon the model, highlighting a trade-off between efficiency and accessibility.
Some of the applications of S4 are language and audio processing (text generation, speech recognition, music and voice synthesis), forecasting (predicting stock prices in financial markets, modelling climate information), and scientific computing (simulations in physics, chemistry, astronomy).
Diagonal State Space Model (DSS)
As mentioned above, S4 relies on the Diagonal Plus Low Rank (DPLR) structure of state matrix [math]\displaystyle{ A }[/math], which improves efficiency but introduces significant complexity in both understanding and implementation. To simplify S4 while maintaining its performance, Diagonal State Space Model (DSS) is proposed. It simplifies the state matrix by replacing it with a purely diagonal form, reducing computational overhead and improving interpretability. It also maintains the ability to capture long-range dependencies.
[math]\displaystyle{ \mathbf{Improvements\ Compared\ with\ S4} }[/math]
- Computational Efficiency (and Model Complexity)
- The DSS model offers a significant computational advantage by simplifying the NPLR state matrix to a diagonal form. This diagonalization enables more efficient recurrence computations and reduces the number of parameters to be estimated, making it computationally efficient. This simplicity allows DSS to scale well to large datasets and real-time systems.
- Interpretability
- The diagonal structure makes it clear how previous hidden states and inputs affect the current state, which helps in understanding the relationships between states. For example, it can be shown that under certain situations, DSS can capture information from extreme distant position in the sequence.
- To illustrate how DSS captures long-range dependencies, consider the diagonalization of the state space representation. Given a diagonalizable state matrix [math]\displaystyle{ A }[/math] with eigenvalues [math]\displaystyle{ \lambda_1, \dots, \lambda_N }[/math] and the diagonal matrix [math]\displaystyle{ \Lambda }[/math], DSS reformulates the recurrence relation as: [math]\displaystyle{ K = \bar{K}_{\Delta,L} \left( \Lambda, \left(e^{L \lambda_i \Delta} - 1 \right)^{-1} \right) }[/math], where [math]\displaystyle{ K }[/math] encodes the sequence propagation in the transformed space. The diagonal form simplifies the recurrence relationship, making it clear how past states influence the current state. Under specific conditions, DSS captures long-range dependencies:
- If [math]\displaystyle{ |\lambda_i| \Delta \approx 0 }[/math], the state evolution reduces to [math]\displaystyle{ x_{i,k} \approx x_{i,k-1} }[/math], leading to persistent memory effects.
- If [math]\displaystyle{ \text{Re}(\lambda_i) \Delta \ll 0 }[/math], information from past states is effectively forgotten, prioritizing local dependencies.
- If [math]\displaystyle{ \text{Re}(\lambda_i) \gt 0 }[/math], DSS can propagate information from distant states due to the exponential weighting term [math]\displaystyle{ e^{\lambda \Delta} }[/math]. This property enables DSS to retain long-range dependencies more effectively than conventional models.
- A key advantage of DSS is that it provides interpretable mechanisms to regulate information retention and forgetting. The row-wise normalization in [math]\displaystyle{ \text{DSS}_{\text{softmax}} }[/math] further stabilizes the dynamics, mitigating numerical instabilities when handling large sequence lengths [math]\displaystyle{ L }[/math]. This simplicity enhances the transparency of the model, providing clear insights into system behavior and making it easier to interpret the underlying dynamics. By comparison, S4 lacks interpretability due to its more complex architecture.
[math]\displaystyle{ \mathbf{Two\ Variants\ of\ DSS} }[/math]
The DSS model mentioned above is one of the variants of DSS called [math]\displaystyle{ DSS_{softmax} }[/math]. Softmax normalization ensures that the contribution of different eigenvalues remains bounded, avoiding numerical instability. Another variant of DSS is called [math]\displaystyle{ DSS_{exp} }[/math]. In this variant, the recurrence relation becomes [math]\displaystyle{ K = \bar{K}_{\Delta,L} \left( \Lambda, \left(1\right)\right) }[/math]. Instead of softmax normalization, this variant forces the real part of eigenvalues to be negative, ensuring that the recurrence does not grow uncontrollably. Note that the restriction may fail in some tasks and not as expressive as general state spaces.
[math]\displaystyle{ \mathbf{Applications} }[/math]
Despite its simplifications, DSS retains strong modeling capabilities for a variety of tasks, including time-series forecasting, raw speech classification, and natural language processing (NLP). Its ability to model temporal dependencies with minimal complexity makes it a highly efficient choice for applications where computational efficiency and interpretability are critical. While S4 excels in capturing intricate, long-range dependencies, DSS's performance is nearly as strong, and in certain cases, it even outperforms S4.
[math]\displaystyle{ \mathbf{Limitations} }[/math]
The initialization of parameters can significantly influence the performance of DSS, as improper initialization may lead to slower convergence or suboptimal solutions. Additionally, DSS tends to be less effective at modeling information-dense data, such as text, where complex patterns and intricate relationships between words or phrases are crucial. In these cases, more sophisticated models may be helpful. However, DSS still provides a viable alternative in scenarios where simplicity and efficiency are prioritized over capturing deep contextual relationships.
Hungry Hungry Hippos (H3)
SSMs vs Attention
Research have shown that SSMs demonstrated state-of-the-art performance in domains like speech recognition, audio generation, etc. However, it underperforms attention in language modelling due to two main reasons:
- Expressivity gap
- Poor hardware utilization
Expressivity Gap
To understand the gap between SSMs and attention on language modelling, the authors examined two synthetic language modelling tasks:
The Induction Head task tests how well a model can recall content after a special token. At the end of the sequence, the model must recall the token that appeared immediately after the special token earlier in the sequence. In the table above, we are trying to recall the first token after the ⊢ symbol, which is f.
Associative Recall is similar to the induction head task, but requires the model to remember multiple key-value pairs. At the end of the sequence, the model must recall a specific value belonging to a specific key. In the table above, we are trying to recall the value associated with character a, which is 2.
The table above shows performance of S4D (specialized S4 for language modelling), Gated State Spaces (GSS) and Attention. We can see that Attention can complete both synthetic tasks perfectly, achieving an accuracy of 100%, significantly outperforming S4D and GSS. Failure of SSMs can be attributed to two missing capabilities: (i) the ability to remember tokens that appear after a particular event (e.g., the special token in the induction head task), and (ii) the ability to compare tokens across the sequence (e.g., comparing keys to decide which value to recall). Attention has both these capabilities: it can compare tokens by constructing the quadratic attention matrix [math]\displaystyle{ \mathbf{QK^T} }[/math], and it can recall tokens by direct copying (multiplying [math]\displaystyle{ softmax(\mathbf{QK^T}) }[/math] with [math]\displaystyle{ \mathbf{V} }[/math]).
H3 Design
H3 is designed to enable these capabilities in SSMs, its structure is given as follows:
The design for H3 layer consists of two SSMs stacked together. The idea of stacking multiple SSM layers is to selectively incorporate attention mechanisms for key operations like recalling past tokens or comparing sequence elements. This allows H3 to perform well on tasks where pure SSMs historically underperformed, making it competitive with Transformers in language modeling while maintaining high computational efficiency. Initially, we convert our input sequence into query, key, and value matrices, as seen in regular attention. We then apply two SSM transformations to these input matrices to generate the final output.
Shift SSM
The first SSM is the shift SSM that you can think of as performing a local lookup across the sequence. In a sliding window fashion, the Shift SSM shifts the state vector by one position at each time to store the most recent inputs. The purpose is to detect specific events and remember the surrounding tokens, As an analogy, this is similar to how we remember the most recent words we have read. Our brain captures those last few words (tokens, for the model). For specific words or events in the book, we associate them with the surrounding context (words) around the specific entity.
In the shift SSM, we constrain [math]\displaystyle{ \mathbf{A} ∈ R^{m×m} }[/math] to be a shift matrix as defined by its entries: [math]\displaystyle{ \mathbf{A}_{i,j} = \begin{cases} 1 & \text{for } i - 1 = j,\\ 0 & \text{otherwise}. \end{cases} }[/math].
If you draw it out, it would be a square matrix where the 1s appear directly below the main diagonal with all other entries 0. The action of this matrix on the hidden state [math]\displaystyle{ x_i }[/math] is to shift each coordinate down by one—thereby creating a “memory” of the previous states. If [math]\displaystyle{ \mathbf{B} = \textit{e}_1 }[/math], the first basis vector, then [math]\displaystyle{ x_i = [u_i, u_{i-1}, . . . , u_{i-m+1}] }[/math] contains the inputs from the previous m time steps. Both [math]\displaystyle{ \mathbf{B} }[/math] and [math]\displaystyle{ \mathbf{C} }[/math] are learnable matrices, but [math]\displaystyle{ \mathbf{B} }[/math] is usually fixed to [math]\displaystyle{ \textit{e}_1 }[/math] for simplicity, in which case the output is a 1D convolution with kernel size m.
Diag SSM
The diagonal SSM serve as a kind of global memory that keeps track of important information over the entire sequence. A diagonal matrix is used to summarize the information we have seen. As an analogy, the diagonal SSM acts like the notes that we take when we are in class. It is super difficult to recall every single detail our professor states during a lecture. We will take notes during lecture to retain important concepts and information. We can then refer to these notes when we review. The diagonal SSM serves as our notes that the input sequence can refer to when recalling the summary of past information.
The diagonal SSM constrains A to be diagonal and initializes it from the diagonal version of HiPPO. This parameterization allows the model to remember state over the entire sequence. The shift SSM can detect when a particular event occurs, and the diagonal SSM can remember a token afterwards for the rest of the sequence.
Multiplicative Interaction
Multiplicative interactions, which is represented by the teal elementwise multiplication symbol, it offers H3 the ability to compare tokens across the sequence. Specifically, we can use this to compare and obtain information between the Shift SSM and Diagonal SSM. This is similar to the similarity score (dot product) seen in vanilla attention.
Holistically, we can kind of view the outputs from Shift SSM as local or short-term information. The outputs from diagonal SSM servers as long-term information. The multiplicative interaction enables us to use both types of information to extract important information. This is critical for tasks like associative recall. For example, if the model needs to recall a value associated with a key, it can compare the current key with all previously seen keys using these interactions.
Mamba
Mamba is a technique which builds on S4 models. It was introduced to increase efficiency for long sequences by leveraging selective attention mechanisms, allowing them to save memory and computational cost by not focusing on irrelevant information. It does so by combining the H3 block traditionally used in SSM models with a gated multilayered perceptron (MLP), as shown in the figure below.
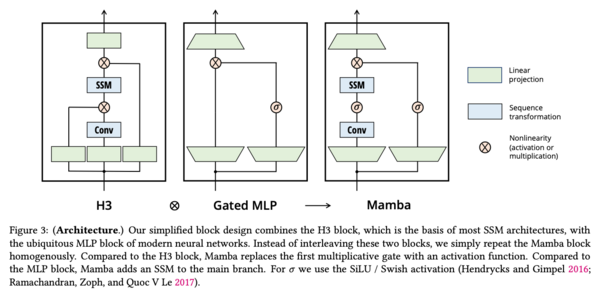
Recall that SSM models calculate the output using the following formulae: [math]\displaystyle{ h'(t) = \mathbf{A} h(t) + \mathbf{B} x(t) }[/math]
[math]\displaystyle{ y(t) = \mathbf{C} h(t) + \mathbf{D} x(t) }[/math]
, where these equations are discretized using an additional parameter [math]\displaystyle{ \Delta }[/math] as shown above, resulting in the updated formulae:
[math]\displaystyle{ h(t) = \bar{\mathbf{A}} h(t-1)+\bar{\mathbf{B}}x(t) }[/math]
[math]\displaystyle{ y(t) = \mathbf{C} h(t) }[/math]
, where the matrices [math]\displaystyle{ {\mathbf{A}} }[/math] and [math]\displaystyle{ {\mathbf{B}} }[/math] are discretized as follows:
[math]\displaystyle{ \begin{aligned} & \overline{\mathbf{A}}=\operatorname{diag}\left(e^{-\Delta_t \omega}\right) \\ & \overline{\mathbf{B}}=\left(1-e^{-\Delta_t \omega}\right) \end{aligned} }[/math]
The matrices may be understood as follows:
- [math]\displaystyle{ \bar{\mathbf{A}} }[/math] represents the transition matrix between discrete hidden states
- [math]\displaystyle{ \bar{\mathbf{B}} }[/math] processes the input data in order to update the hidden state
- [math]\displaystyle{ \mathbf{C} }[/math] interprets the hidden state in order to generate the output.
Mamba introduces an input-dependent gating mechanism [math]\displaystyle{ \Delta_t }[/math], defined as:
[math]\displaystyle{ \Delta_t=\tau_{\Delta}\left(W_{\Delta} x_t+b_{\Delta}\right) }[/math]
where [math]\displaystyle{ \tau_{\Delta} }[/math] is typically a softplus or sigmoid activation function, and [math]\displaystyle{ W_{\Delta}, b_{\Delta} }[/math] are learned parameters. The discrete state update rule incorporating selectivity is:
[math]\displaystyle{ h_t=\left(\mathbf{I}-\Delta_t\right) h_{t-1}+\Delta_t x_t }[/math]
This gating function dynamically adjusts the timescale of information propagation, allowing the model to selectively retain or discard information based on the context provided by input data.
Convolutional Kernel Representation
The Mamba model's dynamics can also be expressed through a convolutional kernel representation for computational efficiency, especially during training. Given an input sequence [math]\displaystyle{ x_{1: T} }[/math], the output [math]\displaystyle{ y_t }[/math] can equivalently be represented as:
[math]\displaystyle{ y_t=\sum_{k=1}^t \mathbf{C} \overline{\mathbf{A}}^{t-k} \overline{\mathbf{B}} x_k }[/math]
This representation highlights that Mamba's hidden states effectively implement a convolution over past inputs with a kernel shaped by the learned gating parameters and state transition matrices. This approach provides efficient parallel training similar to convolutional architectures while maintaining the ability to handle extremely long sequences with linear complexity during inference.
Advantages :
- Dynamic Timescales: Unlike traditional SSMs with fixed transition matrices, Mamba adjusts transition dynamics based on inputs.
- Improved Long-range Dependencies: Dynamic gating allows Mamba to selectively propagate crucial long-range information while ignoring irrelevant short-term fluctuations.
- Computational Efficiency: The convolutional representation significantly reduces computational overhead during parallel training phases.
Selective State Space Models in Mamba
Mamba builds on the success of structured state space models (SSMs) — a family of models that, by design, efficiently capture long-range dependencies through a recurrent or convolutional mechanism. In traditional SSMs, a key benefit is their linear-time scaling, achieved by compressing the entire sequence context into a fixed hidden state. However, this very efficiency can be a double-edged sword: by forcing the state to be constant over time (a property known as linear time invariance or LTI), the model may miss crucial content-specific cues in the data.
Mamba addresses this limitation with a clever twist—it introduces a selection mechanism that makes certain SSM parameters depend on the input. In simple terms, while standard SSMs update their hidden state with the same fixed rules at every time step, the selective variant modulates these update rules based on the current input. This allows the model to "decide" when to ignore irrelevant information and when to focus on key inputs, similar to how gating works in recurrent neural networks.
The mechanism works by turning parameters that usually remain constant (like the discretization parameter [math]\displaystyle{ \Delta }[/math] and others controlling the transition between hidden states) into functions of the input. This extra flexibility means that rather than applying a one-size-fits-all transformation to every token, the model tailors its processing dynamically across the sequence. The result is a network that not only maintains the efficiency of linear scaling but also improves accuracy by being content-aware—even for very long sequences.
An important innovation in Mamba is that it leverages a hardware-aware algorithm to keep the additional computational cost low. Instead of materializing huge intermediate states, the algorithm uses optimized memory strategies. In practice, this means that Mamba can run several times faster than comparable Transformer-based models, especially on longer inputs.
In summary, Mamba's selective state space models marry the efficiency of classical SSMs with the flexibility of input-dependent gating. This combination allows the architecture to handle extremely long sequences—up to millions of tokens—while still capturing the nuanced patterns essential for tasks ranging from language modeling to audio generation.
Mamba-2
Overview
The core idea behind the paper is structured State Space Duality (SSD), which reveals the connections between SSMs and variants of attention using the structured matrices which can be represented using subquadratic parameters. Some key contributions of the paper include:
- SSMs are mathematically equivalent to semiseparable matrices. This interpretation enables more efficient computation of SSMs as structured matrices.
- Prove the recurrent form of linear attention using tensor contractions and extending it to a new family called Structured Masked Attention (SMA)
- A unifying perspective linking SSMs and SMA, meaning they can be expressed in both linear (recurrent) and quadratic (attention-like) forms.
- A faster, more efficient approach to computing SSMs, surpassing optimized Mamba implementations.
- The SSD framework introduces a novel algorithm based on block decompositions of semiseparable matrices balancing compute, memory, and hardware efficiency.
- Mamba-2 introduces heads for SSMs, similar to multi-head attention in transformers.
- Empirical success in language modeling, scaling laws, and recall tasks often surpassing transformers.
This work offers a theoretical perspective by bridging the gap between SSMs and transformers, enhancing our understanding of sequence models. This enables efficient and faster architectures similar to the proposed Mamba-2.
Semiseparable Matrices
Semiseparable Matrices are matrices that have this form:
[math]\displaystyle{ \begin{bmatrix} C_0^\top B_0 & \\ C_1^\top A_1 B_0 & C_1^\top B_1 & \\ C_2^\top A_2A_1 B_0 & C_2^\top A_2 B_1 & C_2^\top B_2 \\ \vdots & \vdots & \ddots & \ddots \\ C_\mathtt{T}^\top A_{\mathtt{T}-1}\dots A_1 B_0 & C_\mathtt{T}^\top A_{\mathtt{T}-1}\dots A_2 B_1 & \dots & C_\mathtt{T}^\top A_{\mathtt{T}-1} B_{\mathtt{T}-2} & C_\mathtt{T}^\top B_{\mathtt{T}-1} \\ \end{bmatrix} }[/math]
By observation, we can immediately spot that all algorithms for computing state space models can be viewed as structured matrix multiplication algorithms on semiseparable matrices. Such matrix have a property that every submatrix contained in the lower-triangular portion is low rank, so we can write then as:
[math]\displaystyle{ \begin{bmatrix} C_j^T A_{j,i}^X B_{i'} & \cdots & C_j^T A_{j,i-1}^X B_{i-1} \\ \vdots & \ddots & \vdots \\ C_{j'-1}^T A_{j'-1,i}^X B_{i'} & \cdots & C_{j'-1}^T A_{j'-1,i-1}^X B_{i-1} \end{bmatrix} = \begin{bmatrix} C_j^T A_{j,j}^X \\ \vdots \\ C_{j'-1}^T A_{j'-1,j}^X \end{bmatrix} A_{j,i-1}^X \begin{bmatrix} A_{i-1,i'}^X B_{i'} & \cdots & A_{i-1,i-1}^X B_{i-1} \end{bmatrix}. }[/math]
This will leads to an efficient algorithm for calculating semiseparable matrices.
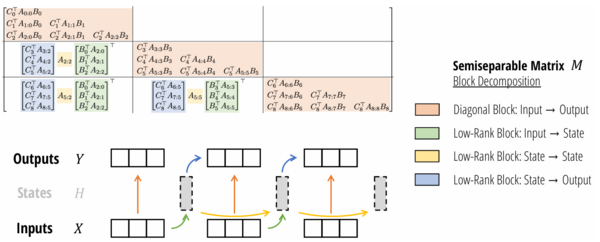
SSD Algorithm: "Block Matrix Decomposition" and "Chunking and State Passing"
- We first partition the semiseparable matrix into blocks of size [math]\displaystyle{ \mathtt{Q} \times \mathtt{Q} }[/math].
- Each diagonal block can be computed using the quadratically, but since [math]\displaystyle{ \mathtt{Q} }[/math] is small, it's hardware efficient. (Orange on the figure)
- Then, we use the properties of semiseparable matrices to factorize each off-diagonal block, which is low rank (Blue, Greem and Yellow on the figure).
- Following a work flow shown, we can have an efficient algorithm that could even incorporate system optimization by running them on different GPUs.
Structured Masked Attention
In RetNet, we used a decay factor which can be seen as a mask on [math]\displaystyle{ \mathtt{Q}^T \mathtt{K} }[/math]. Inspired by Linear Attention and RetNet, we can generalize the idea of using a mask and introduces Structured Masked Attention(SMA). Definition: Structured masked attention (SMA) (or structured attention for short) is defined as a function on queries/keys/values Q,K,V as well as any structured matrix L, through the 4-way tensor contraction.
[math]\displaystyle{ Y = (L \circ Q K^\top) V }[/math]
We can use a special mask called 1-Semiseparable Matrices (1SS) defined as the following.
[math]\displaystyle{ L = \begin{bmatrix} 1 & \\ a_1 & 1 & \\ a_2a_1 & a_2 & 1 \\ \vdots & \vdots & \ddots & \ddots \\ a_{\mathtt{T}-1}\dots a_1 & a_{\mathtt{T}-1}\dots a_2 & \dots & a_{\mathtt{T}-1} & 1 \\ \end{bmatrix} . }[/math]
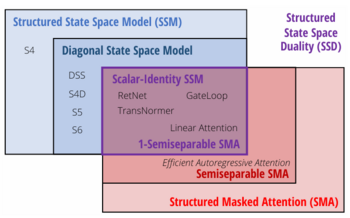
State Space Duality (SSD)
We can recognize that if we use 1SS as the mask for SMA, and if we restrict our SSM'S [math]\displaystyle{ A }[/math] to be a scalar times identity structure (that means [math]\displaystyle{ A }[/math] is a scalar at a given time, so [math]\displaystyle{ A_t = a_t }[/math] at time [math]\displaystyle{ t }[/math]), the are the same thing. This leads to the State Space Duality. It reveals a surprising connection between SSMs and Transformer-based attention mechanisms. The State Space Duality (SSD) framework suggests that certain structured matrices used in SSMs can be reformulated in ways that resemble attention computations. By leveraging this relationship, researchers have proposed efficient algorithms that blend the best of both worlds—retaining the efficiency of SSMs while adopting optimization techniques from Transformers.
We can view the SSD as:
1. A state space models through structured matrix
2. A generalized linear attention through a masking (The duality between SSMs and structured masked attention (SMA) allows us to reinterpret SSMs as a form of linear attention with specific masking strategies.)
Overall, it is an instance that has dual quadratic and linear forms that can be derived from either representation.
Having all this dual form allows us to use some extensions from linear attention such as multi-head attention, grouped-value attention, kernel attention approximations to softmax attention and so on. To name a few specific examples:
- Efficient algorithmic improvements: SSD provides novel ways to compute state transitions, allowing SSMs to leverage techniques such as grouped-value attention and kernelized approximations from the Transformer literature.
- Scalability benefits: Since SSD offers both quadratic and linear formulations, it enables selective adaptation depending on sequence length and computational constraints.
- Bridging architectures: Insights from SSD can guide the development of hybrid architectures that merge SSM-style recurrence with attention-like expressivity.
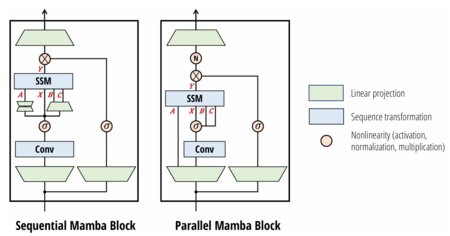
Other ways to explain:
- SSM can be regarded as a controlled dynamical system, where at each time step t, the state xt is influenced by A, while B is responsible for introducing inputs and C is responsible for computing outputs.
- SMA is using a constrained attention model to do information dissemination, but because of the structure of Mask, SMA can only do information flow within a constrained range.
- SSD reveals that they are the same thing, just in a different representation - SSM passes information recursively, whereas SMA propagates through a structured Mask, but the M they compute is structurally equivalent.
Mamba-2 architecture
Using SSD and the a small changes to Mamba’s neural network architecture, we have Mamba-2 architecture.
One change is that we have Parallel Parameter Projections. In Mamba-2, the SSD layer is viewed as a map. It therefore makes sense to produce [math]\displaystyle{ A, B, C, X }[/math] in parallel with a single projection at the beginning of the block.
Another change is that we have an extra Normalization at the end, it could be any normalization, LayerNorm, GroupNorm, or RMSNorm.
Mamba-2 usage and implementation
some examples of Mamba-2 usage includes:
1. Codestral Mamba (Mistral AI): Mistral AI’s open-source code generation model, built on Mamba-2. Competes with Code Llama and Codex, offering longer context (256k tokens) and lower latency.
2. NeMo LLM (NVIDIA): NVIDIA’s large-language model framework now supports Mamba-2 layers. They specifically highlight the use of a hybrid architecture with both Mamba-2 and self-attention layers.
4. Mamba-ND: A multi-dimensional version of Mamba-2 for handling images, video, and climate data. Used in ImageNet-1K classification, HMDB-51 action recognition, and ERA5 weather forecasting.
5. Mambaformer: A hybrid Transformer-Mamba model for time-series forecasting. Achieves better accuracy than both standalone Transformers and Mamba on long-range prediction tasks like stock markets and weather data.
6. Zigzag Mamba (ZigMa): A Mamba-powered diffusion model for image generation. Replaces attention in Diffusion Transformers (DiT), improving speed and memory efficiency for high-resolution image synthesis.
State Space Duality: State Space Models and Transformers
State Space Duality (SSD) gives a mathematization of State Space Models (SSMs)/Transformer duality such that the two models are proven to be definable in terms of structured semiseparable matrices. Duality offers the potential for the development of computationally efficient hybrid models such as Mamba-2 which preserve the expressiveness of Transformers with the benefit of computational efficiency of SSMs.
A discrete-time State Space Model (SSM) can be written as:
[math]\displaystyle{ h_{t+1} = A h_t + B x_t }[/math]
[math]\displaystyle{ y_t = C * h_t + D * x_t }[/math]
where [math]\displaystyle{ h_t }[/math] is the hidden state at time [math]\displaystyle{ t }[/math], [math]\displaystyle{ A, B, C, D }[/math] are learnable state-space matrices, [math]\displaystyle{ x_t }[/math] is the input, and [math]\displaystyle{ y_t }[/math] is the output.
[math]\displaystyle{ K = (CB, CAB, CA^2B, ..., CA^{L-1}B) }[/math]
where [math]\displaystyle{ K }[/math] is some kernel that encodes input dependencies.
SSD establishes that the Transformers and the SSMs share the same structure with respect to semiseparable matrices. A semiseparable matrix is
[math]\displaystyle{ M = D + U^T L }[/math]
where [math]\displaystyle{ D }[/math] is the diagonal matrix for local dependencies, [math]\displaystyle{ L }[/math] is the lower triangular matrix for sequential state transitions, and [math]\displaystyle{ U }[/math] is the upper triangular matrix for long-range interactions.
The self-attention mechanism of Transformers computes
[math]\displaystyle{ M_{att} = Q K^T }[/math]
where [math]\displaystyle{ Q, K }[/math] are the query and key matrices that yield explicit pairwise token interactions. In contrast, transition matrices of SSM make use of:
[math]\displaystyle{ M_{ssm} = C (I - A)^{-1} B }[/math]
where [math]\displaystyle{ A, B, C }[/math] define an implicit recurrence.
SSD offers an optimized block decomposition method for computational efficiency. It splits the sequence into tiny blocks within which intra-chunk dependencies are handled by structured SSMs and inter-chunk information is conducted by structured masked attention (SMA). The structured mechanism hugely reduces the computational complexity so training complexity is [math]\displaystyle{ O(NT) }[/math] for SSMs compared to [math]\displaystyle{ O(N^2T) }[/math] for Transformers and inference complexity is also reduced from [math]\displaystyle{ O(N^2T) }[/math] to [math]\displaystyle{ O(NT) }[/math].
A semiseparable matrix [math]\displaystyle{ M }[/math] of order [math]\displaystyle{ N }[/math] is defined as
[math]\displaystyle{ M_{ji} = C_j^T A_{j:i} B_i }[/math]
where [math]\displaystyle{ A }[/math] is a structured transition matrix that facilitates effective sequence transformations. In the case of 1-semiseparable structured attention, the recurrence is
[math]\displaystyle{ M_{ji} = a_{j:i} (C_j^T B_i) }[/math]
where [math]\displaystyle{ a_{j:i} }[/math] is a generalized positional dependency factor in structured decay.
Structured Masked Attention (SMA) generalizes linear attention with the inclusion of a structured masking matrix [math]\displaystyle{ L }[/math] as follows:
[math]\displaystyle{ L_{ij} = a_{i:j} }[/math]
where [math]\displaystyle{ a_{i:j} }[/math] are the learned decay factors that control the way information flows through the sequence. This makes SSD attain flexibility like attention but with efficiency like SSM.
One of the primary conclusions of SSD is that quadratic (attention-like) as well as linear (SSM-like) computations are enabled for semiseparable matrices.
[math]\displaystyle{ y = M x }[/math]
It can either be computed by a naive quadratic method where [math]\displaystyle{ M }[/math] is used as an explicit attention-like matrix, or an SSM recurrence method that computes [math]\displaystyle{ y }[/math] in [math]\displaystyle{ O(NT) }[/math] time. The dual formulation enables hardware-efficient implementations where structured decompositions are used to enhance computational speed with maintained long-range dependencies.
Mamba-2 exploits SSD through the use of parallel parameter projections to dynamically calculate the parameters of the SSM. There is selective gating of information by a gating mechanism and SSD-based calculation of state transitions facilitates optimal state updates. Expressivity is boosted through structured masked attention (SMA) and the gap with state-space models is bridged.
[math]\displaystyle{ y = \sum_{j=0}^{L-1} W_j (A^j B x_{t-j}) }[/math]
where [math]\displaystyle{ W_j }[/math] are learnable weights derived from structured attention masks. SSD permits hybrid architectures that retain the efficiency of SSMs but with Transformer expressiveness. The future can be anticipated from GPU/TPU acceleration, memory-efficient representations, and retrieval-augmented generation (RAG) for long-context applications. SSD has far-reaching implications for the future of large-scale models that are computationally tractable with 100M-token context windows.
Comparative Analysis of SSM Variants
To provide a clearer understanding of the strengths and weaknesses of State Space Model (SSM) variants—S4, DSS, H3, Mamba, and Mamba-2—this section presents a comparative analysis based on their performance in language modeling tasks, computational efficiency, and scalability. This comparison draws from their architectural designs and empirical results, offering insights into their suitability for various applications.
Performance Metrics
- Perplexity on Language Modeling Tasks
- S4: Achieves competitive perplexity on datasets like WikiText-103 but struggles with extremely long sequences due to its structured parameterization.
- DSS: Matches S4’s perplexity with a simpler diagonal structure, performing well on large-scale datasets with reduced overhead.
- H3: Outperforms S4 and DSS on synthetic tasks like Induction Heads and Associative Recall, closing the expressivity gap with Transformers.
- Mamba: Excels with very low perplexity on long-context tasks, leveraging selective state spaces to rival Transformer performance.
- Mamba-2: Achieves the lowest perplexity among SSMs by enhancing state dimensions and optimization, surpassing Mamba on benchmarks like OpenWebText.
- Computational Efficiency
- S4: Uses Fast Fourier Transform (FFT) for [math]\displaystyle{ O(N \log N) }[/math] training complexity, though its implementation is intricate.
- DSS: Simplifies to [math]\displaystyle{ O(N) }[/math] training and [math]\displaystyle{ O(1) }[/math] inference with a diagonal state matrix, enhancing efficiency.
- H3: Combines two SSMs, resulting in [math]\displaystyle{ O(d^2 N + d N \log N) }[/math] complexity—more expressive but less efficient than others.
- Mamba: Achieves [math]\displaystyle{ O(N) }[/math] training and [math]\displaystyle{ O(1) }[/math] inference with hardware-aware selective mechanisms, optimizing for long sequences.
- Mamba-2: Maintains Mamba’s complexity while improving performance through state space duality and parallelism.
- Scalability
- S4: Scales effectively for moderate sequence lengths but faces challenges with very long contexts.
- DSS: Excels in scalability for large datasets and real-time systems due to its simplicity.
- H3: Limited by higher computational costs, making it less scalable for large models.
- Mamba: Designed for long sequences, scales efficiently to millions of tokens, ideal for extensive context tasks.
- Mamba-2: Enhances scalability with tensor and sequence parallelism, enabling faster training and inference.
Where to Use Each Model
- S4: Best for continuous data tasks (e.g., time series, audio) where moderate sequence lengths are sufficient.
- DSS: Ideal for large-scale, real-time applications needing efficiency and interpretability (e.g., time-series forecasting).
- H3: Suited for language modeling tasks requiring Transformer-like expressivity with moderate sequence lengths.
- Mamba: Optimal for long-sequence tasks (e.g., document modeling, audio generation) needing high efficiency.
- Mamba-2: The go-to choice for large-scale, long-context modeling with enhanced training speed and performance.
Empirical Scaling and Performance Trends
Recent experiments have demonstrated that state space models scale remarkably well as their capacity increases. For instance, when scaled to billions of parameters, models such as Mamba and Mamba-2 achieve language modeling perplexities that rival or even surpass those of similarly sized Transformers. Empirical studies on benchmarks like OpenWebText and the Long Range Arena indicate that as the state dimension grows and longer contexts are leveraged, SSM-based architectures not only maintain their linear computational scaling but also benefit from improved performance. These scaling trends suggest that, with proper architectural tuning and parameter initialization, SSMs are emerging as a viable alternative for large-scale, long-context sequence modeling.
Summary & Key Takeaways
State Space Models (SSMs) offer a scalable alternative to transformers in language modeling by using state space equations to manage and update hidden states for generating outputs from inputs. Since its inception, there has been several important model enhancements. The following table summarizes their development, strengths, weaknesses, and time complexity:
| Year | Model | Contribution | Strengths | Weaknesses | Complexity |
|---|---|---|---|---|---|
| 2022 | Structured State Space (S4) | Leveraged Diagonal Plus Low-Rank parameterization to improve computational efficiency | Captures long-range dependencies efficiently | Complex architecture and implementation | [math]\displaystyle{ O(N log N) }[/math] with [math]\displaystyle{ FFT }[/math] |
| 2022 | Diagonal State Spaces (DSS) | Simplified S4 by using diagonal matrices to achieve comparable performance | Big data and real-time systems scalability | Performance depends on initialization and lacks capacity to handle information-dense data | For batch size [math]\displaystyle{ B }[/math], sequence length [math]\displaystyle{ L }[/math], and hidden size [math]\displaystyle{ H }[/math]: DSS layer requires [math]\displaystyle{ O(NHL) }[/math] time to compute kernels, [math]\displaystyle{ O(BHL logL) }[/math] time for discrete convolution and [math]\displaystyle{ O(BH^2L) }[/math] time for output projection. |
| 2023 | Hungry Hungry Hippos (H3) | Introduced new SSM layer consisting of two SSMs stacked together (a shift and diagonal SSM) to enable token recall and comparison across sequences | Transformer competitive performance on language modeling tasks | Less computationally efficient than other SSMs | For sequence length [math]\displaystyle{ N }[/math], and [math]\displaystyle{ d }[/math] hidden dimension, then [math]\displaystyle{ H3 }[/math] layer takes [math]\displaystyle{ O(d^2N + dN logN) }[/math] |
| 2024 | Mamba | Integrated selective state spaces to filter irrelevant information while being hardware-aware algorithm | Handles long sequences at faster inference and less memory requirements than Transformer | Scaling to compete with LLM requires complex engineering | Training is [math]\displaystyle{ O(N) }[/math], while inference is [math]\displaystyle{ O(1) }[/math] |
| 2024 | Mamba-2 | Used state space duality (SSD) to enable larger state dimensions | Tensor and sequence parallelism which allows for faster training and inference | Lack of inference optimization techniques like quantization and speculative decoding | Training is [math]\displaystyle{ O(N) }[/math], while inference is [math]\displaystyle{ O(1) }[/math] |
Future of SSMs
Ongoing research is focused on improving efficiency, adaptability, and scalability to position State Space Models (SSMs) as a viable alternative to Transformers. While SSMs excel at modeling long-range dependencies, they face hardware inefficiencies and an expressivity gap in tasks like language modeling. Key areas of research include:
1. Better hardware utilization: Optimizing SSM implementations to leverage GPU/TPU acceleration as efficiently as Transformers.
- Enhancing GPU/TPU acceleration through optimized memory access and tensor core utilization.
- Applying kernel fusion techniques to minimize redundant computations.
2. Adaptive SSMs: SSMs currently lack the expressivity of Transformers, particularly for tasks requiring complex reasoning. Developing architectures that can dynamically switch between SSM and attention-based processing depending on the task.
- Structured Masked Attention (SMA) for improved context retention and expressivity.
- Selective Copying & Induction Heads to enhance memory retention.
- State-passing algorithms to better preserve sequence dependencies.
3. Scaling laws for SSMs: SSMs scale efficiently for long-sequence tasks but require further study to match Transformers at large parameter counts. Understanding how these models perform at increasing levels of parameterization compared to standard deep learning architectures.
- Understanding scaling laws to optimize model depth and expressivity.
- Evaluating trade-offs between efficiency and generalization across tasks.
- Expanding SSM applications, particularly in speech, DNA, and document retrieval.
4. Hybrid Architectures with Dynamic Routing:
- Exploring deeper integrations between SSMs and Transformers, potentially using dynamic gating mechanisms or context-based routing, allowing models to dynamically switch processing modes depending on input characteristics or computational constraints.
5. Automated Hyperparameter and Architecture Search:
- Given the sensitivity of SSM performance to hyperparameter choices, research into automated hyperparameter optimization (such as Bayesian optimization or neural architecture search) could greatly reduce manual tuning, making SSMs more broadly applicable in practice.
6. Improved Visualization and Interpretability Techniques:
- Although inherently interpretable, visualization and diagnostic tools tailored specifically to SSM hidden states and transitions remain limited. Developing intuitive visualization tools would significantly improve the practical interpretability of SSM models, especially in high-dimensional or complex data scenarios.
By addressing these key areas, SSMs hold substantial promise for becoming the foundation of next-generation sequence modeling, especially where computational efficiency, adaptability, and interpretability are crucial, such as speech recognition, biological sequence modeling, and real-time inference systems.
Topic 8: Sparse Attention
Introduction
Vanilla Attention is very computationally expensive due to the multiplication of very large matrices required. This results in a complexity of [math]\displaystyle{ O(n^2) }[/math] where n may be very large, potentially even limiting the scalability of this method for long sequences. Sparse attention tries to address this problem by being more selective about what attention is computed. Intuitively, not all tokens need to attend to each other because not all words provide semantic information about all other words in a sentence. How can we determine which token-pairs are important? The goal of Sparse Attention is to answer this question in order to improve the efficiency and scalability of vanilla attention by not computing attention between all tokens without sacrificing performance.
Four methods were presented:
- Sparse Sinkhorn Attention
- Big Bird Sparse Attention
- Attention with Linear Biases (ALiBi)
- SpAtten
Sparse Sinkhorn Attention
Evaluation Metrics for Sparse Attention
To comprehensively evaluate the performance of sparse attention mechanisms, several key metrics are considered:
- Time Complexity
- The number of operations required during inference.
- Vanilla attention has quadratic complexity [math]\displaystyle{ O(n^2) }[/math], while sparse variants aim for linear or sub-quadratic complexity, such as [math]\displaystyle{ O(n \cdot N_k) }[/math] where [math]\displaystyle{ N_k \ll n }[/math].
- Memory Complexity
- Represents the total memory consumption needed for model parameters and intermediate activations.
- Sparse attention reduces this by avoiding full pairwise attention computations.
- Perplexity
- A standard measure to evaluate the predictive performance of language models.
- Defined as:
[math]\displaystyle{ \text{Perplexity}(P) = \exp\left(- \frac{1}{N} \sum_{i=1}^N \log P(w_i | w_1, \dots, w_{i-1}) \right) }[/math]
- Lower perplexity indicates better prediction capability.
These metrics help compare the efficiency and effectiveness of sparse attention methods to the original dense attention in practical applications.
Simplified Intuition
Imagine a crowded room where everyone is trying to talk at once—confusing and inefficient, right? That’s what happens in traditional attention: every token interacts with every other token, like a chaotic party where no one can really focus on the conversation. Sparse Sinkhorn Attention takes a different approach. It first acts like a clever host who quickly sorts the guests into smaller groups based on who’s most likely to have something in common. This sorting, done by a neat algorithm (the Sinkhorn normalization), gently reorders the tokens so that similar ideas end up together, allowing meaningful conversations in manageable clusters.
Once the guests are grouped, each token only needs to chat with its immediate neighbors, much like small, focused discussion groups. Even though tokens now converse locally, the smart grouping ensures that distant yet related ideas are brought close together. This not only cuts down on the chaos and computational cost but also preserves the essential flow of information—much like having productive, focused conversations instead of a noisy, all-out babble.
Overview
To address the computationally intensive of Vanilla Attention, especially for the long input sequence, Sparse Sinkhorn Attention proposes three core ideas:
- [math]\displaystyle{ \mathbf{Block} }[/math] [math]\displaystyle{ \mathbf{Partitioning} }[/math]
- The input sequence with length [math]\displaystyle{ l }[/math] is split into [math]\displaystyle{ N_b }[/math] blocks, each containing [math]\displaystyle{ b }[/math] tokens.
- [math]\displaystyle{ \mathbf{Block} }[/math] [math]\displaystyle{ \mathbf{Sorting} }[/math]
- Input blocks are sorted based on their similarity to the query.
- The Sinkhorn algorithm is then applied to generate a permutation matrix which ensures that relevant blocks are adjacent, and this algorithm also normalizes the sorting matrix to prevent overemphasis on certain input blocks.
- [math]\displaystyle{ \mathbf{Sparse\ (local)} }[/math] [math]\displaystyle{ \mathbf{Attention} }[/math]
- Instead of the full sequence, each token only computes the attention with token within its block (and tokens within its neighbour blocks).

Sorting Network
The original idea of block-based local attention is to allow tokens to only attend to tokens within the same block. However, this restricts the global attention field and limits the ability for local attention models to model long range dependencies, so we need to mitigates this problem by neural sorting of blocks, we learn this sorting through a neural network and gives a permutation matrix. We use a a Meta Sorting Network to learn to sort sequences to enable efficient quasi-global local attention. The equation of the Sorting Network is:
[math]\displaystyle{ R = P(x) = \sigma(W_B \sigma(W_pX+b_p) +b_B) }[/math]
Here, [math]\displaystyle{ R }[/math] becomes the permutation matrix, [math]\displaystyle{ \sigma }[/math] is an activation function and [math]\displaystyle{ W }[/math], [math]\displaystyle{ b }[/math] are the weights and biases. We can see that this is just a two-layer fully-connected neural network.
Sinkhorn normalization with Gumbel noise
We normalize the rows and columns of the sorting matrix using formula:
[math]\displaystyle{ S^0(R) = \frac{\exp(R)+\epsilon}{\tau} }[/math]
[math]\displaystyle{ S^k(R) = F_c(F_r(S^{k-1}(R))) }[/math]
where [math]\displaystyle{ F_r }[/math], [math]\displaystyle{ F_c }[/math] are the row and column wise normalization function, [math]\displaystyle{ \epsilon }[/math] is the injected standard i.i.d Gumbel noise and [math]\displaystyle{ \tau }[/math] is the temperature hyper-parameter.
Advantages over Vanilla Attention
- Reduced memory
- Sparse Sinkhorn Attention only needs [math]\displaystyle{ O\left(\left(\frac{l}{N_b}\right)^2 + N_b^2\right) }[/math], while Vanilla Attention requires [math]\displaystyle{ O(l^2) }[/math].
- Reduced Computational Complexity
- SORTCUT (a Sparse Sinkhorn Attention variant) only requires [math]\displaystyle{ O(lN_k) }[/math], where [math]\displaystyle{ N_k }[/math] is a hyperparameter which is much smaller than [math]\displaystyle{ l }[/math]. In contrast, Vanilla Attention requires [math]\displaystyle{ O(l^2) }[/math] time.
- Ability to Capture Long Range Dependency
- Through block sorting, relevant tokens are grouped adjacently, even if they are originally far apart. Then, through local attention, long range dependencies are captured. By comparison, Vanilla Attention struggles with this since it calculates attention for every tokens with all other tokens, and Softmax entropy collapse naturally reduces the importance of distant tokens, making it difficult to model long-range relationships both computationally and statistically.
Variants of Sparse Sinkhorn Attention
Keeping the core idea of improvements in efficiency and scalability in mind, the authors proposed two variants- Causal and SortCut Sinkhorn Attention to further improve performance.
Causal Sinkhorn Attention
This is a task-specific variant specifically proposed for autoregressive tasks where the future tokens do not have any influence on past and present tokens. Thus, the model is constrained to only attend to past and present tokens and not the future ones.
The original Sinkhorn balancing needs information on the future tokens for normalization, which is undesirable for causal attention. Thus, a new variation of Sinkhorn balancing is performed by masking the future tokens while performing iterative normalization. That is, we convert:
[math]\displaystyle{ F_k^c(X) = F^{k-1}_c(X) - \log \left( \exp(X1_l)1_N^T \right) \text{ and } F_r^k(X) = F^{k-1}_r(X) - \log \left(1_l 1_N^T \exp(X) \right) }[/math]
to
[math]\displaystyle{ F_k^c(X) = F^{k-1}_c(X) - \log \left( \exp(M(X)1_l)1_N^T \right) \text{ and } F_r^k(X) = F^{k-1}_r(X) - \log \left(1_l 1_N^T M(\exp(X)) \right) }[/math]
where,
[math]\displaystyle{ M(x) = \begin{cases} 1, & \text{if } j \geq i \\ 0, & \text{otherwise} \end{cases} }[/math]
This variant thus ensures the preservation of the causal nature for many sequence modeling tasks.
SortCut Attention
SortCut is a dynamic sequence truncation method that improves the efficiency of Sparse Sinkhorn Attention by focusing computational resources on the most relevant parts of the sequence. It first computes the importance scores for each token, followed by sorting them based on the computed relevance scores. Then the algorithm dynamically truncates to retain top-k relevant tokens. Then, it applies block-based attention only to the retained tokens.
The vanilla transformer has a self-attention memory complexity of [math]\displaystyle{ O(l^2) }[/math] and the Sinkhorn Attention model reduces to [math]\displaystyle{ O(B^2 + (\frac{l}{N_B})^2) }[/math] where l is input sequence length and [math]\displaystyle{ B=\frac{l}{N_B} }[/math]. The SortCut Attention model further reduces to O(lN_k + (N_b)^2)</math>, where N_k is the budget hyperparameter. This can further be reduced to [math]\displaystyle{ O(l) }[/math] since [math]\displaystyle{ \frac{l}{l_B}\lt \lt l }[/math]. Thus, the SortCut variant further reduces the computational complexity, allowing for the processing of even longer sequences by focusing on the most relevant parts.
Big Bird Sparse Attention
Background & Motivation
Naive attention has quadratic complexity (mainly in terms of memory) due to full attention calculation, which limits the applicability to tasks that require longer context (i.e., input sequence length). While empirically Transformers and self-attention have shown promising results, theoretical understanding is pretty basic: What aspect of self-attention are needed for its performance? Do we really need the full attention calculation to reach the performance?
By using sparse attention (i.e., not calculating the relationship between each pair of tokens), we hope that it allows us to scale to longer sequences while preserving the majority of the model's performance.
Theoretical Guarantee
The paper prove that sparse attention mechanisms, such as the one used in BigBird, can serve as universal approximators for dense attention Transformers.
- Universal Approximation Theorem:
- Given a class of functions [math]\displaystyle{ \mathcal{F}_{n,p} }[/math], any function [math]\displaystyle{ f \in \mathcal{F}_{n,p} }[/math] can be approximated within [math]\displaystyle{ \epsilon \gt 0 }[/math] by a sparse attention Transformer [math]\displaystyle{ g \in \mathcal{T}_{n,p,r} }[/math]
(i.e.,[math]\displaystyle{ d_{\mathcal{F}}(f, g) \leq \epsilon }[/math])
- This result holds as long as the underlying attention graph contains a star graph.
- Supporting Lemmas:
- Lemma 1: Scalar quantization of inputs using discrete maps.
- Lemma 2: Contextual mapping via learned sparse attention layers.
- Lemma 3 & 4: Construction of approximators with feedforward and attention layers using the sparse mechanism.
These results justify that BigBird retains the expressive power of standard Transformers, while being more scalable.
Intuition & Main Idea
Intuitively, we picture the tokens as nodes in a directed graph where attention is calculated between two tokens if an edge exists to connect their nodes. Then, using the adjacency matrix of this graph, attention is not calculated between disconnected nodes.
In order to decide which nodes to 'connect,' the authors combined several methods:
- Random Attention
- Nodes are connected randomly (whether attention is calculated for a particular token pair is determined randomly)
- Window Attention
- Intuitively, tokens that are closer together probably provide more semantic information about each other. Therefore, attention is calculated between tokens that occur within a particular distance from each other.
- Global Attention
- Some tokens are 'celebrities' so attention between them and all other tokens is calculated. This results in a maximum distance of 2 between any two tokens (nodes in the graph)
The final attention mechanism for BIGBIRD has all three of these parts as illustrated below:
Theoretically, the authors prove that any star-graph (graph which represents global attention) provides a lower bound for performance. Empirically, combining all three of the above methods into what the authors call 'BIGBIRD' results in higher model performance.
We may intepret the naming as:
- "Big": The ability of handling long sequences and overcome complexity of higher orders
- "Bird": A metaphor for bird's eye-view, combining global tokens (ability to observe the whole sequence), local sliding windows (ability to focus on local context), and random attention (ability to account for details that are random left over)
Results
QA tasks tests the model's ability to handle longer sequences and the ability to extract useful context.
Hotpot QA: For given question and documents, model is asked to generate correct answer and identify supporting facts
- Ans (Answer): checks if the answer matches the ground truth.
- Sup (Supporting Facts): checks if the model identifies sentences/evidences that support the answer.
- Joint: A joint evaluation that is considered correct iff both Ans and Sup are correct.
NaturalQ: For given question and documents, extract a short answer or a long answer
- LA (Long Answer): evaluates model's ability to extract longer (paragraph-level) answer from passage
- SA (Short Answer): evaluates model's ability to extract concise (short phrase like) answer from passage
TriviaQA: For given question and documents, generate an answer
- Full: Uses the complete set of questions with automatically paired evidence.
- Verified: Uses the set that is manually paired to ensure correctness.
For WikiHop: For a given question, supporting documents, the model is asked to choose a correct answer from a set of candidate answers
- MCQ (Multiple Choice Question): evaluates model's ability to do MCQ.
BigBird model outperforms RoBERTa and Longformer. At that time, there was also a burst in using deep learning for genomics data, most approaches consume DNA sequence fragments as inputs and BigBird achieved a 99.9 F1 score as well as 1.12 BPC (bits per character) on these tasks.
Limitations
Although BigBird achieves linear complexity, it does not come for free.
- Lower Bounds
- A natural task is displayed by the author that can be evaluated by O(1)-layer full attention mechanism. However, any sparse attention mechanism that has polynomial inner product evaluations and logarithmic length of the shortest path between any two nodes of the mechanism's digraph (thus more than just BigBird) needs to solve the task in at least polynomial layers.
Attention with Linear Biases (ALiBi)
ALiBi Mechanism
Currently, models struggle to extrapolate. Extrapolation is the ability to produce sequence lengths at inference time that are longer than the sequences they were trained on. For example, if a model is trained on a dataset where the longest sequence is 1024 tokens, then it will perform poorly when asked to generate a sequence of 2048 tokens. If we can solve this problem then, in theory, training can become much more efficient as we can train on shorter sequences without sacrificing performance.
The authors hypothesized that the position representation method used in these models influenced extrapolation ability. The authors first tested the extrapolation performance of transformers that use absolute position encodings. This includes sinusoidal position embeddings (as seen in vanilla transformer) and rotary position embeddings (seen in open source GPT-3). The authors found that these transformer models did not extrapolate well.
Then, they tested the extrapolation performance of transformer that employed T5 bias as the position method. This method is a relative position method; it does not add positional information to word embeddings. Instead, after computing the query-key score in attention and before executing softmax, it adds a learned, shared bias that is dependent on the distance between the query and key. This model produced an improve performance. The authors concluded that a relative position method improves extrapolation. However, due to the high computation cost, T5 bias is infeasible.
ALiBi replaces the vanilla transformer [math]\displaystyle{ softmax(QK^T) }[/math] with [math]\displaystyle{ softmax(QK^T + bias) }[/math], adding a lower triangular matrix of biases in order to encode the relative positioning of tokens within the attention calculation.
The bias matrix is of the form [math]\displaystyle{ \begin{bmatrix} 0 & 0 & 0 & 0\\ -1 & 0 & 0 & 0\\ -2 & -1 & 0 & 0\\ -3 & -2 & -1 & 0\\ \end{bmatrix} }[/math]
The addition of this bias leads to a recency bias. A query-key pair that are far apart will have a large bias. The increasing penalty results in less information learned from distant query-key pairs.
The authors hypothesized that this could replace the positional encoding in transformers. For model architectures with multiple attention heads, the weighting of these biases can vary per head (defaulting to a geometric sequence of [math]\displaystyle{ \frac{1}{2^m} }[/math] where m is the number of heads.)
So even through ALiBi is considered to be a spare attention method, it didn't specify sparsity explicitly. As tokens gets far from one another, the bias becomes small and implicitly, we have sparsity.
Experimental Results
Experiments with a 1.3 billion parameter model on the WikiText-103 dataset showed ALiBi, trained on 1024-token sequences, matched the perplexity of sinusoidal models trained on 2048-token sequences when tested on 2048 tokens. ALiBi was 11% faster and used 11% less memory.<ref name="Press2021" /> Results are summarized below:
| Method | Training Length | Test Length | Perplexity | Training Time | Memory Use |
|---|---|---|---|---|---|
| Sinusoidal | 2048 | 2048 | 20.5 | 100% | 100% |
| ALiBi | 1024 | 2048 | 20.6 | 89% | 89% |
| Rotary | 1024 | 2048 | 22.1 | 95% | 92% |
Implications
ALiBi's efficiency and extrapolation ability suggest it could reduce training costs and improve scalability in transformer models. Its recency bias aligns with linguistic patterns, making it a promising advancement.
SpAtten
Introduction
One of the major limitations of LLMs is the computational cost. One of the major inefficiencies is the long input sequence length and large KV cache. The authors have shown that much of the overall latency in attention is computing the [math]\displaystyle{ Q\times K }[/math] matrix. This matrix is [math]\displaystyle{ n\times n }[/math], where [math]\displaystyle{ n }[/math] is the sequence length. The author proposes to reduce the computational cost by shrinking the sequence length [math]\displaystyle{ n }[/math]. The objective is to remove tokens (or words in a sequence) during attention to reduce computation.
Sparse Attention
SpAtten is a method for pruning both tokens and attention heads in transformer models to improve efficiency. By removing tokens and heads with pruning, SpAtten reduces computational complexity and memory usage.
There are four key components to SpAtten:
1. Cascade Token Pruning
2. Cascade Head Pruning
3. Progressive Quantization
4. Specialized High Parallelism top-k Engine.
The first two are motivated by the inherent redundancy in human languages. Cascade token pruning helps to identify and remove unimportant tokens in a sentence; semantically-important tokens remain. For example, in the English language, syntactic words like prepositions, article words, etc... would be considered unimportant, and thus pruned. The reduction in token sequence length reduces the computation cost when executing atttention.
Similarly, cascade head pruning eliminates unnecessary attention heads. Recall that in multi-head attention, one executes attention with multiple heads to capture various token dependency relationships. However, some heads may be redundant to the output. These heads would be pruned.
Unlike traditional weight pruning techniques, cascade token and cascade head pruning operates dynamically and selects tokens and heads to prune on the fly during inference. As an example, given an initial sentence of "As a visual treat, the film is almost perfect." with 11 tokens and 12 heads, cascade pruning results in a final output of "film perfect" with only 2 tokens and 8 heads. The final output retains the essence of the initial sentence but would use less memory and be less computationally expensive to train.
The latter two components play a pivotal role in ensuring the efficient implementation of SpAtten. Progressive quantization is designed to strike a balance between computational efficiency and accuracy by dynamically adjusting the precision of computations. The process begins by handling only the most significant bits (MSBs) of the input data, enabling faster computations and reduced memory access. If the confidence in the result is insufficient, the system progressively incorporates more bits of data to recompute the output with higher precision. This approach is further refined by assigning different bitwidths to different layers, optimizing performance across the model.
Similarly, SpAtten employs a specially designed top-k engine to enable real-time decision-making for pruning tokens and attention heads. This engine efficiently ranks token and head importance scores in linear time, avoiding the inefficiencies of traditional sorting methods. Instead of sorting an entire array, the top-k engine uses a quick-select module to identify the kth largest element and filters the array based on this threshold. This technique is also implemented in a highly parallelized manner, with multiple comparators working simultaneously to achieve linear-time ranking. This streamlined process ensures rapid and accurate pruning decisions, contributing to SpAtten's overall efficiency.
Adaptively Sparse Attention
Motivation
Although Sparse Attention methods like BigBird and Sparse Sinkhorn Attention successfully reduce computational complexity from quadratic to linear or near-linear, they often use predefined patterns (e.g., sliding windows, global tokens, random attention). These predefined patterns may not always reflect the optimal relationships within the sequence for every context. Adaptively Sparse Attention addresses this limitation by dynamically determining which tokens should attend to each other based on their semantic or contextual relationships.
Core Idea
Adaptively Sparse Attention dynamically creates sparse attention patterns by identifying the most significant attention connections for each query token based on current input features. Instead of attending to a fixed set of neighbors, each token selectively attends only to tokens with high relevance scores.
Formulation
Given the queries [math]\displaystyle{ Q \in \mathbb{R}^{T \times d} }[/math], keys [math]\displaystyle{ K \in \mathbb{R}^{T \times d} }[/math], and values [math]\displaystyle{ V \in \mathbb{R}^{T \times d_v} }[/math], the standard attention mechanism computes:
[math]\displaystyle{ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d}}\right)V }[/math]
In Adaptively Sparse Attention, we introduce an adaptive binary mask [math]\displaystyle{ M \in \{0, 1\}^{T \times T} }[/math] that selects which key tokens each query should attend to, effectively pruning unnecessary computations. Specifically, the formulation becomes:
Step 1. Compute standard attention scores: [math]\displaystyle{ S = \frac{QK^T}{\sqrt{d}} }[/math]
Step 2. For each query token [math]\displaystyle{ i }[/math], select a subset of keys by applying a top-[math]\displaystyle{ k }[/math] operator or adaptive thresholding: [math]\displaystyle{ M_{ij} = \begin{cases} 1, & \text{if } S_{ij} \text{ is among the top-} k \text{ scores for row } i\\[6pt] 0, & \text{otherwise} \end{cases} }[/math]
Step 3. Compute the sparse attention: [math]\displaystyle{ \text{Attention}(Q,K,V) = \text{softmax}(S \odot M) V }[/math]
Here, [math]\displaystyle{ \odot }[/math] denotes element-wise multiplication. Softmax normalization is computed over the nonzero elements in each row.
Advantages
- Reduced computational complexity: By dynamically restricting attention computations to the top-[math]\displaystyle{ k }[/math] relevant keys per query, the complexity reduces from [math]\displaystyle{ O(T^2) }[/math] to approximately [math]\displaystyle{ O(Tk) }[/math], which can be near-linear for [math]\displaystyle{ k \ll T }[/math].
- Context-aware sparsity: The adaptive selection allows the model to naturally focus on relevant tokens based on the input context, thus preserving performance while substantially improving efficiency.
- Improved scalability: Suitable for very long sequences, Adaptively Sparse Attention provides computational efficiency needed for large-scale applications (e.g., long-document understanding, genomic sequences).
Example
Suppose we have an attention score matrix [math]\displaystyle{ S \in \mathbb{R}^{4 \times 4} }[/math] (4 tokens for simplicity):
[math]\displaystyle{ S = \begin{bmatrix} 0.1 & 2.0 & 0.5 & 0.2 \\ 1.5 & 0.3 & 0.8 & 0.4 \\ 0.2 & 0.1 & 3.0 & 0.5 \\ 0.7 & 0.6 & 0.4 & 0.2 \\ \end{bmatrix} }[/math]
We set top-2 sparsity per row:
Step 1. Select the top-2 scores per row:
- Row 1: scores 2.0 and 0.5 (columns 2 and 3)
- Row 2: scores 1.5 and 0.8 (columns 1 and 3)
- Row 3: scores 3.0 and 0.5 (columns 3 and 4)
- Row 4: scores 0.7 and 0.6 (columns 1 and 2)
Step 2. Form adaptive mask [math]\displaystyle{ M }[/math]:
[math]\displaystyle{ M = \begin{bmatrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & 1 & 0 & 0 \\ \end{bmatrix} }[/math]
Step 3. Element-wise multiply to get sparse scores:
[math]\displaystyle{ S' = S \odot M = \begin{bmatrix} 0 & 2.0 & 0.5 & 0 \\ 1.5 & 0 & 0.8 & 0 \\ 0 & 0 & 3.0 & 0.5 \\ 0.7 & 0.6 & 0 & 0 \\ \end{bmatrix} }[/math]
Step 4. Apply row-wise softmax on nonzero entries. For example, row 1 nonzero entries (2.0, 0.5):
[math]\displaystyle{ \text{softmax}(2.0, 0.5) \approx [0.82, 0.18] }[/math]
Step 5. The final sparse attention output becomes:
[math]\displaystyle{ \text{Attention}(Q,K,V) = \text{softmax}(S')\,V }[/math]
Only selected entries are used, dramatically reducing computations.
Comparison
| Method | Key Focus | How It Works | Primary Benefit | Primary Trade-off |
|---|---|---|---|---|
| Sparse Sinkhorn | Global interactions via learned sorting | Rearranges tokens to place important ones together in local blocks for efficient attention | Retains global attention while reducing compute | Sorting overhead adds computation; complex implementation |
| BigBird | Local context with selective global/random links | Uses a fixed sparse pattern (local window + some global/random tokens) to approximate full attention | Scales to long sequences without needing per-sequence tuning | Fixed sparsity means some interactions might be missed |
| ALiBi | Recency bias via linear attention penalty, enables extrapolation to longer sequence lengths | Applies a penalty to distant tokens in attention scores, encouraging focus on closer tokens | Extrapolates well to longer sequences without increasing training costs | Does not reduce compute/memory at inference; only helps training |
| SpAtten | Dynamic token and head pruning for efficiency | Dynamically removes unimportant tokens and attention heads at inference for efficiency | Maximizes efficiency while preserving accuracy | Requires custom logic/hardware for full benefits |
| Method | Memory Efficiency | Computational Speed | Accuracy vs Full Attention | Real-World Adoption |
|---|---|---|---|---|
| Sparse Sinkhorn | High (learned local attention reduces need for full attention) | Moderate (sorting overhead but reduced attention computation) | Near-parity (sometimes better, as learned sparsity is adaptive) | Limited (mainly research, complex to implement) |
| BigBird | Very High (reduces O(n²) to O(n) via sparse pattern) | Fast (sparse pattern significantly reduces compute) | Near-parity (captures long-range dependencies well) | High (used in NLP for long-text tasks, available in HuggingFace) |
| ALiBi | Same as full attention (no sparsity, just biasing) but can use smaller context length in training | Same as full attention (no change in complexity) but can use smaller context length in training | Same (performs as well as full attention with added extrapolation) | Very High (adopted in major LLMs like BLOOM, MPT) |
| SpAtten | Extremely High (prunes tokens/heads dynamically) | Extremely Fast (up to 162× faster on specialized hardware) | Same (no accuracy loss, just efficiency gain) | Limited (research and specialized hardware, not common in open-source models) |
Future of Sparse Attention
Sparse attention mechanisms have emerged as a promising approach to improving the efficiency of transformer-based models by reducing computational and memory complexity. However, despite these advantages, they introduce trade-offs that warrant further research. Ongoing and future work in this area aims to enhance their expressivity, efficiency, and adaptability across diverse applications.
1. Enhancing Long-Range Dependency Modeling
Current sparse attention approaches struggle to fully capture distant contextual dependencies, limiting their effectiveness in tasks requiring extended sequence understanding.
- While models like ALiBi demonstrate strong extrapolation, performance degrades beyond twice the training sequence length, indicating room for improvement.
- Future work should focus on developing more robust mechanisms for retaining long-range information without sacrificing efficiency.
2. Reducing Computational Overhead
Despite their efficiency gains, some sparse attention methods introduce additional computational challenges:
- Sparse Sinkhorn Attention requires iterative normalization (Sinkhorn balancing), increasing computational cost.
- Pruning-based methods (e.g., SpAtten) introduce runtime overhead due to dynamic token and head selection.
- Many sparse attention models rely on specialized hardware acceleration (e.g., top-k engines), limiting their accessibility in general-purpose computing environments.
Addressing these issues will be crucial for making sparse attention models more widely applicable.
3. Optimizing Sparse Attention Architectures
A key challenge is designing architectures that achieve high performance while maintaining efficiency. Future research should explore:
- Balancing efficiency and expressivity by reducing the number of layers needed to match the performance of full attention models.
- Hybrid approaches that integrate multiple sparse attention mechanisms to leverage their respective strengths.
By addressing these challenges, future iterations of sparse attention models can push the boundaries of efficiency while preserving the rich contextual modeling capabilities of transformers.
Topic 10: Linear Attention
Introduction
Linear attention tries to address the efficiency limitations of traditional softmax attention. Standard attention (also called vanilla attention) is calculated as:
[math]\displaystyle{ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V }[/math]
The computation complexity of this method is [math]\displaystyle{ O(n^2d) }[/math] for sequence length [math]\displaystyle{ n }[/math] and representation dimension [math]\displaystyle{ d }[/math] and the main reason behind that is the multiplication of [math]\displaystyle{ Q }[/math] and [math]\displaystyle{ K^T }[/math], produces a large [math]\displaystyle{ n \times n }[/math] attention matrix. If we remove the softmax function from this equation, then we can reduce the computational intensity because the matrix multiplication can be reordered to [math]\displaystyle{ Q(K^T V) }[/math]. Multiplying [math]\displaystyle{ K^T V }[/math] first results in smaller matrix multiplications. However, this linear mapping is insufficient to capture the complex relationships in the data. To reintroduce more complexity, we can replace the softmax function with some kernel with approximates it. Recall that for any kernel [math]\displaystyle{ K, K(x, y)= \Phi(x)^T \Phi(y) }[/math] for a matrix [math]\displaystyle{ \Phi }[/math]. If we apply this kernel to Q and K, then we can approximate vanilla attention with a much more efficient mechanism.
Recent research has explored more sophisticated approaches to restore the modelling power of linear attention while preserving efficiency. For instance, Retentive Networks (RetNet) introduce a learnable decay-based recurrence that enables [math]\displaystyle{ O(1) }[/math] inference with strong performance on language tasks. Gated Linear Attention (GLA) incorporates a data-dependent gating mechanism to better capture context, and BASED proposes a hybrid strategy combining linear attention with sliding-window attention to balance throughput and recall. TransNormerLLM refines positional embeddings and normalization while accelerating linear attention with hardware-friendly techniques.
Linear attention is particularly useful for large-scale models and scenarios where memory and computing are constrained. Unlike traditional Transformers, which rely heavily on key-value caching and suffer latency bottlenecks during inference, linear attention variants can support faster decoding with lower memory usage. These properties make them attractive for applications such as real-time processing, edge deployment, and next-generation large language models.
Key Approaches to Linear Attention
Retentive Network (RetNet): A Successor to Transformer for Large Language Models
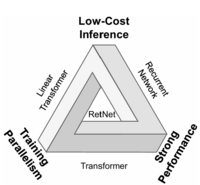
The authors of this paper introduce a new architecture that can achieve parallel training, fast inference, without compromising performance solving the inherent complexity in vanilla attention mechanism. They claim that the new architecture makes the impossible triangle, Figure 1, possible. RetNet combines the advantages of transformer performance and ability for parallel training with the lower-cost inference of RNNs by introducing a multi-scale retention mechanism to replace multi-head attention that incorporates three main representations:
- Parallel: allows GPU utilization during training.
- Recurrent: enables low-cost inference with [math]\displaystyle{ O(1) }[/math] complexity in terms of computation and memory.
- Chunkwise recurrent: models long-sequences efficiently.
Essentially, RetNet replaces the [math]\displaystyle{ softmax }[/math] by adopting a linear representation of the attention mechanism in the form of retention.
Recurrent Representation
We can show that the retention mechanism has a dual form of recurrence and parallelism (Figure2). First let's show RetNet in its recurrent form:
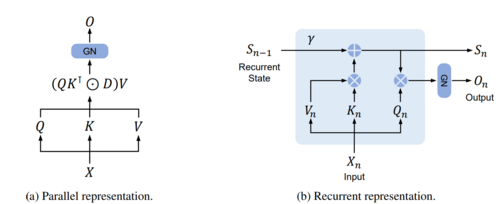
[math]\displaystyle{ S_n = \gamma S_{n-1} + K_n^T V_n }[/math]
[math]\displaystyle{ \text{Retention}(X_n) = Q_n S_n }[/math]
In this formula, [math]\displaystyle{ \gamma }[/math] is a decay factor, ensuring that more recent tokens are weighted more heavily, simulating recency bias without storing all past activations. [math]\displaystyle{ Q }[/math], [math]\displaystyle{ K }[/math], [math]\displaystyle{ V }[/math] are learned projections of the input. During training, this can be computed in parallel form.
Parallel Representation
Now, we can show the parallel representation of retention:
[math]\displaystyle{ \text{Retention}(X) = (QK^T \odot D)V }[/math]
Where [math]\displaystyle{ D }[/math] is a matrix that combines causal masking and exponential decay along relative distance. For better understanding the role of matrix [math]\displaystyle{ D }[/math], let's take a look at its formula:
[math]\displaystyle{ D_{nm} = \begin{cases} \gamma^{n-m}, & n \geq m \ 0, & n \lt m \end{cases} }[/math]
This formulation ensures that tokens can only attend to previous tokens (which they call it, causal masking) and the attention strength decays exponentially with distance (controlled by parameter [math]\displaystyle{ \gamma }[/math]). In other words, as we move forward, less attention is paid to earlier tokens.
Chunkwise Recurrent Representation
The third component, chunkwise recurrent representation, is a hybrid of recurrent and parallel representations aimed at training acceleration for long sequences. Simply, the input sequence is divided into chunks, where in each chunk a parallel representation is utilized to process all the tokens simultaneously. To pass information across chunks, the recurrent representation is used to create a summary of that chunk and pass it to the next. The combination of inner-chunk (parallel) and cross-chunk (recurrent) information produce the retention of the chunk which captures the details within the chunk and the context from previous chunks. To compute the retention of the i-th chunk, let [math]\displaystyle{ B }[/math] be the chunk length, then:
[math]\displaystyle{ Q_{[i]} = Q_{Bi:B(i+1)}, K_{[i]} = K_{Bi:B(i+1)}, V_{[i]} = V_{Bi:B(i+1)} }[/math]
[math]\displaystyle{ R_i = K_{[i]}^T (V_{[i]} \odot \zeta) + \gamma^B R_{i-1}, \quad \zeta_{ij} = \gamma^{B-i-1} }[/math]
[math]\displaystyle{ {Retention}(X_{[i]}) = \underbrace{(Q_{[i]} K_{[i]}^T \odot D) V_{[i]}}_{Inner-Chunk} + \underbrace{(Q_{[i]} R_{i-1}) \odot \xi}_{Cross-Chunk}, \quad \xi_{i,j} = \gamma^{i+1} }[/math]
where [math]\displaystyle{ R_i }[/math] is the state of the current chunk to be passed to the next.
In summary, the overall architecture of RetNet consists of stacked identical L blocks similar to Transformer. Each block consists of two modules: multi-scale retention (MSR) module and a feed-forward network (FFN) module. It takes the embeddings of input sequence [math]\displaystyle{ X^0= [x_1, \dots, x_{|x|}] \in \mathbb R^{|x| \times d_{model}} }[/math] and compute the output [math]\displaystyle{ X^L }[/math]:
[math]\displaystyle{ Y^l = MSR(LN(X^l)) + X^l }[/math]
[math]\displaystyle{ X^{l+1} = FFN(LN(Y^l)) + Y^l }[/math]
where [math]\displaystyle{ LN(.) }[/math] is LayerNorm.
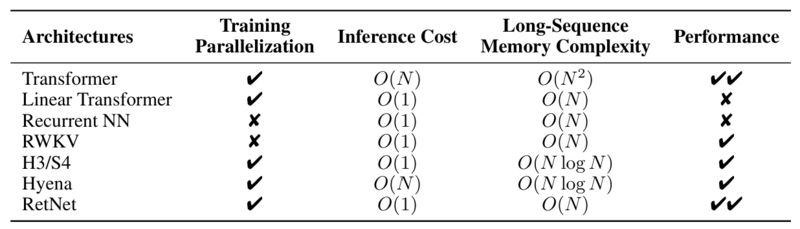
Comparison, Limitations & Future Work
Finally, comparing RetNet to other solutions, we can see that it provides a solid alternative to the Transformer achieving parallel training, fast inference, linear long-sequence memory complexity, and good performance. The limitations of this architecture can be summarized in the following points:
- Limited Cross-Modal Exploration
- The method is primarily validated on language modeling tasks. Its applicability to other modalities (e.g., vision, audio) remains unexplored, requiring further research for broader adoption.
- RetNet achieves superior GPU utilization compared to standard Transformers during training due to its parallel retention mechanism. In practice, it allows training with significantly fewer memory bottlenecks, making it ideal for scaling to longer sequences or deeper models.
Memory-Recall Tradeoff
A fundamental tradeoff exists between the size of a model's recurrent state and its ability to recall past tokens accurately. Some architectures, like BASED, combine linear attention with a sliding window of exact softmax attention to navigate this tradeoff. By adjusting hyperparameters such as the window size and feature dimensions, these models can traverse the Pareto frontier—achieving high recall with a small memory footprint while still benefiting from high throughput.
This paper focuses on the task of associative recall and discusses the memory-recall tradeoff. The memory-recall tradeoff basically states that higher recall requires higher memory consumption, as shown in Figure 3. This tradeoff manifests in different ways across model architectures:
- Vanilla attention models: achieve excellent recall but at the cost of quadratic computational complexity
- Linear attention models: offer better efficiency but often struggle with accurate information retrieval
- State-space models like Mamba: show that increasing recurrent state size generally improves recall accuracy but introduces computational overhead
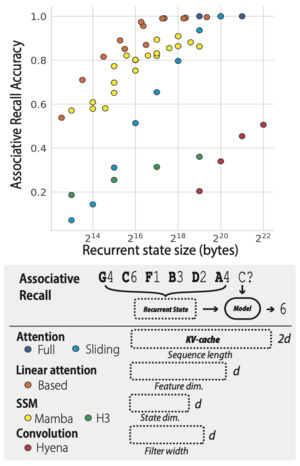
Implementations
The authors introduced Based architecture to improve this tradeoff. They do so by stacking linear attention blocks with sliding window attention blocks. Recall that one of the limitations of linear attention is relatively poor performance compared to vanilla attention. By selecting this type of architecture, the authors compromise on global performance by allowing linear attention to map global dependencies while retaining high performance within a local window by using the sliding window attention to map local dependencies. As seen in figure 4, they achieve this goal.
Chunking Strategy
Chunking involves spliting the input sequence [math]\displaystyle{ X }[/math] into chunks of length [math]\displaystyle{ B }[/math]. For each chunk [math]\displaystyle{ i }[/math], let
[math]\displaystyle{ Q_{[i]} = Q_{B i : B(i+1)}, \quad K_{[i]} = K_{B i : B(i+1)}, \quad V_{[i]} = V_{B i : B(i+1)} }[/math]
be the query, key, and value vectors (respectively) for that chunk. We maintain a recurrent “global” state [math]\displaystyle{ R_i }[/math] that summarizes information from all previous chunks and combine it with a “local” sliding-window attention over the current chunk.
Global Linear Attention (Recurrent “State”)
We use a feature map [math]\displaystyle{ \Phi(\cdot) }[/math] (e.g., a kernel or ELU-based mapping) to make attention linear in the sequence length. We update a global state [math]\displaystyle{ R_i }[/math] for each chunk:
[math]\displaystyle{ R_i = R_{i-1} + \Phi\bigl(K_{[i]}\bigr)^\top , V_{[i]}, }[/math]
and compute the global attention contribution for the [math]\displaystyle{ i }[/math]-th chunk:
[math]\displaystyle{ \mathrm{GlobalAttn}(X_{[i]}) = \Phi\bigl(Q_{[i]}\bigr),R_{i-1}. }[/math]
Intuitively, [math]\displaystyle{ R_{i-1} }[/math] aggregates (in linear time) all key-value information from past chunks.
Taylor Linear Attention
The Based architecture specifically employs a second-order Taylor series expansion as the feature map for linear attention. This approximation offers a good balance between computational efficiency and performance: [math]\displaystyle{ \Phi(x) = \begin{bmatrix} 1 \\ x \\ \frac{x^2}{2} \end{bmatrix} }[/math]
This feature map provides a reasonable approximation of the softmax function while maintaining the linear complexity benefits.
Local Sliding-Window Attention (Exact)
Within the current chunk, we also apply standard (exact) attention to a small window of recent tokens. Denote the set of token indices in this window by [math]\displaystyle{ \mathcal{W}_i }[/math]. Then:
[math]\displaystyle{ \mathrm{LocalAttn}(X_{[i]}) ;=; \sum_{j ,\in, \mathcal{W}i} \mathrm{softmax}!\Bigl(\frac{Q{[i]},K_j^\top}{\sqrt{d}}\Bigr),V_j.! }[/math]
This term captures fine-grained, short-range dependencies at full (exact) attention fidelity, but only over a small neighborhood [math]\displaystyle{ \mathcal{W}_i }[/math].
Final Output per Chunk
The total representation for chunk [math]\displaystyle{ i }[/math] is a sum of global (linear) and local (windowed) attention:
[math]\displaystyle{ h_{[i]} ;=; \mathrm{GlobalAttn}(X_{[i]}) ;+; \mathrm{LocalAttn}(X_{[i]}).! }[/math]
By combining a linear-time global update ([math]\displaystyle{ R_i }[/math]) with high-resolution local attention, the model balances throughput (via the efficient global linear component) and recall (via exact local attention). This addresses the memory-recall tradeoff: large contexts are captured without quadratically scaling memory usage, while local windows preserve high accuracy on short-range dependencies.
Hardware Optimizations
Recent work has shown that linear attention can be made even more practical when its implementation is tailored to the underlying hardware. For example, methods like FLASHLINEARATTENTION integrate I/O-aware techniques to minimize data movement between high-bandwidth memory and faster on-chip memories, resulting in real-world speedups that can even outperform optimized softmax attention implementations on moderate sequence lengths.
The Based Architecture includes several hardware-aware optimizations:
- Memory-efficient linear attention: The implementation fuses the feature map and causal dot product computation in fast memory, reducing high-latency memory operations.
- Optimized sliding window: The window size is carefully selected to align with hardware constraints (typically 64×64 tiles), balancing computation and memory bandwidth.
- Register-level computation: Critical calculations are performed in registers whenever possible, minimizing data movement between different memory hierarchies.
FLASHLINEARATTENTION: Hardware-Efficient Linear Attention for Fast Training and Inference
FLASHLINEARATTENTION is an I/O-aware, hardware-efficient linear attention mechanism for efficient data movement between shared memory (SRAM) and high-bandwidth memory (HBM). The goals are to alleviate memory bottlenecks, maximize GPU parallelism, and accelerate training and inference. The method significantly outperforms even FLASHATTENTION-2 at moderate sequence lengths (~1K tokens). Softmax-based self-attention, which is standard attention mechanism, is quadratic in both computation and memory complexity, making it inefficient for long sequences and scalability-constrained. Linear attention attempts to reduce this complexity, but most of them are not GPU-optimized for modern GPUs and do not provide real-world speed improvements. FLASHLINEARATTENTION solves this by splitting the input sequence into more manageable pieces where computation can independently be performed on each piece before global state updating. This alleviates redundant memory access, decreased latency GPU operations, and keeps tensor cores in effective use.
Mathematically, FLASHLINEARATTENTION builds upon linear attention, which rewrites standard softmax attention as:
[math]\displaystyle{ \text{Attention}(Q, K, V) = \text{softmax} \left(\frac{QK^T}{\sqrt{d}} \right) V }[/math]
instead of explicitly computing the full [math]\displaystyle{ n \times n }[/math] attention matrix, linear attention approximates it using a kernel function [math]\displaystyle{ \phi(x) }[/math] such that:
[math]\displaystyle{ \text{Attention}(Q, K, V) \approx \frac{\phi(Q) (\phi(K)^T V)}{\phi(Q) (\phi(K)^T)} }[/math]
where [math]\displaystyle{ \phi(x) }[/math] is a feature map transformation ensuring that the inner product approximates the softmax function. In standard parallel linear attention, the output is computed as:
[math]\displaystyle{ O = (Q K^T) V }[/math]
which still has quadratic complexity [math]\displaystyle{ O(n^2 d) }[/math]. FLASHLINEARATTENTION, on the other hand, splits the input sequence into pieces and processes them separately while having a hidden state [math]\displaystyle{ S }[/math]. The rule to update the hidden state is in a recurrent form:
[math]\displaystyle{ S[i+1] = S[i] + \sum_{j=1}^{C} K_j^T V_j }[/math]
[math]\displaystyle{ O[i+1] = Q[i+1] S[i] + (Q[i+1] K[i+1]^T \odot M) V[i+1] }[/math]
Here, [math]\displaystyle{ M }[/math] is a causal mask, ensuring attention is calculated only for tokens in the past. Chunkwise computation, minimizing memory overhead by splitting the sequence into smaller chunks to process, is the most crucial optimization in FLASHLINEARATTENTION to enhance efficiency. Chunks can be processed independently, allowing parallel execution. HBM I/O cost minimization is another key optimization, avoiding unnecessary data transfer between HBM and SRAM by reusing on-chip loaded tensors. When [math]\displaystyle{ Q[n] }[/math] is loaded into SRAM, both [math]\displaystyle{ Q[n]S }[/math] and [math]\displaystyle{ (Q[n]K[n]^T \odot M)V[n] }[/math] are computed without reloading [math]\displaystyle{ Q[n] }[/math]. FLASHLINEARATTENTION has two implementations. In the non-materialization version, hidden states [math]\displaystyle{ S[i] }[/math] are stored in SRAM to enable memory-efficient computation. In the materialization version, all [math]\displaystyle{ S[i] }[/math] are stored in HBM to enable full sequence-level parallelism. The materialization version is slightly slower but boosts training throughput by 10-20%. The calculation is parallel for chunks but sequential between chunks. This is for efficiency and handling of memory to render the algorithm suitable for processing long sequences.
The FLASHLINEARATTENTION forward pass algorithm goes as follows. For input matrices [math]\displaystyle{ Q }[/math], [math]\displaystyle{ K }[/math], and [math]\displaystyle{ V }[/math] of size [math]\displaystyle{ L \times d }[/math] and chunk size [math]\displaystyle{ C }[/math], the sequence is divided into [math]\displaystyle{ N = L / C }[/math] blocks as: [math]\displaystyle{ Q = \{ Q[1], Q[2], ..., Q[N] \}, \quad K = \{ K[1], K[2], ..., K[N] \} }[/math]
The hidden state is initialized as [math]\displaystyle{ S = 0 }[/math] in SRAM. For each chunk, [math]\displaystyle{ S }[/math] is stored in HBM if materialization is enabled, and the corresponding [math]\displaystyle{ K[n], V[n] }[/math] values are loaded into SRAM. The hidden state update follows:
[math]\displaystyle{ S = S + K[n]^T V[n] }[/math]
and the output for each chunk is computed in parallel as:
[math]\displaystyle{ O'[n] = Q[n] S + (Q[n] K[n]^T \odot M) V[n] }[/math]
The outputs are then stored in HBM and fed as outputs. The algorithm maintains a trade-off between memory usage and parallelization such that training speeds are higher than previous linear attention versions. FLASHLINEARATTENTION offers significant performance gains compared to several other attention models. Speedup gains involve less than FLASHATTENTION-2 on sequences shorter than 4K tokens and doubling of training speeds compared to standard linear attention. Memory efficiency is improved through reducing HBM I/O expense and removing redundant data movement, with 4x less memory usage compared to baseline softmax attention. Scalability is also a benefit, allowing for processing of sequences longer than 20K tokens without quadratic memory growth. These improvements make FLASHLINEARATTENTION a solid tool for large-scale transformers, improving efficiency in training and inference. By integrating FLASHLINEARATTENTION into traditional transformer designs, large language models can be significantly accelerated, and large-scale deployment made more viable. Future work can explore deeper kernel optimizations, CUDA-specific workloads, and hardware-specific transformations to further enhance efficiency. FLASHLINEARATTENTION is a significant advancement in hardware-efficient deep learning, supporting memory-efficient training at higher speeds for large-scale transformers. By optimizing memory access, chunking input sequences, and parallel intra-chunk computation, it achieves significant speedup with strong recall ability, making it a landmark achievement in the efficient processing of long sequences.
Empirical Results
In Table 3, comparison was made between Transformer and RetNet on a variety of downstream tasks (i.e., HS, BoolQ, etc). In both zero-shot and 4-shot learning, RetNet achieved a higher accuracy on all tasks listed. In Table 4, the authors compared the training speed and memory usage of Transformer, Transformer with FlashAttention and RetNet, the training sequence length is fixed at 8192 tokens. Results show that RetNet consumes less memory while achieving a higher throughput than both Transformer and Transformer with FlashAttention. Recall that in FlashAttention the technique of kernel fusion was applied while here RetNet was implemented naively. Therefore, there's potential for improvements upon the current results, which already exceeds the other two models.
Limitations
While the Based Architecture presents a promising direction, it still faces some challenges:
- Implementation complexity: The dual-attention mechanism and hardware optimizations add complexity to the implementation.
- Hyperparameter sensitivity: The optimal balance between global and local attention components may vary across different tasks and datasets.
- Performance gap: Despite improvements, there remains a gap between Based models and state-of-the-art vanilla attention models on some specific tasks.
Gated Linear Attention (GLA)
RetNet shows us we can achieve parallel training, efficient inference, and more optimized performance. However, despite its innovations, RetNet still has significant limitations. The biggest problem with RetNet was how it handled sequential data. RetNet uses a constant decay factor ([math]\displaystyle{ \gamma }[/math]) that doesn't adapt to the content being processed. Let's imagine a conversation where you treat every fifth word equally regardless of how significant. That is what RetNet does with its constant exponential decay factor. What that means is that RetNet treats all sequential dependencies the same way, regardless of whether the current content requires more emphasis on recent tokens or on tokens much farther back. This process could work, but not necessarily optimally.
Furthermore, while RetNet is theoretically efficient, it is not so effective in practice on real hardware. The algorithms are not I/O-aware, and therefore they do not account for how data is being moved between levels of memory in modern GPUs and this leads to suboptimal performance. Gated Linear Attention (GLA) advances linear attention by solving such key limitations.
The new idea of GLA is the use of data-dependent gates. Unlike RetNet which uses fixed decay factors, these gates dynamically adjust based on the content being processed and this makes the model more powerful. It likes an intelligent filter that decides, at each position in a sequence, how much information should pass through depending on its relevance. For example, when processing the phrase "Prime Minister" in "The Prime Minister of Canada," the model might focus more on "Canada" than on "The". This is something RetNet with fixed decay cannot achieve. GLA introduces a gating mechanism where the output is determined by the below formula:
[math]\displaystyle{ \text{Output} = \text{LinearAttention} \odot \text{ContentGate} }[/math]
The ContentGate is derived directly from the input itself and this modification enhances the model’s ability to capture complex dependencies in text.
The other important feature of GLA is its FLASHLINEARATTENTION algorithm which designed specifically for modern GPU architectures. Unlike theoretical improvements, this optimization gives us real-world performance and outperforming even highly optimized methods like FLASHATTENTION-2. What makes FLASHLINEARATTENTION different is that it is I/O-aware, meaning it efficiently manages data movement between:
- High-bandwidth memory (HBM): Large but slower GPU memory.
- Shared memory (SRAM): Smaller but significantly faster memory.
By minimizing unnecessary data transfers and using specialized compute units (like tensor cores), this method achieves remarkable speed and efficiency. In benchmarks, it even surpasses FLASHATTENTION-2 on relatively short sequences of just 1,000 tokens.
FLASHLINEARATTENTION improves efficiency by using a method called chunkwise processing. Instead of processing the entire sequence at once, it divides it into smaller chunks. Within each chunk, computations are done in parallel to maximize GPU usage. Then, information is passed between chunks in a recurrent way to maintain dependencies. This balances speed and memory efficiency, making it faster than traditional softmax attention and even some optimized methods like FLASHATTENTION-2.
Empirical Results
The table above shows GLA Transformer results against Transformer++, RetNet, and Mamba. Two sets of scales are employed and the same set of language tasks are tested on. The individual task performance is via zero-shot. We can see that GLA outperforms subquadratic models like RetNet on all tasks and achieved comparable performance against quadratic models like Transformer++.
In additional to its performance on various language tasks, GLA also achieves a higher throughput and lower memory consumption, especially on long input sequences.
Limitations & Future Work
- Lack of Large-Scale Validation
- Although the authors anticipate that the training efficiency of GLA become even more favorable compared to model like Mamba at larger scales, it is unclear how GLA would scale to even larger models/datasets.
- The experiments were conducted on moderate-scale language models (up to 1.3B parameters). The performance and efficiency of GLA at larger scales (e.g., >7B parameters) remain uncertain, particularly regarding tensor parallelism and memory constraints.
- Performance Gap in Recall-Intensive Tasks
- While GLA outperforms other subquadratic models in recall-intensive tasks, it still lags behind standard quadratic attention Transformers, indicating room for improvement in tasks requiring precise memory retrieval.
TransNormerLLM: A Faster and Better Large Language Model with Improved TransNormer
The objective of the paper is to address the quadratic time complexity and scalability limitations of conventional transformer-based LLMs by introducing a linear attention-based architecture for improved efficiency and performance. Modern linear attention models like TransNormerLLM push the envelope by integrating several modifications—including improved positional encodings (using LRPE with exponential decay), gating mechanisms, and tensor normalization—to not only match but even outperform conventional Transformer architectures in both accuracy and efficiency. These innovations help address the limitations of earlier linear attention approaches and demonstrate the potential for linear methods in large-scale language modeling.
What is TransNormer?
TransNormer is a linear transformer model introduced in 2022 at the Conference on Empirical Methods in Natural Language Processing (EMNLP). It tackles two primary challenges: unbounded gradients in attention computation, which can destabilize training, and attention dilution, where long sequences reduce focus on local token interactions. To mitigate these, TransNormer replaces traditional scaling operations with normalization techniques to control gradients and employs diagonal attention in early layers to prioritize neighboring tokens.These innovations enhance performance on tasks such as text classification, language modeling, and the Long-Range Arena benchmark, while achieving significant space-time efficiency compared to softmax attention-based transformers.
The original TransNormer model, faced several limitations that impacted its versatility.
- Scalability Constraints: TransNormer was primarily tested on small-scale tasks like text classification and the Long-Range Arena benchmark, with limited evidence of its performance on large-scale language modeling tasks. This restricted its applicability to modern large language models requiring extensive training data and parameters.
- Complexity in Optimization: Despite stabilizing gradients, the model's normalization techniques increased computational overhead in certain configurations, complicating optimization for resource-constrained environments.
- Attention Dilution Trade-offs: While diagonal attention improved local context focus, it potentially limited the model’s ability to capture long-range dependencies in complex sequences, affecting performance on tasks requiring global context.
- Benchmark Scope: The evaluation was confined to specific datasets, lacking comprehensive testing on diverse, real-world applications, which raised questions about its generalizability.
The authors address all of these limitations in TransNormerLLM.
Key Contributions
- Architectural Improvements
- Positional Encoding:
Combines LRPE (Linearized Relative Positional Encoding) with exponential decay to balance global interactions and avoid attention dilution. The expression of positional coding is:
[math]\displaystyle{ a_{st}=\mathbf{q}_s^\top\mathbf{k}_t\lambda^{s-t}\exp(i\theta(s-t)), }[/math]
where [math]\displaystyle{ a_{st} }[/math] is the attention score between token s and t, [math]\displaystyle{ \lambda^{s-t} }[/math] is the exponential decay factor and [math]\displaystyle{ \exp(i\theta(s-t)) }[/math] is the encoding to capture relative positions. - Gating Mechanisms:
Uses Gated Linear Attention (GLA) and Simplified Gated Linear Units (SGLU) to stabilize training and enhance performance.
Gate can enhance the performance of the model and smooth the training process. The structure of Gated LinearAttention (GLA) is:
[math]\displaystyle{ O=\mathrm{Norm}(QK^{\top}V)\odot U, }[/math]
where:[math]\displaystyle{ \quad Q=\phi(XW_q),\quad K=\phi(XW_k),\quad V=XW_v,\quad U=XW_u. }[/math]
To further accelerate the model, the author propose Simple GLU (SGLU), which removes the activation function from the original GLU structure as the gate itself can introduce non-linearity. Therefore, the channel mixing becomes:
[math]\displaystyle{ O=[V\odot U]W_o, }[/math]
where:[math]\displaystyle{ V=XW_v,\quad U=XW_u. }[/math]
- Tensor Normalization:
Replaces RMSNorm with SRMSNorm, a simpler normalization method that accelerates training without performance loss. The new simple normalization function called SimpleRMSNorm, abbreviated as SRMSNorm:
[math]\displaystyle{ \mathrm{SRMSNorm}(x)=\frac{x}{\|x\|_2/\sqrt{d}} }[/math] - Training Optimization Model Parallelism:
- Robust Inference A robust inference algorithm proposed in the paper ensures numerical stability and constant inference speed regardless of sequence length via a recurrent formulation with decay factors.
Adapts Megatron-LM model parallelism for SGLU and GLA, enabling efficient scaling from 7B to 175B parameters.
Model Parallelism on SGLU:
[math]\displaystyle{ O=\left((XW_v)\odot(XW_u)\right)W_o }[/math]
[math]\displaystyle{ \begin{bmatrix} O_1^{\prime},O_2^{\prime} \end{bmatrix}=X \begin{bmatrix} W_v^1,W_v^2 \end{bmatrix}\odot X \begin{bmatrix} W_u^1,W_u^2 \end{bmatrix}= \begin{bmatrix} XW_v^1,XW_v^2 \end{bmatrix}\odot \begin{bmatrix} XW_u^1,XW_u^2 \end{bmatrix} }[/math]
[math]\displaystyle{ O= \begin{bmatrix} O_1^{\prime},O_2^{\prime} \end{bmatrix} \begin{bmatrix} W_o^1,W_o^2 \end{bmatrix}^\top=O_1^{\prime}W_o^1+O_2^{\prime}W_o^2 }[/math]
Model Parallelism on GLA:
[math]\displaystyle{ [O_1,O_2]=\mathrm{SRMSNorm}(QK^\top V)\odot U, }[/math]
where: [math]\displaystyle{ Q = [\phi(X W_q^1), \phi(X W_q^2)],\ K = [\phi(X W_q^1), \phi(X W_q^2)],\ V = X[W_v^1, W_v^2],\ U = X[W_u^1, W_u^2]. }[/math]

Training
TransNormerLLM has been trained in sizes ranging from 385 million to 7 billion parameters, with ongoing development of a 15-billion-parameter version. The training corpus includes 1.0 trillion tokens for the 385M model, 1.2 trillion for the 1B model, and 1.4 trillion for the 7B model, ensuring robust data exposure for diverse language tasks. The model utilizes large-scale clusters, enabling efficient scaling across multiple devices.
Results
TransNormerLLM has demonstrated competitive performance across various benchmarks, particularly in commonsense reasoning and aggregated tasks, matching or approaching state-of-the-art models like LLaMA and OPT. The 7B parameter model is the most extensively evaluated, with results reported as follows:
- Commonsense Reasoning (Zero-Shot):
- BoolQ: 75.87 – Evaluates yes/no question answering based on passages.
- PIQA: 80.09 – Tests understanding of physical world interactions.
- HellaSwag: 75.21 – Assesses commonsense inference from multiple choices.
- Aggregated Benchmarks (Five-Shot):
- MMLU: 43.10 – Measures multitask language understanding in English.
- CMMLU: 47.99 – Chinese version of MMLU.
- C-Eval: 43.18 – Comprehensive Chinese evaluation across 52 disciplines.
These results highlight the model's versatility in handling both English and Chinese tasks, with efficiency gains attributed to its linear attention mechanisms, achieving over 20% acceleration compared to traditional models.
Simple linear attention language models balance the recall-throughput tradeoff
Large language models (LLMs) using Transformers are fantastic at "recalling" details from their input—think of it as their ability to dig up a specific fact buried in a long conversation. However, attention-based language models suffer from high memory consumption during inference due to the growing key-value (KV) cache, which scales with sequence length. This reduces throughput and limits efficiency for long sequences, despite their strong recall ability.
Key Contributions
- BASED: A hybrid architecture blending linear attention and sliding window attention to optimize the recall-memory tradeoff.
- Theoretical and empirical evidence of how memory usage impacts recall.
- Optimized implementation achieving up to 24× higher throughput than FlashAttention-2 for long-sequence generation.
BASED
BASED combines two tricks to strike a balance:
- Linear Attention: This approximates the softmax with a simpler operation. Instead of computing [math]\displaystyle{ \exp(q_i^\top k_j / \sqrt{d}) }[/math], it uses a feature map [math]\displaystyle{ \phi }[/math] so that [math]\displaystyle{ \phi(q_i)^\top \phi(k_j) \approx \exp(q_i^\top k_j / \sqrt{d}) }[/math]. The paper opts for a 2nd-order Taylor series: [math]\displaystyle{ \phi(q_i)^\top \phi(k_j) = 1 + q_i^\top k_j + \frac{(q_i^\top k_j)^2}{2} }[/math]. This lets them rewrite attention as a recurrent process with a fixed-size state, say [math]\displaystyle{ s_i = \sum_{j=1}^i \phi(k_j)^\top v_j }[/math], avoiding the KV-cache explosion. The state size depends on the feature dimension [math]\displaystyle{ d' }[/math], not [math]\displaystyle{ N }[/math], making memory predictable.
- Sliding Window Attention: This adds precision by letting each token attend to a small, local window of past tokens (e.g., 64 tokens) using exact softmax attention. It’s like giving the model a magnifying glass for nearby details, with a KV-cache capped at the window size [math]\displaystyle{ w }[/math].
Together, linear attention handles long-range context with a fixed memory footprint, while sliding window attention sharpens local recall. By tweaking [math]\displaystyle{ w }[/math] and [math]\displaystyle{ d' }[/math], BASED can slide along the recall-memory tradeoff curve—crank up the window for better recall or shrink it for efficiency.
Limitations and Future Work
- Scaling: May struggle with very large models or extremely long sequences.
- Future Work: Could explore improved approximations for linear attention or enhanced hardware optimizations.
Topic 11: Flash Attention
Flash Attention tries to address the resource intensity of vanilla attention by utilizing hardware more effectively. Recent advances in computational speed (particularly in parallelization) have lessened computational intensity as a bottleneck. Consequently, memory usage became a larger bottleneck. Specifically, during training, attention requires data to be read and written multiple times and computations are done in HBM (which is not the fastest memory in the computer). As a result, training takes a lot of time and resource. The goal of Flash Attention is thus to address these inefficiencies in order to reduce training time for LLMs.
Flash Attention began with version 1, which restructured the standard attention mechanism to reduce memory traffic via tiled (block‑wise) computations in on‑chip SRAM. FlashAttention V2 built upon this idea by re‑organizing work partitioning to better utilize GPU resources—optimizing thread block scheduling and reducing non-matmul overhead. Finally, FlashAttention V3 takes advantage of new hardware features present on Hopper/H100 GPUs—most notably asynchronous execution, warp specialization, and low‑precision math (FP8)—resulting in a substantial boost in throughput and higher utilization of tensor cores.
Flash Attention V1
Flash Attention V1 rethinks the standard attention mechanism by minimizing expensive memory transfers. Modern GPUs have high-bandwidth memory (HBM) that is large but relatively slow compared to on‑chip SRAM, which is over 10× faster but limited to about 20 MB. By restructuring the attention computation to operate in small blocks within SRAM, Flash Attention V1 dramatically reduces the number of slow memory reads and writes, resulting in faster training for large language models.
Overview
Traditional attention computes the full [math]\displaystyle{ QK^\top }[/math] matrix in HBM, causing a quadratic memory traffic bottleneck. Flash Attention V1 addresses this by processing the input matrices in smaller, manageable blocks (tiles) that fit in fast SRAM. In doing so, both the matrix multiplication and the softmax normalization are performed piecewise, with local results later merged to produce the exact, globally normalized output.
Block‑Wise (Tiled) Computation
Imagine trying to paint a giant mural using a small canvas. Rather than handling the entire image at once, you divide it into sections that fit on your workbench. In Flash Attention V1, the large [math]\displaystyle{ Q }[/math], [math]\displaystyle{ K }[/math], and [math]\displaystyle{ V }[/math] matrices are partitioned into tiles. For example, with 1024 tokens, the matrices might be split into blocks of 256 tokens each. A block of [math]\displaystyle{ Q }[/math] (e.g. [math]\displaystyle{ 256 \times d }[/math]) is loaded from HBM into SRAM along with the corresponding block of [math]\displaystyle{ K }[/math] (transposed as needed). The multiplication [math]\displaystyle{ QK^\top }[/math] is then computed within SRAM to yield a [math]\displaystyle{ 256 \times 256 }[/math] block of attention scores, eliminating the need to store or compute the entire matrix in slow memory.
Softmax Normalization: Handling Global Dependencies in Small Pieces
The softmax function, defined as [math]\displaystyle{ \text{softmax}(x_i) = \frac{\exp(x_i)}{\sum_j \exp(x_j)} }[/math] requires a global normalization across each row of scores. This poses a challenge when the data is processed in tiles.
Within each tile, a local maximum ([math]\displaystyle{ m_{\text{local}} }[/math]) is computed to stabilize the exponentiation, and a local sum is calculated: [math]\displaystyle{ S_{\text{local}} = \sum_{i \in \text{tile}} \exp(x_i - m_{\text{local}}) }[/math] Simultaneously, the tile computes a partial numerator by weighting each [math]\displaystyle{ \exp(x_i - m_{\text{local}}) }[/math] with the corresponding [math]\displaystyle{ V }[/math] values. These local computations ensure that the softmax can be performed on a small subset of the data without needing the entire row at once.
Algebraic Aggregation: Merging Tile Results for Global Softmax
Since each tile’s softmax is computed relative to its own local maximum, the results must be re‑aligned to a common global reference. Suppose one tile computes a local maximum [math]\displaystyle{ m_1 }[/math] and sum [math]\displaystyle{ S_1 = \sum_{i \in \text{tile 1}} \exp(x_i - m_1) }[/math] and another tile computes [math]\displaystyle{ m_2 }[/math] and [math]\displaystyle{ S_2 = \sum_{j \in \text{tile 2}} \exp(x_j - m_2) }[/math]. The global maximum is given by [math]\displaystyle{ m = \max(m_1, m_2) }[/math] Each local sum is then adjusted to this common reference: [math]\displaystyle{ S_{\text{global}} = \exp(m_1 - m) S_1 + \exp(m_2 - m) S_2 }[/math] A similar adjustment is applied to the local numerators (the weighted sums of [math]\displaystyle{ V }[/math]). The final attention output is obtained by dividing the aggregated numerator by [math]\displaystyle{ S_{\text{global}} }[/math]. This algebraic aggregation process guarantees numerical stability and correctness while never requiring the full matrix to be processed at once.
Memory vs. Compute Trade-offs and Workflow Recap
Flash Attention V1 trades additional computations for a dramatic reduction in memory traffic. Although extra arithmetic is performed—such as recomputing local softmax values and adjusting them—these operations occur in fast SRAM. The overall workflow is as follows:
Load small tiles of [math]\displaystyle{ Q }[/math], [math]\displaystyle{ K }[/math], and [math]\displaystyle{ V }[/math] from HBM into SRAM. Perform block‑wise matrix multiplication and softmax computations within SRAM, including computing local maximums, local sums, and partial numerators. Merge these local results through algebraic aggregation to produce the correct global softmax normalization. Finally, write the computed attention outputs back to HBM.
In contrast, although regular attention to HBM executes fewer arithmetic operations, there is significant overhead. Each intermediate result must be stored back into the HBM and re-loaded for later reuse. This computation overhead significantly increases the elapsed runtime, which makes flash attention much more appealing. The HBM execution workload is analogous to map-reduce operations seen in distributed databases (where intermediate results after map operations are saved into the storage layer, but must be reloaded for reduce operations).
Optional: Block‑Sparse Extension
In some cases, not every tile contributes equally. Flash Attention V1 can be extended to a block‑sparse variant where tiles that fall below a predetermined importance threshold are skipped entirely. This further reduces computation and memory transfers, echoing ideas from sparse attention methods.
Optimizing the Backward Pass
In conventional attention models, the backward pass requires storing and reloading full intermediate activations (the [math]\displaystyle{ QK^\top }[/math] scores) from global memory, which increases both compute and memory costs. FlashAttention avoids this by recomputing necessary intermediate quantities on the fly in the fast SRAM during backpropagation. FlashAttention V2 and V3 further enhance this strategy by overlapping gradient computations with forward passes and partitioning work more finely among warps, thereby reducing I/O and achieving higher overall throughput.
Limitations and Future Directions
- A New CUDA Kernel
- FlashAttention V1 requires a custom CUDA implementation, but the implementation needs significant engineering efforts and it may not be flexibly transferred across different GPU architectures.
- Limited Ability on Other Deep Learning Models
- Since every layer of a deep learning network needs to use GPU HBM, the limitation of IO-Aware implementation to the other deep learning models is believed to be solved in the future
- Single GPU Focus
- The current implementation is optimized for single-GPU setups. The potential of IO analysis in the future on multi-GPU is significant.
Connections to Adaptively Sparse Attention
Flash Attention primarily optimizes standard dense attention through hardware-aware, memory-efficient block computations. However, a complementary approach is “Adaptively Sparse Attention“, which dynamically reduces the quadratic complexity by selecting only key token interactions that matter most, based on content similarity rather than fixed patterns.
Formulation
Given queries [math]\displaystyle{ Q \in \mathbb{R}^{T \times d} }[/math], keys [math]\displaystyle{ K \in \mathbb{R}^{T \times d} }[/math], and values [math]\displaystyle{ V \in \mathbb{R}^{T \times d_v} }[/math], Adaptively Sparse Attention performs:
1. Standard attention scores: [math]\displaystyle{ S = \frac{QK^T}{\sqrt{d}} }[/math]
2. Adaptive sparsity mask [math]\displaystyle{ M \in \{0,1\}^{T\times T} }[/math] generation: [math]\displaystyle{ M_{ij} = \begin{cases} 1, & \text{if } S_{ij} \text{ is among the top-} k \text{ scores for query token } i \\[6pt] 0, & \text{otherwise} \end{cases} }[/math]
3. Compute sparse attention output: [math]\displaystyle{ \text{Attention}(Q,K,V) = \text{softmax}(S \odot M) V }[/math]
Advantages & Complementarity
Adaptively Sparse Attention complements Flash Attention by directly reducing the computational complexity through adaptive token selection:
- Dynamic reduction of computational complexity: While Flash Attention tackles memory inefficiency, Adaptively Sparse Attention further reduces computation from [math]\displaystyle{ O(T^2) }[/math] to nearly [math]\displaystyle{ O(Tk) }[/math].
- Efficient handling of long sequences: The dynamic token selection mechanism pairs naturally with Flash Attention's block-wise memory optimization, combining hardware-aware design with algorithm-level sparsity for maximum efficiency.
- Contextual adaptiveness: Rather than fixed or heuristic sparsity patterns (such as BigBird), the adaptiveness ensures important interactions are always preserved, achieving better accuracy-computation trade-offs.
Flash Attention V2
Background & Motivation
Language models have much longer context than before. Scaling transformers to long sequences is crucial:
- language modelling (GPT-4, Clause, MPT)
- high-resolution image understanding
- code, audio, and video generation
Challenges
- Attention bottleneck: quadratic time complexity, inefficient hardware utilization
- Flash Attention V1: still not nearly as fast as optimized matrix-multiply (GEMM) operations, reaching only 25-40% of the theoretical maximum FLOPs/s
- Suitability to Different Devices: Further research is needed to make Flash Attention V2 available to different devices, such as H100 GPUs, AMD GPUs. So far, the discussion has been focusing on the HBM and SRAM (NVIDIA GPUs with specific memory hierarchies).
Main Idea
In V1, its idea is to use SRAM, compute more, reduce reads/writes. However, it's mentioned previously that only 25%-40% of theoretical maximum FLOPs is reached. This inefficiency is due to suboptimal work partitioning between different thread blocks and warps on the GPU, causing either low-occupancy or unnecessary shared memory reads/writes. In V2, the main idea is to have a better work partitioning algorithm. The core improvements are:
1. Reduce redundant operations: GPU is optimized for matmul operations, although non-matmul FLOPs only takes a fraction of total FLOPs, with optimized hardware, matmul operations are actually performed much faster than non-matmul operations. Thus it's important to reduce non-matmul FLOPs and spend as much time as possible doing matmul FLOPs.
2. Parallelism: Distribute attention computation efficiently across thread blocks and warps.
3. Efficient memory utilization: Optimize intra-thread communication, reducing memory overhead.
Empirical Results
Diagrams above shows how Flash Attention V2 performs across different sequence lengths and compare it to a standard attention implementation in PyTorch, FlashAttention, and FlashAttention in Triton. We can see an improvement in efficiency across all sequence lengths. We can see that FlashAttention-2 is 1.7-3.0× faster than FlashAttention, 1.3-2.5× faster than FlashAttention in Triton, and 3-10× faster than a standard attention implementation. The TFLOPs reached in V2 is about 70% of the theoretical TFLOPs achievable on A100 GPUs.
Flash Attention V3
FlashAttention-2 was a significant improvement in speeding up attention mechanisms, but it only utilized 35% of the computational capacity of H100 GPUs. This left a lot of untapped potential, especially given the advanced features of Hopper GPUs, such as asynchronous execution and support for low-precision math. FlashAttention-3 was developed to fully exploit these capabilities, making attention computations faster, more efficient, and scalable for extremely long sequences.
There are two main ideas in FlashAttention-3:
H100
Before introducing Flash Attention V3, we first learn a little bit about the architecture of H100. Comparing it with A100, the major improvement is on the Asynchronous Execution aspect where we introduced one new hardware component and one one instruction. Apart from Asynchronous Execution aspect, we also introduced a new data precision which is FP8.
- TMA (Tensor Memory Accelerator), which can move data between global and shared memory efficiently
- WGMMA (Warp-Group Matrix Multiply-Accumulate) instructions which allows warp-group-wide operations to run while loading data.
- FP8 precision, delivering 2× speedup over FP16/BFP16.
These designs leads to Warp Specialization. Which means that different warps handle different tasks:
- Producer warps, specialized to transfer data which typically requires less registers
- Consumer warps, specialized to perform computation which typically requires more registers
Overlapping Tasks with Asynchronous Execution

Hopper GPUs feature Tensor Cores which are specialized units for performing matrix multiplications at lightning speed. FlashAttention-3 takes advantage of these Tensor Cores by using warp specialization, where some GPU threads handle data movement (producers) while others focus on computation (consumers). These roles swap and run simultaneously, leading to "pingpong" scheduling to ensure the GPU is always busy and no time is wasted.
- Why do we do Ping pong Scheduling?
Matrix multiplication (matmul) is significantly more compute-intensive than other operations. In attention specifically, Matmul FLOPS is 512× exponential FLOPS and exponential FLOPS bottleneck reduces overall efficiency by 256× in FP8.
- Trade-off
This Ping pong Scheduling do, however, have a trade-off, it provides higher register pressure, requiring more registers to store GEMM accumulators and softmax I/O. And overall, we need effective balance between performance and resource usage.
Low-Precision Math (FP8)
FlashAttention-3 introduces support for FP8 precision, which reduces memory usage and speeds up calculations compared to FP16. To maintain accuracy, it uses techniques like block quantization (storing one scalar per block) and incoherent processing, which smooths out numerical outliers. This results in a 2.6x reduction in numerical error compared to baseline FP8 implementations.
Comparison to FlashAttention-2:
- 1.5–2x faster attention computations
- Up to 75% GPU utilization with FP16 precision
Empirical Results
We reached 75% of the theoretical maximum TFLOPs/s on H100 GPUs using Flash Attention V3. And FlashAttention 3 reaches up to 740 TFLOPs/s which is up to 2.0× faster than V2.
Flash Fast Fourier Transform Convolution (FlashFFT Conv)
Introduction
Efficient sequence processing is always a fundamental challenge in deep learning, especially for natural language processing (NLP). Although convolutional models provide the state-of-the-art performance across various tasks, including NLP and time-series forecasting, their efficiency is often limited due to suboptimal hardware utilization. A potential solution to this problem is the Fast Fourier Transform (FFT), which theoretically operates in [math]\displaystyle{ O(N\text{log}N) }[/math] time complexity. However, conventional FFT implementations fail to fully leverage modern GPU architectures, leading to suboptimal efficiency. To address this, a highly optimized FFT-based convolution algorithm, namely Flash Fast Fourier Transform Convolution (Flash FFT Conv), is introduced.
Innovation
A key innovation in Flash FFT Conv is the Monarch FFT Decomposition, which significantly improves the efficiency of Fast Fourier Transform (FFT)-based convolutions. Unlike traditional FFT algorithms, such as the Cooley-Tukey FFT, Monarch FFT Decomposition reformulates the FFT computation into a structured matrix representation that can be efficiently executed using matrix multiplications on tensor cores.
Importance of Monarch FFT Decomposition
The objective of Monarch FFT decomposition is to express FFT as a series of matrix multiplication. Doing so, it enables efficient GPU computation on specialized compute units (e.g., tensor cores of NVIDIA GPUS or matrix multiply units of TPUs). An order-[math]\displaystyle{ p }[/math] Monatch decomposition rewrites the FFT into [math]\displaystyle{ p }[/math] matrix-matrix multiply operations (which implies that we can map them onto these fast compute units efficiently). The value of [math]\displaystyle{ p }[/math] has a tradeoff. A higher [math]\displaystyle{ p }[/math] value imply smaller matrices to multiply, and thus, a lower number of FLOPs. But there is greater I/O communication overhead due to greater number of intermediate results.

An illusrtation of Monarch FFT decomposition can be seen to the right. To give an example of Monarch FFT decomposition, consider a matrix [math]\displaystyle{ N=N_1N_2 }[/math]. An order-2 Monarch FFT decomposition expresses the FFT of [math]\displaystyle{ N }[/math] as [math]\displaystyle{ \mathcal{F}_N=\mathbf{P}(\mathbf{I}_{N_2}\otimes\mathcal{F}_{N_1})\mathbf{D}\mathbf{P}^{-1}(\mathbf{I}_{N_1}\otimes\mathcal{F}_{N_2})\mathbf{P} }[/math], where [math]\displaystyle{ \oslash }[/math] is the Kronecker product, [math]\displaystyle{ \mathbf{P} }[/math] is the permutate matrix that reshapes the input to [math]\displaystyle{ N_1\times N_2 }[/math], transposes the intermediate matrix,and then reshape it back to [math]\displaystyle{ N }[/math]m, and [math]\displaystyle{ \mathbf{D}\in\mathbb{C}^{N\times N} }[/math] is a dinagonal matrix containing correctional values Twiddle factors. Twiddle factors are roots of unity [math]\displaystyle{ W^k_N=\exp{\left(-j\frac{2\pi k}{N}\right)} }[/math] where [math]\displaystyle{ N }[/math] is the number of points in the FFT, that are used to combine the results of smaller DFTs to generate larger DFTs (recall that FFT is a divide-and-conquer algorithm to compute DFT efficiently).
To execute higher-order Monarch FFT decompositions, one can recursively apply the order-2 decomposition to [math]\displaystyle{ \mathcal{F}_{N_1} }[/math] and [math]\displaystyle{ \mathcal{F}_{N_2} }[/math].
Domain-Specific Optimizations
FlashFFTConv incorporates domain-specific strategies to reduce overhead:
- Uses real-valued FFT for real-input convolutions, reducing FFT length by half.
- Special-cases zero padding to avoid redundant matrix multiplies.
- Fuses gating operations (e.g., [math]\displaystyle{ y = v \odot ((u \odot w) * k) }[/math]) common in Hyena or M2 models into the core kernel.
Benefits
By leveraging this structured decomposition, FlashFFTConv achieves highly parallelized execution across the input sequence. This maximizes hardware utilization, resulting in faster computation. Furthermore, this approach minimizes high-latency global memory (HBM) access by performing most computations within on-chip memory (SRAM or shared memory). This reduces the I/O bottleneck that often limits FFT performance on modern GPUs. This leads to significant speedups over conventional FFT-based convolution methods. Additionally, the use of sparse and low-rank matrix structures further enhances computational efficiency, eliminating unnecessary operations and improving scalability for long-sequence processing.
Through efficient memory access and tensor core optimization, Flash FFT Conv becomes a highly effective solution for accelerating FFT-based convolutions tasks, such as NLP and audio generation.
Cost Model of order-p Monarch Decomposition
An adaptive cost modeling for GPU efficiency is employed by dynamically optimizing the Monarch decomposition order (p) based on sequence length and hardware capabilities. The previous subsection discusses how the FLOP cost decreases with higher p-orders due to the small matrix operations and that I/O costs linearly increase with p. Thus, a cost function combining FLOP cost and I/O cost is designed as:
[math]\displaystyle{ C = C_{\text{flop}} + C_{\text{I/O}} }[/math]
[math]\displaystyle{ C = BH \sum_{i=1}^{p} \frac{16NN_i}{\gamma(N_i)} + \frac{4N}{\omega(i)} }[/math]
where, [math]\displaystyle{ N }[/math] is the sequence length with [math]\displaystyle{ N = \sum^p_{i=1}{N_i} }[/math], [math]\displaystyle{ \omega }[/math] is the memory bandwidth at step [math]\displaystyle{ I }[/math]. Here, [math]\displaystyle{ \gamma }[/math] is FLOP efficiency represented as:
[math]\displaystyle{ \gamma(N_i) = \begin{cases} \tau_G, & \text{if } N_i \lt \mu \\ \tau_M, & \text{if } N_i \geq \mu \end{cases} }[/math]
where, [math]\displaystyle{ \tau_G }[/math] and [math]\displaystyle{ \tau_M }[/math] are empirically-achievable FLOPs on the GPU for general-purpose arithmetic and matrix-matrix multiply arithmetic, respectively. [math]\displaystyle{ \mu }[/math] denotes the matrix unit size.
Figure visualizes the cost model for FFT convolution with order-2, order-3, and order-4 decompositions when sequence length increases on an A100 GPU computed from the cost calculations from the above equations. The FLOP cost of an order-p decomposition grows as [math]\displaystyle{ O(N^{((p+1)/p)}) }[/math]. However, shorter sequences ([math]\displaystyle{ N }[/math]<1K and [math]\displaystyle{ N }[/math]<4k) for higher-order decompositions (p=3 and 4, respectively) are more expensive because they produce matrices smaller than the GPU's matrix-matrix multiply unit. Additionally, at p=3, noticeable bumps are observed at around 64k. This occurs because intermediate results exceed SRAM capacity and spill into slower HBM memory (memory specs discussed in FlashAttention V1). The extra I/O cost increases runtime which is circumvented in p=4 with an extra decomposition.
Summary
FlashFFTConv’s architecture offers:
- Matrix-based decomposition for high FLOP utilization.
- Broadcast and tiling over sequence to maximize fusion and reuse.
- Efficient on-chip memory access, reducing I/O bottlenecks.
- Scalability to 4M+ sequence lengths with reduced memory footprint and faster wall-clock time than standard FFTs.
This architecture unlocks fast and memory-efficient FFT convolutions for NLP, audio, and genomics applications.
Simple Hardware-Efficient Long Convolutions for Sequence Modeling
Introduction
State space models (SSMs) have emerged as a powerful general-purpose sequence modeling framework. It scale nearly linearly in sequence length and have shown SOTA performance on a range of sequence modeling tasks. However, SSMs rely on sophisticated mathematical structures to train effectively in deep networks. These structures generate a convolution kernel as long as the input sequence by repeatedly multiplying a hidden state matrices. This process could become unstable and requires hand-crafted initialization. Hence, people have tried parameterize the long convolution kernel directly. In doing so, people have to overcome two challenges, the quality of model and the runtime performance. This paper, by employing simple regularization techniques and an IO-aware convolution algorithm, have addressed these challenges and made improvements.
FlashButterfly
FlashButterfly is an IO-aware convolution algorithm that enhances runtime efficiency for long sequences. It employs Butterfly decomposition, inspired by Fast Fourier Transform (FFT) algorithms, to break down convolutions into smaller, hierarchical computations.
- Mechanism: By structuring convolutions as a series of matrix multiplies, FlashButterfly reduces memory I/O, optimizing data movement between GPU global and shared memory. Blockwise kernel execution further minimizes SRAM usage.
- Regularization: Techniques like kernel squashing ensure smoothness, recovering SSM performance on tasks like the Long Range Arena (LRA).
- Performance: Achieves a 2.2× speedup over standard convolutions and sets state-of-the-art results on Path256 (64K sequence length) by 29.1 points, with 7.2× faster training than prior models.
Butterfly decomposition, central to FlashButterfly, mirrors FFT’s hierarchical structure, as depicted in diagrams like the one referenced. It recursively breaks convolutions into smaller units, optimizing GPU memory access and computation, and extends to FlashFFTConv’s matrix-based FFTs.
Butterfly Decomposition
Butterfly decomposition is a computational framework central to FlashButterfly’s optimization of long convolutions, drawing from the hierarchical structure of Fast Fourier Transform (FFT) algorithms.It recursively breaks down convolutions into smaller operations, reducing memory I/O and computational complexity on GPUs. In this framework, the Butterfly matrices (which replace the standard DFT matrices) are parameterized and trained end-to-end. This approach increases the expressiveness of the convolutional kernels without incurring additional FLOPs; in practice, it has been shown to reduce the number of parameters while maintaining or even improving model accuracy. For instance, replacing Transformer MLPs with learned Butterfly layers can achieve similar performance with 30% fewer parameters on WikiText103.
The decomposition mirrors FFT’s butterfly diagram, where a transform is split into smaller units combined via butterfly operations. For a sequence of length [math]\displaystyle{ N }[/math], a convolution [math]\displaystyle{ y = x \ast h }[/math] is represented as a matrix-vector product [math]\displaystyle{ y = T_h x }[/math], where [math]\displaystyle{ T_h }[/math] is a Toeplitz matrix. FlashButterfly approximates [math]\displaystyle{ T_h }[/math] as a product of sparse butterfly matrices:
- [math]\displaystyle{ T_h \approx \prod_{i=1}^L B_i, }[/math]
where each [math]\displaystyle{ B_i }[/math] performs a stage of computation, and [math]\displaystyle{ L \approx \log N }[/math]. A single butterfly, for inputs [math]\displaystyle{ x_i }[/math] and [math]\displaystyle{ x_{i+N/2} }[/math], computes:
- [math]\displaystyle{ \begin{bmatrix} y_i \\ y_{i+N/2} \end{bmatrix} = \begin{bmatrix} 1 & h_k \\ 1 & -h_k \end{bmatrix} \begin{bmatrix} x_i \\ x_{i+N/2} \end{bmatrix}, }[/math]
with [math]\displaystyle{ h_k }[/math] as a kernel weight, regularized for smoothness.<ref name="SimpleConv"/> This yields [math]\displaystyle{ O(N \log N) }[/math] complexity, compared to [math]\displaystyle{ O(N^2) }[/math] for direct convolution.
By structuring computations hierarchically, FlashButterfly minimizes GPU global memory accesses, using blockwise execution to fit operations within shared memory. This enables tasks like Path256 (64K tokens) to achieve a 29.1-point accuracy gain and 7.2× faster training. The approach extends to FlashFFTConv’s frequency-domain optimizations, where similar decompositions enhance FFT efficiency.
FlashFFTConv: Efficient IO-Aware Convolution
FlashFFTConv is an IO-efficient convolution algorithm designed for long sequence modeling, and complements the challenges addressed in this paper. While traditional convolutions have [math]\displaystyle{ O(N^2) }[/math] complexity, FlashFFTConv leverages Fast Fourier Transform (FFT) and GPU tensor cores to reduce this to [math]\displaystyle{ O(N \log N) }[/math], while maintaining model quality.
- Key Components
- FFT-Based Convolution: Replaces standard convolution with FFT, reducing asymptotic complexity.
- Monarch Decomposition: Decomposes FFTs into matrix multiplies, allowing optimized execution on GPU tensor cores.
- Blockwise Kernel Execution: Reduces SRAM requirements by performing smaller matrix multiplications.
- Hardware Optimization
- Uses mixed precision (e.g., FP8) and warp-group tensor core instructions (WGMMA) on H100 GPUs.
- Supports asynchronous scheduling via TMA and ping-pong buffering.
- Performance Results
- Up to 7.9× faster than PyTorch convolution.
- Up to 5.6× memory savings.
- Faster than FlashAttention-v2 at sequence lengths of 2k+.
- Enables models to process sequences as long as 4 million tokens.
This method provides an alternative path to efficient long-sequence modeling through Fourier-based convolution rather than attention, with strong empirical and hardware-level performance.
Topic 5: KD / Pruning / Sharing
Introduction
Knowledge Distillation (KD), Pruning, and Sharing are three strategies to make language models smaller, faster, and more efficient without sacrificing their performance. KD works by having a large, powerful "teacher" model that teachs a smaller "student" model how to behave similarly so the student model can do almost as well as the teacher but with less effort. Pruning can be thought of trimming a tree by which it removes unnecessary or less important parts of the model, making it more compact and faster while keeping its core abilities intact. Sharing is about reusing parts of the model across different tasks or layers, so there is no need to build everything from scratch, saving time and resources.
While KD focuses on teaching a smaller model to imitate a larger one, pruning cuts away the unnecessary parts to make the model cleaner, and sharing reuses parts to avoid having unnecessary extra work. These techniques contribute together to create language models that are not only powerful but also efficient enough to run on devices with limited resources, like smartphones or laptops.
Knowledge Distillation (KD)
KD transfers knowledge from a large, well-trained teacher model to a smaller student model. The student learns not only from the hard labels but also by mimicking the teacher’s soft output distributions or internal representations. In the work by Muralidharan et al. , KD is a critical component in recovering the performance lost during the compression of a 15B-parameter model. By distilling knowledge during retraining, the authors were able to produce smaller models (MINITRON 8B and 4B) that not only match but, in some cases, outperform models trained from scratch—even while using a fraction of the training data.
Improvements to Knowledge Distillation
1. Born-Again Networks (BANs):
Repeated training iterations to simplify the dataset.
Improves performance for lower-capacity NAT models.
2. Mixture of Experts (MoE):
Reduces data diversity by training on simpler expert translations.
3. Sequence-Level Interpolation:
Selects the best candidate translation based on BLEU score, improving high-capacity NAT models.
Metrics for Distilled Data
- Data Complexity measures how much variability is present in the translations, which is calculated by fitting an alignment model and compute the average of token-level conditional entropy.
- Data faithfulness evaluates how closely the distilled data aligns with the original real-world data.
[math]\displaystyle{ F(d)=\frac{1}{\left|\mathcal{V}_x\right|} \sum_{x \in \mathcal{V}_x} \sum_{y \in \mathcal{V}_y} p_r(y \mid x) \log \frac{p_r(y \mid x)}{p_d(y \mid x)} }[/math]
Distillation Best Practices
- KD should focus primarily on logit-based loss rather than using a weighted combination of multiple losses.
- Use Kullback-Leibler Divergence (KLD) loss as it outperforms MSE and cosine losses in pruned settings.
- Incorporate intermediate state distillation only when model depth is significantly reduced.
- Distilling from the final training stage model (instead of early checkpoints) yields better results.
Compact Language Models via Pruning and Knowledge Distillation
Introduction
In this paper, the authors propose a data‑efficient approach that prunes an existing 15 B‑parameter Nemotron‑4 model and retrains it with less than 3 % of the original training data to derive smaller variants by factors of 2–4× . This method achieves up to 40× reduction in training tokens per model and delivers 1.8× compute cost savings across the full model family. The resulting Minitron‑8B and Minitron‑4B models exhibit up to 16 % improvement in MMLU scores compared to scratch‑trained counterparts, and perform on par with or better than popular community models like Mistral 7B, Gemma 7B, and Llama‑3 8B.
Model Compression Approach
This work follows a structured approach to model compression:
- Structured Pruning Across Multiple Axes: The paper prunes various dimensions of the model—neurons (in MLPs), attention heads, embedding channels, and even layers—using an activation‐based importance metric.
- Knowledge Distillation Retraining: After pruning, the model is retrained with a knowledge distillation loss that transfers the “knowledge” of the original (teacher) model to the pruned (student) model. This retraining is done efficiently using only a small fraction of the original training tokens.
- Neural Architecture Search: A lightweight search is performed to select feasible pruned architectures that meet a target parameter budget, ensuring both efficiency and performance.
Pruning Techniques
Width Pruning (Pruning Individual Model Components)
This is how importance scores are calculated for each component (neuron, head, embedding channels)
Neurons in MLPs
For a given neuron in an MLP layer, the importance score is computed based on the activations it produces. The activation of a neuron is the output of the non-linear function (e.g., ReLU) applied to the weighted sum of its inputs.
Mathematically, the importance score for the [math]\displaystyle{ i^{th} }[/math] neuron in an MLP layer is given by:
[math]\displaystyle{ F_{\text{neuron}}^{(i)} = \sum_{\mathbf{B},\mathbf{S}} \mathbf{X} \big(\boldsymbol{W}_{1}^{i}\big{)}^{T} }[/math]
Here:
- [math]\displaystyle{ \mathbf{X} }[/math] is the input to the MLP layer.
- [math]\displaystyle{ \boldsymbol{W}_{1}^{i} }[/math] is the [math]\displaystyle{ i^{th} }[/math] row of the weight matrix [math]\displaystyle{ \boldsymbol{W}_{1} }[/math].
- [math]\displaystyle{ \sum_{\mathbf{B},\mathbf{S}} }[/math] denotes aggregation over the batch and sequence dimensions.
The paper experiment with different aggregation functions (e.g., mean, L2 norm, variance) to compute the importance score. They find that using the L2 norm for batch aggregation and the mean for sequence aggregation yields the best results.
Attention Heads in MHA Layers
For attention heads, the importance score is based on the attention output produced by each head. The attention output is computed using the standard multi-head attention mechanism:
[math]\displaystyle{ \text{MHA}(\mathbf{X}) = \text{Concat}(\text{head}_{1}, \ldots, \text{head}_{L}) \cdot \boldsymbol{W}^{O} }[/math]
where each head is computed as:
[math]\displaystyle{ \text{head}_{i} = \text{Attn}(\mathbf{X}\boldsymbol{W}^{Q,i}, \mathbf{X}\boldsymbol{W}^{K,i}, \mathbf{X}\boldsymbol{W}^{V,i}) }[/math]
The importance score for the [math]\displaystyle{ i^{th} }[/math] attention head is then computed as:
[math]\displaystyle{ F_{\text{head}}^{(i)} = \sum_{\mathbf{B},\mathbf{S}} \|\text{Attn}(\mathbf{X}\boldsymbol{W}^{Q,i}, \mathbf{X}\boldsymbol{W}^{K,i}, \mathbf{X}\boldsymbol{W}^{V,i})\|_{2} }[/math]
Here:
- [math]\displaystyle{ \|\cdot\|_{2} }[/math] denotes the L2 norm of the attention output.
- [math]\displaystyle{ \sum_{\mathbf{B},\mathbf{S}} }[/math] aggregates over the batch and sequence dimensions.
L2 norm for batch aggregation and the mean for sequence aggregation work best.
Embedding Channels
For embedding channels, the importance score is based on the Layer Normalization (LayerNorm) output. LayerNorm is applied to the embeddings to normalize the activations across the embedding dimensions. The importance score for the [math]\displaystyle{ i^{th} }[/math] embedding channel is computed as:
[math]\displaystyle{ F_{\text{emb}}^{(i)} = \sum_{\mathbf{B},\mathbf{S}} \text{LayerNorm}(\mathbf{X})_{i} }[/math]
Here:
- [math]\displaystyle{ \text{LayerNorm}(\mathbf{X})_{i} }[/math] is the [math]\displaystyle{ i^{th} }[/math] dimension of the LayerNorm output.
- [math]\displaystyle{ \sum_{\mathbf{B},\mathbf{S}} }[/math] aggregates over the batch and sequence dimensions.
Depth (Layers) Pruning
For depth pruning (removing entire layers), the authors use two metrics to compute layer importance: 1. Perplexity (PPL): The effect of removing a layer on the model’s perplexity (a measure of how well the model predicts a sequence). 2. Block Importance (BI): The cosine distance between the input and output of a layer, which measures how much the layer transforms its input.
The BI score for layer [math]\displaystyle{ i }[/math] is computed as:
[math]\displaystyle{ \text{BI}_{i} = 1 - \mathbb{E}_{\mathbf{X},t} \frac{\mathbf{X}_{i,t}^{T} \mathbf{X}_{i+1,t}}{\|\mathbf{X}_{i,t}\|_{2} \|\mathbf{X}_{i+1,t}\|_{2}} }[/math]
Here:
- [math]\displaystyle{ \mathbf{X}_{i} }[/math] is the input to layer [math]\displaystyle{ i }[/math].
- [math]\displaystyle{ \mathbf{X}_{i,t} }[/math] is the [math]\displaystyle{ t^{th} }[/math] row of [math]\displaystyle{ \mathbf{X}_{i} }[/math].
- [math]\displaystyle{ \mathbb{E}_{\mathbf{X},t} }[/math] denotes the expectation over the input and sequence dimensions.
The authors find that BI is faster to compute than PPL and provides a good approximation of layer importance. Additionally, removing layers selectively can retain strong model performance while reducing computational costs.
Residual Transfer for Attention Head Pruning
To reduce accuracy loss after pruning attention heads, the authors introduce a residual transfer technique. Instead of discarding pruned heads entirely, their information is redistributed to the remaining heads using a symmetric formula:
[math]\displaystyle{ \text{new\_head}_i = \text{head}_i + (\text{head}_i - \text{head}_{2K - i + 1}) }[/math] This helps preserve knowledge from pruned heads, improving performance during retraining. In models with grouped-query attention, this is applied only to query heads. The method is lightweight and boosts model accuracy, especially in aggressive pruning settings.
Pruning Best Practices
- Width pruning (e.g., neurons, heads, embedding channels) is more effective than depth pruning after retraining.
- Activation-based importance metrics are effective and computationally cheap, avoiding the need for backward gradients.
- (Batch=L2, Sequence=Mean) aggregation functions yield the best results when calculating importance scores.
- Iterative pruning (prune → retrain → prune) significantly outperforms one-shot pruning for high compression targets like 4B from 15B.
- Adding residual information from pruned attention heads back into remaining heads boosts performance.
- Order matters: performing one width‑prune cycle first, then a shallow depth‑prune, then a second width pass yields up to +2.6 MMLU over any other ordering at 4 B
Knowledge Distillation Retraining
Knowledge distillation is used to retain knowledge from the original large model after pruning. In this process, a smaller "student" model is trained using a distillation loss that aligns its output with the original "teacher" model.
The retraining phase leverages only a small fraction of the original training tokens, significantly reducing computational costs. The key components of knowledge distillation include:
- Distillation loss: A combination of cross-entropy and KL divergence loss is applied to match the student’s output distribution with the teacher’s predictions.
- Token-efficient training: Only a subset of the original dataset is used, as full retraining would negate the benefits of compression.
- Iterative pruning and retraining: The best results are achieved when distillation is applied iteratively with pruning rather than in a one-shot manner.
Empirical results show that knowledge distillation allows the pruned models to maintain high perplexity accuracy and generalization performance, even at significantly smaller model sizes.
Neural Architecture Search (NAS)
After pruning, Neural Architecture Search (NAS) is employed to identify optimal architectural configurations under a given parameter budget. Instead of manually selecting pruned architectures, NAS automates the process to maximize efficiency and performance.
The NAS process involves:
- Evaluating pruned architectures based on computational efficiency and accuracy trade-offs.
- Selecting optimal configurations for both width-pruned and depth-pruned models.
- Fine-tuning the final pruned model to maximize performance.
Findings indicate that NAS-selected architectures outperform manually pruned baselines of the same model size. The approach ensures that the compressed models retain the highest possible accuracy while significantly reducing computational costs.
Experimental Results and Findings
The structured pruning approach combined with distillation yields compressed models that retain a high degree of accuracy:
- The 8B and 4B models retain over 95% of the original model’s accuracy while being significantly smaller.
- The 4B model achieves a 4× reduction in parameters with minimal loss in perplexity performance.
- The 8B model maintains nearly full accuracy compared to the original 15B model, making it a viable alternative with lower compute requirements.
Conclusion and Implications
This study presents a systematic and cost-efficient method for compressing large-scale language models with minimal retraining. The combination of structured pruning, knowledge distillation, and NAS enables significant reductions in model size while maintaining strong performance.
Key takeaways include:
- Pruning across multiple axes (width and depth) effectively reduces model size while preserving accuracy.
- Distillation requires only a fraction of training tokens, making retraining computationally feasible.
- NAS automates architectural optimization, leading to better compressed models than manual selection.
These techniques are broadly applicable to other large models beyond Nemotron-4, making them relevant for real-world deployment scenarios. Future work could explore:
- Extending pruning techniques to multimodal and vision-language models.
- Investigating more aggressive pruning strategies for extreme model compression.
- Optimizing pruned models for real-time inference on edge devices.
Attention Is All You Need But You Don’t Need All Of It For Inference of Large Language Models
This paper explores how strategically omitting layers at inference can drastically cut compute and latency while preserving performance. They focus on Llama‑v2 models and show that dropping up to 33 % of deeper attention sublayers in the 13 B variant incurs only a 1.8 % average drop on the OpenLLM benchmark, yet yields significant speedups without extra fine‑tuning. This simple “inference‑time attention removal” (ITAR) method outperforms more complex pruning schemes by targeting the most redundant components post‑training.
The Problem: Inference Complexity
Inference in LLMs is costly because of the self-attention mechanism, which scales quadratically with input length. This creates a challenge, especially for applications requiring real-time responses. Researchers have previously explored various methods to optimize inference, including pruning, quantization, and speculative decoding, but this paper focuses on a more direct approach: skipping unnecessary layers.
Key Idea: Skipping Layers Without Significant Performance Loss
The core hypothesis of the paper is that not all layers contribute equally to the final output of an LLM. Specifically, the deeper layers (closer to the output) exhibit higher similarity with their preceding layers, meaning that dropping some of them may have minimal impact on performance. To test this, the authors conduct experiments on Llama-v2 (7B and 13B models) and compare different strategies for skipping layers.
Method: Selective Layer Skipping
Consider a Transformer model with [math]\displaystyle{ L }[/math] layers, where each layer consists of an attention sub-layer and a multi-layer perceptron (MLP) sub-layer. We define each layer as:
[math]\displaystyle{ \text{Layer}_i = (\text{Attention}_i, \text{MLP}_i) }[/math]
for [math]\displaystyle{ i \in \{1, 2, \dots, L\} }[/math].
The paper evaluates three techniques for skipping components of Transformer layers:
1. Skipping MLP Layers: The feedforward (MLP) sub-layers from the last few layers are removed.
If we skip the last [math]\displaystyle{ k }[/math] MLP layers while keeping the attention layers, the modified model is:
[math]\displaystyle{ M_{\text{skip MLP}} = \left\{ (\text{Attention}_i, \text{MLP}_i) \mid i \in [1, L-k] \right\} \cup \left\{ (\text{Attention}_i, \emptyset) \mid i \in [L-k+1, L] \right\} }[/math]
2. Skipping Attention Layers: The self-attention sub-layers from the last few layers are removed.
If we skip the last [math]\displaystyle{ k }[/math] attention layers while keeping the MLP layers, the modified model is represented as:
[math]\displaystyle{ M_{\text{skip attention}} = \left\{ (\text{Attention}_i, \text{MLP}_i) \mid i \in [1, L-k] \right\} \cup \left\{ (\emptyset, \text{MLP}_i) \mid i \in [L-k+1, L] \right\} }[/math]
3. Skipping Entire Transformer Blocks: Both attention and MLP components are removed from some of the last layers.
If we skip both the attention and MLP sub-layers in the last [math]\displaystyle{ k }[/math] layers, we obtain:
[math]\displaystyle{ M_{\text{skip block}} = \left\{ (\text{Attention}_i, \text{MLP}_i) \mid i \in [1, L-k] \right\} \cup \left\{ (\emptyset, \emptyset) \mid i \in [L-k+1, L] \right\} }[/math]
The image below gives the skip mechanisms for skipping single layers and attention layers during inference:
The models were tested across four benchmarks: ARC, HellaSwag, TruthfulQA, and MMLU, which measure reasoning, common sense, truthfulness, and general knowledge.
Empirical Results & Findings: Attention Layers Are Less Crucial Than MLP Layers
The empirical results are shown below:
As expected, results dropped after skipping layers except for TruthfulQA. It had already been observed that larger language models are less truthful, but this interesting result now shows that reducing the size of already trained models can actually make them more truthful. The observation still holds even if the last layer is preserved. Skipping attention layers only results in a 1.8% drop in accuracy when keeping 66% of the network compared to a 13.1% decrease in performance when dropping only the MLP layers.
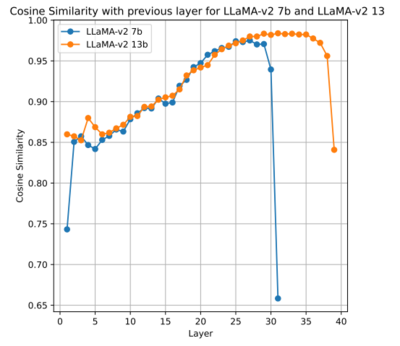
The results demonstrate a clear pattern:
- Dropping entire Transformer blocks leads to a significant performance drop.
- Dropping MLP layers leads to larger performance degradation compared to dropping attention layers.
- Dropping attention layers results in the best trade-off between speed and performance, with only a 1.8% drop in accuracy when 33% of attention layers are removed. Removing 33% of attention layers led to an 18% speedup in Llama-2-13B.
Interestingly, the TruthfulQA benchmark showed an increase in accuracy when some layers were skipped, suggesting that reducing model complexity might reduce hallucinations.
The paper provides empirical evidence that deeper layers contribute less unique information compared to earlier layers. The figure below shows cosine similarity between successive layers, highlighting that deeper layers are more redundant.
Conclusion
The paper investigated the effect of dropping the last layers from the 7B and 13B Llama2 models. The authors observed that dropping attention layers leads to less performance decrease than MLP layers. This demonstrates the potential that improvements can be made over dropping entire layers compared to just dropping the attention layers.
SliceGPT: Compress Large Language Models by deleting rows and columns
Overview
SliceGPT is a post‑training sparsification method that compresses large language models by deleting entire rows and columns from weight matrices via orthonormal transformations and principal-component projections, reducing up to 30 % of parameters while maintaining over 90 % of zero-shot performance across LLAMA‑2, OPT, and Phi‑2 models with minimal recovery fine‑tuning. It leverages a novel concept called computational invariance—in which applying an orthogonal matrix to weights leaves the model functionally unchanged—enabling structured pruning without additional sparsity‑specific data structures. The sliced models run 34 %–36 % faster on both consumer (24 GB) and data‑center (40 GB A100) GPUs without custom kernel optimizations, offering a practical path to deploy high‑capacity LLMs on fewer resources.
Background
This section introduces some necessary background on transformer architectures and notations used in this paper.
Transformer networks
Embeddings: Let [math]\displaystyle{ D }[/math] be the embedding dimension of our transformer, [math]\displaystyle{ N }[/math] be the sequence length. Embedding matrix [math]\displaystyle{ \mathbf{W}_{\mathrm{embd}} }[/math] is indexed by input sequence [math]\displaystyle{ s }[/math] to produce the initial signal [math]\displaystyle{ X }[/math] with shape [math]\displaystyle{ N × D }[/math]
LayerNorm: LayerNorm operation subtracts the mean from each row of the input matrix, divides the row by its standard deviation, rescales (columnwise), and adds an offset.
[math]\displaystyle{ \mathrm{LayerNorm}(\mathbf{X})=\mathrm{RMSNorm}(\mathbf{XM})\mathrm{diag}(\boldsymbol{\alpha})\sqrt{D}+\mathbf{1}_{N}\boldsymbol{\beta}^{\top} }[/math]
Attention Blocks:The attention block has four matrices: [math]\displaystyle{ \mathbf{W}_{\mathrm{k}} }[/math] , [math]\displaystyle{ \mathbf{W}_{\mathrm{q}} }[/math] , [math]\displaystyle{ \mathbf{W}_{\mathrm{v}} }[/math] and [math]\displaystyle{ \mathbf{W}_{\mathrm{o}} }[/math] , each of dimension [math]\displaystyle{ D × D }[/math]. The input signal arriving into the block is projected into the Key ([math]\displaystyle{ \mathbf{XW}_{\mathrm{k}} }[/math] ), Query ([math]\displaystyle{ \mathbf{XW}_{\mathrm{q}} }[/math] ), and Value ([math]\displaystyle{ \mathbf{XW}_{\mathrm{v}} }[/math] ) matrices, which are then split into multiple heads. A nonlinear operation [math]\displaystyle{ \sigma }[/math] is applied at each head before the signals are combined and multiplied by the output weight matrix [math]\displaystyle{ \mathbf{W}_{\mathrm{o}} }[/math].
FFN Blocks:This is a Multi-layer Perceptron (MLP), which consists of a linear layer [math]\displaystyle{ \mathbf{W}_{\mathrm{1}} }[/math], followed by an element-wise operation [math]\displaystyle{ \sigma }[/math], followed by a second linear layer: [math]\displaystyle{ \sigma(\mathbf{X}\mathbf{W}_1+\boldsymbol{b}_1)\mathbf{W}_2+\boldsymbol{b}_2 }[/math].
Key Contributions
Computational invariance
If [math]\displaystyle{ \mathbf{Q} }[/math] is an orthogonal matrix, i.e, [math]\displaystyle{ \mathbf{Q}^\top\mathbf{Q}=\mathbf{Q}\mathbf{Q}^\top=\mathbf{I} }[/math] . Multiplying a vector [math]\displaystyle{ \boldsymbol{x} }[/math] by [math]\displaystyle{ \mathbf{Q} }[/math] does not change the norm of the vector, since [math]\displaystyle{ \|\mathbf{Q}\boldsymbol{x}\|=\sqrt{\boldsymbol{x}^\top\mathbf{Q}^\top\mathbf{Q}\boldsymbol{x}}=\sqrt{\boldsymbol{x}^\top\boldsymbol{x}}=\|\boldsymbol{x}\| }[/math]. The authors demonstrated that orthogonal transformations can be applied to weight matrices in transformer networks without altering the model's output. We can apply any orthogonal transformation [math]\displaystyle{ \mathbf{Q} }[/math] to the weights of the transformer without changing the result, so the computation can be performed in any transformed state. We refer to this as a computational invariance, and define it in the following theorem.
This invariance enables structured pruning by modifying weights while preserving functionality, a foundational insight for post-training compression.
SliceGPT
The computational invariance is only effctive to RMSNorm-connected networks, so we convert the network to RMSNorm by absorbing the linear blocks of LayerNorm into the adjacent blocks first.
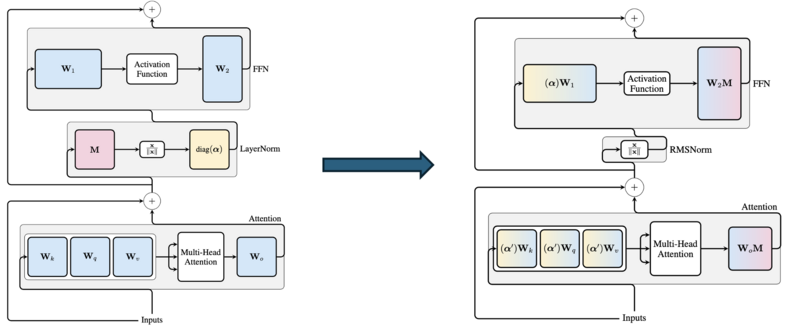
After every LayerNorm in the transformer has been converted to RMSNorm, we will apply the computational-invariance idea, and can select any [math]\displaystyle{ Q }[/math] to modify the model.
To compute the matrices [math]\displaystyle{ \mathbf{Q}_{\ell} }[/math] , we use PCA. We select a calibration dataset from the training set, run it through the model (after converting LayerNorm operations into RMSNorm), and extract the orthogonal matrix of the layer. We use the output of the transformed network to calculate the orthogonal matrices of the next layers. More precisely, if [math]\displaystyle{ \mathbf{X}_{\mathrm{\ell,i}} }[/math] is the output of the [math]\displaystyle{ \boldsymbol{\ell}^{\mathbf{th}} }[/math] RMSNorm block for the [math]\displaystyle{ \boldsymbol{i}^{\mathbf{th}} }[/math] sequence in the calibration dataset, we compute [math]\displaystyle{ \mathbf{C}_\ell=\sum_i\mathbf{X}_{\ell,i}^\top\mathbf{X}_{\ell,i} }[/math] and set [math]\displaystyle{ \mathbf{Q}_{\ell} }[/math] to the be the eigenvectors of [math]\displaystyle{ \mathbf{C}_{\ell} }[/math], sorted by decreasing eigenvalues.
Then we apply the deletion matrix [math]\displaystyle{ \mathbf{D} }[/math] ([math]\displaystyle{ D\times D_{\mathrm{small}} }[/math]) to the operations preceding and succeeding the construction of that matrix, which have already been multiplied by [math]\displaystyle{ \mathbf{Q} }[/math] in the above. That will delete rows of [math]\displaystyle{ \mathbf{W}_{\mathrm{in}} }[/math] and columns of [math]\displaystyle{ \mathbf{W}_{\mathrm{out}} }[/math] and [math]\displaystyle{ \mathbf{W}_{\mathrm{embd}} }[/math], and also delete both rows and columns of the matrix [math]\displaystyle{ \mathbf{Q}_{\ell-1}^\top\mathbf{Q}_\ell }[/math] (in Figure RMSNorm with [math]\displaystyle{ \mathbf{Q} }[/math] transformation).
method
SliceGPT’s approach is elegant and practical:
- Unlocking Invariance: Transformers often use normalization layers like RMSNorm. The paper shows that applying an orthogonal matrix [math]\displaystyle{ \mathbf{Q} }[/math] (where [math]\displaystyle{ \mathbf{Q}^\top \mathbf{Q} = \mathbf{I} }[/math]) to weights doesn’t change the output because RMSNorm ignores such rotations. Mathematically: [math]\displaystyle{ \text{RMSNorm}(\mathbf{X} \mathbf{Q}) \mathbf{Q}^\top = \text{RMSNorm}(\mathbf{X}) }[/math]. If the model uses LayerNorm instead, it’s first converted to RMSNorm.
- Slicing with PCA:
- For each transformer block, activations from a small calibration dataset (e.g., WikiText-2) are collected.
- Principal Component Analysis (PCA) finds the most important directions in these activations, encoded in [math]\displaystyle{ \mathbf{Q}_\ell }[/math] for layer [math]\displaystyle{ \ell }[/math].
- Weight matrices are rotated with [math]\displaystyle{ \mathbf{Q}_\ell }[/math], and the least important rows and columns (low PCA components) are sliced off, shrinking the embedding dimension.
- Residual connections get a tweak: a small matrix [math]\displaystyle{ \mathbf{Q}_{\ell-1}^\top \mathbf{Q}_\ell }[/math] keeps everything aligned.
- No Fine-Tuning Needed: This runs on a single GPU in hours (e.g., 3.5 hours for LLAMA-2 70B) and skips retraining, though optional fine-tuning can boost results.
Empirical Result
Generation Task
The table below shows the perplexity obtained by various slicing levels using the WikiText-2 dataset on both the OPT and LLAMA-2 model families. The performance of SliceGPT improves as the model size increases. Comparing SliceGPT with SparseGPT, we see that SparseGPT 2:4 performs worse than SliceGPT with 25% slicing in all LLAMA-2 models. For OPT, we see that 30% sliced models beat 2:4 sparsity for all model sizes except 2.7B.
Zero-shot Tasks
SliceGPT is assessed across five well-known zero-shot tasks: PIQA; WinoGrande; HellaSwag; ARC-e and ARC-c. The following figure shows the average scores achieved by the sliced models across these tasks.
Limitation and Future Work
SliceGPT effectively reduces inference costs by slicing weight matrices using an orthogonal transformation computed via PCA, but it still retains more parameters than methods like SparseGPT and is less beneficial for smaller models where dense architectures perform better. The method’s reliance on PCA can be sensitive to numerical precision and may not be optimal, and it currently operates as a standalone technique without combining with complementary approaches such as quantization or additional structural pruning. Future work could explore alternative ways to compute the transformation, integrate other compression strategies, and further investigate the theoretical aspects of computational invariance to design even more efficient models.
- Smaller Models Struggle: SliceGPT shines on giants like LLAMA-2 70B, but smaller models (under 13B parameters) lose more accuracy when sliced.
- Calibration Matters: The dataset used for PCA (e.g., WikiText-2 vs. Alpaca) affects results—choosing the right one is key.
- No Sparse Magic: It doesn’t create hardware-friendly sparse patterns (like 2:4 sparsity), though its dense matrices still speed things up.
- Room to Grow: Combining SliceGPT with quantization or exploring smarter ways to pick [math]\displaystyle{ \mathbf{Q}_\ell }[/math] (beyond PCA) could push efficiency further.
EchoAtt: Attend, Copy, then Adjust for More Efficient Large Language Models
This paper introduces a novel framework to make transformer-based LLMs more efficient while maintaining their performance. The motivation behind their work is that when studying larger models, it is observed that inner layers contain highly similar attention matrices. The similarity is determined by computing the cosine similarity between attention matrices at different layers. Therefore, they suggest a knowledge distillation-based framework that shares attention between layers containing similar matrices while unique layers are maintained as they contain distinct attention patterns. These critical layers are usually located within the first layers of the network.
Contributions
- Introduce EchoAtt framework to optimize transformer-based LLMs.
- Propose a method to share attention matrix.
- Apply this approach in a knowledge distillation setting.
- Demonstrate the effectiveness of EchoAtt reducing inference and training speed and number of parameters while being competitive in zero-shot tasks.
Framework
The developed method is divided into two steps:
- Construct a shared attention student model.
- Transfer knowledge from a pre-trained teacher model to the student through knowledge distillation.
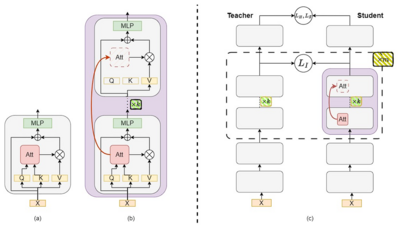
To construct the student model, the first and last layers are retained. To select these layers, the following procedure was followed:
- Calculate the average cosine similarity of each layer with all other layers.
- Sort the layers based on the scores.
- Choose the cutoff point to be the distance between the lowest and highest scores.
- Maintain first or last layers with a score below the threshold.
To share the attention mechanism within inner layers, a shared attention block is constructed. Every block consists of [math]\displaystyle{ k }[/math] consecutive inner layers, and attention matrices are shared among these blocks. Shared attention figure (b) clearly illustrates how multiple blocks are sharing attention. It is worth noting that [math]\displaystyle{ k }[/math] is a hyperparameter controlling the degree of compression and parameter sharing; larger values of [math]\displaystyle{ k }[/math] mean more parameter sharing and high compression and vice versa.
In vanilla transformers, the attention matrix is computed at each layer [math]\displaystyle{ i }[/math]:
[math]\displaystyle{ Att_i = softmax(\frac{Q_i K_i^T}{\sqrt{d}}) V_i }[/math]
In the proposed technique, a single set of [math]\displaystyle{ Q }[/math] and [math]\displaystyle{ K }[/math] matrices is used for all the layers within a block; indexed by [math]\displaystyle{ j }[/math]. To compute shared attention, we first calculate the [math]\displaystyle{ softmax }[/math] of [math]\displaystyle{ Q }[/math] and [math]\displaystyle{ K }[/math] across the layers belonging to the same block then we multiply it by [math]\displaystyle{ V }[/math] matrix that is unique to the block:
[math]\displaystyle{ A_{shared} = softmax(\frac{Q_{shared} K_{shared}^T}{\sqrt{d}}) }[/math]
[math]\displaystyle{ Att_j = A_{shared}V_j, \quad j \in [i, i+k] }[/math]
Knowledge Distillation
To compensate for parameters cut, which may affect performance, a knowledge distillation framework is utilized to pass the knowledge from a pre-trained teacher to the student. The process consists of two stages:
- Distillation with teacher's Pseudo-Labels.
- Refinement with True Labels.
Before going into the details of each stage, let's define the following keywords:
- Pseudo label: pre-trained model output (prediction) that is used to train the student. For example, for a certain input if the model outputs 'apple', then it becomes the label for the same input for the student.
- Soft label: probability distribution across class labels. For example, if we have 3 classes and one to be predicted, then the soft label would be something like [0.2, 0.6, 0.2].
- Hard label: it is like one-hot encoded version of the soft label where only the predicted label has a probability of 1. For the previous example, it would be [0, 1, 0].
Distillation with teacher's Pseudo-Labels
In this stage both models are provided the same input tokens, and the student's training objective is to match the teacher's prediction at several levels. As shown in the figure above, three losses are utilized to optimize the process:
- Intermediate Layer Loss ([math]\displaystyle{ \mathcal{L}_I }[/math]): this loss encourages the student to minimize the difference between its shared attention blocks and the teacher's corresponding mid-layers. This will push the student to learn to convey the teacher's knowledge with fewer parameters.
[math]\displaystyle{ \mathcal{L}_I = \frac{1}{m} \sum_{i=1}^{m} \| S_{ki+b}(x) - T_{ki+b}(x) \|_2^2 }[/math]
where [math]\displaystyle{ m }[/math] is the number of shared attention blocks, [math]\displaystyle{ k }[/math] is the number of attention layers within each block, and [math]\displaystyle{ b }[/math] is the number of early skipped layers while [math]\displaystyle{ S_j }[/math] and [math]\displaystyle{ T_j }[/math] are the outputs of the student and the teacher at layer [math]\displaystyle{ j }[/math].
- Soft Label Loss ([math]\displaystyle{ \mathcal{L}_S }[/math]): guides the student to learn the teacher's probability distribution over the labels. Hence it is calculated by KL-divergence.
[math]\displaystyle{ \mathcal{L}_S = \text{KL}\left(\sigma(S(x)) \parallel \sigma(T(x))\right) }[/math]
- Hard Label Loss ([math]\displaystyle{ \mathcal{L}_H }[/math]): this loss's goal is to teach the student about the most confident predictions of the teacher.
[math]\displaystyle{ \mathcal{L}_H = \text{CE}\left(\sigma(S(x)), \tau(T(x))\right) }[/math]
[math]\displaystyle{ \sigma }[/math] and [math]\displaystyle{ \tau }[/math] are the softmax and argmax functions, respectively. [math]\displaystyle{ S(x) }[/math] and [math]\displaystyle{ T(x) }[/math] are the outputs of the student and teacher models.
The final loss function is a weighted sum of the three losses: [math]\displaystyle{ \mathcal{L} = \alpha \mathcal{L}_I + \beta \mathcal{L}_S + \gamma \mathcal{L}_H }[/math] where [math]\displaystyle{ \alpha }[/math], [math]\displaystyle{ \beta }[/math], and [math]\displaystyle{ \gamma }[/math] control the contribution of each loss function.
Refinement with True Labels
At this stage, the student is fine-tuned on the ground truth labels from the training dataset. It is more of a polishing step to improve predictions. For that purpose, cross-entropy is used for loss calculation.
Results
To evaluate the performance of the proposed architecture, TinyLlaMA was selected as the baseline. Two main tests were conducted, the first with continual training only and the second with continual training and knowledge distillation. Three versions of the model were evaluated with [math]\displaystyle{ 77\% }[/math], [math]\displaystyle{ 41\% }[/math], and [math]\displaystyle{ 23\% }[/math] attention sharing ratios. Table 1 shows that with continual training only, without distillation, the model with [math]\displaystyle{ 23\% }[/math] sharing ratio outperforms the baseline. However, Table 2 proves that when knowledge distillation is incorporated, both models with [math]\displaystyle{ 41\% }[/math] and [math]\displaystyle{ 23\% }[/math] outperform the baseline indicating performance improvement with fewer parameters. Finally, Table 3 shows how shared attention improves inference and training speeds and the number of reduced parameters.
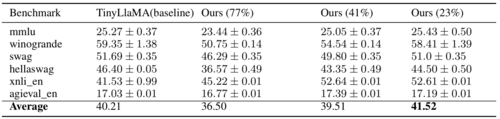
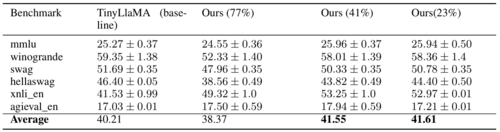

Attention Similarity Analysis and Selection Strategy
EchoAtt is based on a key observation in transformer-based models: the attention matrices in intermediate layers are often highly redundant. To quantify this, EchoAtt computes the cosine similarity between attention scores across different layers. Let [math]\displaystyle{ A_i }[/math] and [math]\displaystyle{ A_j }[/math] be the flattened attention matrices at layers [math]\displaystyle{ i }[/math] and [math]\displaystyle{ j }[/math], respectively. The similarity is computed as:
[math]\displaystyle{ \text{cosine_sim}(A_i, A_j) = \frac{A_i \cdot A_j}{\|A_i\| \cdot \|A_j\|} }[/math]
By comparing this measure over all pairs of layers, a similarity matrix is constructed. The layers that have the highest average similarity are redundant and can be shared. What this analysis proves is that middle layers generate similar attention maps, while first and final layers are different and hence kept in their original form.
To determine which layers should share attention, EchoAtt computes the average similarity of each layer to all others:
[math]\displaystyle{ S_i = \frac{1}{L} \sum_{j=1}^{L} \text{cosine_sim}(A_i, A_j) }[/math]
where [math]\displaystyle{ L }[/math] represents the number of layers. Layers are sorted by [math]\displaystyle{ S_i }[/math], and the maximum gap between neighboring sorted values is used to find a threshold for attention sharing. Layers below the threshold are shaped into shared-attention blocks. This ensures high efficiency without significant degradation in model performance, as evidenced by empirical results.
Summary & Key Takeaways
Knowledge Distillation (KD), pruning, and parameter sharing make a great effort to address the challenges of computational and memory efficiency. The following table summarizes their contribution, strengths and weaknesses:
| Year | Method | Contribution | Strengths | Weaknesses | Speedup Type | Distillation Loss Design |
|---|---|---|---|---|---|---|
| 2024 | Attention Layer Skipping |
|
Efficiently reduces computational costs with minor performance loss; deeper attention layers can be pruned effectively. | Performance impact varies depending on which layers are skipped; requires careful selection of attention vs. MLP layers for optimal results. | Inference-time only | None (no distillation used) |
| 2024 | Minitron |
|
Highly data-efficient, significantly reduces compute needs, and outperforms similar-sized models trained from scratch. | Further optimization needed through neural architecture search and expanded application to even larger models. | Inference-time and training-time (via reduced retraining tokens) | Logit-based KL divergence, optional intermediate state loss, hard label cross-entropy |
| 2024 | SliceGPT |
|
Effective model compression (up to 25% fewer parameters) without significant retraining; compatible with common hardware. | May not scale optimally with certain hardware architectures; deeper transformers may require more fine-grained pruning combinations. | Inference-time only | Optional (not required; works without fine-tuning) |
| 2024 | EchoAtt |
|
Enhances efficiency significantly through attention mechanism sharing; promising scalability for larger models. | Effectiveness depends on similarity patterns across layers; over-sharing can lead to degradation without distillation. | Inference-time and training-time | Intermediate state loss, soft label KL, hard label cross-entropy (weighted) |
Topic 4: Quantization
Introduction
Quantization is another model compression approach to address the large memory and computational requirements of models. Specifically, the multiplication and storage of very large matrices is expensive - is there a way to reduce these costs? The main idea with quantization is to represent the values in the various weight matrices and biases of the model with integers instead of floating point numbers. This requires a mapping from floating point value (e.g FP32) into integers (e.g INT4) and various techniques have been developed to preserve model accuracy. By doing so, we can significantly reduces memory consumption (FP32 to INT4 saves 8 times the memory), as well as computation cost. Thus, research in this area aims to sacrifice as little accuracy as possible while making this substitution in numerical representation.
Notably there are two main forms of quantization:
- Post-Training Quantization (PTQ): Applied after the model has been fully trained using high-precision (e.g., 32-bit floating point) weights
- Quantization-Aware Training (QAT): Applied during the forward pass of model training to allow the optimization process to account for the quantized inference
A tabular overview of the recent advancements in quantization methods is shown below with further details provided for each method in the subsequent sections.
| Method | Type | Bit Precision | Key Features | Best Suited For |
|---|---|---|---|---|
| Integer-Only | QAT | INT8 | Enables integer-only inference and requires quantization-aware training | Various neural network architectures |
| ZeroQuant | PTQ | INT8 | Efficient for large transformers, minimal accuracy impact and significant speedup vs FP16 | Large transformer models |
| GPTQ | PTQ | 2.5-4 bits | Highly efficient for very large models, high compression rate, maintains accuracy | GPT-like models with billions of parameters |
| SmoothQuant | PTQ | 8-bit weight, 8-bit activation (W8A8) | Training-free, accuracy-preserving and ready-to-use solution for Large Language Models (LLMs) | LLMs |
Emerging Trends: Mixed-Precision Quantization and Adaptive Methods
Beyond traditional fixed-bit quantization (e.g., INT8 or INT4), recent research has explored mixed-precision quantization and adaptive quantization methods, aiming to achieve even better trade-offs between computational efficiency and model accuracy.
Mixed-Precision Quantization
Mixed-precision quantization involves assigning different numerical precisions to different layers or components of the model, depending on their sensitivity to quantization errors. The intuition behind this approach is that not all layers equally contribute to accuracy degradation when quantized. For instance, embedding layers might retain higher precision (e.g., INT8), while deeper layers, which typically have lower sensitivity, could be quantized more aggressively (e.g., INT4 or INT2).
Formally, consider a model with layers [math]\displaystyle{ L_1, L_2, \dots, L_n }[/math]. Each layer [math]\displaystyle{ L_i }[/math] has a quantization bit-width [math]\displaystyle{ b_i }[/math]. The optimization problem for mixed-precision quantization can be defined as minimizing the weighted sum of accuracy loss and computational resource constraints:
[math]\displaystyle{ \min_{b_1, b_2, \dots, b_n} \mathcal{L}(b_1, b_2, \dots, b_n) + \lambda \cdot \mathcal{C}(b_1, b_2, \dots, b_n), }[/math]
where:
- [math]\displaystyle{ \mathcal{L}(b_1, b_2, \dots, b_n) }[/math] denotes the accuracy degradation associated with quantization bit-widths.
- [math]\displaystyle{ \mathcal{C}(b_1, b_2, \dots, b_n) }[/math] represents the computational cost, such as inference latency or memory usage.
- [math]\displaystyle{ \lambda }[/math] is a hyperparameter balancing accuracy and cost.
For example, layers performing critical operations like attention or embeddings might maintain higher precision (INT8), while dense layers or less sensitive modules could use lower precision (INT4), significantly optimizing performance without major accuracy losses.
Adaptive Quantization
Adaptive quantization dynamically adjusts the quantization range or precision based on input data distributions or runtime feedback. Instead of using a fixed quantization scale, adaptive quantization recalculates scales periodically or continuously during inference, allowing it to handle outliers effectively and maintain higher accuracy in scenarios where input distributions vary significantly.
Mathematically, adaptive quantization recalculates the quantization scale [math]\displaystyle{ S }[/math] dynamically for each batch or time step:
[math]\displaystyle{ S_t = \frac{\max(X_t) - \min(X_t)}{2^{b} - 1}, }[/math]
where [math]\displaystyle{ X_t }[/math] is the activation or weight matrix at inference step [math]\displaystyle{ t }[/math], and [math]\displaystyle{ b }[/math] is the quantization bit-width.
This adaptive recalibration ensures that quantization better reflects the current data distribution, significantly reducing quantization errors, especially in long-context models or models encountering highly varied input.
Hardware-Aware Quantization
Additionally, recent trends emphasize hardware-aware quantization methods, which directly consider the characteristics of the deployment hardware (e.g., GPUs, TPUs, CPUs). These methods jointly optimize the quantization scheme along with hardware constraints, such as memory hierarchy and computational unit (tensor core) size.
A typical optimization objective becomes:
[math]\displaystyle{ \min_{Q} \left( \text{Accuracy Loss}(Q) + \gamma \cdot \text{Latency}(Q; H) \right), }[/math]
where:
- [math]\displaystyle{ Q }[/math] denotes the quantization scheme.
- [math]\displaystyle{ H }[/math] denotes the hardware platform.
- [math]\displaystyle{ \gamma }[/math] is a hyperparameter controlling trade-off between accuracy loss and hardware latency.
Hardware-aware methods such as ZeroQuant leverage GPU-specific instructions (e.g., NVIDIA Ampere's WMMA instructions) to maximize performance gains by aligning quantization granularity with hardware architecture.
Example: Mixed-Precision in GPT-Style Models
A concrete example of mixed-precision quantization is demonstrated in quantizing GPT-style models, where different precision levels are applied across layers to minimize accuracy loss:
- Embedding Layers: INT8 (higher precision due to sensitivity).
- Attention Layers: INT4 (balanced precision due to importance and redundancy).
- Feed-Forward Layers: INT2 or INT4 (lowest precision due to redundancy).
Empirical results show that mixed-precision quantization can significantly reduce memory footprint by over 70%, compared to uniform INT8 quantization, with negligible loss of accuracy (less than 0.5% drop in benchmark tasks).
Thus, these emerging quantization techniques—mixed-precision, adaptive scaling, and hardware-aware optimization—provide powerful methods for deploying extremely large models efficiently, marking a significant step forward from traditional uniform quantization approaches.
Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference
This paper sets up the basis for further research in quantization. The broad idea is to find a mapping from real numbers to integers (in the weight and activation matrices) which does not compromise model accuracy.
In order to derive this mapping, the authors start by examining the affine mapping which maps an integer to a real number while preserving collinearity and distance ratios. For two constants [math]\displaystyle{ S \in \mathbb{R}, Z \in \mathbb{Z} }[/math] (called quantization parameters), the mapping of an integer q to a real number r is defined as [math]\displaystyle{ r = S(q-Z) }[/math]. To apply this to the context of matrix multiplication, consider the following problem. Let:
- [math]\displaystyle{ r_1, r_2 \in \mathbb{R}^{N \times N} }[/math] be two real-valued matrices
- [math]\displaystyle{ r_3 = r_1r_2 }[/math]
- [math]\displaystyle{ \alpha \in \{1, 2, 3\} }[/math] be subscripts referring to [math]\displaystyle{ r_1, r_2, r_3 }[/math]
- [math]\displaystyle{ S_{\alpha}, Z_{\alpha} }[/math] be the quantization parameters
- [math]\displaystyle{ q_{\alpha} }[/math] be the quantized version of [math]\displaystyle{ r_{\alpha} }[/math]
- [math]\displaystyle{ 1 \le i, j \le N }[/math] where [math]\displaystyle{ r_{\alpha}^{(i,j)}, q_{\alpha}^{(i,j)} }[/math] refer to the entry in the [math]\displaystyle{ i^{th} }[/math] row and [math]\displaystyle{ j^{th} }[/math] column of the matrices
Then [math]\displaystyle{ r = S(q-Z) }[/math] can be written as [math]\displaystyle{ r_{\alpha}^{(i,j)} = S_\alpha(q_{\alpha}^{(i,j)}-Z_\alpha) }[/math]. Recall that [math]\displaystyle{ r_3 = r_1r_2 }[/math]. If we consider a particular entry (i, k) in this matrix multiplication formula and substitute each term with this quantization, we get that [math]\displaystyle{ S_3(q_3^{(i,k)} - Z_3) = \Sigma_{j=1}^{N} S_1(q_1^{(i,j)} - Z_1) S_2(q_2^{(j,k)} - Z_2) }[/math]. Then rearranging this formula to give isolate the term of interest, we get that
[math]\displaystyle{ q_3^{(i,k)} = Z_3 + \dfrac{S_1S_2}{S_3} \Sigma_{j=1}^{N} (q_1^{(i,j)} - Z_1) (q_2^{(j,k)} - Z_2) }[/math]
Defining [math]\displaystyle{ M = \dfrac{S_1S_2}{S_3} }[/math] to represent the constants, the authors found empirically that [math]\displaystyle{ M \in (0,1) }[/math] and can thus be expressed in the compressed form [math]\displaystyle{ M = 2^{-n} M_0 }[/math] for some non-negative integer n and [math]\displaystyle{ M_0 \in [0.5, 1) }[/math]. This allows the computation of the constant M to be performed using fixed point multiplication. All remaining terms in the formula are integers, this the quantized version of the matrix multiplication [math]\displaystyle{ q_3 \approx r_3 = r_1r_2 }[/math] can be computed using fixed point arithmetic which is much more efficient than the previously used floating point operations.
Note that here [math]\displaystyle{ r_1 }[/math] represents an activation matrix, [math]\displaystyle{ r_2 }[/math] represents the weight and [math]\displaystyle{ r_3 }[/math] is thus the output matrix. S here is called quantization scale, which converts the integer [math]\displaystyle{ (q-Z) }[/math] into real number [math]\displaystyle{ r }[/math]. Z is called zero-point, which decides the map of real number [math]\displaystyle{ r=0 }[/math] into the quantization [math]\displaystyle{ q=Z }[/math].
Efficient Handling of zero-points
From the equation [math]\displaystyle{ q_3^{(i,k)} = Z_3 + M \Sigma_{j=1}^{N} (q_1^{(i,j)} - Z_1) (q_2^{(j,k)} - Z_2) }[/math] mentioned above, we can see that it performs subtractions of zero-points inside a triple loop (in total [math]\displaystyle{ 2N^3 }[/math] subtraction operations) and it is expensive, meaning that two subtractions are performed every multiplication. Thus we move some calculations outside the expensive inner loop to make it less expensive.
We algebraically expend this equation and get the expression: [math]\displaystyle{ q_3^{(i,k)} = Z_3 + M(NZ_1Z_2 - Z_1\Sigma_{j=1}^{N}q_2^{(j,k)} - Z_2\Sigma_{j=1}^{N}q_1^{(i,j)} + \Sigma_{j=1}^{N}q_1^{(i,j)}q_2^{(j,k)}) }[/math]. Here since [math]\displaystyle{ \Sigma_{j=1}^{N}q_1^{(i,j)} }[/math] only need to be calculated once at each [math]\displaystyle{ i }[/math], and similarly, [math]\displaystyle{ \Sigma_{j=1}^{N}q_2^{(j,k)} }[/math] only need to be calculated once at each [math]\displaystyle{ k }[/math], we can see that these two terms take only [math]\displaystyle{ 2N^2 }[/math] additions. While [math]\displaystyle{ Z_3, M, N, Z_1, Z_2 }[/math] are all constants, it means that the rest cost of the calculation concentrates on the term [math]\displaystyle{ \Sigma_{j=1}^{N}q_1^{(i,j)}q_2^{(j,k)} }[/math], which takes [math]\displaystyle{ 2N^3 }[/math] operations. This reduces the problem to the same core integer matrix multiplication of [math]\displaystyle{ \Sigma_{j=1}^{N}q_1^{(i,j)}q_2^{(j,k)} }[/math] as other quantization scheme that does not contains zero-points and saves [math]\displaystyle{ O(2N^3) }[/math] subtractions.
[math]\displaystyle{ \mathbf{Training} }[/math]
The core idea behind simulated quantization is to mimic quantization behavior during training while still allowing gradients to flow smoothly for optimization. This enables the model to adapt to the reduced numerical precision it will face during inference. During the forward pass, we apply the quantization function that we have covered above:
[math]\displaystyle{ \hspace{10cm} q(r; a,b,n)=\text{Round}\left(\frac{\text{clip}(r;a,b)}{S(a,b,n)}\right) S(a,b,n)+a }[/math]
where [math]\displaystyle{ S(a,b,n) = \frac{b-a}{n-1} }[/math], [math]\displaystyle{ a,b }[/math] are the limits of the quantization range, n is the number of unique integers in quantization. This process can be done very efficiently by bypassing floating point operations.
While this function mimics quantization during the forward pass, it poses a challenge for gradient-based optimization. The Round() operation is non-differentiable. Thus, during backpropagation, it is ignored as an identity function. This approximation allows gradients to pass through as if the rounding do not exist, enabling standard training techniques like SGD or Adam to continue working.
This two-step process allows the network to learn using floating-point numbers initially, and subsequently adapt to working effectively with quantized integer values. As a result, the network can perform consistently and reliably when deployed in environments that apply integer-only arithmetic.
Once training is complete, the model is prepared for deployment with quantized values. The first step is to quantize all components, including inputs, weights, and activations at each layer. Then, scale factors [math]\displaystyle{ S }[/math] are computed for each layer to map floating-point values to integers. The model operates all calculations using integer arithmetic, ensuring efficient execution on hardware. Finally, if needed, the output is dequantized back to floating-point values for compatibility with other systems or processes. This approach maintains both performance and efficiency in deployment.
Computation-Efficient Implementation of Integer-Only Arithmetic
Although the quantization constant [math]\displaystyle{ M = \frac{S_1 S_2}{S_3} }[/math] is a real number, Jacob et al. showed that it can be efficiently implemented using integer operations. Empirically, [math]\displaystyle{ 0 \lt M \lt 1 }[/math], which allows it to be rewritten in the form:
[math]\displaystyle{ M = 2^{-n} M_0 }[/math]
Where: - [math]\displaystyle{ n \in \mathbb{Z}_{\ge 0} }[/math] is an integer, and - [math]\displaystyle{ M_0 \in [0.5, 1) }[/math] is the normalized scaling factor.
This reformulation allows: - [math]\displaystyle{ 2^{-n} }[/math] to be implemented as a bit-shift operation, which is computationally cheap. - [math]\displaystyle{ M_0 }[/math] to be implemented in fixed-point form using a single integer bit.
Thus, all computation in [math]\displaystyle{ q_3^{(i,k)} = Z_3 + M \sum_{j=1}^{N} (q_1^{(i,j)} - Z_1)(q_2^{(j,k)} - Z_2) }[/math] can be performed using fixed-point arithmetic, enabling fast integer-only inference.
ZeroQuant: Efficient and Affordable Post-Training Quantization for Large-Scale Transformers
With the increasing size of Generative Pre-Trained Transformers (GPTs), it has become a significant challenge to deploy these models efficiently on resource-constrained hardware. Traditional methods of compression and quantization often lead to severe accuracy degradation, which limits their practicality in real-world applications. In this paper, the authors present ZeroQuant, an end-to-end post-training quantization method to address the challenges and this method is designed to compress large transformer models without losing much accuracy. But what do we mean by Post-Training Quantization? Quantization can take place at various stages. In this context, we have two well-known approaches: Post-Training Quantization (PTQ) and Quantization-Aware Training (QAT).
- Post-Training Quantization is a technique in which we first have a pre-trained model and quantize its parameters down to lower precision during inference time. This technique doesn't alter the real training process itself. During PTQ, the dynamic ranges of parameters are calculated on-the-fly at runtime. PTQ is essentially a post-processing step which happens after the model has completed its training and making it a relatively straightforward approach to implement.
- On the other hand, Quantization-Aware Training incorporates quantization directly into the training procedure. In QAT, the training procedure itself is particularly modified to simulate the effects of quantization while the model is learning. This allows the model to be robust against quantization noise throughout its training. Something unique about QAT is that, during training, there are two versions of the weights in memory simultaneously: a quantized version that's used for forward passes (inference), and the original unquantized version that is updated during backpropagation. By performing this double trick, the model can learn with the awareness of how quantization will affect its performance. As a result, QAT tends to be more accurate than PTQ for the same bit-width quantization, but at the expense of more computational resources for training.
Now we can better explain the original necessity for ZeroQuant. Traditional quantization methods required extensive retraining with original data and computational resources that were often unavailable to organizations deploying large language models. Quantization-Aware Training (QAT) works, but in practice, it is not feasible on large models due to its time-consuming and data-intensive nature. As you understand from our recent explanation, PTQ exhibits great compression efficiency compared to QAT because PTQ is typically applied to quantize the model without retraining. However, existing Post-Training Quantization techniques (before this article) were primarily designed for computer vision rather than language models. We have some previous works before ZeroQuant on language models that use PTQ and achieve good results on BERT. This work used INT8 weight and mixed INT8/FP16 activation quantization. The problem with this work is that there was no investigation into even lower bit-precision PTQ on BERT models and large-scale GPT-3-style models. It is better to say that their main focus was on high-precision quantization for the BERT base model and did not consider other billion-scale generative models like GPT-3-style models. These limitations created a need for a specialized quantization approach which can compress language models efficiently.
ZeroQuant has three main components, which we will explain in detail.
1- Fine-grained Hardware-friendly Quantization Scheme
Unfortunately, based on previous research conducted prior to this article, it is evident that even applying INT8 PTQ to BERT/GPT-3-style models results in significant accuracy degradation. The primary challenge lies in the inability of INT8 representation to fully capture the varying numerical ranges of different rows in weight matrices and different activation tokens. One approach to address this issue is to implement group-wise (token-wise) quantization for the weight matrices (activations). So, let’s define these terms first.
- Group-wise Quantization for Weights: Quantization typically occurs on weight matrices. A straightforward approach is to compress the values into int8 format by columns (or rows), but this can lead to a significant loss in prediction accuracy. Group-wise weight matrix quantization splits a weight matrix [math]\displaystyle{ W \in \mathbb{R}^{n \times m} }[/math] into [math]\displaystyle{ g }[/math] smaller groups and quantizes each group separately. Compared to the traditional single-matrix quantization, this approach enables finer-grained control and is thus better able to maintain critical weight information. Group-wise quantization in earlier research was applied mostly during Quantization-Aware Training (QAT) without considerations of hardware efficiency and backend system support. As a result, such methods did not achieve practical improvements in inference latency. In this work, the authors combine hardware constraints from NVIDIA's Ampere GPU architecture (e.g., A100), which is built on Warp Matrix Multiply and Accumulate (WMMA) with specific tiling sizes. By aligning group-wise quantization with these hardware capabilities, they are able to reduce latency considerably without sacrificing accuracy. This method outperforms single-matrix quantization because of its higher granularity thus enabling it to enjoy better model performance and speed.
- Token-wise Quantization for Activations: A common practice in post-training quantization (PTQ) is to use static quantization for activations. This means that the minimum and maximum values of activations are calculated ahead of time during an offline calibration phase. This approach can work well for small models where activation ranges are relatively stable. But, in large transformer models like GPT-style or BERT models, the ranges of activation values can be quite different for different tokens. Having a static range for all tokens can lead to a loss of accuracy. Since it does not account for unique behavior of each input. To solve this, token-wise quantization is introduced. In this method, the min and max range is computed dynamically for every token during inference time. This reduces quantization error and model accuracy increases. Token-wise quantization is more accurate, but applying it directly to popular deep learning libraries (e.g., PyTorch) may not be efficient. It often introduces extra operations that require moving data between GPU compute units and main memory, which slows down inference. To solve this problem, an optimized inference backend is developed. For example, kernel fusion is used to combine the quantization step with the previous operation (such as layer normalization). This reduces the need for extra data movement. Similarly, to reduce the cost of converting data back to floating point after matrix multiplications (GEMMs), the system uses a technique that applies the quantization scale directly to the intermediate result before storing it in memory. In this way, the entire process quicker and efficient. Token-wise quantization helps to reduce representation errors and does not require an extra calibration step for activation ranges. Therefore, 8-bit weights and 8-bit activations become a viable and accurate choice for quantizing large language models without adding significant overhead.
Both group-wise and token-wise quantization are forms of fine-grained quantization.
In order to further improve performance and reduce the deployment cost of large models like GPT and BERT, ZeroQuant goes one step beyond group-wise and token-wise quantization. It also includes two other important elements: a lightweight layer-by-layer knowledge distillation method (LKD) and a highly optimized inference backend.
2- Layer-by-layer Knowledge Distillation (LKD) with Affordable Cost
Traditional knowledge distillation operations are memory-bound, where the student and teacher models are both loaded into memory for training. This is especially impractical for billion-parameter models. ZeroQuant avoids this overhead through a better approach: it quantizes the model layer by layer.
For each of the layers which are being quantized, their unquantized version is taken as the teacher. The input is passed through both the original and the quantized version of the layer and the difference in their outputs is minimized. Because only one extra layer needs to be stored in memory during this process, LKD is even scalable to highly large models like GPT-NeoX_20B.
Another valuable benefit of LKD is that it does not require access to the original training data. Since it works layer by layer and is only interested in matching internal outputs, it can work with any dataset — even random or unrelated text like Wikipedia. Experiments verified that with the use of Wikipedia or even random sequences of tokens, it still achieved dramatic improvements in accuracy and perplexity. This makes ZeroQuant especially useful in privacy-sensitive or low-resource settings.
3- Quantization-Optimized Transformer Kernels
Post-training quantization is often slowed down because of the overhead of converting between quantized and floating-point values. ZeroQuant solves this with a highly optimized system backend. Instead of performing separate operations for quantization, normalization, and activation, ZeroQuant fuses them into single GPU kernels. This reduces memory access and speeds up inference. For example, in dequantization, ZeroQuant scales the INT32 results with precomputed quantization scales before converting back to FP16 and do all within the same kernel. This method reduces expensive data transfers and improves latency and achieving the expected benefits of lower precision.
GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers
Concept
GPTQ is a layer-wise post-training quantization technique specifically tailored for generative pretrained transformers. It aims in making more informed decisions on quantizing of weights allowing lower bandwidth quantization using approximate second-order information. The technique addresses some major challenges in terms of computation and memory for massive models like GPT3 which has 175B parameters and takes 326GB in float16 format. GPTQ can quantize GPT3 under 4 GPU hours reducing to 3/4 bits with minimal accuracy degradation. The significant contribution of GPTQ is the ability to execute post-training quantization on significantly large models (billions of parameters) compared to previous models like ZeroQuant. Furthermore, previous models could only quantize weights to 8-bit integers, otherwise accuracy would plummet. However, GPT can quickly quantize large transformer models using 3-4 bits without major accuracy loss.
Introducing Optimal Brain Quantization
To understand GPTQ, we first examine another quantization technique called optimal brain quantization (OBQ). This is necessary to learn GPTQ as it is essentially OBQ with some improvement.
1. Core Concepts:
The core concept behind OBQ is to minimize the performance degradation between the quantized integer weights [math]\displaystyle{ \hat{W} }[/math] and the input floating point weights [math]\displaystyle{ W }[/math], expressed as:
[math]\displaystyle{ \hat{W} = \arg\min_\hat{W} \|WX - \hat{W}X\| }[/math]
where [math]\displaystyle{ X }[/math] is the input activations to the layer.
2. Implementation:
To do so, optimal Brain Quantization employs quantization based on the Optimal Brain Surgery (OBS) approach. The OBS approach is simple. Many neural network weights are quite redundant, or have minimal impact on the output. To reduce parameters (and thus make models more compact), one can drop weights. Of course, one must be selective about dropping weights, since some weights are more important than others. Dropping the most impactful weights will significantly reduce model performance. Therefore, the objective of OBS is to selectively remove weights to reduce model parameters with minimal performance degradation. In OBQ, the strategy is similar. Instead of dropping weights, we quantize weights.
Mathematically, consider the quantized weights [math]\displaystyle{ \hat{W} = \arg\min_\hat{W} \|WX - \hat{W}X\| }[/math], This can be re-expressed as a sum of the squared errors, over each row of [math]\displaystyle{ W }[/math]. OBQ can execute row-wise quantization in a parallel fashion. For each row, OBQ will quantize a single weight parameter while always updating all not-yet-quantized weights (to compensate for error). Mathematically, the quantization process can be expressed by the following:
[math]\displaystyle{ w_q=\text{argmin}_{w_q} \frac{(\text{quant}(w_q)-w_q)^2}{[H_F^{-1}]_{qq}},\qquad\delta_F=-\frac{w_q-\text{quant}(w_q)}{[H_f^{-1}]_{qq}}\cdot(H_F^{-1})_{:q} }[/math]
where the Herssian of the matrix that contains the remaining full-precision weights [math]\displaystyle{ H_F=2X_FX_F^\intercal }[/math], [math]\displaystyle{ w_q }[/math] is the quantized weight, and [math]\displaystyle{ \delta_F }[/math] is the corresponding weight update to compensate for errors.
Using an iterative approach, OBQ quantizes weights until all weights are quantized. The significant advantage with this approach is the Hessian matrix [math]\displaystyle{ H^{-1} }[/math] does not have to be fully recomputed at every step.
GPTQ: An Improved OBQ
Compared with OBQ, GPTQ has 3 major improvements.
1. Order of quantization does not matter
We empirically discovered that order in quantizing the weight does not matter. So now we can quantize weights sequentially from the first column to the last compared to previous work such as optimal brain quantization (OBQ) which quantize weight starting with the weights that have smallest impact on the loss function. This improvement drastically decrease the need to recompute Hessian Matrix and resulted in a faster computation.
2. Block-wise update
Since we discovered that the order of quantization does not matter, now when updating sequentially, the quantization on column [math]\displaystyle{ i }[/math] does not depend on subsequent columns [math]\displaystyle{ i + 1, i + 2 }[/math], and etc. This enabled a new way to update which is the block-wise update.
The block-wise update is performed as follows:
1. Split the rows into blocks and perform the update on current block.
2. Perform a big update when finished updating the current block.
3. Cholesky Reformulation
Since directly updating [math]\displaystyle{ H^{-1} }[/math] for every column removal can accumulate floating-point errors, we need a more stable way to update. As mentioned in the method, we uses the Cholesky decomposition, which involves computing and storing a stable Cholesky factor of [math]\displaystyle{ H^{-1} }[/math] once, so we avoid repeated redundant updates. This Cholesky Reformulation naturally fits our block-wise updates mentioned earlier since each block only needs to reference the relevant rows/columns of the factor.
Algorithm

Figure shows the algorithm of GPTQ explained above. As seen, GPTQ utilizes three key steps.
The first step is to understand how the loss is updating as an impact of the weights during the process of quantization. Instead of directly using the hessian [math]\displaystyle{ H }[/math] to do this, GPTQ uses the hessian inverse ([math]\displaystyle{ H^{-1} }[/math]) for each layer's weight matrix since it provides better insights on the loss sensitivity while updating the weights. The weight importance is then determined using the [math]\displaystyle{ H^{-1} }[/math] values, such that weights associated with smaller [math]\displaystyle{ H^{-1} }[/math] are more important since small changes in weights lead to significant performance degradation. A dampening factor is applied to [math]\displaystyle{ H^{-1} }[/math] to reduce the numerical instability.
Then, to further reduces memory usage, GPTQ applies Cholesky decomposition on the [math]\displaystyle{ H^{-1} }[/math], such that:
[math]\displaystyle{ H^{-1} = LL^t }[/math]
where, [math]\displaystyle{ L }[/math] is the lower triangular matrix from Cholesky decomposition.
The final step involves quantizing of weights column by column in blocks. Columns are processed in batches of size [math]\displaystyle{ B }[/math], keeping track of error [math]\displaystyle{ E_{:,j-i} }[/math] to update the weights [math]\displaystyle{ W_{:,j:(i+B)} }[/math] in the block. Upon processing of the entire block, the remaining weights are updated using the tracked errors, which happens only for [math]\displaystyle{ C/B }[/math] times, making the process fast.
SmoothQuant
Motivation
Large language models have demonstrated excellent performances on various tasks such as language modelling, reasoning. However, due to the size of the model, it's computational and memory intensive. Quantization is a method that can reduce memory and accelerate inference by quantizing weights and activations with low-bit integers. For example, quantizing an FP16 number to a INT8 number can halve the GPU memory usage and double the throughput. One major challenge in quantization of LLMs are quantization of activations. When LLMs are scaled to billions of parameters, systematic outliers began to appear. Due to the existence of outliers (i.e., values particularly large compared to other activations), the quantization range is stretched and most activations will be close to 0 after quantization. This significantly decreased the accuracy of LLMs and large quantization errors. ZeroQuant achieved good performance on LLMs with millions of parameters but failed to maintain accuracy on models with billions of parameters.
Intuition
As mentioned previously and shown in the image above, in LLMs, activations are hard to quantize due to presence of outliers while weights are usually smooth and can preserve most of the information during quantization. In (a) we see that activations are HARD to quantize while weights are VERY EASY to quantize. In (b), after applying SmoothQuant, the activations are EASY to quantize while weights are EASY to quantize as well. Therefore, the main/high-level idea of SmoothQuant is simply transfer some of the difficulty in activations to weights so that both activations and weights are now feasible for quantization instead of activations being super hard to quantize and weights almost trivial to quantize. The image below clearly demonstrates this "transfer of difficulty":
We will discuss below how this migration of difficulty is done.
SmoothQuant's Smoothing Factor
Recall that matrix multiplication is linear (e.g., [math]\displaystyle{ Y = XW = (0.01X)(100W) }[/math]). So we can smooth the input activation by dividing it by a per channel smoothing factor: If [math]\displaystyle{ \mathbf{X} \in \mathbb{R}^{T \times C_i} }[/math] is the input matrix and [math]\displaystyle{ \mathbf{W} \in \mathbb{R}^{C_i \times C_o} }[/math] is the weight matrix, we can introduce a smoothing factor [math]\displaystyle{ \mathbf{s} \in \mathbb{R}^{C_i} }[/math] and scale the input and weight by [math]\displaystyle{ \mathbf{Y} = \mathbf{X} \mathbf{W} = \left( \mathbf{X} \, \mathrm{diag}(\mathbf{s})^{-1} \right) \left( \mathrm{diag}(\mathbf{s}) \, \mathbf{W} \right) = \hat{\mathbf{X}} \hat{\mathbf{W}} . }[/math]
How much difficulty should we migrate from activations to weights? We certainly do not want to migrate all difficulty because that would make weights too hard to quantize, the gist is all about maintaining the balance of easiness to quantize for both activations and weights.
The authors proposed [math]\displaystyle{ s_j = \frac{\max(|\mathbf{X}_j|)^{\alpha}}{\max(|\mathbf{W}_j|)^{1 - \alpha}}, }[/math]
where [math]\displaystyle{ j = 1, 2, \ldots, C_i }[/math] is the [math]\displaystyle{ j^{th} }[/math] channel and [math]\displaystyle{ \alpha }[/math] is the migration strength which controls the amount of difficulty we want to move from activations to weights. A larger [math]\displaystyle{ \alpha }[/math] migrates more quantization difficulty to weights.
As shown below, the right [math]\displaystyle{ \alpha }[/math] makes quantization easier for both activations and weights. If [math]\displaystyle{ \alpha }[/math] is too large, most difficulty will be transferred to weights, making weights hard to quantize. If it's too small, most difficulty still remains in activations.
Example
We will demonstrate Smooth Quant with an example to better illustrate.
Consider this [math]\displaystyle{ X }[/math] and [math]\displaystyle{ W }[/math]:
[math]\displaystyle{ X = \begin{pmatrix} 1& -16 & 2 & 6 \\ -2 & 8 & -1 & -9 \\ \end{pmatrix} \quad W = \begin{pmatrix} 2 & -1 & -2 \\ 1 & -1 & 1 \\ 2 & -1 & -2 \\ -1 & -1 & 1 \\ \end{pmatrix} }[/math]
We first get the [math]\displaystyle{ \max(|\cdot|) }[/math] along the column of [math]\displaystyle{ X }[/math] and row of [math]\displaystyle{ W }[/math] and divide them, we get.
[math]\displaystyle{ \frac{\max(|\mathbf{X}_j|)}{\max(|\mathbf{W}_j|)}= \begin{pmatrix} \frac{|-2|}{|-2|}& 0 & 0 & 0 \\ 0 & \frac{|-16|}{|1|} & 0 & 0 \\ 0 & 0 & \frac{|2|}{|2|} & 0 \\ 0 & 0 & 0 & \frac{|-9|}{|-1|}\\ \end{pmatrix} = \begin{pmatrix} 1& 0 & 0 & 0 \\ 0 & 16 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 9\\ \end{pmatrix} }[/math]
If we pick [math]\displaystyle{ \alpha = 0.5 }[/math], the smoothing factor [math]\displaystyle{ S }[/math] matrix will become [math]\displaystyle{ S = \sqrt{\begin{pmatrix} 1& 0 & 0 & 0 \\ 0 & 16 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 9\\ \end{pmatrix}} = \begin{pmatrix} 1& 0 & 0 & 0 \\ 0 & 4 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 3\\ \end{pmatrix} }[/math]
So we divide each column [math]\displaystyle{ i }[/math] of [math]\displaystyle{ X }[/math] by [math]\displaystyle{ \text{diag}(S_i) }[/math] and multiple each row [math]\displaystyle{ i }[/math] of [math]\displaystyle{ W }[/math] by [math]\displaystyle{ \text{diag}(S_i) }[/math] to get their new Smooth Quant version. [math]\displaystyle{ \hat{X} = \begin{pmatrix} 1& -4 & 2 & 2 \\ -2 & 2 & -1 & -3 \\ \end{pmatrix} \quad \hat{W} = \begin{pmatrix} 2 & -1 & -2 \\ 4 & -4 & 4 \\ 2 & -1 & -2 \\ -3 & -3 & 3 \\ \end{pmatrix} }[/math]
Note the result of [math]\displaystyle{ XW = \hat{X}\hat{W} }[/math] since we divide by [math]\displaystyle{ \text{diag}(S_i) }[/math] and then multipled by [math]\displaystyle{ \text{diag}(S_i) }[/math].
Topic 6: KV Cache Compression
Background
In a basic transformer, given an input token sequence X, each token’s Q, K, V are computed using learned projection matrices:
[math]\displaystyle{ Q = X W^Q = \begin{bmatrix} q_1 \\ q_2 \\ \vdots \\ q_n \end{bmatrix}, \quad K = X W^K = \begin{bmatrix} k_1 \\ k_2 \\ \vdots \\ k_n \end{bmatrix}, \quad V = X W^V = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} }[/math]
The full self-attention computation is:
[math]\displaystyle{ A = \mathrm{softmax} \left( \frac{Q K^T}{\sqrt{d_k}} \right) V }[/math]
This leads to quadratic time complexity.
We know that during inference, we do not want current tokens to access future tokens, therefore we apply a mask that restricts access:
[math]\displaystyle{ S = QK^T = \begin{bmatrix} q_1 k_1^T & q_1 k_2^T & \cdots & q_1 k_t^T \\ q_2 k_1^T & q_2 k_2^T & \cdots & q_2 k_t^T \\ \vdots & \vdots & \ddots & \vdots \\ q_t k_1^T & q_t k_2^T & \cdots & q_t k_t^T \end{bmatrix}, \quad M = \begin{bmatrix} 0 & -\infty & \cdots & -\infty \\ 0 & 0 & \cdots & -\infty \\ \vdots & \vdots & \ddots & -\infty \\ 0 & 0 & \cdots & 0 \end{bmatrix} }[/math]
After applying the mask, we can see below that the current token can only attend to itself and previous tokens:
[math]\displaystyle{ S' = S + M = \begin{bmatrix} q_1 k_1^T & -\infty & \cdots & -\infty \\ q_2 k_1^T & q_2 k_2^T & \cdots & -\infty \\ \vdots & \vdots & \ddots & \vdots \\ q_t k_1^T & q_t k_2^T & \cdots & q_t k_t^T \end{bmatrix}, \quad A = \begin{bmatrix} a_{11} & 0 & \cdots & 0 \\ a_{21} & a_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ a_{t1} & a_{t2} & \cdots & a_{tt} \end{bmatrix} }[/math]
Note that softmax here is applied row-wise so that masked values have 0 probability after softmax. This ensures that current token only has access to past tokens and itself.
You may notice that there are a lot of repetitive calculations here, repetitive calculations between K and V to be specific. For example, when we have two tokens [a, b], the number of key-value pairs we need to calculate are (a, a), (a, b), (b, a), (b, b). If we have three tokens [a, b, c], the pairs we need to calculate are (a, a), (a, b), (a, c), (b, a), (b, b), (b, c), (c, a), (c, b) and (c, c). Note that if we can somehow store the key-value pairs in [a, b], then when we look at the next query from token c, we can simply do a lookup of previous key-value pairs and only calculate new ones that contains c. This is the main idea behind KV caching:
Instead of recomputing K, V at every step, we define two caches and store previously computed values in them:
[math]\displaystyle{ K_{\text{cache}} = \begin{bmatrix} k_1 \\ k_2 \\ \vdots \\ k_{t-1} \end{bmatrix}, \quad V_{\text{cache}} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_{t-1} \end{bmatrix} }[/math]
At time step t, we generate token [math]\displaystyle{ x_t }[/math] and compute the new query: [math]\displaystyle{ q_t = x_t W^Q }[/math]
Compute [math]\displaystyle{ k_t }[/math], [math]\displaystyle{ v_t }[/math] and add to the cache.
Compute attention only against cached keys:
[math]\displaystyle{ A_t = \mathrm{softmax} \left( \frac{q_t K_{\text{cache}}^T}{\sqrt{d_k}} \right) }[/math]
This reduces the time complexity at inference from O(n²) to O(n), which is much faster for long sequences.
Challenges
While reducing the time complexity of inference from O(n²) to O(n) significantly speeds up long-sequence generation, it comes at the cost of increased memory usage. Storing all past keys and values results in memory growth linear to sequence length. Cache compression techniques help mitigate this, but they introduce a new challenge: low parallelizability. Since each token depends on compressed past states, the model must sequentially load weights, retrieve the KV cache, and compute attention for every generated token, limiting potential speed gains.
Ideal KV Cache
An ideal KV cache should balance memory efficiency and performance by meeting the following criteria:
- Small cache size – Minimizes memory footprint without compromising effectiveness.
- Low miss rate – Ensures the model retains enough context to generate coherent long-form text.
- Low-cost eviction policy – Reduces computation overhead and speeds up inference.
H[math]\displaystyle{ _2 }[/math]O: Efficient KV Cache Compression for Large Language Models
Introduction
Large language models (LLMs) are memory hogs, especially during text generation. A big culprit is the KV cache, which stores attention keys and values to skip redundant computations as new tokens are generated. This cache grows linearly with sequence length and batch size, gobbling up GPU memory fast. For a 30-billion-parameter model with a batch size of 128 and sequence length of 1024, the KV cache alone can demand 180 GB. This limitation makes long-context tasks (like stories, chats, or code generation) very expensive to run, especially in real-time or on resource-constrained devices.
Most existing methods which are mentioned in previous parts of this wiki, have some problems. First, models like Reformer and Flash Attention, are designed to overcome the quadratic memory required by attention mechanisms when modeling long sequences but still require a large cache size. Second, variants like sparse transformer, low-rank based transformers, or multi-query attention can reduce the cache size, but directly applying them on pre-trained LLMs for generation results in high miss rates and degrades the accuracy. This problem is shown in Figure 1. Finally, some recent advances such as gisting tokens can learn to compress the KV cache for documents, but their expensive eviction policies are difficult to deploy during generation.
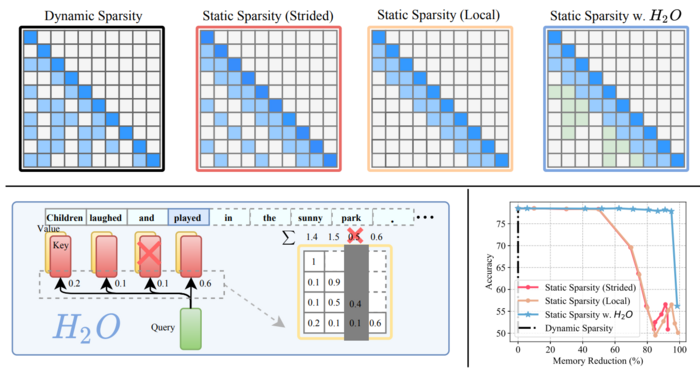
Key Contributions
The paper introduces H[math]\displaystyle{ _2 }[/math]O (Heavy Hitter Oracle), a clever way to slim down the KV cache. Here’s what stands out:
- Dynamic Token Selection: H[math]\displaystyle{ _2 }[/math]O keeps only the most impactful tokens—called "heavy hitters"—based on their attention scores, slashing memory use by up to 20× while preserving 99% of the original performance.
- No Retraining Required: Unlike some methods that need model tweaks, H[math]\displaystyle{ _2 }[/math]O works during inference, making it plug-and-play.
- Big Performance Boost: It outperforms popular inference systems like DeepSpeed Zero-Inference, Hugging Face Accelerate, and FlexGen, boosting throughput by up to 29× on models like OPT-6.7B and OPT-30B.
In addition, H2O introduces a low-cost greedy eviction algorithm that maintains a balance between recent and heavy hitter tokens in the KV cache. It formulates the cache eviction problem as a dynamic submodular maximization task and shows that under mild assumptions, the greedy approach offers near-optimal performance. Importantly, H2O does not require future token information and instead using local statistics at each decoding step to approximate attention contribution and this makes it practical for real-time deployment.
The framework is validated across a wide range of tasks and model families, including OPT, LLaMA, and GPT-NeoX, and this shows that H2O with just 20% KV cache budget can match or even surpass the accuracy of full-cache models. Besides saving memory, it enables larger batch sizes and eliminates the need for CPU offloading. This delivers spectacular latency and throughput gains. H2O also proves compatible with other efficiency techniques like quantization and even enhances diversity in generated text and making it a robust, versatile solution for scalable LLM inference.
Problem Formulation
In large language models (LLMs), the process of generating text requires the creation of a memory structure known as the KV cache, which stores the key and value vectors of all previously processed tokens. This cache enables the model to compute attention efficiently during autoregressive generation. However, as the sequence grows longer or as the batch size increases, the KV cache grows linearly, eventually consuming a significant amount of memory.
To address this issue, the paper studies a constrained setting where the size of the KV cache is limited to a fixed budget [math]\displaystyle{ k }[/math], which is much smaller than the sequence length [math]\displaystyle{ n }[/math]. The challenge is to design a policy that selects which key-value pairs to retain in this limited cache at each generation step, without compromising the model’s generation quality.
To formalize this problem, the model’s attention mechanism is described using two matrices: the query matrix [math]\displaystyle{ Q \in \mathbb{R}^{n \times d} }[/math] and the key matrix [math]\displaystyle{ K \in \mathbb{R}^{n \times d} }[/math], where [math]\displaystyle{ d }[/math] is the hidden dimension size. Each row [math]\displaystyle{ Q_{i,*} }[/math] represents the query vector for the [math]\displaystyle{ i }[/math]-th token, and similarly [math]\displaystyle{ K_{i,*} }[/math] is the key vector for that token. Let [math]\displaystyle{ S_i }[/math] denote the set of token indices whose KV pairs are retained in the cache at step [math]\displaystyle{ i }[/math]. The goal is to define an eviction policy that updates the cache from [math]\displaystyle{ S_{i-1} }[/math] to [math]\displaystyle{ S_i }[/math] such that the size of the cache remains fixed at [math]\displaystyle{ k }[/math], and only one token is evicted or added per step. Formally, this means the policy must satisfy two constraints: [math]\displaystyle{ |S_i| = k }[/math], and [math]\displaystyle{ |S_i \setminus S_{i-1}| \leq 1 }[/math], which also implies that at least [math]\displaystyle{ k - 1 }[/math] tokens are preserved between steps.
The attention output for the current token is computed using only the keys in [math]\displaystyle{ S_i }[/math], not the full history. This introduces the need to adjust the attention calculation to account for the missing tokens. Specifically, the model computes a vector [math]\displaystyle{ o_i }[/math], which contains the attention scores normalized over the tokens in the current cache. To calculate this, a scalar [math]\displaystyle{ D_i }[/math] is first defined as the sum of the exponentiated attention logits between the current query [math]\displaystyle{ Q_{i,*} }[/math] and the selected keys [math]\displaystyle{ K_{S_i,*} }[/math], subtracting out the contributions of evicted tokens using an indicator vector [math]\displaystyle{ 1_{[i] \setminus S_i} }[/math]. The formula is given by:
[math]\displaystyle{ D_i := \left( \exp(Q_{i,*}(K_{S_i,*})^\top) - 1_{[i] \setminus S_i} \right) \cdot 1_i }[/math]
The normalized attention vector [math]\displaystyle{ o_i }[/math] is then obtained by:
[math]\displaystyle{ o_i := D_i^{-1} \cdot \left( \exp(Q_{i,*}(K_{S_i,*})^\top) - 1_{[i] \setminus S_i} \right) }[/math]
This effectively zeroes out the scores of tokens that are no longer in the cache, while properly normalizing the remaining attention weights.
The core goal of this setup is to design an eviction strategy such that the generative process of the model, when operating under this cache constraint, behaves as similarly as possible to the original, full-cache process. This formulation establishes the mathematical foundation for the method proposed in the next section, where the paper introduces a greedy but effective policy—H[math]\displaystyle{ _2 }[/math]O (Heavy Hitter Oracle)—that determines which tokens to keep in the cache based on their attention contributions. All variables and concepts defined here will be directly used to describe and implement that method.
Method
H[math]\displaystyle{ _2 }[/math]O hinges on two key empirical observations about attention behavior in large language models (LLMs):
- Sparsity Rules: Though trained with dense attention, actual attention matrices during inference are very sparse—more than 95% of entries are close to zero. Such means most tokens have negligible contribution to attention computation at any step.
- Heavy Hitters Shine: A small number of tokens consistently receive high cumulative attention across layers and heads. These "Heavy Hitters" stronggly influence generation and often correspond to frequently co-occurring words.
Now let's see how it works, in the following sections.
1. Spotting Heavy Hitters
In LLMs, the attention mechanism often shows that a small subset of tokens, termed Heavy Hitters (H[math]\displaystyle{ _2 }[/math]), disproportionately influence the model’s output. They have to be identified to enable cost-efficient memory usage at inference time with minimal loss of generation quality.
At each generation step, the model computes attention scores that shows how much influnce each past token has on the current one. In H[math]\displaystyle{ _2 }[/math]O, these attention scores are accumulated across all layers and atttention heads to determine a token’s overall importanc. This accumulated score represent that how often and how strongly a token is attended to in subsequent decoding steps.
Formally, let [math]\displaystyle{ a_{i,j}^{(l,h)} }[/math] represent the attention score from token [math]\displaystyle{ j }[/math] to token [math]\displaystyle{ i }[/math] at layer [math]\displaystyle{ l }[/math] and head [math]\displaystyle{ h }[/math]. The cumulative attention score for token [math]\displaystyle{ j }[/math] is calculated as:
[math]\displaystyle{ A_j = \sum_{l=1}^{L} \sum_{h=1}^{H} \sum_{i=j+1}^{n} a_{i,j}^{(l,h)} }[/math]
Here, [math]\displaystyle{ L }[/math] denotes the number of layers, [math]\displaystyle{ H }[/math] the number of attention heads, and [math]\displaystyle{ n }[/math] the total number of generated tokens. This formulation aggregates the influence of token [math]\displaystyle{ j }[/math] across all future tokens. The tokens with the highest [math]\displaystyle{ A_j }[/math] scores are selected as Heavy Hitters. in this paper empirical evidence shows that removing these tokens from the cache severely decrease model performance and validating their critical role.
2. Smart Eviction
When the Heavy Hitters have been identified, the H[math]\displaystyle{ _2 }[/math]O framework applies a dynamic eviction policy to manage a fixed-size key-value (KV) cach during autoregressive generation. The goal is to balance two things: first, preserving long-term influential tokens (Heavy Hitters) and second, retaining recent tokens that help maintain local coherenc.
At each generation step, when a new token is generated and added to the cache, the number of stored tokens may exceed the limit [math]\displaystyle{ k }[/math]. For having a constant cache size, one token must be evicted. The Smart Eviction mechanism uses a greedy algorithm to make this decision, combining two guiding principles:
- Recency — recent tokens are often important for short-term context;
- Global importance — tokens with high cumulative attention should be preserved.
The problem of choosing which token to evict is modeled as a dynamic selection problem with a submodular structure. At each step [math]\displaystyle{ i }[/math], the goal is to maintain a set [math]\displaystyle{ S_i }[/math] of size [math]\displaystyle{ k }[/math] that maximizes an attention-based utility function. Although the model does not use future information directly, it approximates importance using current attention scores.
The update rule guarantees that the cache evolves incrementally:
- The size of the cache is fixed: [math]\displaystyle{ |S_i| = k }[/math],
- At most one token is changed per step: [math]\displaystyle{ |S_i \setminus S_{i-1}| \leq 1 }[/math].
This strategy allows the model to focus memory on the most useful tokens at every point in generation. Specially, the method works entirely at inference time and requires no retraining, and this makes it efficient and easily deployable.
3. Math Under the Hood
The mathematical core of H[math]\displaystyle{ _2 }[/math]O lies in how it formulates the cache update process as a dynamic submodular maximization problem. Submodular functions naturally model diminishing returns, the idea that adding a new token to an already strong set provides less gain than adding it to a weaker one. This fits the nature of attention which we say as more tokens are cached, the marginal benefit of each additional one decreases.
To formalize the eviction decision, the paper defines a utility function [math]\displaystyle{ F_{\text{score}}(T) }[/math] over token sets [math]\displaystyle{ T }[/math] that estimates the contribution of each token in attention. At decoding step [math]\displaystyle{ i }[/math], this is computed as:
[math]\displaystyle{ F_{\text{score}}(T) := \sum_{s \in T} o_s }[/math]
where [math]\displaystyle{ o_s }[/math] is the attention score of token [math]\displaystyle{ s }[/math] based on the query vector at step [math]\displaystyle{ i }[/math]. These scores are derived from the attention matrix, considering only keys in the current cache.
The cache update rule in the algorithm works as follows: it considers the candidate set [math]\displaystyle{ G_i = S_{i-1} \cup \{i\} }[/math], and finds the token [math]\displaystyle{ u }[/math] whose removal least harms the total score. Then the new cache is updated by:
[math]\displaystyle{ S_i \leftarrow (S_{i-1} \cup \{i\}) \setminus \{u\} }[/math]
The algorithm is both simple and effective. Under mild assumptions, the paper proves that this greedy approach achieves a near-optimal solution, with performance bounded by [math]\displaystyle{ (1 - 1/e) }[/math] of the optimal score, minus a small error. This theoretical guarantee shows why the method works so good in practic and providing high-quality results with low overhead.
Together, these mathematical principles enable H2O to retain the most important tokens, adapt dynamically during generation, and deliver efficient inference with minimal memory.
Algorithm Overview
The Figure2 Shows anilustration of the H[math]\displaystyle{ _2 }[/math] Eviction Algorithm, and we can understand how tokens are managed in the constrained KV cache during autoregressive text generation process. The algorithm dynamically updates the cache to keep only the most useful tokens based on their local attention contributtion.

The algorithm assumes a fixed cache size budget [math]\displaystyle{ k }[/math]. Initially, the cache is empty. For the first [math]\displaystyle{ k }[/math] tokens, no eviction is necessary and they are simply added to the cache. It starts from the [math]\displaystyle{ (k+1) }[/math]-th token, the algorithm must make space for each new token by removing one existing entry from the cache.
At each generation step [math]\displaystyle{ i }[/math], the algorithm performs the following steps:
- It computes the attention logits betwen the current query [math]\displaystyle{ Q_{i,*} }[/math] and the cached keys [math]\displaystyle{ K_{S_{i-1},*} }[/math].
- These logits are masked by using the indicator [math]\displaystyle{ 1_{[i] \setminus S_{i-1}} }[/math] to ignore the influence of evicted tokens and normalized to obtain the attention output [math]\displaystyle{ o_i }[/math].
- A scoring function [math]\displaystyle{ F_{\text{score}}(T) }[/math] is defined as the sum of attention contributions over any token subset [math]\displaystyle{ T }[/math].
- The candidate cache set [math]\displaystyle{ G_i = S_{i-1} \cup \{i\} }[/math] includes all current cache entries plus the new token.
- The algorithm greedily selects one token [math]\displaystyle{ u \in G_i }[/math] whose removal would cause the least drop in the total attention score, and evicts it.
- The updated cache [math]\displaystyle{ S_i }[/math] becomes [math]\displaystyle{ (S_{i-1} \cup \{i\}) \setminus \{u\} }[/math].
As an example, let's assume that the cache size is limited to 3 tokens. After the fourth decoding step, the algorithm evaluates the attention contributions of all tokens in the current cache and the new one. If the third token’s score is the lowest, its key and value embeddings are removed. These evicted embeddings are no longer accessible in subsequent steps and saving memory while maintaining output quality.
This cache management strategy makesH[math]\displaystyle{ _2 }[/math]O to operate efficiently even under memory constraints. It avoids recomputation and adapts dynamically to the context. In practice, this approach has been successfully implemented on models such as OPT, LLaMA, and GPT-NeoX, and achieve substantial memory reduction and faster generation speeds without any need to model retraining.
Heavy Hitters (H₂)
H₂O addresses the problem of KV cache bloat by retaining only tokens that contribute significantly to attention—called Heavy Hitters (H₂)—and discarding others with negligible impact.
- Heavy Hitters in MLPs: Beyond attention, H₂s also appear in MLP blocks. A small number of neurons are activated almost universally (100% frequency), while others remain rarely used. Eliminating these critical neurons causes severe performance drops but recovery is possible with just 1% of training data, highlighting their core influence.
- Early-Bird Emergence: H₂s tend to emerge early in training and show positional stability over time, reinforcing their fundamental role.
- Infinite-Length Generation: H₂O supports generation over ultra-long contexts (up to 4 million tokens), outperforming StreamLLM in perplexity while reducing memory consumption.
- Compatibility: It integrates well with quantization (e.g., 4-bit weights), allowing memory savings and throughput improvements even on low-resource GPUs.
- Shot Robustness: H₂O performs effectively in zero-shot, one-shot, and few-shot inference, maintaining quality while reducing memory use by up to 5×.
- Complementarity: H₂ tokens can enhance Top-K pruning methods and outperform static sparse alternatives like SpAtten, thanks to dynamic submodular optimization and per-head retention strategies.
Attention Sink
While designing KV cache compression strategies, it's important to understand which tokens are actually being attended to over long sequences. One key observation introduced in the paper is the presence of an "Attention Sink" effect.
Definition
- Attention Sink refers to tokens that disproportionately attract attention across future tokens, regardless of their semantic importance.
- This is due to the nature of causal attention: the earlier a token appears, the more future tokens can see it.
- Combined with the row-wise softmax in the attention mechanism, early tokens tend to accumulate large attention scores.
Impact on Token Retention and KV Cache Design
- Attention sinks often receive high scores not because they're informative, but because of positional bias.
- Retaining these tokens in the KV cache can waste space and reduce the effectiveness of compression.
- H2O proposes to distinguish true "heavy hitters" from attention sinks by analyzing cumulative attention in context and designing smarter eviction policies.
This insight improves both the interpretability and efficiency of autoregressive models, especially when applying selective KV caching.
Limitations and Future Work
H[math]\displaystyle{ _2 }[/math]O isn’t perfect and it has some limitations:
- Dataset Dependency: To identify heavy hitters initially, a small dataset is needed and its success relies on a calibration dataset to spot heavy hitters. If that dataset doesn’t match the task, performance could dip.
- Threshold Sensitivity: Setting the threshold too high or too low can hurt performance or waste memory. Picking the right cutoff for "heavy" tokens is a balancing act—too strict, and you lose context; too lenient, and memory savings shrink.
In future work, using adaptive thresholds based on recent token statistics can help to more improve accuracy and efficiency. Blending H[math]\displaystyle{ _2 }[/math]O with tricks like quantization could push efficiency further. Also, finding alternatives to attention scores (like gradients or entropy) for token importance can lead to better pruning.
Visualization & Intuition Behind H₂O
To understand how H[math]\displaystyle{ _2 }[/math]O achieves efficient KV cache compression, it helps to visualize the decoding process. During generation, not all tokens contribute equally to future outputs. H[math]\displaystyle{ _2 }[/math]O tracks accumulated attention scores to identify a small subset of tokens—called "heavy hitters"—that are repeatedly referenced in attention computation.
By keeping only these tokens in the cache, H[math]\displaystyle{ _2 }[/math]O reduces memory usage without harming performance. This approach not only accelerates inference but also improves generation quality by avoiding repetitive or trivial patterns. The retained tokens form a sparse but semantically meaningful context window, balancing precision with efficiency.
Practical Benefits and Use Cases
H[math]\displaystyle{ _2 }[/math]O presents a compelling solution for real-world deployment of large language models, particularly when memory and speed are bottlenecks.
Key benefits include:
- Memory Efficiency: Dramatically reduces the size of the KV cache by discarding unimportant tokens.
- Inference Speed: Compatible with quantized models, enabling low-latency inference even on moderate hardware.
- Improved Output Diversity: Reduces redundancy by preventing the model from over-attending to trivial tokens.
These properties make H[math]\displaystyle{ _2 }[/math]O particularly useful in applications such as edge computing, real-time generation systems, and large-batch inference pipelines where throughput and memory footprint are critical.
Comparison with Baselines
Different KV caching strategies yield significantly different outcomes in generation quality and efficiency.
- Full Cache: Retains all tokens. This approach maintains full context but consumes large amounts of memory and may lead to repetitive outputs.
- Local Cache: Retains only the most recent tokens. While this improves efficiency, it often degrades performance by omitting long-term dependencies.
- H[math]\displaystyle{ _2 }[/math]O (Selective Cache): Retains only the heavy hitters. This strategy maintains semantic coherence while dramatically reducing memory cost.
Compared to traditional methods, H[math]\displaystyle{ _2 }[/math]O preserves meaningful context, avoids information overload, and produces fluent, diverse outputs with minimal redundancy.
Attention Sink Mitigation Strategy
One challenge in transformer-based models is the "attention sink" phenomenon, where certain tokens—often those appearing early in the sequence—attract excessive attention regardless of their semantic relevance.
This is primarily caused by two factors:
- Token Visibility Bias: Early tokens have more opportunities to be attended by subsequent tokens.
- Softmax Dynamics: The normalization in softmax exaggerates even slight score advantages, reinforcing initial token dominance.
H[math]\displaystyle{ _2 }[/math]O implicitly mitigates this by not relying on position alone. Instead, it dynamically evaluates each token’s importance via cumulative attention. This ensures that retained tokens are selected based on utility rather than position, effectively filtering out irrelevant sinks and improving generation balance.
Transformer-VQ: Linear-Time Transformers via Vector Quantization
Introduction
Transformer models have demonstrated remarkable success in natural language processing and other sequential data tasks. However, their standard self-attention mechanism has quadratic time complexity with respect to sequence length. Transformer-VQ addresses this bottleneck by introducing a linear-time attention mechanism using vector quantization (VQ). This approach makes it feasible to apply transformers to much longer sequences efficiently.
Key Innovations
1. Vector-Quantized Keys:
- Standard self-attention requires computing pairwise interactions between queries and keys, leading to quadratic complexity.
- Transformer-VQ clusters keys into a smaller set of representative vectors (codewords) using a learned vector quantization codebook.
- Queries attend to these codewords rather than raw keys, reducing the computational load.
2. Efficient Attention Mechanism:
- Instead of computing full pairwise interactions, attention weights are calculated between queries and quantized keys.
- This allows a factorization of the attention matrix, leading to linear time complexity.
3. Compressive Key-Value Cache:
- Transformer-VQ introduces a caching mechanism that stores only the quantized representations of past keys, maintaining efficiency without losing important information.
- Unlike traditional key-value caching, which scales linearly in storage requirements, this approach enables efficient long-context modeling.
Mathematical Formulation
Self-Attention in Transformers
Given input sequence representations [math]\displaystyle{ X }[/math], standard attention computes:
[math]\displaystyle{ A = \text{softmax} \left( \frac{QK^T}{\sqrt{d_k}} \right) V }[/math]
where:
- [math]\displaystyle{ Q = XW_Q }[/math] (queries)
- [math]\displaystyle{ K = XW_K }[/math] (keys)
- [math]\displaystyle{ V = XW_V }[/math] (values)
- [math]\displaystyle{ W_Q, W_K, W_V }[/math] are learnable projection matrices.
Vector Quantization (VQ) Mechanism
Instead of using raw [math]\displaystyle{ K }[/math], Transformer-VQ applies vector quantization (VQ) to reduce the number of unique keys:
1. Assign each key [math]\displaystyle{ K_t }[/math] to its closest codeword [math]\displaystyle{ C_s }[/math] from a learned codebook [math]\displaystyle{ C }[/math]: [math]\displaystyle{ z_t = \arg\min_s || K_t - C_s ||^2 }[/math]
2. Replace [math]\displaystyle{ K_t }[/math] with the quantized representation: [math]\displaystyle{ \hat{K}_t = C_{z_t} }[/math]
3. Compute attention using the quantized keys: [math]\displaystyle{ A = \text{softmax} \left( \frac{Q \hat{K}^T}{\sqrt{d_k}} \right) V }[/math]
This replacement significantly reduces the computational cost of self-attention while preserving key information.
Linear-Time Attention Computation
To enable linear-time self-attention, the authors introduce a factorization of the attention matrix:
[math]\displaystyle{ W = \text{softmax} (Q \hat{K}^T) }[/math]
which can be rewritten as:
[math]\displaystyle{ W = \text{softmax} (Q C^T) \Delta }[/math]
where [math]\displaystyle{ \Delta }[/math] is a sparse matrix mapping token indices to their assigned codebook vectors.
Additionally, a recurrence relation is used to update the cache efficiently:
[math]\displaystyle{ U(n) = U(n-1) + \Delta(:,n) V(n,:) }[/math]
where [math]\displaystyle{ U(n) }[/math] accumulates grouped values based on quantized keys, ensuring efficient memory use.
In an effort to reduce the computation cost of attention and KV caching, a new method has been proposed that combines vector quantization with shared attention models. Since it exploits the property that attention patterns over multiple layers of deep language models have significant similarity, it quantizes keys and shares attention weights over layers, permitting compression of both memory and FLOPs at the inference time.
Let [math]\displaystyle{ K \in \mathbb{R}^{n \times d} }[/math] be the matrix of key vectors for a sequence of [math]\displaystyle{ n }[/math] tokens and [math]\displaystyle{ d }[/math] the dimensionality. A quantization codebook [math]\displaystyle{ C \in \mathbb{R}^{S \times d} }[/math] is introduced, where [math]\displaystyle{ S \ll n }[/math]. Each key [math]\displaystyle{ k_i }[/math] is mapped to its nearest codeword via:
[math]\displaystyle{ z_i = \arg\min_{s} \| k_i - C_s \|^2, \quad \hat{k}_i = C_{z_i} }[/math]
Instead of computing attention directly with raw keys, the model uses the quantized keys [math]\displaystyle{ \hat{K} }[/math]. The attention score for a query [math]\displaystyle{ q_t }[/math] becomes:
[math]\displaystyle{ A_t = \mathrm{softmax} \left( \frac{q_t \hat{K}^\top}{\sqrt{d}} \right) }[/math]
To enable efficient factorization, define a sparse assignment matrix [math]\displaystyle{ \Delta \in \{0,1\}^{S \times n} }[/math] where [math]\displaystyle{ \Delta_{s,i} = 1 }[/math] if [math]\displaystyle{ k_i }[/math] maps to [math]\displaystyle{ C_s }[/math]. Then the attention computation simplifies to:
[math]\displaystyle{ A_t \approx \mathrm{softmax} \left( \frac{q_t C^\top}{\sqrt{d}} \right) \Delta }[/math]
This factorization enables [math]\displaystyle{ q_t C^\top }[/math] to be calculated once and reused for multiple heads or layers. It avoids redundancy by avoiding repeated softmax calculation and caching a few full sets of keys. This representation also enables re-use during decoding time with a minimal cache of quantized key embeddings.
In practical deployments, this provides significant memory and computational reductions without compromising precision. The technique integrates smoothly with vector-quantized models like Transformer-VQ and naturally extends to shared-attention techniques where the same attention matrices are reused across consecutive layers.
Training Objective
The training loss consists of two components:
[math]\displaystyle{ L(X; \theta, C) = L_{CE}(X; \theta, C) + \beta L_{VQ}(X; \theta, C) }[/math]
where: [math]\displaystyle{ L_{CE} }[/math] is the cross-entropy loss for next-token prediction:
[math]\displaystyle{ L_{CE}(X; \theta, C) = -\frac{1}{T} \sum_{t=0}^{T-1} \ln p(x_{t+1} | x_{\leq t}, \theta, C) }[/math]
[math]\displaystyle{ L_{VQ} }[/math] is the vector quantization loss ensuring the model commits to learned codebook entries:
[math]\displaystyle{ L_{VQ}(X; \theta, C) = \frac{1}{T} \sum_{t=0}^{T-1} \sum_{\ell=0}^{N-1} || K^{(\ell)}_t - SG(C^{(\ell)}_{z_t}) ||^2_2 }[/math]
where [math]\displaystyle{ SG(\cdot) }[/math] is a stop-gradient operator, preventing codebook updates via backpropagation.
Advantages and Performance
- At sequence length 8k, Transformer-VQ is 3x faster than standard transformers.
- At sequence length 32k, it is 12x faster.
- Can scale to 131k tokens with stable throughput.
Conclusion
Transformer-VQ offers an efficient way to process long sequences, making transformers more scalable. It uses vector quantization and a smart caching system to keep the advantages of full attention while using fewer computing resources. This improvement makes it possible to apply transformers to tasks like analyzing long documents and generating extended conversations.
Dynamic Context Pruning for Efficient and Interpretable Autoregressive Transformers
Motivation
In this paper, the authors pose the following question: Can we dynamically prune past content based on the available context, while preserving as much as possible the expressivity of the model? In response to it, they propose a technique that dynamically prunes the context while maintaining the model capacity, hence, reduced memory and computational resources during inference. The method simply learns a mechanism to determine uninformative tokens and drop them during the generation process. This way not only performance is being improved, but also the model decision-making process becomes more interpretable.
Background
Assume the input sequence is [math]\displaystyle{ \mathbf{T}\in\{0,1,\ldots,n_{\mathrm{vocab}}\}^{n} }[/math], where [math]\displaystyle{ n }[/math] is the length of the sequence and [math]\displaystyle{ n_{\mathrm{vocab}} }[/math] is the vocabulary size. The emdedding layer will embedded the tokens into matrix [math]\displaystyle{ \mathbf{X}^0\in\mathbb{R}^{n\times d} }[/math], where [math]\displaystyle{ d }[/math] is the embedding dimension of the model.
One layer of the Transformer-decoder architecture is defined as:
[math]\displaystyle{ \begin{aligned} & \mathbf{X}=\mathsf{MHA}(\mathsf{LayerNorm}(\mathbf{X}^{\ell-1}))+\mathbf{X}^{\ell-1}, \\ & \mathbf{X}^\ell=\mathsf{FF}(\mathsf{LayerNorm}(\mathbf{X}))+\mathbf{X}, \end{aligned} }[/math]
where MHA stands for Multi-head self-attention defined as, [math]\displaystyle{ \mathsf{MHA}(\mathbf{X})=\text{Concatenate}(\mathsf{head}_1(\mathbf{X}),\mathsf{head}_2(\mathbf{X}),\ldots,\mathsf{head}_h(\mathbf{X}))\mathbf{W}_O }[/math], [math]\displaystyle{ \ell\in\{1,2,\ldots,L\} }[/math] denotes different layers.
The feed-forward part of the Transformer is defined as:
[math]\displaystyle{ \mathrm{FF}(\mathbf{X})=\sigma_{\mathrm{FF}}(\mathbf{XW}_{F_1})\mathbf{W}_{F_2}, }[/math] where [math]\displaystyle{ \sigma_{\mathrm{FF}} }[/math] is a nonlinearity, and [math]\displaystyle{ \mathbf{W}_{F_1} }[/math],[math]\displaystyle{ \mathbf{W}_{F_2} }[/math] are linear layers with typical dimensions [math]\displaystyle{ \mathbf{W}_{F_1}\in\mathbb{R}^{d\times4\cdot d} }[/math] and [math]\displaystyle{ \mathbf{W}_{F_2}\in\mathbb{R}^{4 \cdot d \times d} }[/math].
A final projection layer [math]\displaystyle{ \mathbf{W}_{\mathrm{logits~}}\in\mathbb{R}^{d\times n_{\mathrm{vocab}}} }[/math] is used to project back to thevocabulary space and predict the next token from the representations [math]\displaystyle{ X^{L} }[/math].
Methodology
Firstly, adaptively sparse attention is introduced to allow the network to drop unimportant parts of the context (as Figure below).

To achieve this, two learnable parameters [math]\displaystyle{ \mathbf{W}_{Q_{int}}^\ell, \mathbf{W}_{K_{int}}^\ell \in \mathbb{R}^{d \times r} }[/math] that calculate the interaction queries and keys as [math]\displaystyle{ \mathbf{Q}_{int}^\ell = \mathbf{X}^\ell \mathbf{W}_{Q_{{int}}}^\ell }[/math], [math]\displaystyle{ \mathbf{K}_{int}^\ell = \mathbf{X}^\ell \mathbf{W}_{K_{int}}^\ell }[/math] are added to each layer. Then the interaction of token [math]\displaystyle{ k }[/math] with token [math]\displaystyle{ j }[/math] at layer [math]\displaystyle{ \ell }[/math] is calculated as:
[math]\displaystyle{ \mathbf{I}_{k,j}^\ell = \begin{cases} \prod_{n=j+1}^k \mathbf{\overline{I}}_{n,j}^\ell \text{ and } \mathbf{\overline{I}}_{n,j}^\ell = \sigma\left(\frac{(\mathbf{Q}_{int}^\ell)_n^\top (\mathbf{K}_{int}^\ell)_j}{\sqrt{r}} + \beta^\ell\right), & \text{if } j \lt k \\ 1, & \text{if } j = k \\ 0, & \text{if } j \gt k \end{cases} }[/math]
where [math]\displaystyle{ \sigma(\cdot) }[/math] is the sparse sigmoid function and [math]\displaystyle{ \beta^\ell \in \mathbb{R} }[/math] is a layer specific parameter that controls initial sparsity.
When [math]\displaystyle{ j = k }[/math], the value is [math]\displaystyle{ 1 }[/math], meaning that the token has to remain, as no token can drop itself. In addition, the interaction is [math]\displaystyle{ 0 }[/math] when [math]\displaystyle{ j \gt k }[/math] to enforce causal masking so that future tokens are not attended to.
The sparse sigmoid is defined as:
[math]\displaystyle{ \sigma(x)=\alpha\mathrm{-sigmoid}(x)=\mathrm{argmax}_{p\in[0,1]}\left(p\cdot x+H_\alpha(p)\right), }[/math]
where
[math]\displaystyle{ H_\alpha(p)= \begin{cases} \frac{1}{\alpha(\alpha-1)}(p-p^\alpha+(1-p)-(1-p)^\alpha),\text{if } \alpha\neq1 \\ -p\log p-(1-p)\log(1-p),\text{if } \alpha=1. & \end{cases} }[/math]
The hyperparameter [math]\displaystyle{ \alpha }[/math] can control the sparsity of the network, practically, we will start from small value and increase it to a cosine scheduler.
Experiment
The experiment involved fine-tuning several pre-trained GPT‑2 models (small, medium, large, and xl) on language modeling tasks using subsets of English Wikipedia and BookCorpus. The approach, termed Adaptively Sparse Attention, introduces a learnable mechanism that dynamically prunes uninformative tokens from the input context during generation by using a modified α‑sigmoid function. The method was integrated with existing models through a fine-tuning process, and its performance was compared against baselines such as dense, local, and static sparse attention configurations. The experiments measured traditional language modeling metrics like perplexity as well as zero-shot performance on benchmarks including WinoGrande, HellaSwag, PIQA, and LAMBADA, while also evaluating improvements in inference speed and memory efficiency.
Results
High Pruning with Minimal Loss: The method is able to prune up to 80% of the context with very little degradation in perplexity (in some settings, even a slight improvement was observed compared to the dense baseline).
Improved Efficiency: Significant gains in inference speed were demonstrated. For instance, a GPT‑2-small model achieved nearly double the throughput (tokens per second) with only a minor increase in perplexity. Similarly, GPT‑2-medium models showed an almost 189% throughput boost for a context of 1000 tokens with negligible performance drop.
Maintained Zero-shot Capability: Despite the aggressive pruning, the zero-shot performance on standard benchmarks remained comparable—and in some cases even better—than the dense models.
Interpretability Insights: The analysis revealed that the pruning mechanism predominantly drops tokens that tend to be less critical (such as punctuation or stop words), and that different layers exhibit distinct pruning behaviors, offering insights into the model’s decision-making.
Limitations & Future Work
Limitations
While dynamic context pruning significantly improves efficiency and interpretability, it has several limitations:
- Loss of Long-Range Dependencies: Although pruning preserves key tokens, certain long-range dependencies (e.g., legal text, programming code) may still be affected, leading to subtle performance degradation.
- Layer-Specific Sensitivity: Different transformer layers exhibit varying pruning behaviors, which may require additional fine-tuning to balance efficiency and expressivity.
- Interaction with Decoding Strategies: The method assumes a standard autoregressive decoding process, but its impact on diverse strategies like beam search or nucleus sampling remains underexplored.
- Computational Overhead During Training: While inference efficiency improves, the model introduces extra computations during training to learn the pruning mechanism, which may limit scalability.
Future Work
Several directions can further refine and expand this approach:
- Multimodal Extensions: Adapting dynamic pruning to transformers handling text + images (e.g., GPT-4V) or speech models could improve efficiency in broader AI applications.
- Task-Specific Adaptations: Investigating pruning in different NLP tasks (e.g., summarization, translation) could reveal domain-specific advantages or weaknesses.
- Adaptive Pruning for RLHF: Exploring how pruning interacts with reinforcement learning from human feedback (RLHF) could enhance efficiency in fine-tuned language models.
- Integration with Hardware-Aware Optimization: Aligning pruning with efficient hardware execution (e.g., sparsity-aware accelerators) could maximize real-world benefits.
This method presents a promising step toward efficient and interpretable transformers, but further research is needed to address trade-offs in expressivity, robustness, and task-specific generalization.
Overview

In order to increase the efficiency of LLMs during inference, this paper introduces a unique technique called Shared Attention (SA), which shares the computed attention weights directly across many layers. The fundamental idea is that, upon pretraining, the attention weight distribution in complex LLMs becomes comparable across the majority of layers. For example, it was observed that a majority of the layers (roughly layers 3 to 30 in Llama2-7B) are similar when checked with cosine similarity metric. This suggests that for many layers, the model attends to different parts of the input sequence in a similar manner.
Isotropic Attention Distribution
An in-depth analysis of layer-specific attention weights across multiple LLMs, including Llama2-7B-chat, Llama3-8B-instruct, and Qwen2-72B-instruct, reveals a striking self-organization pattern in attention distributions, termed Isotropic Attention Distribution. This pattern, observed across models evaluated on MMLU, segments layers into four functional groups. The first group (layers 0-1) abstracts token-level semantic information with highly data-dependent attention patterns. The second group (layers up to index 5) acts as a transitional phase, refining intermediate semantic features. The third and largest group spans most of the model, displaying high attention weight similarity, signifying a stable and isotropic attention mechanism that informs deeper contextual understanding. Finally, the fourth group, consisting solely of the output layer, diverges significantly in attention distribution, emphasizing its specialized role in final decision-making. These findings reinforce the structural organization within LLMs and further validate the computational optimization potential of Shared Attention (SA), as it strategically exploits this inherent similarity to minimize redundant computations while preserving model expressivity.
Method
The core of this method is to directly share a single pre-calculated attention matrix over a selected multi-layer span. With SA, the first layer in the shared span computes the attention weights, and all subsequent layers in that span use the same computed weights. This is in contrast to each layer independently calculating its attention weights using its own query and key matrices, followed by the softmax function. Although the attention distribution that determines how much weight to assign to each value is the same, each layer in the shared span still computes the output using its own value matrix. This eliminates the need for repeated softmax computations and reduces the need to store separate key matrices for each layer within the shared span.
By sharing the attention matrices, they aim to reduce the computational redundancy by avoiding repeated softmax and utilizing fewer unique key caches. The algorithm is shown in Figure (right).
Experiment
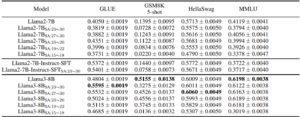
Experimentation was done using the Llama2-7B and Llama3-8B base models conducted on two NVIDIA A100 80GB GPUs. Table (right) compares the performance by directly applying the SA to different layers in the pretrained models across various language tasks. The results highlight that applying SA in upper layers for Llama2-7B maintained stable performance in the GLUE and MMLU benchmarks, but SA in middle layers led to a drop in GSM8K reasoning task.
When tested on the Llama3-8B model, SA in the upper layers improved the performance on the GLUE benchmark and was quite comparable in other benchmarked tasks as well. This model had a minimal performance decrease when SA was used since it had a better layer-wise attention similarity by nature.
Topic 7: Dynamic Models: Many-in-One Language Models
Introduction
The popularity of machine learning has been growing immensely in the recent decade. There is a growing number of industries and applications that leverage machine learning for growth. With various applications, there is immense difficulty when trying to find a perfect solution for a specific application. For instance, there is a plethora of deep neural networks that apply to different applications (e.g., CNNs for image processing). With the rise of LLMs, the challenge of finding suitable models becomes more difficult to solve. One has to consider the performance and computational needs of their tasks and target devices, especially with very large models. There are many techniques to improve the efficiency of LLMs, such as knowledge distillation, pruning, and quantization. However, this approach has a fundamental flaw: a static model. The model does not change, which can be problematic; when executing on simple task, the model may be too complex. On the contrary, the model may be too simple when executing difficult tasks.
To resolve the issue, we try to build a many-in-one-model. It is a single neural network that can run in different sizes for a given task. When the computation resource is abundant, more parameters are activated for inference whereas when the computation resource is insufficient, less parameters are activated. In doing so, we avoided training models of different sizes and drastically reduces the complexity of managing multiple independently trained models while still offering different "performance vs cost" trade-offs. Note many-in-one model is different from Multi-model. The former is a single model that has the ability to activate more/less parameters on a single task where as the latter is the architecture that combines several independently trained models, each performing a specific tasks.
There is no "one-size-fits-all" model due to present constraints. In this section, one can explore various techniques to make more dynamic models to suit different needs.
Challenges and Opportunities in Dynamic Models
While dynamic models offer tremendous flexibility and efficiency, several open challenges remain to be addressed:
- Balance Between Complexity and Performance:
- Designing dynamic models requires careful management of complexity. Overly complex routing mechanisms or sub-model architectures may lead to additional computational overhead during inference, reducing the potential gains. Efficiently balancing model complexity and computational overhead remains an ongoing research area.
- Training Stability and Convergence Issues:
- Due to simultaneous training of multiple sub-networks, dynamic models may face difficulties in ensuring stable training and convergence. Specifically, smaller sub-models may not receive sufficient training signals, potentially leading to underfitting. Techniques such as adaptive sampling strategies or curriculum learning could address these challenges.
- Interpretability and Explainability:
- Dynamic routing mechanisms inherently introduce complexity in understanding model behavior. How and why specific sub-networks are activated for certain inputs can become opaque, making model interpretability challenging. Improved visualization and diagnostic tools that elucidate routing decisions could significantly enhance interpretability.
- Robustness to Input Variability:
- Dynamic models must robustly handle diverse input distributions. Variations in input complexity or unexpected input scenarios can impact the routing quality, potentially degrading performance. Future research can explore adaptive routing mechanisms incorporating real-time feedback or uncertainty estimation to improve robustness.
These challenges provide rich opportunities for future research, emphasizing the importance of continuing innovation in architectures, routing algorithms, and training methodologies for dynamic models. Addressing these issues will be critical to fully realizing the potential of Many-in-One models for scalable, efficient, and adaptive AI deployment.
SortedNet: A Scalable and Generalized Framework for Training Modular Deep Neural Networks
Motivation
Traditional deep neural network (DNN) training often requires building and maintaining many individual models to meet the diverse computational budgets and accuracy requirements of different users and devices. This approach is:
- Expensive in terms of training time and storage,
- Hard to scale to many architectures,
- Inefficient when adapting to dynamic conditions such as variable latency or memory constraints.
Existing dynamic/many-in-one model approaches (e.g., Once-for-All, DynaBERT) attempt to alleviate these issues but have major drawbacks:
- Significant accuracy drop in sub-models,
- Require architecture-specific designs or teacher-student knowledge distillation,
- Can only train a limited number of sub-models,
- Involve heavy architecture search during training or inference.
To address these challenges, the authors propose SortedNet — a general, scalable, and architecture-agnostic solution that enables training of hundreds of sub-models simultaneously without sacrificing performance.
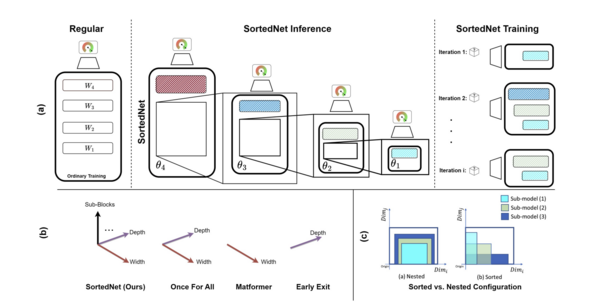
Model Architecture
SortedNet introduces a general and scalable architecture called the Sorted Architecture, designed to support the simultaneous training of a main model and a large number of sub-models. The key idea is to structure sub-models in a sorted (rather than strictly nested) fashion, enabling modular sharing of parameters across various architectural dimensions (e.g., depth, width, attention heads).
Key Concepts
- Sorted vs. Nested sub-models:
- In nested architectures, each smaller sub-model is fully contained within larger sub-models (e.g., layer 2 is inside layer 3).
- In sorted architectures, sub-models are defined by consistent origin indices across dimensions (e.g., always starting from layer 1), but are not strictly nested. This increases flexibility and scalability.
- All sub-models share weights with the main model and with each other, reducing storage and training overhead.
- Target Dimensions:
- SortedNet supports modularization and sorting across multiple dimensions:
- Depth (number of layers),
- Width (number of channels, neurons, or hidden units),
- Attention heads (for Transformers),
- Embedding size.
- Sub-models are created by truncating these dimensions from a sampled index up to the full model size.
- SortedNet supports modularization and sorting across multiple dimensions:
Training Procedure
At each training iteration:
- A sub-model is sampled randomly from the predefined sorted pool.
- Its corresponding parameters (e.g., selected layers and channels) are activated.
- The model is trained on a standard loss (e.g., cross-entropy), either:
- With only the selected sub-model (stochastic loss), or
- With a subset of related sub-models (summation loss).
To ensure stability and fairness in training:
- A shared classifier head is used across all sub-models.
- A gradient accumulation mechanism is employed to aggregate updates across multiple sampled sub-models efficiently.
Architecture Summary
- Shared parameters across all sub-models → memory efficient.
- Sorted origin-based slicing → enables fast sub-model selection at inference.
- No architectural changes required → works on CNNs, Transformers, and others.
- No need for knowledge distillation or architecture search.
This architecture allows SortedNet to achieve:
- Efficient training of up to 160 sub-models in parallel,
- Dynamic sub-model selection during inference (e.g., for faster or cheaper computation),
- High performance across all sub-models without retraining.
MatFormer: Nested Transformer for Elastic Inference
Motivation
Suppose in this scenario that you wanted to run a large language model for some application. There is a variety of different LLMs to choose from, and each LLM can differ by the number of parameters (e.g., the LLAMA-2 family contains models with 7B, 13B, 34B, or 70B parameters). Which model to choose? You consider the compute device you have and decide that LLAMA-2 with 7B parameters suffices. Great, the model ran successfully! Ambitiously, you try the 13B-parameter model. Oh no! The model could not be loaded onto your GPU.
In this scenario, your computer can handle the 7B-parameter model, but not the 13B-parameter model. This means that when your computer ran the smaller model, there was still some additional GPU memory that could be leveraged; the entire GPU was not used. Of course, you cannot run the bigger model. Maybe, if say a 12B-parameter model existed, it would have been perfect! The GPU would have been fully used, and we would have (hopefully) better performance than the 7B-parameter model.
The motivation behind MatFormer is to solve this dilemma. The objective of MatFormer is to enable on-demand slicing of a single trained LLM model to precisely fit various deployment constraints. Whether your compute device can handle models with 10 billion parameters to 1 trillion or more, MatFormer can satisfy your compute needs.
Slicing: Enabling Elastic Inference
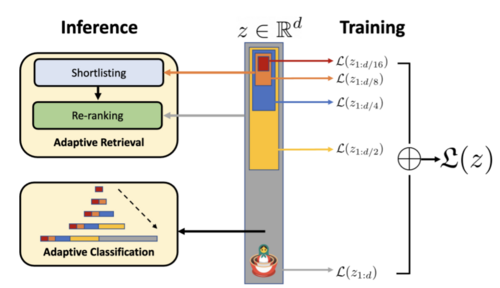
Intuition
In order to make elastic inference possible, we need a special articheture desgin and a special way of training the model. Inspired by Matryoshka Representation Learning, we can nest the entire model where each smaller submodel as nested inside the larger one. The smaller the submodel is, the more robust and "core” information is has for the larger ones to reuse.
If we train in this nested way. Any sub-block of the model can be directly used at inference for smaller capacity needs. Ensures consistent behavior across submodels.
Specifically with LLMs, VITs, and other transformer-based models, the author determined that a majority of the computational cost and model size can be attributed to the FFN block. Therefore, they applied this learning technique to the FFN block.
Training Process
We first pick [math]\displaystyle{ g }[/math] granularities to be used. Then, for each training run:
1. For each batch, randomly pick one submodel (from g granularities).
- Uniform sampling typically suffices, but if you want emphasize on certain submodel, you can do weighted if sampling.
2. Perform forward/backward pass only on that submodel.
- Forward pass' weights
[math]\displaystyle{ \text{FFN}_i(x) = \sigma \left( x W_1[0:m_i]^\top \right) W_2[0:m_i] }[/math]
- Losses for submodel [math]\displaystyle{ M_i }[/math]
[math]\displaystyle{ \mathcal{L}_{\text{Sampling}}(x, y) = \mathcal{L}(M_i(x), y), }[/math]
3. Update the shared parameter matrix accordingly.
Deployment: Mix’n’Match
You can choose different slices per layer to form new submodels beyond the explicitly trained ones.
Results: Scaling Laws for MatFormer LMs
Empirically, MatFormer follows similar or better scaling trends compared to vanilla Transformers. This means that this nesting and slicing does not degrade model scaling behavior in both log-perplexity and 1-shot tasks even as model sizes grow.
Future working directions
- Submodel structure is still “global”, so when deploying, the entire layers are chosen, compared to per-token or per-sequence width changes.
- Too many slices could under-train certain submodels if we pick too large a [math]\displaystyle{ g }[/math]. This leads the the thoughts that We could pick a better sampling strategy to balance these submodels.
- Could potentially combine with pruning/quantization.
SHARCS: Efficient Transformers through Routing with Dynamic Width Sub-networks
Why SHARCS?
Transformers, while powerful, come with the drawback of high computational costs. Their static inference process applies the same level of computation to all inputs, regardless of complexity. However, not all inputs require equal processing—some are simpler and can be handled with fewer resources. This inefficiency inspired SHARCS (Sample Hardness Aware Routing based on Confidence Scores), a framework designed to make transformers more efficient by dynamically adjusting computation based on input difficulty.
How Does SHARCS Work?
SHARCS introduces a lightweight router that predicts the difficulty (or "hardness") of each input sample and routes it to a sub-network of appropriate computational width.
The following details the three key steps in SHARCS:
1. Estimating Sample Hardness
- SHARCS assigns a "hardness label" to each input based on the model's prediction history during training.
- Hardness levels range from 1 (easy) to [math]\displaystyle{ M }[/math] (hard), determined by the model's confidence in predicting the correct class over a sliding window of [math]\displaystyle{ W }[/math] epochs.
- Lower confidence thresholds reduce computational cost but may impact accuracy, making [math]\displaystyle{ M }[/math] and [math]\displaystyle{ W }[/math] critical hyperparameters for balancing efficiency and performance.
2. Training the Router
- The transformer is split into two parts: non-adaptive layers (shared across all inputs) and adaptive layers (adjustable based on hardness).
- The router, placed between these layers, predicts the hardness level using outputs from the non-adaptive layers. This is a key design choice as the placement of the router (early vs late decision) results in a trade-off between accuracy and speed.
- Each hardness level corresponds to a specific width reduction factor for the adaptive layers.
- During training:
- A reduction factor is sampled for each input.
- The corresponding sub-network processes the input and both the sub-networks and router are trained jointly using a weighted loss function that is the weighted sum of the task loss and router loss
3. Adjusting the Network's Inference Capacity
- At inference time, the router directs each input to an appropriate sub-network based on its predicted hardness.
- Computational savings are achieved by reducing the number of neurons in linear layers and heads in multi-head attention by a factor proportional to the reduction factor ([math]\displaystyle{ r }[/math]).
- A pooler module adjusts dimensions before entering adaptive layers, while an unpooler module restores them before final classification.
Why Does SHARCS Matter?
SHARCS improves efficiency by dynamically allocating resources where needed, achieving up to a 2x speedup with minimal accuracy loss. It generalizes across different transformer architectures and can complement other efficiency methods like model compression. As such, SHARCS represents a significant step toward making transformers more scalable for real-world applications. By tailoring computational effort to input complexity, it addresses one of the core inefficiencies in modern AI systems: treating all data equally.
Limitations & Future Work
SHARCS only focuses on transformer encoders and experimentation with only classification tasks which leaves decoder-only and encoder-decoder models along with other modelling tasks left to be explored. The hyperparameter sensitivity of SHARCS also means that careful tuning is required when development. Subsequently, future work would include extending SHARCS to other architectures and tasks with further integration with other efficiency methods and automated hyperparameter tuning.
FLEXTRON: Many-in-One Flexible Large Language Model
Large language models (LLMs) are incredibly powerful, but they are often impractical due to their high computational costs and lack of flexibility. Training multiple model sizes to fit different devices is inefficient. While experts have proposed potential solutions, they still have limitations. For example, MatFormer and SortedNet focus on elasticity but lack input-adaptive routing, and SHARCS adjusts models only based on input hardness. FLEXTRON addresses these challenges by offering a single LLM that dynamically adapts to accuracy, latency, and compute constraints, providing a versatile solution for real-world applications. More specifically, Flextron is a neural architecture and post-training optimization framework that enables flexible model deployment. Unlike traditional models, Flextron can quickly adapt to meet user-defined latency and accuracy requirements during inference by utilizing a nested elastic structure without the need of additional fine-tuning. Its input-adaptive design also automatically routes tokens through its sub-networks, improving both the performance and computational efficiency.
Contributions
- Flexible Inference: FLEXTRON enables a single model to operate in multiple configurations, dynamically adapting to different computational constraints without requiring extra fine-tuning.
- Efficient Post-Training Optimization: The framework systematically converts pretrained LLMs into elastic networks, using only a fraction of the tokens required for full pretraining.
- Advanced Routing Mechanisms: By introducing both static and input-adaptive routing—supported by a surrogate model—FLEXTRON optimally selects sub-networks based on latency and input difficulty.
- Comprehensive Elasticity: Unlike previous approaches that focus only on MLP elasticity, FLEXTRON extends flexibility to both MHA and FFN layers, significantly broadening the operational search space.
How Does FLEXTRON Work
Key Idea
A single model can flexibly act as multiple models by applying nested and elastic layers that dynamically adjust computations. It can be transformed into any existing LLM and adapts at inference time without requiring retraining.
Steps
Step 0: Pretraining
- Pretrain an LLM with multi-head attention (MHA) and Feedforward Neural Network (FFN).
[math]\displaystyle{ \hspace 6 cm MHA^{(j)}(x) = Concat(head_1,...,head_{d_{j}}) \cdot (I_{d_{j}H}W^O) \hspace 0.3 cm }[/math]
[math]\displaystyle{ \hspace 6 cm head_i = Attn(XW^{Q,i}, XW^{K,i}, XW^{V,i}) \hspace 0.3 cm }[/math] where [math]\displaystyle{ H }[/math] is size of a single head, [math]\displaystyle{ L }[/math] is total number of heads
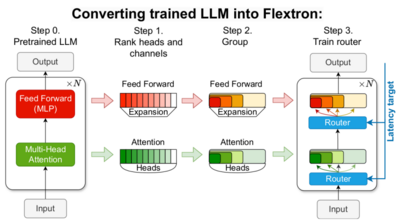
Step 1: Ranking the Importance of Attention Heads and Neurons
- For Attention Heads, importance is measured by
[math]\displaystyle{ \hspace 6 cm F_{head}^{(i)} = \sum_x ||Atten(XW^{Q,i}, XW^{K,i}, XW^{V,i})||_1 \hspace 0.3 cm }[/math] where [math]\displaystyle{ W^{Q}, W^{K}, W^{V} }[/math] are Query, Key, Value weight matrix, respectively
- For Neurons in FFN, importance is measured by
[math]\displaystyle{ \hspace 6 cm F_{neuron}^{(i)} = \sum_x ||X(W^{(i), r})^T||_1 \hspace 0.3 cm }[/math] where [math]\displaystyle{ W^{(1)} }[/math] are one of the associated weight matrices in FFN, and [math]\displaystyle{ r }[/math] means the [math]\displaystyle{ r^{th} }[/math] row of the matrix.
- Next, depending on their importance, sort neurons and heads.
Step 2: Elastic Continued-Training
- Select sub-networks dynamically: MHA layers adjust the number of attention heads, and MLP layers vary in width (e.g., 25% to 100%).
- Train multiple sub-networks simultaneously by randomly sampling k sub-networks during training.
- Optimize a joint loss that combines cross-entropy loss and a latency penalty to ensure efficiency.
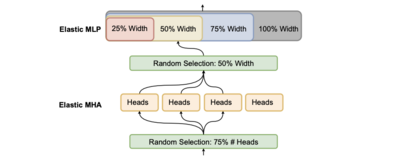
Step 3: Automatic Network Selection via Routers
- Routers dynamically choose the best sub-network for a given input, optimizing efficiency based on latency and input complexity.
- There are two types of routers:
- 1. Static: Selects based only on inference speed.
- 2. Dynamic: Considers both inference speed and hidden states.
Step 4: Training the Routers using a Surrogate Model
- The process of training routers does not goes smoothly even after the elastic continued-training stage because the gradient doesn't flow back effectively from the model's final loss to the router. As a result, the surrogate model is introduced.
- A Surrogate Model (SM) is a simplified model used to approximate the behavior of a more complex system. It is trained to predict the LLM’s performance based solely on the router’s decisions. The surrogate model is defined as below:
[math]\displaystyle{ \hspace 6cm r = Concat(R_0(T), R_1(T), ..., R_{N-1}(T)) \hspace 0.3cm }[/math]
[math]\displaystyle{ \hspace 6cm S(r) = \sigma(rW^T_{S_1})W_{S_2} \hspace 0.3cm }[/math]
where [math]\displaystyle{ T }[/math] is a target latency without input-adaptivity, [math]\displaystyle{ R_i }[/math] is a small FFN for each layer [math]\displaystyle{ i }[/math], and [math]\displaystyle{ W_{S_1} }[/math] and [math]\displaystyle{ W_{S_2} }[/math] are weights. Note that the SM is just a two-layer MLP.
- While training:
- Surrogate Model Update: The surrogate model learns to estimate performance accurately.
- Router Update: The router adjusts its selection strategy based on surrogate model feedback.
- Joint Tuning: The LLM, router, and surrogate model are fine-tuned together for optimal performance.
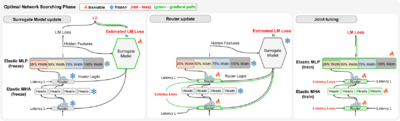
Performance
Experimental results show that FLEXTRON effectively balances accuracy and efficiency across a variety of downstream tasks. When evaluated on benchmarks such as ARC-easy, LAMBADA, PIQA, WinoGrande, MMLU, and HellaSwag, FLEXTRON shows that its dynamic sub-network configurations can achieve performance levels close to those of the full model while significantly reducing computational cost.
The full FLEXTRON-8B model exhibits strong performance across tasks, but even when operating in lower-latency configurations (e.g., 0.7× or 0.6× the full model’s latency), the model maintains competitive accuracy with only a modest drop in average performance. Similarly, FLEXTRON-Llama2-7B retains high accuracy when adapted for lower latency; dynamic variants slightly outperform their static counterparts, highlighting the benefits of input-adaptive routing.

Limitations
- Training Complexity: Integrating elastic layers, dynamic routing, and a surrogate model increases the overall system complexity, posing challenges in implementation and tuning.
- Router Optimization Challenges: Training routers is nontrivial due to issues such as gradient vanishing and expert collapse, which require careful handling.
- Performance Trade-Offs: Lower latency configurations may incur some performance degradation relative to the full model, representing an inherent trade-off in flexible design.
Comparisons
One sentence summaries
- SortedNet | Train many nested submodels in one run via sorted modularity and sampling for efficient deployment across compute budgets.
- MatFormer | Add nested MLPs inside transformers so a single model can behave like many submodels depending on width—all without re-training.
- SHARCS | Route inputs through sub-networks of different widths based on input hardness, reducing FLOPs via learned confidence-based routers.
- FLEXTRON | Convert a pretrained LLM into a fully elastic, input-adaptive, and latency-aware system using nested MLPs/MHAs and surrogate-trained routers.
Method comparisons
| Feature | SortedNet | MatFormer | SHARCS | FLEXTRON | Description |
|---|---|---|---|---|---|
| Training Cost | Train from scratch | Train from scratch | Finetune from scratch | Post-training (~7.6% of tokens) | How much training is needed to support flexible inference |
| Elastic Dimensions | Depth, width, heads, embedding | MLP width | MHA/MLP width | MLP + MHA width | Which axes of the model can be sliced elastically |
| Nested Weight Sharing | yes | yes | yes | yes | Whether smaller submodels reuse parameters via prefix indexing |
| Input-Adaptive Routing | no | no | yes | yes | Whether the model selects different sub-networks based on input characteristics |
| Static Submodel Selection | yes | yes | yes | yes | Whether fixed submodels can be selected at inference (e.g., by latency or budget) |
| Dynamic Routing Granularity | none | none | Sample-level | Token-level | The resolution at which routing decisions are made |
| Router Design | none | none | Lightweight classifier | MLP with surrogate model supervision | How the routing decision is made during inference |
| Surrogate Model for Router Training | no | no | no | yes | Whether a learned surrogate model helps stabilize and supervise router training |
| Speculative Decoding Support | Partial | yes | no | yes | Whether the framework supports fast draft-then-verify decoding using submodels |
| Token Dropping Compatibility | no | no | yes | yes | Whether token dropping techniques can be combined with the method |
| Inference Adaptivity | no | no | yes | yes | Whether inference time behavior changes based on the sample (input- or latency-aware) |
| Model Type Generality | CNN + Transformer | Transformer-only | Encoder-only Transformers | Decoder-style LLMs | Which kinds of architectures are supported |
| Routing Objective | none | none | Confidence-based + BCE | Surrogate-model-predicted LM loss + latency loss | How the router is supervised to make routing decisions |
| Output Layer Sharing | yes | yes | yes | yes | Whether all submodels share the same final classifier head |
| Intended Use Case | Efficient multi-size training | Inference-time width flexibility | Sample-wise compute scaling | Unified, flexible LLM deployment with latency/accuracy control | What deployment or usage need the method is designed for |
Topic 19: MM-LLMs
Introduction
Humans perceive the world through multiple senses—sight, hearing, touch, taste, and smell—which work together to form a coherent understanding of our environment. In artificial intelligence, multimodal large language models (MLLMs) aim to replicate this ability by integrating and processing information from two or more modalities, such as text, images, or audio. Traditional large language models (LLMs) excel at understanding language by embedding text into a high-dimensional semantic space. However, to build systems that mimic the multisensory integration of the human brain, we need mechanisms that can connect and align embeddings from different modalities with LLMs. Vision-Language Models (VLMs) represent a key subset of MLLMs that focus on combining image and text modalities. These models, including CLIP, DALL·E, and BLIP, form the foundation of modern multimodal reasoning and generation, offering new ways to bridge visual and linguistic understanding in a unified framework.
Learning Transferable Visual Models From Natural Language Supervision
Introduction and Motivation
Traditional supervised learning in computer vision relies on large labeled datasets, such as ImageNet, where human annotators manually assign labels to images. While effective, this approach has several limitations:
- High annotation costs: Manually labeling images is time-consuming and expensive.
- Limited label space: Fixed label sets restrict the model’s ability to generalize beyond predefined categories.
- Domain adaptation issues: Models trained on specific datasets often struggle with real-world data due to distribution shifts.
This paper proposes an alternative approach: training vision models using large-scale natural language supervision. Instead of manually labeled datasets, the model learns from image-text pairs collected from the internet, where the accompanying text descriptions act as a free-form supervision signal. The hypothesis is that language provides a rich and flexible learning signal, allowing models to understand broader concepts and generalize better in a zero-shot setting (i.e., classifying new categories without additional training).
Key Contribution: CLIP
The authors introduce CLIP (Contrastive Language-Image Pre-training), a model that learns visual concepts directly from natural language supervision at an unprecedented scale.
- Scalable Learning: CLIP was trained on a massive new dataset (WIT - WebImageText) of 400 million (image, text) pairs gathered from the internet. This leverages the broad supervision available online.
- Efficient Training: Instead of predicting the exact text for an image (computationally expensive), CLIP uses a simpler, more efficient contrastive objective. It learns to predict which text caption, out of a batch of possibilities, is correctly paired with a given image.
- Impressive Zero-Shot Transfer: The key breakthrough is CLIP's ability to perform zero-shot transfer to new tasks and datasets without any specific training for them. By providing the names or descriptions of the target classes in natural language, CLIP can generate a classifier on the fly and perform competitively, sometimes even matching fully supervised models trained on millions of labelled examples. For instance, zero-shot CLIP matched the accuracy of a ResNet-50 trained on ImageNet, without using any ImageNet training data.
- Broad Task Capability: CLIP learns a wide range of visual concepts during pre-training, enabling it to perform tasks like OCR, action recognition, geo-localization, and fine-grained classification across numerous benchmarks.
Architecture and Methodology
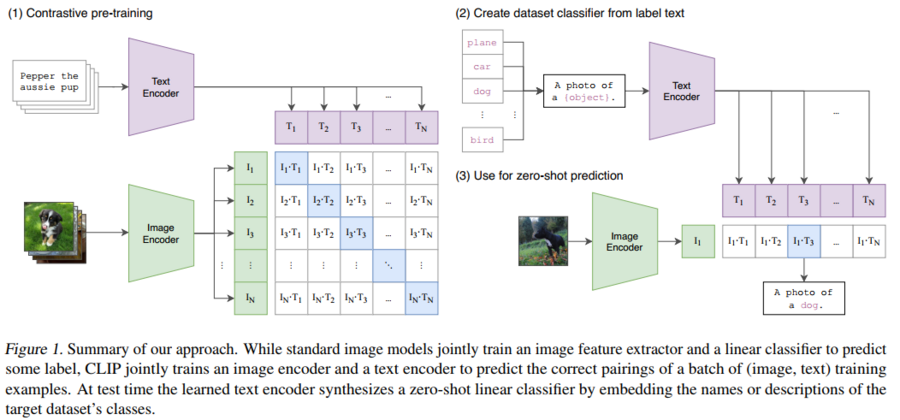
The proposed method, Contrastive Language-Image Pretraining (CLIP), consists of three main components:
- An image encoder (ResNet or Vision Transformer) that extracts image features.
- A text encoder (Transformer similar to GPT) that converts text descriptions into feature vectors.
- A contrastive learning objective that aligns image and text representations in a shared embedding space.
Pretraining with Contrastive Learning
CLIP is trained using a contrastive loss, which encourages correct image-text pairs to have similar representations while pushing apart incorrect pairs. Given a batch of N image-text pairs [math]\displaystyle{ \{(I_i, T_i)\}_{i=1}^{N} }[/math], the model follows these steps:
1. Encoding Images and Texts:
- The image encoder extracts a feature vector [math]\displaystyle{ f_I }[/math] from each image [math]\displaystyle{ I_i }[/math].
- The text encoder converts each textual description [math]\displaystyle{ T_i }[/math] into a feature vector [math]\displaystyle{ f_T }[/math].
2. Projection into a Shared Embedding Space:
- Both the image and text embeddings are mapped into a 512-dimensional space using learned linear projections.
- The embeddings are L2-normalized so that their magnitudes do not affect similarity calculations.
3. Computing Similarity Scores:
- A similarity score matrix is computed as: [math]\displaystyle{ S_{ij} = \tau \cdot \langle f_{I_i}, f_{T_j} \rangle }[/math] where [math]\displaystyle{ \tau }[/math] is a learnable temperature parameter that scales the dot product similarity.
4. Contrastive Loss Function:
- The model is trained using a symmetric cross-entropy loss, which maximizes the similarity of correct (image, text) pairs while minimizing incorrect pair similarities.
- The final loss is computed as: [math]\displaystyle{ L = \frac{1}{2N} \sum_{i=1}^{N} \left( \text{CrossEntropy}(S_i, y_i) + \text{CrossEntropy}(S^T_i, y_i) \right) }[/math]
This formulation ensures that images are embedded closer to their correct text descriptions and farther from incorrect ones.
Zero-Shot Transfer & Evaluation
One of CLIP’s key strengths is its ability to classify new images without additional training. This is done by leveraging the text encoder at inference time:
1. Creating Text Prompts: Instead of training a classifier, the text encoder processes textual class descriptions (e.g., "A photo of a cat").
2. Computing Image-Text Similarity: The similarity between an image and each text prompt is computed.
3. Selecting the Best Match: The class with the highest similarity score is assigned to the image.
This allows CLIP to perform competitively with fully supervised models on over 30 benchmark datasets without fine-tuning, demonstrating strong generalization capabilities.
Why Multimodal Learning Matters
Multimodal learning mimics the human brain’s ability to integrate multiple senses. By combining modalities such as text, image, and audio, models can form richer, more grounded representations of the world.
This integration enables more robust understanding, better generalization to real-world tasks, and more intuitive interaction with users. For example, an image alone may lack context, and a caption alone may be ambiguous—but together, they can disambiguate meaning.
Multimodal models are therefore critical for applications like:
- Vision-language reasoning (e.g., captioning, VQA)
- Text-to-image generation
- Speech-to-text transcription with context-awareness
Empirical Results
The table above compares Visual N-Grams to CLIP. The CLIP outperforms Visual N-Grams by a large margin, a significant step towards zero-shot computer vision classifiers.
The figure shows linear probe performance of CLIP models in comparison with SOTA computer vision models. The left plot shows the result after averaging on 17 datasets while the right is the result on all datasets. It's clear that CLIP-ViT outperforms every model on average score for various forward-pass GFLOPSs/image.
Limitation and Future Work
- Performance Gaps: While strong, zero-shot CLIP doesn't always beat state-of-the-art task-specific supervised models, especially on highly specialized or complex tasks. It struggles with abstract tasks like counting objects or differentiating fine-grained details that might not be well-represented in its web text pre-training data.
- Data Bias: Training on unfiltered internet data means CLIP inherits societal biases present in the text and images. This requires careful consideration for real-world deployment, as the model might exhibit undesirable biases related to gender, race, etc.. The ease with which developers can create classifiers using natural language also raises concerns about misuse.
- Compute Intensive: Training the largest CLIP models required significant computational resources (e.g., 18 days on 592 V100 GPUs for RN50x64).
- Struggles with fine-grained reasoning or image-specific captions.
- Not suited for text generation.
- Future Directions: Exploring the integration of CLIP's approach with more structured vision-language tasks (like VQA or multimodal entailment), improving data efficiency further, investigating methods to mitigate biases, and applying the natural language supervision concept to other domains remain open areas. Using masked self-attention in the text encoder leaves open the possibility of adding language modeling as an auxiliary objective or initializing with pre-trained language models.
Zero-Shot Text-to-Image Generation
This paper approaches the problem of text-to-image generation by developing a simple architecture of an autoregressive transformer, DALL-E, that models image and text tokens as a unified data stream.
Problem to Address
Generating realistic images from text descriptions is inherently difficult. Previous approaches often relied on specific datasets (like MS-COCO or CUB-200), complex architectures, or extra information like object parts or segmentation masks provided during training. These methods often produced images with artifacts, distorted objects, or illogical arrangements. Furthermore, they were typically limited by the scale of the datasets used. Could simply scaling up the model size and the amount of diverse (image, text) data lead to a breakthrough in high-fidelity, controllable image generation?
Method
Since dealing with image pixels requires significant memory and likelihood cost functions tend to focus on high-frequency details and leave out low-frequency ones, which makes an image recognizable to humans, the authors designed a two-stage training methodology to develop the model.
Stage One: Learning the Visual Codebook
In this stage, a discrete variational autoencoder (dVAE), Figure 1, was trained to compress images from 256x256 to a 32x32 grid. Although the size is significantly reduced, it still preserves the main features of the image. The encoder, Figure 2, processes the input 256x256 image and produces a 32x32 grid of logits where each entry is a categorical distribution over 8192 possible tokens. However, this representation is unsuitable for transformer processing in the second stage.
In order to tokenize this latent representation, a visual codebook, a dictionary consisting of 8192 tokens as keys and feature vectors of 512 dimensions as values, is learned as a map from discrete tokens to feature vectors. Since what we have is a distribution of probabilities, the token at each position is assigned using argmax sampling from the encoder logits. This way we end up with a 32x32 array of 1024 tokens ready to be passed to the transformer.
On the other hand, the decoder, Figure 3, is responsible for reconstructing the original image from the tokenized grid. It does so by retrieving the corresponding feature vectors from the codebook, then upsamples them until the output image is generated.
Stage Two: Learning the Prior
In this stage, the authors utilized a transformer to model the relationship between text and image tokens. For every text/image pair, the text is encoded with the BPE-encode model, producing 256 text tokens, which are concatenated with image embeddings, constructing a list of 1280 tokens that are fed to the transformer. The transformer learns to predict image tokens autoregressively guided by the text, outputting a total of 1024 tokens. As depicted in Figure 4, the codebook will be used to get the corresponding feature vectors based on the predicted image tokens then the dVAE generates the image.
Generation
At inference, the model takes a text description as input and generates a candidate image, then passes it to a pre-trained contrastive model to rank generation quality. The highest-ranked image gets selected as the output. As shown in Figure 5, more sampling leads to more refined results.
Results
DALL·E’s performance in zero-shot text-to-image generation was evaluated across multiple datasets and metrics, showcasing its ability to produce high-fidelity, diverse images from text prompts. The table below summarizes key results, highlighting visual quality, text-image alignment, and creative generation capabilities.
| Metric | Dataset/Task | Value | Notes |
|---|---|---|---|
| FID | MS-COCO | 27.5 | Competitive with supervised GANs (e.g., AttnGAN’s 35.2) |
| FID (CLIP-reranked, top-32) | MS-COCO | 22.4 | Improved by reranking for human preference |
| FID | CUB-200 (birds) | 45.8 | Higher than fine-tuned models (e.g., StackGAN’s 18.7) |
| Caption-Image Alignment | Conceptual Captions | 0.82 | Normalized cosine similarity |
| Human Accuracy (Simple Prompts) | General Prompts | 87% | Correctly matches text (e.g., "a red apple") |
| Human Accuracy (Complex Prompts) | General Prompts | 74% | For prompts like "a futuristic city at sunset" |
| Creativity Score | Diverse Prompts | 92% | Unique designs (e.g., "avocado-shaped armchair") |
| Log-Likelihood Gain | Image-Text Modeling | +1.2 nats | Over VQ-VAE-2 baseline |
| Success Rate vs. TediGAN | Zero-Shot Objects | +15% | Higher recognizable object generation |
The results demonstrate DALL·E’s strength in general-purpose image synthesis, particularly on broad datasets like MS-COCO, with challenges in specialized domains like CUB-200. Its diversity and creativity stood out, producing up to 512 unique images per prompt, often surpassing baselines like X-LXMERT and TediGAN in alignment and visual coherence.
Key Innovations in DALL·E
DALL·E introduces several novel ideas that distinguish it from prior text-to-image models:
- Two-stage training: First learns a discrete latent space using a VQ-style auto-encoder, then trains an autoregressive transformer on text and image tokens jointly.
- Codebook tokenization: Each image is represented as a grid of discrete tokens, allowing the transformer to model images like sequences of words.
- Creative generation: Unlike previous GAN-based approaches, DALL·E can synthesize imaginative and abstract images that align semantically with complex prompts.
These innovations enable DALL·E to generate diverse, high-quality visuals from free-form language.
Limitation and Future Work
- Sample Quality Variation: While capable of impressive results, the model's performance can be inconsistent, especially with complex prompts requiring precise variable binding (e.g., correctly assigning attributes only to specific objects). The quality often relies heavily on the CLIP reranking step.
- Fidelity vs. Compression: The dVAE compression step, while necessary for tractability, inherently limits the model's ability to generate very fine, high-frequency details, which affects metrics like FID unless images are slightly blurred.
- Dataset Specificity: The model performs less favorably in zero-shot evaluations on highly specialized datasets like CUB (birds) compared to broader datasets like MS-COCO, suggesting domain specificity is still a challenge.
- Computational Cost: Training requires massive computational resources and sophisticated engineering for distributed training and numerical stability.
- Future Work: The authors suggest fine-tuning on specific datasets as a promising direction to improve performance on specialized tasks. Further investigation into improving compositional generalization and reducing reliance on reranking could also be beneficial.
Robust Speech Recognition via Large-Scale Weak Supervision
Introduction and Motivation
Automatic Speech Recognition (ASR) models typically rely on curated datasets like LibriSpeech, containing around 1,000 hours of labeled audio. However, these models struggle with real-world variations such as accents, noisy environments, and unseen vocabulary.
This paper introduces Whisper, a model trained on 680,000 hours of weakly supervised internet audio data. The goal is to reduce reliance on human-labeled datasets and improve ASR robustness across languages and domains.
Architecture and Methodology
Whisper is a Transformer-based encoder-decoder model trained for multiple speech-related tasks.
Model Architecture
- Audio Encoder: A convolutional feature extractor followed by Transformer layers. The first layers process the log-mel spectrogram, a representation of the audio signal where frequency information is mapped using the Mel scale, which aligns more closely with human auditory perception. The spectrogram captures both time and frequency features of the audio, making it a crucial input representation for speech models.
- Text Decoder: An autoregressive Transformer decoder that generates text transcriptions token by token, conditioned on the encoder’s output.
- Positional Encodings: Both the encoder and decoder incorporate sinusoidal positional encodings to retain temporal information.
Training Data and Preprocessing
- The dataset consists of 680,000 hours of transcribed speech, covering 98 languages.
- Audio is converted to 30-second log-mel spectrograms with 80 frequency bins.
- Text transcripts are normalized using standard preprocessing techniques (lowercasing, punctuation removal, and Unicode normalization).
Multitask Training Objective
Whisper is trained with task-specific tokens to perform:
1. Speech Recognition: Converting audio into text.
2. Speech Translation: Transcribing non-English speech into English.
3. Voice Activity Detection: Identifying speech vs. silence.
4. Language Identification: Detecting the spoken language.
The decoder is prompted with a sequence of special tokens like <|transcribe|>, <|translate|>, and <|language:xx|> to guide the output behavior.
Training Loss
Whisper is trained using cross-entropy loss over the decoder’s token predictions:
[math]\displaystyle{ L = -\sum_{t=1}^{T} \log P(y_t | y_{\lt t}, X) }[/math]
where [math]\displaystyle{ X }[/math] is the input audio, and [math]\displaystyle{ y_t }[/math] is the target token at time step [math]\displaystyle{ t }[/math].
Zero-Shot Evaluation and Results
- Whisper achieves state-of-the-art results on benchmarks like LibriSpeech.
- It generalizes without fine-tuning, showing robustness to accents, noise, and domain shifts.
- The model significantly reduces word error rates (WER) compared to traditional ASR systems.
- Evaluations across 98 languages show that Whisper outperforms previous multilingual ASR models in both low-resource and high-resource languages.
Whisper's Unified Speech Capabilities
Whisper handles a wide range of speech tasks in a unified framework, including:
- Transcription
- Translation
- Language identification
- Timestamp prediction
What sets Whisper apart is its use of multitask conditioning tokens, which allow the same model to switch between tasks without retraining. This makes Whisper highly flexible and efficient for multilingual and multitask deployments.
It is also resilient to real-world variability, performing well on noisy or out-of-distribution speech, such as TV interviews or live conversations.
Limitations & Future Directions
Current Limitations:
- Errors in long-form (e.g., full speeches, full interviews) such as repetition & hallucination.
- Underperforms on lower-resource (e.g., limited training data, corpora) languages.
- Unexplored benefits of fine-tuning and auxiliary objectives.
Future Directions:
- Employ more advanced decoding strategies like reinforcement learning or fine-tuning.
- Conduct data enrichment for low-resource languages by augmenting or enhancing limited existing data.
- Systematic exploration of fine-tuning impacts by varying different factors like amount of data used for fine-tuning, number of epochs, etc.
- Incorporate auxiliary training methods like self-supervision/self-training.
BLIP: Bootstrapping Language-Image Pre-training for Unified Vision-Language Understanding and Generation
Motivation
The motivation behind BLIP arises from two major limitations in existing vision-language pretraining methods: model inefficiencies and data quality issues. Most vision-language models either use an encoder-based architecture, like CLIP and ALBEF, or an encoder-decoder architecture, like SimVLM. However, encoder-based models struggle with text generation tasks such as image captioning, while encoder-decoder models have not been successfully applied to retrieval-based tasks like image-text matching. This lack of flexibility prevents a single model from excelling at both vision-language understanding (retrieval, classification) and generation (captioning, reasoning).
Additionally, current pretraining approaches rely on large-scale image-text datasets scraped from the web, which often contain noisy and misaligned captions. These inconsistencies degrade model performance, as models trained on such data fail to learn meaningful vision-language associations. To overcome this, a method is needed to filter out irrelevant text while generating high-quality captions to enhance pretraining.
Key Contributions
BLIP introduces two key innovations:
- Multimodal Mixture of Encoder-Decoder (MED): a flexible and unified transformer architecture that can operate in three modes:
- As a unimodal encoder for contrastive learning between image and text representations (ITC loss).
- As an image-grounded encoder for matching tasks (ITM loss).
- As an image-grounded decoder for text generation (LM loss).
This design enables BLIP to handle both understanding and generation tasks within a single model.
- CapFilt (Captioning + Filtering): a new dataset bootstrapping method to enhance pretraining data.
- A captioner module generates synthetic captions for web images.
- A filter module removes noisy or irrelevant image–text pairs (from both original and synthetic data).
Together, these modules improve the quality of training data, which leads to significant gains across downstream tasks.
Model Architecture
BLIP is built upon a unified architecture called the Multimodal Mixture of Encoder-Decoder (MED), which enables flexible switching between three functional modes for vision-language pretraining. These modes correspond to three key training objectives:
1. ITC: Image-Text Contrastive Learning
- The model operates in an encoder-only configuration.
- An image is encoded using a Vision Transformer (ViT), and the text is encoded using a BERT-style transformer with a [CLS] token.
- The model is trained to align the visual and textual representations using a contrastive loss, encouraging matching pairs to have similar embeddings while pushing apart mismatched ones.
- This setting is used for vision-language understanding tasks like image-text retrieval.
2. ITM: Image-Text Matching
- In this mode, the text encoder is enhanced with Cross Attention layers to integrate visual information from the image encoder.
- The model takes an image-text pair as input and predicts whether they match (binary classification).
- The text input is prepended with a special [Encode] token whose final embedding is used for classification.
- This improves fine-grained alignment and is trained using an Image-Text Matching (ITM) loss.
- This setup also supports reasoning and retrieval tasks.
3. LM: Language Modeling
- This mode enables text generation, such as image captioning.
- The image encoder remains the same, but the text transformer is converted into a decoder by:
- Replacing the bi-directional self-attention layers with causal self-attention, allowing the model to generate tokens autoregressively.
- Retaining the same cross-attention layers to incorporate image features.
- A [Decode] token is used to initiate generation, and the model is trained using a language modeling (LM) loss to generate captions based on image inputs.
Parameter Sharing
- To ensure efficient training, most parameters (like feed-forward networks and cross-attention layers) are shared across the encoder and decoder.
- Only the self-attention layers are separated:
- The encoder uses bi-directional self-attention.
- The decoder uses causal self-attention for generation.
Why It Matters
BLIP is significant because it bridges the gap between vision–language understanding and generation within a single model, excelling in tasks like image-text retrieval, captioning, and even video-language applications. By effectively transforming noisy web data into high-quality training material, BLIP reduces the dependency on costly human annotations and enhances scalability. Its unified framework simplifies system design for real-world applications such as automated captioning and visual question answering, while its innovative approach to data refinement and model integration lays a solid foundation for advancing future multimodal research.
Empirical Results
The left table shows result for a comparative study on image-text retrieval. BLIP achieves a significant performance improvement compared with existing methods. Using the same number (14M) of pre-train images, BLIP outperforms the previous best model ALBEF by +2.7% in average recall.
The right table shows result for a comparative study on image captioning. Again, BLIP with 14M pre-train images significantly outperforms methods using a similar amount of pre-training data. BLIP with 129M pre-train images achieved comparable performance to LEMON with 200M pre-train images. However, BLIP does inference much faster than LEMON due to the fact that LEMON requires a computationally expensive object detector and high-res input images.
Limitations and Future Directions
While BLIP sets a new benchmark by unifying vision–language understanding and generation, it faces several challenges. Its reliance on the bootstrapping method (CapFilt) means that any residual noise or suboptimal synthetic captions can still impact performance. Moreover, the current treatment of video data via simple frame concatenation overlooks temporal dynamics, potentially limiting its effectiveness for time-sensitive tasks. The complexity and computational demands of the model also pose scalability and reproducibility challenges, and some inherent biases from noisy web data may persist despite filtering. Future work could explore iterative bootstrapping to further refine data quality, generate multiple captions for richer diversity, integrate dedicated temporal modeling for video tasks, and optimize parameter sharing to reduce computational costs.
BLIP V2
Introduction and Motivation
Though BLIP introduced a novel method for combining image and textual data, its end to end training process is very expensive and computationally complex. Thus, the authors address these shortcomings by introducing BLIP V2 which uses a pretrained frozen image encoder and LLM. They then use a Q-Former model to connect the modules, drastically reducing the model's training overhead. Q-Former stands for querying transformer and it is a transformer model trained in 2 stages: the first stage connects to the frozen image encoder to learn vision-language representation and the second connects to the LLM to learn vision-to-language generation. The full architecture is shown in the figure below.
Architecture and Training Efficiency
BLIP V2 leverages a frozen ViT image encoder (e.g., ViT-L/14 or ViT-g/14) and a frozen large language model (LLM) (e.g., OPT or FlanT5). The Q-Former acts as a lightweight bridging module between the two, composed of BERT-style transformer layers enhanced with cross-attention to absorb visual features from the image encoder. The cross-attention layers are only inserted every other block to balance efficiency and capacitytopic 19 5.
The Q-Former has 32 learnable query embeddings, each of dimensionality 768. These serve as the bottleneck for passing information from vision to language and are considered trainable parameterstopic 19 5.
To ensure efficient interaction control, three distinct attention masking strategies are employed for the pretraining objectives:
- Uni-modal self-attention for contrastive learning.
- Multi-modal causal self-attention for text generation.
- Bi-directional self-attention for matching (queries and text fully interact).
Methods
The Q-Former learns a set of 32 embedding vectors through cross-attention layers with the image encoder. Each query learns to attend to various aspects of the image features for information extraction, is passed through the Q-Former layers, and then is passed as input to the LLM. To train the Q-Former, the authors use a set of image-text pairs and optimize Image-Text Contrastive Learning, Image-grounded Text Generation, and Image-Text matching jointly.
The Image-Text Contrastive Learning attempts to align the visual representations of the images with the text representation which come from the Q-Former's output queries and text encoder respectively by maximizing the similarity between matching image-text pairs while minimizing similarity for pairs which are not matched. Image-Grounded Text Generation focuses on aligning the generated text with the images (in the form of embeddings from the image encoder) using self-attention with the learned queries. Because the training data comes as image-text pairs, this is analogous to fine-tuning an LLM by calculating the loss with respect to the ground truth captions. Finally, Image-Text Matching is a binary classification task which evaluates whether the image and the generated text are suitable as a pair. It does so using bi-directional self attention between the Q-Former's learned queries and the generated text, and takes the query values (after they have passed through the Q-Former's transformer layers) as the matching score.
The Q-Former's second module concerns connecting the trained image representations with the (again, frozen and pretrained) LLM. Thus far, the image has been passed through the frozen image encoder and the partially-trained Q-Former to obtain the output query embeddings. Now, the query embeddings are projected by a trainable fully connected linear layer (which is quite small) to match the hidden dimension of the frozen LLM's word embeddings. These embeddings act are prepended to the input text embeddings fed into the LLM and are meant to represent visual information extracted from the input image. The LLM's goal is to generate the text caption, conditioned on the visual information passed by the Q-Former. The authors use cross-entropy loss function, however the gradients only pass through the fully connected layer (which projects the dimension of the Q-Former outputs onto the dimension of the word embeddings of the pre-trained LLM) and the Q-Former itself.
Why It Matters
BLIP-2 is significant as it demonstrates a highly compute-efficient method for vision–language pre-training by effectively harnessing the power of frozen pre-trained image encoders and large language models. Its lightweight querying transformer successfully bridges the modality gap, enabling state-of-the-art performance on tasks such as visual question answering, image captioning, and image–text retrieval, all while requiring a fraction of the trainable parameters compared to end-to-end approaches. By leveraging mature, robust unimodal models, BLIP-2 not only achieves strong performance but also showcases emerging zero-shot generation capabilities that follow natural language instructions. This breakthrough paves the way for more practical and scalable multimodal systems, potentially accelerating the development of conversational AI agents that can understand and generate both visual and textual content with minimal additional training.
Results
BLIP V2 presents a significant improvement over BLIP as it achieves comparable results with a much more lightweight model that has much fewer trainable parameters. Specifically, using the Q-Former as a connection module between a pre-trained frozen image encoder and LLM, BLIP V2 is able to bypass the expensive end-to-end training scheme required by BLIP.
Limitations and Future Directions
BLIP-2 exhibits impressive performance across various vision–language tasks; however, certain limitations remain. For instance, the current pre-training dataset provides only one image–text pair per sample, which appears to constrain the model’s ability to leverage in-context learning for visual question answering. This limitation prevents the large language model from effectively correlating multiple image–text examples within a single sequence, a capability that has been beneficial in other approaches using interleaved multimodal data. Furthermore, the image-to-text generation process can sometimes yield inaccurate or unsatisfactory results—stemming from outdated or imprecise knowledge in the frozen language models, misdirected reasoning, or exposure to erroneous inputs. Additionally, by relying on frozen unimodal models, BLIP-2 inherently inherits risks such as bias propagation, offensive language generation, and potential leaks of private information. Future work may focus on constructing richer pre-training datasets that include multiple image–text pairs per sample to better support in-context learning, refining the querying mechanism to enhance visual feature extraction, and developing more robust guidance or filtering strategies to mitigate undesired outputs.
Additional limitations include the fixed-size query bottleneck, which may restrict fine-grained spatial reasoning and dense image understanding, the lack of temporal modeling for sequential or video-based tasks, and the inability to handle interleaved multimodal inputs needed for visual dialogue or multi-turn interaction. Extending BLIP-2 to support multi-image input, temporal dynamics, and instruction tuning across both modalities would be valuable directions for improving generalization and task versatility.
From BLIP to BLIP-V2: Evolving the Vision-Language Paradigm
BLIP-V2 builds upon the success of BLIP by improving both architecture and training efficiency:
- Introduces Querying Transformer (Q-Former) to mediate between vision encoder outputs and language modelling.
- Supports unified vision-language tasks with one model, from captioning to visual QA.
- Demonstrates better zero-shot performance across multiple datasets compared to previous models.
This evolution marks a shift toward foundation multimodal models that can adapt to diverse tasks through prompt tuning or minimal finetuning.
Extension: InstructBLIP & BLIP-Diffusion
Two important extensions to BLIP-2 are InstructBLIP and BLIPDiffusion.
- InstructBLIP introduces instruction tuning on top of BLIP-2 to equip the model with the ability to process task instructions, thus improving its generalisation performance in a multi-tasking environment.
- BLIPDiffusion, a version that combines BLIP-2 with Stable Diffusion, incorporates powerful text-to-image generation capabilities, further expanding the model's generative capabilities and application scope.
These two extensions demonstrate the flexibility and extensibility of the BLIP-2 framework and provide new directions for multimodal understanding and generation.
Summary Table of Multimodal LLMs
This table summarizes five major multimodal LLMs—CLIP, DALL·E, Whisper, BLIP, and BLIP V2—highlighting their core architectures, innovative contributions, strengths, and limitations. These models represent significant advancements in combining vision, language, and audio modalities for tasks such as image classification, generation, speech recognition, and unified vision-language understanding. Each approach introduces a unique strategy for bridging modalities, offering trade-offs between generalization, computational efficiency, and training complexity.
| Model | Architecture | Key Innovations | Strengths | Limitations |
|---|---|---|---|---|
| CLIP | Dual-encoder (ViT + Transformer) | Contrastive learning with image-text pairs from the web | Zero-shot generalization; handles broad visual tasks; scalable | Struggles with abstract reasoning and fine-grained tasks; data bias; high training cost |
| DALL·E | dVAE + Transformer (autoregressive) | Discrete codebook representation for images; text-image sequence modeling | High-quality text-to-image generation; creative outputs | Quality varies with prompt complexity; compression limits detail; high compute cost |
| Whisper | Transformer encoder-decoder | Large-scale weak supervision; multitask learning with task tokens | Robust ASR across domains and languages; unified speech model | Errors in long-form tasks; underperforms in low-resource languages; needs fine-tuning |
| BLIP | Multimodal Mixture of Encoder-Decoder (MED) | Unified vision-language pretraining; CapFilt for data cleaning | Excels at both understanding and generation; improved data quality | Expensive end-to-end training; still impacted by noisy web data |
| BLIP V2 | Frozen ViT + Frozen LLM bridged by Q-Former | Efficient bridging with Q-Former; modular architecture | Lightweight, compute-efficient; strong zero-shot and generative performance | Limited in-context learning; inherits limitations from frozen models |
Topic 20: Diffusion Language Model
Motivation and Limitations of Autoregressive Models
Exposure Bias in AR Models
Autoregressive language models like GPT-2 and GPT-3 generate text one token at a time, with each token conditioned on previously generated ones. During training, they are fed ground-truth sequences; however, during inference, they rely on their own outputs. This mismatch causes *exposure bias*—early mistakes in generation can snowball, leading to unnatural or incoherent text.
Lack of Global Control
Because generation is strictly left-to-right, it's challenging for autoregressive models to incorporate global structure or constraints. This limits their ability to meet user-specified generation goals such as:
- Sentence length
- Part-of-speech patterns
- Syntax trees
- Semantic tones (e.g., positivity or formality)
Even when given specific instructions, such as generating a sentence with a fixed number of words, these models often fail to comply precisely due to their greedy token-by-token decoding. For example, suppose you a generation model to produce a sentence with 20 words. Because of the left-to-right generation nature, the model may forget the user-defined requirements (such as the 20-word restriction), and thus produce a sentence with less than or more than 20 words. Even if the model had identified the issue, it would be difficult to amend. For instance, it would be difficult to add or remove words to satisfy the 20-word constraint without bungling grammar or semantics.
One approach to address this issue is to teach LLMs to adhere to the conditions (i.e., train on input text with constraints). However, this technique is extremely expensive and becomes super difficult to teach LLMs to adhere to various constraints. For instance, it is difficult to train an LLM to make 1-page essays in active voice with specific tones. Alternatively, researchers have tried an alternative approach of freezing LLMs (use pre-trained LLMs and never adjust its weights) and applying an external classifier to learn various conditions. But, this technique has been difficult to execute and only works on limited conditions (specific semantic or topic).
Difficulty with Infilling and Structured Generation
Many real-world tasks—like text infilling, editing, or constrained rewriting—require access to both past and future context. Since autoregressive models are inherently one-directional, they are not well suited for such bidirectional or structure-aware tasks without significant architectural modifications.
Why Diffusion Offers a Solution
Diffusion-based language models present an alternative approach that addresses these limitations. Instead of generating text sequentially, they treat the entire sequence as a whole and generate it through an iterative denoising process. This allows for:
- Joint control over all tokens during the generation
- Flexible incorporation of global constraints
- Seamless infilling by fixing certain tokens and sampling the rest
By removing the strict left-to-right dependency, diffusion models open new possibilities for controllable and structured text generation.
General Drawbacks of Diffusion Language Models
- Diffusion models do indeed improve controllable generation. However, most day-to-day uses of LLMs do not require controllable generation.
- Diffusion models need to convert continuous embeddings back into discrete tokens, which leads to errors and inefficiencies.
- Diffusion models rely on k-NN rounding, which tends to be unstable when having some high-dimensional embeddings and large vocabularies.
- It’s hard to maintain the context for open generation tasks (limited to the context present in the sequence, and any other external classifiers being used), this means that diffusion models struggle with longer context.
- During training, diffusion models need to store intermediate latent states for every diffusion step, increasing the GPU memory usage.
Further Challenges and Open Questions
Beyond the outlined limitations, there are additional open challenges and research opportunities in diffusion language modeling:
- Robustness to Noise and Errors in Intermediate Steps:
- Diffusion models depend heavily on the accuracy of intermediate denoising steps. Even minor inaccuracies can accumulate, causing significant deviations from the target distribution. Developing methods to detect, correct, or mitigate such errors during the diffusion steps is an open challenge.
- Token Space Coverage and Diversity:
- While diffusion models facilitate controlled generation, they can also face mode-collapse or insufficient diversity in generated outputs, especially when rounding or discretizing embeddings. Ensuring sufficient coverage of the token space without sacrificing fluency remains a critical research direction.
- Alignment Between Continuous and Discrete Spaces:
- Continuous diffusion models operate in embedding spaces, requiring a reliable mechanism for mapping embeddings back to discrete tokens. Current rounding techniques like nearest-neighbor search or clamping can introduce semantic distortions. More sophisticated, semantically-aware rounding mechanisms could greatly improve generation quality.
- Computational Efficiency and Scalability:
- Diffusion models typically involve computationally intensive iterative processes for both training and inference. Optimizing these processes through accelerated sampling, improved architectures (e.g., structured or sparse diffusion), or hardware-aware implementations is essential to enable real-world deployment.
- Long-Range Context Management:
- Diffusion models, particularly continuous ones, face challenges in effectively modeling long-range dependencies due to their iterative nature. How to preserve coherence and global context in lengthy text sequences or documents remains a challenging and promising research area.
Addressing these open questions will significantly enhance diffusion language models' capabilities and applicability, positioning them as competitive alternatives or complementary methods alongside established autoregressive approaches.
Gaussian Diffusion for Text
Recall a diffusion model. We take the input (such as an image) and apply Gaussian noise to eventually produce white noise. We then apply iterative denoising techniques to recover an image from the input distribution. To apply diffusion for text, text sequences are embedded and treated as continuous data (like grayscale images). Gaussian noise is added in training, and a denoising network recovers clean embeddings. A final rounding step maps vectors to tokens. This supports flexible generation but is computationally expensive. The application and removal of noise is expensive. Furthermore, it may be expensive to convert our final vector embeddings into tokens.
Core Idea
In the diffusion language modelling framework, text sequences are represented as continuous embeddings. Instead of generating tokens autoregressively, the model learns to reverse a noise process that gradually corrupts these embeddings. Generation is reframed as iterative denoising: the model starts from pure noise and gradually refines it into meaningful embeddings.
Each text sequence of [math]\displaystyle{ n }[/math] tokens is embedded into an [math]\displaystyle{ n \times d }[/math] matrix, where [math]\displaystyle{ d }[/math] is the embedding dimension. This continuous matrix is treated like a grayscale image and becomes the object of the diffusion process.
Forward and Backward Process
The forward process adds Gaussian noise to the embedding sequence over multiple steps. The backward (denoising) process aims to reconstruct the clean sequence by removing this noise in reverse.
This is achieved using a score model, which is trained to estimate the gradient of the log-probability density function at each time step. Conceptually, the model:
- Samples a noisy input from the prior
- Predicts the direction toward the data manifold
- Repeats this over several steps
- Eventually outputs a denoised embedding close to the real data
This continuous diffusion process eliminates the need for direct token prediction at each step.
Embedding and Rounding
The embedding step is the same as in autoregressive models: each token is mapped to a vector using a trainable embedding layer.
However, diffusion models operate purely in the continuous space. They output a matrix of [math]\displaystyle{ n \times d }[/math] vectors rather than token probabilities. Thus, a rounding step is needed to convert these vectors back into discrete tokens.
This is done via nearest-neighbour search: each generated vector is clamped to the closest token embedding at every diffusion step. This ensures that the denoising trajectory stays close to the valid token space, but the rounding process is costly and can be a bottleneck during inference.
End-to-End Training
Training is done end-to-end by jointly optimizing both the embedding network and the Gaussian denoising model. The loss function extends the classic diffusion loss by incorporating the learnable embedding parameters.
By training in the continuous domain while supervising against discrete targets, the model learns both the semantic structure of language and how to reconstruct it from corrupted embeddings.
Diffusion-LM: A Continuous Diffusion Model for Controllable Text Generation
Introduction
Diffusion‑LM is a non‑autoregressive, continuous diffusion–based language model that iteratively denoises Gaussian latents into word embeddings to form a hierarchical latent representation for text generation. This continuous diffusion process enables simple gradient‑based updates on those latents to enforce complex, fine‑grained controls—such as text length, part‑of‑speech constraints, exact syntactic trees, or semantic attributes—without any model re‑training or fine‑tuning. On six challenging controllable generation tasks, it significantly outperforms previous plug‑and‑play methods (e.g., PPLM, FUDGE), trading off an approximately 7× slower decoding speed for far superior control fidelity.
Controlling the behavior of language models without re-training is a major open problem in natural language generation. It is true that previous works have had success with simple attribute-level control tasks like sentiment or topic, but they struggle with more complex, fine-grained constraints like syntactic structure. This motivates light-weight, modular plug-and-play approaches that keep the language model frozen and insteaad use external classifiers or potential functions for generation. However, these methods—especially those based on autoregressive models, have been limited in their effectiveness and scope. Diffusion-LM is designed to handle a wide range of controllable generation tasks that are difficult for traditional autoregressive models. These include:
- Semantic control (e.g., generating positive vs. negative text)
- Part-of-speech control (e.g., enforcing specific POS sequences)
- Syntax control (e.g., constraining generation to match a parse tree)
- Length control (e.g., generate exactly 10 tokens)
- Infilling (e.g., filling blanks in a partially masked sentence)
Diffusion-LM addresses these challenges by adapting continuous diffusion models, which have shown great success in vision and audio domains, to the discrete domain of language. The model begins with a sequence of Gaussian noise vectors and incrementally denoises them into meaningful word representations. These denoising steps produce a hierarchy of continuous latent variables that enable efficient, gradient-based control during generation.
Key advantages of Diffusion-LM include:
- Support for complex, global constraints: Unlike autoregressive models, which generate text left-to-right and they can only condition on past tokens, Diffusion-LM operates on the full sequence, and this allows it to enforce constraints that depend on both left and right contexts, such as syntax trees or long-range dependencies.
- Plug-and-play controllability: Diffusion-LM enables classifier-guided generation by using gradient updates directly to the continuous latent variables. This allows the generation process to satisfy control objectives (e.g., sentiment, structure) while maintaining fluency, without requiring any model retraining.
- Infilling and span-anchored controls: The model can hold parts of a sentence fixed and only sample the missing spans, and naturally supporting infilling tasks. These tasks can be performed without the need for a clasifier, and Diffusion-LM achieves results competitive with autoregressive models trained specifically for such tasks.
- Compatibility with existing methods: The model builds on a standard diffusion process but incorporates critical adaptations for language, such as a learned embedding space, rounding back to discrete tokens, and training techniques to handle the continuous-discrete interface.
Diffusion-LM significantly outperforms prior plug-and-play methods on a variety of challenging control tasks—including syntax, semantics, and structure—and often matches or exceeds the performance of models that are fine-tuned for each individual control. Moreover, it demonstrates strong composability: multiple controls (e.g., non-toxic and positive sentiment) can be jointly applied with minimal overhead. These results show that Diffusion-LM is a promising way for controllable text generation.
Mathematical Formulation
Diffusion-LM applies a continuous diffusion process to language modeling by representing text sequences as continuous embeddings. These embeddings are progressively noised and then denoised to recover coherent text. Let's take a look at its formulas in the following parts.
Forward Diffusion Process
The forward process gradually adds Gaussian noise to the embedded text representation. A sequence of tokens [math]\displaystyle{ w = [w_1, \ldots, w_n] }[/math] is mapped to a continuous vector matrix [math]\displaystyle{ x_0 \in \mathbb{R}^{n \times d} }[/math]. A fixed Markov chain adds noise at each step to produce [math]\displaystyle{ x_1, \ldots, x_T }[/math]:
[math]\displaystyle{ q(x_t \mid x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} , x_{t-1}, \beta_t I) }[/math]
Here, [math]\displaystyle{ \beta_t }[/math] is a hyperparameter controlling the noise at step [math]\displaystyle{ t }[/math]. The final noisy sample [math]\displaystyle{ x_T }[/math] approximates a Gaussian prior:
[math]\displaystyle{ q(x_T \mid x_0) \approx \mathcal{N}(0, I) }[/math]
This process is illustrated in Figure 1.

Reverse Denoising Process
The model learns the reverse transitions to remove noise and recover the original text embeddings. Each step of the reverse process is modeled as:
[math]\displaystyle{ p_\theta(x_{t-1} \mid x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t, t)) }[/math]
The mean [math]\displaystyle{ \mu_\theta(x_t, t) }[/math] and optionally the variance [math]\displaystyle{ \Sigma_\theta(x_t, t) }[/math] are predicted by a neural network (e.g., Transformer or U-Net).
Training Objective
Training aims to maximize the marginal likelihood [math]\displaystyle{ \log p_\theta(x_0) }[/math], but this is intractable. Instead, the model minimizes a variational lower bound (ELBO):
[math]\displaystyle{ \mathcal{L}_{\text{vlb}}(x_0) = \mathbb{E}_{q(x_{1:T} \mid x_0)} \left[ \log \frac{q(x_T \mid x_0)}{p_\theta(x_T)} + \sum_{t=2}^{T} \log \frac{q(x_{t-1} \mid x_0, x_t)}{p_\theta(x_{t-1} \mid x_t)} - \log p_\theta(x_0 \mid x_1) \right] }[/math] Since this objective is unstable, the paper adopts the simplified denoising loss proposed by Ho et al.:
[math]\displaystyle{ \mathcal{L}_{\text{simple}}(x_0) = \sum_{t=1}^{T} \mathbb{E}_{q(x_t \mid x_0)} \left[ \| \mu_\theta(x_t, t) - \hat{\mu}(x_t, x_0) \|^2 \right] }[/math] Here, [math]\displaystyle{ \hat{\mu}(x_t, x_0) }[/math] is the mean of the true posterior [math]\displaystyle{ q(x_{t-1} \mid x_t, x_0) }[/math], which is analytically known for Gaussian noise.
While [math]\displaystyle{ \mathcal{L}_{\text{simple}} }[/math] is no longer a valid lower bound, prior work has found that it empirically made training more stable and improved sample quality.
Embedding and Rounding
After denoising, the model obtains [math]\displaystyle{ x_0 }[/math], a continuous representation. A final decoding step maps this to discrete tokens using:
[math]\displaystyle{ p_\theta(w \mid x_0) = \prod_i p_\theta(w_i \mid x_{0, i}) }[/math] Each [math]\displaystyle{ w_i }[/math] is predicted from its embedding [math]\displaystyle{ x_{0, i} }[/math] using a softmax over the vocabulary.
To improve alignment with the discrete token space during generation, the model optionally applies the clamping trick, which replaces the predicted vector with its nearest token embedding at intermediate steps. This helps reduce rounding errors during generation.
Model Architecture and Training Methods
Diffusion-LM adapts the standard diffusion model to handle discrete text. As we know, text is inherently discrete and constructing Diffusion-LM requires several key changes. This section walks through those changes step by step, covering embedding design, training strategy, rounding, and controllable decoding. As we described before, in the Mathematical Formulation section, the model starts with Gaussian noise and learns to iteratively denoise it back to meaningful embeddings. Now we explain how this process is practically implemented.
Embedding and End-to-End Training
For using diffusion in language modeling, first we should convert text into continuous embeddings. Each token in a sequence [math]\displaystyle{ w = [w_1, w_2, \dots, w_n] }[/math] is mapped to a continuous vector in [math]\displaystyle{ \mathbb{R}^d }[/math] by an embedding function [math]\displaystyle{ \text{EMB}(w_i) }[/math]. The full sentence is represented as:
[math]\displaystyle{ \text{EMB}(w) = [\text{EMB}(w_1), \dots, \text{EMB}(w_n)] \in \mathbb{R}^{n \times d} }[/math]
Then, these embeddings are used in a diffusion process that gradualy adds noise and then learns to reverse this process. The embedding function is learned end-to-end along with the model parameters using a modified version of the standard diffusion loss. (Recall from the Mathematical Formulation section that this loss is based on a variational lower bound and a simplified mean squared objective.)
The modified objective is:
[math]\displaystyle{ \mathcal{L}^{\text{e2e}}{\text{vlb}}(w) = \mathbb{E}{q(x_0|w)} \left[\mathcal{L}{\text{vlb}}(x_0) + \log q\phi(x_0|w) - \log p_\theta(w|x_0)\right] }[/math]
The learned embeddings (Figure 2) show interesting clustering patterns, where tokens with similar part-of-speech tags tend to group together in embedding space.
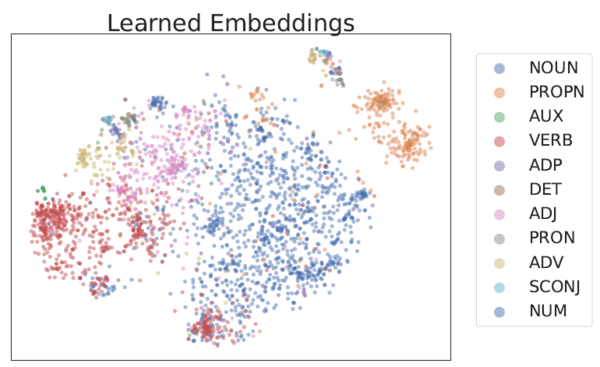
Reducing Rounding Errors
As we discussed earlier, once denoising ends and the model reaches a final continuous state [math]\displaystyle{ x_0 }[/math], it needs to be mapped back to a discrete sentence. We call this process as "rounding". The standard approach is to choose the word with the highest likelihood given [math]\displaystyle{ x_0 }[/math]:
[math]\displaystyle{ p_\theta(w | x_0) = \prod_{i=1}^n p_\theta(w_i | x_{0,i}) }[/math]
But, this naïve rounding often fails because [math]\displaystyle{ x_0 }[/math] may not map cleanly to one token per position. To fix this, the model modifies the training objective to explicitly encourage [math]\displaystyle{ x_0 }[/math] to align with discrete word vectors. The improved loss is:
[math]\displaystyle{ \mathcal{L}^{\text{e2e}}{\text{simple}}(x_0) = \sum{t=1}^T \mathbb{E}{q(x_t|x_0)} \left[ | f\theta(x_t, t) - x_0 |^2 \right] }[/math]
Here, [math]\displaystyle{ f_\theta(x_t, t) }[/math] is a neural network that predicts [math]\displaystyle{ x_0 }[/math] from any [math]\displaystyle{ x_t }[/math], and this enforces that the model should maintain a clear mapping throughout the diffusion steps. This mirrors the score-based denoising strategy which we introduced in the mathematical formulation section.
Additionally, the "clamping trick" helps by snaping intermediate states closer to valid token embeddings. The clamping update is:
[math]\displaystyle{ x_{t-1} = \sqrt{\bar{\alpha}t} \cdot \text{Clamp}(f\theta(x_t, t)) + \sqrt{1 - \bar{\alpha}_t} \cdot \epsilon }[/math]
This trick improves word alignment and reduces rounding errors.
Controllable Text Generation
As we mentioned in the Introduction, Diffusion-LM is particularly powerful for controllable generation. This is done by applying plug-and-play control at the latent level. Rather than steering the output text directly, we apply gradients to the latent variables [math]\displaystyle{ x_{0:T} }[/math] so that the denoised output satisfies the control objective.
The goal is to sample from:
[math]\displaystyle{ p(x_{0:T} | c) = \prod_{t=1}^T p(x_{t-1} | x_t, c) }[/math]
This is approximated using gradient ascent on [math]\displaystyle{ x_{t-1} }[/math]:
[math]\displaystyle{ \nabla_{x_{t-1}} \log p(x_{t-1} | x_t, c) = \nabla_{x_{t-1}} \log p(x_{t-1} | x_t) + \nabla_{x_{t-1}} \log p(c | x_{t-1}) }[/math]
The first term is from the language model, and the second from the control classifier. This allows the model to adjust generation to satisfy constraints like syntax or semantics.
To improve decoding, two enhancements are introduced:
- Fluency Regularization: Add a term that balances fluency with control satisfaction.
- Multiple Gradient Steps: Run several gradient steps per denoising step to better fulfill constraints.
These techniques directly reflect the plug-and-play controllable generation strategy we mentioned in the introduction.
Score-Based Gradient Control in Diffusion-LM
One of the key benefits of Diffusion-LM is that it can incorporate external control signals at generation time using gradient guidance. At denoising time, the model refines latent representations using the gradient of a control objective. For a control variable [math]\displaystyle{ c }[/math] (e.g., sentiment, length, syntax), the posterior over trajectories is refined as [math]\displaystyle{ p(x_{0:T} \mid c) \propto p(x_{0:T}) \cdot p(c \mid x_0) }[/math]. This construction enables us to optimize the path to meet language fluency and the control constraint at the same time.
To approximate this posterior, Diffusion-LM updates gradients in latent states [math]\displaystyle{ x_t }[/math] using a classifier (or potential function) [math]\displaystyle{ p(c \mid x_0) }[/math]. Specifically, for each reverse step, the model updates [math]\displaystyle{ x_{t-1} }[/math] by:
[math]\displaystyle{ \nabla_{x_{t-1}} \log p(x_{t-1} \mid x_t, c) = \nabla_{x_{t-1}} \log p(x_{t-1} \mid x_t) + \nabla_{x_{t-1}} \log p(c \mid x_{t-1}) }[/math]
The first term ensures language fluency following the diffusion model, while the second term channels the output for ensuring the control requirement. Plug-and-play controllability is thus ensured without altering the language model weights.
For stable and interpretable updates, the model can optionally incorporate fluency regularization and multiple gradient steps. Adding a fluency loss such as [math]\displaystyle{ \lambda \cdot \| x_{t-1} - \hat{x}_{t-1} \|^2 }[/math], where [math]\displaystyle{ \hat{x}_{t-1} }[/math] is the initial prediction of the model, can be used. Also, performing multiple steps of gradient ascent on [math]\displaystyle{ x_{t-1} }[/math] before sampling [math]\displaystyle{ x_{t-2} }[/math] can help constraint satisfaction. These mechanisms enable control of the generation process at a fine-grained level, producing a more expressive and flexible alternative to autoregressive approaches.
Minimum Bayes Risk Decoding
For generation tasks that demand high-accuracy outputs—such as machine translation, summarization, or infilling—it is often not enough to generate a single fluent sentence. Instead, we want the output that best aligns with some evaluation metric, such as BLEU, ROUGE, or semantic similarity. In these scenarios, Diffusion-LM supports a decoding strategy called Minimum Bayes Risk (MBR) decoding.
MBR decoding works by generating a set of candidate outputs (e.g., 10 or 100 samples) from the model and then selecting the one that has the lowest expected loss under a given utility function. In other words, instead of choosing the most likely sentence, the model picks the one that is most similar to the other high-quality samples, according to some reference-free scoring criterion.
Formally, the MBR decoding selects: [math]\displaystyle{ \hat{w} = \arg\min_{w \in S} \sum_{w' \in S} \frac{1}{|S|} \cdot \mathcal{L}(w, w') }[/math]
where:
- [math]\displaystyle{ S }[/math] is the set of generated samples,
- [math]\displaystyle{ \mathcal{L}(w, w') }[/math] is a task-specific loss (e.g., 1 - BLEU),
- [math]\displaystyle{ \hat{w} }[/math] is the output that minimizes the expected loss over the set.
This method is useful. why? because even if the model’s sampling process is noisy or diverse, the MBR step ensures that the selected output is representative of the best qualities among all samples. This is especially helpful in controllable generation, where we care about both fluency and constraint satisfaction.
In practice, MBR decoding often improves the final quality of generated sequences without needing to modify the model itself. It serves as a powerful post-processing technique for refining outputs, and this makes it highly complementary to the plug-and-play control strategies used in Diffusion-LM.
Evaluation and Results
Diffusion-LM is evaluated on five controllable generation tasks, using both control accuracy (how well the constraint is followed) and fluency (measured via perplexity and human evaluation).
Compared to baselines like:
- PPLM – a plug-and-play autoregressive method
- FUDGE – classifier-based control on GPT-2
- FT – fine-tuned GPT-2 on each control task

Diffusion-LM achieves higher control accuracy and comparable or better fluency, demonstrating its effectiveness in multi-property generation without needing task-specific retraining.
Limitations
- Higher Perplexity
- Diffusion-LM relies on continuous diffusion processes for text generation, which differ fundamentally from the discrete autoregressive approach used in models like GPT or BERT.
- As a result, the generated text may exhibit slightly lower fluency or grammatical coherence, leading to higher perplexity scores.
- This suggests that the model's ability to capture natural language distributions is not yet on par with state-of-the-art language models. Improving the architecture or introducing auxiliary losses may help reduce perplexity.
- Substantially Slower Decoding
- Unlike autoregressive models that generate tokens sequentially in a single forward pass, diffusion models require hundreds of iterative denoising steps to produce output.
- This makes the decoding process significantly slower, limiting the model’s usability in real-time applications such as interactive writing assistants or conversational agents.
- Speed optimization and accelerated sampling techniques are essential for improving practical deployment.
- Slower Training Convergence
- Training a diffusion-based language model involves learning across a wide range of noise levels, which introduces a more complex optimization landscape than traditional language modeling tasks.
- This complexity leads to longer training times and makes the training process more sensitive to hyperparameters, such as noise schedules and model architecture.
- Effective convergence often requires careful tuning and potentially more compute resources compared to standard fine-tuning or pretraining.
Conclusion
Diffusion-LM, a novel language model based on continuous diffusion processes, introduces new possibilities for controlling text generation with fine-grained precision. With a modified loss function and end-to-end training, Diffusion-LM outperforms previous methods in six distinct control tasks, significantly improving success rates and competing well with fine-tuning approaches that require additional training. Despite some challenges, such as increased perplexity, slower decoding, and slower training convergence, Diffusion-LM shows great promise. With further optimization and development, it has the potential to offer a highly effective solution for large-scale controllable text generation tasks.
Masked-Diffusion LM: Faster and Smarter
The key limitation of traditional diffusion models in handling discrete data like text is their application of uniform noise. In language modelling, it is important to model the fact that different words have different levels of importance. Simply adding a rounding step is expensive as it leads to slower training and inference times.
Masked-Diffusion LM improves efficiency by applying noise selectively based on word importance. Important tokens are masked earlier in the process so that the model is exposed to their features earlier. It replaces nearest-neighbour rounding with a cross-entropy loss between predicted and original tokens. Then, at generation, less important words are predicted first (as they are masked later) with more important words generated towards the end. The result is better performance and faster inference.
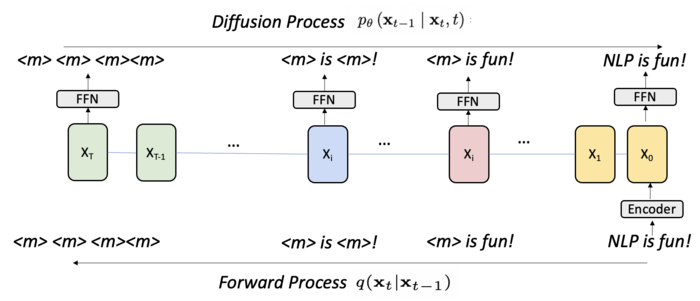
Method/Experiment
The paper introduces a new diffusion language model called Masked-Diffuse LM that aims to generate text more efficiently and with higher quality with three key innovations.
1. Selective Noise Application: Instead of applying uniform noise as in earlier methods, it uses a “soft-masking” strategy that gradually corrupts text by targeting more important words first. These important words are identified using simple linguistic metrics like TF-DF and word entropy. TF-IDF enables us to measure the relevance of a word with respect to a specific sentence. A higher score means the particular word is more important in the sentence. Entropy determines the amount of information a word contains. A word with lower entropy suggests that the word contains less information. Thus, these words have lower importance than those with higher entropy.
Word Relevancy (TF-IDF): [math]\displaystyle{ w_{\text{tf-idf}}(w, d) = \frac{f_{w,d}}{\sum_{w' \in d} f_{w',d}} \log \frac{N}{1 + |\{d \in D : w \in d\}|} }[/math]
Entropy: [math]\displaystyle{ H(w) = -p(w) \log(p(w)), \quad p(w) = \frac{f_w}{\sum_{j=1}^J f_j} }[/math]
In practice, we combine both measures (with normalization) to produce a new importance metric (as seen below) to evaluate the importance of words in a given sentence.
Importance: [math]\displaystyle{ I(w) = \frac{x_{\text{tf-idf}}(w, d)}{\sum_{w' \in d} w_{\text{tf-idf}}(w', d)} + \frac{H(w)}{\sum_{w' \in d} H(w')} }[/math]
2. Soft-Masking Process: During the forward process, the model corrupts token embeddings progressively, starting with the most meaningful words to ensure that the model learns to prioritize recovering critical information during the reverse process. For example, given the text "NLP is fun!", the most meaningful word ("NLP") would be masked first and then "fun" and then "is".
3. Cross-Entropy Loss for Stability: In the reverse diffusion process, the model denoises the embeddings step-by-step to reconstruct the original text by directly predicting the original tokens using a cross-entropy loss. This approach effectively bridges the gap between continuous embeddings and discrete tokens and ensures stable and coherent text generation. Using the example from above, during denoising, "is" would be generated first and then "fun" and then "NLP".
The model can also be combined with large pre-trained language models like BERT to further boost performance on various controllable generation tasks.
Results
The experiments show that Masked-Diffuse LM outperforms previous diffusion language models on several controllable generation tasks. For example, on tasks like generating specific semantic content, the model achieved higher accuracy and better fluency compared to baselines like Diffusion-LM and FUDGE. It consistently improved accuracy across tasks such as parts-of-speech, syntax tree, syntax spans, and controlling sentence length. Moreover, the new method is more efficient, requiring significantly less training and inference time. Human evaluators also ranked it higher for quality, confirming that it produces more natural and controlled text. Overall, the results demonstrate that this new model is both cheaper to train and better at generating coherent and controlled text.
Why It Matters
Masked-Diffusion LM represents a shift in how diffusion models handle discrete data like text. By leveraging linguistic insights and optimizing the noise application process, it not only generates better-quality text but also does so at a lower computational cost. This makes it a promising tool for applications requiring controlled and efficient language generation.
Limitations
1. Dependence on Heuristic Importance Metrics: The model relies on simple heuristic-based metrics like TF-IDF and entropy to estimate word importance. While effective and interpretable, these metrics may not always capture deep semantic relevance or context-dependent importance. Future work could explore learned importance functions or attention-based saliency models that dynamically adjust based on task or context.
2. Evaluation Limited to Controllable Tasks: The experiments are primarily focused on controllable generation tasks (e.g., POS constraints, syntax structure, sentence length). It remains unclear how well the model performs in open-ended generation, dialogue systems, or low-resource settings. Broader evaluation would help validate general applicability.
Conclusion
Masked-Diffusion LM marks a meaningful step forward in bridging the gap between continuous diffusion processes and the discrete world of natural language. By leveraging lightweight linguistic signals to guide noise injection and replacing costly rounding with stable cross-entropy loss, it introduces a more efficient and semantically aware approach to controllable text generation. The model not only improves performance across key generation tasks but also does so with reduced computational overhead—making it both practical and powerful. As diffusion models continue to gain traction in NLP, innovations like this offer a glimpse into a future where language generation is not just accurate and fluent, but also interpretable, controllable, and efficient. With its thoughtful design and strong results, Masked-Diffusion LM lays important groundwork for the next generation of discrete generative models.
DiffuSum: Generation Enhanced Extractive Summarization with Diffusion
Overview
DiffuSum introduces a novel paradigm for extractive summarization by leveraging continuous diffusion models to generate summary‐level sentence embeddings and then extract sentences via representation matching, rather than treating extraction as a binary sequence‐labeling task. It jointly trains a contrastive sentence encoder—with matching and diversity losses—and a diffusion‐based generator that iteratively denoises Gaussian latents into target embeddings. On CNN/DailyMail, DiffuSum achieves a new state‑of‑the‑art ROUGE of 44.83/22.56/40.56 and generalizes robustly to XSum and PubMed with only minor performance drops and no domain‑specific tuning.
Method
Sentence Encoding Module:
- Initial Embedding: The document and summary sentences are first processed using Sentence-BERT to obtain initial sentence embeddings. These embeddings are fixed and will not be updated during the training.
- Contextualization: These embeddings are refined through a transformer-based encoder and a projection (MLP) layer to produce contextualized sentence representations.
- Optimization: The module is trained using a matching loss (ensuring the generated summary representations align with oracle summaries) and a multi-class contrastive loss (promoting diversity and distinguishability among sentence representations).
Diffusion Generation Module:
- Forward Process:The module gradually injects Gaussian noise into the summary sentence embeddings, simulating a diffusion process that corrupts the embeddings over several steps.
- Reverse Process: A transformer-based model then learns to iteratively remove the noise, recovering the target summary sentence representations in a reverse diffusion process.
- Simultaneous Generation: This approach enables the model to generate all summary sentence representations concurrently, bypassing token-level generation challenges.
Sentence Extraction via Matching:
- Matching Mechanism: The generated summary embeddings are compared with the document’s sentence embeddings using a similarity measure (e.g., dot product followed by softmax).
- Extraction: For each generated summary representation, the document sentence with the highest matching score is selected to form the final extractive summary.
Experimental Results and Analysis
DiffuSum demonstrates state-of-the-art performance on benchmark datasets such as CNN/DailyMail, XSum, and PubMed. Key findings include:
1. Performance Gains:
The model achieves high ROUGE-1/2/L scores, particularly improving ROUGE-2, compared to both one-stage and two-stage extractive summarization baselines.
2. Ablation Studies:
- Using Sentence-BERT for initial sentence embeddings is critical.
- Both the matching loss and contrastive loss substantially enhance the quality of sentence representations.
- The number of diffusion steps and the dimensionality of the embeddings (h) significantly influence performance, indicating the need for an optimal balance between noise injection and recovery.
3. Cross-Dataset Adaptability:
Evaluations across different domains (news and scientific papers) show that DiffuSum adapts well to varying summary lengths and document complexities.
Limitations
- Only supports extractive summarization (i.e. select one or more summary sentences directly)
- The diffusion module generates sentence-level embeddings only
- Lacks token-level generation, making it unsuitable for abstractive summarization (i.e. generate a new summary sentence)
- Evaluated only on single-document datasets
- Not tested on multi-document or long-document summarization
- Requires further investigation for adaptation to these settings
- More complex generation process
- Involves multiple steps of noise injection and denoising
- More computationally intensive than discriminator-based extractive systems
Conclusion
DiffuSum pioneers the application of diffusion models in extractive summarization by generating continuous summary sentence representations and using a matching mechanism for sentence extraction. This generation-enhanced framework not only achieves superior performance compared to traditional methods but also opens new avenues for applying generative models in text summarization. Future work could extend this approach to abstractive summarization, multi-document scenarios, and integration with pre-trained language models to further boost performance.
Discrete Diffusion Modeling by Estimating the Ratios of the Data Distribution
This paper introduces Score Entropy Discrete Diffusion (SEDD), a new framework that brings the power of continuous diffusion models to discrete data—especially language—by learning probability ratios via a novel “score entropy” loss. SEDD matches or surpasses existing diffusion‑based language models (cutting perplexity by 25–75 %), outperforms GPT‑2 on zero‑shot perplexity without any annealing (6–8× better), and allows rich control (e.g., arbitrary infilling) while trading compute for quality (32× fewer network evaluations). By framing the reverse diffusion as estimation of conditional probability ratios between token pairs using a Bregman‑divergence–based objective, SEDD ensures nonnegativity and convexity in its loss, yielding stable training dynamics across timesteps. It also derives a tractable evidence lower bound (ELBO) for direct maximum‑likelihood training and perplexity evaluation, enabling head‑to‑head comparisons with autoregressive baselines on benchmarks like Penn Treebank and WikiText‑103.
Introduction
Diffusion models have revolutionized image generation, creating stunningly realistic visuals. However, translating this success to discrete data like natural language has proven challenging. While standard diffusion models build on the solid foundation of score matching in continuous spaces, attempts to adapt this for discrete domains haven't yielded comparable results. This paper introduces a novel approach that aims to bridge this gap.
The Problem This Paper Tried to Address
Generating high-quality, coherent text has long been dominated by autoregressive models (like GPT). While powerful, these models have limitations: sequential generation is slow, controlling the output is tricky, and they often require sampling tricks like temperature scaling or nucleus sampling to avoid degraded text quality.
Inspired by the success of diffusion models in generating continuous data (like images), researchers have tried adapting them for discrete sequences (like text). However, these discrete diffusion models have generally lagged behind autoregressive models. They often struggle with likelihood performance (perplexity), are slow to sample from, and produce lower-quality text without significant modifications or annealing techniques. Existing methods for training discrete diffusion models, like mean prediction or ratio matching, have practical drawbacks or don't perform as well empirically. Concrete score matching, while theoretically promising, suffers from instability due to its loss function.
Key Contribution: Score Entropy Discrete Diffusion (SEDD)
This work introduces Score Entropy Discrete Diffusion (SEDD), a new framework for discrete diffusion modeling that significantly boosts performance, particularly for language tasks.
- Score Entropy Loss: The core innovation is the "score entropy" loss function. This loss naturally extends the concept of score matching from continuous to discrete spaces by focusing on learning the ratios of probabilities between adjacent states,[math]\displaystyle{ \frac{p_t(y)}{p_t(x)} }[/math], often called the concrete score. Score entropy is designed to handle the positivity requirement of these ratios, overcoming stability issues faced by previous discrete score matching attempts.
- State-of-the-Art Discrete Diffusion: SEDD significantly outperforms previous discrete and continuous diffusion language models on standard benchmarks, reducing perplexity by 25-75%.
- Competitive with Autoregressive Models: For comparable model sizes, SEDD achieves perplexity scores competitive with strong autoregressive baselines, notably outperforming GPT-2 on several zero-shot perplexity tasks.
- High-Quality Generation & Compute Trade-off: SEDD generates high-quality text samples without needing distribution annealing techniques like temperature or nucleus sampling. It significantly outperforms un-annealed GPT-2 in generative perplexity (6-8x better) and allows trading compute for quality – matching GPT-2 quality with up to 32x fewer network evaluations.
- Controllable Generation: By directly modeling probability ratios, SEDD enables flexible conditional generation, including controllable infilling (generating text to fill gaps between prompts) without specialized training, matching the quality of nucleus sampling in autoregressive models.
Method: Learning Ratios via Denoising Score Entropy
- Discrete Diffusion Process: The SEDD model defines a forward discrete diffusion process where data distribution evolves via a continuous-time Markov process defined by a rate matrix (diffusion matrix) [math]\displaystyle{ Q_t \in \mathbb{R}^{N \times N} }[/math], and a family of distributions [math]\displaystyle{ p_t \in \mathbb{R}^N }[/math] where [math]\displaystyle{ \frac{dp_t}{dt} = Q_t p_t }[/math] and [math]\displaystyle{ p_0 }[/math] is approximately the original data probability distribution. Note that [math]\displaystyle{ Q_t }[/math] here has non-negative non-diagonal entries and the sum of each column of [math]\displaystyle{ Q_t }[/math] is 0. This makes sure that the rate [math]\displaystyle{ \frac{dp_t}{dt}\ }[/math]'s entries have a sum of zero, meaning that there is no change of total mass. The goal is to learn the reverse process, which depends on the probability ratios[math]\displaystyle{ \frac{p_t(y)}{p_t(x)} }[/math]
- Score Entropy Loss: Instead of directly minimizing an [math]\displaystyle{ l^2 }[/math]difference (like Concrete Score Matching), SEDD uses the score entropy loss [math]\displaystyle{ \mathcal{L}_{SE} = \mathbb{E}_{x \sim p} \left[ \sum_{y \ne x} w_{xy} \left( s_\theta(x)_y - \frac{p(y)}{p(x)} \log s_\theta(x)_y + K\left(\frac{p(y)}{p(x)}\right) \right) \right] }[/math], where [math]\displaystyle{ s_\theta(x)_y }[/math] is the model's estimate of the ratio[math]\displaystyle{ \frac{p(y)}{p(x)}, }[/math][math]\displaystyle{ w_{xy} }[/math] are weights, and [math]\displaystyle{ K(a) = a(log(a)-1) }[/math] is a constant function that makes sure the score entropy loss is non-negative. It is better behaved than the [math]\displaystyle{ l^2 }[/math] loss.
- Denoising Score Entropy (DSE): Calculating [math]\displaystyle{ \mathcal{L}_{SE} }[/math] directly requires knowing the true ratios [math]\displaystyle{ \frac{p(y)}{p(x)} }[/math], but they are unknown. Similar to denoising score matching, the authors derive a tractable denoising score entropy [math]\displaystyle{ \mathcal{L}_{DSE} }[/math] objective that is equivalent to [math]\displaystyle{ \mathcal{L}_{SE} }[/math] up to a constant independence of [math]\displaystyle{ \theta }[/math] and depends only on the transition probabilities [math]\displaystyle{ p(y|x_0) }[/math] and [math]\displaystyle{ p(x|x_0) }[/math] of the forward diffusion process: [math]\displaystyle{ \mathcal{L}_{DSE} = \mathbb{E}_{x_0 \sim p_0, x \sim p(\cdot|x_0)} \left[ \sum_{y \ne x} w_{xy} \left( s_\theta(x)_y - \frac{p(y|x_0)}{p(x|x_0)} \log s_\theta(x)_y \right) \right] }[/math], where [math]\displaystyle{ p_0 }[/math] is a base density.
- Diffusion Weighted DSE (DWDSE): For training diffusion models, this loss is integrated over time and weighted by the forward process transition rates, yielding the Diffusion Weighted Denoising Score Entropy [math]\displaystyle{ \mathcal{L}_{DWDSE} }[/math] where DWDSE at data point [math]\displaystyle{ x_0 }[/math] is [math]\displaystyle{ \mathcal{L}_{DWDSE}(x_0) = \int_0^T \mathbb{E}_{x_t \sim p_{t|0}(\cdot|x_0)} \sum_{y \neq x_t} Q_t(x_t, y) \left( s_\theta(x_t, t)_y - \frac{p_{t|0}(y|x_0)}{p_{t|0}(x_t|x_0)} \log s_\theta(x_t, t)_y + K( \frac{p_{t|0}(y|x_0)}{p_{t|0}(x_t|x_0)}) \right) dt }[/math], and [math]\displaystyle{ p_{t|0}(\cdot|x_0) }[/math] and [math]\displaystyle{ K }[/math] remain the same meaning as above. DWDSE provides an upper bound on the negative log-likelihood (similar to the ELBO).
- Structured Transitions: For tractability with sequences (like text), the diffusion process [math]\displaystyle{ Q_t }[/math] perturbs tokens independently using simpler token-level transition matrices [math]\displaystyle{ Q^{tok}_t }[/math] such as uniform noise [math]\displaystyle{ Q^{uniform} = \begin{bmatrix} 1-N & 1 & \dots & 1 \\ 1 & 1-N & \dots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & \dots & 1-N \end{bmatrix} }[/math] or transitions to a special MASK token [math]\displaystyle{ Q^{absorb} = \begin{bmatrix} -1 & 0 & \dots & 0 & 0 \\ 0 & -1 & \dots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \dots & -1 & 0 \\ 1 & 1 & \dots & 1 & 0 \end{bmatrix} }[/math]. This allows the score network [math]\displaystyle{ s_\theta }[/math] to predict ratios only between sequences differing by one token, and all values in [math]\displaystyle{ \mathcal{L}_{DWDSE} }[/math] are able to be efficiently calculated with such [math]\displaystyle{ Q's }[/math].
- Sampling & Control: Generation uses the learned scores [math]\displaystyle{ s_\theta }[/math] to simulate the reverse process, typically using [math]\displaystyle{ \tau }[/math]-leaping. A "Tweedie[math]\displaystyle{ \tau }[/math]-leaping" variant leverages the ratio information for potentially better sampling. Conditional generation (like infilling) is achieved by applying Bayes' rule to the learned unconditional scores, allowing prompts at arbitrary positions without retraining.
Conclusion and performance
In terms of perplexity across common task, a small SEDD model outperformed GPT-2 in the Wikitext2, PTB and Wikitext103 dataset. Similarly things happened for the medium SEDD model which again they outperformed GPT2 medium in Wikitext2, PTB and Wikitext103 dataset.
In terms of efficiency, both SEDD small and SEDD medium achieve comparable perplexity with GPT2 with less iterations.
Limitation and Future Work
- Sampling Speed: While SEDD offers a compute-quality trade-off, and the network evaluation itself is efficient (no KV cache needed), achieving the highest quality still requires many sampling steps (e.g., 2048), which can be slower overall than autoregressive sampling with KV caching, depending on the hardware and batch size. Future work could focus on reducing the required number of steps, similar to advances in continuous diffusion.
- Annealing: The current work focuses on demonstrating high-quality generation without distribution annealing. Incorporating annealing techniques (like thresholding or guidance) could potentially further improve results or offer different control trade-offs.
- Scaling: While SEDD outperforms GPT-2, bridging the gap to modern large language models remains a challenge for future research, potentially building upon the SEDD framework.
- Hyperparameters: The current study didn't perform extensive hyperparameter tuning (e.g., noise schedules, loss weightings), suggesting potential for further improvements.
Compare Discrete and Continuous Diffusion
Discrete Diffusion
How it works
- IT Operates in discrete data space like word tokens level.
- Each token transitions from one word to another during the noising and denoising process (sometimes the token are masked)
- Often uses a diffusion matrix to guide the transitions
Advantages
- Language is discrete, so modeling it directly preserves the original structure and semantics better.
- We don't need to learn a separate mapping ("rounding") from vectors back to language since we are already in the token space.
Disadvantage and Challenges
- The symbolic space doesn’t allow for gradients to flow easily since it's non-differentiable .
- Everything happens in discrete steps, the denoising has to predict exact tokens which could be difficult.
Continuous Diffusion
How it works
- Maps tokens into a continuous embedding space
- Noising and denoising happen in this continuous space
- May include clamping mechanisms to keep values in valid ranges
- After denoising, the final vector is rounded or projected back to the nearest sentence
Advantages
- Since everything happens in the continuous domain, it better aligned with the original diffusion and could allow gradients to flow smoothly through the model, making training more stable and efficient.
- Thanks to embeddings, the continuous space captures richer semantics domain, so the model can generalize to unseen combinations or variations more easily.
Disadvantage and Challenges
- We need a strong rounding technique to map from the continuous space back to valid token and valid language.
Topic 18: Retrival Augmented Generation (RAG)
Motivation
Language models often struggle with hallucinations, outdated knowledge, and lack of factual grounding. Retrieval-Augmented Generation (RAG) addresses these issues by incorporating external knowledge into the generation process in a modular, efficient way.
Why Do Language Models Hallucinate?
Large language models (LLMs) are trained on massive corpora using self-supervised objectives, which makes them excellent at generating fluent text. However, they often produce hallucinations—confident but factually incorrect statements. This happens because:
- LLMs store information implicitly in parameters, which may become outdated.
- Their knowledge is static, limited to the training corpus.
- They lack direct access to external knowledge sources during inference.
As a result, even the most powerful models may fail to answer factual questions reliably, especially when dealing with rare or time-sensitive topics.
Limitations of Parametric Knowledge
Traditional LLMs rely solely on parametric memory—i.e., knowledge encoded in weights. This approach has several key limitations:
- Scalability – Retraining a model to update its knowledge is expensive and slow.
- Transparency – It is hard to trace the origin of a generated fact.
- Updatability – Knowledge becomes stale quickly in dynamic domains like news or medicine.
These issues become critical in open-domain question answering, where users expect accuracy, citation, and timeliness.
The Promise of Retrieval-Augmented Generation
Retrieval-Augmented Generation (RAG) aims to solve these problems by separating retrieval from generation.
Instead of generating from memory alone, RAG models:
- Accept a query
- Retrieve relevant documents from an external knowledge source (e.g., Wikipedia, search engine, vector DB)
- Generate a response grounded in those documents
This offers several advantages:
- Reduced hallucinations – Answers are supported by retrieved evidence.
- Updatable knowledge – The retrieval index can be updated without retraining.
- Improved interpretability – Retrieved sources can be cited directly.
- Efficient scaling – Small models can perform well with strong retrieval.
This separation between knowledge access and text generation introduces a new paradigm that is more modular, flexible, and robust for real-world applications.
What is Retrieval-Augmented Generation
RAG combines a retriever and a generator. Given a query, the retriever fetches relevant documents from a knowledge base, and the generator uses them to produce grounded responses. This architecture bridges retrieval-based QA and language generation.
Core Definition
Retrieval-Augmented Generation (RAG) is a hybrid framework that integrates information retrieval into the generation pipeline of language models. Instead of relying solely on internal parametric memory, a RAG system:
- Retrieves external documents relevant to a given query
- Conditions the generation process on the retrieved evidence
This enables models to access current, specific, and factual knowledge at inference time.
RAG is not a single architecture but a general paradigm. It can be combined with various retrievers (e.g., dense or sparse) and generators (e.g., GPT-style models) to suit different applications such as question-answering, summarization, and fact-grounded dialogue.
Key Components
A typical RAG system consists of two modules:
- Retriever Takes a query and retrieves the most relevant documents from an external corpus, such as Wikipedia or a search engine. This can be a dense retriever (like Contriever or DPR) or a sparse one (like BM25).
- Generator Given the query and retrieved documents, the generator produces an answer that ideally reflects and integrates the retrieved content. It is usually a pre-trained language model such as T5, BART, or GLM.
This structure allows knowledge to flow from the retriever to the generator, enhancing factual correctness and grounding.
Retrieval vs. Parametric Generation
The core contrast between RAG and the traditional generation lies in how knowledge is accessed:
- Parametric LMs are generated based on internal representations learned during pretraining.
- RAG explicitly pulls in external evidence for each query.
This means RAG can stay up-to-date, offer transparent answers, and dynamically adapt to user input without needing retraining.
A Practical Example
The concept of RAG is embodied in real-world systems like Perplexity.ai, a web-based chatbot that:
- Issues live search queries
- Aggregates results from real web documents
- Generates fluent answers with clickable citations
Perplexity.ai demonstrates the practical use of RAG in open-domain QA. It incorporates real-time retrieval with fluent generation, offering citeable, source-aware answers in an interactive system. This setup illustrates how RAG can be deployed for scalable, user-facing knowledge access with human-readable and traceable output.
WebGLM: Efficient Web-Enhanced Question Answering
Overview and Objectives
WebGLM is a web-enhanced question-answering system designed to solve one of the biggest limitations of large language models (LLMs) which is the lack of up-to-date or rare external knowledge. Traditional “closed-book” models like GPT-3 that rely solely on pre-trained parameters, but WebGLM integrates real-time web search to generate accurate, long-form, and well-cited answers.
The system is built on the General Language Model (GLM), specifically a 10-billion-parameter version (GLM-10B). It improves the base model by adding three key features:
- A retriever that collects relevant web content,
- A generator that synthesizes answers according to those references,
- A human preference-aware scorer that ranks answers according to what users prefer.
This design allows WebGLM to achieve accuracy, efficiency, and cost-effectiveness advantages over similar systems like WebGPT. Specifically, it performs better than WebGPT (13B) and nearly matches WebGPT (175B) in human evaluation, all while using far fewer resources. WebGPT, rely heavily on costly expert annotations and slow browser simulations but WebGLM is optimized for efficiency and cost-effectiveness, and minimizes the need for manual annotation. It introduces practical strategies that allow for rapid response times, with more than 90% of queries processed in under 10 seconds. Another key aspect of WebGLM is its focus on human-aligned answer generation. Instead of expert ranking, the system learns from real user feedback—for example, upvotes on QA forums like Reddit, to guide what a good answer is.
To better understand, look at Figure 1. It illustrates a typical output from WebGLM: a user asks “Why do people try to maintain eye contact while communicating?” and receives a well-organized, properly cited answer generated in real-time based on live web results.
To summarize, the key objectives of WebGLM are:
- To augment LLMs with real-world information via the web.
- To minimize the use of expensive human annotation.
- To produce long-form, citation-rich answers that are aligned with human preferences.
And to do so efficiently, so that the system is practical for real-world use.
WebGPT
WebGPT is a question-answering model developed by OpenAI, extending GPT-3 to browse the web for answering open-ended queries. Introduced in 2021, it simulates human research by submitting search queries, following links, and citing sources, enhancing factual accuracy over static language models.
Methodology
WebGPT operates in a text-based web-browsing environment, using the Microsoft Bing Web Search API for document retrieval. It was fine-tuned via imitation learning, mimicking human research behavior, followed by reinforcement learning with human feedback to optimize answer quality. A key component is dense passage retrieval (DPR), where the probability of a passage given a query is modeled as:
- [math]\displaystyle{ p(\text{passage} \mid \text{query}) \propto \exp(\text{embed}(\text{passage}) \cdot \text{embed}(\text{query})) }[/math]
This contrastive objective maximizes similarity for relevant passage-query pairs. The model, scaled up to 175 billion parameters, uses best-of-64 sampling for high-quality outputs.
Results
WebGPT was evaluated on the ELI5 dataset, showing strong performance in long-form question-answering. The table below summarizes key metrics.
| Metric | Value | Notes |
|---|---|---|
| Human Preference vs. Demonstrations | 56% | Preferred over human research demos |
| Human Preference vs. Reddit Answers | 69% | Outperformed highest-voted ELI5 answers |
| TruthfulQA Improvement | Higher | Better than GPT-3, especially at 175B |
| Reward Model Score Gain | +0.13 | From doubling demonstration data |
| Reward Model Accuracy Gain | +1.8% | From doubling comparison data |
These results highlight WebGPT’s ability to generate accurate, verifiable answers, with larger models excelling in truthfulness and user preference.
Limitations
WebGPT, despite its advancements in web-assisted question-answering, faced several constraints that highlighted the need for improved models like WebGLM.
- Dependence on Human Feedback: The model’s reliance on human demonstrations and feedback for fine-tuning made training resource-intensive. Scaling to diverse query types was limited by the availability of high-quality human annotations, often requiring thousands of comparisons to achieve modest gains (e.g., 1.8% accuracy boost from doubled comparisons).
- Web Retrieval Inefficiencies: Using the Bing Web Search API restricted WebGPT to predefined search results, sometimes missing niche or real-time information. The dense passage retrieval approach struggled with ambiguous queries, leading to irrelevant citations or incomplete answers.
- Factual Inconsistencies: WebGPT occasionally produced inaccurate responses, especially for affirming questions, where it was less likely to refute incorrect assumptions. This was evident in evaluations showing higher error rates on certain query stances.
- Scalability Challenges: The 175B parameter model demanded significant computational resources, with best-of-64 sampling increasing inference time. Smaller models (e.g., 760M) underperformed, limiting deployment in resource-constrained settings.
- Limited Multimodal Integration: WebGPT was confined to text-based web browsing, unable to process images or other media, which restricted its ability to handle queries requiring visual context (e.g., "describe a painting").
Essential Background & Inspiration
The construction of web-enhanced QA systems is a systematic project that requires cross-domain collaboration. To understand the contribution of WebGLM, we need to first look at them so here we briefly introduce them.
1) Large Language Models (LLMs)
Modern LLMs like GPT-3, PaLM, OPT, and GLM-130B are trained on massive corpora in a self-supervised way. They have shown good performance in various tasks, from translation to summarization and question answering. A critical ability of LLMs is in-context learning, where the model is guided by examples within the prompt, instead of retraining. This allows them to transfer skills across tasks with no fine-tuning. WebGLM extensively uses ICL in its generator and data bootstrapping phases.
2) Open-Domain Question Answering (Open QA)
Traditional datasets like SQuAD assumes a fixed context, but open-domain QA works with real-world questions where relevant context must be retrieved dynamically. Classic datasets include:
- Natural Questions: from Google search, answered using Wikipedia.
- WebQuestions: from Freebase.
- MS MARCO: QA over passages with binary labels.
Most of the models in this field focus on short answers, but users often expect long-form explanations with references and this need is something WebGLM try to address.
3) Retrieval-Augmented Generation (RAG)
RAG systems combine a retriever and a generator. Classic retrieval models include:
- Sparse methods: TF-IDF, BM25.
- Dense methods: DPR, Contriever.
WebGLM is inspired by systems like REALM, RAG, FiD, and Atlas, which jointly train retrieval and generation. However, WebGLM’s key innovation is its use of LLMs to augment a small dense retriever without retraining the LLM at runtime—making it fast and efficient.
4) Reinforcement Learning from Human Feedback (RLHF)
Systems like WebGPT and InstructGPT use RLHF to align models with human values. But RLHF is expensive, because it requires:
- Expert-written answers,
- Pairwise ranking by humans,
- Iterative fine-tuning with policy gradients.
WebGLM sidesteps this by training a scorer on crowdsourced human signals, specifically, Reddit thumbs-ups—offering a scalable and effective alternative.
System Overview and Architecture
Ok, we got familiar with the background, let’s now look at the overall structure of WebGLM. Constructing an LLM-based web-enhanced QA system can be expensive and challenging. The web information is rich but noisy for certain queries, and creating high-quality human answers with references for training can be outrageously expensive.
To address these challenges, WebGLM suggests a practical, modular solution which has three tightly connected components: the Retriever, the Generator, and the Scorer. Each plays a critical role in ensuring that the system is accurate, efficient, cost-effective, and aligned with human expectations. Figure 2 shows these modules togehter.
Retriever Module: From Web Search to Clean Context
The first component in the WebGLM is the Retriever. This module recognizes relevant informations from the web for any givn question. This process has two stages:
(a) Coarse-Grained Web Search
In the first stage, WebGLM sends the user’s query to a third-party web search engine (like the Google Search API). Then, It retrieves a list of top-ranked URLs, usually fewer than 10. Then, it follows below steps:
- Fetch: Crawls and downloads the HTML content of these URLs.
- Extract: Converts HTML into clean, plain text using html2text.
- Split: Breaks the page content in to paragraphs and they will be used as candidats for final selection.
This entire process is optimized for speed using asynchronous parallel crawling. For example, instead of loading one page at a time (which might take over 2 minutes), WebGLM loads all pages in parallel and finishing 90% of retrievals in under 10 seconds. Figure3 shows this better.
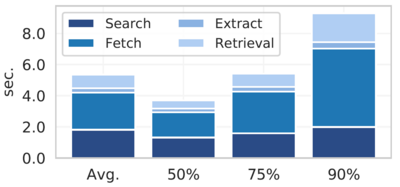
(b) Fine-Grained LLM-Augmented Retrieval
Now, at this stage, WebGLM has collected a big set of candidat paragraphs from various web pages. But, all of them are not useful or directly relevant to the question. So we need to refine the pool. For doing so, WebGLM uses a dense retriever called Contriever, which is designed to encode both questions and passages into dense vector embeddings and rank them based on similarity. Traditional sparse retrieval methods like BM25, rely on keyword overlap, but Contriever can identify semantically related text, even when the exact words don’t match.
But, Contriever in its vanilla form still has limitations and it doesn’t always prioritize the most contextually appropriate references. To improve this, WebGLM incorporates a trick: it fine-tunes Contriever using reference adoption patterns learned from GPT-3 through in-context learning. This process uses GPT-3’s natural ability to cite relevant information when answering questions, using it as a proxy teacher.
This approach is very effective. In a benchmark of 200 sampled queries, the original Contriever was able to select relevant references with 68.6% accuracy, while GPT-3 using ICL achieved a much higher 90.2% accuracy. By training Contriever to imitate GPT-3’s citation behavior, which evaluated using ROUGE-1 precision scores, WebGLM successfully transfers high-quality reference selection abilities to a smaller, more efficient retriever that can operate at scale and speed. See Table 1 for these reference adoption results
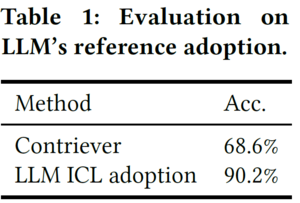
This LLM-augmented retriever becomes a critical component of WebGLM, enabling precise, low-latency filtering of noisy web content and ensuring that the Generator receives only the most relevant and trustworthy paragraphs to base its answers on.
Generator Module: Long-Form Answers with References
When the top-5 reference paragraphs have been retrieved and filtered, then WebGLM uses its 10-billion-parameter language model, GLM-10B, to generate long-form answers. These answers are not only fluent and informative but also include inline ctations. this is similar to how academic writing references source material. This is important in real-world applications to ensuring factual accuracy and trustworthiness.
One of the novel aspects of WebGLM is that it avoids relying on expensive, expert-annotated training data. Instead, it bootstraps its training set using in-context learning with GPT-3. In this process, WebGLM feeds GPT-3 a prompt that includes a user question and a small set of retrieved references. GPT-3 then generates a full, long-form answer that includes direct quotations with reference markers. This bootstrapping process is used in a large corpus of questions, specifically, 83,000 entries sampled from the ELI5 dataset, to generate a diverse and extensive set of question-answer-reference triplets.
However, because GPT-3 occasionally produces citation errors, such as quoting the wrong reference or hallucinating sources, WebGLM implements a citation correction step to improve data reliability. Each generated answer is broken into segments, and the system verifies whether the cited sources are appropriate for the content. This is done by using a ROUGE-1 precision similarity function to compare each answer segment [math]\displaystyle{ s_i }[/math] against all retrieved references [math]\displaystyle{ r }[/math]. If a reference has a sufficiently high similarity score with a sentence, it is going to be considered a valid citation. Formally, this is expressed as:
[math]\displaystyle{ \mathcal{V}_i = \left\{ r \mid f(s_i, r) \ge T \right\}, \quad r \in \mathcal{R} }[/math]
Here, [math]\displaystyle{ f(s_i, r) }[/math] is the ROUGE-1 precision scor between the segment and the refferenc, [math]\displaystyle{ T }[/math] is an empirical threshold set to [math]\displaystyle{ 0.57 }[/math], and [math]\displaystyle{ \mathcal{V}_i }[/math] is the set of valid references for sentence [math]\displaystyle{ s_i }[/math]. This method ensures that only accurate and semantically aligned references are retained during training.
According to citation correction, WebGLM uses additional filtering to ensure dataset quality. It removes samples that contain hallucinated content not grounded in any references, answers with too few citations, or answers with invalid citation formatting. After this filtering step, the original 83,000 bootstrapped examples are narrowed down to 45,000 high-quality question-answer-reference triplets. This refined dataset is then used to fine-tune the GLM-10B model. this forms the backbone of WebGLM’s answer generation module.
This generator design enables WebGLM to deliver long-form, referenced answers with high factual accuracy, without the labor-intensive cost of expert supervision.
Scorer Module: Learning Human Preferences Without RLHF
WebGPT uses reinforcement learning from expert feedback (RLHF), but WebGLM trains its answer selector using crowdsourced feedback. Specifically the number of upvotes on QA foroms like Reddit. The idea is simple: if many users preferred a particular answer, it likely reflects human-aligned quality.
To collect this data, WebGLM crawls Reddit QA threads and filters the examples to ensure high signal quality. Only answers with at least [math]\displaystyle{ 3 }[/math] upvotes are saved and retained, and each qualifying question must have a minimume of [math]\displaystyle{ 8 }[/math] candidat answers. To reduce length-related biases, long responses are Shortened, and extremely short answers are ignored. From this filtered pool, the authors construct pairwise comparison data by selecting pairs of answers with large ranking gaps, e.g., a top-ranked answer versus a much lower one. This results in a dataset of approximately [math]\displaystyle{ 249{,}000 }[/math] contrastive answer pairs, of which [math]\displaystyle{ 230{,}000 }[/math] are used for training and [math]\displaystyle{ 19{,}000 }[/math] for evaluation.
The scoring model itself is a 6-billion-parameter GLM trained to predict a scalar value for each candidate answer. Training begins with supervised fine-tuning using Reddit TL;DR data, after that the model is optimized via a pairwise ranking loss to ensure that better answers consistently receive higher scores than their lower-quality counterparts. To prevent overfitting, the authors freeze the bottom 70% of transformer layers and apply regularization strategies during training.
The output of this scorer is used to select the highest-quality answer from a set of candidates generated by the GLM-10B model. According to their results, the model’s scores correlate strongly with real user preferences, and this shows that WebGLM can effectively approximate RLHF using only implicit human signals, without the need for expensive manual annotations.
Retriever Module:
- Coarse-Grained Web Search: Uses standard web search APIs to retrieve candidate URLs, fetches corresponding web pages, and extracts textual content rapidly.
- Fine-Grained LLM-Augmented Retrieval: Enhances a dense retriever (like Contriever) via in-context learning, enabling the model to adopt only relevant references, thus improving accuracy and efficiency.
Generator Module:
The answer generator is based on the GLM-10B model and is fine-tuned on a bootstrapped dataset of long-form, quoted QA samples.
- Bootstrapped Data Generation: Employs few-shot in-context learning with a small set of high-quality examples to automatically generate a large dataset of long-form, quoted QA pairs.
- Citation Correction: Applies correction techniques based on similarity metrics (e.g., Rouge‑1) to ensure that each quoted segment accurately corresponds to its web reference.
- Efficient Answer Synthesis: This setup enables the generator to produce coherent, well-referenced answers without relying on expensive expert annotations.
Data Bootstrapping and Preference Scoring:
- Automated Data Bootstrapping: WebGLM leverages the in-context learning ability of large language models (e.g., GPT-3) to automatically generate a large pool of QA pairs. The resulting dataset, which initially contains many noisy samples, is then filtered-using automatic metrics and citation checks-to extract a high-quality subset for training.
- Human Preference-Aware Scoring: Instead of relying solely on expert feedback, the system trains a scorer using real user feedback (such as upvotes from online QA forums). This scorer is designed to evaluate multiple aspects of generated answers (fluency, correctness, citation accuracy, etc.) and rank them so that the final output aligns with human quality preferences.
Limitations and Future Directions
Despite its promising performance, WebGLM faces several challenges that open avenues for future work. First, the system’s reliance on web retrieval can introduce variability in response time and quality; network delays and inconsistent web content may sometimes lead to outdated or imprecise answers. In addition, although the bootstrapped generator benefits from LLM in-context learning, the process of citation correction and filtering is not foolproof—incorrect or missing citations may still occur, affecting the factual grounding of generated answers. Moreover, the human preference-aware scorer, trained on online forum feedback, might not always reflect broader user expectations due to inherent biases in the source data. Future work may focus on improving retrieval efficiency through more robust asynchronous techniques, enhancing dataset quality by incorporating richer multi-turn or multi-reference contexts, and refining the scoring mechanism with more diverse and calibrated human feedback. These enhancements could further bridge the gap between rapid web retrieval and high-quality, factually accurate answer generation.
Interleaving Retrieval with Chain-of-Thought Reasoning
Introduction & Motivation
Large language models excel at many tasks but still struggle with complex, multi‑step questions that require up‑to‑date or aggregated information. Traditional chain‑of‑thought (CoT) prompting helps by breaking reasoning into steps, and retrieval augmentation brings in external documents, but neither alone reliably handles queries needing facts from multiple sources. To address this, the authors propose IRCoT (Interleaved Retrieval with Chain‑of‑Thought), which alternates between generating a CoT step and using that step as a new retrieval query—iterating until an answer emerges. This tight feedback loop lets the model iteratively refine its understanding and gather the most relevant evidence, improving retrieval recall by up to 22 points and downstream QA F1 by up to 15 points over one‑shot retrieval on multi‑step benchmarks (HotPotQA, 2WikiMultihopQA, MuSiQue, IIRC). It works out‑of‑the‑box with both GPT‑3 and much smaller Flan‑T5 models (no fine‑tuning required) and cuts factual errors in generated CoTs by up to 50 %, yielding more accurate, reliable answers for open‑domain, multi‑hop question answering.
Background: Standard Retrieval vs. Interleaving
A straightforward way to augment an LLM with outside knowledge is to do the following:
1. Retrieve a set of documents based on the user’s question (one-step retrieval).
2. Concatenate those documents with the original question.
3. Prompt the large language model to answer, possibly with chain-of-thought.
While this approach works well for simple or straightforward questions, it has problems with more complex, multi-step queries. Why? Because the system doesn’t know ahead of time which facts or key terms will come up during the model’s partial reasoning. If the first round of retrieval misses an important piece of text, there’s no opportunity to fix that mistake later.
In contrast, IRCoT goes back and forth between finding new documents and building the chain-of-thought. The chain-of-thought is actually used as a new search query. For example, if it says “this item was created by a company named X,” the retriever then looks for more information about “company X.” This method is more flexible, similar to how a person might research a question by reading some information, noticing new keywords, and then doing another focused search.
The IRCoT Approach
Overall Method
The IRCoT pipeline works in several steps:
1. Initial Retrieval Step: The process starts with the user’s question [math]\displaystyle{ Q }[/math]. A standard search engine (like BM25) or another retrieval method is used to fetch an initial set of documents. Let’s call these documents: [math]\displaystyle{ D_1, D_2, \ldots, D_k }[/math]
2. Reason Step: The language model is given:
- The question [math]\displaystyle{ Q }[/math]
- The chain-of-thought generated so far (initially empty)
- The documents retrieved so far
Using this information, the model is asked to generate one more sentence of reasoning. This new sentence is denoted as: [math]\displaystyle{ s_i }[/math]
3. New Retrieval Step: The model treats the newly generated sentence [math]\displaystyle{ s_i }[/math] (sometimes combined with the original question [math]\displaystyle{ Q }[/math]) as a new search query. The retrieval system then fetches up to [math]\displaystyle{ k }[/math] new documents that match this sentence. These new documents are added to the existing set of retrieved documents.
4. Iteration and Stopping: Steps 2 and 3 are repeated: the model keeps extending the chain-of-thought, and new documents keep getting added. This loop continues until one of the following conditions is met:
- The model produces a sentence like “The answer is …,” indicating it has reached a final answer, or
- A maximum number of steps (e.g., 8 rounds) is reached.
After the loop finishes, the complete set of retrieved documents is passed to a question-answering module. This final module, either using chain-of-thought or a direct answer prompt, reads all the information and produces a concise answer.
Prompt Design
IRCoT uses few-shot learning with example prompts. Each example includes:
- A short question (e.g., “In what country was Lost Gravity manufactured?”)
- A small set of related paragraphs (including correct ones and possibly some irrelevant ones)
- A detailed chain-of-thought that explains how to reason through those paragraphs step by step
These examples teach the language model both how to reason using specific parts of the text and when to retrieve new documents based on partial reasoning.
Formal Structure (Like Pseudocode)
We can describe IRCoT’s loop in a more structured format:
Initialization:
[math]\displaystyle{ C \leftarrow \{ \}; \quad R \leftarrow \text{Retrieve}(Q) }[/math]
- [math]\displaystyle{ C }[/math] is the chain-of-thought built so far
- [math]\displaystyle{ R }[/math] is the current set of retrieved documents
At each step [math]\displaystyle{ i }[/math]:
Reason:
[math]\displaystyle{ s_i = \text{LM}(Q, R, C) }[/math]
The language model (LM) takes in the question [math]\displaystyle{ Q }[/math], the documents [math]\displaystyle{ R }[/math], and the current chain-of-thought [math]\displaystyle{ C }[/math], and generates a new sentence [math]\displaystyle{ s_i }[/math]. Add this sentence to the chain-of-thought:
[math]\displaystyle{ C \leftarrow C \cup \{ s_i \} }[/math]
Retrieve:
[math]\displaystyle{ R \leftarrow R \cup \text{Retrieve}(s_i) }[/math]
In other words, the new sentence [math]\displaystyle{ s_i }[/math] is used as a search query, and the resulting documents are added to [math]\displaystyle{ R }[/math].
Stopping Condition: Stop if the new sentence includes a phrase like “the answer is…” or if the maximum number of steps is reached.
This loop shows how IRCoT builds up reasoning step-by-step, using each new piece of information to improve both the search results and the next part of the reasoning chain.
Experimental Setup
Datasets
The paper evaluates IRCoT using four well-known multi-step question answering datasets:
- HotpotQA: A dataset focused on multi-hop reasoning, where each question usually requires combining information from two separate Wikipedia articles.
- 2WikiMultihopQA: Similar to HotpotQA, but specifically designed to ensure that answering each question involves connecting two related Wikipedia pages.
- MuSiQue: A newer dataset built to require multiple reasoning steps. In some cases, more than two pieces of evidence must be linked together to answer the question.
- IIRC: Each question is based on a main passage, but answering it requires looking at other linked Wikipedia pages to find the needed information.
For all of these datasets, the paper uses an open-domain setting. This means the model is not given just the correct paragraphs, instead, it must search for the relevant information from a large collection of Wikipedia articles.
Compared Methods
The paper compares IRCoT with two baseline methods:
- NoR QA: A simple baseline that does no retrieval at all. It relies only on the language model’s built-in knowledge (its parametric memory).
- OneR QA: A method that performs one retrieval step using the question. It then passes both the question and the retrieved documents to the language model for answering.
- IRCoT QA: The method proposed in the paper. It uses iterative retrieval, adding new information after each reasoning step in the chain-of-thought.
The results are measured using:
1. Document recall: How many of the relevant documents were successfully retrieved by the end.
2. Answer accuracy or F1 score: How well the model answered the questions.
The experiments show that IRCoT significantly improves performance on multi-step questions compared to both baselines.
Why It Matters
The significance of interleaving retrieval with chain-of-thought reasoning lies in its capacity to improve multi-step question answering by iteratively refining reasoning and evidence gathering. By enabling the retrieval of more contextually relevant information at each step, the approach enhances retrieval recall and factual accuracy, thereby reducing model hallucination and yielding more reliable, evidence-based reasoning. This advancement addresses the inherent limitations of traditional one-shot retrieval methods and offers a scalable, adaptable solution for complex, knowledge-intensive tasks—an achievement with important implications for applications in research, decision support, and any domain that demands precise, contextual understanding.
Key Findings
- Better Retrieval: IRCoT finds the right supporting documents more reliably than one-shot methods, with 10–20% higher recall of gold paragraphs.
- Improved QA Accuracy: It outperforms both baselines on standard metrics (Exact Match and F1), often by 5–10+ points. For example, in HotpotQA, it can follow multiple steps (e.g., finding a roller coaster’s manufacturer, then their country) to get the right answer.
- Fewer Mistakes: IRCoT reduces false or made-up facts (hallucinations) by grounding each reasoning step in real documents, cutting factual errors by up to 40–50%.
- Works Across Model Sizes: Even smaller models using IRCoT can beat much larger models that use basic retrieval. It also performs well on new datasets without custom examples, showing strong generalization.
Limitations and Future Directions
The proposed IRCoT framework demonstrates notable improvements over one-step retrieval methods on multi-step open-domain question answering; however, several limitations persist. The method relies on the base language model possessing effective zero-shot or few-shot chain-of-thought generation capability—a strength largely confined to very large models—which restricts its applicability to smaller-scale models. In addition, the approach requires the language model to handle long input sequences in order to integrate multiple retrieved paragraphs and demonstration examples. The iterative process, with separate language model calls for each reasoning step, incurs additional computational cost, potentially impacting efficiency in real-world deployments. Future research should consider strategies for dynamic decision-making regarding when to retrieve additional information, methods for compressing or efficiently ranking retrieved content, and techniques that enhance chain-of-thought robustness in out-of-distribution settings.
Iterative Retrieval-Generation Synergy (Iter-RetGen)
Iterative Retrieval‑Generation Synergy (ITER‑RETGEN) introduces a simple yet powerful loop between retrieval and generation that yields substantial quality gains with minimal overhead. It first retrieves documents based on the original query, prompts an LLM to generate an initial answer, and then concatenates that answer with the query to guide a second, more focused retrieval—using the newly fetched documents to produce a refined response. Unlike prior methods that interleave retrieval within a single generation pass, ITER‑RETGEN processes all retrieved context at once, preserving flexibility in the generation stage while still benefiting from multi‑step knowledge gathering. Evaluated on multi‑hop QA benchmarks (HotPotQA, 2WikiMultiHopQA, MuSiQue, Bamboogle), fact verification (Feverous), and commonsense reasoning (StrategyQA), it achieves up to an 8.6 % absolute improvement over state‑of‑the‑art retrieval‑augmented baselines under few‑shot chain‑of‑thought prompting. Furthermore, by distilling generation‑informed relevance judgments from a re‑ranker into a dense retriever, the method further boosts performance while reducing the number of retrieval‑generation iterations required.
Motivation
Retrieval-augmented generation (RAG) methods aim to mitigate the limitations of large language models (LLMs)—such as outdated knowledge and hallucinations—by incorporating external information from retrieved documents. However, most existing techniques rely on one-time retrieval based solely on the initial input query. This often falls short for complex tasks like multi-hop question answering, where queries require holistic reasoning across multiple knowledge pieces.
Additionally, interleaved methods like ReAct and Self-Ask tightly bind retrieval with generation during each output step, requiring multiple retrieval calls (3–5 per query) and constraining generation flexibility. These approaches incrementally process retrieved content and are not designed to collectively utilize all retrieved information in the generation phase.
To overcome these limitations, the authors propose Iter-RetGen, a simple yet effective framework that decouples retrieval and generation structurally while maintaining synergy between them. It leverages intermediate generations as feedback signals to refine subsequent retrievals, resulting in iterative improvements in both relevance and answer quality.
Method
Iter-RetGen operates through a synergistic loop of retrieval and generation, following these steps:
- In the initial iteration, knowledge is retrieved based on the task input (e.g., a question).
- An LLM generates a response using this retrieved knowledge.
- The generated output is then used as additional context for the next retrieval round, guiding the retriever toward more relevant or missing knowledge.
- The newly retrieved knowledge is again used to generate a refined response.
- This process is repeated for a fixed number of iterations (e.g., T = 2–4).
This structure enables holistic knowledge integration in each generation step, unlike interleaved approaches that only use partial retrievals at each stage. Iter-RetGen also maintains generation flexibility by avoiding structural constraints on prompt formatting or fixed retrieval patterns.
Generation-Augmented Retrieval Adaptation
To further improve retrieval quality, Iter-RetGen incorporates a method called generation-augmented retrieval adaptation. This uses the generation outputs to inform a re-ranker, which then distills its knowledge into a dense retriever.
- Dense Retriever Parameters: [math]\displaystyle{ \theta = \{\theta_q, \theta_d\} }[/math]
- Similarity Score: [math]\displaystyle{ s_\theta(q,d)=\left\langle E(q;\theta_q),E(d;\theta_d)\right\rangle }[/math]
- Re-ranker Score: [math]\displaystyle{ s_\phi(q,d) }[/math]
- Knowledge Distillation Objective:
[math]\displaystyle{ \theta_q^*=arg\min_{\theta_q}\mathrm{~KL}(P_\phi(\cdot|y_1,q),P_\theta(\cdot|q)) }[/math] where [math]\displaystyle{ P_\phi(d|y_1,q)=\frac{\exp(s_\phi(y_1||q,d)/\tau)}{\sum_{d^{\prime}\in\mathcal{D}_{y_1}||q}\exp(s_\phi(y_1||q,d^{\prime})/\tau)} }[/math] and [math]\displaystyle{ P_\theta(d|q)=\frac{\exp(s_\theta(q,d)/\tau)}{\sum_{d^{\prime}\in\mathcal{D}_{y_1}||q}\exp(s_\theta(q,d^{\prime})/\tau)} }[/math]
This distillation process aligns the retriever's output distribution with that of the re-ranker, significantly boosting retrieval relevance and performance with fewer iterations.
Simplicity and Efficiency
Iter-RetGen is conceptually simple, requiring minimal architectural changes or complex prompt engineering. It efficiently balances performance and cost by reducing the number of API calls and total retrieved documents. For example, with just two iterations and five paragraphs retrieved per iteration, Iter-RetGen can outperform other retrieval-augmented methods that require more resources.
Experiments and Results
The authors evaluated Iter-RetGen across six datasets involving multi-hop QA, fact verification, and commonsense reasoning. The method consistently outperformed strong baselines such as Direct Prompting, Chain-of-Thought (CoT), ReAct, Self-Ask, and DSP. Using text-davinci-003 as the LLM and Contriever-MSMARCO for retrieval, Iter-RetGen achieved:
- Up to 8.6% higher accuracy on HotPotQA compared to Self-Ask.
- 73.4% accuracy in just four iterations.
- Up to 75.7% accuracy with generation-augmented retriever adaptation.
Notably, Iter-RetGen required fewer retrieval steps and API calls, demonstrating superior cost-efficiency. Traditional metrics like Exact Match (EM) often underestimated its true performance, but human-aligned accuracy (Acc†) revealed its ability to produce semantically correct answers despite surface form differences.
Ablation studies showed that generation-augmented retrieval is critical, increasing answer recall by 16–25% in later iterations. Case studies highlighted the model's self-correction ability, such as fixing an error about arena seating capacity after retrieving better contextual information.
Limitations and Future Directions
While Iter-RetGen achieves strong performance, it relies heavily on the chain-of-thought capabilities of large LLMs, limiting its applicability to smaller or less capable models. The iterative approach also incurs overhead due to multiple retrieval and generation steps, though it is still more efficient than some interleaved methods.
Future work includes:
- Adaptive iteration strategies to dynamically determine the optimal number of retrieval-generation steps.
- Enhancing prompt-specific optimization for better use of parametric and non-parametric knowledge.
- Expanding evaluations to long-form generation and other complex reasoning tasks.
Overall, Iter-RetGen sets a new standard for iterative retrieval-augmented generation by achieving both efficiency and effectiveness in complex information-seeking tasks.
Graph-RAG for Document Set Summarization
The paper introduces GraphRAG, a novel approach that uses graph-based retrieval-augmented generation to answer broad, global questions about large text collections. It proposes a graph-based extension to RAG that enables global context modeling across documents, improving performance on query-specific summarization tasks.
Introduction and Motivation
While retrieval-augmented generation (RAG) is effective for answering fact-based or localized questions, it struggles with global questions—broad, sensemaking questions that require synthesizing themes or trends across an entire corpus. Examples include:
- “What are the key trends in health policy over the last decade?”
- “How do tech leaders perceive government regulation in podcasts?”
Such questions require a level of holistic understanding that vector-based RAG systems (which retrieve semantically similar chunks) cannot provide. These systems work well for narrow queries but break down when the answer isn’t confined to a few passages.
GraphRAG addresses this limitation by constructing a knowledge graph from the corpus and using it to support hierarchical summarization. This transforms the task into one that is less about retrieving matching passages and more about building a structured understanding of content relationships.
Methodology
The graph above shows the architectural overview of GraphRAG and can be broken down into the following procedure:
Source Documents → Text Chunks
Documents are split into manageable text chunks. The chunk size is a trade-off: larger chunks reduce the number of LLM calls but may miss finer-grained details.
Text Chunks → Entities & Relationships
From each chunk, the LLM extracts key entities and their relationships. These are then converted into node and edge candidates for a knowledge graph.
Entities & Relationships → Knowledge Graph
Multiple extractions across the corpus are merged into a weighted knowledge graph. Edge weights correspond to how frequently a relationship appears. Claims—statements of verifiable facts—are also extracted.
Knowledge Graph → Graph Communities
Using the Leiden community detection algorithm, the graph is partitioned into coherent thematic communities in a hierarchical structure.
Graph Communities → Community Summaries
Each community is summarized independently using the LLM, and summaries at higher levels recursively incorporate lower-level summaries. These summaries act as a condensed representation of the source corpus.
Community Summaries → Community Answers → Global Answer
When a question is asked, each community provides a partial answer. These are scored by helpfulness, then aggregated using a map-reduce approach to generate the final global answer.
Evaluation Process
To evaluate GraphRAG, the authors developed a novel benchmark for global sensemaking questions by:
- Generating user personas (e.g., journalist, educator).
- Defining realistic tasks for each persona.
- Asking the LLM to generate global questions for each (e.g., “How is public health discussed in news?”).
Then, answers from GraphRAG and baseline methods were compared using the LLM-as-a-judge technique based on three criteria:
- Comprehensiveness – How well does the answer cover all facets of the query?
- Diversity – Does the answer provide multiple perspectives or angles?
- Empowerment – Does the answer help the user form a judgment or understanding?
These criteria aim to capture the richness and utility of answers in real-world analytical contexts.
Results
Experiments were conducted on two large-scale datasets—podcast transcripts and news articles (each ~1M tokens). GraphRAG was evaluated at multiple community levels (C0–C3), and against:
- A baseline vector RAG using semantic search (SS).
- A graph-free map-reduce summarization method using raw source texts (TS).
Key findings include:
- Superior Comprehensiveness & Diversity: GraphRAG outperformed vector RAG across all global sensemaking criteria, with win rates between 72–83% in comprehensiveness and 62–82% in diversity.
- Empowerment: GraphRAG also generally helped users better understand and make judgments about the data, although results here were more mixed compared to other metrics.
- Token Efficiency vs Quality Trade-off:
- Structured semantic global search (GraphRAG) is more expensive in terms of total LLM calls at inference than standard vector RAG.
- However, it offers a trade-off: root-level community summaries (C0) provide strong performance (e.g., 72% comprehensiveness win rate) at a fraction of the token cost—sometimes requiring over 90% fewer tokens than full source summarization.
- Claim-Based Validation: A claim extraction method (Claimify) confirmed that GraphRAG answers contain more factual claims and more diverse clusters of ideas than vector RAG.
Conclusion
GraphRAG significantly extends the reach of RAG systems to encompass broad, sensemaking queries. By constructing and leveraging a hierarchical knowledge graph, it enables query-focused summarization across large corpora. While more computationally intensive than vector RAG, its performance benefits and structured summarization make it a compelling tool for global understanding tasks.
Mathematical Formulation of RAG Systems
Retrieval-Augmented Generation (RAG) can strictly be formulated as a conditioned probabilistic text generation over both the input query and externally retrieved documents. With query [math]\displaystyle{ q }[/math] and corpus [math]\displaystyle{ \mathcal{C} }[/math], the model outputs a subset of documents [math]\displaystyle{ D_q \subset \mathcal{C} }[/math] and produces an answer [math]\displaystyle{ a }[/math] by maximizing the conditional probability:
- [math]\displaystyle{ P(a \mid q) = \sum_{d \in D_q} P(a \mid q, d) \cdot P(d \mid q) }[/math]
In this, [math]\displaystyle{ P(d \mid q) }[/math] refers to the retriever's confidence in the relevance of document [math]\displaystyle{ d }[/math] to query [math]\displaystyle{ q }[/math], and [math]\displaystyle{ P(a \mid q, d) }[/math] refers to the probability of the generator generating answer [math]\displaystyle{ a }[/math] based on query [math]\displaystyle{ q }[/math] and evidence [math]\displaystyle{ d }[/math]. This framework makes generation dependent on what is retrieved in order to reduce hallucinations and increase factuality.
The retriever uses dense vector similarity. Query [math]\displaystyle{ q }[/math] and document [math]\displaystyle{ d }[/math] are both represented via learned encoders [math]\displaystyle{ E_q(\cdot) }[/math] and [math]\displaystyle{ E_d(\cdot) }[/math]. The similarity score between them is denoted as the inner product:
- [math]\displaystyle{ s(q, d) = \langle E_q(q), E_d(d) \rangle }[/math]
The top-k documents are selected by ranking documents in [math]\displaystyle{ \mathcal{C} }[/math] based on [math]\displaystyle{ s(q, d) }[/math]. These scores are then converted into probabilities with a softmax:
- [math]\displaystyle{ P(d \mid q) = \frac{\exp(s(q, d)/\tau)}{\sum_{d' \in \mathcal{C}} \exp(s(q, d')/\tau)} }[/math]
where [math]\displaystyle{ \tau }[/math] is a temperature parameter controlling sharpness.
For generation, given the retrieved set [math]\displaystyle{ D_q = \{d_1, \dots, d_k\} }[/math], the generator produces a response token-by-token. Assuming an autoregressive model, the generation probability is:
- [math]\displaystyle{ P(a \mid q, D_q) = \prod_{t=1}^{T} P(a_t \mid a_{\lt t}, q, D_q) }[/math]
where [math]\displaystyle{ a_t }[/math] is the [math]\displaystyle{ t }[/math]-th token of the answer. Some architectures concatenate all [math]\displaystyle{ d_i }[/math] into one context, while others marginalize or attend to them one at a time. This modular structure allows the RAG framework to decouple retrieval from generation, and therefore becomes more interpretable, scalable, and adaptable to real-world question answering systems.
Summary and Future Directions
- RAG improves factual grounding and adaptability of LMs.
- Combining retrieval with structured reasoning (IRCoT, graphs) enhances complex task performance.
- Challenges remain in latency, retrieval quality, and hallucination control.
Future Directions in Retrieval-Augmented Generation
Beyond current advances, several promising future directions can enhance RAG's effectiveness, efficiency, and usability in real-world applications:
Adaptive and Context-Aware Retrieval: Current retrieval approaches typically rely on fixed similarity metrics (e.g., cosine similarity or BM25) to fetch relevant documents. Future systems could leverage dynamically adaptive retrieval strategies, integrating real-time context or user preferences. For example, retrieval systems could adjust weights based on user feedback or query intent, optimizing retrieval results iteratively.
Multi-modal Retrieval-Augmented Generation: While current RAG systems primarily retrieve textual knowledge, extending retrieval to multi-modal sources—such as images, audio, and video—can enrich the information context. Future work might integrate vision-language models or video indexing to facilitate richer responses, particularly in domains such as news summarization, education, and healthcare.
Improving Retrieval Efficiency: Retrieval latency remains a bottleneck for real-time applications. Techniques like retrieval index compression, hierarchical retrieval (coarse-to-fine), and approximate nearest neighbor searches optimized for LLM embedding spaces could substantially reduce response times without significantly affecting retrieval accuracy.
Enhanced Interpretability and Source Attribution:Users increasingly demand transparency regarding the sources behind generated answers. Future RAG models can develop advanced mechanisms for source attribution and interpretability, clearly delineating how retrieved evidence contributes to the generated response. Interactive interfaces allowing users to explore cited sources could enhance trust and usability.
Personalized Retrieval-Augmented Generation: Integrating user profiles or historical interaction data into the retrieval-generation loop could enable more personalized responses. For instance, healthcare applications might retrieve patient-specific medical history or preferences to tailor responses more precisely to individual contexts.
Reducing Hallucinations with Self-verification: Future RAG models could incorporate explicit verification steps within the retrieval-generation cycle. Models might internally query their own outputs for consistency checks, leveraging an iterative self-query mechanism to detect and correct potential hallucinations before providing the final output.
Scalable, Decentralized Knowledge Retrieval: Centralized retrieval systems become increasingly challenging at scale. Future research could explore decentralized or distributed retrieval mechanisms, employing blockchain or federated retrieval networks to securely and efficiently access up-to-date knowledge from diverse, globally distributed databases.
Integration with External Reasoning Modules: Combining RAG with external symbolic reasoning or logic modules could enable complex inferential reasoning tasks, going beyond simple fact retrieval. Systems could leverage knowledge graphs or reasoning engines to validate and extend reasoning within the RAG pipeline, providing more accurate and logically consistent answers.
Pursuing these directions will further position RAG as a robust and versatile approach for accurate, efficient, and reliable knowledge-grounded generation.