CRITICAL ANALYSIS OF SELF-SUPERVISION: Difference between revisions
No edit summary |
|||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 6: | Line 6: | ||
This paper evaluated the performance of the state-of-the-art self-supervised methods on learning weights of convolutional neural networks (CNNs) and on a per-layer basis. They were motivated by the fact that low-level features in the first layers of networks may not require the high-level semantic information captured by manual labels. This paper also aims to figure out whether current self-supervision techniques can learn deep features from only one image. | This paper evaluated the performance of the state-of-the-art self-supervised methods on learning weights of convolutional neural networks (CNNs) and on a per-layer basis. They were motivated by the fact that low-level features in the first layers of networks may not require the high-level semantic information captured by manual labels. This paper also aims to figure out whether current self-supervision techniques can learn deep features from only one image. | ||
The main goal of self-supervised learning is to take advantage of a vast amount of unlabeled data to train CNNs and find | The main goal of self-supervised learning is to take advantage of a vast amount of unlabeled data to train CNNs and find good generalized image representations. | ||
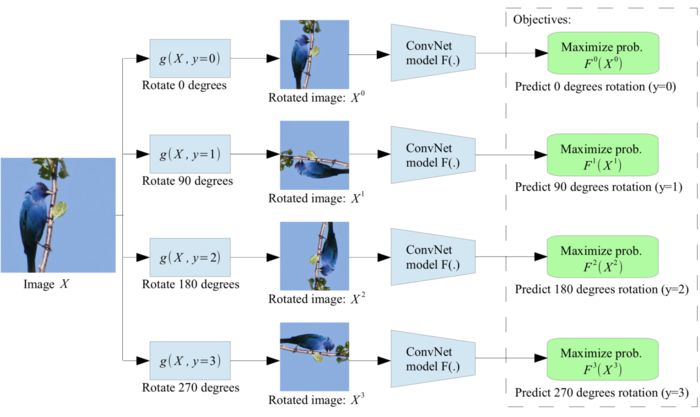
In self-supervised learning, unlabeled data generate ground truth labels | In self-supervised learning, unlabeled data is used to generate ground truth labels, such as the Jigsaw puzzle task[6], and the rotation estimation[3]. For example, in the rotation task, we have a picture of a bird without the label "bird". We rotate the bird image by 90 degrees clockwise and the CNN is trained in a way to find the rotation axis, as can be seen in the figure below. The intuition is that if a deep network can tell if a bird is upside down or not, perhaps it has learned a semantically relevant representation without the need for hand-labelling. | ||
[[File:self-sup-rotation.png|700px|center]] | [[File:self-sup-rotation.png|700px|center]] | ||
| Line 34: | Line 34: | ||
To evaluate the impact of the size of the training set, they have compared the results of a million images in the ImageNet dataset with a million augmented images generated from only one single image. Various data augmentation methods including cropping, rotation, scaling, contrast changes, and adding noise, have been used to generate the mentioned artificial dataset from one image. Augmentation can be seen as imposing a prior on how we expect the manifold of natural images to look like. When training with very few images, these priors become more important since the model cannot extract them directly from data. | To evaluate the impact of the size of the training set, they have compared the results of a million images in the ImageNet dataset with a million augmented images generated from only one single image. Various data augmentation methods including cropping, rotation, scaling, contrast changes, and adding noise, have been used to generate the mentioned artificial dataset from one image. Augmentation can be seen as imposing a prior on how we expect the manifold of natural images to look like. When training with very few images, these priors become more important since the model cannot extract them directly from data. | ||
To measure the quality of deep features on a per-layer basis, a linear classifier is trained on top of each convolutional layer of AlexNet. Linear classifier probes are commonly used to monitor the features at every layer of a CNN and are trained entirely independently of the CNN itself [5]. Note that the main purpose of CNNs is to reach a linearly discriminable representation for images. Accordingly, the linear probing technique aims to evaluate the training of each layer of a CNN and inspect how much information each of the layers learned. | To measure the quality of deep features on a per-layer basis, a linear classifier is trained on top of each convolutional layer of AlexNet. Linear classifier probes are commonly used to monitor the features at every layer of a CNN and are trained entirely independently of the CNN itself [5]. Note that the main purpose of CNNs is to reach a linearly discriminable representation for images. Accordingly, the linear probing technique aims to evaluate the training of each layer of a CNN and inspect how much information each of the layers learned. The discrimination power at each layer under self-supervision is then compared to that of a fully supervised model classically trained. | ||
The same experiment has been done using the CIFAR10/100 dataset. | The same experiment has been done using the CIFAR10/100 dataset. | ||
| Line 53: | Line 53: | ||
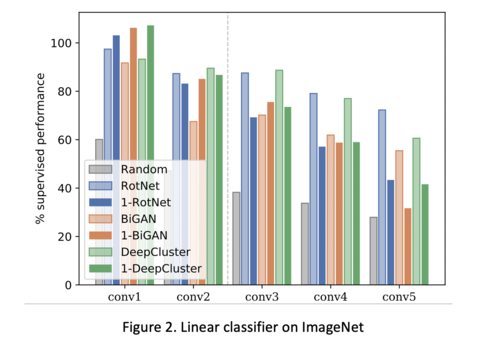
Figure 2 shows how well representations at each level are linearly separable. | Figure 2 shows how well representations at each level are linearly separable using a single image, as compared to fully supervised performance using the entire dataset. Table 1 indicates the classification accuracy of the linear classifier trained on the top of each convolutional layer. | ||
According to the results, training the CNN with self-supervision methods can match the performance of fully supervised learning in the first two convolutional layers. It must be pointed out that only one single image with massive augmentation is utilized in this experiment. | According to the results, training the CNN with self-supervision methods can match the performance of fully supervised learning in the first two convolutional layers. It must be pointed out that only one single image with massive augmentation is utilized in this experiment. | ||
[[File:histo.png|500px|center]] | [[File:histo.png|500px|center]] | ||
| Line 63: | Line 63: | ||
[[File:critical_analysis.png|500px|center]] | [[File:critical_analysis.png|500px|center]] | ||
The above table ( | The above table (Table 3) corresponds to the Accuracy of linear classifiers on different network layers on CIFAR-10 and CIFAR-100 datasets. | ||
[[File:pretrain.png|500px|center]] | |||
In table 4, the authors fine-tuned a convolution neural network with the first two filters left frozen. They achieved almost benchmark results with just a single image. This tells us that a single image is sufficient for training the first two convolutional filter banks. | |||
== Source Code == | == Source Code == | ||
| Line 71: | Line 75: | ||
== Conclusion == | == Conclusion == | ||
In this paper, the authors conducted interesting experiments to show that the first few layers of CNNs contain only limited information for analyzing natural images. They saw this by examining the weights of the early layers in cases where they only trained using only a single image with much data augmentation. Specifically, sufficient data augmentation was enough to make up for a lack of data in early CNN layers. However, this technique was not able to elicit proper learning in deeper CNN layers. In fact, even millions of images were not enough to elicit proper learning without supervision. | In this paper, the authors conducted interesting experiments to show that the first few layers of CNNs contain only limited information for analyzing natural images. They saw this by examining the weights of the early layers in cases where they only trained using only a single image with much data augmentation. Specifically, sufficient data augmentation was enough to make up for a lack of data in early CNN layers. However, this technique was not able to elicit proper learning in deeper CNN layers. In fact, even millions of images were not enough to elicit proper learning without supervision. Thus, current unsupervised learning benefits from data augmentation more than a larger dataset. The results seem to indicate that we probably do not use the full semantic capacity of a million images yet. | ||
== Critique == | == Critique == | ||
| Line 78: | Line 82: | ||
It would be interesting to consider and compare the effects of each augmentation strategy in terms of performance. Additionally, it may be worthwhile to try other augmentation techniques like Gaussian smoothing and see the impact on the learning performance. | It would be interesting to consider and compare the effects of each augmentation strategy in terms of performance. Additionally, it may be worthwhile to try other augmentation techniques like Gaussian smoothing and see the impact on the learning performance. | ||
It would be really beneficial to apply a more challenging dataset, with objects in clutter, occlusion, and wider pose variation, inter-image invariance can be more effective. | It would be really beneficial to apply a more challenging dataset, with objects in clutter, occlusion, and wider pose variation, inter-image invariance can be more effective, as it is used in this paper [10]. It will help us to understand the author's methodology if it encourages intra image invariance, unlike the objective of contrastive learning like the proposed in [10] or not. | ||
== References == | == References == | ||
| Line 101: | Line 105: | ||
[9] I. Misra and L. van der Maaten, "Self-Supervised Learning of Pretext-Invariant Representations," 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020. | [9] I. Misra and L. van der Maaten, "Self-Supervised Learning of Pretext-Invariant Representations," 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020. | ||
[10] Cheng, Z., Su, J.-C., and Maji, S., “Unsupervised Discovery of Object Landmarks via Contrastive Learning”, <i>arXiv e-prints</i>, 2020. | |||
Latest revision as of 00:08, 13 December 2020
Presented by
Maral Rasoolijaberi
Introduction
This paper evaluated the performance of the state-of-the-art self-supervised methods on learning weights of convolutional neural networks (CNNs) and on a per-layer basis. They were motivated by the fact that low-level features in the first layers of networks may not require the high-level semantic information captured by manual labels. This paper also aims to figure out whether current self-supervision techniques can learn deep features from only one image.
The main goal of self-supervised learning is to take advantage of a vast amount of unlabeled data to train CNNs and find good generalized image representations. In self-supervised learning, unlabeled data is used to generate ground truth labels, such as the Jigsaw puzzle task[6], and the rotation estimation[3]. For example, in the rotation task, we have a picture of a bird without the label "bird". We rotate the bird image by 90 degrees clockwise and the CNN is trained in a way to find the rotation axis, as can be seen in the figure below. The intuition is that if a deep network can tell if a bird is upside down or not, perhaps it has learned a semantically relevant representation without the need for hand-labelling.
Previous Work
In recent literature, several papers addressed self-supervised learning methods.
- Generative models: Generative Adversarial Networks (GANs), learn to generate images in an adversarial manner. They consist of a generator network which maps noise samples to image samples and a discriminator network whose task is to distinguish the fake images from the real ones. These two are trained together until the point where the fake images are indistinguishable. BiGAN [2], or Bidirectional GAN, is simply a generative adversarial network plus an encoder. The generator maps latent samples to generated data and the encoder performs as the opposite of the generator. After training BiGAN, the encoder has learned to generate a rich image representation.
- In RotNet method [3], images are rotated and the CNN learns to figure out the direction. Therefore, this task is a 4-way classification task. Most images are taken upright which could be considered as labeled images with label 90 degrees. The authors of RotNet argue that the concept of 'upright' is hard to understand and requires high-level knowledge about the image, so this task encourages the network to discover more complex information about the images.
- DeepCluster [4] alternates between k-means clustering step, in which pseudo-labels are assigned to the data by k-means on the PCA-reduced features, and the learning step in which the model tries to learn to fit the representation to these labels(cluster IDs) under several image transformations. These transformations include random resized crops with [math]\displaystyle{ \beta = 0.08 }[/math] and [math]\displaystyle{ \gamma = \frac{3}{4} }[/math] and horizontal flips.
- In Jigsaw task [6], the unlabelled images are divided into nine patches and then, the patches are permuted randomly to create a new image. Then, a deep neural network is trained to predict the permutation of patches in the perturbed image.
Following is the work done in the domain of learning from a single image:
- Rodriguez et al. [7] used max-margin correlation filters to learn robust tracking templates from a single sample of the patch.
- Malisiewicz et al. [8] used a semi-parametric exemplar SVM model where the model uses one positive sample and separates it from thousands of negative samples mined from the background.
Method & Experiment
In this paper, BiGAN, RotNet, and DeepCluster are employed for training AlexNet in a self-supervised manner. The author uses the ResNet-50 to compute the image and the transpose of this image. The method is evaluated by multiple datasets, and the tasks majorly focus on object detection and image classification. Jigsaw ResNet-50, introduced by Priya Goyal, was utilized as a baseline of the experiment.
To evaluate the impact of the size of the training set, they have compared the results of a million images in the ImageNet dataset with a million augmented images generated from only one single image. Various data augmentation methods including cropping, rotation, scaling, contrast changes, and adding noise, have been used to generate the mentioned artificial dataset from one image. Augmentation can be seen as imposing a prior on how we expect the manifold of natural images to look like. When training with very few images, these priors become more important since the model cannot extract them directly from data.
To measure the quality of deep features on a per-layer basis, a linear classifier is trained on top of each convolutional layer of AlexNet. Linear classifier probes are commonly used to monitor the features at every layer of a CNN and are trained entirely independently of the CNN itself [5]. Note that the main purpose of CNNs is to reach a linearly discriminable representation for images. Accordingly, the linear probing technique aims to evaluate the training of each layer of a CNN and inspect how much information each of the layers learned. The discrimination power at each layer under self-supervision is then compared to that of a fully supervised model classically trained. The same experiment has been done using the CIFAR10/100 dataset.
Choice of augmentations
Here we describe how [math]\displaystyle{ N }[/math] surce images get expanded to an additional [math]\displaystyle{ d-N }[/math]images, where [math]\displaystyle{ d }[/math] is much larger and independent to [math]\displaystyle{ N }[/math].
Given a source image of size [math]\displaystyle{ H \times W }[/math], extract random patches of size [math]\displaystyle{ (w,h) }[/math]. Set [math]\displaystyle{ \beta , \gamma }[/math] such that [math]\displaystyle{ \beta \leq \frac{wh}{WH} }[/math] and [math]\displaystyle{ \gamma \leq \frac{h}{w} \leq \gamma^{-1} }[/math]. The smalles size of crops is at least [math]\displaystyle{ \beta WH }[/math]. Changes in aspect ratio are limited by [math]\displaystyle{ \gamma }[/math]. In practice [math]\displaystyle{ \beta = 0.0001, \gamma = 0.75 }[/math] are good choices.
Second, images are rotated by [math]\displaystyle{ \alpha }[/math] degrees, where [math]\displaystyle{ -35 \leq \alpha \leq 35 }[/math]. Images are flipped with 50% probability.
Finally, colour and intensity of single pixels are linearly transformed to provide changes of illumination, as is common in natural images.
Quantitative Analysis
They compared the learned filters of all first-layer convolutions of an AlexNet trained with the different methods and a single image. Showed how the results of retraining a network with the first two convolutional filters, or the scattering transform from (Oyallon et al., 2017), left frozen. They also observed that their single image trained DeepCluster and BiGAN models achieve performances closes to the supervised benchmark. Lastly, they show how their features trained on only a single image can be used for other applications.
Results
Figure 2 shows how well representations at each level are linearly separable using a single image, as compared to fully supervised performance using the entire dataset. Table 1 indicates the classification accuracy of the linear classifier trained on the top of each convolutional layer. According to the results, training the CNN with self-supervision methods can match the performance of fully supervised learning in the first two convolutional layers. It must be pointed out that only one single image with massive augmentation is utilized in this experiment.
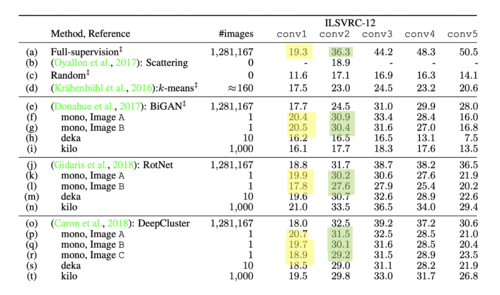
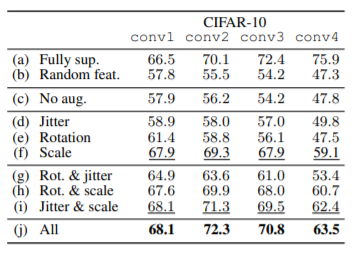
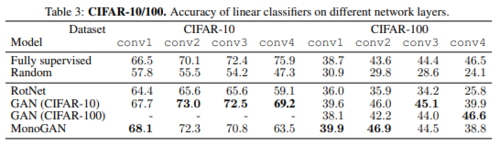
The above table (Table 3) corresponds to the Accuracy of linear classifiers on different network layers on CIFAR-10 and CIFAR-100 datasets.
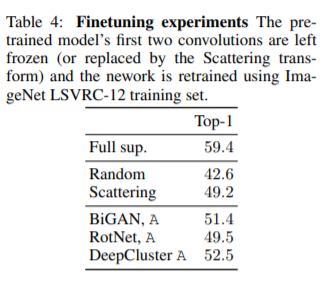
In table 4, the authors fine-tuned a convolution neural network with the first two filters left frozen. They achieved almost benchmark results with just a single image. This tells us that a single image is sufficient for training the first two convolutional filter banks.
Source Code
The source code for the paper can be found here: https://github.com/yukimasano/linear-probes
Conclusion
In this paper, the authors conducted interesting experiments to show that the first few layers of CNNs contain only limited information for analyzing natural images. They saw this by examining the weights of the early layers in cases where they only trained using only a single image with much data augmentation. Specifically, sufficient data augmentation was enough to make up for a lack of data in early CNN layers. However, this technique was not able to elicit proper learning in deeper CNN layers. In fact, even millions of images were not enough to elicit proper learning without supervision. Thus, current unsupervised learning benefits from data augmentation more than a larger dataset. The results seem to indicate that we probably do not use the full semantic capacity of a million images yet.
Critique
This is a well-written paper. However, as the main contribution of the paper is experimental, I expected a more in-depth analysis. For example, it is interesting to see how these results change if we change AlexNet with a more powerful CNN like EfficientNet? Also, the authors could try other types of Self-Supervised tasks such as jigsaw task and state-of-the-art PIRL [8].
It would be interesting to consider and compare the effects of each augmentation strategy in terms of performance. Additionally, it may be worthwhile to try other augmentation techniques like Gaussian smoothing and see the impact on the learning performance.
It would be really beneficial to apply a more challenging dataset, with objects in clutter, occlusion, and wider pose variation, inter-image invariance can be more effective, as it is used in this paper [10]. It will help us to understand the author's methodology if it encourages intra image invariance, unlike the objective of contrastive learning like the proposed in [10] or not.
References
[1] Y. Asano, C. Rupprecht, and A. Vedaldi, “A critical analysis of self-supervision, or what we can learn from a single image,” in International Conference on Learning Representations, 2019
[2] J. Donahue, P. Kr ̈ahenb ̈uhl, and T. Darrell, “Adversarial feature learning,”arXiv preprint arXiv:1605.09782, 2016.
[3] S. Gidaris, P. Singh, and N. Komodakis, “Unsupervised representation learning by predicting image rotations,”arXiv preprintarXiv:1803.07728, 2018
[4] M. Caron, P. Bojanowski, A. Joulin, and M. Douze, “Deep clustering for unsupervised learning of visual features,” in Proceedings of the European Conference on Computer Vision (ECCV), 2018, pp. 132–149
[5] G. Alain and Y. Bengio, “Understanding intermediate layers using linear classifier probes,”arXiv preprint arXiv:1610.01644, 2016.
[6] Mehdi Noroozi and Paolo Favaro. Unsupervised learning of visual representations by solving jigsaw puzzles. In ECCV, 2016.
[7] T. Malisiewicz, A. Gupta, and A. A. Efros. Ensemble of exemplar-SVMs for object detection and beyond. In Proc. ICCV, 2011.
[8] A. Rodriguez, V. Naresh Boddeti, BVK V. Kumar, and A. Mahalanobis. Maximum margin correlation filter: A new approach for localization and classification. IEEE Transactions on Image Processing, 22(2):631–643, 2013
[9] I. Misra and L. van der Maaten, "Self-Supervised Learning of Pretext-Invariant Representations," 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020.
[10] Cheng, Z., Su, J.-C., and Maji, S., “Unsupervised Discovery of Object Landmarks via Contrastive Learning”, arXiv e-prints, 2020.