User:J46hou: Difference between revisions
| (103 intermediate revisions by 48 users not shown) | |||
| Line 3: | Line 3: | ||
Jinjiang Lian, Yisheng Zhu, Jiawen Hou, Mingzhe Huang | Jinjiang Lian, Yisheng Zhu, Jiawen Hou, Mingzhe Huang | ||
== Introduction == | == Introduction == | ||
In this | In this paper, the “one-class” classification, whose goal is to obtain accurate discriminators for a special class, has been studied. Popular uses of this technique include anomaly detection, which is widely used to detect unusual patterns in data. Anomaly detection is a well-studied area of research that aims to learn a model that accurately describes "normality". It has many applications, such as risk assessment for security purposes in many fields, health, and medical risk. However, the conventional approach of modeling with typical data using a simple function falls short when it comes to complex domains such as vision or speech. Another case where this would be useful is when recognizing a “wake-word” while waking up AI systems such as Alexa. | ||
Deep learning based on anomaly detection methods attempts to learn features automatically but has some limitations. One approach is based on extending the classical data modeling techniques over the learned representations, but in this case, all the points may be mapped to a single point, making the layer look "perfect". The second approach is based on learning the salient geometric structure of data and training the discriminator to predict the applied transformation. The result could be considered anomalous if the discriminator fails to predict the transformation accurately. Appropriate structures or transformations are necessary for these works in general, but are hard to find in practice, especially for domains like time-series or speech, for image data from several orientations, or when generative models are used for deep anomaly detection. | |||
Thus, in this paper, a new approach called Deep Robust One-Class Classification (DROCC) was presented to solve the above concerns. DROCC is based on the assumption that the points from the class of interest lie on a well-sampled, locally linear low-dimensional manifold. More specifically, we are presenting DROCC-LF which is an outlier-exposure style extension of DROCC. This extension combines the DROCC's anomaly detection loss with standard classification loss over the negative data and exploits the negative examples to learn a Mahalanobis distance. | |||
== Previous Work == | == Previous Work == | ||
The current state of art | Traditional approaches for one-class problems include one-class SVM (Scholkopf et al., 1999) and Isolation Forest (Liu et al., 2008)[9]. One drawback of these approaches is that they involve careful feature engineering when applied to structured domains like images. The current state-of-the-art methodologies to tackle these kinds of problems are: | ||
1. Approach based on prediction transformations (Golan & El-Yaniv, 2018; | |||
2. Approach of minimizing a classical one-class loss on the learned final layer representations such as DeepSVDD. (Ruff et al.,2018)[2] | 1. Approach based on prediction transformations (Golan & El-Yaniv, 2018; Hendricks et al.,2019a) [1]. This work is based on learning the salient geometric structure of typical data by applying specific transformations to the input data and training the discriminator to predict the applied transformation. This approach has some shortcomings in the sense that it depends heavily on an appropriate domain-specific set of transformations that are in general hard to obtain. | ||
2. Approach of minimizing a classical one-class loss on the learned final layer representations such as DeepSVDD. (Ruff et al.,2018)[2]. Such work has proposed some heuristics to mitigate issues like setting the bias to zero but it is often insufficient in practice. This method suffers from the fundamental drawback of representation collapse, where the learned transformation might map all the points to a single point (like the origin), leading to a degenerate solution and poor discrimination between normal points and the anomalous points. | |||
3. Approach based on balancing unbalanced training datasets using methods such as SMOTE to synthetically create outlier data to train models on. | |||
== Motivation == | == Motivation == | ||
Anomaly detection is a well-studied problem with a large body of research (Aggarwal, 2016; Chandola et al., 2009) [3]. Classical approaches for anomaly detection are based on modeling the typical data using simple functions over the | Anomaly detection is a well-studied problem with a large body of research (Aggarwal, 2016; Chandola et al., 2009) [3]. The goal is to identify the outliers: points which are not following a typical distribution. The following image provides a visual representation of an outlier/anomaly. | ||
DROCC is robust to representation collapse by involving a discriminative component that is general and | [[File:abnormal.jpeg | thumb | center | 1000px | Abnormal Data (Data Driven Investor, 2020)]] | ||
Classical approaches for anomaly detection are based on modeling the typical data using simple functions over the low-dimensional subspace or a tree-structured partition of the input space to detect anomalies (Schölkopf et al., 1999; Liu et al., 2008; Lakhina et al., 2004) [4], such as constructing a minimum-enclosing ball around the typical data points (Tax & Duin, 2004) [5]. They broadly fall into three categories: AD via generative modeling, Deep Once Class SVM, Transformations based methods, and Side-information based AD. While these techniques are well-suited when the input is featured appropriately, they struggle on complex domains like vision and speech, where hand-designing features are difficult. | |||
'''AD via Generative Modeling:''' involves deep autoencoders and GAN based methods and have been deeply studied. But, this method solves a much harder problem than required and reconstructs the entire input during the decoding step. | |||
'''Deep Once Class SVM:''' Deep SVDD attempts to learn a neural network which maps data into a hypersphere. Mappings which fall within the hypersphere are considered "normal". It was the first method to introduce deep one-class classification for the purpose of anomaly detection, but is impeded by representation collapse. | |||
'''Transformations based methods:''' Are more recent methods that are based on self-supervised training. The training process of these methods applies transformations to the regular points and training the classifier to identify the transformations used. The model relies on the assumption that a point is normal iff the transformations applied to the point can be identified. Some proposed transformations are as simple as rotations and flips, or can be handcrafted and much more complicated. The various transformations that have been proposed are heavily domain dependent and are hard to design. | |||
'''Side-information based AD:''' incorporate labelled anomalous data or out-of-distribution samples. DROCC makes no assumptions regarding access to side-information. | |||
Another related problem is the one-class classification under limited negatives (OCLN). In this case, only a few negative samples are available. The goal is to find a classifier that would not misfire close negatives so that the false positive rate will be low. | |||
DROCC is robust to representation collapse by involving a discriminative component that is general and empirically accurate on most standard domains like tabular, time-series and vision without requiring any additional side information. DROCC is motivated by the key observation that generally, the typical data lies on a low-dimensional manifold, which is well-sampled in the training data and thus tends to be more accurate in practical problems. This is believed to be true even in complex domains such as vision, speech, and natural language (Pless & Souvenir, 2009). [6] | |||
== Model Explanation == | == Model Explanation == | ||
[[File:drocc_f1.jpg | center]] | [[File:drocc_f1.jpg | center]] | ||
<div align="center">Figure 1</div> | <div align="center">'''Figure 1'''</div> | ||
(a) A normal data manifold with red dots representing generated anomalous points in Ni(r). | |||
(a): A normal data manifold with red dots representing generated anomalous points in Ni(r). | |||
(b) Decision boundary learned by DROCC when applied to the data from (a). Blue represents points classified as normal and red points are classified as abnormal. | (b): Decision boundary learned by DROCC when applied to the data from (a). Blue represents points classified as normal and red points are classified as abnormal. We observe from here that DROCC is able to capture the manifold accurately; whereas the classical methods, OC-SVM and DeepSVDD perform poorly as they both try to learn a minimum enclosing ball for the whole set of positive data points. | ||
(c), (d): | (c), (d): First two dimensions of the decision boundary of DROCC and DROCC–LF, when applied to noisy data (Section 5.2). DROCC–LF is nearly optimal while DROCC’s decision boundary is inaccurate. Yellow color sine wave depicts the train data. | ||
== DROCC == | == DROCC == | ||
The model is based on the assumption that the true data | The model is based on the assumption that the true data lies on a manifold. As manifolds resemble Euclidean space locally, our discriminative component is based on classifying a point as anomalous if it is outside the union of small L2 norm balls around the training typical points (See Figure 1a, 1b for an illustration). Importantly, the above definition allows us to synthetically generate anomalous points, and we adaptively generate the most effective anomalous points while training via a gradient ascent phase reminiscent of adversarial training. In other words, DROCC has a gradient ascent phase to adaptively add anomalous points to our training set and a gradient descent phase to minimize the classification loss by learning a representation and a classifier on top of the representations to separate typical points from the generated anomalous points. In this way, DROCC automatically learns an appropriate representation (like DeepSVDD) but is robust to a representation collapse as mapping all points to the same value would lead to poor discrimination between normal points and the generated anomalous points. | ||
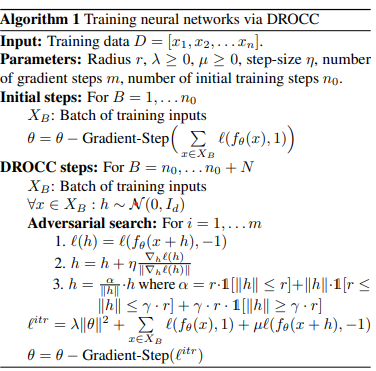
The algorithm that was used to train the model is laid out below in pseudocode. | |||
<center> | |||
[[File:DROCCtrain.png]] | |||
</center> | |||
For a DNN <math>f_\theta: \mathbb{R}^d \to \mathbb{R}</math> that is parameterized by a set of parameters <math>\theta</math>, DROCC estimates <math>\theta^{dr} = \min_\theta\ell^{dr}(\theta)</math> where | |||
$$\ell^{dr}(\theta) = \lambda\|\theta\|^2 + \sum_{i=1}^n[\ell(f_\theta(x_i),1)+\mu\max_{\tilde{x}_i \in N_i(r)}\ell(f_\theta(\tilde{x}_i),-1)]$$ | |||
Here, <math>N_i(r) = \{\|\tilde{x}_i-x_i\|_2\leq\gamma\cdot r; r \leq \|\tilde{x}_i - x_j\|, \forall j=1,2,...n\}</math> contains all the points that are at least distance <math>r</math> from the training points. The <math>\gamma \geq 1</math> is a regularization term, and <math>\ell:\mathbb{R} \times \mathbb{R} \to \mathbb{R}</math> is a loss function. The <math>x_i</math> are normal points that should be classified as positive and the <math>\tilde{x}_i</math> are anomalous points that should be classified as negative. This formulation is a saddle point problem. | |||
== DROCC-LF == | == DROCC-LF == | ||
To especially tackle problems such as anomaly detection and outlier exposure (Hendrycks et al., 2019a) [7] | To especially tackle problems such as anomaly detection and outlier exposure (Hendrycks et al., 2019a) [7], DROCC–LF, an outlier-exposure style extension of DROCC was proposed. Intuitively, DROCC–LF combines DROCC’s anomaly detection loss (that is over only the positive data points) with standard classification loss over the negative data. In addition, DROCC–LF exploits the negative examples to learn a Mahalanobis distance to compare points over the manifold instead of using the standard Euclidean distance, which can be inaccurate for high-dimensional data with relatively fewer samples. (See Figure 1c, 1d for illustration) | ||
== Popular Dataset Benchmark Result == | == Popular Dataset Benchmark Result == | ||
[[File:drocc_auc.jpg | center]] | [[File:drocc_auc.jpg | center]] | ||
<div align="center">Figure 2: AUC result</div> | <div align="center">'''Figure 2: AUC result'''</div> | ||
The CIFAR-10 dataset consists of 60000 32x32 color images in 10 classes, with 6000 images per class. There are 50000 training images and 10000 test images. The dataset is divided into five training batches and one test batch, each with 10000 images. The test batch contains exactly 1000 randomly selected images from each class. The training batches contain the remaining images in random order, but some training batches may contain more images from one class than another. Between them, the training batches contain exactly 5000 images from each class. The average AUC (with standard deviation) for one-vs-all anomaly detection on CIFAR-10 is shown in table 1. DROCC outperforms baselines on most classes, with gains as high | |||
The CIFAR-10 dataset consists of 60000 32x32 color images in 10 classes, with 6000 images per class. There are 50000 training images and 10000 test images. The dataset is divided into five training batches and one test batch, each with 10000 images. The test batch contains exactly 1000 randomly selected images from each class. The training batches contain the remaining images in random order, but some training batches may contain more images from one class than another. Between them, the training batches contain exactly 5000 images from each class. The average AUC (with standard deviation) for one-vs-all anomaly detection on CIFAR-10 is shown in table 1. DROCC outperforms baselines on most classes, with gains as high as 20%, and notably, nearest neighbors (NN) beats all the baselines on 2 classes. | |||
[[File:drocc_f1score.jpg | center]] | [[File:drocc_f1score.jpg | center]] | ||
<div align="center">Figure 3: F1-Score</div> | <div align="center">'''Figure 3: F1-Score'''</div> | ||
Figure 3 shows F1-Score (with standard deviation) for one-vs-all anomaly detection on Thyroid, Arrhythmia, and Abalone datasets from the UCI Machine Learning Repository. DROCC outperforms the baselines on all three datasets by a minimum of 0.07 which is about an 11.5% performance increase. | |||
Results on One-class Classification with Limited Negatives (OCLN): | Results on One-class Classification with Limited Negatives (OCLN): | ||
[[File:ocln.jpg | center]] | [[File:ocln.jpg | center]] | ||
<div align="center">Figure 4: Sample | <div align="center">'''Figure 4: Sample positives, negatives and close negatives for MNIST digit 0 vs 1 experiment (OCLN).'''</div> | ||
MNIST 0 vs. 1 Classification: | MNIST 0 vs. 1 Classification: | ||
We consider an experimental setup on MNIST dataset, where the training data consists of Digit 0, the normal class, and | We consider an experimental setup on the MNIST dataset, where the training data consists of Digit 0, the normal class, and Digit 1 as the anomaly. During the evaluation, in addition to samples from training distribution, we also have half zeros, which act as challenging OOD points (close negatives). These half zeros are generated by randomly masking 50% of the pixels (Figure 2). BCE performs poorly, with a recall of 54% only at a fixed FPR of 3%. DROCC–OE gives a recall value of 98:16% outperforming DeepSAD by a margin of 7%, which gives a recall value of 90:91%. DROCC–LF provides further improvement with a recall of 99:4% at 3% FPR. | ||
[[File:ocln_2.jpg | center]] | [[File:ocln_2.jpg | center]] | ||
<div align="center">Figure 5: OCLN on Audio Commands.</div> | <div align="center">'''Figure 5: OCLN on Audio Commands.'''</div> | ||
Wake word Detection: | Wake word Detection: | ||
Finally, we evaluate DROCC–LF on the practical problem of wake word detection with low FPR against arbitrary OOD negatives. To this end, we identify a keyword, say “Marvin” from the audio commands dataset (Warden, 2018) [8] as the positive class, and the remaining 34 keywords are labeled as the negative class. For training, we sample points uniformly at random from the above-mentioned dataset. However, for evaluation, we sample positives from the train distribution, but negatives contain a few challenging OOD points as well. Sampling challenging negatives itself is a hard task and is the key motivating reason for studying the problem. So, we manually list close-by keywords to Marvin such as | Finally, we evaluate DROCC–LF on the practical problem of wake word detection with low FPR against arbitrary OOD negatives. To this end, we identify a keyword, say “Marvin” from the audio commands dataset (Warden, 2018) [8] as the positive class, and the remaining 34 keywords are labeled as the negative class. For training, we sample points uniformly at random from the above-mentioned dataset. However, for evaluation, we sample positives from the train distribution, but negatives contain a few challenging OOD points as well. Sampling challenging negatives itself is a hard task and is the key motivating reason for studying the problem. So, we manually list close-by keywords to Marvin such as Mar, Vin, Marvelous, etc. We then generate audio snippets for these keywords via a speech synthesis tool 2 with a variety of accents. | ||
Figure | Figure 5 shows that for 3% and 5% FPR settings, DROCC–LF is significantly more accurate than the baselines. For example, with FPR=3%, DROCC–LF is 10% more accurate than the baselines. We repeated the same experiment with the keyword "Seven" and observed a similar trend. In summary, DROCC–LF is able to generalize well against negatives that are “close” to the true positives even when such negatives were not supplied with the training data. | ||
== Conclusion and Future Work == | == Conclusion and Future Work == | ||
We introduced DROCC method for deep anomaly detection. It | We introduced the DROCC method for deep anomaly detection. It uses low-dimensional modeling normal data point manifold to compare the closed point distance by Euclidean. The optimization of DROCC is formulated as a saddle point problem solved by the standard gradient descent-rise algorithm. Then we extend DROCC to the OCLN problem. The goal is to assume that samples of any category are fully sampled, and a small number of samples are negative so that it can be well summarized for any negative words. Both methods are significantly better than the strong benchmark problem setting in their respective performance. | ||
For computational efficiency, we simplified the projection set | For computational efficiency, we simplified the projection set of both methods which can perhaps slow down the convergence of the two methods. Designing optimization algorithms that can work with the stricter set is an exciting research direction. Further, we would also like to rigorously analyze DROCC, assuming enough samples from a low-curvature manifold. Finally, as OCLN is an exciting problem that routinely comes up in a variety of real-world applications, we would like to apply DROCC–LF to a few high impact scenarios. Possible applications of this work are financial fraud detection, medical anomalies, or key words in audio processing. | ||
The results of this study showed that DROCC is comparatively better for anomaly detection across many different areas, such as tabular data, images, audio, and time series, when compared to existing state-of-the-art techniques. | |||
== References == | == References == | ||
| Line 65: | Line 106: | ||
[8]: Warden, P. Speech commands: A dataset for limited vocabulary speech recognition, 2018. URL https: //arxiv.org/abs/1804.03209. | [8]: Warden, P. Speech commands: A dataset for limited vocabulary speech recognition, 2018. URL https: //arxiv.org/abs/1804.03209. | ||
[9]: Liu, F. T., Ting, K. M., and Zhou, Z.-H. Isolation forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, 2008. | |||
== Critiques/Insights == | |||
1. It would be interesting to see this implemented in self-driving cars, for instance, to detect unusual road conditions. | |||
2. Figure 1 shows a good representation on how this model works. However, how can we know that this model is not prone to overfitting? There are many situations where there are valid points that lie outside of the line, especially new data that the model has never see before. An explanation on how this is avoided would be good. | |||
3.In the introduction part, it should first explain what is "one class", and then make a detailed application. Moreover, special definition words are used in many places in the text. No detailed explanation was given. In the end, the future application fields of DROCC and the research direction of the group can be explained. | |||
4. It will also be interesting to see if one change from using <math>\ell_{2}</math> Euclidean distance to other distances. When the low-dimensional manifold is highly non-linear, using the local linear distance to characterize anomalous points might fail. | |||
5. This is a nice summary and the authors introduce clearly on the performance of DROCC. It is nice to use Alexa as an example to catch readers' attention. I think it will be nice to include the algorithm of the DROCC or the architecture of DROCC in this summary to help us know the whole view of this method. Maybe it will be interesting to apply DROCC in biomedical studies? since one-class classification is often used in biomedical studies. | |||
6. For the second sentence in the motivation section, it's better to change "The goal is to identify the outliers: points which are not following a typical distribution" to "The goal is to identify the outliers: points that are not following a typical distribution". In addition, it should be noted that there is an important assumption which assumes the points from the class of interest lie on a well-sampled, locally linear low dimensional manifold when someone wants to use DROCC. | |||
7. The training method resembles adversarial learning with gradient ascent, however, there is no evaluation of this method on adversarial examples. This is quite unusual considering the paper proposed a method for robust one-class classification, and can be a security threat in real life in critical applications. | |||
8. The underlying idea behind OCLN is very similar to how neural networks are implemented in recommender systems and trained over positive/negative triplet models. In that case as well, due to the nature of implicit and explicit feedback, positive data tends to dominate the system. It would be interesting to see if insights from that area could be used to further boost the model presented in this paper. | |||
9. The paper shows the performance of DROCC being evaluated for time series data. It is interesting to see high AUC scores for DROCC against baselines like nearest neighbours and REBMs.Because detecting abnormal data in time series datasets is not common to practice. | |||
10. Figure1 presented results on a simple 2-D sine wave dataset to visualize the kind of classifiers learnt by DROCC. And the 1a is the positive data lies on a 1-D manifold. We can see from 1b that DROCC is able to capture the manifold accurately. | |||
11. In the MNIST 0 vs. 1 Classification dataset, why is 1 the only digit that is considered an anomoly? Couldn't all of the non-0 digits be left in the dataset to serve as "anomolies"? | |||
12. For future work the authors suggest considering DROCC for a low curvature manifold but do not motivate the benefits of such a direction. | |||
13. One of the problems is that in this model we might need to map all the points to one point to make the layer looks "perfect". However, this might not be a good choice since each point is distinct and if we map them together to one point, then this point cannot tell everything. If authors can specify more details on this it would be better. | |||
14. This project introduced DROCC for “one-class” classification. It will be interesting if such kind of classification can be compared with any other classification such as binary classification, etc. If “one-class” classification would be more speedy than the others. | |||
15. The dimensions and feature values must be so different across datasets in different domains. I would love to see how this algorithm is performing so well applied on different domains as it is mentioned that it could be used on datasets including images, audio, time-series, etc. | |||
16. It would be interesting to show the performance of DROCC against popular models used for outlier prediction such as PCA, EVA, etc. Perhaps show their accuracy scores so we can better compare. | |||
17. It would be greater if an visualization of how much performance DROCC improved compare to traditional binary classifier like SVM, isolation Forest. | |||
19. The paper is well organized and informative. It would be great if it included more details about the datasets. For example, some detailed information about CIFAR-10 can be found in this paper: [https://arxiv.org/pdf/1207.0580.pdf] | |||
Latest revision as of 15:12, 7 December 2020
DROCC: Deep Robust One-Class Classification
Presented by
Jinjiang Lian, Yisheng Zhu, Jiawen Hou, Mingzhe Huang
Introduction
In this paper, the “one-class” classification, whose goal is to obtain accurate discriminators for a special class, has been studied. Popular uses of this technique include anomaly detection, which is widely used to detect unusual patterns in data. Anomaly detection is a well-studied area of research that aims to learn a model that accurately describes "normality". It has many applications, such as risk assessment for security purposes in many fields, health, and medical risk. However, the conventional approach of modeling with typical data using a simple function falls short when it comes to complex domains such as vision or speech. Another case where this would be useful is when recognizing a “wake-word” while waking up AI systems such as Alexa.
Deep learning based on anomaly detection methods attempts to learn features automatically but has some limitations. One approach is based on extending the classical data modeling techniques over the learned representations, but in this case, all the points may be mapped to a single point, making the layer look "perfect". The second approach is based on learning the salient geometric structure of data and training the discriminator to predict the applied transformation. The result could be considered anomalous if the discriminator fails to predict the transformation accurately. Appropriate structures or transformations are necessary for these works in general, but are hard to find in practice, especially for domains like time-series or speech, for image data from several orientations, or when generative models are used for deep anomaly detection.
Thus, in this paper, a new approach called Deep Robust One-Class Classification (DROCC) was presented to solve the above concerns. DROCC is based on the assumption that the points from the class of interest lie on a well-sampled, locally linear low-dimensional manifold. More specifically, we are presenting DROCC-LF which is an outlier-exposure style extension of DROCC. This extension combines the DROCC's anomaly detection loss with standard classification loss over the negative data and exploits the negative examples to learn a Mahalanobis distance.
Previous Work
Traditional approaches for one-class problems include one-class SVM (Scholkopf et al., 1999) and Isolation Forest (Liu et al., 2008)[9]. One drawback of these approaches is that they involve careful feature engineering when applied to structured domains like images. The current state-of-the-art methodologies to tackle these kinds of problems are:
1. Approach based on prediction transformations (Golan & El-Yaniv, 2018; Hendricks et al.,2019a) [1]. This work is based on learning the salient geometric structure of typical data by applying specific transformations to the input data and training the discriminator to predict the applied transformation. This approach has some shortcomings in the sense that it depends heavily on an appropriate domain-specific set of transformations that are in general hard to obtain.
2. Approach of minimizing a classical one-class loss on the learned final layer representations such as DeepSVDD. (Ruff et al.,2018)[2]. Such work has proposed some heuristics to mitigate issues like setting the bias to zero but it is often insufficient in practice. This method suffers from the fundamental drawback of representation collapse, where the learned transformation might map all the points to a single point (like the origin), leading to a degenerate solution and poor discrimination between normal points and the anomalous points.
3. Approach based on balancing unbalanced training datasets using methods such as SMOTE to synthetically create outlier data to train models on.
Motivation
Anomaly detection is a well-studied problem with a large body of research (Aggarwal, 2016; Chandola et al., 2009) [3]. The goal is to identify the outliers: points which are not following a typical distribution. The following image provides a visual representation of an outlier/anomaly.
Classical approaches for anomaly detection are based on modeling the typical data using simple functions over the low-dimensional subspace or a tree-structured partition of the input space to detect anomalies (Schölkopf et al., 1999; Liu et al., 2008; Lakhina et al., 2004) [4], such as constructing a minimum-enclosing ball around the typical data points (Tax & Duin, 2004) [5]. They broadly fall into three categories: AD via generative modeling, Deep Once Class SVM, Transformations based methods, and Side-information based AD. While these techniques are well-suited when the input is featured appropriately, they struggle on complex domains like vision and speech, where hand-designing features are difficult.
AD via Generative Modeling: involves deep autoencoders and GAN based methods and have been deeply studied. But, this method solves a much harder problem than required and reconstructs the entire input during the decoding step.
Deep Once Class SVM: Deep SVDD attempts to learn a neural network which maps data into a hypersphere. Mappings which fall within the hypersphere are considered "normal". It was the first method to introduce deep one-class classification for the purpose of anomaly detection, but is impeded by representation collapse.
Transformations based methods: Are more recent methods that are based on self-supervised training. The training process of these methods applies transformations to the regular points and training the classifier to identify the transformations used. The model relies on the assumption that a point is normal iff the transformations applied to the point can be identified. Some proposed transformations are as simple as rotations and flips, or can be handcrafted and much more complicated. The various transformations that have been proposed are heavily domain dependent and are hard to design.
Side-information based AD: incorporate labelled anomalous data or out-of-distribution samples. DROCC makes no assumptions regarding access to side-information.
Another related problem is the one-class classification under limited negatives (OCLN). In this case, only a few negative samples are available. The goal is to find a classifier that would not misfire close negatives so that the false positive rate will be low.
DROCC is robust to representation collapse by involving a discriminative component that is general and empirically accurate on most standard domains like tabular, time-series and vision without requiring any additional side information. DROCC is motivated by the key observation that generally, the typical data lies on a low-dimensional manifold, which is well-sampled in the training data and thus tends to be more accurate in practical problems. This is believed to be true even in complex domains such as vision, speech, and natural language (Pless & Souvenir, 2009). [6]
Model Explanation
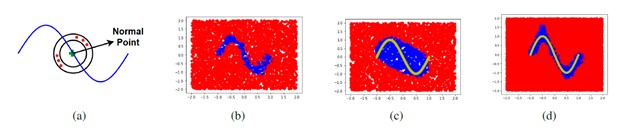
(a): A normal data manifold with red dots representing generated anomalous points in Ni(r).
(b): Decision boundary learned by DROCC when applied to the data from (a). Blue represents points classified as normal and red points are classified as abnormal. We observe from here that DROCC is able to capture the manifold accurately; whereas the classical methods, OC-SVM and DeepSVDD perform poorly as they both try to learn a minimum enclosing ball for the whole set of positive data points.
(c), (d): First two dimensions of the decision boundary of DROCC and DROCC–LF, when applied to noisy data (Section 5.2). DROCC–LF is nearly optimal while DROCC’s decision boundary is inaccurate. Yellow color sine wave depicts the train data.
DROCC
The model is based on the assumption that the true data lies on a manifold. As manifolds resemble Euclidean space locally, our discriminative component is based on classifying a point as anomalous if it is outside the union of small L2 norm balls around the training typical points (See Figure 1a, 1b for an illustration). Importantly, the above definition allows us to synthetically generate anomalous points, and we adaptively generate the most effective anomalous points while training via a gradient ascent phase reminiscent of adversarial training. In other words, DROCC has a gradient ascent phase to adaptively add anomalous points to our training set and a gradient descent phase to minimize the classification loss by learning a representation and a classifier on top of the representations to separate typical points from the generated anomalous points. In this way, DROCC automatically learns an appropriate representation (like DeepSVDD) but is robust to a representation collapse as mapping all points to the same value would lead to poor discrimination between normal points and the generated anomalous points.
The algorithm that was used to train the model is laid out below in pseudocode.
For a DNN [math]\displaystyle{ f_\theta: \mathbb{R}^d \to \mathbb{R} }[/math] that is parameterized by a set of parameters [math]\displaystyle{ \theta }[/math], DROCC estimates [math]\displaystyle{ \theta^{dr} = \min_\theta\ell^{dr}(\theta) }[/math] where $$\ell^{dr}(\theta) = \lambda\|\theta\|^2 + \sum_{i=1}^n[\ell(f_\theta(x_i),1)+\mu\max_{\tilde{x}_i \in N_i(r)}\ell(f_\theta(\tilde{x}_i),-1)]$$ Here, [math]\displaystyle{ N_i(r) = \{\|\tilde{x}_i-x_i\|_2\leq\gamma\cdot r; r \leq \|\tilde{x}_i - x_j\|, \forall j=1,2,...n\} }[/math] contains all the points that are at least distance [math]\displaystyle{ r }[/math] from the training points. The [math]\displaystyle{ \gamma \geq 1 }[/math] is a regularization term, and [math]\displaystyle{ \ell:\mathbb{R} \times \mathbb{R} \to \mathbb{R} }[/math] is a loss function. The [math]\displaystyle{ x_i }[/math] are normal points that should be classified as positive and the [math]\displaystyle{ \tilde{x}_i }[/math] are anomalous points that should be classified as negative. This formulation is a saddle point problem.
DROCC-LF
To especially tackle problems such as anomaly detection and outlier exposure (Hendrycks et al., 2019a) [7], DROCC–LF, an outlier-exposure style extension of DROCC was proposed. Intuitively, DROCC–LF combines DROCC’s anomaly detection loss (that is over only the positive data points) with standard classification loss over the negative data. In addition, DROCC–LF exploits the negative examples to learn a Mahalanobis distance to compare points over the manifold instead of using the standard Euclidean distance, which can be inaccurate for high-dimensional data with relatively fewer samples. (See Figure 1c, 1d for illustration)
Popular Dataset Benchmark Result
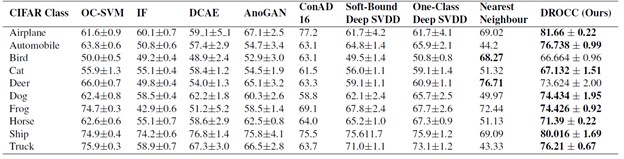
The CIFAR-10 dataset consists of 60000 32x32 color images in 10 classes, with 6000 images per class. There are 50000 training images and 10000 test images. The dataset is divided into five training batches and one test batch, each with 10000 images. The test batch contains exactly 1000 randomly selected images from each class. The training batches contain the remaining images in random order, but some training batches may contain more images from one class than another. Between them, the training batches contain exactly 5000 images from each class. The average AUC (with standard deviation) for one-vs-all anomaly detection on CIFAR-10 is shown in table 1. DROCC outperforms baselines on most classes, with gains as high as 20%, and notably, nearest neighbors (NN) beats all the baselines on 2 classes.
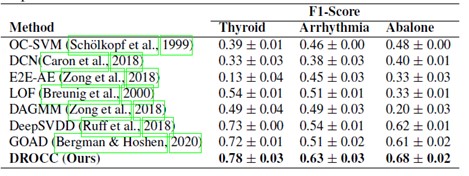
Figure 3 shows F1-Score (with standard deviation) for one-vs-all anomaly detection on Thyroid, Arrhythmia, and Abalone datasets from the UCI Machine Learning Repository. DROCC outperforms the baselines on all three datasets by a minimum of 0.07 which is about an 11.5% performance increase. Results on One-class Classification with Limited Negatives (OCLN):

MNIST 0 vs. 1 Classification: We consider an experimental setup on the MNIST dataset, where the training data consists of Digit 0, the normal class, and Digit 1 as the anomaly. During the evaluation, in addition to samples from training distribution, we also have half zeros, which act as challenging OOD points (close negatives). These half zeros are generated by randomly masking 50% of the pixels (Figure 2). BCE performs poorly, with a recall of 54% only at a fixed FPR of 3%. DROCC–OE gives a recall value of 98:16% outperforming DeepSAD by a margin of 7%, which gives a recall value of 90:91%. DROCC–LF provides further improvement with a recall of 99:4% at 3% FPR.
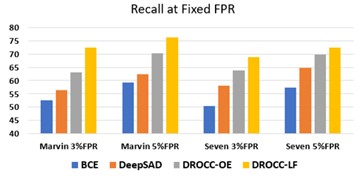
Wake word Detection: Finally, we evaluate DROCC–LF on the practical problem of wake word detection with low FPR against arbitrary OOD negatives. To this end, we identify a keyword, say “Marvin” from the audio commands dataset (Warden, 2018) [8] as the positive class, and the remaining 34 keywords are labeled as the negative class. For training, we sample points uniformly at random from the above-mentioned dataset. However, for evaluation, we sample positives from the train distribution, but negatives contain a few challenging OOD points as well. Sampling challenging negatives itself is a hard task and is the key motivating reason for studying the problem. So, we manually list close-by keywords to Marvin such as Mar, Vin, Marvelous, etc. We then generate audio snippets for these keywords via a speech synthesis tool 2 with a variety of accents. Figure 5 shows that for 3% and 5% FPR settings, DROCC–LF is significantly more accurate than the baselines. For example, with FPR=3%, DROCC–LF is 10% more accurate than the baselines. We repeated the same experiment with the keyword "Seven" and observed a similar trend. In summary, DROCC–LF is able to generalize well against negatives that are “close” to the true positives even when such negatives were not supplied with the training data.
Conclusion and Future Work
We introduced the DROCC method for deep anomaly detection. It uses low-dimensional modeling normal data point manifold to compare the closed point distance by Euclidean. The optimization of DROCC is formulated as a saddle point problem solved by the standard gradient descent-rise algorithm. Then we extend DROCC to the OCLN problem. The goal is to assume that samples of any category are fully sampled, and a small number of samples are negative so that it can be well summarized for any negative words. Both methods are significantly better than the strong benchmark problem setting in their respective performance.
For computational efficiency, we simplified the projection set of both methods which can perhaps slow down the convergence of the two methods. Designing optimization algorithms that can work with the stricter set is an exciting research direction. Further, we would also like to rigorously analyze DROCC, assuming enough samples from a low-curvature manifold. Finally, as OCLN is an exciting problem that routinely comes up in a variety of real-world applications, we would like to apply DROCC–LF to a few high impact scenarios. Possible applications of this work are financial fraud detection, medical anomalies, or key words in audio processing.
The results of this study showed that DROCC is comparatively better for anomaly detection across many different areas, such as tabular data, images, audio, and time series, when compared to existing state-of-the-art techniques.
References
[1]: Golan, I. and El-Yaniv, R. Deep anomaly detection using geometric transformations. In Advances in Neural Information Processing Systems (NeurIPS), 2018.
[2]: Ruff, L., Vandermeulen, R., Goernitz, N., Deecke, L., Siddiqui, S. A., Binder, A., M¨uller, E., and Kloft, M. Deep one-class classification. In International Conference on Machine Learning (ICML), 2018.
[3]: Aggarwal, C. C. Outlier Analysis. Springer Publishing Company, Incorporated, 2nd edition, 2016. ISBN 3319475770.
[4]: Sch¨olkopf, B., Williamson, R., Smola, A., Shawe-Taylor, J., and Platt, J. Support vector method for novelty detection. In Proceedings of the 12th International Conference on Neural Information Processing Systems, 1999.
[5]: Tax, D. M. and Duin, R. P. Support vector data description. Machine Learning, 54(1), 2004.
[6]: Pless, R. and Souvenir, R. A survey of manifold learning for images. IPSJ Transactions on Computer Vision and Applications, 1, 2009.
[7]: Hendrycks, D., Mazeika, M., and Dietterich, T. Deep anomaly detection with outlier exposure. In International Conference on Learning Representations (ICLR), 2019a.
[8]: Warden, P. Speech commands: A dataset for limited vocabulary speech recognition, 2018. URL https: //arxiv.org/abs/1804.03209.
[9]: Liu, F. T., Ting, K. M., and Zhou, Z.-H. Isolation forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, 2008.
Critiques/Insights
1. It would be interesting to see this implemented in self-driving cars, for instance, to detect unusual road conditions.
2. Figure 1 shows a good representation on how this model works. However, how can we know that this model is not prone to overfitting? There are many situations where there are valid points that lie outside of the line, especially new data that the model has never see before. An explanation on how this is avoided would be good.
3.In the introduction part, it should first explain what is "one class", and then make a detailed application. Moreover, special definition words are used in many places in the text. No detailed explanation was given. In the end, the future application fields of DROCC and the research direction of the group can be explained.
4. It will also be interesting to see if one change from using [math]\displaystyle{ \ell_{2} }[/math] Euclidean distance to other distances. When the low-dimensional manifold is highly non-linear, using the local linear distance to characterize anomalous points might fail.
5. This is a nice summary and the authors introduce clearly on the performance of DROCC. It is nice to use Alexa as an example to catch readers' attention. I think it will be nice to include the algorithm of the DROCC or the architecture of DROCC in this summary to help us know the whole view of this method. Maybe it will be interesting to apply DROCC in biomedical studies? since one-class classification is often used in biomedical studies.
6. For the second sentence in the motivation section, it's better to change "The goal is to identify the outliers: points which are not following a typical distribution" to "The goal is to identify the outliers: points that are not following a typical distribution". In addition, it should be noted that there is an important assumption which assumes the points from the class of interest lie on a well-sampled, locally linear low dimensional manifold when someone wants to use DROCC.
7. The training method resembles adversarial learning with gradient ascent, however, there is no evaluation of this method on adversarial examples. This is quite unusual considering the paper proposed a method for robust one-class classification, and can be a security threat in real life in critical applications.
8. The underlying idea behind OCLN is very similar to how neural networks are implemented in recommender systems and trained over positive/negative triplet models. In that case as well, due to the nature of implicit and explicit feedback, positive data tends to dominate the system. It would be interesting to see if insights from that area could be used to further boost the model presented in this paper.
9. The paper shows the performance of DROCC being evaluated for time series data. It is interesting to see high AUC scores for DROCC against baselines like nearest neighbours and REBMs.Because detecting abnormal data in time series datasets is not common to practice.
10. Figure1 presented results on a simple 2-D sine wave dataset to visualize the kind of classifiers learnt by DROCC. And the 1a is the positive data lies on a 1-D manifold. We can see from 1b that DROCC is able to capture the manifold accurately.
11. In the MNIST 0 vs. 1 Classification dataset, why is 1 the only digit that is considered an anomoly? Couldn't all of the non-0 digits be left in the dataset to serve as "anomolies"?
12. For future work the authors suggest considering DROCC for a low curvature manifold but do not motivate the benefits of such a direction.
13. One of the problems is that in this model we might need to map all the points to one point to make the layer looks "perfect". However, this might not be a good choice since each point is distinct and if we map them together to one point, then this point cannot tell everything. If authors can specify more details on this it would be better.
14. This project introduced DROCC for “one-class” classification. It will be interesting if such kind of classification can be compared with any other classification such as binary classification, etc. If “one-class” classification would be more speedy than the others.
15. The dimensions and feature values must be so different across datasets in different domains. I would love to see how this algorithm is performing so well applied on different domains as it is mentioned that it could be used on datasets including images, audio, time-series, etc.
16. It would be interesting to show the performance of DROCC against popular models used for outlier prediction such as PCA, EVA, etc. Perhaps show their accuracy scores so we can better compare.
17. It would be greater if an visualization of how much performance DROCC improved compare to traditional binary classifier like SVM, isolation Forest.
19. The paper is well organized and informative. It would be great if it included more details about the datasets. For example, some detailed information about CIFAR-10 can be found in this paper: [1]