User:Gtompkin: Difference between revisions
| (106 intermediate revisions by 34 users not shown) | |||
| Line 4: | Line 4: | ||
== Introduction == | == Introduction == | ||
One of the fundamental challenges in machine learning | One of the fundamental challenges in machine learning and data science is dealing with missing and incomplete data. This paper proposes a theoretically justified methodology for using incomplete data in neural networks, eliminating the need for direct completion of data by imputation or other commonly used methods in the existing literature. The authors propose identifying missing data points with a parametric density and then training it together with the rest of the network's parameters. The neuron's response at the first hidden layer is generalized by taking its expected value to process this probabilistic representation. This process is essentially calculating the average activation of the neuron over imputations drawn from the missing data's density and this proposed approach is advantageous because it has the ability to train neural networks using incomplete observations from datasets, which are ubiquitous in practice. Furthermore, this approach also requires minimal adjustments and modifications to existing architectures. Theoretical results of this study show that this process does not lead to a loss of information, while experimental results showed the practical uses of this methodology on several different types of networks. | ||
== Related Work == | == Related Work == | ||
Currently, dealing with incomplete inputs in machine learning requires filling absent attributes based on complete, observed data. Two commonly used methods are mean imputation and k-NN imputation. Other methods for dealing with missing data involve training separate neural networks | Currently, dealing with incomplete inputs in machine learning requires filling absent attributes based on complete, observed data. Two commonly used methods are mean imputation and <math>k</math>-nearest neighbors (k-NN) imputation. In the former (mean imputation), the missing value is replaced by the mean of all available values of that feature in the dataset. In the latter (k-NN imputation), the missing value is also replaced by the mean, however, it is now computed using only the k "closest" samples in the dataset. For example, if the dataset is numerical, Euclidean distance could be used as a measure of "closeness". Other methods for dealing with missing data involve training separate neural networks and extreme learning machines. Probabilistic models of incomplete data can also be built depending on the mechanism missingness (i.e. whether the data is Missing At Random (MAR), Missing Completely At Random (MCAR), or Missing Not At Random (MNAR)), which can be fed into a particular learning model. Further, the decision function can also be trained using available/visible inputs alone. Previous work using neural networks for missing data includes a paper by Bengio and Gringras [1] where the authors used recurrent neural networks with feedback into the input units to fill absent attributes solely to minimize the learning criterion. Goodfellow et. al. [2] also used neural networks by introducing a multi-prediction deep Boltzmann machine that could perform classification on data with missingness in the inputs. | ||
== Layer for Processing Missing Data == | == Layer for Processing Missing Data == | ||
In this approach, the adaptation of a given neural network to incomplete data relies on two steps: the estimation of the missing data and the generalization of the neuron's activation. | |||
Let <math>(x,J)</math> represent a missing data point, where <math>x \in \mathbb{R}^D </math>, and <math>J \subset {1,...,D} </math> is a set of attributes with missing data. | Let <math>(x,J)</math> represent a missing data point, where <math>x \in \mathbb{R}^D </math>, and <math>J \subset \{1,...,D\} </math> is a set of attributes with missing data. <math>(x,J)</math> therefore represents an "incomplete" data point for which <math>|J|</math>-many entries are unknown - examples of this could be a list of daily temperature readings over a week where temperature was not recorded on the third day (<math>x\in \mathbb{R}^7, J= \{3\}</math>), an audio transcript that goes silent for certain timespans, or images that are partially masked out (as discussed in the examples). | ||
For each missing point <math>(x,J)</math>, define an affine subspace consisting of all points which coincide with <math>x</math> on known coordinates <math>J'=\{1,…,N\}/J</math>: | For each missing point <math>(x,J)</math>, define an affine subspace consisting of all points which coincide with <math>x</math> on known coordinates <math>J'=\{1,…,N\}/J</math>: | ||
<center><math>S=Aff[x,J]=span(e_J) </math></center> | <center><math>S=Aff[x,J]=span(e_J) </math></center> | ||
where <math>e_J=[e_j]_{j\in J}</math> and <math>e_j</math> is the <math> j^{th}</math> canonical vector in <math>\mathbb{R}^D </math>. | |||
Assume that the missing data points come from the D-dimensional probability distribution, <math>F</math>. In their approach, the authors assume that the data points follow a mixture of Gaussians (GMM) with diagonal covariance matrices. By choosing diagonal covariance matrices, the number of model parameters is reduced. To model the missing points <math>(x,J)</math>, the density <math>F</math> is restricted to the affine subspace <math>S</math>. Thus, possible values of <math>(x,J)</math> are modelled using the conditional density <math>F_S: S \to \mathbb{R} </math>, | |||
<center><math>F_S(x) = \begin{cases} | |||
\frac{1}{\int_{S} F(s) \,ds}F(x) & \text{if $x \in S$,} \\ | |||
0 & \text{otherwise.} | |||
\end{cases} </math></center> | |||
To process the missing data by a neural network, the authors propose that only the first hidden layer needs modification. Specifically, they generalize the activation functions of all the neurons in the first hidden layer of the network to process the probability density functions representing the missing data points. For the conditional density function <math>F_S</math>, the authors define the generalized activation of a neuron <math>n: \mathbb{R}^D \to \mathbb{R}</math> on <math>F_S </math> as: | |||
<center><math>n(F_S)=E[n(x)|x \sim F_S]=\int n(x)F_S(x) \,dx</math>,</center> | |||
provided that the expectation exists. | |||
The following two theorems describe how to apply the above generalizations to both the ReLU and the RBF neurons, respectively. | |||
'''Theorem 3.1''' Let <math>F = \sum_i{p_iN(m_i, \Sigma_i)}</math> be the mixture of (possibly degenerate) Gaussians. Given weights <math>w=(w_1, ..., w_D) \in \mathbb{R}^D,</math><math> b \in \mathbb{R} </math>, we have | |||
<center><math>\text{ReLU}_{w,b}(F)=\sum_i{p_iNR\big(\frac{w^{\top}m_i+b}{\sqrt{w^{\top}\Sigma_iw}}}\big)</math></center> | |||
where <math>NR(x)=\text{ReLU}[N(x,1)]</math> and <math>\text{ReLU}_{w,b}(x)=\text{max}(w^{\top}+b, 0)</math>, <math>w \in \mathbb{R}^D </math> and <math> b \in \mathbb{R}</math> is the bias. | |||
'''Theorem 3.2''' Let <math>F = \sum_i{p_iN(m_i, \Sigma_i)}</math> be the mixture of (possibly degenerate) Gaussians and let the RBF unit be parametrized by <math>N(c, \Gamma) </math>. We have: | |||
<center><math>\text{RBF}_{c, \Gamma}(F) = \sum_{i=1}^k{p_iN(m_i-c, \Gamma+\Sigma_i)}(0)</math>.</center> | |||
In the case where the data set contains no missing values, the generalized neurons reduce to classical ones, since the distribution <math>F</math> is only used to estimate possible values at missing attributes. However, if one wishes to use an incomplete data set in the testing stage, then an incomplete data set must be used to train the model. | |||
<math> </math> | <math> </math> | ||
== Theoretical Analysis == | == Theoretical Analysis == | ||
The main theoretical results, which are summarized below, show that using generalized neuron's activation at the first layer does not lead to the loss of information. | |||
Let the generalized response of a neuron <math>n: \mathbb{R}^D \rightarrow \mathbb{R}</math> evaluated on a probability measure <math>\mu</math> which is given by | |||
<center><math>n(\mu) := \int n(x)d\mu(x)</math></center> | |||
'''Theorem 4.1.''' Let <math>\mu</math>, <math>v</math> be probabilistic measures satisfying <math>\int ||x|| d \mu(x) < \infty</math>. If | |||
<center><math>ReLU_{w,b}(\mu) = ReLU_{w,b}(\nu) \text{ for } w \in \mathbb{R}^D, b \in \mathbb{R}</math></center> then <math>\nu = \mu</math>. | |||
Theorem 4.1 shows that a neural network with generalized ReLU units is able to identify any two probability measures. The proof presented by the authors uses the Universal Approximation Property (UAP), and is summarized as follows. | |||
''Sketch of Proof'' Let <math>w \in \mathbb{R}^D</math> be fixed and define the set <center><math>F_w = \{p: \mathbb{R} \rightarrow \mathbb{R}: \int p(w^Tx)d\mu(x) = \int p(w^Tx)d\nu(x)\}.</math></center> The first step of the proof involves showing that <math>F_w</math> contains all continuous and bounded functions. The authors show this by showing that a piecewise continuous function that is affine linear on specific intervals, <math>Q</math>, is in the set <math>F_w</math>. This involves re-writing <math>Q</math> as a sum of tent-like piecewise linear functions, <math>T</math> and showing that <math>T \in F_w</math> (since it is sufficient to only show <math>T \in F_w</math>). | |||
Next, the authors show that an arbitrary bounded continuous function <math>G</math> is in <math>F_w</math> by the Lebesgue dominated convergence theorem. | |||
Then, as <math>cos(\cdot), sin(\cdot) \in F_w</math>, the function <center><math>exp(ir) = cos(r) + i sin(r) \in F_w</math></center> and we have the equality <center><math>\int exp(iw^Tx)d\mu(x) = \int exp(iw^Tx)d\nu(x).</math></center> Since <math>w</math> was arbitrarily chosen, we can conclude that <math>\mu = \nu</math> as the characteristic functions of the two measures coincide. | |||
A result analogous to Theorem 4.1 for RBF can also be obtained. | |||
'''Theorem 2.1''' Let <math>\mu, \nu</math> be probabilistic measures. If | |||
$$ RBF_{m,\alpha}(\mu) = RBF_{m,\alpha}(\nu) \text{ for every } m \in \mathbb{R}^D, \alpha > 0,$$ | |||
then <math>\nu = \mu</math>. | |||
More general results can be obtained making stronger assumptions on the probability measures. For example, if a given family of neurons satisfies UAP, then their generalization can identify any probability measure with compact support. | |||
'''Theorem 2.2''' Let <math>\mu, \nu</math> be probabilistic measures with compact support. Let <math>\mathcal{N}</math> be a family of functions having UAP. If | |||
$$n(\mu) = n(\nu) \text{ for every } n \in \mathcal{N},$$ | |||
then <math>\nu = \mu</math>. | |||
A detailed proof Theorems 2.1 and 2.2 can be found in section 2 of the Supplementary Materials, which can be downloaded [https://proceedings.neurips.cc/paper/2018/hash/411ae1bf081d1674ca6091f8c59a266f-Abstract.html here]. | |||
== Experimental Results == | == Experimental Results == | ||
The model was applied to three types of algorithms: an Autoencoder (AE), a multilayer perceptron, and a radial basis function network. | |||
'''Autoencoder''' | |||
Corrupted images were restored as a part of this experiment. Grayscale handwritten digits were obtained from the MNIST database. A 13 by 13 (169 pixels) square was removed from each 28 by 28 (784 pixels) image. The location of the square was uniformly sampled for each image. The autoencoder used included 5 hidden layers. The first layer used ReLU activation functions while the subsequent layers utilized sigmoids. The loss function was computed using pixels from outside the mask. | |||
Popular imputation techniques were compared against the conducted experiment: | |||
''k-nn:'' Replaced missing features with the mean of respective features calculated using K nearest training samples. Here, K=5. | |||
''mean:'' Replaced missing features with the mean of respective features calculated using all incomplete training samples. | |||
''dropout:'' Dropped input neutrons with missing values. | |||
Moreover, a context encoder (CE) was trained by replacing missing features with their means. Unlike mean imputation, the complete data was used in the training phase. The method under study performed better than the imputation methods inside and outside the mask. Additionally, the method under study outperformed CE based on the whole area and area outside the mask. | |||
The mean square error of reconstruction is used to test each method. The errors calculated over the whole area, inside and outside the mask are shown in Table 1, which indicates the method introduced in this paper is the most competitive. | |||
[[File:Group3_Table1.png |center]] | |||
<div align="center">Table 1: Mean square error of reconstruction on MNIST incomplete images scaled to [0, 1]</div> | |||
'''Multilayer Perceptron''' | |||
A multilayer perceptron with 3 ReLU hidden layers was applied to a multi-class classification problem on the Epileptic Seizure Recognition (ESR) data set taken from [3]. Each 178-dimensional vector (out of 11500 samples) is the EEG recording of a given person for 1 second, categorized into one of 5 classes. To generate missing attributes, 25%, 50%, 75%, and 90% of observations were randomly removed. The aforementioned imputation methods were used in addition to Multiple Imputation by Chained Equation (mice) and a mixture of Gaussians (GMM). The former utilizes the conditional distribution of data by Markov chain Monte Carlo techniques to draw imputations. The latter replaces missing features with values sampled from GMM estimated from incomplete data using the EM algorithm. | |||
Double 5-fold cross-validation was used to report classification results. The classical accuracy measure is usually being used for accessing the results. The model under study outperformed classical imputation methods, which give reasonable results only for a low number of missing values. The method under study performs nearly as well as CE, even though CE had access to complete training data. | |||
'''Radial Basis Function Network''' | |||
RBFN can be considered as a minimal architecture implementing our model, which contains only one hidden layer. A cross-entropy function was applied to a softmax in the output layer. Two-class data sets retrieved from the UCI repository [4] with internally missing attributes were used. Since the classification is binary, two additional SVM kernel models which work directly with incomplete data without performing any imputations were included in the experiment: | |||
''geom:'' The objective function is based on the geometric interpretation of the margin and aims to maximize the margin of each sample in its own subspace [5]. | |||
''karma:'' This algorithm iteratively tunes kernel classifier under low-rank assumptions [6]. | |||
The above SVM methods were combined with RBF kernel function. The number of RBF units was selected in the inner cross-validation from the range {25, 50, 75, 100}. Initial centers of RBFNs were randomly selected from training data while variances were samples from <math>N(0,1)</math> distribution. For SVM methods, the margin parameter <math>C</math> and kernel radius <math>\gamma</math> were selected from <math>\{2^k :k=−5,−3,...,9\}</math> for both parameters. For karma, additional parameter <math>\gamma_{karma}</math> was selected from the set <math>\{1, 2\}</math>. | |||
The model under study outperformed imputation techniques in almost all cases. It partially confirms that the use of raw incomplete data in neural networks is a usually better approach than filling missing attributes before the learning process. Moreover, it obtained more accurate results than modified kernel methods, which directly work on incomplete data. The performance of the model was once again comparable to, and in some cases better than CE, which had access to the complete data. | |||
== Conclusion == | == Conclusion == | ||
The results with these experiments along with the theoretical results conclude that this novel approach for dealing with missing data through a modification of a neural network is beneficial and outperforms many existing methods. This approach, which utilizes representing missing data with a probability density function, allows a neural network to determine a more generalized and accurate response of the neuron. | |||
== Critiques == | == Critiques == | ||
- A simulation study where the mechanism of missingness is known will be interesting to examine. Doing this will allow us to see when the proposed method is better than existing methods, and under what conditions. | |||
- This method of imputing incomplete data has many limitations. In most cases, we have a missing data point. Consequently, we are facing a relatively small amount of data that does not require training of a neural network. For a large dataset, missing records do not seem to be very crucial because obtaining data will be relatively easier. Thus, using an empirical way of imputing data such as a majority vote will be sufficient. | |||
- An interesting application of this problem is in NLP. In NLP, especially Question Answering, there is a problem where a query is given and an answer must be retrieved, but the knowledge base is incomplete. There is therefore a requirement for the model to be able to infer information from the existing knowledge base in order to answer the question. Although this problem is a little more contrived than the one mentioned here, it is nevertheless similar in nature because it requires the ability to probabilistically determine some value which can then be used as a response. | |||
- For the first sentence in the introduction section, it might be better to use "to deal with missing and incomplete data" rather than use "dealing with missing and incomplete data" | |||
- Based on my R experience, there is one useful function "knnImputation" under the package DMwR, which is very helpful when dealing with missing and incomplete data. This function uses the k-nearest neighbors to fill in the unknown (NA) values in a data set. The users can modify the number of neighbors required in the calculation of each missing value. | |||
- The experiments in this paper evaluate this method against low amounts of missing data. It would be interesting to see the properties of this imputation when a majority of the data is missing, and see if this method can outperform dropout training in this setting (dropout is known to be surprisingly robust even at high drop levels). | |||
- This problem can possibly be applied to face recognition were given a blurry image of a person's face, the neural network can make the image clearer such that the face of the person would be visible for humans to see and also possible for the software to identify who the person is. | |||
- This novel approach can also be applied to restoring damaged handwritten historical documents. By feeding in a damaged document with portions of unreadable texts, the neural network can add missing information utilizing a trained context encoder | |||
- It will be interesting to see how this method performs with audio data, i.e. say if there are parts of an audio file that are missing, whether the neural network will be able to learn the underlying distribution and impute the missing sections of speech. | |||
- In general, data are usually missing in a specific part of the content. For example, old books usually have first couple page or last couple pages that are missing. It would be interesting to see that how the distribution of "missing data" will be applied in those cases. | |||
- In this paper, the researchers were able to outperform existing imputation methods using neural networks. It would be really nice to see how does the usage of neural networks impacts the need for amount of data, and how much more training is required in comparison to the other algorithms provided in this paper. | |||
- It might be an interesting approach to investigate how the size of missing data may influence the training. For example, in the MNIST AutoEncoder, some algorithms involve masks to generate more general images and avoid overfitting. The approach could compare the result by changing the size of the "missing" part to illustrate to what degree can we ignore the missing data and view them as assistance. | |||
- It would be nice to see how the method under study outperforms both the Multilayer Perceptron and Radial Basis Function Network methods mentioned in the summary. Since these two methods are placed under the Experimental Results section, it is expected that they consist of more justifications and supporting evidence (analytical results, tables, graphs, etc.) than what have been presented, so that it is more convincing for the readers. | |||
- Both KNN imputation and mean imputation are valid techniques to solve the problem, one possible future study on this topic is to explore which one of the two methods above will perform better given the sparsity of the dataset. Another possible study is that if there are methods that can make better inferences on original input, an example is described in the paper (https://cs.uwaterloo.ca/~ilyas/papers/WuMLSys2020.pdf), where imputation is performed based on learning structural properties of data distributions. | |||
- This project has many applications in the real world. One of the examples is to forecast the average height in Canada. We know that people are born and die every second. Also, many people are not accessible which means we cannot obtain the exactly true data. Thus, we can just feed the observed data to the neural network then we will get the predicted result. This can also be applied to the investment world since the data are changing every second. | |||
-If the performance and efficiency of training neural network models with the original dataset directly are generally better than traditional algorithms, this would be a practical method to use. | |||
- It is interesting to see how we can fill missing data with machine learning. The standard way to fill missing numeric data is to use mean, and using KNN is really a talented way of doing this. | |||
- This project focus on dealing with incomplete or missing data which has a wide application on many aspects such as image recognition and damaged documents, etc. This is a novel application for machine learning and inspires us for the usage of the missing data. | |||
- Sometimes, these methods to deal with miss data is not cost-worthy, as a result, when the missing data doesn't exceed a certain threshold, we need to consider whether we need to use this method for missing data or not. | |||
- Since there are bunch of equations and math in the analysis part, it will be helpful if examples with application of these equations included in this summary. | |||
-As the author explains there is no loss in the information in the introduction section, it could explain more about how much missing there are that leads to this conclusion and provide a threshold which that the percentage of missing data is within an acceptable range. | |||
== References == | == References == | ||
| Line 36: | Line 174: | ||
[2] Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep learning. MIT press, 2016. | [2] Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep learning. MIT press, 2016. | ||
[3] Ralph G Andrzejak, Klaus Lehnertz, Florian Mormann, Christoph Rieke, Peter David, and Christian E Elger. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Physical Review E, 64(6):061907, 2001. | |||
[4] Arthur Asuncion and David J. Newman. UCI Machine Learning Repository, 2007. | |||
[5] Gal Chechik, Geremy Heitz, Gal Elidan, Pieter Abbeel, and Daphne Koller. Max-margin classification of data with absent features. Journal of Machine Learning Research, 9:1–21, 2008. | |||
[6] Elad Hazan, Roi Livni, and Yishay Mansour. Classification with low rank and missing data. In Proceedings of The 32nd International Conference on Machine Learning, pages 257–266, 2015. | |||
Latest revision as of 14:36, 6 December 2020
Presented by
Grace Tompkins, Tatiana Krikella, Swaleh Hussain
Introduction
One of the fundamental challenges in machine learning and data science is dealing with missing and incomplete data. This paper proposes a theoretically justified methodology for using incomplete data in neural networks, eliminating the need for direct completion of data by imputation or other commonly used methods in the existing literature. The authors propose identifying missing data points with a parametric density and then training it together with the rest of the network's parameters. The neuron's response at the first hidden layer is generalized by taking its expected value to process this probabilistic representation. This process is essentially calculating the average activation of the neuron over imputations drawn from the missing data's density and this proposed approach is advantageous because it has the ability to train neural networks using incomplete observations from datasets, which are ubiquitous in practice. Furthermore, this approach also requires minimal adjustments and modifications to existing architectures. Theoretical results of this study show that this process does not lead to a loss of information, while experimental results showed the practical uses of this methodology on several different types of networks.
Related Work
Currently, dealing with incomplete inputs in machine learning requires filling absent attributes based on complete, observed data. Two commonly used methods are mean imputation and [math]\displaystyle{ k }[/math]-nearest neighbors (k-NN) imputation. In the former (mean imputation), the missing value is replaced by the mean of all available values of that feature in the dataset. In the latter (k-NN imputation), the missing value is also replaced by the mean, however, it is now computed using only the k "closest" samples in the dataset. For example, if the dataset is numerical, Euclidean distance could be used as a measure of "closeness". Other methods for dealing with missing data involve training separate neural networks and extreme learning machines. Probabilistic models of incomplete data can also be built depending on the mechanism missingness (i.e. whether the data is Missing At Random (MAR), Missing Completely At Random (MCAR), or Missing Not At Random (MNAR)), which can be fed into a particular learning model. Further, the decision function can also be trained using available/visible inputs alone. Previous work using neural networks for missing data includes a paper by Bengio and Gringras [1] where the authors used recurrent neural networks with feedback into the input units to fill absent attributes solely to minimize the learning criterion. Goodfellow et. al. [2] also used neural networks by introducing a multi-prediction deep Boltzmann machine that could perform classification on data with missingness in the inputs.
Layer for Processing Missing Data
In this approach, the adaptation of a given neural network to incomplete data relies on two steps: the estimation of the missing data and the generalization of the neuron's activation.
Let [math]\displaystyle{ (x,J) }[/math] represent a missing data point, where [math]\displaystyle{ x \in \mathbb{R}^D }[/math], and [math]\displaystyle{ J \subset \{1,...,D\} }[/math] is a set of attributes with missing data. [math]\displaystyle{ (x,J) }[/math] therefore represents an "incomplete" data point for which [math]\displaystyle{ |J| }[/math]-many entries are unknown - examples of this could be a list of daily temperature readings over a week where temperature was not recorded on the third day ([math]\displaystyle{ x\in \mathbb{R}^7, J= \{3\} }[/math]), an audio transcript that goes silent for certain timespans, or images that are partially masked out (as discussed in the examples).
For each missing point [math]\displaystyle{ (x,J) }[/math], define an affine subspace consisting of all points which coincide with [math]\displaystyle{ x }[/math] on known coordinates [math]\displaystyle{ J'=\{1,…,N\}/J }[/math]:
where [math]\displaystyle{ e_J=[e_j]_{j\in J} }[/math] and [math]\displaystyle{ e_j }[/math] is the [math]\displaystyle{ j^{th} }[/math] canonical vector in [math]\displaystyle{ \mathbb{R}^D }[/math].
Assume that the missing data points come from the D-dimensional probability distribution, [math]\displaystyle{ F }[/math]. In their approach, the authors assume that the data points follow a mixture of Gaussians (GMM) with diagonal covariance matrices. By choosing diagonal covariance matrices, the number of model parameters is reduced. To model the missing points [math]\displaystyle{ (x,J) }[/math], the density [math]\displaystyle{ F }[/math] is restricted to the affine subspace [math]\displaystyle{ S }[/math]. Thus, possible values of [math]\displaystyle{ (x,J) }[/math] are modelled using the conditional density [math]\displaystyle{ F_S: S \to \mathbb{R} }[/math],
To process the missing data by a neural network, the authors propose that only the first hidden layer needs modification. Specifically, they generalize the activation functions of all the neurons in the first hidden layer of the network to process the probability density functions representing the missing data points. For the conditional density function [math]\displaystyle{ F_S }[/math], the authors define the generalized activation of a neuron [math]\displaystyle{ n: \mathbb{R}^D \to \mathbb{R} }[/math] on [math]\displaystyle{ F_S }[/math] as:
provided that the expectation exists.
The following two theorems describe how to apply the above generalizations to both the ReLU and the RBF neurons, respectively.
Theorem 3.1 Let [math]\displaystyle{ F = \sum_i{p_iN(m_i, \Sigma_i)} }[/math] be the mixture of (possibly degenerate) Gaussians. Given weights [math]\displaystyle{ w=(w_1, ..., w_D) \in \mathbb{R}^D, }[/math][math]\displaystyle{ b \in \mathbb{R} }[/math], we have
where [math]\displaystyle{ NR(x)=\text{ReLU}[N(x,1)] }[/math] and [math]\displaystyle{ \text{ReLU}_{w,b}(x)=\text{max}(w^{\top}+b, 0) }[/math], [math]\displaystyle{ w \in \mathbb{R}^D }[/math] and [math]\displaystyle{ b \in \mathbb{R} }[/math] is the bias.
Theorem 3.2 Let [math]\displaystyle{ F = \sum_i{p_iN(m_i, \Sigma_i)} }[/math] be the mixture of (possibly degenerate) Gaussians and let the RBF unit be parametrized by [math]\displaystyle{ N(c, \Gamma) }[/math]. We have:
In the case where the data set contains no missing values, the generalized neurons reduce to classical ones, since the distribution [math]\displaystyle{ F }[/math] is only used to estimate possible values at missing attributes. However, if one wishes to use an incomplete data set in the testing stage, then an incomplete data set must be used to train the model.
[math]\displaystyle{ }[/math]
Theoretical Analysis
The main theoretical results, which are summarized below, show that using generalized neuron's activation at the first layer does not lead to the loss of information.
Let the generalized response of a neuron [math]\displaystyle{ n: \mathbb{R}^D \rightarrow \mathbb{R} }[/math] evaluated on a probability measure [math]\displaystyle{ \mu }[/math] which is given by
Theorem 4.1. Let [math]\displaystyle{ \mu }[/math], [math]\displaystyle{ v }[/math] be probabilistic measures satisfying [math]\displaystyle{ \int ||x|| d \mu(x) \lt \infty }[/math]. If
then [math]\displaystyle{ \nu = \mu }[/math].
Theorem 4.1 shows that a neural network with generalized ReLU units is able to identify any two probability measures. The proof presented by the authors uses the Universal Approximation Property (UAP), and is summarized as follows.
Sketch of Proof Let [math]\displaystyle{ w \in \mathbb{R}^D }[/math] be fixed and define the set
The first step of the proof involves showing that [math]\displaystyle{ F_w }[/math] contains all continuous and bounded functions. The authors show this by showing that a piecewise continuous function that is affine linear on specific intervals, [math]\displaystyle{ Q }[/math], is in the set [math]\displaystyle{ F_w }[/math]. This involves re-writing [math]\displaystyle{ Q }[/math] as a sum of tent-like piecewise linear functions, [math]\displaystyle{ T }[/math] and showing that [math]\displaystyle{ T \in F_w }[/math] (since it is sufficient to only show [math]\displaystyle{ T \in F_w }[/math]).
Next, the authors show that an arbitrary bounded continuous function [math]\displaystyle{ G }[/math] is in [math]\displaystyle{ F_w }[/math] by the Lebesgue dominated convergence theorem.
Then, as [math]\displaystyle{ cos(\cdot), sin(\cdot) \in F_w }[/math], the function
and we have the equality
Since [math]\displaystyle{ w }[/math] was arbitrarily chosen, we can conclude that [math]\displaystyle{ \mu = \nu }[/math] as the characteristic functions of the two measures coincide.
A result analogous to Theorem 4.1 for RBF can also be obtained.
Theorem 2.1 Let [math]\displaystyle{ \mu, \nu }[/math] be probabilistic measures. If $$ RBF_{m,\alpha}(\mu) = RBF_{m,\alpha}(\nu) \text{ for every } m \in \mathbb{R}^D, \alpha > 0,$$ then [math]\displaystyle{ \nu = \mu }[/math].
More general results can be obtained making stronger assumptions on the probability measures. For example, if a given family of neurons satisfies UAP, then their generalization can identify any probability measure with compact support.
Theorem 2.2 Let [math]\displaystyle{ \mu, \nu }[/math] be probabilistic measures with compact support. Let [math]\displaystyle{ \mathcal{N} }[/math] be a family of functions having UAP. If $$n(\mu) = n(\nu) \text{ for every } n \in \mathcal{N},$$ then [math]\displaystyle{ \nu = \mu }[/math].
A detailed proof Theorems 2.1 and 2.2 can be found in section 2 of the Supplementary Materials, which can be downloaded here.
Experimental Results
The model was applied to three types of algorithms: an Autoencoder (AE), a multilayer perceptron, and a radial basis function network.
Autoencoder
Corrupted images were restored as a part of this experiment. Grayscale handwritten digits were obtained from the MNIST database. A 13 by 13 (169 pixels) square was removed from each 28 by 28 (784 pixels) image. The location of the square was uniformly sampled for each image. The autoencoder used included 5 hidden layers. The first layer used ReLU activation functions while the subsequent layers utilized sigmoids. The loss function was computed using pixels from outside the mask.
Popular imputation techniques were compared against the conducted experiment:
k-nn: Replaced missing features with the mean of respective features calculated using K nearest training samples. Here, K=5.
mean: Replaced missing features with the mean of respective features calculated using all incomplete training samples.
dropout: Dropped input neutrons with missing values.
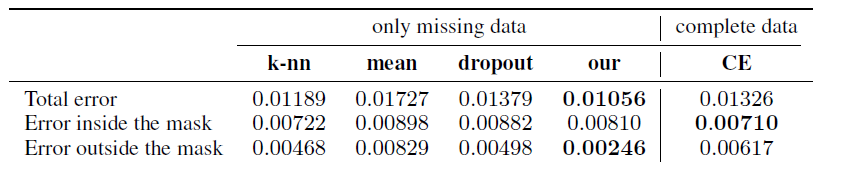
Moreover, a context encoder (CE) was trained by replacing missing features with their means. Unlike mean imputation, the complete data was used in the training phase. The method under study performed better than the imputation methods inside and outside the mask. Additionally, the method under study outperformed CE based on the whole area and area outside the mask.
The mean square error of reconstruction is used to test each method. The errors calculated over the whole area, inside and outside the mask are shown in Table 1, which indicates the method introduced in this paper is the most competitive.
Multilayer Perceptron
A multilayer perceptron with 3 ReLU hidden layers was applied to a multi-class classification problem on the Epileptic Seizure Recognition (ESR) data set taken from [3]. Each 178-dimensional vector (out of 11500 samples) is the EEG recording of a given person for 1 second, categorized into one of 5 classes. To generate missing attributes, 25%, 50%, 75%, and 90% of observations were randomly removed. The aforementioned imputation methods were used in addition to Multiple Imputation by Chained Equation (mice) and a mixture of Gaussians (GMM). The former utilizes the conditional distribution of data by Markov chain Monte Carlo techniques to draw imputations. The latter replaces missing features with values sampled from GMM estimated from incomplete data using the EM algorithm.
Double 5-fold cross-validation was used to report classification results. The classical accuracy measure is usually being used for accessing the results. The model under study outperformed classical imputation methods, which give reasonable results only for a low number of missing values. The method under study performs nearly as well as CE, even though CE had access to complete training data.
Radial Basis Function Network
RBFN can be considered as a minimal architecture implementing our model, which contains only one hidden layer. A cross-entropy function was applied to a softmax in the output layer. Two-class data sets retrieved from the UCI repository [4] with internally missing attributes were used. Since the classification is binary, two additional SVM kernel models which work directly with incomplete data without performing any imputations were included in the experiment:
geom: The objective function is based on the geometric interpretation of the margin and aims to maximize the margin of each sample in its own subspace [5].
karma: This algorithm iteratively tunes kernel classifier under low-rank assumptions [6].
The above SVM methods were combined with RBF kernel function. The number of RBF units was selected in the inner cross-validation from the range {25, 50, 75, 100}. Initial centers of RBFNs were randomly selected from training data while variances were samples from [math]\displaystyle{ N(0,1) }[/math] distribution. For SVM methods, the margin parameter [math]\displaystyle{ C }[/math] and kernel radius [math]\displaystyle{ \gamma }[/math] were selected from [math]\displaystyle{ \{2^k :k=−5,−3,...,9\} }[/math] for both parameters. For karma, additional parameter [math]\displaystyle{ \gamma_{karma} }[/math] was selected from the set [math]\displaystyle{ \{1, 2\} }[/math].
The model under study outperformed imputation techniques in almost all cases. It partially confirms that the use of raw incomplete data in neural networks is a usually better approach than filling missing attributes before the learning process. Moreover, it obtained more accurate results than modified kernel methods, which directly work on incomplete data. The performance of the model was once again comparable to, and in some cases better than CE, which had access to the complete data.
Conclusion
The results with these experiments along with the theoretical results conclude that this novel approach for dealing with missing data through a modification of a neural network is beneficial and outperforms many existing methods. This approach, which utilizes representing missing data with a probability density function, allows a neural network to determine a more generalized and accurate response of the neuron.
Critiques
- A simulation study where the mechanism of missingness is known will be interesting to examine. Doing this will allow us to see when the proposed method is better than existing methods, and under what conditions.
- This method of imputing incomplete data has many limitations. In most cases, we have a missing data point. Consequently, we are facing a relatively small amount of data that does not require training of a neural network. For a large dataset, missing records do not seem to be very crucial because obtaining data will be relatively easier. Thus, using an empirical way of imputing data such as a majority vote will be sufficient.
- An interesting application of this problem is in NLP. In NLP, especially Question Answering, there is a problem where a query is given and an answer must be retrieved, but the knowledge base is incomplete. There is therefore a requirement for the model to be able to infer information from the existing knowledge base in order to answer the question. Although this problem is a little more contrived than the one mentioned here, it is nevertheless similar in nature because it requires the ability to probabilistically determine some value which can then be used as a response.
- For the first sentence in the introduction section, it might be better to use "to deal with missing and incomplete data" rather than use "dealing with missing and incomplete data"
- Based on my R experience, there is one useful function "knnImputation" under the package DMwR, which is very helpful when dealing with missing and incomplete data. This function uses the k-nearest neighbors to fill in the unknown (NA) values in a data set. The users can modify the number of neighbors required in the calculation of each missing value.
- The experiments in this paper evaluate this method against low amounts of missing data. It would be interesting to see the properties of this imputation when a majority of the data is missing, and see if this method can outperform dropout training in this setting (dropout is known to be surprisingly robust even at high drop levels).
- This problem can possibly be applied to face recognition were given a blurry image of a person's face, the neural network can make the image clearer such that the face of the person would be visible for humans to see and also possible for the software to identify who the person is.
- This novel approach can also be applied to restoring damaged handwritten historical documents. By feeding in a damaged document with portions of unreadable texts, the neural network can add missing information utilizing a trained context encoder
- It will be interesting to see how this method performs with audio data, i.e. say if there are parts of an audio file that are missing, whether the neural network will be able to learn the underlying distribution and impute the missing sections of speech.
- In general, data are usually missing in a specific part of the content. For example, old books usually have first couple page or last couple pages that are missing. It would be interesting to see that how the distribution of "missing data" will be applied in those cases.
- In this paper, the researchers were able to outperform existing imputation methods using neural networks. It would be really nice to see how does the usage of neural networks impacts the need for amount of data, and how much more training is required in comparison to the other algorithms provided in this paper.
- It might be an interesting approach to investigate how the size of missing data may influence the training. For example, in the MNIST AutoEncoder, some algorithms involve masks to generate more general images and avoid overfitting. The approach could compare the result by changing the size of the "missing" part to illustrate to what degree can we ignore the missing data and view them as assistance.
- It would be nice to see how the method under study outperforms both the Multilayer Perceptron and Radial Basis Function Network methods mentioned in the summary. Since these two methods are placed under the Experimental Results section, it is expected that they consist of more justifications and supporting evidence (analytical results, tables, graphs, etc.) than what have been presented, so that it is more convincing for the readers.
- Both KNN imputation and mean imputation are valid techniques to solve the problem, one possible future study on this topic is to explore which one of the two methods above will perform better given the sparsity of the dataset. Another possible study is that if there are methods that can make better inferences on original input, an example is described in the paper (https://cs.uwaterloo.ca/~ilyas/papers/WuMLSys2020.pdf), where imputation is performed based on learning structural properties of data distributions.
- This project has many applications in the real world. One of the examples is to forecast the average height in Canada. We know that people are born and die every second. Also, many people are not accessible which means we cannot obtain the exactly true data. Thus, we can just feed the observed data to the neural network then we will get the predicted result. This can also be applied to the investment world since the data are changing every second.
-If the performance and efficiency of training neural network models with the original dataset directly are generally better than traditional algorithms, this would be a practical method to use.
- It is interesting to see how we can fill missing data with machine learning. The standard way to fill missing numeric data is to use mean, and using KNN is really a talented way of doing this.
- This project focus on dealing with incomplete or missing data which has a wide application on many aspects such as image recognition and damaged documents, etc. This is a novel application for machine learning and inspires us for the usage of the missing data.
- Sometimes, these methods to deal with miss data is not cost-worthy, as a result, when the missing data doesn't exceed a certain threshold, we need to consider whether we need to use this method for missing data or not.
- Since there are bunch of equations and math in the analysis part, it will be helpful if examples with application of these equations included in this summary.
-As the author explains there is no loss in the information in the introduction section, it could explain more about how much missing there are that leads to this conclusion and provide a threshold which that the percentage of missing data is within an acceptable range.
References
[1] Yoshua Bengio and Francois Gingras. Recurrent neural networks for missing or asynchronous data. In Advances in neural information processing systems, pages 395–401, 1996.
[2] Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep learning. MIT press, 2016.
[3] Ralph G Andrzejak, Klaus Lehnertz, Florian Mormann, Christoph Rieke, Peter David, and Christian E Elger. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Physical Review E, 64(6):061907, 2001.
[4] Arthur Asuncion and David J. Newman. UCI Machine Learning Repository, 2007.
[5] Gal Chechik, Geremy Heitz, Gal Elidan, Pieter Abbeel, and Daphne Koller. Max-margin classification of data with absent features. Journal of Machine Learning Research, 9:1–21, 2008.
[6] Elad Hazan, Roi Livni, and Yishay Mansour. Classification with low rank and missing data. In Proceedings of The 32nd International Conference on Machine Learning, pages 257–266, 2015.