Visual Reinforcement Learning with Imagined Goals: Difference between revisions
(Technical) |
|||
| (107 intermediate revisions by 27 users not shown) | |||
| Line 1: | Line 1: | ||
[ | Video and details of this work are available [https://sites.google.com/site/visualrlwithimaginedgoals/ here] | ||
=Introduction and Motivation= | =Introduction and Motivation= | ||
Humans are able to accomplish many tasks without any explicit or supervised training, simply by exploring their environment | Humans are able to accomplish many tasks without any explicit or supervised training, simply by exploring their environment. We are able to set our own goals and learn from our experiences, and thus are able to accomplish specific tasks without ever having been trained explicitly for them. It would be ideal if an autonomous agent can also set its own goals and learn from its environment. | ||
In the paper “Visual Reinforcement Learning with Imagined Goals”, the authors are able to devise such an unsupervised reinforcement learning system. They introduce a system that sets abstract (self-generated) goals and autonomously learns to achieve those goals. They then show that the system can use these autonomously learned skills to perform a variety of user-specified goals, such as pushing objects, grasping objects, and opening doors, without any additional learning. Lastly, they demonstrate that their method is efficient enough to work in the real world on a Sawyer robot. The robot learns to set and achieve goals with only images as the input to the system. | |||
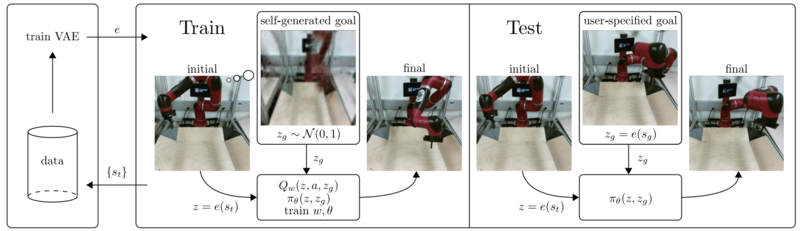
The | The algorithm proposed by the authors is summarized below. A Variational Auto Encoder (VAE) on the (left) learns a latent representation of images gathered during training time (center). These latent variables are used to train a policy on imagined goals (center), which can then be used for accomplishing user-specified goals (right). | ||
[[File: WF_Sec_11Nov25_01.png |center| 800px]] | |||
=Related Work = | =Related Work = | ||
Many previous works on vision-based deep reinforcement learning for robotics studied a variety of behaviors such as grasping [1], pushing [2], navigation [3], and other manipulation tasks [4]. However, their assumptions on the models limit their suitability for training general-purpose robots. Some previous works such as Levine et al. [11] proposed time-varying models which require episodic setups and thus are hard to generalize to non-episodic and continuous learning scenarios. There are also other works such as Pinto et al. [12] that proposed an approach using goal images, but it requires instrumented training simulations. Lillicrap et al. [13] use fully model-free training (Model-based RL uses experience to construct an internal model of the transitions and immediate outcomes in the environment. Appropriate actions are then chosen by searching or planning in this world model. Model-free RL, on the other hand, uses experience to learn directly one or both of two simpler quantities (state/action values or policies) which can achieve the same optimal behavior but without estimation or use of a world model. Given a policy, a state has a value, defined in terms of the future utility that is expected to accrue starting from that state [https://www.princeton.edu/~yael/Publications/DayanNiv2008.pdf Reinforcement learning: The Good, The Bad and The Ugly].), but does not learn goal-conditioned skills. The authors' experiments indicate that this technique is difficult to extend to goal-conditioned setting | |||
with image inputs. There are currently no examples that use model-free reinforcement learning for learning policies to train on real-world robotic systems without having ground-truth information. | |||
In this paper, the authors utilize a goal-conditioned value function to tackle more general tasks through goal relabelling, which improves sample efficiency. Goal relabelling is to retroactively relabel samples in the replay buffer with goals sampled from the latent representation. The paper uses sample random goals from learned latent space to use as replay goals for off-policy Q-learning rather than restricting to states seen along the sampled trajectory as was done in the earlier works. Specifically, they use a model-free Q-learning method that operates on raw state observations and actions. This approach allows for a single transition tuple to be converted into potentially infinite valid training examples. | |||
Unsupervised learning has been used in a number of prior works to acquire better representations of reinforcement learning. In these methods, the learned representation is used as a substitute for the state for the policy. However, these methods require additional information, such as access to the ground truth reward function based on the true state during training time [5], expert trajectories [6], human demonstrations [7], or pre-trained object-detection features [8]. In contrast, the authors learn to generate goals and use the learned representation to get a reward function for those goals without any of these extra sources of supervision. | |||
=Goal-Conditioned Reinforcement Learning= | |||
The ultimate goal in reinforcement learning is to learn a policy <math>\pi</math>, that when given a state <math>s_t</math> and goal <math>g</math> (desired state), can dictate the optimal action <math>a_t</math>. The optimal action <math>a_t</math> is defined as an action which maximizes the expected return denoted by <math>R_t</math> and defined as <math>R_t = \mathbb{E}[\sum_{i = t}^T\gamma^{(i-t)}r_i]</math>, where <math>r_i = r(s_i, a_i, s_{i+1})</math> is the reward for performing action <math>a_i</math> when the current state is <math>s_i</math> and the goal state is <math>s_{i+1}</math> and <math>\gamma</math> is a discount factor which determines the relative importance given to rewards at different times. | |||
In the | In this paper, goals are not explicitly defined during training. If a goal is not explicitly defined, the agent must be able to generate a set of synthetic goals automatically. Suppose we let an autonomous agent explore an environment with a random policy. After executing each action, start and stop state observations are collected and stored. All state observations are images. For training, the agent can randomly select starting states and goals images from the set of state observations. | ||
Moreover, if we aim to accomplish a variety of tasks, we can construct a goal-conditioned policy and reward, and optimize the expected return with respect to a goal distribution | |||
<center><math>E_{g \sim G}[E_{r_i,s_i \sim E, a_i \sim \pi}[R_0]]</math></center> | |||
where <math>G</math> is the set of goals and the reward is also a function of <math>g</math> | |||
Now given a set of all possible states, a goal, and an initial state, a reinforcement learning framework can be used to find the optimal policy such that a chosen value function is maximized. However, to implement such a framework, a reward function needs to be defined. One choice for the reward is the negative distance between the current state and the goal state, so that maximizing the reward corresponds to minimizing the distance to the goal state. | |||
[[File:human-giving-goal.png|center|thumb|400px|The task: Make the world look like this image. [9]]] | |||
In reinforcement learning, a goal-conditioned Q-function can be used to find a single policy to maximize rewards and therefore reach goal states. A goal-conditioned Q-function <math>Q(s,a,g)</math> tells us how good an action <math>a</math> is, given the current state <math>s</math> and goal <math>g</math>. For example, a Q-function tells us, “How good is it to move my hand up (action <math>a</math>), if I’m holding a plate (state <math>s</math>) and want to put the plate on the table (goal <math>g</math>)?” Once this Q-function is trained, a goal-conditioned policy can be obtained by performing the following optimization | |||
= | <div align="center"> | ||
<math>\pi(s,g) = max_a Q(s,a,g)</math> | |||
</div> | |||
which effectively says, “choose the best action according to this Q-function.” By using this procedure, one can obtain a policy that maximizes the sum of rewards, i.e. reaches various goals. | |||
The reason why Q-learning is popular is that it can be trained in an off-policy manner. Therefore, the only things a Q-function needs are samples of state, action, next state, goal, and reward <math>(s,a,s′,g,r)</math>. This data can be collected by any policy and can be reused across multiples tasks. So a preliminary goal-conditioned Q-learning algorithm looks like this: | |||
[[File:ql.png|center|600px]] | |||
From the tuple <math>(s,a,s',g,r)</math>, an approximate Q-function paramaterized by <math>w</math> can be trained by minimizing the Bellman error: | |||
<div | <div align="center"> | ||
<math>\mathcal{E}(w) = \frac{1}{2} || Q_w(s,a,g) -(r + \gamma \max_{a'} Q_{\overline{w}}(s',a',g)) ||^2 </math> | |||
</div> | |||
where <math>\overline{w}</math> is treated as some constant. | |||
The | The main drawback in this training procedure is collecting data. In theory, one could learn to solve various tasks without even interacting with the world if more data are available. Unfortunately, it is difficult to learn an accurate model of the world, so sampling is usually performed to get state-action-next-state data, <math> (s,a,s′)</math> . However, if the reward function <math>r(s,g)</math> can be accessed, one can retroactively relabel goals and recompute rewards. This way, more data can be artificially generated given a single <math>(s,a,s′)</math> tuple. As a result, the training procedure can be modified like so: | ||
[[File:qlr.png|center|600px]] | |||
This goal resampling makes it possible to simultaneously learn how to reach multiple goals at once without needing more data from the environment. Thus, this simple modification can result in substantially faster learning. However, the method described above makes two major assumptions: (1) you have access to a reward function and (2) you have access to a goal sampling distribution <math>p(g)</math>. When moving to vision-based tasks where goals are images, both of these assumptions introduce practical concerns, as the task of generating goal images is fairly intensive. | |||
This | |||
For one, a fundamental problem with this reward function is that it assumes that the distance between raw images will yield semantically useful information. But images are noisy and a large amount of information in an image may not be related to the object we analyze. Thus, the distance between the two images may not correlate with their semantic distance. | |||
Second, because the goals are images, a goal image distribution <math>p(g)</math> is needed so that one can sample goal images. Manually designing a distribution over goal images is a non-trivial task and image generation is still an active field of research. It would be ideal if the agent can autonomously imagine its own goals and learn how to reach them. | |||
Retroactively generating goals is also explored in tabular domains in [15]and in continuous domains in [14] using hindsight experience replay (HER). However, HER is | |||
limited to sampling goals seen along a trajectory, which greatly limits the number and diversity of goals with which one can relabel a given transition. | |||
=Variational Autoencoder= | |||
Variational autoencoders can learn structured latent representations of high dimensional data. VAE contains an encoder <math>p_\phi</math> and a decoder <math>p_\psi</math>. The former maps states to latent distributions, while the later maps latents to distributions over states. these two are jointly trained to maximize: | |||
<math>L(\psi,\phi;s^{(i)})=-\beta D_{KL}(q_\phi(z|s^{(i)}||p(z))+E_{q\phi(z|s^(i))}[log p_\psi(s^{(i)})|z])</math> | |||
</ | |||
where p(z) is a prior distribution, which is chosen to be unit Gaussian, <math>D_{KL}</math> is the Kullback-Leibler divergence, and <math>\beta</math> is a hyper-parameter that balances the two terms. | |||
This generative model | |||
converts high-dimensional observations <math>x</math>, like images, into low-dimensional latent variables <math>z</math>, and vice versa. The model is trained so that the latent variables capture the underlying factors of variation in an image. A current image <math>x</math> and goal image <math>x_g</math> can be converted into latent variables <math>z</math> and <math>z_g</math>, respectively. These latent variables can then be used to represent the state and goal for the reinforcement learning algorithm. Learning Q functions and policies on top of this low-dimensional latent space rather than directly on images result in faster learning. | |||
[[File:robot-interpreting-scene.png|center|thumb|600px|The agent encodes the current image (<math>x</math>) and goal image (<math>x_g</math>) into a latent space and use distances in that latent space for reward. [9]]] | |||
</ | |||
Using the latent variable representations for the images and goals also solves the problem of computing rewards. Instead of using pixel-wise error as our reward, the distance in the latent space is used as the reward to train the agent to reach a goal. The paper shows that this corresponds to rewarding reaching states that maximize the probability of the latent goal <math>z_g</math>. | |||
This generative model is also important because it allows an agent to easily generate goals in the latent space. In particular, the authors design the generative model so that latent variables are sampled from the VAE prior. This sampling mechanism is used for two reasons: First, it provides a mechanism for an agent to set its own goals. The agent simply samples a value for the latent variable from the generative model and tries to reach that latent goal. Second, this resampling mechanism is also used to relabel goals as mentioned above. Since the VAE prior is trained by real images, meaningful latent goals can be sampled from the latent variable prior. This will help the agent set its own goals and practice towards them if no goal is provided at test time. | |||
[[File:robot-imagining-goals.png|center|thumb|600px|Even without a human providing a goal, our agent can still generate its own goals, both for exploration and for goal relabeling. [9]]] | |||
The authors summarize the purpose of the latent variable representation of images as follows: (1) captures the underlying factors of a scene, (2) provides meaningful distances to optimize, and (3) provides an efficient goal sampling mechanism which can be used by the agent to generate its own goals. The overall method is called reinforcement learning with imagined goals (RIG) by the authors. | |||
The process involves starts with collecting data through a simple exploration policy. Possible alternative explorations could be employed here including off-the-shelf exploration bonuses or unsupervised reinforcement learning methods. Then, a VAE latent variable model is trained on state observations and fine-tuned during training. The latent variable model is used for multiple purposes: sampling a latent goal <math>z_g</math> from the model and conditioning the policy on this goal. All states and goals are embedded using the model’s encoder and then used to train the goal-conditioned value function. The authors then resample goals from the prior and compute rewards in the latent space. | |||
=Goal-Conditioned Policies with Unsupervised Representation Learning= | |||
The choice of a suitable goal representation is required for the devising of practical goal-conditioned value functions. When there is absence of domain specific knowledge and instrumentation, a choice is to set the goal space G to be the same as the state observation space S. However, when state is high-dimensional learning a goal-conditioned Q-function and policy becomes exceedingly difficult. One challenging problem with end-to-end approaches for visual RL tasks is that the resulting policy needs to learn both perception and control. Training the goal-conditioned value function requires defining a goal-conditioned reward. | |||
= | Their method jointly addresses a number of problems that arise when working with high-dimensional | ||
inputs such as images: sample efficient learning, reward specification, and automated goal-setting. These problems are addressed by learning a latent embedding using a <math>/beta - VAE</math>. This latent space is then used to represent the goal and state and retroactively relabel data with latent goals sampled from the VAE prior to improve sample efficiency. | |||
=Algorithm= | |||
[[File:algorithm1.png|center|thumb|600px|]] | |||
Algorithm 1 is called reinforcement learning with imagined goals (RIG). The data is first collected via a simple exploration policy. The proposed model allows for alternate exploration policies to be used which include off-the-shelf exploration bonuses or unsupervised reinforcement learning methods. Then, the authors train a VAE latent variable model on state observations and finetune it over the course of training. VAE latent space modeling is used to allow the conditioning of policy on the goal which is sampled from the latent model. The VAE model is also used to encode all the goals and the states. When the goal-conditioned value function is trained, the authors resample prior goals and compute rewards in the latent space using the equation | |||
<center><math display="inline"> r(s, g) = - || z - z_g ||_A \propto \sqrt{log(e_{\Phi}(z_g | s))} </math></center>. | |||
This equation is derived from the equation below. This is based on the choice to use the negative Mahalanobis distance in the latent space for the reward: | |||
<center><math display="inline"> r(s, g) = - || e(s) - e(g) ||_A = - || z - z_g ||_A </math></center> | |||
=Experiments= | |||
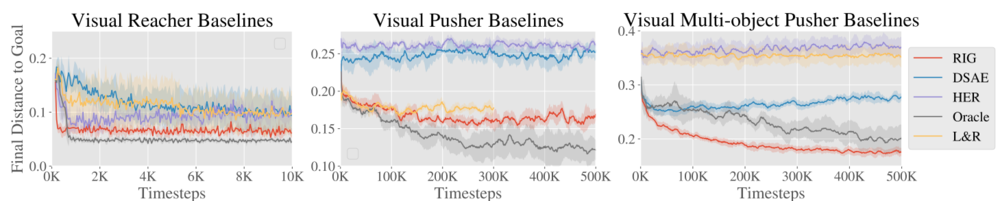
The authors evaluated their method against some prior algorithms and ablated versions of their approach on a suite of simulated and real-world tasks: Visual Reacher, Visual Pusher, and Visual Multi-Object Pusher. They compared their model with the following prior works: L&R, DSAE, HER, and Oracle. It is concluded that their approach substantially outperforms the previous methods and is close to the state-based "oracle" method in terms of efficiency and performance. | |||
This | The figure below shows the performance of different algorithms on this task. This involved a simulated environment with a Sawyer arm. The authors' algorithm was given only visual input, and the available controls were end-effector velocity. The plots show the distance to the goal state as a function of simulation steps. The Oracle, as a baseline, was given true object location information, as opposed to visual pixel information. | ||
[[File:WF_Sec_11Nov_25_02.png|1000px]] | |||
They then investigated the effectiveness of distances in the VAE latent space for the Visual Pusher task. They observed that latent distance significantly outperforms the log probability and pixel mean-squared error. The resampling strategies are also varied while fixing other components of the algorithm to study the effect of relabeling strategy. In this experiment, the RIG, which is an equal mixture of the VAE and Future sampling strategies, performs best. Subsequently, learning with variable numbers of objects was studied by evaluating on a task where the environment, based on the Visual Multi-Object Pusher, randomly contains zero, one, or two objects during testing. The results show that their model can tackle this task successfully. | |||
Finally, the authors tested the RIG in a real-world robot for its ability to reach user-specified positions and push objects to desired locations, as indicated by a goal image. The robot is trained with access only to 84x84 RGB images and without access to joint angles or object positions. The robot first learns by settings its own goals in the latent space and autonomously practices reaching different positions without human involvement. After a reasonable amount of time of training, the robot is given a goal image. Because the robot has practiced reaching so many goals, it is able to reach this goal without additional training: | |||
[[File:reaching.JPG|center|thumb|600px|(Left) The robot setup is pictured. (Right) Test rollouts of the learned policy.]] | |||
The method for reaching only needs 10,000 samples and an hour of real-world interactions. | |||
They also used RIG to train a policy to push objects to target locations: | |||
The | [[File:pushing.JPG|center|thumb|600px|The robot pushing setup is | ||
pictured, with frames from test rollouts of the learned policy.]] | |||
The pushing task is more complicated and the method requires about 25,000 samples. Since the authors do not have the true position during training, so they used test episode returns as the VAE latent distance reward. As learning proceeds, RIG makes steady progress at optimizing the latent distance. | |||
=Conclusion & Future Work= | |||
The | In this paper, a new RL algorithm is proposed to efficiently solve goal-conditioned, vision-based tasks without any ground truth state information or reward functions. The author suggests that one could instead use other representations, such as language and demonstrations, to specify goals. Also, while the paper provides a mechanism to sample goals for autonomous exploration, one can combine the proposed method with existing work by choosing these goals in a more principled way, i.e. a procedure that is not only goal-oriented, but also information seeking or uncertainty aware, to perform even better exploration. Furthermore, combining the idea of this paper with methods from multitask learning and meta-learning is a promising path to create general-purpose agents that can continuously and efficiently acquire skill. Lastly, there are a variety of robot tasks whose state representation would be difficult to capture with sensors, such as manipulating deformable objects or handling scenes with variable number of objects. It is interesting to see whether the RIG can be scaled up to solve these tasks. A new paper [10] was published last week that built on the framework of goal conditioned Reinforcement Learning to extract state representations based on the actions required to reach them, which is abbreviated ARC for actionable representation for control. | ||
=Critique= | |||
1. This paper is novel because it uses visual data and trains in an unsupervised fashion. The algorithm has no access to a ground truth state or to a pre-defined reward function. It can perform well in a real-world environment with no explicit programming. | |||
2. From the videos, one major concern is that the output of robotic arm's position is not stable during training and test time. It is likely that the encoder reduces the image features too much so that the images in the latent space are too blurry to be used goal images. It would be better if this can be investigated in the future. It would be better, if a method is investigated with multiple data sources, and the agent is trained to choose the source which has more complete information. | |||
3. | 3. The algorithm seems to perform better when there is only one object in the images. For example, in Visual Multi-Object Pusher experiment, the relative positions of two pucks do not correspond well with the relative positions of two pucks in goal images. The same situation is also observed in Variable-object experiment. We may guess that the more information contained in an image, the less likely the robot will perform well. This limits the applicability of the current algorithm to solving real-world problems. | ||
4. The instability mentioned in #2 is even more apparent in the multi-object scenario and appears to result from the model attempting to optimize on the position of both objects at the same time. Reducing the problem to a sequence of single-object targets may reduce the amount of time the robots spend moving between the multiple objects in the scene (which it currently does quite frequently). | |||
=References= | |||
1. Lerrel Pinto, Marcin Andrychowicz, Peter Welinder, Wojciech Zaremba, and Pieter Abbeel. Asymmetric | |||
Actor Critic for Image-Based Robot Learning. arXiv preprint arXiv:1710.06542, 2017. | |||
2. Pulkit Agrawal, Ashvin Nair, Pieter Abbeel, Jitendra Malik, and Sergey Levine. Learning to Poke by | |||
Poking: Experiential Learning of Intuitive Physics. In Advances in Neural Information Processing Systems | |||
(NIPS), 2016. | |||
3. Deepak Pathak, Parsa Mahmoudieh, Guanghao Luo, Pulkit Agrawal, Dian Chen, Yide Shentu, Evan | |||
Shelhamer, Jitendra Malik, Alexei A Efros, and Trevor Darrell. Zero-Shot Visual Imitation. In International | |||
Conference on Learning Representations (ICLR), 2018. | |||
4. Timothy P Lillicrap, Jonathan J Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David | |||
Silver, and Daan Wierstra. Continuous control with deep reinforcement learning. In International | |||
Conference on Learning Representations (ICLR), 2016. | |||
5. Irina Higgins, Arka Pal, Andrei A Rusu, Loic Matthey, Christopher P Burgess, Alexander Pritzel, Matthew | |||
Botvinick, Charles Blundell, and Alexander Lerchner. Darla: Improving zero-shot transfer in reinforcement | |||
learning. International Conference on Machine Learning (ICML), 2017. | |||
6. Aravind Srinivas, Allan Jabri, Pieter Abbeel, Sergey Levine, and Chelsea Finn. Universal Planning | |||
Networks. In International Conference on Machine Learning (ICML), 2018. | |||
7. Pierre Sermanet, Corey Lynch, Yevgen Chebotar, Jasmine Hsu, Eric Jang, Stefan Schaal, and Sergey | |||
Levine. Time-contrastive networks: Self-supervised learning from video. arXiv preprint arXiv:1704.06888, | |||
2017. | |||
8. Alex Lee, Sergey Levine, and Pieter Abbeel. Learning Visual Servoing with Deep Features and Fitted | |||
Q-Iteration. In International Conference on Learning Representations (ICLR), 2017. | |||
9. Online source: https://bair.berkeley.edu/blog/2018/09/06/rig/ | |||
10. https://arxiv.org/pdf/1811.07819.pdf | |||
11. Sergey Levine, Chelsea Finn, Trevor Darrell, and Pieter Abbeel. End-to-End Training of Deep Visuomotor Policies. Journal of Machine Learning Research (JMLR), 17(1):1334–1373, 2016. ISSN 15337928. | |||
12. Lerrel Pinto, Marcin Andrychowicz, Peter Welinder, Wojciech Zaremba, and Pieter Abbeel. Asymmetric Actor Critic for Image-Based Robot Learning. arXiv preprint arXiv:1710.06542, 2017. | |||
13. Timothy P Lillicrap, Jonathan J Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver, and Daan Wierstra. Continuous control with deep reinforcement learning. In International Conference on Learning Representations (ICLR), 2016. | |||
14. Marcin Andrychowicz, Filip Wolski, Alex Ray, Jonas Schneider, Rachel Fong, Peter Welinder, Bob Mcgrew, Josh Tobin, Pieter Abbeel, and Wojciech Zaremba. Hindsight Experience Replay. In | |||
Advances in Neural Information Processing Systems (NIPS) 2017. | |||
15. L P Kaelbling. Learning to achieve goals. In IJCAI-93. Proceedings of the Thirteenth International Joint Conference on Artificial Intelligence, volume vol.2, pages 1094 – 8, 1993. | |||
Latest revision as of 20:47, 11 December 2018
Video and details of this work are available here
Introduction and Motivation
Humans are able to accomplish many tasks without any explicit or supervised training, simply by exploring their environment. We are able to set our own goals and learn from our experiences, and thus are able to accomplish specific tasks without ever having been trained explicitly for them. It would be ideal if an autonomous agent can also set its own goals and learn from its environment.
In the paper “Visual Reinforcement Learning with Imagined Goals”, the authors are able to devise such an unsupervised reinforcement learning system. They introduce a system that sets abstract (self-generated) goals and autonomously learns to achieve those goals. They then show that the system can use these autonomously learned skills to perform a variety of user-specified goals, such as pushing objects, grasping objects, and opening doors, without any additional learning. Lastly, they demonstrate that their method is efficient enough to work in the real world on a Sawyer robot. The robot learns to set and achieve goals with only images as the input to the system.
The algorithm proposed by the authors is summarized below. A Variational Auto Encoder (VAE) on the (left) learns a latent representation of images gathered during training time (center). These latent variables are used to train a policy on imagined goals (center), which can then be used for accomplishing user-specified goals (right).
Related Work
Many previous works on vision-based deep reinforcement learning for robotics studied a variety of behaviors such as grasping [1], pushing [2], navigation [3], and other manipulation tasks [4]. However, their assumptions on the models limit their suitability for training general-purpose robots. Some previous works such as Levine et al. [11] proposed time-varying models which require episodic setups and thus are hard to generalize to non-episodic and continuous learning scenarios. There are also other works such as Pinto et al. [12] that proposed an approach using goal images, but it requires instrumented training simulations. Lillicrap et al. [13] use fully model-free training (Model-based RL uses experience to construct an internal model of the transitions and immediate outcomes in the environment. Appropriate actions are then chosen by searching or planning in this world model. Model-free RL, on the other hand, uses experience to learn directly one or both of two simpler quantities (state/action values or policies) which can achieve the same optimal behavior but without estimation or use of a world model. Given a policy, a state has a value, defined in terms of the future utility that is expected to accrue starting from that state Reinforcement learning: The Good, The Bad and The Ugly.), but does not learn goal-conditioned skills. The authors' experiments indicate that this technique is difficult to extend to goal-conditioned setting with image inputs. There are currently no examples that use model-free reinforcement learning for learning policies to train on real-world robotic systems without having ground-truth information.
In this paper, the authors utilize a goal-conditioned value function to tackle more general tasks through goal relabelling, which improves sample efficiency. Goal relabelling is to retroactively relabel samples in the replay buffer with goals sampled from the latent representation. The paper uses sample random goals from learned latent space to use as replay goals for off-policy Q-learning rather than restricting to states seen along the sampled trajectory as was done in the earlier works. Specifically, they use a model-free Q-learning method that operates on raw state observations and actions. This approach allows for a single transition tuple to be converted into potentially infinite valid training examples.
Unsupervised learning has been used in a number of prior works to acquire better representations of reinforcement learning. In these methods, the learned representation is used as a substitute for the state for the policy. However, these methods require additional information, such as access to the ground truth reward function based on the true state during training time [5], expert trajectories [6], human demonstrations [7], or pre-trained object-detection features [8]. In contrast, the authors learn to generate goals and use the learned representation to get a reward function for those goals without any of these extra sources of supervision.
Goal-Conditioned Reinforcement Learning
The ultimate goal in reinforcement learning is to learn a policy [math]\displaystyle{ \pi }[/math], that when given a state [math]\displaystyle{ s_t }[/math] and goal [math]\displaystyle{ g }[/math] (desired state), can dictate the optimal action [math]\displaystyle{ a_t }[/math]. The optimal action [math]\displaystyle{ a_t }[/math] is defined as an action which maximizes the expected return denoted by [math]\displaystyle{ R_t }[/math] and defined as [math]\displaystyle{ R_t = \mathbb{E}[\sum_{i = t}^T\gamma^{(i-t)}r_i] }[/math], where [math]\displaystyle{ r_i = r(s_i, a_i, s_{i+1}) }[/math] is the reward for performing action [math]\displaystyle{ a_i }[/math] when the current state is [math]\displaystyle{ s_i }[/math] and the goal state is [math]\displaystyle{ s_{i+1} }[/math] and [math]\displaystyle{ \gamma }[/math] is a discount factor which determines the relative importance given to rewards at different times.
In this paper, goals are not explicitly defined during training. If a goal is not explicitly defined, the agent must be able to generate a set of synthetic goals automatically. Suppose we let an autonomous agent explore an environment with a random policy. After executing each action, start and stop state observations are collected and stored. All state observations are images. For training, the agent can randomly select starting states and goals images from the set of state observations.
Moreover, if we aim to accomplish a variety of tasks, we can construct a goal-conditioned policy and reward, and optimize the expected return with respect to a goal distribution
where [math]\displaystyle{ G }[/math] is the set of goals and the reward is also a function of [math]\displaystyle{ g }[/math]
Now given a set of all possible states, a goal, and an initial state, a reinforcement learning framework can be used to find the optimal policy such that a chosen value function is maximized. However, to implement such a framework, a reward function needs to be defined. One choice for the reward is the negative distance between the current state and the goal state, so that maximizing the reward corresponds to minimizing the distance to the goal state.
In reinforcement learning, a goal-conditioned Q-function can be used to find a single policy to maximize rewards and therefore reach goal states. A goal-conditioned Q-function [math]\displaystyle{ Q(s,a,g) }[/math] tells us how good an action [math]\displaystyle{ a }[/math] is, given the current state [math]\displaystyle{ s }[/math] and goal [math]\displaystyle{ g }[/math]. For example, a Q-function tells us, “How good is it to move my hand up (action [math]\displaystyle{ a }[/math]), if I’m holding a plate (state [math]\displaystyle{ s }[/math]) and want to put the plate on the table (goal [math]\displaystyle{ g }[/math])?” Once this Q-function is trained, a goal-conditioned policy can be obtained by performing the following optimization
[math]\displaystyle{ \pi(s,g) = max_a Q(s,a,g) }[/math]
which effectively says, “choose the best action according to this Q-function.” By using this procedure, one can obtain a policy that maximizes the sum of rewards, i.e. reaches various goals.
The reason why Q-learning is popular is that it can be trained in an off-policy manner. Therefore, the only things a Q-function needs are samples of state, action, next state, goal, and reward [math]\displaystyle{ (s,a,s′,g,r) }[/math]. This data can be collected by any policy and can be reused across multiples tasks. So a preliminary goal-conditioned Q-learning algorithm looks like this:

From the tuple [math]\displaystyle{ (s,a,s',g,r) }[/math], an approximate Q-function paramaterized by [math]\displaystyle{ w }[/math] can be trained by minimizing the Bellman error:
[math]\displaystyle{ \mathcal{E}(w) = \frac{1}{2} || Q_w(s,a,g) -(r + \gamma \max_{a'} Q_{\overline{w}}(s',a',g)) ||^2 }[/math]
where [math]\displaystyle{ \overline{w} }[/math] is treated as some constant.
The main drawback in this training procedure is collecting data. In theory, one could learn to solve various tasks without even interacting with the world if more data are available. Unfortunately, it is difficult to learn an accurate model of the world, so sampling is usually performed to get state-action-next-state data, [math]\displaystyle{ (s,a,s′) }[/math] . However, if the reward function [math]\displaystyle{ r(s,g) }[/math] can be accessed, one can retroactively relabel goals and recompute rewards. This way, more data can be artificially generated given a single [math]\displaystyle{ (s,a,s′) }[/math] tuple. As a result, the training procedure can be modified like so:
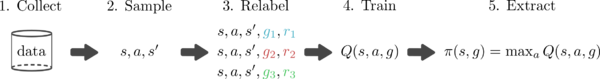
This goal resampling makes it possible to simultaneously learn how to reach multiple goals at once without needing more data from the environment. Thus, this simple modification can result in substantially faster learning. However, the method described above makes two major assumptions: (1) you have access to a reward function and (2) you have access to a goal sampling distribution [math]\displaystyle{ p(g) }[/math]. When moving to vision-based tasks where goals are images, both of these assumptions introduce practical concerns, as the task of generating goal images is fairly intensive.
For one, a fundamental problem with this reward function is that it assumes that the distance between raw images will yield semantically useful information. But images are noisy and a large amount of information in an image may not be related to the object we analyze. Thus, the distance between the two images may not correlate with their semantic distance.
Second, because the goals are images, a goal image distribution [math]\displaystyle{ p(g) }[/math] is needed so that one can sample goal images. Manually designing a distribution over goal images is a non-trivial task and image generation is still an active field of research. It would be ideal if the agent can autonomously imagine its own goals and learn how to reach them.
Retroactively generating goals is also explored in tabular domains in [15]and in continuous domains in [14] using hindsight experience replay (HER). However, HER is limited to sampling goals seen along a trajectory, which greatly limits the number and diversity of goals with which one can relabel a given transition.
Variational Autoencoder
Variational autoencoders can learn structured latent representations of high dimensional data. VAE contains an encoder [math]\displaystyle{ p_\phi }[/math] and a decoder [math]\displaystyle{ p_\psi }[/math]. The former maps states to latent distributions, while the later maps latents to distributions over states. these two are jointly trained to maximize:
[math]\displaystyle{ L(\psi,\phi;s^{(i)})=-\beta D_{KL}(q_\phi(z|s^{(i)}||p(z))+E_{q\phi(z|s^(i))}[log p_\psi(s^{(i)})|z]) }[/math]
where p(z) is a prior distribution, which is chosen to be unit Gaussian, [math]\displaystyle{ D_{KL} }[/math] is the Kullback-Leibler divergence, and [math]\displaystyle{ \beta }[/math] is a hyper-parameter that balances the two terms.
This generative model converts high-dimensional observations [math]\displaystyle{ x }[/math], like images, into low-dimensional latent variables [math]\displaystyle{ z }[/math], and vice versa. The model is trained so that the latent variables capture the underlying factors of variation in an image. A current image [math]\displaystyle{ x }[/math] and goal image [math]\displaystyle{ x_g }[/math] can be converted into latent variables [math]\displaystyle{ z }[/math] and [math]\displaystyle{ z_g }[/math], respectively. These latent variables can then be used to represent the state and goal for the reinforcement learning algorithm. Learning Q functions and policies on top of this low-dimensional latent space rather than directly on images result in faster learning.
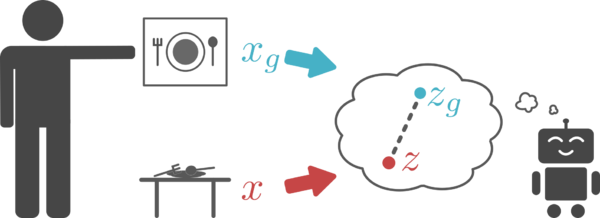
Using the latent variable representations for the images and goals also solves the problem of computing rewards. Instead of using pixel-wise error as our reward, the distance in the latent space is used as the reward to train the agent to reach a goal. The paper shows that this corresponds to rewarding reaching states that maximize the probability of the latent goal [math]\displaystyle{ z_g }[/math].
This generative model is also important because it allows an agent to easily generate goals in the latent space. In particular, the authors design the generative model so that latent variables are sampled from the VAE prior. This sampling mechanism is used for two reasons: First, it provides a mechanism for an agent to set its own goals. The agent simply samples a value for the latent variable from the generative model and tries to reach that latent goal. Second, this resampling mechanism is also used to relabel goals as mentioned above. Since the VAE prior is trained by real images, meaningful latent goals can be sampled from the latent variable prior. This will help the agent set its own goals and practice towards them if no goal is provided at test time.
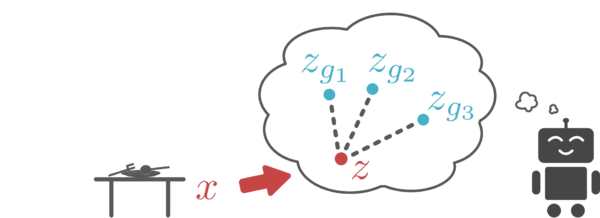
The authors summarize the purpose of the latent variable representation of images as follows: (1) captures the underlying factors of a scene, (2) provides meaningful distances to optimize, and (3) provides an efficient goal sampling mechanism which can be used by the agent to generate its own goals. The overall method is called reinforcement learning with imagined goals (RIG) by the authors. The process involves starts with collecting data through a simple exploration policy. Possible alternative explorations could be employed here including off-the-shelf exploration bonuses or unsupervised reinforcement learning methods. Then, a VAE latent variable model is trained on state observations and fine-tuned during training. The latent variable model is used for multiple purposes: sampling a latent goal [math]\displaystyle{ z_g }[/math] from the model and conditioning the policy on this goal. All states and goals are embedded using the model’s encoder and then used to train the goal-conditioned value function. The authors then resample goals from the prior and compute rewards in the latent space.
Goal-Conditioned Policies with Unsupervised Representation Learning
The choice of a suitable goal representation is required for the devising of practical goal-conditioned value functions. When there is absence of domain specific knowledge and instrumentation, a choice is to set the goal space G to be the same as the state observation space S. However, when state is high-dimensional learning a goal-conditioned Q-function and policy becomes exceedingly difficult. One challenging problem with end-to-end approaches for visual RL tasks is that the resulting policy needs to learn both perception and control. Training the goal-conditioned value function requires defining a goal-conditioned reward.
Their method jointly addresses a number of problems that arise when working with high-dimensional inputs such as images: sample efficient learning, reward specification, and automated goal-setting. These problems are addressed by learning a latent embedding using a [math]\displaystyle{ /beta - VAE }[/math]. This latent space is then used to represent the goal and state and retroactively relabel data with latent goals sampled from the VAE prior to improve sample efficiency.
Algorithm
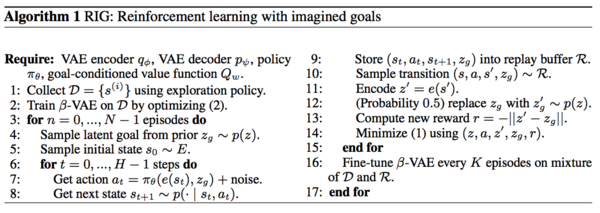
Algorithm 1 is called reinforcement learning with imagined goals (RIG). The data is first collected via a simple exploration policy. The proposed model allows for alternate exploration policies to be used which include off-the-shelf exploration bonuses or unsupervised reinforcement learning methods. Then, the authors train a VAE latent variable model on state observations and finetune it over the course of training. VAE latent space modeling is used to allow the conditioning of policy on the goal which is sampled from the latent model. The VAE model is also used to encode all the goals and the states. When the goal-conditioned value function is trained, the authors resample prior goals and compute rewards in the latent space using the equation
.
This equation is derived from the equation below. This is based on the choice to use the negative Mahalanobis distance in the latent space for the reward:
Experiments
The authors evaluated their method against some prior algorithms and ablated versions of their approach on a suite of simulated and real-world tasks: Visual Reacher, Visual Pusher, and Visual Multi-Object Pusher. They compared their model with the following prior works: L&R, DSAE, HER, and Oracle. It is concluded that their approach substantially outperforms the previous methods and is close to the state-based "oracle" method in terms of efficiency and performance.
The figure below shows the performance of different algorithms on this task. This involved a simulated environment with a Sawyer arm. The authors' algorithm was given only visual input, and the available controls were end-effector velocity. The plots show the distance to the goal state as a function of simulation steps. The Oracle, as a baseline, was given true object location information, as opposed to visual pixel information.
They then investigated the effectiveness of distances in the VAE latent space for the Visual Pusher task. They observed that latent distance significantly outperforms the log probability and pixel mean-squared error. The resampling strategies are also varied while fixing other components of the algorithm to study the effect of relabeling strategy. In this experiment, the RIG, which is an equal mixture of the VAE and Future sampling strategies, performs best. Subsequently, learning with variable numbers of objects was studied by evaluating on a task where the environment, based on the Visual Multi-Object Pusher, randomly contains zero, one, or two objects during testing. The results show that their model can tackle this task successfully.
Finally, the authors tested the RIG in a real-world robot for its ability to reach user-specified positions and push objects to desired locations, as indicated by a goal image. The robot is trained with access only to 84x84 RGB images and without access to joint angles or object positions. The robot first learns by settings its own goals in the latent space and autonomously practices reaching different positions without human involvement. After a reasonable amount of time of training, the robot is given a goal image. Because the robot has practiced reaching so many goals, it is able to reach this goal without additional training:

The method for reaching only needs 10,000 samples and an hour of real-world interactions.
They also used RIG to train a policy to push objects to target locations:

The pushing task is more complicated and the method requires about 25,000 samples. Since the authors do not have the true position during training, so they used test episode returns as the VAE latent distance reward. As learning proceeds, RIG makes steady progress at optimizing the latent distance.
Conclusion & Future Work
In this paper, a new RL algorithm is proposed to efficiently solve goal-conditioned, vision-based tasks without any ground truth state information or reward functions. The author suggests that one could instead use other representations, such as language and demonstrations, to specify goals. Also, while the paper provides a mechanism to sample goals for autonomous exploration, one can combine the proposed method with existing work by choosing these goals in a more principled way, i.e. a procedure that is not only goal-oriented, but also information seeking or uncertainty aware, to perform even better exploration. Furthermore, combining the idea of this paper with methods from multitask learning and meta-learning is a promising path to create general-purpose agents that can continuously and efficiently acquire skill. Lastly, there are a variety of robot tasks whose state representation would be difficult to capture with sensors, such as manipulating deformable objects or handling scenes with variable number of objects. It is interesting to see whether the RIG can be scaled up to solve these tasks. A new paper [10] was published last week that built on the framework of goal conditioned Reinforcement Learning to extract state representations based on the actions required to reach them, which is abbreviated ARC for actionable representation for control.
Critique
1. This paper is novel because it uses visual data and trains in an unsupervised fashion. The algorithm has no access to a ground truth state or to a pre-defined reward function. It can perform well in a real-world environment with no explicit programming.
2. From the videos, one major concern is that the output of robotic arm's position is not stable during training and test time. It is likely that the encoder reduces the image features too much so that the images in the latent space are too blurry to be used goal images. It would be better if this can be investigated in the future. It would be better, if a method is investigated with multiple data sources, and the agent is trained to choose the source which has more complete information.
3. The algorithm seems to perform better when there is only one object in the images. For example, in Visual Multi-Object Pusher experiment, the relative positions of two pucks do not correspond well with the relative positions of two pucks in goal images. The same situation is also observed in Variable-object experiment. We may guess that the more information contained in an image, the less likely the robot will perform well. This limits the applicability of the current algorithm to solving real-world problems.
4. The instability mentioned in #2 is even more apparent in the multi-object scenario and appears to result from the model attempting to optimize on the position of both objects at the same time. Reducing the problem to a sequence of single-object targets may reduce the amount of time the robots spend moving between the multiple objects in the scene (which it currently does quite frequently).
References
1. Lerrel Pinto, Marcin Andrychowicz, Peter Welinder, Wojciech Zaremba, and Pieter Abbeel. Asymmetric Actor Critic for Image-Based Robot Learning. arXiv preprint arXiv:1710.06542, 2017.
2. Pulkit Agrawal, Ashvin Nair, Pieter Abbeel, Jitendra Malik, and Sergey Levine. Learning to Poke by Poking: Experiential Learning of Intuitive Physics. In Advances in Neural Information Processing Systems (NIPS), 2016.
3. Deepak Pathak, Parsa Mahmoudieh, Guanghao Luo, Pulkit Agrawal, Dian Chen, Yide Shentu, Evan Shelhamer, Jitendra Malik, Alexei A Efros, and Trevor Darrell. Zero-Shot Visual Imitation. In International Conference on Learning Representations (ICLR), 2018.
4. Timothy P Lillicrap, Jonathan J Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver, and Daan Wierstra. Continuous control with deep reinforcement learning. In International Conference on Learning Representations (ICLR), 2016.
5. Irina Higgins, Arka Pal, Andrei A Rusu, Loic Matthey, Christopher P Burgess, Alexander Pritzel, Matthew Botvinick, Charles Blundell, and Alexander Lerchner. Darla: Improving zero-shot transfer in reinforcement learning. International Conference on Machine Learning (ICML), 2017.
6. Aravind Srinivas, Allan Jabri, Pieter Abbeel, Sergey Levine, and Chelsea Finn. Universal Planning Networks. In International Conference on Machine Learning (ICML), 2018.
7. Pierre Sermanet, Corey Lynch, Yevgen Chebotar, Jasmine Hsu, Eric Jang, Stefan Schaal, and Sergey Levine. Time-contrastive networks: Self-supervised learning from video. arXiv preprint arXiv:1704.06888, 2017.
8. Alex Lee, Sergey Levine, and Pieter Abbeel. Learning Visual Servoing with Deep Features and Fitted Q-Iteration. In International Conference on Learning Representations (ICLR), 2017.
9. Online source: https://bair.berkeley.edu/blog/2018/09/06/rig/
10. https://arxiv.org/pdf/1811.07819.pdf
11. Sergey Levine, Chelsea Finn, Trevor Darrell, and Pieter Abbeel. End-to-End Training of Deep Visuomotor Policies. Journal of Machine Learning Research (JMLR), 17(1):1334–1373, 2016. ISSN 15337928.
12. Lerrel Pinto, Marcin Andrychowicz, Peter Welinder, Wojciech Zaremba, and Pieter Abbeel. Asymmetric Actor Critic for Image-Based Robot Learning. arXiv preprint arXiv:1710.06542, 2017.
13. Timothy P Lillicrap, Jonathan J Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver, and Daan Wierstra. Continuous control with deep reinforcement learning. In International Conference on Learning Representations (ICLR), 2016.
14. Marcin Andrychowicz, Filip Wolski, Alex Ray, Jonas Schneider, Rachel Fong, Peter Welinder, Bob Mcgrew, Josh Tobin, Pieter Abbeel, and Wojciech Zaremba. Hindsight Experience Replay. In Advances in Neural Information Processing Systems (NIPS) 2017.
15. L P Kaelbling. Learning to achieve goals. In IJCAI-93. Proceedings of the Thirteenth International Joint Conference on Artificial Intelligence, volume vol.2, pages 1094 – 8, 1993.