Do Deep Neural Networks Suffer from Crowding: Difference between revisions
| (19 intermediate revisions by 15 users not shown) | |||
| Line 1: | Line 1: | ||
= Introduction = | = Introduction = | ||
Since the increase in popularity of Deep Neural Networks (DNNs), there has been | Since the increase in popularity of Deep Neural Networks (DNNs), there has been increased research in making machines capable of recognizing objects the same way humans do. Humans can recognize objects in ways that are invariant to scale, translation, and clutter. Crowding is visual effect suffered by humans, in which an object that can be recognized in isolation can no longer be recognized when other objects, called flankers, are placed close to it. This paper focuses on studying the impact of crowding on DNNs trained for object recognition by adding clutter to the images and then analyzing which models and settings suffer less from such effects. | ||
[[File:paper25_fig_crowding_ex.png|center|600px]] | [[File:paper25_fig_crowding_ex.png|center|600px]] | ||
The figure shows a visual example of crowding [3]. Keep your eyes still and look at the dot in the center and try to identify the "A" in the two circles. You should see that it is much easier to make out the "A" in the right than in the left circle. The same "A" exists in both circles, however, the left circle contains flankers which are those line segments. | The figure shows a visual example of crowding [3]. Keep your eyes still and look at the dot in the center and try to identify the "A" in the two circles. You should see that it is much easier to make out the "A" in the right than in the left circle. The same "A" exists in both circles, however, the left circle contains flankers which are those line segments. | ||
The paper investigates two types of DNNs for crowding: traditional deep convolutional neural networks (DCNN) and a multi-scale eccentricity-dependent model which is an extension of the DCNNs and inspired by the retina where the receptive field size of the convolutional filters in the model grows with increasing distance from the center of the image, called the eccentricity and | Another common example to visualize the same: | ||
[[File:crowding-tigger.jpg|center|600px]] | |||
===Drawbacks of CNNs=== | |||
CNNs fall short in explaining human perceptual invariance. Firstly, CNNs typically take input at a single uniform resolution. Biological measurements suggest that resolution is not uniform across the human visual field, but rather decays with eccentricity, i.e. distance from the center of focus. The major cause of this issue is the pooling layer in CNN structure. The pooling is an efficient technique but loses important spatial information. Pooling is also not capable to capture the hierarchical structure in the image, which is also crucial to view point problems. Even more importantly, CNNs rely not only on weight-sharing but also on data augmentation to achieve transformation invariance and so obviously a lot of processing is needed for CNNs. | |||
The paper investigates two types of DNNs for crowding: traditional deep convolutional neural networks (DCNN) and a multi-scale eccentricity-dependent model which is an extension of the DCNNs and inspired by the retina where the receptive field size of the convolutional filters in the model grows with increasing distance from the center of the image, called the eccentricity and is explained below. The authors focus on the dependence of crowding on image factors, such as flanker configuration, target-flanker similarity, target eccentricity and premature pooling in particular. Along with that, there is major emphasis on reducing the training time of the networks since the motive is to have a simple network capable of learning space-invariant features. | |||
= Models = | = Models = | ||
The authors describe two kinds of DNN architectures: Deep Convolutional Neural Networks, and eccentricity dependent networks, with varying pooling strategies across space and scale. Of particular note is the pooling operation, as many researchers have suggested that this may be the cause of crowding in human perception. | |||
== Deep Convolutional Neural Networks == | == Deep Convolutional Neural Networks == | ||
| Line 18: | Line 25: | ||
As highlighted earlier, the effect of pooling is into main consideration and hence three different configurations have been investigated as below: | As highlighted earlier, the effect of pooling is into main consideration and hence three different configurations have been investigated as below: | ||
# '''No total pooling''' Feature maps sizes decrease only due to boundary effects, as the 3x3 max pooling has stride 1. The square feature maps sizes after each pool layer are 60-54-48-42. | |||
# '''Progressive pooling''' 3x3 pooling with a stride of 2 halves the square size of the feature maps, until we pool over what remains in the final layer, getting rid of any spatial information before the fully connected layer. (60-27-11-1). | |||
# '''At end pooling''' Same as no total pooling, but before the fully connected layer, max-pool over the entire feature map. (60-54-48-1). | |||
==Eccentricity-dependent Model== | ==Eccentricity-dependent Model== | ||
In order to take care of the scale invariance in the input image, the eccentricity dependent DNN is utilized. The main intuition behind this architecture is that as we increase eccentricity, the receptive fields also increase and hence the model will become invariant to changing input scales. The authors note that the width of each scale is roughly related to the amount of translation invariance for objects at that scale, simply because once the object is outside that window, the filter no longer observes it. Therefore, the authors say that the architecture emphasizes scale invariance over translation invariance, in contrast to traditional DCNNs. In this model, the input image is cropped into varying scales (11 crops increasing by a factor of <math>\sqrt{2}</math> which are then resized to 60x60 pixels) and then fed to the network. The model computes an invariant representation of the input by sampling the inverted pyramid at a discrete set of scales with the same number of filters at each scale. Since the same number of filters are used for each scale, the smaller crops will be sampled at a high resolution while the larger crops will be sampled with a low resolution. These scales are fed into the network as an input channel to the convolutional layers and share the weights across scale and space. | In order to take care of the scale invariance in the input image, the eccentricity dependent DNN is utilized. This was proposed as a model of the human visual cortex by [https://arxiv.org/pdf/1406.1770.pdf, Poggio et al] and later further studied in [2]. The main intuition behind this architecture is that as we increase eccentricity, the receptive fields also increase and hence the model will become invariant to changing input scales. The authors note that the width of each scale is roughly related to the amount of translation invariance for objects at that scale, simply because once the object is outside that window, the filter no longer observes it. Therefore, the authors say that the architecture emphasizes scale invariance over translation invariance, in contrast to traditional DCNNs. From a biological perspective, eye movement can compensate for the limitations of translation invariance, but compensating for scale invariance requires changing distance from the object. In this model, the input image is cropped into varying scales (11 crops increasing by a factor of <math>\sqrt{2}</math> which are then resized to 60x60 pixels) and then fed to the network. Exponentially interpolated crops are used over linearly interpolated crops since they produce fewer boundary effects while maintaining the same behavior qualitatively. The model computes an invariant representation of the input by sampling the inverted pyramid at a discrete set of scales with the same number of filters at each scale. Since the same number of filters are used for each scale, the smaller crops will be sampled at a high resolution while the larger crops will be sampled with a low resolution. These scales are fed into the network as an input channel to the convolutional layers and share the weights across scale and space. Due to the downsampling of the input image, this is equivalent to having receptive fields of varying sizes. Intuitively, this means that the network generalizes learnings across scales and is guaranteed by during back-propagation by averaging the error derivatives over all scale channels, then using the averages to compute weight adjustments. The same set of weight adjustments to the convolutional units across different scale channels is applied. | ||
[[File:EDM.png|2000x450px|center]] | [[File:EDM.png|2000x450px|center]] | ||
The architecture of this model is the same as the previous DCNN model with the only change being the extra filters added for each of the scales, so the number of parameters remains the same as DCNN models. The authors perform spatial pooling, the aforementioned ''At end pooling'' is used here, and scale pooling which helps in reducing | |||
The architecture of this model is the same as the previous DCNN model with the only change being the extra filters added for each of the scales, so the number of parameters remains the same as DCNN models. The authors perform spatial pooling, the aforementioned ''At end pooling'' is used here, and scale pooling which helps in reducing the number of scales by taking the maximum value of corresponding locations in the feature maps across multiple scales. It has three configurations: (1) at the beginning, in which all the different scales are pooled together after the first layer, 11-1-1-1-1 (2) progressively, 11-7-5-3-1 and (3) at the end, 11-11-11-11-1, in which all 11 scales are pooled together at the last layer. | |||
===Contrast Normalization=== | ===Contrast Normalization=== | ||
Since | Since there are multiple scales of an input image, in some experiments, normalization is performed such that the sum of the pixel intensities in each scale is in the same range [0,1] (this is to prevent smaller crops, which have more non-black pixels, from disproportionately dominating max-pooling across scales). The normalized pixel intensities are then divided by a factor proportional to the crop area [[File:sqrtf.png|60px]] where i=1 is the smallest crop. | ||
=Experiments= | =Experiments= | ||
Targets are the set of objects to be recognized and flankers are the set of objects the model has not been trained to recognize, which act as clutter with respect to these target objects. The target objects are the even MNIST numbers having translational variance (shifted at different locations of the image along the horizontal axis), while flankers are from odd MNIST numbers, | Targets are the set of objects to be recognized and flankers are the set of objects the model has not been trained to recognize, which act as clutter with respect to these target objects. The target objects are the even MNIST numbers having translational variance (shifted at different locations of the image along the horizontal axis), while flankers are from odd MNIST numbers, not MNIST dataset (contains alphabet letters) and Omniglot dataset (contains characters). Examples of the target and flanker configurations are shown below: | ||
[[File:eximages.png|800px|center]] | [[File:eximages.png|800px|center]] | ||
| Line 42: | Line 47: | ||
# One central flanker closer to the center of the image than the target. (xa) | # One central flanker closer to the center of the image than the target. (xa) | ||
# One peripheral flanker closer to the boundary of the image that the target. (ax) | # One peripheral flanker closer to the boundary of the image that the target. (ax) | ||
# Two flankers spaced equally around the target, being both the same object (xax). | # Two flankers spaced equally around the target, being both the same object, see Figure 1 above for an example (xax). | ||
Training is done using | Training is done using backpropagation with images of size <math>1920 px^2</math> with embedded targets objects and flankers of size of <math>120 px^2</math>. The training and test images are divided as per the usual MNIST configuration. To determine if there is a difference between the peripheral flankers and the central flankers, all the tests are performed in the right half image plane. | ||
==DNNs trained with Target and Flankers== | ==DNNs trained with Target and Flankers== | ||
This is a constant spacing training setup where identical flankers are placed at a distance of 120 pixels either side of the target(xax) with the target having translational variance. The tests are evaluated on (i) DCNN with at the end pooling, and (ii) eccentricity-dependent model with 11-11-11-11-1 scale pooling, at the end spatial pooling and contrast normalization. The | This is a constant spacing training setup where identical flankers are placed at a distance of 120 pixels either side of the target(xax) with the target having translational variance. The tests are evaluated on (i) DCNN with at the end pooling, and (ii) eccentricity-dependent model with 11-11-11-11-1 scale pooling, at the end spatial pooling and contrast normalization. The results are reported by different flanker types <math>(xax,ax, xa)</math> at test. | ||
[[File:result1.png|x450px|center]] | [[File:result1.png|x450px|center]] | ||
| Line 57: | Line 62: | ||
==DNNs trained with Images with the Target in Isolation== | ==DNNs trained with Images with the Target in Isolation== | ||
Here the target objects are in isolation and with translational variance while the test-set is the same set of flanker configurations as used before. | Here the target objects are in isolation and with translational variance while the test-set is the same set of flanker configurations as used before. The constant spacing and constant eccentricity effect have been evaluated. | ||
[[File:result2.png|750x400px|center]] | [[File:result2.png|750x400px|center]] | ||
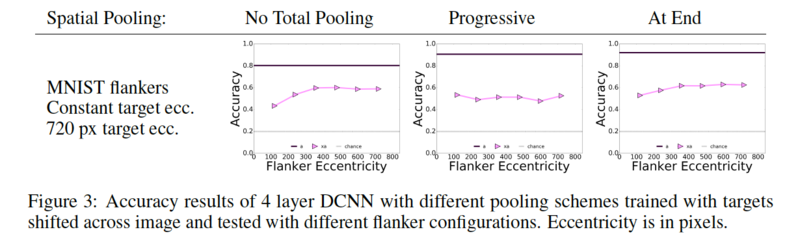
In addition to the evaluation of DCNNs in constant target eccentricity at 240 pixels, here they are tested with images in which the target is fixed at 720 pixels from the center of the image, as shown in Fig 3. Since the target is already at the edge of the visual field, a flanker cannot be more peripheral in the image than the target. Same results as for the 240 pixels target eccentricity can be extracted. The closer the flanker is to the target, the more accuracy decreases. Also, it can be seen that when the target is close to the image boundary, recognition is poor because of boundary effects eroding away information about the target | |||
In addition to the evaluation of DCNNs in constant target eccentricity at 240 pixels, here they are tested with images in which the target is fixed at 720 pixels from the center of the image, as shown in Fig 3. Since the target is already at the edge of the visual field, a flanker cannot be more peripheral in the image than the target. Same results as for the 240 pixels target eccentricity can be extracted. The closer the flanker is to the target, the more accuracy decreases. Also, it can be seen that when the target is close to the image boundary, recognition is poor because of boundary effects eroding away information about the target. | |||
[[File:paper25_supplemental1.png|800px|center]] | [[File:paper25_supplemental1.png|800px|center]] | ||
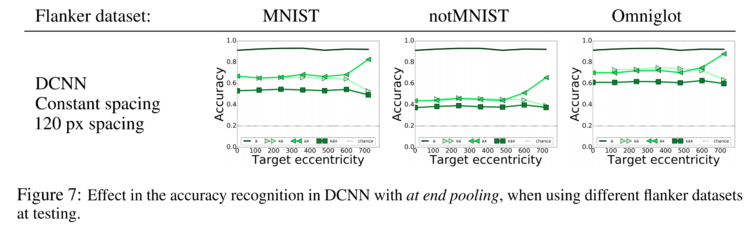
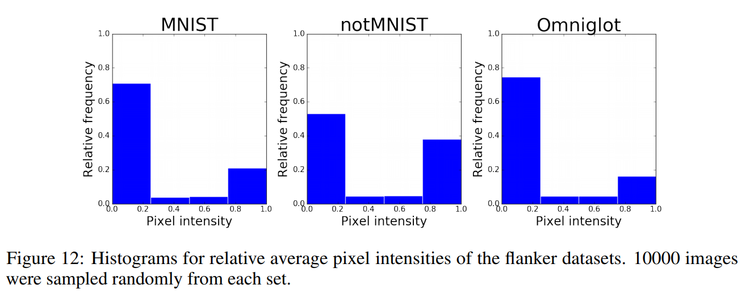
The authors also test the effect of flankers from different datasets on a DCNN model with at end pooling, with results shown in Fig. 7 below. Omniglot flankers crowd less than MNIST digits, and the authors note that this is because they are visually similar to MNIST digits, but are not actually digits, and thus activate the model's convolutional filters less than MNIST digits. The notMNIST digits however, result it more crowding. This is due to the fact that the different font style results in more high intensity pixels and edges. The intensity distributions for the 3 datasets is shown in the histograms in Fig. 12 below. The correlation between crowding and relative frequency of high intensity pixels can be seen from this figure. | |||
[[File:crowding_at_end_pooling.png|750px|center]] | |||
[[File:DCNN dataset histogram.png|750px|center]] | |||
===DCNN Observations=== | ===DCNN Observations=== | ||
* | * Accuracy decreases with the increase in the number of flankers. | ||
* | * Unsurprisingly, CNNs are capable of being invariant to translations. | ||
* In the constant target eccentricity setup, where the target is fixed at the center of the image with varying target-flanker spacing, we observe that as the distance between target and flankers increase, recognition gets better. | * In the constant target eccentricity setup, where the target is fixed at the center of the image with varying target-flanker spacing, we observe that as the distance between target and flankers increase, recognition gets better. | ||
* Spatial pooling helps in learning invariance. | * Spatial pooling helps the network in learning invariance. | ||
*Flankers similar to the target object helps in recognition since they | * Flankers similar to the target object helps in recognition since they activate the convolutional filter more. | ||
* notMNIST data affects leads to more crowding since they have many more edges and white image pixels which activate the convolutional layers more. | * notMNIST data affects leads to more crowding since they have many more edges and white image pixels which activate the convolutional layers more. | ||
===Eccentric Model=== | ===Eccentric Model=== | ||
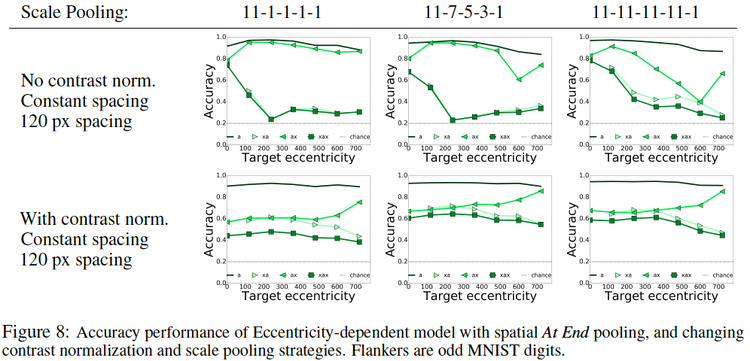
The set-up is the same as explained earlier. | The set-up is the same as explained earlier. The spacial pooling keeps constant. The effect of pooling across scales are investigated. The three configurations for scale pooling are (i) at the beginning, (ii)progressively and (iii) at the end. | ||
[[File:result3.png|750x400px|center]] | [[File:result3.png|750x400px|center]] | ||
====Observations==== | ====Observations==== | ||
* The recognition accuracy is dependent on the eccentricity of the target object. | |||
* If the target is placed at the center and no contrast normalization is done, then the recognition accuracy is high since this model concentrates the most on the central region of the image. | * If the target is placed at the center and no contrast normalization is done, then the recognition accuracy is high since this model concentrates the most on the central region of the image. | ||
* If contrast normalization is done, then all the scales will contribute equal amount and hence the eccentricity dependence is removed. | * If contrast normalization is done, then all the scales will contribute equal amount and hence the eccentricity dependence is removed. | ||
* Early pooling is harmful since it might take away the useful information very early which might be useful to the network. | * Early pooling is harmful since it might take away the useful information very early which might be useful to the network. | ||
Without contrast normalization, the middle portion of the image can be focused more with high resolution so the target at the center with no normalization performs well in that case. But if normalization is done, then all the segments of the image contribute to the classification and hence the overall accuracy is not that great but the system becomes robust to the changes in eccentricity. | |||
==Complex Clutter== | ==Complex Clutter== | ||
| Line 86: | Line 104: | ||
====Observations==== | ====Observations==== | ||
* Only eccentricity model without contrast normalization can recognize the target and only when the target is close to the image center. | * Only eccentricity model without contrast normalization can recognize the target and only when the target is close to the image center. | ||
* The eccentricity model does not need to be trained on different types of clutter to become robust to those types of clutter, but it needs to fixate on the relevant part of the image to recognize the target. | * The eccentricity model does not need to be trained on different types of clutter to become robust to those types of clutter, but it needs to fixate on the relevant part of the image to recognize the target. If it can fixate on the relevant part of the image, it can still discriminate it, even at different scales. This implies that the eccentricity model is robust to clutter. | ||
=Conclusions= | =Conclusions= | ||
We often think that just training the network with data similar to the test data would achieve good results in a general scenario too but that's not the case as we trained the model with flankers and it did not give us the ideal results for the target objects. | This paper investigates the effect of crowding on a DNN. Using a simple technique of adding clutter in the model didn't improve the performance. We often think that just training the network with data similar to the test data would achieve good results in a general scenario too but that's not the case as we trained the model with flankers and it did not give us the ideal results for the target objects. The following 4 techniques influenced crowding in DNN: | ||
*'''Flanker Configuration''': When models are trained with images of objects in isolation, adding flankers harms recognition. Adding two flankers is the same or worse than adding just one and the smaller the spacing between flanker and target, the more crowding occurs. This is because the pooling operation merges nearby responses, such as the target and flankers if they are close. | *'''Flanker Configuration''': When models are trained with images of objects in isolation, adding flankers harms recognition. Adding two flankers is the same or worse than adding just one and the smaller the spacing between flanker and target, the more crowding occurs. This is because the pooling operation merges nearby responses, such as the target and flankers if they are close. | ||
*'''Similarity between target and flanker''': Flankers more similar to targets cause more crowding, because of the selectivity property of the learned DNN filters. | *'''The Similarity between target and flanker''': Flankers more similar to targets cause more crowding, because of the selectivity property of the learned DNN filters. | ||
*'''Dependence on target location and contrast normalization''': In DCNNs and eccentricity-dependent models with contrast normalization, recognition accuracy is the same across all eccentricities. In eccentricity-dependent networks without contrast normalization, recognition does not decrease despite the presence of clutter when the target is at the center of the image. | *'''Dependence on target location and contrast normalization''': In DCNNs and eccentricity-dependent models with contrast normalization, recognition accuracy is the same across all eccentricities. In eccentricity-dependent networks without contrast normalization, recognition does not decrease despite the presence of clutter when the target is at the center of the image. | ||
*'''Effect of pooling''': adding pooling leads to better recognition accuracy of the models. Yet, in the eccentricity model, pooling across the scales too early in the hierarchy leads to lower accuracy. | *'''Effect of pooling''': adding pooling leads to better recognition accuracy of the models. Yet, in the eccentricity model, pooling across the scales too early in the hierarchy leads to lower accuracy. | ||
* The Eccentricity Dependent Models can be used for modeling the feedforward path of the primate visual cortex. | |||
* If target locations are proposed, then the system can become even more robust and hence a simple network can become robust to clutter while also reducing the amount of training data and time needed | |||
=Critique= | =Critique= | ||
This paper | This paper only tries to check the impact of flankers on targets as to how crowding can affect recognition but it does not propose anything novel in terms of architecture to take care of such type of crowding. The paper only shows that the eccentricity based model does better (than plain DCNN model) when the target is placed at the center of the image but maybe windowing over the frames the same way that a convolutional model passes a filter over an image, instead of taking crops starting from the middle, might help. | ||
This paper focuses on image classification. For a stronger argument, their model could be applied to the task of object detection. Perhaps crowding does not have as large of an impact when the objects of interest are localized by a region proposal network. | This paper focuses on image classification. For a stronger argument, their model could be applied to the task of object detection. Perhaps crowding does not have as large of an impact when the objects of interest are localized by a region proposal network. Further, the artificial crowding introduced in the paper may not be random enough for the neural network to learn to classify the object of interest as opposed to the entire cluster of objects. For example, in the case of an even MNIST digit being flanked by two odd MNIST digits, there are only 25 possible combinations of flankers and targets. | ||
This paper does not provide a convincing argument that the problem of crowding as experienced by humans somehow shares a similar mechanism to the problem of DNN accuracy falling when there is more clutter in the scene. The multi-scale architecture does not | This paper does not provide a convincing argument that the problem of crowding as experienced by humans somehow shares a similar mechanism to the problem of DNN accuracy falling when there is more clutter in the scene. The multi-scale architecture does not appear similar to the distribution of rods and cones in the retina[https://www.ncbi.nlm.nih.gov/books/NBK10848/figure/A763/?report=objectonly]. It might be that the eccentric model does well when the target is centered because it is being sampled by more scales, not because it is similar to a primate visual cortex, and primates are able to recognize an object in clutter when looking directly at it. | ||
=References= | =References= | ||
# Volokitin A, Roig G, Poggio T:"Do Deep Neural Networks Suffer from Crowding?" Conference on Neural Information Processing Systems (NIPS). 2017 | |||
# Francis X. Chen, Gemma Roig, Leyla Isik, Xavier Boix and Tomaso Poggio: "Eccentricity Dependent Deep Neural Networks for Modeling Human Vision" Journal of Vision. 17. 808. 10.1167/17.10.808. | |||
# J Harrison, W & W Remington, R & Mattingley, Jason. (2014). Visual crowding is anisotropic along the horizontal meridian during smooth pursuit. Journal of vision. 14. 10.1167/14.1.21. http://willjharrison.com/2014/01/new-paper-visual-crowding-is-anisotropic-along-the-horizontal-meridian-during-smooth-pursuit/ | |||
Latest revision as of 00:21, 21 April 2018
Introduction
Since the increase in popularity of Deep Neural Networks (DNNs), there has been increased research in making machines capable of recognizing objects the same way humans do. Humans can recognize objects in ways that are invariant to scale, translation, and clutter. Crowding is visual effect suffered by humans, in which an object that can be recognized in isolation can no longer be recognized when other objects, called flankers, are placed close to it. This paper focuses on studying the impact of crowding on DNNs trained for object recognition by adding clutter to the images and then analyzing which models and settings suffer less from such effects.

The figure shows a visual example of crowding [3]. Keep your eyes still and look at the dot in the center and try to identify the "A" in the two circles. You should see that it is much easier to make out the "A" in the right than in the left circle. The same "A" exists in both circles, however, the left circle contains flankers which are those line segments.
Another common example to visualize the same:

Drawbacks of CNNs
CNNs fall short in explaining human perceptual invariance. Firstly, CNNs typically take input at a single uniform resolution. Biological measurements suggest that resolution is not uniform across the human visual field, but rather decays with eccentricity, i.e. distance from the center of focus. The major cause of this issue is the pooling layer in CNN structure. The pooling is an efficient technique but loses important spatial information. Pooling is also not capable to capture the hierarchical structure in the image, which is also crucial to view point problems. Even more importantly, CNNs rely not only on weight-sharing but also on data augmentation to achieve transformation invariance and so obviously a lot of processing is needed for CNNs.
The paper investigates two types of DNNs for crowding: traditional deep convolutional neural networks (DCNN) and a multi-scale eccentricity-dependent model which is an extension of the DCNNs and inspired by the retina where the receptive field size of the convolutional filters in the model grows with increasing distance from the center of the image, called the eccentricity and is explained below. The authors focus on the dependence of crowding on image factors, such as flanker configuration, target-flanker similarity, target eccentricity and premature pooling in particular. Along with that, there is major emphasis on reducing the training time of the networks since the motive is to have a simple network capable of learning space-invariant features.
Models
The authors describe two kinds of DNN architectures: Deep Convolutional Neural Networks, and eccentricity dependent networks, with varying pooling strategies across space and scale. Of particular note is the pooling operation, as many researchers have suggested that this may be the cause of crowding in human perception.
Deep Convolutional Neural Networks
The DCNN is a basic architecture with 3 convolutional layers, spatial 3x3 max-pooling with varying strides and a fully connected layer for classification as shown in the below figure.
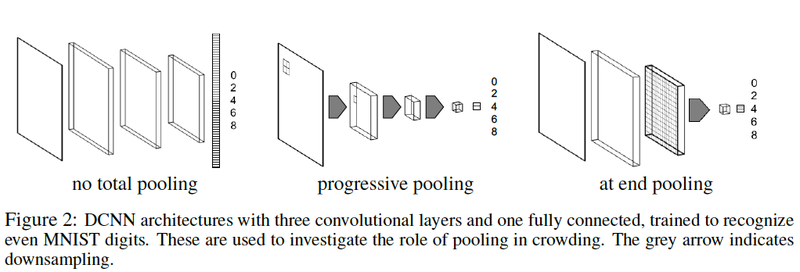
The network is fed with images resized to 60x60, with mini-batches of 128 images, 32 feature channels for all convolutional layers, and convolutional filters of size 5x5 and stride 1.
As highlighted earlier, the effect of pooling is into main consideration and hence three different configurations have been investigated as below:
- No total pooling Feature maps sizes decrease only due to boundary effects, as the 3x3 max pooling has stride 1. The square feature maps sizes after each pool layer are 60-54-48-42.
- Progressive pooling 3x3 pooling with a stride of 2 halves the square size of the feature maps, until we pool over what remains in the final layer, getting rid of any spatial information before the fully connected layer. (60-27-11-1).
- At end pooling Same as no total pooling, but before the fully connected layer, max-pool over the entire feature map. (60-54-48-1).
Eccentricity-dependent Model
In order to take care of the scale invariance in the input image, the eccentricity dependent DNN is utilized. This was proposed as a model of the human visual cortex by Poggio et al and later further studied in [2]. The main intuition behind this architecture is that as we increase eccentricity, the receptive fields also increase and hence the model will become invariant to changing input scales. The authors note that the width of each scale is roughly related to the amount of translation invariance for objects at that scale, simply because once the object is outside that window, the filter no longer observes it. Therefore, the authors say that the architecture emphasizes scale invariance over translation invariance, in contrast to traditional DCNNs. From a biological perspective, eye movement can compensate for the limitations of translation invariance, but compensating for scale invariance requires changing distance from the object. In this model, the input image is cropped into varying scales (11 crops increasing by a factor of [math]\displaystyle{ \sqrt{2} }[/math] which are then resized to 60x60 pixels) and then fed to the network. Exponentially interpolated crops are used over linearly interpolated crops since they produce fewer boundary effects while maintaining the same behavior qualitatively. The model computes an invariant representation of the input by sampling the inverted pyramid at a discrete set of scales with the same number of filters at each scale. Since the same number of filters are used for each scale, the smaller crops will be sampled at a high resolution while the larger crops will be sampled with a low resolution. These scales are fed into the network as an input channel to the convolutional layers and share the weights across scale and space. Due to the downsampling of the input image, this is equivalent to having receptive fields of varying sizes. Intuitively, this means that the network generalizes learnings across scales and is guaranteed by during back-propagation by averaging the error derivatives over all scale channels, then using the averages to compute weight adjustments. The same set of weight adjustments to the convolutional units across different scale channels is applied.
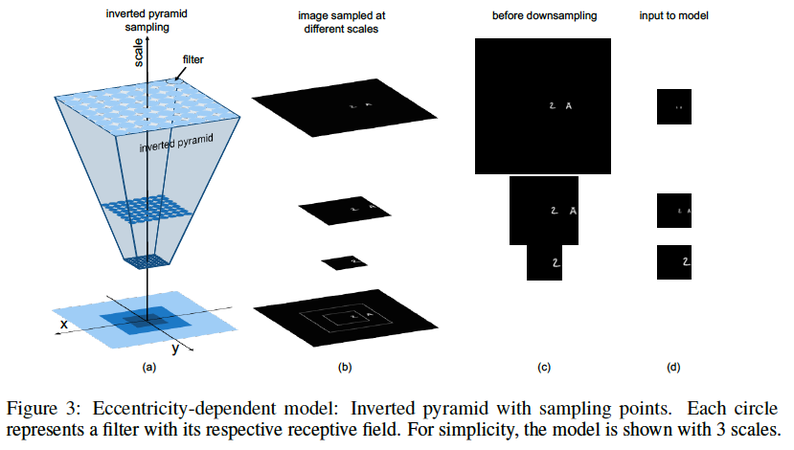
The architecture of this model is the same as the previous DCNN model with the only change being the extra filters added for each of the scales, so the number of parameters remains the same as DCNN models. The authors perform spatial pooling, the aforementioned At end pooling is used here, and scale pooling which helps in reducing the number of scales by taking the maximum value of corresponding locations in the feature maps across multiple scales. It has three configurations: (1) at the beginning, in which all the different scales are pooled together after the first layer, 11-1-1-1-1 (2) progressively, 11-7-5-3-1 and (3) at the end, 11-11-11-11-1, in which all 11 scales are pooled together at the last layer.
Contrast Normalization
Since there are multiple scales of an input image, in some experiments, normalization is performed such that the sum of the pixel intensities in each scale is in the same range [0,1] (this is to prevent smaller crops, which have more non-black pixels, from disproportionately dominating max-pooling across scales). The normalized pixel intensities are then divided by a factor proportional to the crop area ![]() where i=1 is the smallest crop.
where i=1 is the smallest crop.
Experiments
Targets are the set of objects to be recognized and flankers are the set of objects the model has not been trained to recognize, which act as clutter with respect to these target objects. The target objects are the even MNIST numbers having translational variance (shifted at different locations of the image along the horizontal axis), while flankers are from odd MNIST numbers, not MNIST dataset (contains alphabet letters) and Omniglot dataset (contains characters). Examples of the target and flanker configurations are shown below:

The target and the object are referred to as a and x respectively with the below four configurations:
- No flankers. Only the target object. (a in the plots)
- One central flanker closer to the center of the image than the target. (xa)
- One peripheral flanker closer to the boundary of the image that the target. (ax)
- Two flankers spaced equally around the target, being both the same object, see Figure 1 above for an example (xax).
Training is done using backpropagation with images of size [math]\displaystyle{ 1920 px^2 }[/math] with embedded targets objects and flankers of size of [math]\displaystyle{ 120 px^2 }[/math]. The training and test images are divided as per the usual MNIST configuration. To determine if there is a difference between the peripheral flankers and the central flankers, all the tests are performed in the right half image plane.
DNNs trained with Target and Flankers
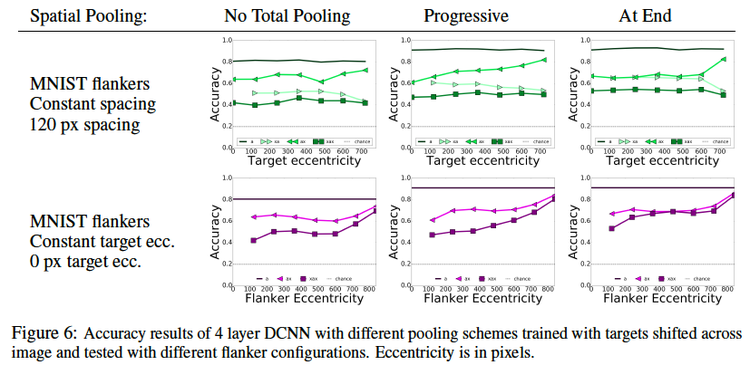
This is a constant spacing training setup where identical flankers are placed at a distance of 120 pixels either side of the target(xax) with the target having translational variance. The tests are evaluated on (i) DCNN with at the end pooling, and (ii) eccentricity-dependent model with 11-11-11-11-1 scale pooling, at the end spatial pooling and contrast normalization. The results are reported by different flanker types [math]\displaystyle{ (xax,ax, xa) }[/math] at test.
Observations
- With the flanker configuration same as the training one, models are better at recognizing objects in clutter rather than isolated objects for all image locations
- If the target-flanker spacing is changed, then models perform worse
- the eccentricity model is much better at recognizing objects in isolation than the DCNN because the multi-scale crops divide the image into discrete regions, letting the model learn from image parts as well as the whole image
- Only the eccentricity-dependent model is robust to different flanker configurations not included in training when the target is centered.
DNNs trained with Images with the Target in Isolation
Here the target objects are in isolation and with translational variance while the test-set is the same set of flanker configurations as used before. The constant spacing and constant eccentricity effect have been evaluated.
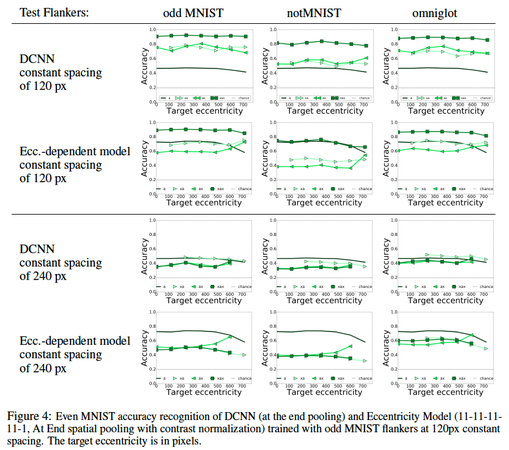
In addition to the evaluation of DCNNs in constant target eccentricity at 240 pixels, here they are tested with images in which the target is fixed at 720 pixels from the center of the image, as shown in Fig 3. Since the target is already at the edge of the visual field, a flanker cannot be more peripheral in the image than the target. Same results as for the 240 pixels target eccentricity can be extracted. The closer the flanker is to the target, the more accuracy decreases. Also, it can be seen that when the target is close to the image boundary, recognition is poor because of boundary effects eroding away information about the target.
The authors also test the effect of flankers from different datasets on a DCNN model with at end pooling, with results shown in Fig. 7 below. Omniglot flankers crowd less than MNIST digits, and the authors note that this is because they are visually similar to MNIST digits, but are not actually digits, and thus activate the model's convolutional filters less than MNIST digits. The notMNIST digits however, result it more crowding. This is due to the fact that the different font style results in more high intensity pixels and edges. The intensity distributions for the 3 datasets is shown in the histograms in Fig. 12 below. The correlation between crowding and relative frequency of high intensity pixels can be seen from this figure.
DCNN Observations
- Accuracy decreases with the increase in the number of flankers.
- Unsurprisingly, CNNs are capable of being invariant to translations.
- In the constant target eccentricity setup, where the target is fixed at the center of the image with varying target-flanker spacing, we observe that as the distance between target and flankers increase, recognition gets better.
- Spatial pooling helps the network in learning invariance.
- Flankers similar to the target object helps in recognition since they activate the convolutional filter more.
- notMNIST data affects leads to more crowding since they have many more edges and white image pixels which activate the convolutional layers more.
Eccentric Model
The set-up is the same as explained earlier. The spacial pooling keeps constant. The effect of pooling across scales are investigated. The three configurations for scale pooling are (i) at the beginning, (ii)progressively and (iii) at the end.
Observations
- The recognition accuracy is dependent on the eccentricity of the target object.
- If the target is placed at the center and no contrast normalization is done, then the recognition accuracy is high since this model concentrates the most on the central region of the image.
- If contrast normalization is done, then all the scales will contribute equal amount and hence the eccentricity dependence is removed.
- Early pooling is harmful since it might take away the useful information very early which might be useful to the network.
Without contrast normalization, the middle portion of the image can be focused more with high resolution so the target at the center with no normalization performs well in that case. But if normalization is done, then all the segments of the image contribute to the classification and hence the overall accuracy is not that great but the system becomes robust to the changes in eccentricity.
Complex Clutter
Here, the targets are randomly embedded into images of the Places dataset and shifted along horizontally in order to investigate model robustness when the target is not at the image center. Tests are performed on DCNN and the eccentricity model with and without contrast normalization using at end pooling. The results are shown in Figure 9 below.

Observations
- Only eccentricity model without contrast normalization can recognize the target and only when the target is close to the image center.
- The eccentricity model does not need to be trained on different types of clutter to become robust to those types of clutter, but it needs to fixate on the relevant part of the image to recognize the target. If it can fixate on the relevant part of the image, it can still discriminate it, even at different scales. This implies that the eccentricity model is robust to clutter.
Conclusions
This paper investigates the effect of crowding on a DNN. Using a simple technique of adding clutter in the model didn't improve the performance. We often think that just training the network with data similar to the test data would achieve good results in a general scenario too but that's not the case as we trained the model with flankers and it did not give us the ideal results for the target objects. The following 4 techniques influenced crowding in DNN:
- Flanker Configuration: When models are trained with images of objects in isolation, adding flankers harms recognition. Adding two flankers is the same or worse than adding just one and the smaller the spacing between flanker and target, the more crowding occurs. This is because the pooling operation merges nearby responses, such as the target and flankers if they are close.
- The Similarity between target and flanker: Flankers more similar to targets cause more crowding, because of the selectivity property of the learned DNN filters.
- Dependence on target location and contrast normalization: In DCNNs and eccentricity-dependent models with contrast normalization, recognition accuracy is the same across all eccentricities. In eccentricity-dependent networks without contrast normalization, recognition does not decrease despite the presence of clutter when the target is at the center of the image.
- Effect of pooling: adding pooling leads to better recognition accuracy of the models. Yet, in the eccentricity model, pooling across the scales too early in the hierarchy leads to lower accuracy.
- The Eccentricity Dependent Models can be used for modeling the feedforward path of the primate visual cortex.
- If target locations are proposed, then the system can become even more robust and hence a simple network can become robust to clutter while also reducing the amount of training data and time needed
Critique
This paper only tries to check the impact of flankers on targets as to how crowding can affect recognition but it does not propose anything novel in terms of architecture to take care of such type of crowding. The paper only shows that the eccentricity based model does better (than plain DCNN model) when the target is placed at the center of the image but maybe windowing over the frames the same way that a convolutional model passes a filter over an image, instead of taking crops starting from the middle, might help.
This paper focuses on image classification. For a stronger argument, their model could be applied to the task of object detection. Perhaps crowding does not have as large of an impact when the objects of interest are localized by a region proposal network. Further, the artificial crowding introduced in the paper may not be random enough for the neural network to learn to classify the object of interest as opposed to the entire cluster of objects. For example, in the case of an even MNIST digit being flanked by two odd MNIST digits, there are only 25 possible combinations of flankers and targets.
This paper does not provide a convincing argument that the problem of crowding as experienced by humans somehow shares a similar mechanism to the problem of DNN accuracy falling when there is more clutter in the scene. The multi-scale architecture does not appear similar to the distribution of rods and cones in the retina[1]. It might be that the eccentric model does well when the target is centered because it is being sampled by more scales, not because it is similar to a primate visual cortex, and primates are able to recognize an object in clutter when looking directly at it.
References
- Volokitin A, Roig G, Poggio T:"Do Deep Neural Networks Suffer from Crowding?" Conference on Neural Information Processing Systems (NIPS). 2017
- Francis X. Chen, Gemma Roig, Leyla Isik, Xavier Boix and Tomaso Poggio: "Eccentricity Dependent Deep Neural Networks for Modeling Human Vision" Journal of Vision. 17. 808. 10.1167/17.10.808.
- J Harrison, W & W Remington, R & Mattingley, Jason. (2014). Visual crowding is anisotropic along the horizontal meridian during smooth pursuit. Journal of vision. 14. 10.1167/14.1.21. http://willjharrison.com/2014/01/new-paper-visual-crowding-is-anisotropic-along-the-horizontal-meridian-during-smooth-pursuit/