Dynamic Routing Between Capsules: Difference between revisions
| (26 intermediate revisions by 3 users not shown) | |||
| Line 95: | Line 95: | ||
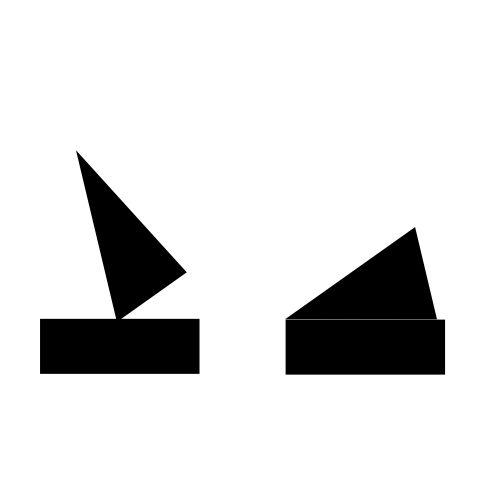
As can be shown in the ambiguous figure below. There are two different ways to interpret it. One way is to interpret the rectangle and triangle in the middle as an upside down house, but this leaves the bottom rectangle and the top triangle unexplained. The other way to interpret the image is that there is a house at the top tilting approximately 30 degree to the left and a boat at the bottom tilting approximately 20 degree to the right. Routing by agreement will tend to choose the latter explanation, since each of the capsules makes perfect predictions for the capsules in the next layer. | As can be shown in the ambiguous figure below. There are two different ways to interpret it. One way is to interpret the rectangle and triangle in the middle as an upside down house, but this leaves the bottom rectangle and the top triangle unexplained. The other way to interpret the image is that there is a house at the top tilting approximately 30 degree to the left and a boat at the bottom tilting approximately 20 degree to the right. Routing by agreement will tend to choose the latter explanation, since each of the capsules makes perfect predictions for the capsules in the next layer. | ||
[[File: | [[File:Screen Shot 2018-03-21 at 5.40.54 PM.png|800px]] | ||
=== Classification and Regularizaiton=== | === Classification and Regularizaiton=== | ||
'''Classifier''' | |||
Once we know how routing between capsules works, we can have one capsule per class in the top layer in order to have an image classifier. Add a layer that computes the length of the top layer activation vectors, which gives the estimated class probabilities. | |||
In the paper, they use a margin loss that makes it possible to detect multiple classes. | |||
</math> L_k = T_k max(0,m^+-||v_k||)^2+&lamda(1-T_k)max(0,||v_k||-m^-) </math> | |||
This margin loss is such that if an object of class k is present in the image, then the corresponding top-level capsule should output a vector whose square length is at least 0.9. Conversely, if an object of class k is not present in the image, then the capsule should output a short vector, whose length is shorter than 0.1. So the total loss is the sum of losses for all classes. | |||
'''Regularization by Reconstruction''' | |||
In the paper, they also add a decoder network on top of the capsule network. There are 3 fully connected layers with a sigmoid activation function in the output layer. It learns to reconstruct the input image by minimizing the squared difference between the reconstructed image and the input image. The full loss is the margin loss plus the reconstruction loss (scaled down considerably so as to ensure that the margin loss dominates training). The benefit of applying this reconstruction loss is that it forces the network to preserve all the information required to reconstruct the image, up to the top layer of the capsule network (its output layer). This constraint acts a bit like a regularizer: it reduces the risk of overfitting and helps generalize to new examples. | |||
== Modelling using MNIST == | == Modelling using MNIST == | ||
[[File:mnist_modeling_graph.png | center | 800px]] | |||
A simple CapsNet with 3 layers has been proposed MNIST dataset. | |||
This model gives comparable results to deep convolutional networks (such as Chang and Chen [arXiv:1511.02583, 2015]). | |||
The first convolutional layer has kernel_size=9, stride=1. It produces one image(20 X 20) with 256 channels. | |||
The second convolutional layer has kernel_size=9, stride=2. It produces 32 images(6X6) with 8 channels. Now, we have 32 images, each image has 6X6 pixels and each pixel has 8 dimensions. Thus we have 32*6*6 pixels at this point. | |||
Consider each pixel is an capsule. We have 32*6*6 capsules <math>u_i</math> from second Conv layer. Thus, we have <math>\hat{u}_{ij} = W_{ij}u_i</math> as output from capsule i (from lower layer) to capsule j (from DigitCaps layer). | |||
DigitsCaps layer has 10 capsules <math>v_j</math>, each has length 16.<math>v_j = squash(\sum_i \alpha_{ij} \hat{u}_{ij})</math>, and <math>\alpha_{ij}</math> is scalar determined by dynamic routing. | |||
The capsule that has the largest length (e.g. capsule j)represent the model has most confidence that this image shows digits j. | |||
== Evaluation == | == Evaluation == | ||
'''Benefits of the Capsule Network:''' | |||
1. Capsule network offers equivariance | |||
2. Less training data required | |||
3. High accuracy on MNIST dataset | |||
4. Good performance at segmenting highly overlapping digits | |||
5. Activation vectors are interpretable | |||
6. Robustness to Affine Transformations | |||
'''Limitations of the Capsule Network:''' | |||
1. Low accuracy on CIFAR10 dataset | |||
2. Lack of testing on larger images (e.g. ImageNet) | |||
3. Training process is slow | |||
4. Capsule network cannot see very close identical objects | |||
(Reference: https://www.youtube.com/watch?v=pPN8d0E3900) | |||
Latest revision as of 12:36, 29 March 2018
Group Member
Siqi Chen, Weifeng Liang, Yi Shan, Yao Xiao, Yuliang Xu, Jiajia Yin, Jianxing Zhang
Introduction and Background
Over the past decades, convolutional neural network has been proven to be one of the most effective methods in voice and image recognition. Back in the 90's, Geoffrey Hinton, one of the authors of this paper, also THE scientist in machine learning field, lead a project which was regarded more as a science fiction rather than a research vocation at that time. Decades later, with the computational power and huge data collected today, scientists are racing to start their careers in machine learning field.
(Reference: https://www.recode.net/2015/7/15/11614684/ai-conspiracy-the-scientists-behind-deep-learning)
However, CNN is not guaranteed to be perfect all the time. With the pursing of perfection in image recognition field, we are glad to present this paper, which offers a modification to solve for the flaws in CNN and largely improves the prediction precision.
Motivation
Why CNN doesn't always work?
In CNN, there's always at least one pooling stage. If we take max-pooling method as an example, the idea is to take the maximum value from a neighborhood, so that when the information is passed to the next layer, we can adjust the dimensions whatever ways we want, and in most cases, we want to reduce the number of dimensions because we always want to save computations. The reason behind this kind of pooling method is based on the correlations within adjacent area. There’re two examples: one (Netflix users’ preferences )is from the example in Ali’s Youtube videos, the other is about the observation of pictures. We will illustrate these two examples in class. So we can see, the problem with local pooling method is that, it only passes the local patterns into the next layer. That is to say, if our original data set doesn't have the good property of neighborhood resemblance, or is simply rearranged by different components, our machine can no longer recognize the picture or make predictions. Although pooling methods save lots of computational power, but it leads the whole CNN methods (i.e. the machine) towards recognizing the local patterns in an image to make judgement instead of looking at the whole picture. Our goal is to train the machine do things in a way, if not beyond human, resembles human thinking.
"They do not encode the position and orientation of the object into their predictions. They completely lose all their internal data about the pose and the orientation of the object and they route all the information to the same neurons that may not be able to deal with this kind of information.
A CNN makes predictions by looking at an image and then checking to see if certain components are present in that image or not. If they are, then it classifies that image accordingly.
In a CNN, all low-level details are sent to all the higher level neurons. These neurons then perform further convolutions to check whether certain features are present. This is done by striding the receptive field and then replicating the knowledge across all the different neurons
According to Professor Hinton, if a lower level neuron has identified an ear, it then makes sense to send this information to a higher level neuron that deals with identifying faces and not to a neuron that identifies chairs. If the higher level face neuron gets a lot of information that contains both the position and the degree of certainty from lower level neurons of the presence of a nose, two eyes and an ear, then the face neuron can identify it as a face.
His solution is to have capsules, or a group of neurons, in lower layers to identify certain patterns. These capsules would then output a high-dimensional vector that contains information about the probability of the position of a pattern and its pose. These values would then be fed to the higher-level capsules that take multiple inputs from many lower-level capsules."
Reference: https://www.quora.com/What-are-some-of-the-limitations-or-drawbacks-of-Convolutional-Neural-Networks
Moreover, there are two more examples which can visualize the defect of CNN.
The first one is "One pixel attack". Look at the following graph:
One-pixel attacks created with the proposed algorithm that successfully fooled three types of DNNs trained on CIFAR-10 dataset: The All convolutional network(AllConv), Network in network(NiN) and VGG. The original class labels are in black color while the target class labels and the corresponding confidence are in blue.
In addition, CNN is good at detecting features but less effective at exploring the spatial relationships among features (perspective, size, orientation). For example, the following picture may fool a simple CNN model in believing that this a good sketch of a human face.
A simple CNN model can extract the features for nose, eyes and mouth correctly but will wrongly activate the neuron for the face detection. Without realize the mis-match in spatial orientation and size, the activation for the face detection will be too high.
So, how to train the machine to look at the whole picture?
In this paper, Professor Geoffrey Hinton gave a solution—using a group of neurons as a capsule to pass the information of orientation and pose.
Introduction to Capsules and Dynamic Routing
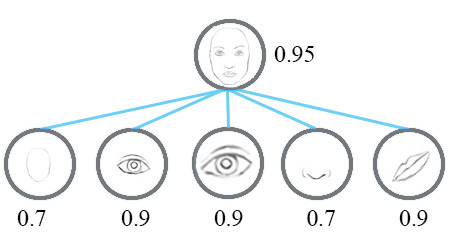
In the following section, we will use an example of classifying images of house and boat (both constructed with rectangles and triangles as shown in Fig 1.) to demonstrate the general idea of capsules and how dynamic routing works.
Introduction to Capsules
First, let's start with the definition of Capsule. Capsule is a group of neurons that tries to predict the presence and the instantiation parameter of a particular object at the given location. The length of the activity vector of a capsule represent the probability that the object exists, and the orientation of the activity vector represents the instantiation parameters. In the figure below, there are 50 arrows in the left square, and each of them is a capsule. The blue arrows are predicting triangles, and the black ones are predicting the rectangle. In this example, the orientation of the arrows represents the rotation of the shapes. But in reality, the activity vector may have much more dimensions.
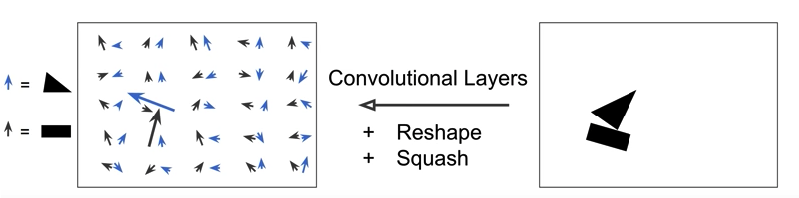
Usually multiple Convolutional Layers are applied to implement capsules, which outputs an array containing feature maps. Then the array is reshaped to get a set of vectors for each location. At the same time, we also need to squash the vectors by [math]\displaystyle{ Squash(u) = \frac{||u||^2}{1+||u||^2} \frac{u}{||u||} }[/math], which preserves the direction of the vector but rescales the range to [0, 1]. We want this range because the length need to represent the probability of the existence of the object.
In the example above, if we rotate the ship, the errors will change their pointing direction correspondingly as well, since they always detect the orientation of the object. This is called [math]\displaystyle{ Equivariance }[/math]. This is an important feature that is not captured by convolutional net. The key difference between capsule and neural network architectures is that others add layers after a layer, but capsule nests a layer inside another layer.
Prediction and Routing
In the above boat and house example, we have two capsules to detect rectangle and triangle. The left part of Figure 2 shows the result from the primary capsule layer. The prediction contains two parts: probability of existence of certain element and the direction. Suppose they will be feed into 2 capsules in the next layer: house-capsule and boat-capsule.
Assume that the rectangle capsule detect a rectangle rotated by 30 degrees, this feed into the next layer will result into house-capsule detecting a house rotated by 30 degrees. Similar for boat-capsule, where a boat rotated by 30 degrees will be detected in the next layer. Mathematically speaking, this can be written as: [math]\displaystyle{ \hat{u}_{ij} = W_{ij} u_i }[/math] where [math]\displaystyle{ u_i }[/math] is the own activation function of this capsule and [math]\displaystyle{ W_{ij} }[/math] is a transformation matrix being developed during training process.
Then look at the prediction from triangle capsule, which provides a different result in house-capsule and boat-capsule.
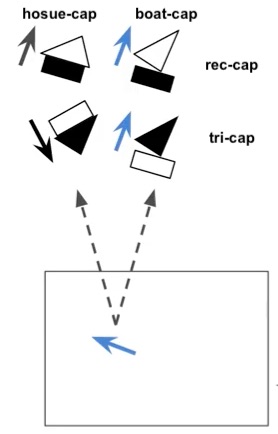
Now we have four outputs in total, and we can see that the prediction in boat-capsule strongly agree to each other, which means we can reach the conclusion that the rectangle and triangle are parts of a boat; therefore, they should be routed to the boat-capsule. There is no need to send the output from primary capsule to any other capsules in the next layer, since this action will only add noise. This is the procedure called routing by agreement. Since only necessary outputs will be directed to the next layer, clearer signal will be received, and more accurate result will be produced. To implement routing by agreement, a clustering technique will be used and introduced in the next section.
Clustering and Updating
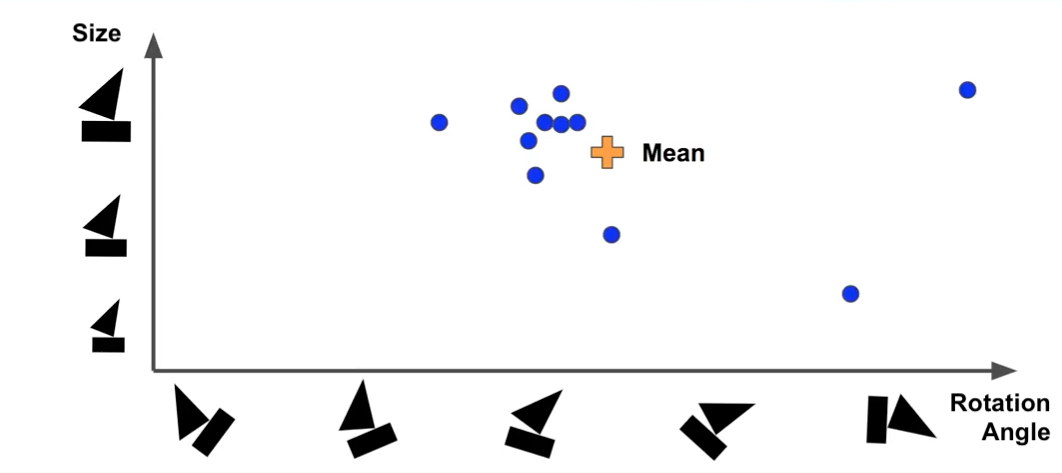
Suppose we represent capsules in the above graph, with x-axis representing rotation angle of the boat and y-axie representing the size. After find out the mean of data, we need to measure the distance between mean and prediction points on the graph by applying Euclidean distance or scalar product. The purpose of this step is to understand how much each prediction vector agrees with the mean, so that the weights of predicted vector can be output and updated. If the prediction matches mean well (i.e. the distance is small), more weights will be assigned to it. After getting the new weights, a weighted-mean will be computed, and it will be used to compute the distance again, and updated iteratively until reaches a steady state.
Mathematically speaking, the procedure starts with 0 weights for all prediction initially. Round1:
bij = 0 for all i and j ci = softmax(bi) sj = weighted sum of predictions of each capsule in the next layer vj = squash(sj), which will be the actual outputs of the next layers
After round1, we will update all [math]\displaystyle{ b_{ij} }[/math] as: [math]\displaystyle{ b_{ij} += \hat{u}_j * v_{ji} }[/math], then perform the next steps iteratively.
Handling Overlap Images
Routing by agreement is really good at handling crowded scenes/overlap images compared with CNN.
As can be shown in the ambiguous figure below. There are two different ways to interpret it. One way is to interpret the rectangle and triangle in the middle as an upside down house, but this leaves the bottom rectangle and the top triangle unexplained. The other way to interpret the image is that there is a house at the top tilting approximately 30 degree to the left and a boat at the bottom tilting approximately 20 degree to the right. Routing by agreement will tend to choose the latter explanation, since each of the capsules makes perfect predictions for the capsules in the next layer.
Classification and Regularizaiton
Classifier
Once we know how routing between capsules works, we can have one capsule per class in the top layer in order to have an image classifier. Add a layer that computes the length of the top layer activation vectors, which gives the estimated class probabilities.
In the paper, they use a margin loss that makes it possible to detect multiple classes.
</math> L_k = T_k max(0,m^+-||v_k||)^2+&lamda(1-T_k)max(0,||v_k||-m^-) </math>
This margin loss is such that if an object of class k is present in the image, then the corresponding top-level capsule should output a vector whose square length is at least 0.9. Conversely, if an object of class k is not present in the image, then the capsule should output a short vector, whose length is shorter than 0.1. So the total loss is the sum of losses for all classes.
Regularization by Reconstruction
In the paper, they also add a decoder network on top of the capsule network. There are 3 fully connected layers with a sigmoid activation function in the output layer. It learns to reconstruct the input image by minimizing the squared difference between the reconstructed image and the input image. The full loss is the margin loss plus the reconstruction loss (scaled down considerably so as to ensure that the margin loss dominates training). The benefit of applying this reconstruction loss is that it forces the network to preserve all the information required to reconstruct the image, up to the top layer of the capsule network (its output layer). This constraint acts a bit like a regularizer: it reduces the risk of overfitting and helps generalize to new examples.
Modelling using MNIST
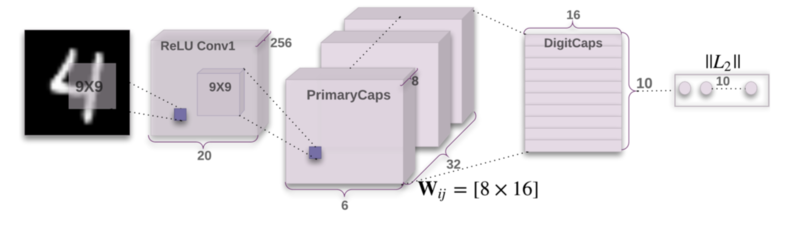
A simple CapsNet with 3 layers has been proposed MNIST dataset.
This model gives comparable results to deep convolutional networks (such as Chang and Chen [arXiv:1511.02583, 2015]).
The first convolutional layer has kernel_size=9, stride=1. It produces one image(20 X 20) with 256 channels.
The second convolutional layer has kernel_size=9, stride=2. It produces 32 images(6X6) with 8 channels. Now, we have 32 images, each image has 6X6 pixels and each pixel has 8 dimensions. Thus we have 32*6*6 pixels at this point.
Consider each pixel is an capsule. We have 32*6*6 capsules [math]\displaystyle{ u_i }[/math] from second Conv layer. Thus, we have [math]\displaystyle{ \hat{u}_{ij} = W_{ij}u_i }[/math] as output from capsule i (from lower layer) to capsule j (from DigitCaps layer).
DigitsCaps layer has 10 capsules [math]\displaystyle{ v_j }[/math], each has length 16.[math]\displaystyle{ v_j = squash(\sum_i \alpha_{ij} \hat{u}_{ij}) }[/math], and [math]\displaystyle{ \alpha_{ij} }[/math] is scalar determined by dynamic routing.
The capsule that has the largest length (e.g. capsule j)represent the model has most confidence that this image shows digits j.
Evaluation
Benefits of the Capsule Network:
1. Capsule network offers equivariance
2. Less training data required
3. High accuracy on MNIST dataset
4. Good performance at segmenting highly overlapping digits
5. Activation vectors are interpretable
6. Robustness to Affine Transformations
Limitations of the Capsule Network:
1. Low accuracy on CIFAR10 dataset
2. Lack of testing on larger images (e.g. ImageNet)
3. Training process is slow
4. Capsule network cannot see very close identical objects
(Reference: https://www.youtube.com/watch?v=pPN8d0E3900)