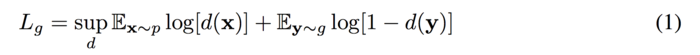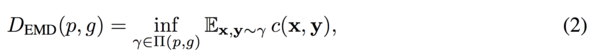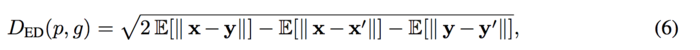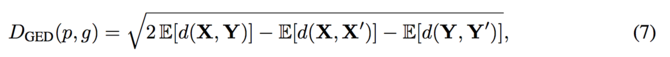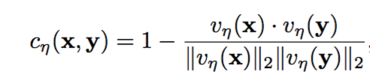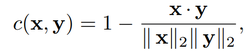stat946w18/IMPROVING GANS USING OPTIMAL TRANSPORT: Difference between revisions
| (154 intermediate revisions by 20 users not shown) | |||
| Line 1: | Line 1: | ||
== Introduction == | == Introduction == | ||
Generative | Recently, the problem of how to learn models that generate media such as images, video, audio and text has become very popular and is called Generative Modeling. One of the main benefits of such an approach is that generative models can be trained on unlabeled data that is readily available . Therefore, generative networks have a huge potential in the field of deep learning. | ||
Generative Adversarial Networks (GANs) are powerful generative models used for unsupervised learning techniques where the 2 agents compete to generate a zero-sum model. A GAN model consists of a generator and a discriminator or critic. The generator is a neural network which is trained to generate data having a distribution matched with the distribution of the real data. The critic is also a neural network, which is trained to separate the generated data from the real data. A loss function that measures the distribution distance between the generated data and the real one is important to train the generator. | |||
This paper presents a variant GANs named OT-GAN, which incorporates a discriminative metric called ' | Optimal transport theory, which is another approach to measuring distances between distributions, evaluates the distribution distance between the generated data and the training data based on a metric, which provides another method for generator training. The main advantage of optimal transport theory over the distance measurement in GAN is its closed form solution for having a tractable training process. But the theory might also result in inconsistency in statistical estimation due to the given biased gradients if the mini-batches method is applied (Bellemare et al., | ||
2017). | |||
This paper presents a variant GANs named OT-GAN, which incorporates a discriminative metric called 'Mini-batch Energy Distance' into its critic in order to overcome the issue of biased gradients. | |||
== GANs and Optimal Transport == | == GANs and Optimal Transport == | ||
| Line 13: | Line 16: | ||
[[File:equation1.png|700px]] | [[File:equation1.png|700px]] | ||
The goal of GANs is to train the generator g and the discriminator d finding a pair of (g,d) to achieve Nash equilibrium. However, it could cause failure of converging since the generator and the discriminator are trained based on gradient descent techniques. | The goal of GANs is to train the generator g and the discriminator d finding a pair of (g,d) to achieve Nash equilibrium(such that either of them cannot reduce their cost without changing the others' parameters). However, it could cause failure of converging since the generator and the discriminator are trained based on gradient descent techniques. | ||
===Wasserstein | ===Wasserstein Distance (Earth-Mover Distance)=== | ||
In order to solve the problem of convergence failure, Arjovsky et. al. (2017) suggested Wasserstein distance (Earth-Mover distance) based on the optimal transport theory. | In order to solve the problem of convergence failure, Arjovsky et. al. (2017) suggested Wasserstein distance (Earth-Mover distance) based on the optimal transport theory. | ||
| Line 21: | Line 24: | ||
[[File:equation2.png|600px]] | [[File:equation2.png|600px]] | ||
where <math> \prod (p,g) </math> is the set of all joint distributions <math> \gamma (x,y) </math> with marginals <math> p(x), g(y) </math> | where <math> \prod (p,g) </math> is the set of all joint distributions <math> \gamma (x,y) </math> with marginals <math> p(x) </math> (real data), <math> g(y) </math> (generated data). <math> c(x,y) </math> is a cost function and the Euclidean distance was used by Arjovsky et. al. in the paper. | ||
The | The Wasserstein distance can be considered as moving the minimum amount of points between distribution <math> g(y) </math> and <math> p(x) </math> such that the generator distribution <math> g(y) </math> is similar to the real data distribution <math> p(x) </math>. | ||
Computing the Wasserstein distance is intractable. The proposed Wasserstein GAN (W-GAN) provides an estimated solution by switching the optimal transport problem into Kantorovich-Rubinstein dual formulation using a set of 1-Lipschitz functions. A neural network can then be used to obtain an estimation. | |||
[[File:equation3.png|600px]] | [[File:equation3.png|600px]] | ||
W-GAN | W-GAN helps to solve the unstable training process of original GAN and it can solve the optimal transport problem approximately, but it is still intractable. | ||
===Sinkhorn Distance=== | |||
Genevay et al. (2017) proposed to use the primal formulation of optimal transport instead of the dual formulation to generative modeling. They introduced Sinkhorn distance which is a smoothed generalization of the Wasserstein distance. | |||
[[File: equation4.png|600px]] | |||
It introduced entropy restriction (<math> \beta </math>) to the joint distribution <math> \prod_{\beta} (p,g) </math>. This distance could be generalized to approximate the mini-batches of data <math> X ,Y</math> with <math> K </math> vectors of <math> x, y</math>. The <math> i, j </math> th entry of the cost matrix <math> C </math> can be interpreted as the cost it needs to transport the <math> x_i </math> in mini-batch X to the <math> y_i </math> in mini-batch <math>Y </math>. The resulting distance will be: | |||
[[File: equation5.png|550px]] | |||
where <math> M </math> is a <math> K \times K </math> matrix, each row of <math> M </math> is a joint distribution of <math> \gamma (x,y) </math> with positive entries. The summmation of rows or columns of <math> M </math> is always equal to 1. | |||
This mini-batch Sinkhorn distance is not only fully tractable but also capable of solving the instability problem of GANs. However, it is not a valid metric over probability distribution when taking the expectation of <math> \mathcal{W}_{c} </math> and the gradients are biased when the mini-batch size is fixed. | |||
===Energy Distance (Cramer Distance)=== | |||
In order to solve the above problem, Bellemare et al. proposed Energy distance: | |||
[[File: equation6.png|700px]] | |||
== | where <math> x, x' </math> and <math> y, y'</math> are independent samples from data distribution <math> p </math> and generator distribution <math> g </math>, respectively. Based on the Energy distance, Cramer GAN is to minimize the ED distance metric when training the generator. | ||
[[File: | ==Mini-Batch Energy Distance== | ||
Salimans et al. (2016) mentioned that comparing to use distributions over individual images, mini-batch GAN is more powerful when using the distributions over mini-batches <math> g(X), p(X) </math>. The distance measure is generated for mini-batches. | |||
===Generalized Energy Distance=== | |||
The generalized energy distance allowed to use non-Euclidean distance functions d. It is also valid for mini-batches and is considered better than working with individual data batch. | |||
[[File: equation7.png|670px]] | |||
Similarly as defined in the Energy distance, <math> X, X' </math> and <math> Y, Y'</math> can be the independent samples from data distribution <math> p </math> and the generator distribution <math> g </math>, respectively. While in Generalized engergy distance, <math> X, X' </math> and <math> Y, Y'</math> can also be valid for mini-batches. The <math> D_{GED}(p,g) </math> is a metric when having <math> d </math> as a metric. Thus, taking the triangle inequality of <math> d </math> into account, <math> D(p,g) \geq 0,</math> and <math> D(p,g)=0 </math> when <math> p=g </math>. | |||
===Mini-Batch Energy Distance=== | |||
As <math> d </math> is free to choose, authors proposed Mini-batch Energy Distance by using entropy-regularized Wasserstein distance as <math> d </math>. | |||
[[File: equation8.png|650px]] | |||
where <math> X, X' </math> and <math> Y, Y'</math> are independent sampled mini-batches from the data distribution <math> p </math> and the generator distribution <math> g </math>, respectively. This distance metric combines the energy distance with primal form of optimal transport over mini-batch distributions <math> g(Y) </math> and <math> p(X) </math>. Inside the generalized energy distance, the Sinkhorn distance is a valid metric between each mini-batches. By adding the <math> - \mathcal{W}_c (Y,Y')</math> and <math> \mathcal{W}_c (X,Y)</math> to equation (5) and using energy distance, the objective becomes statistically consistent (meaning the objective converges to the true parameter value for large sample sizes) and mini-batch gradients are unbiased. | |||
==Optimal Transport GAN (OT-GAN)== | |||
The mini-batch energy distance which was proposed depends on the transport cost function <math>c(x,y)</math>. One possibility would be to choose c to be some fixed function over vectors, like Euclidean distance, but the authors found this to perform poorly in preliminary experiments. For simple fixed cost functions like Euclidean distance, there exists many bad distributions <math>g</math> in higher dimensions for which the mini-batch energy distance is zero such that it is difficult to tell <math>p</math> and <math>g</math> apart if the sample size is not big enough. To solve this the authors propose learning the cost function adversarially, so that it can adapt to the generator distribution <math>g</math> and thereby become more discriminative. | |||
In practice, in order to secure the statistical efficiency (i.e. being able to tell <math>p</math> and <math>g</math> apart without requiring an enormous sample size when their distance is close to zero), authors suggested using cosine distance between vectors <math> v_\eta (x) </math> and <math> v_\eta (y) </math> based on the deep neural network that maps the mini-batch data to a learned latent space. Here is the transportation cost: | |||
[[File: euqation9.png|370px]] | |||
where the <math> v_\eta </math> is chosen to maximize the resulting minibatch energy distance. | |||
Unlike the practice when using the original GANs, the generator was trained more often than the critic, which keep the cost function from degeneration. The resulting generator in OT-GAN has a well defined and statistically consistent objective through the training process. | |||
The algorithm is defined below. The backpropagation is not used in the algorithm since ignoring this gradient flow is justified by the envelope theorem (i.e. when changing the parameters of the objective function, changes in the optimizer do not contribute to a change in the objective function). Stochastic gradient descent is used as the optimization method in algorithm 1 below, although other optimizers are also possible. In fact, Adam was used in experiments. | |||
[[File: al.png|600px]] | |||
[[File: al_figure.png|600px]] | |||
==Experiments== | |||
In order to demonstrate the supermum performance of the OT-GAN, authors compared it with the original GAN and other popular models based on four experiments: Dataset recovery; CIFAR-10 test; ImageNet test; and the conditional image synthesis test. | |||
===Mixture of Gaussian Dataset=== | |||
OT-GAN has a statistically consistent objective when it is compared with the original GAN (DC-GAN), such that the generator would not update to a wrong direction even if the signal provided by the cost function to the generator is not good. In order to prove this advantage, authors compared the OT-GAN with the original GAN loss (DAN-S) based on a simple task. The task was set to recover all of the 8 modes from 8 Gaussian mixers in which the means were arranged in a circle. MLP with RLU activation functions were used in this task. The critic was only updated for 15K iterations. The generator distribution was tracked for another 25K iteration. The results showed that the original GAN experiences the model collapse after fixing the discriminator while the OT-GAN recovered all the 8 modes from the mixed Gaussian data. | |||
[[File: 5_1.png|600px]] | |||
===CIFAR-10=== | |||
The dataset CIFAR-10 was then used for inspecting the effect of batch-size to the model training process and the image quality. OT-GAN and four other methods were compared using "inception score" as the criteria for comparison. Figure 3 shows the change of inceptions scores (y-axis) by the increased of the iteration number. Scores of four different batch sizes (200, 800, 3200 and 8000) were compared. The results show that a larger batch size, which would more likely cover more modes in the distribution of data, lead to a more stable model showing a larger value in inception score. However, a large batch size would also require a high-performance computational environment. The sample quality across all 5 methods, ran using a batch size of 8000, are compared in Table 1 where the OT_GAN has the best score. | |||
The OT-GAN was trained using Adam optimizer. The learning rate was set to <math> 0.0003, \beta_1 = 0.5, \beta_2 = 0.999 </math> . The introduced OT-GAN algorithm also includes two additional hyperparameters for the Sinkhorn algorithm. The first hyperparameters indicated the number of iterations to run the algorithm and the second <math> 1 / \lambda </math> the entropy penalty of alignments. The authors found that a value of 500 worked well for both mentioned hyperparameters. The network uses the following architecture: | |||
[[File: cf10gc.png|600px]] | |||
[[File: 5_2.png|600px]] | |||
Figure 4 below shows samples generated by the OT-GAN trained with a batch size of 8000. Figure 5 below shows random samples from a model trained with the same architecture and hyperparameters, but with random matching of samples in place of optimal transport. | |||
[[File: ot_gan_cifar_10_samples.png|600px]] | |||
In order to show the advantage of learning the cost function adversarially, the CIFAR-10 experiment was re-run with the cost as follows: | |||
[[File: OTGAN_CosineDist.png|250px]] | |||
When using this fixed cost and keeping the other experiment settings constant, the max inception score dropped from 8.47 with learned to 4.93 with fixed cost functions. The results of the fixed cost are seen in Figure 8 below. | |||
[[File: OTGAN_fixedDist.png|600px]] | |||
===ImageNet Dogs=== | |||
In order to investigate the performance of OT-GAN when dealing with the high-quality images, the dog subset of ImageNet (128*128) was used to train the model. Figure 6 shows that OT-GAN produces less nonsensical images and it has a higher inception score compare to the DC-GAN. | |||
[[File: 5_3.png|600px]] | |||
To analyze mode collapse in GANs the authors trained both types of GANs for a large number of epochs. They find the DCGAN shows mode collapse as soon as 900 epochs. They trained the OT-GAN for 13000 epochs and saw no evidence of mode collapse or less diversity in the samples. Samples can be viewed in Figure 9. | |||
[[File: ModelCollapseImageNetDogs.png|600px]] | |||
===Conditional Generation of Birds=== | |||
The last experiment was to compare OT-GAN with three popular GAN models for processing the text-to-image generation demonstrating the performance on conditional image synthesis. As can be found from Table 2, OT-GAN received the highest inception score than the scores of the other three models. | |||
[[File: 5_4.png|600px]] | |||
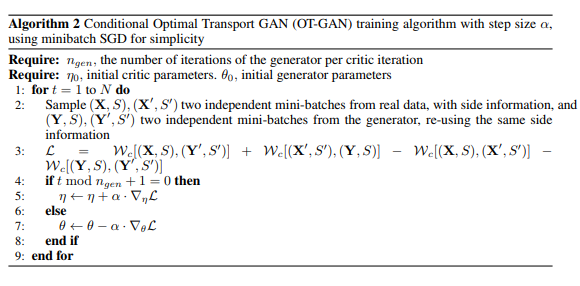
The algorithm used to obtain the results above is conditional generation generalized from '''Algorithm 1''' to include conditional information <math>s</math> such as some text description of an image. The modified algorithm is outlined in '''Algorithm 2'''. | |||
[[File: paper23_alg2.png|600px]] | |||
==Conclusion== | |||
In this paper, an OT-GAN method was proposed based on the optimal transport theory. A distance metric that combines the primal form of the optimal transport and the energy distance was given was presented for realizing the OT-GAN. The results showed OT-GAN to be uniquely stable when trained with large mini batches and state of the art results were achieved on some datasets. One of the advantages of OT-GAN over other GAN models is that OT-GAN can stay on the correct track with an unbiased gradient even if the training on critic is stopped or presents a weak cost signal. The performance of the OT-GAN can be maintained when the batch size is increasing, though the computational cost has to be taken into consideration. | |||
==Critique== | |||
The paper presents a variant of GANs by defining a new distance metric based on the primal form of optimal transport and the mini-batch energy distance. The stability was demonstrated through the four experiments that comparing OP-GAN with other popular methods. However, limitations in computational efficiency were not discussed much. Furthermore, in section 2, the paper lacks explanation on using mini-batches instead of a vector as input when applying Sinkhorn distance. It is also confusing when explaining the algorithm in section 4 about choosing M for minimizing <math> \mathcal{W}_c </math>. Lastly, it is found that it is lack of parallel comparison with existing GAN variants in this paper. Readers may feel jumping from one algorithm to another without necessary explanations. However, one downside of OT-GAN, as mentioned in the paper, is that it requires large amounts of computation and memory. | |||
= Discussion = | |||
We have presented OT-GAN, a new variant of GANs where the generator is trained to minimize | |||
a novel distance metric over probability distributions. This metric, which we call mini-batch energy | |||
distance, combines optimal transport in primal form with an energy distance defined in an | |||
adversarially learned feature space, resulting in a highly discriminative distance function with unbiased | |||
mini-batch gradients. OT-GAN was shown to be uniquely stable when trained with large | |||
mini-batches and to achieve state-of-the-art results on several common benchmarks. | |||
One downside of OT-GAN, as currently proposed, is that it requires large amounts of computation | |||
and memory. We achieve the best results when using very large mini-batches, which increases the | |||
time required for each update of the parameters. All experiments in this paper, except for the mixture | |||
of Gaussians toy example, were performed using 8 GPUs and trained for several days. In future work, | |||
we hope to make the method more computationally efficient, as well as to scale up our approach to | |||
multi-machine training to enable generation of even more challenging and high-resolution image | |||
data sets. | |||
A unique property of OT-GAN is that the mini-batch energy distance remains a valid training objective | |||
even when we stop training the critic. Our implementation of OT-GAN updates the generative | |||
model more often than the critic, where GANs typically do this the other way around (see e.g. Gulrajani | |||
et al., 2017). As a result, we learn a relatively stable transport cost function c(x, y), describing | |||
how (dis)similar two images are, as well as an image embedding function vη(x) capturing the geometry | |||
of the training data. Preliminary experiments suggest these learned functions can be used | |||
successfully for unsupervised learning and other applications, which we plan to investigate further | |||
in future work. | |||
==Reference== | |||
Salimans, Tim, Han Zhang, Alec Radford, and Dimitris Metaxas. "Improving GANs using optimal transport." (2018). | |||
Latest revision as of 00:23, 21 April 2018
Introduction
Recently, the problem of how to learn models that generate media such as images, video, audio and text has become very popular and is called Generative Modeling. One of the main benefits of such an approach is that generative models can be trained on unlabeled data that is readily available . Therefore, generative networks have a huge potential in the field of deep learning.
Generative Adversarial Networks (GANs) are powerful generative models used for unsupervised learning techniques where the 2 agents compete to generate a zero-sum model. A GAN model consists of a generator and a discriminator or critic. The generator is a neural network which is trained to generate data having a distribution matched with the distribution of the real data. The critic is also a neural network, which is trained to separate the generated data from the real data. A loss function that measures the distribution distance between the generated data and the real one is important to train the generator.
Optimal transport theory, which is another approach to measuring distances between distributions, evaluates the distribution distance between the generated data and the training data based on a metric, which provides another method for generator training. The main advantage of optimal transport theory over the distance measurement in GAN is its closed form solution for having a tractable training process. But the theory might also result in inconsistency in statistical estimation due to the given biased gradients if the mini-batches method is applied (Bellemare et al., 2017).
This paper presents a variant GANs named OT-GAN, which incorporates a discriminative metric called 'Mini-batch Energy Distance' into its critic in order to overcome the issue of biased gradients.
GANs and Optimal Transport
Generative Adversarial Nets
Original GAN was firstly reviewed. The objective function of the GAN:
The goal of GANs is to train the generator g and the discriminator d finding a pair of (g,d) to achieve Nash equilibrium(such that either of them cannot reduce their cost without changing the others' parameters). However, it could cause failure of converging since the generator and the discriminator are trained based on gradient descent techniques.
Wasserstein Distance (Earth-Mover Distance)
In order to solve the problem of convergence failure, Arjovsky et. al. (2017) suggested Wasserstein distance (Earth-Mover distance) based on the optimal transport theory.
where [math]\displaystyle{ \prod (p,g) }[/math] is the set of all joint distributions [math]\displaystyle{ \gamma (x,y) }[/math] with marginals [math]\displaystyle{ p(x) }[/math] (real data), [math]\displaystyle{ g(y) }[/math] (generated data). [math]\displaystyle{ c(x,y) }[/math] is a cost function and the Euclidean distance was used by Arjovsky et. al. in the paper.
The Wasserstein distance can be considered as moving the minimum amount of points between distribution [math]\displaystyle{ g(y) }[/math] and [math]\displaystyle{ p(x) }[/math] such that the generator distribution [math]\displaystyle{ g(y) }[/math] is similar to the real data distribution [math]\displaystyle{ p(x) }[/math].
Computing the Wasserstein distance is intractable. The proposed Wasserstein GAN (W-GAN) provides an estimated solution by switching the optimal transport problem into Kantorovich-Rubinstein dual formulation using a set of 1-Lipschitz functions. A neural network can then be used to obtain an estimation.
W-GAN helps to solve the unstable training process of original GAN and it can solve the optimal transport problem approximately, but it is still intractable.
Sinkhorn Distance
Genevay et al. (2017) proposed to use the primal formulation of optimal transport instead of the dual formulation to generative modeling. They introduced Sinkhorn distance which is a smoothed generalization of the Wasserstein distance.
![]()
It introduced entropy restriction ([math]\displaystyle{ \beta }[/math]) to the joint distribution [math]\displaystyle{ \prod_{\beta} (p,g) }[/math]. This distance could be generalized to approximate the mini-batches of data [math]\displaystyle{ X ,Y }[/math] with [math]\displaystyle{ K }[/math] vectors of [math]\displaystyle{ x, y }[/math]. The [math]\displaystyle{ i, j }[/math] th entry of the cost matrix [math]\displaystyle{ C }[/math] can be interpreted as the cost it needs to transport the [math]\displaystyle{ x_i }[/math] in mini-batch X to the [math]\displaystyle{ y_i }[/math] in mini-batch [math]\displaystyle{ Y }[/math]. The resulting distance will be:
where [math]\displaystyle{ M }[/math] is a [math]\displaystyle{ K \times K }[/math] matrix, each row of [math]\displaystyle{ M }[/math] is a joint distribution of [math]\displaystyle{ \gamma (x,y) }[/math] with positive entries. The summmation of rows or columns of [math]\displaystyle{ M }[/math] is always equal to 1.
This mini-batch Sinkhorn distance is not only fully tractable but also capable of solving the instability problem of GANs. However, it is not a valid metric over probability distribution when taking the expectation of [math]\displaystyle{ \mathcal{W}_{c} }[/math] and the gradients are biased when the mini-batch size is fixed.
Energy Distance (Cramer Distance)
In order to solve the above problem, Bellemare et al. proposed Energy distance:
where [math]\displaystyle{ x, x' }[/math] and [math]\displaystyle{ y, y' }[/math] are independent samples from data distribution [math]\displaystyle{ p }[/math] and generator distribution [math]\displaystyle{ g }[/math], respectively. Based on the Energy distance, Cramer GAN is to minimize the ED distance metric when training the generator.
Mini-Batch Energy Distance
Salimans et al. (2016) mentioned that comparing to use distributions over individual images, mini-batch GAN is more powerful when using the distributions over mini-batches [math]\displaystyle{ g(X), p(X) }[/math]. The distance measure is generated for mini-batches.
Generalized Energy Distance
The generalized energy distance allowed to use non-Euclidean distance functions d. It is also valid for mini-batches and is considered better than working with individual data batch.
Similarly as defined in the Energy distance, [math]\displaystyle{ X, X' }[/math] and [math]\displaystyle{ Y, Y' }[/math] can be the independent samples from data distribution [math]\displaystyle{ p }[/math] and the generator distribution [math]\displaystyle{ g }[/math], respectively. While in Generalized engergy distance, [math]\displaystyle{ X, X' }[/math] and [math]\displaystyle{ Y, Y' }[/math] can also be valid for mini-batches. The [math]\displaystyle{ D_{GED}(p,g) }[/math] is a metric when having [math]\displaystyle{ d }[/math] as a metric. Thus, taking the triangle inequality of [math]\displaystyle{ d }[/math] into account, [math]\displaystyle{ D(p,g) \geq 0, }[/math] and [math]\displaystyle{ D(p,g)=0 }[/math] when [math]\displaystyle{ p=g }[/math].
Mini-Batch Energy Distance
As [math]\displaystyle{ d }[/math] is free to choose, authors proposed Mini-batch Energy Distance by using entropy-regularized Wasserstein distance as [math]\displaystyle{ d }[/math].
where [math]\displaystyle{ X, X' }[/math] and [math]\displaystyle{ Y, Y' }[/math] are independent sampled mini-batches from the data distribution [math]\displaystyle{ p }[/math] and the generator distribution [math]\displaystyle{ g }[/math], respectively. This distance metric combines the energy distance with primal form of optimal transport over mini-batch distributions [math]\displaystyle{ g(Y) }[/math] and [math]\displaystyle{ p(X) }[/math]. Inside the generalized energy distance, the Sinkhorn distance is a valid metric between each mini-batches. By adding the [math]\displaystyle{ - \mathcal{W}_c (Y,Y') }[/math] and [math]\displaystyle{ \mathcal{W}_c (X,Y) }[/math] to equation (5) and using energy distance, the objective becomes statistically consistent (meaning the objective converges to the true parameter value for large sample sizes) and mini-batch gradients are unbiased.
Optimal Transport GAN (OT-GAN)
The mini-batch energy distance which was proposed depends on the transport cost function [math]\displaystyle{ c(x,y) }[/math]. One possibility would be to choose c to be some fixed function over vectors, like Euclidean distance, but the authors found this to perform poorly in preliminary experiments. For simple fixed cost functions like Euclidean distance, there exists many bad distributions [math]\displaystyle{ g }[/math] in higher dimensions for which the mini-batch energy distance is zero such that it is difficult to tell [math]\displaystyle{ p }[/math] and [math]\displaystyle{ g }[/math] apart if the sample size is not big enough. To solve this the authors propose learning the cost function adversarially, so that it can adapt to the generator distribution [math]\displaystyle{ g }[/math] and thereby become more discriminative.
In practice, in order to secure the statistical efficiency (i.e. being able to tell [math]\displaystyle{ p }[/math] and [math]\displaystyle{ g }[/math] apart without requiring an enormous sample size when their distance is close to zero), authors suggested using cosine distance between vectors [math]\displaystyle{ v_\eta (x) }[/math] and [math]\displaystyle{ v_\eta (y) }[/math] based on the deep neural network that maps the mini-batch data to a learned latent space. Here is the transportation cost:
where the [math]\displaystyle{ v_\eta }[/math] is chosen to maximize the resulting minibatch energy distance.
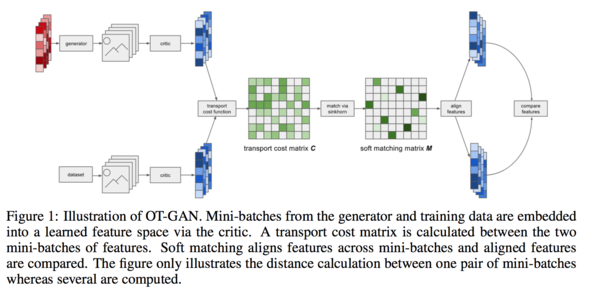
Unlike the practice when using the original GANs, the generator was trained more often than the critic, which keep the cost function from degeneration. The resulting generator in OT-GAN has a well defined and statistically consistent objective through the training process.
The algorithm is defined below. The backpropagation is not used in the algorithm since ignoring this gradient flow is justified by the envelope theorem (i.e. when changing the parameters of the objective function, changes in the optimizer do not contribute to a change in the objective function). Stochastic gradient descent is used as the optimization method in algorithm 1 below, although other optimizers are also possible. In fact, Adam was used in experiments.
Experiments
In order to demonstrate the supermum performance of the OT-GAN, authors compared it with the original GAN and other popular models based on four experiments: Dataset recovery; CIFAR-10 test; ImageNet test; and the conditional image synthesis test.
Mixture of Gaussian Dataset
OT-GAN has a statistically consistent objective when it is compared with the original GAN (DC-GAN), such that the generator would not update to a wrong direction even if the signal provided by the cost function to the generator is not good. In order to prove this advantage, authors compared the OT-GAN with the original GAN loss (DAN-S) based on a simple task. The task was set to recover all of the 8 modes from 8 Gaussian mixers in which the means were arranged in a circle. MLP with RLU activation functions were used in this task. The critic was only updated for 15K iterations. The generator distribution was tracked for another 25K iteration. The results showed that the original GAN experiences the model collapse after fixing the discriminator while the OT-GAN recovered all the 8 modes from the mixed Gaussian data.
CIFAR-10
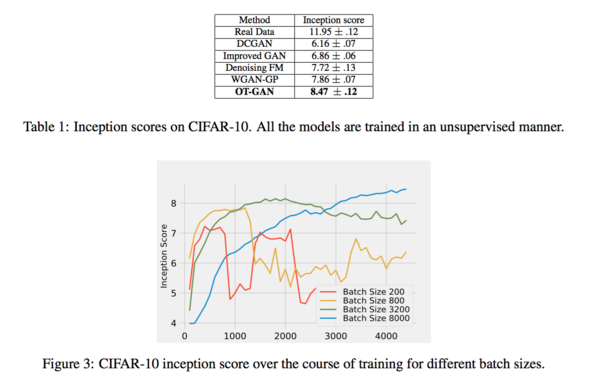
The dataset CIFAR-10 was then used for inspecting the effect of batch-size to the model training process and the image quality. OT-GAN and four other methods were compared using "inception score" as the criteria for comparison. Figure 3 shows the change of inceptions scores (y-axis) by the increased of the iteration number. Scores of four different batch sizes (200, 800, 3200 and 8000) were compared. The results show that a larger batch size, which would more likely cover more modes in the distribution of data, lead to a more stable model showing a larger value in inception score. However, a large batch size would also require a high-performance computational environment. The sample quality across all 5 methods, ran using a batch size of 8000, are compared in Table 1 where the OT_GAN has the best score.
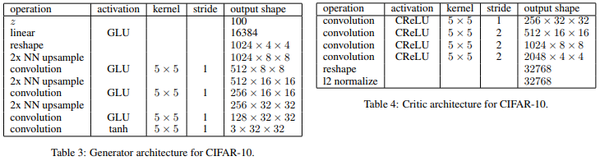
The OT-GAN was trained using Adam optimizer. The learning rate was set to [math]\displaystyle{ 0.0003, \beta_1 = 0.5, \beta_2 = 0.999 }[/math] . The introduced OT-GAN algorithm also includes two additional hyperparameters for the Sinkhorn algorithm. The first hyperparameters indicated the number of iterations to run the algorithm and the second [math]\displaystyle{ 1 / \lambda }[/math] the entropy penalty of alignments. The authors found that a value of 500 worked well for both mentioned hyperparameters. The network uses the following architecture:
Figure 4 below shows samples generated by the OT-GAN trained with a batch size of 8000. Figure 5 below shows random samples from a model trained with the same architecture and hyperparameters, but with random matching of samples in place of optimal transport.
In order to show the advantage of learning the cost function adversarially, the CIFAR-10 experiment was re-run with the cost as follows:
When using this fixed cost and keeping the other experiment settings constant, the max inception score dropped from 8.47 with learned to 4.93 with fixed cost functions. The results of the fixed cost are seen in Figure 8 below.
ImageNet Dogs
In order to investigate the performance of OT-GAN when dealing with the high-quality images, the dog subset of ImageNet (128*128) was used to train the model. Figure 6 shows that OT-GAN produces less nonsensical images and it has a higher inception score compare to the DC-GAN.
To analyze mode collapse in GANs the authors trained both types of GANs for a large number of epochs. They find the DCGAN shows mode collapse as soon as 900 epochs. They trained the OT-GAN for 13000 epochs and saw no evidence of mode collapse or less diversity in the samples. Samples can be viewed in Figure 9.
Conditional Generation of Birds
The last experiment was to compare OT-GAN with three popular GAN models for processing the text-to-image generation demonstrating the performance on conditional image synthesis. As can be found from Table 2, OT-GAN received the highest inception score than the scores of the other three models.
The algorithm used to obtain the results above is conditional generation generalized from Algorithm 1 to include conditional information [math]\displaystyle{ s }[/math] such as some text description of an image. The modified algorithm is outlined in Algorithm 2.
Conclusion
In this paper, an OT-GAN method was proposed based on the optimal transport theory. A distance metric that combines the primal form of the optimal transport and the energy distance was given was presented for realizing the OT-GAN. The results showed OT-GAN to be uniquely stable when trained with large mini batches and state of the art results were achieved on some datasets. One of the advantages of OT-GAN over other GAN models is that OT-GAN can stay on the correct track with an unbiased gradient even if the training on critic is stopped or presents a weak cost signal. The performance of the OT-GAN can be maintained when the batch size is increasing, though the computational cost has to be taken into consideration.
Critique
The paper presents a variant of GANs by defining a new distance metric based on the primal form of optimal transport and the mini-batch energy distance. The stability was demonstrated through the four experiments that comparing OP-GAN with other popular methods. However, limitations in computational efficiency were not discussed much. Furthermore, in section 2, the paper lacks explanation on using mini-batches instead of a vector as input when applying Sinkhorn distance. It is also confusing when explaining the algorithm in section 4 about choosing M for minimizing [math]\displaystyle{ \mathcal{W}_c }[/math]. Lastly, it is found that it is lack of parallel comparison with existing GAN variants in this paper. Readers may feel jumping from one algorithm to another without necessary explanations. However, one downside of OT-GAN, as mentioned in the paper, is that it requires large amounts of computation and memory.
Discussion
We have presented OT-GAN, a new variant of GANs where the generator is trained to minimize a novel distance metric over probability distributions. This metric, which we call mini-batch energy distance, combines optimal transport in primal form with an energy distance defined in an adversarially learned feature space, resulting in a highly discriminative distance function with unbiased mini-batch gradients. OT-GAN was shown to be uniquely stable when trained with large mini-batches and to achieve state-of-the-art results on several common benchmarks. One downside of OT-GAN, as currently proposed, is that it requires large amounts of computation and memory. We achieve the best results when using very large mini-batches, which increases the time required for each update of the parameters. All experiments in this paper, except for the mixture of Gaussians toy example, were performed using 8 GPUs and trained for several days. In future work, we hope to make the method more computationally efficient, as well as to scale up our approach to multi-machine training to enable generation of even more challenging and high-resolution image data sets. A unique property of OT-GAN is that the mini-batch energy distance remains a valid training objective even when we stop training the critic. Our implementation of OT-GAN updates the generative model more often than the critic, where GANs typically do this the other way around (see e.g. Gulrajani et al., 2017). As a result, we learn a relatively stable transport cost function c(x, y), describing how (dis)similar two images are, as well as an image embedding function vη(x) capturing the geometry of the training data. Preliminary experiments suggest these learned functions can be used successfully for unsupervised learning and other applications, which we plan to investigate further in future work.
Reference
Salimans, Tim, Han Zhang, Alec Radford, and Dimitris Metaxas. "Improving GANs using optimal transport." (2018).