Modular Multitask Reinforcement Learning with Policy Sketches: Difference between revisions
No edit summary |
|||
| (108 intermediate revisions by 21 users not shown) | |||
| Line 1: | Line 1: | ||
='''Introduction'''= | ='''Introduction & Background'''= | ||
[[File:MRL0.png|border|right|400px]] | |||
This paper describes a framework for learning | [[File:MRL_diagram.jpg|thumb|right|400px| Figure 1b: the diagram for policy sketches]] | ||
[[File:MRL_encode.jpg|thumb|right|600px| Figure 1c: All sub tasks are encoded without any semantic meanings]] | |||
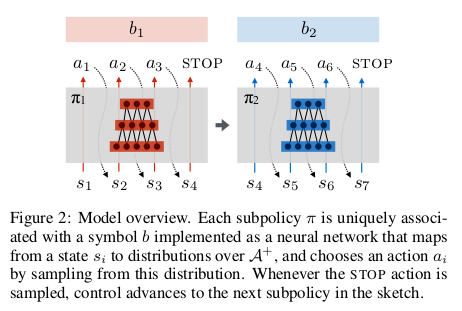
This paper describes a framework for learning composable deep subpolicies in a multitask setting. These policies are guided only by abstract sketches which are representative of the high-level behavior in the environment. Sketches annotate tasks with sequences of named subtasks, providing information about high-level structural relationships among tasks but not how to implement them—specifically not providing the detailed guidance used by much previous work on learning policy abstractions for RL (e.g. intermediate rewards, subtask completion signals, or intrinsic motivations). General reinforcement learning algorithms allow agents to solve tasks in complex environments. Vanilla policies find it difficult to deal with tasks featuring extremely delayed rewards. Most approaches often require in-depth supervision in the form of explicitly specified high-level actions, subgoals, or behavioral primitives. The proposed methodology is particularly suitable where rewards are difficult to engineer by hand. It is enough to tell the learner about the abstract policy structure, without indicating how high-level behaviors should try to use primitive percepts or actions. | |||
This paper explores a multitask reinforcement learning setting where the learner is presented with policy sketches. Policy sketches are defined as short, ungrounded, symbolic representations of a task. It describes its components, as shown in Figure 1. While symbols might be shared across different tasks ( the predicate "get wood" appears in sketches for both the tasks: "make planks" and "make sticks"). The learner is not shown or told anything about what these symbols mean, either in terms of observations or intermediate rewards. These sketches are initially meaningless but eventually the sketches get mapped into real policies. As shown in Figure 1c, the tasks are divided into human readable sub tasks. However, in the actual settings, the learner can only get access to encoded results. | |||
The agent learns from policy sketches by associating each high-level action with a parameterization of a low-level subpolicy. It jointly optimizes over concatenated task-specific policies by tying/sharing parameters across common subpolicies. They find that this architecture uses the high-level guidance provided by sketches to drastically accelerate learning of complex multi-stage behaviors. The experiments show that most benefits of learning from very detailed low-level supervision (e.g. from subgoal rewards) can also be obtained from fairly coarse high-level policy sketches. Most importantly, sketches are much easier to construct. They require no additions or modifications to the environment dynamics or reward function and can be easily provided by non-experts (third party mechanical turk providers). This makes it possible to extend the benefits of hierarchical RL to challenging environments where it may not be possible to specify by hand the details of relevant subtasks. This paper shows that their approach drastically outperforms purely unsupervised methods that do not provide the learner with any task-specific guidance. The specific use of sketches to parameterize modular subpolicies makes better use of sketches than conditioning on them directly. | |||
The modular structure of this whole approach, which associates every high-level action symbol with a discrete subpolicy, naturally leads to a library of interpretable policy fragments which can be are easily recombined. The authors evaluate the approach in a variety of different data conditions: | |||
# Learning the full collection of tasks jointly via reinforcement learning | |||
# In a zero-shot setting where a policy sketch is available for a held-out task | |||
# In an adaptation setting, where sketches are hidden and the agent must learn to use and adapt a pretrained policy to reuse high-level actions in a new task. | |||
The code has been released at http://github.com/jacobandreas/psketch. | |||
The | |||
='''Related Work'''= | ='''Related Work'''= | ||
The | The approach in this paper is a specific case of the options framework developed by Sutton et al., 1999. In that work, options are introduced as "closed-loop policies for taking action over the period of time". They show that options enable temporally abstract information to be included in reinforcement learning algorithms, though it was published before the large-scale popularity of neural networks for reinforcement. | ||
The authors in this paper focus on learning in an interactive environment. However, they have done similar work in other applications [14]. There, they developed models for question answering tasks. However, in the present work, there is no longer direct supervision of the learning process. The authors claim that the two problems are complementary and propose that in the future natural language hints are used instead of semi-structured sketches. | |||
Other authors have recently explored techniques for learning policies which require less prior knowledge of the environment than the method presented in this paper. For example, in Vezhnevets et al. (2016), the authors propose an RNN architecture to build "implicit plans" only through interacting with the environment as in the classic reinforcement learning problem formulation. | |||
One closely related line of work is the Hierarchical Abstract Machines (HAM) framework introduced by Parr & Russell, 1998 [11]. Like the approach which the Modular Multitask Reinforcement Learning with Policy Sketches uses, HAMs begin with a representation of a high-level policy as an automaton (or a more general computer program; Andre & Russell, | |||
2001 [7]; Marthi et al., 2004 [12]) and use reinforcement learning to fill in low-level details. | |||
='''Learning Modular Policies from Sketches'''= | |||
The paper considers a multitask reinforcement learning problem arising from a family of infinite-horizon discounted Markov decision processes in a shared environment. This environment is specified by a tuple $(S, A, P, \gamma )$, with | |||
* $S$ a set of states | |||
* $A$ a set of low-level actions | |||
* $P : S \times A \times S \to R$ a transition probability distribution | |||
* $\gamma$ a discount factor | |||
Each task $t \in T$ is then specified by a pair $(R_t, \rho_t)$, with $R_t : S \to R$ a task-specific reward function and $\rho_t: S \to R$, an initial distribution over states. For a fixed sequence ${(s_i, a_i)}$ of states and actions obtained from a rollout of a given policy, we will denote the empirical return starting in state $s_i$ as $q_i = \sum_{j=i+1}^\infty \gamma^{j-i-1}R(s_j)$. In addition to the components of a standard multitask RL problem, we assume that tasks are annotated with sketches $K_t$ , each consisting of a sequence $(b_{t1},b_{t2},...)$ of high-level symbolic labels drawn from a fixed vocabulary $B$. | |||
==Model== | ==Model== | ||
The authors exploit the structural information provided by sketches by constructing for each symbol ''b'' a corresponding subpolicy $\pi_b$. By sharing each subpolicy across all tasks annotated with the corresponding symbol, their approach naturally learns the tied/shared abstraction for the corresponding subtask. Symbolic sketches can be thought of as a high level symbolic labels drawn from some fixed vocabulary, which initially are devoid of any meaning. Eventually the sketches get mapped into real policies and enable policy transfer and temporal abstraction. Learning occurs through a variant of the standard actor critic architecture that will be explained in later sections. | |||
[[File:Algorithm_MRL2.png|center|frame|Pseudo Algorithms for Modular Multitask Reinforcement Learning with Policy Sketches]] | [[File:Algorithm_MRL2.png|center|frame|Pseudo Algorithms for Modular Multitask Reinforcement Learning with Policy Sketches]] | ||
At | At every timestep, a subpolicy selects either a low-level action $a \in A$ or a special STOP action. The augmented state space is denoted as $A^+ := A \cup \{STOP\}$. At a high level, this framework is agnostic to the implementation of subpolicies: any function that takes a representation of the current state onto a distribution over $A^+$ will work fine with the approach. | ||
In this paper, | In this paper, $\pi_b$ is represented as a neural network. These subpolicies may be viewed as options of the kind described by [2], with the key distinction that they have no initiation semantics, but are instead invokable everywhere, and have no explicit representation as a function from an initial state to a distribution over final states (instead this paper uses the STOP action to terminate). | ||
Given a fixed sketch $(b_1, b_2,....)$, a task-specific policy $\Pi_r$ is formed by concatenating its associated subpolicies in sequence. In particular, the high-level policy maintains a sub-policy index ''i'' (initially 0), and executes actions from $\pi_{b_i}$ until the STOP symbol is emitted, at which point control is passed to bi+1 . We may thus think of as inducing a Markov chain over the state space $S \times B$, with transitions: | Given a fixed sketch $(b_1, b_2,....)$, a task-specific policy $\Pi_r$ is formed by concatenating its associated subpolicies in sequence. In particular, the high-level policy maintains a sub-policy index ''i'' (initially 0), and executes actions from $\pi_{b_i}$ until the STOP symbol is emitted, at which point control is passed to bi+1 . We may thus think of as inducing a Markov chain over the state space $S \times B$, with transitions: | ||
[[File:MRL1.png|center|border|]] | [[File:MRL1.png|center|border|]] | ||
Note that is semi-Markov with respect to projection of the augmented state space $S \times B$ onto the underlying state space ''S''. | Note that $\Pi_r$ is semi-Markov with respect to projection of the augmented state space $S \times B$ onto the underlying state space ''S''. The complete family of task-specific policies is denoted as $\Pi := \bigcup_r \{ \Pi_r \}$. Assume each $\pi_b$ be an arbitrary function of the current environment state parameterized by some weight vector $\theta_b$. The learning problem is to optimize overall $\theta_b$ to maximize expected discounted reward | ||
[[File:MRL2.png|center|border|]] | [[File:MRL2.png|center|border|]] | ||
across all tasks $t \in T$. | across all tasks $t \in T$. | ||
| Line 58: | Line 53: | ||
==Policy Optimization== | ==Policy Optimization== | ||
Here that optimization is accomplished | Control policy parameterized by parameter vector $\theta$, $$\displaystyle \max_{\Theta}E[\sum_{t=0}^{H}R(s_{t})|\pi_{\theta}]$$ $\pi_{\theta}(u|s)$ is the probability of action u in state s. The details of policy optimization can be found here: https://people.eecs.berkeley.edu/~pabbeel/nips-tutorial-policy-optimization-Schulman-Abbeel.pdf | ||
Here that optimization is accomplished through a simple decoupled actor–critic method. In a standard policy gradient approach, with a single policy $\pi$ with parameters $\theta$, the gradient steps are of the form: | |||
[[File:MRL3.png|center|border|]] | [[File:MRL3.png|center|border|]] | ||
where the baseline or “critic” c can be chosen independently of the future without introducing bias into the gradient. Recalling | where the baseline or “critic” c can be chosen independently of the future without introducing bias into the gradient. Recalling the previous definition of $q_i$ as the empirical return starting from $s_i$, this form of the gradient corresponds to a generalized advantage estimator with $\lambda = 1$. Here ''c'' achieves close to the optimal variance[6] when it is set exactly equal to the state-value function $V_{\pi} (s_i) = E_{\pi} q_i$ for the target policy $\pi$ starting in state $s_i$. | ||
[[File:MRL4.png|frame|]] | [[File:MRL4.png|frame|]] | ||
In the case of generalizing to modular policies built by sequencing sub-policies the authors suggest to have one subpolicy per symbol but one critic per task. This is because subpolicies $\pi_b$ might participate in many compound policies $\Pi_r$, each associated with its own reward function $R_r$ . Thus individual subpolicies are not uniquely identified or differentiated with value functions. The actor–critic method is extended to allow decoupling of policies from value functions by allowing the critic to vary per-sample (per-task-and-timestep) based on the reward function with which that particular sample is associated. Noting that | |||
[[File:MRL5.png|center|border|]] | [[File:MRL5.png|center|border|]] | ||
i.e. the sum of gradients of expected rewards across all tasks in which $\pi_b$ participates, we have: | i.e. the sum of gradients of expected rewards across all tasks in which $\pi_b$ participates, we have: | ||
| Line 69: | Line 67: | ||
where each state-action pair $(s_{t_i}, a_{t_i})$ was selected by the subpolicy $\pi_b$ in the context of the task ''t''. | where each state-action pair $(s_{t_i}, a_{t_i})$ was selected by the subpolicy $\pi_b$ in the context of the task ''t''. | ||
Now minimization of the gradient variance requires that each $c_t$ actually depend on the task identity. (This follows immediately by applying the corresponding argument in | Now minimization of the gradient variance requires that each $c_t$ actually depend on the task identity. (This follows immediately by applying the corresponding argument in [6] individually to each term in the sum over ''t'' in Equation 2.) Because the value function is itself unknown, an approximation must be estimated from data. Here it is allowed that these $c_t$ to be implemented with an arbitrary function approximator with parameters $\eta_t$ . This is trained to minimize a squared error criterion, with gradients given by | ||
[[File:MRL7.png|center|border|]] | [[File:MRL7.png|center|border|]] | ||
Alternative forms of the advantage estimator (e.g. the TD residual $R_t (s_i) + \gamma V_t(s_{i+1} - V_t(s_i))$ or any other member of the generalized advantage estimator family) can be | Alternative forms of the advantage estimator (e.g. the TD residual $R_t (s_i) + \gamma V_t(s_{i+1} - V_t(s_i))$ or any other member of the generalized advantage estimator family) can be used to substitute by simply maintaining one such estimator per task. Experiments show that conditioning on both the state and the task identity results in dramatic performance improvements, suggesting that the variance reduction given by this objective is important for efficient joint learning of modular policies. | ||
The complete | The complete algorithm for computing a single gradient step is given in Algorithm 1. (The outer training loop over these steps, which is driven by a curriculum learning procedure, is shown in Algorithm 2.) Note that this is an on-policy algorithm. In every step, the agent samples tasks from a task distribution provided by a curriculum (described in the following subsection). The current family of policies '''$\Pi$''' is used to perform rollouts for every sampled task, accumulating the resulting tuples of (states, low-level actions, high-level symbols, rewards, and task identities) into a dataset ''$D$''. Once ''$D$'' reaches a maximum size D, it is used to compute gradients with respect to both policy and critic parameters, and the parameter vectors are updated accordingly. The step sizes $\alpha$ and $\beta$ in Algorithm 1 can be chosen adaptively using any first-order method. | ||
==Curriculum Learning== | ==Curriculum Learning== | ||
For complex tasks, like the one depicted in Figure 3b, it is difficult for the agent to discover any states with positive reward until many subpolicy behaviors have already been learned. It is thus a better use of the learner’s time to focus on “easy” tasks, where many rollouts will result in high reward from which | For complex tasks, like the one depicted in Figure 3b, it is difficult for the agent to discover any states with positive reward until many subpolicy behaviors have already been learned. It is thus a better use of the learner’s time (and computational resources) to focus on “easy” tasks, where many rollouts will result in high reward from which relevant subpolicy behavior can be obtained. But there is a fundamental tradeoff involved here: if the learner spends a lot of its time on easy tasks before being told of the existence of harder ones, it may overfit and learn subpolicies that exhibit the desired structural properties or no longer generalize. | ||
To resolve these issues, a curriculum learning scheme (Bengio et al.,2009) is used that allows the model to smoothly scale up from easy tasks to more difficult ones without overfitting. Initially, the model is presented with tasks associated with short sketches. Once average reward on all these tasks reaches a certain threshold, the length limit is incremented. It is assumed that rewards across tasks are normalized with maximum achievable reward $0 < q_i < 1$ . Let $Er_t$ denote the empirical estimate of the expected reward for the current policy on task T. Then at each timestep, tasks are sampled in proportion $1-Er_t$, which by assumption must be positive. | |||
Intuitively, the tasks that provide the strongest learning signal are those in which | |||
# The agent does not on average achieve reward close to the upper bound | |||
# Many episodes result in a high reward. | |||
The expected reward component of the curriculum solves condition (1) by making sure that time is not spent on nearly solved tasks, while the length bound component of the curriculum addresses condition (2) by ensuring that tasks are not attempted until high-reward episodes are likely to be encountered. The experiments performed show that both components of this curriculum learning scheme improve the rate at which the model converges to a good policy. | |||
The complete curriculum-based training | The complete curriculum-based training algorithm is written as Algorithm 2 above. Initially, the maximum sketch length $l_{max}$ is set to 1, and the curriculum initialized to sample length-1 tasks uniformly. For each setting of $l_{max}$, the algorithm uses the current collection of task policies to compute and apply the gradient step described in Algorithm 1. The rollouts obtained from the call to TRAIN-STEP can also be used to compute reward estimates $Er_t$ ; these estimates determine a new task distribution for the curriculum. The inner loop is repeated until the reward threshold $r_{good}$ is exceeded, at which point $l_{max}$ is incremented and the process repeated over a (now-expanded) collection of tasks. | ||
='''Experiments'''= | ='''Experiments'''= | ||
[[File:MRL8.png|border|right|400px]] | |||
This paper considers three families of tasks: a 2-D Minecraft-inspired crafting game (Figure 3a), in which the agent must acquire particular resources by finding raw ingredients, combining them together in the correct order, and in some cases building intermediate tools that enable the agent to alter the environment itself; a 2-D maze navigation task that requires the agent to collect keys and open doors, and a 3-D locomotion task (Figure 3b) in which a quadrupedal robot must actuate its joints to traverse a narrow winding cliff. | |||
In all tasks, the agent receives a reward only after the final goal is accomplished. For the most challenging tasks, involving sequences of four or five high-level actions, a task-specific agent initially following a random policy essentially never discovers the reward signal, so these tasks cannot be solved without considering their hierarchical structure. These environments involve various kinds of challenging low-level control: agents must learn to avoid obstacles, interact with various kinds of objects, and relate fine-grained joint activation to high-level locomotion goals. | |||
==Implementation== | ==Implementation== | ||
In all | In all of the experiments, each subpolicy is implemented as a neural network with ReLU nonlinearities and a hidden layer with 128 hidden units. Each critic is a linear function of the current state. Each subpolicy network receives as input a set of features describing the current state of the environment and outputs a distribution over actions. The agent acts at every timestep by sampling from this distribution. The gradient steps given in lines 8 and 9 of Algorithm 1 are implemented using RMSPROP with a step size of 0.001 and gradient clipping to a unit norm. They take the batch size D in Algorithm 1 to be 2000 and set $\gamma$= 0.9 in both environments. For curriculum learning, the improvement threshold $r_{good}$ is 0.8. | ||
==Environments== | ==Environments== | ||
The | The environment in Figure 3a is inspired by the popular game Minecraft, but is implemented in a discrete 2-D world. The agent interacts with objects in the environment by executing a special USE action when it faces them. Picking up raw materials initially scattered randomly around the environment adds to an inventory. Interacting with different crafting stations causes objects in the agent’s inventory to be combined or transformed. Each task in this game corresponds to some crafted object the agent must produce; the most complicated goals require the agent to also craft intermediate ingredients, and in some cases build tools (like a pickaxe and a bridge) to reach ingredients located in initially inaccessible regions of the world. | ||
[[File:MRL_maze.png|boarder|right|400px]] | |||
The maze environment is very similar to “light world” described by [4], which can be seen in Figure 3c. The agent is placed in a discrete world consisting of a series of rooms, some of which are connected by doors. The agent needs to first pick up a key to open them. For our experiments, each task corresponds to a goal room that the agent must reach through a sequence of intermediate rooms. The agent senses the distance to keys, closed doors, and open doors in each direction. Sketches specify a particular sequence of directions for the agent to traverse between rooms to reach the goal. The sketch always corresponds to a viable traversal from the start to the goal position, but other (possibly shorter) traversals may also exist. | |||
The cliff environment (Figure 3b) | The cliff environment (Figure 3b) proves the effectiveness of the approach in a high-dimensional continuous control environment where a quadrupedal robot [5] is placed on a variable-length winding path, and must navigate to the end without falling off. This is a challenging RL problem since the walker must learn the low-level walking skill before it can make any progress. The agent receives a small reward for making progress toward the goal, and a large positive reward for reaching the goal square, with a negative reward for falling off the path. | ||
==Multitask Learning== | ==Multitask Learning== | ||
[[File: | |||
The primary experimental question in this paper is whether the extra structure provided by policy sketches alone is enough to enable fast learning of coupled policies across tasks. | [[File:MRL9.png|border|center|800px]] | ||
The primary experimental question in this paper is whether the extra structure provided by policy sketches alone is enough to enable fast learning of coupled policies across tasks. The aim is to explore the differences between the approach described and relevant prior work that performs either unsupervised or weakly supervised multitask learning of hierarchical policy structure. Specifically, they compare their '''modular''' approach to: | |||
# Structured hierarchical reinforcement learners: | # Structured hierarchical reinforcement learners: | ||
#* the fully unsupervised '''option–critic''' algorithm of Bacon & Precup | #* the fully unsupervised '''option–critic''' algorithm of Bacon & Precup[1] | ||
#* a '''Q automaton''' that attempts to explicitly represent the Q function for each task / subtask combination (essentially a HAM | #* a '''Q automaton''' that attempts to explicitly represent the Q function for each task/subtask combination (essentially a HAM [8] with a deep state abstraction function) | ||
# Alternative ways of incorporating sketch data into standard policy gradient methods: | # Alternative ways of incorporating sketch data into standard policy gradient methods: | ||
#* learning an '''independent''' policy for each task | #* learning an '''independent''' policy for each task | ||
| Line 113: | Line 120: | ||
The joint and independent models performed best when trained with the same curriculum described in Section 3.3, while the option–critic model performed best with a length–weighted curriculum that has access to all tasks from the beginning of training. | The joint and independent models performed best when trained with the same curriculum described in Section 3.3, while the option–critic model performed best with a length–weighted curriculum that has access to all tasks from the beginning of training. | ||
Learning curves for baselines and the modular model | Learning curves for baselines and the modular model is shown in Figure 4. It can be seen that in all environments, our approach substantially outperforms the baselines: it induces policies with substantially higher average reward and converges more quickly than the policy gradient baselines. It can further be seen in Figure 4c that after policies have been learned on simple tasks, the model is able to rapidly adapt to more complex ones, even when the longer tasks involve high-level actions not required for any of the short tasks. | ||
==Ablations== | |||
[[File:MRL10.png|border|right|400px]] | |||
In addition to the overall modular parameter-tying structure induced by sketches, the other critical component of the training procedure is the decoupled critic and the curriculum. Ablation analysis investigates the extent to which these components contribute to the performance. | |||
To evaluate the critic, consider three ablations: | |||
# Removing the dependence of the model on the environment state, in which case the baseline is a single scalar per task | |||
# Removing the dependence of the model on the task, in which case the baseline is a conventional generalized advantage estimator | |||
# Removing both, in which case the baseline is a single scalar, as in a vanilla policy gradient approach. | |||
Experiment results are shown in Figure 5a. Introducing both state and task dependence into the baseline leads to faster convergence of the model: the approach with a constant baseline achieves less than half the overall performance of the full critic after 3 million episodes. Introducing task and state dependence independently improve this performance; combining them gives the best result. | |||
Two other experiments are also performed as Figure 5b: starting with short examples and moving to long ones, and sampling tasks in inverse proportion to their accumulated reward. It is shown that both components help; prioritization by both length and weight gives the best results. | |||
==Zero-shot and Adaptation Learning== | ==Zero-shot and Adaptation Learning== | ||
[[File:MRL11.png| | [[File:MRL11.png|border|left|320px]] | ||
In | In the final experiments, the authors test the model’s ability to generalize beyond the standard training condition. Consider two tests of generalization: a zero-shot setting, in which the model is provided with a sketch for the new task and must immediately achieve good performance, and an adaptation setting, where no sketch is provided, leaving the model to learn a suitable sketch via interaction. For zero-shot experiments, the concatenated policy is formed to describe the sketches of the held-out tasks, and repeatedly executing this policy (without learning) to obtain an estimate of its effectiveness. For adaptation experiments, consider ordinary RL over high-level actions B rather than low-level actions A, implementing the high-level learner with the same agent architecture as described in the section 'Learning Modular Policies from Sketches'. Results are shown in the table to the left. The held-out tasks are sufficiently challenging that the baselines are unable to obtain more than negligible reward: in particular, the joint model overfits to the training tasks and cannot generalize to new sketches, while the independent model cannot discover enough of a reward signal to learn in the adaptation setting. The modular model does comparatively well: individual subpolicies succeed in novel zero-shot configurations (suggesting that they have in fact discovered the behavior suggested by the semantics of the sketch) and provide a suitable basis for adaptive discovery of new high-level policies. | ||
='''Conclusion & Critique'''= | ='''Conclusion & Critique'''= | ||
The paper's contributions are: | |||
* A general paradigm for multitask, hierarchical, deep reinforcement learning guided by abstract sketches of task-specific policies. | |||
* A concrete recipe for learning from these sketches, built on a general family of modular deep policy representations and a multitask actor–critic training objective. | |||
This paper studies the problem of abstract hierarchical multiagent RL with policy sketches, high level descriptions of abstract actions. The work is related to much previous work in hierarchical RL, and adds some new elements by using neural implementations of prior work on hierarchical learning and skill representations. They have described an approach for multitask learning of deep multitask policies guided by symbolic policy sketches. By associating each symbol appearing in a sketch with a modular neural sub policy, they have shown that it is possible to build agents that share behavior across tasks in order to achieve success in tasks with sparse and delayed rewards. This process induces an inventory of reusable and interpretable sub policies which can be employed for zero-shot generalization when further sketches are available, and hierarchical reinforcement learning when they are not. | |||
Hierarchical Reinforcement Learning is a popular research topic now, it is interesting to compare this paper(which was presented in this class)[13], where the architecture follows the manager-and-workers style. In that work, the sub policy is decided by manager network. To finish a hierarchical task, each worker focuses on the sub task and optimizes the sub task. The difference is in that work, the sub policy is implicit and is trained in the training process. A further question for future work for this paper: would these sub policy be learned automatically instead of pre-defined? | |||
There are four drawbacks of the presented work. First, the presented ideas portrayed in this paper (for instance: symbolic specifications, actor-critic, shared representations) have all been explored in other works. Secondly, the aforementioned approach relies heavily on curriculum learning - which is, as we know, difficult to design as it is pretty complicated depending on the task in-hand. Thirdly, there has been no discussion on how the curriculum can be designed for larger problems. Finally, this approach could be that building of different neural networks for each sub tasks could lead to overly complicated networks and is not in the spirit of building an efficient structure. | |||
When the paper is considered in the context of the OpenReview discussion with the authors [https://openreview.net/forum?id=H1kjdOYlx] some interesting criticisms of the paper are brought to light. Many of the criticisms are based on the novelty of the approach. Reviewers contest that, the paper doesn't seem to offer anything new, except for providing a new implementation in the context of deep learning. The problem solved here can be seen as an extension to the option-learning problem with richer supervision. Hence it makes the problem simple to tackle with existing RL schemes. For example, learning from natural language instructions makes it easy to learn. And the model proposed in the paper shares many things common with existing hierarchical RL methods. The authors maintain, however, that the use of diagram instruction is indeed novel. Moreover, the authors focus on the ease of generation of these policy sketches (noting "The extra annotation we use here literally fits in a 10-line text file.") and commenting on the dramatic improvements that this approach provides. They further argue that this approach is fundamentally different from the traditional NLP approaches which are claimed to be equivalent. Traditional approaches are useless in the absence of natural language instructions as the model conditions on both the state and the instructions. Experiment 1 in this paper shows the added generality of the approach presented. | |||
A more salient criticism has to do with the utility of such an approach. Even if it is taken as granted that this approach, as presented, is novel and the results are replicable, what does this mean for future work or for applications of reinforcement learning? While the authors suggest that the sketches are, in fact, straightforward to create, practitioners are less likely to desire the generation of such sketches versus providing natural language instructions, for instance. | |||
= '''Resources''' = | |||
You can find a talk on this paper [https://www.google.ca/url?sa=t&rct=j&q=&esrc=s&source=video&cd=3&cad=rja&uact=8&ved=0ahUKEwjNzPuBqM7XAhVK6mMKHQICAdEQtwIILDAC&url=https%3A%2F%2Fwww.youtube.com%2Fwatch%3Fv%3DNRIcDEB64x8&usg=AOvVaw1NHi2XExGXwhzzeJn5AcnR here]. | |||
='''References'''= | ='''References'''= | ||
[1] Bacon, Pierre-Luc and Precup, Doina. The option-critic architecture. In NIPS Deep Reinforcement Learning Work-shop, 2015. | |||
[2] Sutton, Richard S, Precup, Doina, and Singh, Satinder. Be-tween MDPs and semi-MDPs: A framework for temporal abstraction in reinforcement learning. Artificial intel-ligence, 112(1):181–211, 1999. | |||
[3] Stolle, Martin and Precup, Doina. Learning options in reinforcement learning. In International Symposium on Abstraction, Reformulation, and Approximation, pp. 212– 223. Springer, 2002. | |||
[4] Konidaris, George and Barto, Andrew G. Building portable options: Skill transfer in reinforcement learning. In IJ-CAI, volume 7, pp. 895–900, 2007. | |||
[5] Schulman, John, Moritz, Philipp, Levine, Sergey, Jordan, Michael, and Abbeel, Pieter. Trust region policy optimization. In International Conference on Machine Learning, 2015b. | |||
[6] Greensmith, Evan, Bartlett, Peter L, and Baxter, Jonathan. Variance reduction techniques for gradient estimates in reinforcement learning. Journal of Machine Learning Research, 5(Nov):1471–1530, 2004. | |||
[7] Andre, David and Russell, Stuart. Programmable reinforce-ment learning agents. In Advances in Neural Information Processing Systems, 2001. | |||
[8] Andre, David and Russell, Stuart. State abstraction for pro-grammable reinforcement learning agents. In Proceedings of the Meeting of the Association for the Advance-ment of Artificial Intelligence, 2002. | |||
[9] Author Jacob Andreas presenting the paper - https://www.youtube.com/watch?v=NRIcDEB64x8 | |||
[10] Vezhnevets, A., Mnih, V., Osindero, S., Graves, A., Vinyals, O., & Agapiou, J. (2016). Strategic attentive writer for learning macro-actions. In Advances in Neural Information Processing Systems (pp. 3486-3494). | |||
[11] Parr, Ron and Russell, Stuart. Reinforcement learning with hierarchies of machines. In Advances in Neural Information Processing Systems, 1998. | |||
[12] Marthi, Bhaskara, Lantham, David, Guestrin, Carlos, and Russell, Stuart. Concurrent hierarchical reinforcement learning. In Proceedings of the Meeting of the Association for the Advancement of Artificial Intelligence, 2004. | |||
[13] A. S. Vezhnevets, S. Osindero, T. Schaul, N. Heess, M. Jaderberg, D. Silver, and K. Kavukcuoglu. Feudal networks for hierarchical reinforcement learning. arXiv preprint arXiv:1703.01161, 2017. | |||
[14] J. Andreas, M. Rohrbach, T. Darrell, D. Klein. Learning to compose neural networks for question answering. In ''Proceedings of the Annual Meeting of the North American Chapter of the Association for Computational Linguistics'', 2016. | |||
[15] Bengio, Yoshua, et al. "Curriculum learning." Proceedings of the 26th annual international conference on machine learning. ACM, 2009. | |||
= Appendix = | |||
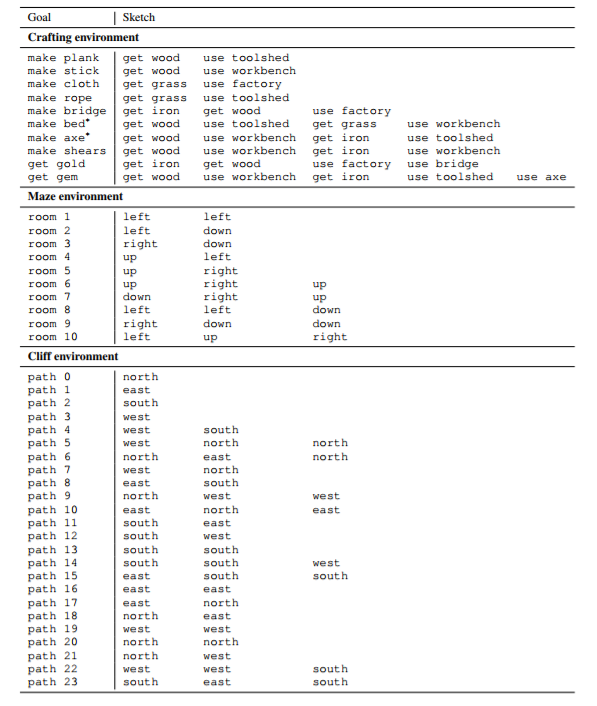
The authors provide a brief appendix that gives a complete list of tasks and sketches. Asterisk * indicates that the task was held out for generalization experiments in Section 4.5, but included in the multitask experiments of Sections 4.3 and 4.4. | |||
[[File: tasks.PNG]] | |||
Latest revision as of 14:25, 3 December 2017
Introduction & Background
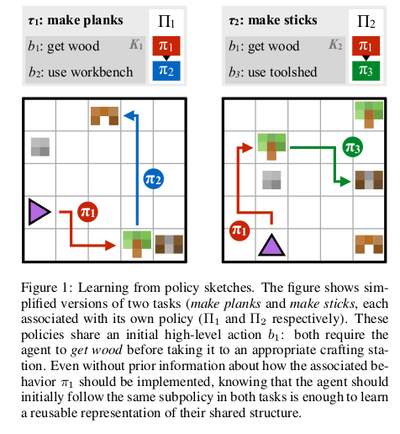
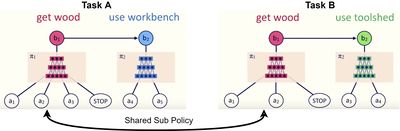

This paper describes a framework for learning composable deep subpolicies in a multitask setting. These policies are guided only by abstract sketches which are representative of the high-level behavior in the environment. Sketches annotate tasks with sequences of named subtasks, providing information about high-level structural relationships among tasks but not how to implement them—specifically not providing the detailed guidance used by much previous work on learning policy abstractions for RL (e.g. intermediate rewards, subtask completion signals, or intrinsic motivations). General reinforcement learning algorithms allow agents to solve tasks in complex environments. Vanilla policies find it difficult to deal with tasks featuring extremely delayed rewards. Most approaches often require in-depth supervision in the form of explicitly specified high-level actions, subgoals, or behavioral primitives. The proposed methodology is particularly suitable where rewards are difficult to engineer by hand. It is enough to tell the learner about the abstract policy structure, without indicating how high-level behaviors should try to use primitive percepts or actions.
This paper explores a multitask reinforcement learning setting where the learner is presented with policy sketches. Policy sketches are defined as short, ungrounded, symbolic representations of a task. It describes its components, as shown in Figure 1. While symbols might be shared across different tasks ( the predicate "get wood" appears in sketches for both the tasks: "make planks" and "make sticks"). The learner is not shown or told anything about what these symbols mean, either in terms of observations or intermediate rewards. These sketches are initially meaningless but eventually the sketches get mapped into real policies. As shown in Figure 1c, the tasks are divided into human readable sub tasks. However, in the actual settings, the learner can only get access to encoded results.
The agent learns from policy sketches by associating each high-level action with a parameterization of a low-level subpolicy. It jointly optimizes over concatenated task-specific policies by tying/sharing parameters across common subpolicies. They find that this architecture uses the high-level guidance provided by sketches to drastically accelerate learning of complex multi-stage behaviors. The experiments show that most benefits of learning from very detailed low-level supervision (e.g. from subgoal rewards) can also be obtained from fairly coarse high-level policy sketches. Most importantly, sketches are much easier to construct. They require no additions or modifications to the environment dynamics or reward function and can be easily provided by non-experts (third party mechanical turk providers). This makes it possible to extend the benefits of hierarchical RL to challenging environments where it may not be possible to specify by hand the details of relevant subtasks. This paper shows that their approach drastically outperforms purely unsupervised methods that do not provide the learner with any task-specific guidance. The specific use of sketches to parameterize modular subpolicies makes better use of sketches than conditioning on them directly.
The modular structure of this whole approach, which associates every high-level action symbol with a discrete subpolicy, naturally leads to a library of interpretable policy fragments which can be are easily recombined. The authors evaluate the approach in a variety of different data conditions:
- Learning the full collection of tasks jointly via reinforcement learning
- In a zero-shot setting where a policy sketch is available for a held-out task
- In an adaptation setting, where sketches are hidden and the agent must learn to use and adapt a pretrained policy to reuse high-level actions in a new task.
The code has been released at http://github.com/jacobandreas/psketch.
Related Work
The approach in this paper is a specific case of the options framework developed by Sutton et al., 1999. In that work, options are introduced as "closed-loop policies for taking action over the period of time". They show that options enable temporally abstract information to be included in reinforcement learning algorithms, though it was published before the large-scale popularity of neural networks for reinforcement.
The authors in this paper focus on learning in an interactive environment. However, they have done similar work in other applications [14]. There, they developed models for question answering tasks. However, in the present work, there is no longer direct supervision of the learning process. The authors claim that the two problems are complementary and propose that in the future natural language hints are used instead of semi-structured sketches.
Other authors have recently explored techniques for learning policies which require less prior knowledge of the environment than the method presented in this paper. For example, in Vezhnevets et al. (2016), the authors propose an RNN architecture to build "implicit plans" only through interacting with the environment as in the classic reinforcement learning problem formulation.
One closely related line of work is the Hierarchical Abstract Machines (HAM) framework introduced by Parr & Russell, 1998 [11]. Like the approach which the Modular Multitask Reinforcement Learning with Policy Sketches uses, HAMs begin with a representation of a high-level policy as an automaton (or a more general computer program; Andre & Russell, 2001 [7]; Marthi et al., 2004 [12]) and use reinforcement learning to fill in low-level details.
Learning Modular Policies from Sketches
The paper considers a multitask reinforcement learning problem arising from a family of infinite-horizon discounted Markov decision processes in a shared environment. This environment is specified by a tuple $(S, A, P, \gamma )$, with
- $S$ a set of states
- $A$ a set of low-level actions
- $P : S \times A \times S \to R$ a transition probability distribution
- $\gamma$ a discount factor
Each task $t \in T$ is then specified by a pair $(R_t, \rho_t)$, with $R_t : S \to R$ a task-specific reward function and $\rho_t: S \to R$, an initial distribution over states. For a fixed sequence ${(s_i, a_i)}$ of states and actions obtained from a rollout of a given policy, we will denote the empirical return starting in state $s_i$ as $q_i = \sum_{j=i+1}^\infty \gamma^{j-i-1}R(s_j)$. In addition to the components of a standard multitask RL problem, we assume that tasks are annotated with sketches $K_t$ , each consisting of a sequence $(b_{t1},b_{t2},...)$ of high-level symbolic labels drawn from a fixed vocabulary $B$.
Model
The authors exploit the structural information provided by sketches by constructing for each symbol b a corresponding subpolicy $\pi_b$. By sharing each subpolicy across all tasks annotated with the corresponding symbol, their approach naturally learns the tied/shared abstraction for the corresponding subtask. Symbolic sketches can be thought of as a high level symbolic labels drawn from some fixed vocabulary, which initially are devoid of any meaning. Eventually the sketches get mapped into real policies and enable policy transfer and temporal abstraction. Learning occurs through a variant of the standard actor critic architecture that will be explained in later sections.

At every timestep, a subpolicy selects either a low-level action $a \in A$ or a special STOP action. The augmented state space is denoted as $A^+ := A \cup \{STOP\}$. At a high level, this framework is agnostic to the implementation of subpolicies: any function that takes a representation of the current state onto a distribution over $A^+$ will work fine with the approach.
In this paper, $\pi_b$ is represented as a neural network. These subpolicies may be viewed as options of the kind described by [2], with the key distinction that they have no initiation semantics, but are instead invokable everywhere, and have no explicit representation as a function from an initial state to a distribution over final states (instead this paper uses the STOP action to terminate).
Given a fixed sketch $(b_1, b_2,....)$, a task-specific policy $\Pi_r$ is formed by concatenating its associated subpolicies in sequence. In particular, the high-level policy maintains a sub-policy index i (initially 0), and executes actions from $\pi_{b_i}$ until the STOP symbol is emitted, at which point control is passed to bi+1 . We may thus think of as inducing a Markov chain over the state space $S \times B$, with transitions:
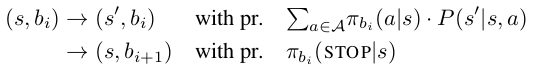
Note that $\Pi_r$ is semi-Markov with respect to projection of the augmented state space $S \times B$ onto the underlying state space S. The complete family of task-specific policies is denoted as $\Pi := \bigcup_r \{ \Pi_r \}$. Assume each $\pi_b$ be an arbitrary function of the current environment state parameterized by some weight vector $\theta_b$. The learning problem is to optimize overall $\theta_b$ to maximize expected discounted reward
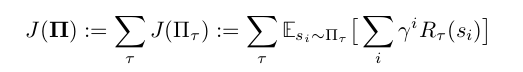
across all tasks $t \in T$.
Policy Optimization
Control policy parameterized by parameter vector $\theta$, $$\displaystyle \max_{\Theta}E[\sum_{t=0}^{H}R(s_{t})|\pi_{\theta}]$$ $\pi_{\theta}(u|s)$ is the probability of action u in state s. The details of policy optimization can be found here: https://people.eecs.berkeley.edu/~pabbeel/nips-tutorial-policy-optimization-Schulman-Abbeel.pdf
Here that optimization is accomplished through a simple decoupled actor–critic method. In a standard policy gradient approach, with a single policy $\pi$ with parameters $\theta$, the gradient steps are of the form:
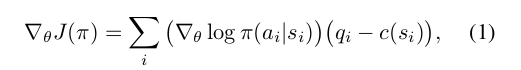
where the baseline or “critic” c can be chosen independently of the future without introducing bias into the gradient. Recalling the previous definition of $q_i$ as the empirical return starting from $s_i$, this form of the gradient corresponds to a generalized advantage estimator with $\lambda = 1$. Here c achieves close to the optimal variance[6] when it is set exactly equal to the state-value function $V_{\pi} (s_i) = E_{\pi} q_i$ for the target policy $\pi$ starting in state $s_i$.
In the case of generalizing to modular policies built by sequencing sub-policies the authors suggest to have one subpolicy per symbol but one critic per task. This is because subpolicies $\pi_b$ might participate in many compound policies $\Pi_r$, each associated with its own reward function $R_r$ . Thus individual subpolicies are not uniquely identified or differentiated with value functions. The actor–critic method is extended to allow decoupling of policies from value functions by allowing the critic to vary per-sample (per-task-and-timestep) based on the reward function with which that particular sample is associated. Noting that
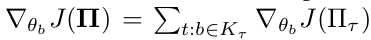
i.e. the sum of gradients of expected rewards across all tasks in which $\pi_b$ participates, we have:
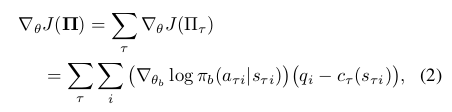
where each state-action pair $(s_{t_i}, a_{t_i})$ was selected by the subpolicy $\pi_b$ in the context of the task t.
Now minimization of the gradient variance requires that each $c_t$ actually depend on the task identity. (This follows immediately by applying the corresponding argument in [6] individually to each term in the sum over t in Equation 2.) Because the value function is itself unknown, an approximation must be estimated from data. Here it is allowed that these $c_t$ to be implemented with an arbitrary function approximator with parameters $\eta_t$ . This is trained to minimize a squared error criterion, with gradients given by
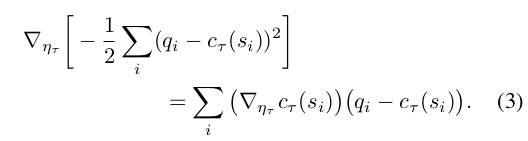
Alternative forms of the advantage estimator (e.g. the TD residual $R_t (s_i) + \gamma V_t(s_{i+1} - V_t(s_i))$ or any other member of the generalized advantage estimator family) can be used to substitute by simply maintaining one such estimator per task. Experiments show that conditioning on both the state and the task identity results in dramatic performance improvements, suggesting that the variance reduction given by this objective is important for efficient joint learning of modular policies.
The complete algorithm for computing a single gradient step is given in Algorithm 1. (The outer training loop over these steps, which is driven by a curriculum learning procedure, is shown in Algorithm 2.) Note that this is an on-policy algorithm. In every step, the agent samples tasks from a task distribution provided by a curriculum (described in the following subsection). The current family of policies $\Pi$ is used to perform rollouts for every sampled task, accumulating the resulting tuples of (states, low-level actions, high-level symbols, rewards, and task identities) into a dataset $D$. Once $D$ reaches a maximum size D, it is used to compute gradients with respect to both policy and critic parameters, and the parameter vectors are updated accordingly. The step sizes $\alpha$ and $\beta$ in Algorithm 1 can be chosen adaptively using any first-order method.
Curriculum Learning
For complex tasks, like the one depicted in Figure 3b, it is difficult for the agent to discover any states with positive reward until many subpolicy behaviors have already been learned. It is thus a better use of the learner’s time (and computational resources) to focus on “easy” tasks, where many rollouts will result in high reward from which relevant subpolicy behavior can be obtained. But there is a fundamental tradeoff involved here: if the learner spends a lot of its time on easy tasks before being told of the existence of harder ones, it may overfit and learn subpolicies that exhibit the desired structural properties or no longer generalize.
To resolve these issues, a curriculum learning scheme (Bengio et al.,2009) is used that allows the model to smoothly scale up from easy tasks to more difficult ones without overfitting. Initially, the model is presented with tasks associated with short sketches. Once average reward on all these tasks reaches a certain threshold, the length limit is incremented. It is assumed that rewards across tasks are normalized with maximum achievable reward $0 < q_i < 1$ . Let $Er_t$ denote the empirical estimate of the expected reward for the current policy on task T. Then at each timestep, tasks are sampled in proportion $1-Er_t$, which by assumption must be positive.
Intuitively, the tasks that provide the strongest learning signal are those in which
- The agent does not on average achieve reward close to the upper bound
- Many episodes result in a high reward.
The expected reward component of the curriculum solves condition (1) by making sure that time is not spent on nearly solved tasks, while the length bound component of the curriculum addresses condition (2) by ensuring that tasks are not attempted until high-reward episodes are likely to be encountered. The experiments performed show that both components of this curriculum learning scheme improve the rate at which the model converges to a good policy.
The complete curriculum-based training algorithm is written as Algorithm 2 above. Initially, the maximum sketch length $l_{max}$ is set to 1, and the curriculum initialized to sample length-1 tasks uniformly. For each setting of $l_{max}$, the algorithm uses the current collection of task policies to compute and apply the gradient step described in Algorithm 1. The rollouts obtained from the call to TRAIN-STEP can also be used to compute reward estimates $Er_t$ ; these estimates determine a new task distribution for the curriculum. The inner loop is repeated until the reward threshold $r_{good}$ is exceeded, at which point $l_{max}$ is incremented and the process repeated over a (now-expanded) collection of tasks.
Experiments
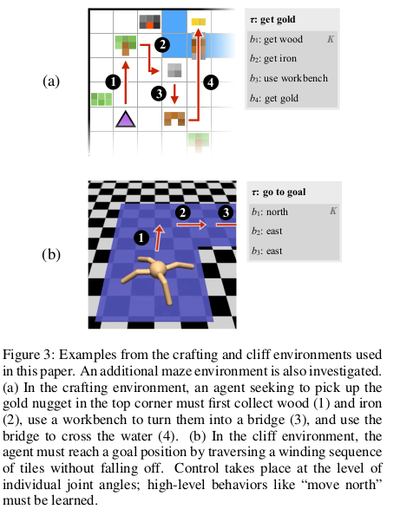
This paper considers three families of tasks: a 2-D Minecraft-inspired crafting game (Figure 3a), in which the agent must acquire particular resources by finding raw ingredients, combining them together in the correct order, and in some cases building intermediate tools that enable the agent to alter the environment itself; a 2-D maze navigation task that requires the agent to collect keys and open doors, and a 3-D locomotion task (Figure 3b) in which a quadrupedal robot must actuate its joints to traverse a narrow winding cliff.
In all tasks, the agent receives a reward only after the final goal is accomplished. For the most challenging tasks, involving sequences of four or five high-level actions, a task-specific agent initially following a random policy essentially never discovers the reward signal, so these tasks cannot be solved without considering their hierarchical structure. These environments involve various kinds of challenging low-level control: agents must learn to avoid obstacles, interact with various kinds of objects, and relate fine-grained joint activation to high-level locomotion goals.
Implementation
In all of the experiments, each subpolicy is implemented as a neural network with ReLU nonlinearities and a hidden layer with 128 hidden units. Each critic is a linear function of the current state. Each subpolicy network receives as input a set of features describing the current state of the environment and outputs a distribution over actions. The agent acts at every timestep by sampling from this distribution. The gradient steps given in lines 8 and 9 of Algorithm 1 are implemented using RMSPROP with a step size of 0.001 and gradient clipping to a unit norm. They take the batch size D in Algorithm 1 to be 2000 and set $\gamma$= 0.9 in both environments. For curriculum learning, the improvement threshold $r_{good}$ is 0.8.
Environments
The environment in Figure 3a is inspired by the popular game Minecraft, but is implemented in a discrete 2-D world. The agent interacts with objects in the environment by executing a special USE action when it faces them. Picking up raw materials initially scattered randomly around the environment adds to an inventory. Interacting with different crafting stations causes objects in the agent’s inventory to be combined or transformed. Each task in this game corresponds to some crafted object the agent must produce; the most complicated goals require the agent to also craft intermediate ingredients, and in some cases build tools (like a pickaxe and a bridge) to reach ingredients located in initially inaccessible regions of the world.
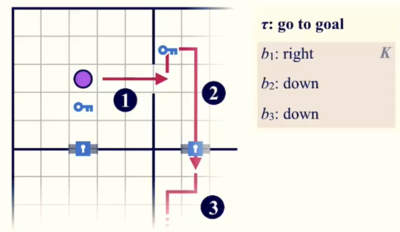
The maze environment is very similar to “light world” described by [4], which can be seen in Figure 3c. The agent is placed in a discrete world consisting of a series of rooms, some of which are connected by doors. The agent needs to first pick up a key to open them. For our experiments, each task corresponds to a goal room that the agent must reach through a sequence of intermediate rooms. The agent senses the distance to keys, closed doors, and open doors in each direction. Sketches specify a particular sequence of directions for the agent to traverse between rooms to reach the goal. The sketch always corresponds to a viable traversal from the start to the goal position, but other (possibly shorter) traversals may also exist.
The cliff environment (Figure 3b) proves the effectiveness of the approach in a high-dimensional continuous control environment where a quadrupedal robot [5] is placed on a variable-length winding path, and must navigate to the end without falling off. This is a challenging RL problem since the walker must learn the low-level walking skill before it can make any progress. The agent receives a small reward for making progress toward the goal, and a large positive reward for reaching the goal square, with a negative reward for falling off the path.
Multitask Learning
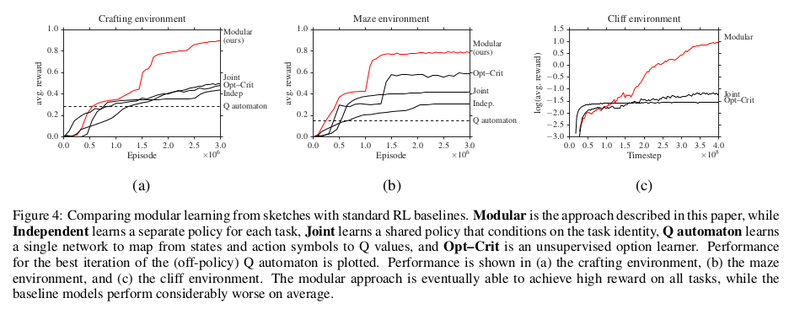
The primary experimental question in this paper is whether the extra structure provided by policy sketches alone is enough to enable fast learning of coupled policies across tasks. The aim is to explore the differences between the approach described and relevant prior work that performs either unsupervised or weakly supervised multitask learning of hierarchical policy structure. Specifically, they compare their modular approach to:
- Structured hierarchical reinforcement learners:
- the fully unsupervised option–critic algorithm of Bacon & Precup[1]
- a Q automaton that attempts to explicitly represent the Q function for each task/subtask combination (essentially a HAM [8] with a deep state abstraction function)
- Alternative ways of incorporating sketch data into standard policy gradient methods:
- learning an independent policy for each task
- learning a joint policy across all tasks, conditioning directly on both environment features and a representation of the complete sketch
The joint and independent models performed best when trained with the same curriculum described in Section 3.3, while the option–critic model performed best with a length–weighted curriculum that has access to all tasks from the beginning of training.
Learning curves for baselines and the modular model is shown in Figure 4. It can be seen that in all environments, our approach substantially outperforms the baselines: it induces policies with substantially higher average reward and converges more quickly than the policy gradient baselines. It can further be seen in Figure 4c that after policies have been learned on simple tasks, the model is able to rapidly adapt to more complex ones, even when the longer tasks involve high-level actions not required for any of the short tasks.
Ablations
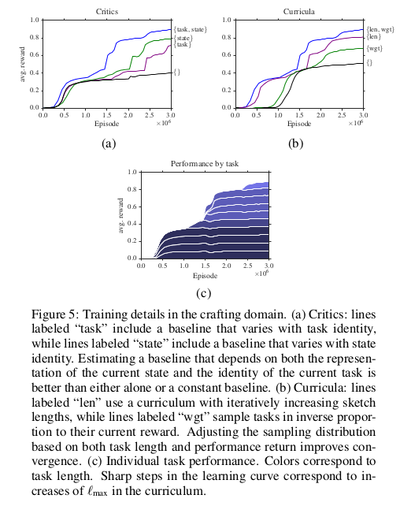
In addition to the overall modular parameter-tying structure induced by sketches, the other critical component of the training procedure is the decoupled critic and the curriculum. Ablation analysis investigates the extent to which these components contribute to the performance.
To evaluate the critic, consider three ablations:
- Removing the dependence of the model on the environment state, in which case the baseline is a single scalar per task
- Removing the dependence of the model on the task, in which case the baseline is a conventional generalized advantage estimator
- Removing both, in which case the baseline is a single scalar, as in a vanilla policy gradient approach.
Experiment results are shown in Figure 5a. Introducing both state and task dependence into the baseline leads to faster convergence of the model: the approach with a constant baseline achieves less than half the overall performance of the full critic after 3 million episodes. Introducing task and state dependence independently improve this performance; combining them gives the best result.
Two other experiments are also performed as Figure 5b: starting with short examples and moving to long ones, and sampling tasks in inverse proportion to their accumulated reward. It is shown that both components help; prioritization by both length and weight gives the best results.
Zero-shot and Adaptation Learning
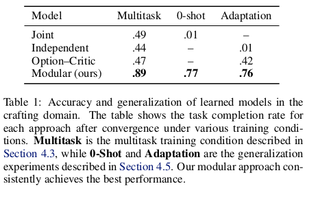
In the final experiments, the authors test the model’s ability to generalize beyond the standard training condition. Consider two tests of generalization: a zero-shot setting, in which the model is provided with a sketch for the new task and must immediately achieve good performance, and an adaptation setting, where no sketch is provided, leaving the model to learn a suitable sketch via interaction. For zero-shot experiments, the concatenated policy is formed to describe the sketches of the held-out tasks, and repeatedly executing this policy (without learning) to obtain an estimate of its effectiveness. For adaptation experiments, consider ordinary RL over high-level actions B rather than low-level actions A, implementing the high-level learner with the same agent architecture as described in the section 'Learning Modular Policies from Sketches'. Results are shown in the table to the left. The held-out tasks are sufficiently challenging that the baselines are unable to obtain more than negligible reward: in particular, the joint model overfits to the training tasks and cannot generalize to new sketches, while the independent model cannot discover enough of a reward signal to learn in the adaptation setting. The modular model does comparatively well: individual subpolicies succeed in novel zero-shot configurations (suggesting that they have in fact discovered the behavior suggested by the semantics of the sketch) and provide a suitable basis for adaptive discovery of new high-level policies.
Conclusion & Critique
The paper's contributions are:
- A general paradigm for multitask, hierarchical, deep reinforcement learning guided by abstract sketches of task-specific policies.
- A concrete recipe for learning from these sketches, built on a general family of modular deep policy representations and a multitask actor–critic training objective.
This paper studies the problem of abstract hierarchical multiagent RL with policy sketches, high level descriptions of abstract actions. The work is related to much previous work in hierarchical RL, and adds some new elements by using neural implementations of prior work on hierarchical learning and skill representations. They have described an approach for multitask learning of deep multitask policies guided by symbolic policy sketches. By associating each symbol appearing in a sketch with a modular neural sub policy, they have shown that it is possible to build agents that share behavior across tasks in order to achieve success in tasks with sparse and delayed rewards. This process induces an inventory of reusable and interpretable sub policies which can be employed for zero-shot generalization when further sketches are available, and hierarchical reinforcement learning when they are not.
Hierarchical Reinforcement Learning is a popular research topic now, it is interesting to compare this paper(which was presented in this class)[13], where the architecture follows the manager-and-workers style. In that work, the sub policy is decided by manager network. To finish a hierarchical task, each worker focuses on the sub task and optimizes the sub task. The difference is in that work, the sub policy is implicit and is trained in the training process. A further question for future work for this paper: would these sub policy be learned automatically instead of pre-defined?
There are four drawbacks of the presented work. First, the presented ideas portrayed in this paper (for instance: symbolic specifications, actor-critic, shared representations) have all been explored in other works. Secondly, the aforementioned approach relies heavily on curriculum learning - which is, as we know, difficult to design as it is pretty complicated depending on the task in-hand. Thirdly, there has been no discussion on how the curriculum can be designed for larger problems. Finally, this approach could be that building of different neural networks for each sub tasks could lead to overly complicated networks and is not in the spirit of building an efficient structure.
When the paper is considered in the context of the OpenReview discussion with the authors [1] some interesting criticisms of the paper are brought to light. Many of the criticisms are based on the novelty of the approach. Reviewers contest that, the paper doesn't seem to offer anything new, except for providing a new implementation in the context of deep learning. The problem solved here can be seen as an extension to the option-learning problem with richer supervision. Hence it makes the problem simple to tackle with existing RL schemes. For example, learning from natural language instructions makes it easy to learn. And the model proposed in the paper shares many things common with existing hierarchical RL methods. The authors maintain, however, that the use of diagram instruction is indeed novel. Moreover, the authors focus on the ease of generation of these policy sketches (noting "The extra annotation we use here literally fits in a 10-line text file.") and commenting on the dramatic improvements that this approach provides. They further argue that this approach is fundamentally different from the traditional NLP approaches which are claimed to be equivalent. Traditional approaches are useless in the absence of natural language instructions as the model conditions on both the state and the instructions. Experiment 1 in this paper shows the added generality of the approach presented.
A more salient criticism has to do with the utility of such an approach. Even if it is taken as granted that this approach, as presented, is novel and the results are replicable, what does this mean for future work or for applications of reinforcement learning? While the authors suggest that the sketches are, in fact, straightforward to create, practitioners are less likely to desire the generation of such sketches versus providing natural language instructions, for instance.
Resources
You can find a talk on this paper here.
References
[1] Bacon, Pierre-Luc and Precup, Doina. The option-critic architecture. In NIPS Deep Reinforcement Learning Work-shop, 2015.
[2] Sutton, Richard S, Precup, Doina, and Singh, Satinder. Be-tween MDPs and semi-MDPs: A framework for temporal abstraction in reinforcement learning. Artificial intel-ligence, 112(1):181–211, 1999.
[3] Stolle, Martin and Precup, Doina. Learning options in reinforcement learning. In International Symposium on Abstraction, Reformulation, and Approximation, pp. 212– 223. Springer, 2002.
[4] Konidaris, George and Barto, Andrew G. Building portable options: Skill transfer in reinforcement learning. In IJ-CAI, volume 7, pp. 895–900, 2007.
[5] Schulman, John, Moritz, Philipp, Levine, Sergey, Jordan, Michael, and Abbeel, Pieter. Trust region policy optimization. In International Conference on Machine Learning, 2015b.
[6] Greensmith, Evan, Bartlett, Peter L, and Baxter, Jonathan. Variance reduction techniques for gradient estimates in reinforcement learning. Journal of Machine Learning Research, 5(Nov):1471–1530, 2004.
[7] Andre, David and Russell, Stuart. Programmable reinforce-ment learning agents. In Advances in Neural Information Processing Systems, 2001.
[8] Andre, David and Russell, Stuart. State abstraction for pro-grammable reinforcement learning agents. In Proceedings of the Meeting of the Association for the Advance-ment of Artificial Intelligence, 2002.
[9] Author Jacob Andreas presenting the paper - https://www.youtube.com/watch?v=NRIcDEB64x8
[10] Vezhnevets, A., Mnih, V., Osindero, S., Graves, A., Vinyals, O., & Agapiou, J. (2016). Strategic attentive writer for learning macro-actions. In Advances in Neural Information Processing Systems (pp. 3486-3494).
[11] Parr, Ron and Russell, Stuart. Reinforcement learning with hierarchies of machines. In Advances in Neural Information Processing Systems, 1998.
[12] Marthi, Bhaskara, Lantham, David, Guestrin, Carlos, and Russell, Stuart. Concurrent hierarchical reinforcement learning. In Proceedings of the Meeting of the Association for the Advancement of Artificial Intelligence, 2004.
[13] A. S. Vezhnevets, S. Osindero, T. Schaul, N. Heess, M. Jaderberg, D. Silver, and K. Kavukcuoglu. Feudal networks for hierarchical reinforcement learning. arXiv preprint arXiv:1703.01161, 2017.
[14] J. Andreas, M. Rohrbach, T. Darrell, D. Klein. Learning to compose neural networks for question answering. In Proceedings of the Annual Meeting of the North American Chapter of the Association for Computational Linguistics, 2016.
[15] Bengio, Yoshua, et al. "Curriculum learning." Proceedings of the 26th annual international conference on machine learning. ACM, 2009.
Appendix
The authors provide a brief appendix that gives a complete list of tasks and sketches. Asterisk * indicates that the task was held out for generalization experiments in Section 4.5, but included in the multitask experiments of Sections 4.3 and 4.4.