deep Generative Stochastic Networks Trainable by Backprop: Difference between revisions
m (Conversion script moved page Deep Generative Stochastic Networks Trainable by Backprop to deep Generative Stochastic Networks Trainable by Backprop: Converting page titles to lowercase) |
|||
| (One intermediate revision by one other user not shown) | |||
| Line 38: | Line 38: | ||
The estimation of <math>P(X)</math> is as follows: create <math>\bar{X}</math> from corrupted distribution <math>C(\bar{X}|X)</math>. <math>C</math> is created by adding some type of noise to the original data. The model is then trained to reconstruct <math>X</math> from <math>\bar{X}</math> and thus obtain <math>P(X|\bar{X})</math>. This is easier to model then the whole of <math>P(X)</math> since <math>P(X|\bar{X})</math> is dominated by fewer modes than <math>P(X)</math>. Bayes rule then dictates that <math>P(X|\bar{X}) = \frac{1}{z}C(\bar{X}|X)P(X)</math>, z is an independent normalizing constant. This leads to the ability to construct <math>P(X)</math> based off the other two distributions. | The estimation of <math>P(X)</math> is as follows: create <math>\bar{X}</math> from corrupted distribution <math>C(\bar{X}|X)</math>. <math>C</math> is created by adding some type of noise to the original data. The model is then trained to reconstruct <math>X</math> from <math>\bar{X}</math> and thus obtain <math>P(X|\bar{X})</math>. This is easier to model then the whole of <math>P(X)</math> since <math>P(X|\bar{X})</math> is dominated by fewer modes than <math>P(X)</math>. Bayes rule then dictates that <math>P(X|\bar{X}) = \frac{1}{z}C(\bar{X}|X)P(X)</math>, z is an independent normalizing constant. This leads to the ability to construct <math>P(X)</math> based off the other two distributions. | ||
Using a | Using a parametrized model (i.e. a neural network) it was found that the approximation made by the model, <math>P_{\theta}(X|\bar{X})</math> could be used to approximate <math>P_{\theta}(X)</math>. The Markov chain distribution <math>\pi(X)</math> will eventually converge to <math>P(X)</math>. Figure 2 shows this process. | ||
One may wonder where the complexity of the original data distribution went?! If <math>P_{\theta}(X|\bar{X})</math> and <math>C(\bar{X}|X)</math> are not complex, then how can they model the complex distribution <math>P(X)</math>? They explain that even though <math>P_{\theta}(X|\bar{X})</math> has few modes, the location of the modes is dependent on <math>\bar{X}</math>. Since the estimation is based off of many values of <math>\bar{X}</math> and a mapping of <math>\bar{X}</math> to a mode location that allows the problem to become a supervised function approximation problem (which is easy). | One may wonder where the complexity of the original data distribution went?! If <math>P_{\theta}(X|\bar{X})</math> and <math>C(\bar{X}|X)</math> are not complex, then how can they model the complex distribution <math>P(X)</math>? They explain that even though <math>P_{\theta}(X|\bar{X})</math> has few modes, the location of the modes is dependent on <math>\bar{X}</math>. Since the estimation is based off of many values of <math>\bar{X}</math> and a mapping of <math>\bar{X}</math> to a mode location that allows the problem to become a supervised function approximation problem (which is easy). | ||
Training the GSN involves moving along a Markov chain that uses the transition distribution between nodes as a way to update the weights of the GSM. The transition | Training the GSN involves moving along a Markov chain that uses the transition distribution between nodes as a way to update the weights of the GSM. The transition distribution <math>f(h,h', x)</math> is trained to maximize reconstruction likelihood. The following picture demonstrates the Markov chain that allows for the training of the model. Note the similarities to Hinton's contrastive divergence. | ||
[[File:bengio_markov.png |centre|]] | [[File:bengio_markov.png |centre|]] | ||
Latest revision as of 08:46, 30 August 2017
Introduction
The Deep Learning boom that has been seen in recent years was spurred initially by research in unsupervised learning techniques.<ref> Bengio, Yoshua. Learning deep architectures for AI. Now Publishers, 2009.</ref>However, most of the major successes over the last few years have mostly been based on supervised techniques. A drawback for the unsupervised methods stems from their need for too many calculations and intractable sums in their models (inference, learning, sampling and partition functions). The paper presented puts forth an idea for a network that creates a model of a conditional distribution, [math]\displaystyle{ P(X|\bar{X}) }[/math], which can be seen as a local (usually) unimodal representation of [math]\displaystyle{ P(X) }[/math]. [math]\displaystyle{ \bar{X} }[/math] is a corrupted example of the original data [math]\displaystyle{ {X} }[/math]. The Generative Stochastic Network (GSN) combines arbitrary latent variables [math]\displaystyle{ H }[/math] that serve as input for a Markov chain which build in layers that eventually create a representation of the original data. Training of the network does not need Gibb's sampling or large partition functions but is trained with backpropagation and all the tools that come with it.
In DBM <ref> Salakhutdinov, Ruslan and Hinton, Geoffrey E. Deep Boltzmann machines. In AISTATS’2009, pp. 448–455, 2009 </ref>, sampling [math]\displaystyle{ P(x, h) }[/math] is estimated based on inference and sampling (contrastive divergence algorithm). To obtain a gradient there are intractable sums that must to calculated, however there are ways around this. The problem with these methods is that they make strong assumptions. In essence, the sampling methods for these calculations are biased towards certain distribution types (i.e. small number of modes). The attempt is to get around this.
The reasoning for wanting to have a tractable generative model that uses unsupervised training is that within the realm of data, there is a far greater amount of unlabelled data than labelled data. Future models should be able to take advantage of this information.
Generative Stochastic Network (GSN)
The paper describes the Generative Stochastic Network as a generalization of generative denoising autoencoders. This can be said as the estimations of the data are based on noised sampling. As opposed to directly estimating the data distribution, the model ventures to parametrize the transition of a Markov chain. This is the change that allows the problem to be transformed into a problem more similar to a supervised training problem. GSN relies on estimating the transition operator of a Markov chain, that is [math]\displaystyle{ P(x_t | x_{t-1}) }[/math] or [math]\displaystyle{ P(x_t, h_t|x_{t-1}, h_{t-1}) }[/math], which contain a small number of important modes. This leads to a simple gradient of a partition function. Tries to leverage the strength of function approximation. GSN parametrizes the transition operators of Markov chain rather than [math]\displaystyle{ P(X) }[/math]. Allows for training of unsupervised methods by gradient descent and maximum likelihood with no partition functions, just back-propagation.
The estimation of [math]\displaystyle{ P(X) }[/math] is as follows: create [math]\displaystyle{ \bar{X} }[/math] from corrupted distribution [math]\displaystyle{ C(\bar{X}|X) }[/math]. [math]\displaystyle{ C }[/math] is created by adding some type of noise to the original data. The model is then trained to reconstruct [math]\displaystyle{ X }[/math] from [math]\displaystyle{ \bar{X} }[/math] and thus obtain [math]\displaystyle{ P(X|\bar{X}) }[/math]. This is easier to model then the whole of [math]\displaystyle{ P(X) }[/math] since [math]\displaystyle{ P(X|\bar{X}) }[/math] is dominated by fewer modes than [math]\displaystyle{ P(X) }[/math]. Bayes rule then dictates that [math]\displaystyle{ P(X|\bar{X}) = \frac{1}{z}C(\bar{X}|X)P(X) }[/math], z is an independent normalizing constant. This leads to the ability to construct [math]\displaystyle{ P(X) }[/math] based off the other two distributions.
Using a parametrized model (i.e. a neural network) it was found that the approximation made by the model, [math]\displaystyle{ P_{\theta}(X|\bar{X}) }[/math] could be used to approximate [math]\displaystyle{ P_{\theta}(X) }[/math]. The Markov chain distribution [math]\displaystyle{ \pi(X) }[/math] will eventually converge to [math]\displaystyle{ P(X) }[/math]. Figure 2 shows this process.
One may wonder where the complexity of the original data distribution went?! If [math]\displaystyle{ P_{\theta}(X|\bar{X}) }[/math] and [math]\displaystyle{ C(\bar{X}|X) }[/math] are not complex, then how can they model the complex distribution [math]\displaystyle{ P(X) }[/math]? They explain that even though [math]\displaystyle{ P_{\theta}(X|\bar{X}) }[/math] has few modes, the location of the modes is dependent on [math]\displaystyle{ \bar{X} }[/math]. Since the estimation is based off of many values of [math]\displaystyle{ \bar{X} }[/math] and a mapping of [math]\displaystyle{ \bar{X} }[/math] to a mode location that allows the problem to become a supervised function approximation problem (which is easy).
Training the GSN involves moving along a Markov chain that uses the transition distribution between nodes as a way to update the weights of the GSM. The transition distribution [math]\displaystyle{ f(h,h', x) }[/math] is trained to maximize reconstruction likelihood. The following picture demonstrates the Markov chain that allows for the training of the model. Note the similarities to Hinton's contrastive divergence.
Experimental Results
Some initial experimental results were created without extensive parameter alteration. This was done to maintain consistency over the tests and likely to show that even without optimization that the results approached the performance of more established unsupervised learning networks. The main comparison was made to Deep Boltzmann Machines (DBM) and Deep Belief Networks (DBN).
MNIST
The non-linearity for the units in the GSN was applied as [math]\displaystyle{ h_i = \eta_{out} + \tanh (\eta_{in} + a_i) }[/math], with [math]\displaystyle{ a_i }[/math] as the linear activation for unit [math]\displaystyle{ i }[/math] and [math]\displaystyle{ \eta_{in} }[/math] and [math]\displaystyle{ \eta_{out} }[/math] are both zero mean Gaussian noise. Sampling of unfinished or incomplete data can be done in a similar manner to DBM, where representations can propagate upwards and downwards in the network. This allows for pattern completion similar to that achieved by DBM. The third image in Figure 3 demonstrates the GSN's ability to move from only half an image (where the rest is noise) and complete the digit, showing it has a internal representation of the digit that can be sampled to complete the digit.
Faces
The following figure shows the GSN's ability to perform facial reconstruction.
Comparison
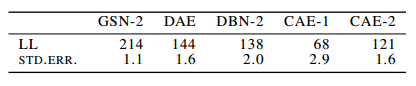
Test set log-likelihood lower bound (LL) obtained by a Parzen density estimator constructed using 10000 generated samples, for different generative models trained on MNIST. The LL is not directly comparable to AIS likelihood estimates because we use a Gaussian mixture rather than a Bernoulli mixture to compute the likelihood. A DBN-2 has 2 hidden layers, a (Contrastive Autoencoder) CAE-1 has 1 hidden layer, and a CAE-2 has 2. The (Denoising Autoencoder)DAE is basically a GSN-1, with no injection of noise inside the network.
 <ref>Rifai, Salah, Bengio, Yoshua, Dauphin, Yann, and Vincent,
Pascal. A generative process for sampling contractive
auto-encoders. In ICML’12, 2012</ref>
<ref>Rifai, Salah, Bengio, Yoshua, Dauphin, Yann, and Vincent,
Pascal. A generative process for sampling contractive
auto-encoders. In ICML’12, 2012</ref>
Conclusions and Critique
The main objective of the paper and technique was to avoid the intractable aspects of traditional generative models. This was achieved by training a model to reconstruct noisy data, which created a local and simple approximation of the whole data distribution. This was done over and over, treated as a Markov chain, with each transition distribution corresponding to a new representation of the data distribution. This can be trained with supervised neural network tools. Experiments shows similarity between results from the GSN and the DBM. However, there is no need for layer wise pre-training on the GSN.
One critique for this paper is that they continually point out that there method should, in theory, be faster than the traditional models. They show that a similar model can achieve similar results but they do not provide any information on the time each network took to train. This could be done by having networks with approximately the same numbers of parameters train for a specific task and be timed and evaluated based upon that. The paper does not do a very good job of describing how the training is done in relation to the Markov chain. The relationship can be teased out eventually, though it is not immediately apparent and could have been elaborated upon further. There is one section that briefly glosses over Sum Product Networks (SPN) as an alternative tractable graphical model. Since the SPN are solving the same problem that they are proposing to solve, it would have made sense for them to evaluate their model compared to the SPN as well, however they failed to do this.
References
<references>