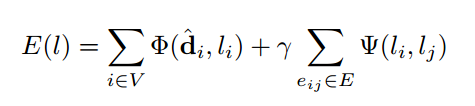learning Hierarchical Features for Scene Labeling: Difference between revisions
m (Conversion script moved page Learning Hierarchical Features for Scene Labeling to learning Hierarchical Features for Scene Labeling: Converting page titles to lowercase) |
|||
| (17 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
= Introduction = | = Introduction = | ||
This paper considers the problem of ''scene parsing'', in which every pixel in the image is assigned to a category that delineates a distinct object or region. For instance, an image of a cow on a field can be segmented into an image of a cow and an image of a field, with a clear delineation between the two. An example input image and resultant output is shown below to demonstrate this. | |||
'''Test input''': The input into the network was a static image such as the one below: | '''Test input''': The input into the network was a static image such as the one below: | ||
| Line 17: | Line 19: | ||
A multi-scale convolutional network is trained from raw pixels to extract dense feature vectors that encode regions of multiple sizes centered on each pixel for scene labeling. Also a technique is proposed to automatically retrieve an optimal set of components that best explain the scene from a pool of segmentation components. | A multi-scale convolutional network is trained from raw pixels to extract dense feature vectors that encode regions of multiple sizes centered on each pixel for scene labeling. Also a technique is proposed to automatically retrieve an optimal set of components that best explain the scene from a pool of segmentation components. | ||
= Related work = | |||
A preliminary work <ref> | |||
Grangier, David, Léon Bottou, and Ronan Collobert. [http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.183.8571&rep=rep1&type=pdf "Deep convolutional networks for scene parsing."] ICML 2009 Deep Learning Workshop. Vol. 3. 2009. | |||
</ref> on using convolutional neural networks for scene parsing showed that CNNs fed with raw pixels could be trained to perform scene parsing with decent accuracy. | |||
Another previous work <ref> | |||
Hannes Schulz and Sven Behnke. [https://www.elen.ucl.ac.be/Proceedings/esann/esannpdf/es2012-160.pdf "Learning Object-Class Segmentation with Convolutional Neural Networks."] 11th European Symposium on Artificial Neural Networks (ESANN). Vol. 3. 2012. | |||
</ref> also uses convolution neural networks for image segmentation. Pairwise class location filters are used to improve the raw output. The current work uses image gradient instead, which was found to increase accuracy and better respect image boundaries. | |||
= Methodology = | = Methodology = | ||
| Line 22: | Line 34: | ||
Below we can see a flow of the overall approach. | Below we can see a flow of the overall approach. | ||
[[File:yann_flow.png | 1200px ]] | [[File:yann_flow.png | 1200px | frame | center |Figure 1. Diagram of the scene parsing system. The raw input image is transformed through a Laplacian pyramid. Each scale is fed to a 3-stage convolutional network, which produces a set of feature maps. The feature maps of all | ||
scales are concatenated, the coarser-scale maps being upsampled to match the size of the finest-scale map. Each feature vector thus represents a large contextual window around each pixel. In parallel, a single segmentation (i.e. superpixels), or a family of segmentations (e.g. a segmentation tree) are computed to exploit the natural contours of the image. The final labeling is produced from the feature vectors and the segmentation(s) using different methods. ]] | |||
This model consists of two parallel components which are two complementary image representations. In the first component, an image patch is seen as a point in <math>\mathbb R^P</math> and we seek to find a transform <math>f:\mathbb R^P \to \mathbb R^Q</math> that maps each path into <math>\mathbb R^Q</math>, a space where it can be classified linearly. This stage usually suffers from two main problems with traditional convolutional neural networks: (1) the window considered rarely contains an object that is centred and scaled, (2) integrating a large context involves increasing the grid size and therefore the dimensionality of <math>P</math> and hence, it is then necessary to enforce some invariance in the function <math>f</math> itself. This is usually achieved through pooling but this degrades the model to precisely locate and delineate objects. In this paper, <math>f</math> is implemented by a mutliscale convolutional neural network, which allows integrating large contexts in local decisions while remaining manageable in terms of parameters/dimensionality. In the second component, the image is seen as an edge-weighted graph, on which one or several oversegmentations can be constructed. The components are spatially accurate and naturally delineates objects as this representation conserves pixel-level precision. A classifier is then applied to the aggregated feature grid of each node. | |||
In the second | |||
== Pre-processing == | == Pre-processing == | ||
| Line 32: | Line 43: | ||
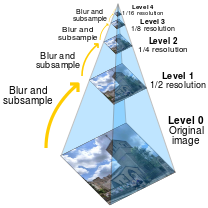
Before being put into the Convolutional Neural Network (CNN) multiple scaled versions of the image are generated. The set of these scaled images is called a ''pyramid''. There were three different scale outputs of the image created, in a similar manner shown in the picture below | Before being put into the Convolutional Neural Network (CNN) multiple scaled versions of the image are generated. The set of these scaled images is called a ''pyramid''. There were three different scale outputs of the image created, in a similar manner shown in the picture below | ||
[[File:Image_pyramid.png]] | [[File:Image_pyramid.png ]] | ||
The scaling can be done by different transforms; the paper suggests to use the Laplacian transform. The Laplacian is the sum of partial second derivatives <math>\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}</math>. A two-dimensional discrete approximation is given by the matrix <math>\left[\begin{array}{ccc}0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0\end{array}\right]</math>. | The scaling can be done by different transforms; the paper suggests to use the Laplacian transform. The Laplacian is the sum of partial second derivatives <math>\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}</math>. A two-dimensional discrete approximation is given by the matrix <math>\left[\begin{array}{ccc}0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0\end{array}\right]</math>. | ||
| Line 42: | Line 53: | ||
In the first representation, for each scale of the Laplacian pyramid, a typical 3-stage (Each of the first 2 stages is composed of three layers: convolution of kernel with feature map, non-linearity, pooling) CNN architecture was used. The function tanh served as the non-linearity. The kernel being used were 7x7 Toeplitz matrices (matrices with constant values along their diagonals). The pooling operation was performed by the 2x2 max-pool operator. The same CNN was applied to all different sized images. Since the parameters were shared between the networks, the ''same'' connection weights were applied to all of the images, thus allowing for the detection of scale-invariant features. The outputs of all CNNs at each scale are upsampled and concatenated to produce a map of feature vectors. The author believe that the more scales used to jointly train the models, the better the representation becomes for all scales. | In the first representation, for each scale of the Laplacian pyramid, a typical 3-stage (Each of the first 2 stages is composed of three layers: convolution of kernel with feature map, non-linearity, pooling) CNN architecture was used. The function tanh served as the non-linearity. The kernel being used were 7x7 Toeplitz matrices (matrices with constant values along their diagonals). The pooling operation was performed by the 2x2 max-pool operator. The same CNN was applied to all different sized images. Since the parameters were shared between the networks, the ''same'' connection weights were applied to all of the images, thus allowing for the detection of scale-invariant features. The outputs of all CNNs at each scale are upsampled and concatenated to produce a map of feature vectors. The author believe that the more scales used to jointly train the models, the better the representation becomes for all scales. | ||
In the second representation, the image is seen as an edge-weighted graph, on which one or several over-segmentations can be constructed and used to group the feature descriptors. This [http:// | In the second representation, the image is seen as an edge-weighted graph<ref> | ||
Shotton, Jamie, et al.[http://www.csd.uwo.ca/~olga/Courses/Fall2013/CS9840/PossibleStudentPapers/eccv06.pdf "Textonboost: Joint appearance, shape and context modeling for multi-class object recognition and segmentation." ]Computer Vision–ECCV 2006. Springer Berlin Heidelberg, 2006. 1-15. | |||
</ref><ref> | |||
Fulkerson, Brian, Andrea Vedaldi, and Stefano Soatto. [http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.150.4613&rep=rep1&type=pdf "Class segmentation and object localization with superpixel neighborhoods."] Computer Vision, 2009 IEEE 12th International Conference on. IEEE, 2009. | |||
</ref>, on which one or several over-segmentations can be constructed and used to group the feature descriptors. This graph segmentation technique was taken from another paper<ref> | |||
Felzenszwalb, Pedro F., and Daniel P. Huttenlocher.[http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.150.4613&rep=rep1&type=pdf "Efficient graph-based image segmentation."] International Journal of Computer Vision 59.2 (2004): 167-181. | |||
</ref>. Three techniques are proposed to produce the final image labelling as discussed below in the Post-Processing section. | |||
Stochastic gradient descent was used for training the filters. To avoid over-fitting the training images were edited via jitter, horizontal flipping, rotations between +8 and -8, and rescaling between 90 and 110%. The objective function was the ''cross entropy'' loss function, [https://jamesmccaffrey.wordpress.com/2013/11/05/why-you-should-use-cross-entropy-error-instead-of-classification-error-or-mean-squared-error-for-neural-network-classifier-training/ which is a way to take into account the closeness of a prediction into the error]. | Stochastic gradient descent was used for training the filters. To avoid over-fitting the training images were edited via jitter, horizontal flipping, rotations between +8 and -8, and rescaling between 90 and 110%. The objective function was the ''cross entropy'' loss function, [https://jamesmccaffrey.wordpress.com/2013/11/05/why-you-should-use-cross-entropy-error-instead-of-classification-error-or-mean-squared-error-for-neural-network-classifier-training/ which is a way to take into account the closeness of a prediction into the error]. With respect to the actual training procedure, once the output feature maps for each image in the laplacian pyramid are concatenated to produce the final map of feature vectors, these feature vectors are passed through a linear classifier that produces a probability distribution over class labels for each pixel location <math>i</math> via the softmax function. In other words, multi-class logistic regression is used to predict class labels for each pixel. Since each pixel in the image has a ground-truth class label, there is target distribution for each pixel that can be compared to the distribution produced by the linear classifier. This comparison allows one to define the cross-entropy loss function that is used to train the filters in the CNN. In short, the derivative of the cross entropy error with respect to the input to each class label unit can be backpropogated through the CNN to iteratively minimize the loss function. Once training is complete, taking the argmax of the predicted class distribution for each pixel gives a labelling to the entire scene. However, this labelling lacks spatial coherence, and hence the post processing techniques described in the next section are used to introduce refinements. | ||
== Post-Processing == | == Post-Processing == | ||
| Line 50: | Line 67: | ||
Unlike previous approaches, the emphasis of this scene-labelling method was to rely on a highly accurate pixel labelling system. So, despite the fact that a variety of approaches were attempted, including SuperPixels, Conditional Random Fields and gPb, the simple approach of super-pixels yielded state of the art results. | Unlike previous approaches, the emphasis of this scene-labelling method was to rely on a highly accurate pixel labelling system. So, despite the fact that a variety of approaches were attempted, including SuperPixels, Conditional Random Fields and gPb, the simple approach of super-pixels yielded state of the art results. | ||
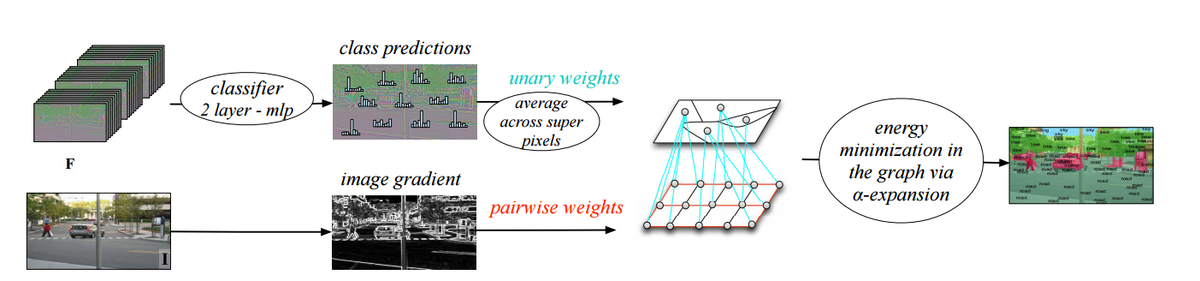
SuperPixels are randomly generated chunks of pixels. To label these pixels, a two layer neural network was used. Given | SuperPixels are randomly generated chunks of pixels. To label these pixels, a two layer neural network was used. Given inputs from the map of feature vectors produced by the CNN, the 2-layer network produces a distribution over class labels for each pixel in the superpixel. These distributions are averaged, and the argmax of the resulting average is then chosen as the final label for the super pixel. The picture below shows the general approach> | ||
[[File:super_pix.png]] | [[File:super_pix.png]] | ||
| Line 56: | Line 73: | ||
=== Conditional Random Fields === | === Conditional Random Fields === | ||
A standard approach for labelling is training a CRF model on the superpixels. It consists of associating the image to a graph and | A standard approach for labelling is training a CRF model on the superpixels. It consists of associating the image to a graph <math>(V,E)</math> where each vertex <math>v \in V</math> is a pixel of the image, and the edges <math>E = V \times V</math> exist for all neighbouring pixels. Let <math>l_i</math> be the labelling for the <math>i</math>th pixel. The CRF energy function is used to minimize the difference between the predicted label <math>d</math>, as well as a term that penalizes local changes in labels. The first difference term is <math>\Phi(d_i,l_i)</math> for all pixels. The second term is motivated by the idea that labels should have broad spatial range in general for good segmentations. As such, a penalty term is applied for each pixel <math>v_i</math> adjacent to a pixel <math>v_j</math> having a ''different'' label, as <math>\Phi(l_i,l_j)</math> for each <math>e_{ij} \in E</math>. Hence the energy function has the form | ||
[[File:Paper1p1.png ]] | [[File:Paper1p1.png ]] | ||
The entire process of using CRF can be summarized below | where <math>\Phi(d_i,l_i) = \begin{cases} | ||
e^{-\alpha d_i}& (l_i \neq d_i) \\ | |||
0 & \text{else}\\ | |||
\end{cases},</math> | |||
and | |||
<math>\Psi(l_i,l_j) = \begin{cases} | |||
e^{-\beta \|\nabla I\|_i}& (l_i \neq d_i) \\ | |||
0 & \text{else}\\ | |||
\end{cases}</math> | |||
for constants <math>\alpha,\beta,\gamma > 0</math>. | |||
The entire process of using CRF can be summarized below. | |||
[[File:Paper2p2.png | 1200px ]] | [[File:Paper2p2.png | 1200px ]] | ||
| Line 81: | Line 111: | ||
Finally, the output of N networks are upsampled and concatenated so as to produce F: | Finally, the output of N networks are upsampled and concatenated so as to produce F: | ||
<math>\ F= [f_1, u(f_2), ... , u(f_N)]</math>, where <math> u</math> is an upsampling function. | <math>\ F= [f_1, u(f_2), ... , u(f_N)]</math>, where <math> u</math> is an upsampling function. | ||
<br /> | |||
''' Learning discriminative scale-invariant features''' | |||
Ideally a linear classifier should produce the correct categorization for all pixel locations ''i'', from the feature vectors <math>F_{i}</math>. We train the parameters <math>\theta_{s}</math> to achieve this goal, using the multiclass ''cross entropy'' loss function. Let <math>\hat{c_{i}}</math> be the normalized prediction vector from the linear classifier for pixel ''i''. We compute normalized predicted probability distributions over classes <math>\hat{c}_{i,a}</math> using the softmax function: | |||
<math> | |||
\hat{c}_{i,a} = \frac{e^{w^{T}_{a} F_{i}}}{\sum\nolimits_{b \in classes} e^{w^{T}_{b} F_{i}}} | |||
</math> | |||
where <math>w</math> is a temporary weight matrix only used to learn the features. The cross entropy between the predicted class distribution <math>\hat{c}</math> and the target class distribution <math>c</math> penalizes their deviation and is measured by | |||
<math> | |||
L_{cat} = \sum\limits_{i \in pixels} \sum\limits_{a \in classes} c_{i,a} ln(\hat{c}_{i,a}) | |||
</math> | |||
The true target probability <math>c_{i,a}</math> of class <math>a</math> to be present at location <math>i</math> can either be a distribution of classes at location <math>i</math>, in a given neighborhood or a hard target vector: <math>c_{i,a} = 1</math> if pixel <math>i</math> is labeled <math>a</math>, and <math>0</math> otherwise. For training maximally discriminative features, we use hard target vectors in this first stage. Once the parameters <math>\theta s</math> are trained, the classifier is discarded, and the feature vectors <math>F_{i}</math> are used using different strategies, as explained later. | |||
''' Classification ''' | ''' Classification ''' | ||
| Line 102: | Line 149: | ||
<math>\ l_k=argmax_{a\in classes}{\hat{d_{k,a}}}</math> | <math>\ l_k=argmax_{a\in classes}{\hat{d_{k,a}}}</math> | ||
= Results = | = Results = | ||
| Line 133: | Line 179: | ||
There would also be considerable benefit from improving the metrics used in scene parsing. The current pixel-wise accuracy is a somewhat uninformative measure of the quality of the result. Spotting rare objects is often more important than correctly labeling every boundary pixel of a large region such as the sky. The average per-class accuracy is a step in the right direction, but the authors would prefer a system that correctly spots every object or region, while giving an approximate boundary to a system that produces accurate boundaries for large regions (sky, road, grass, etc), but fails to spot small objects. | There would also be considerable benefit from improving the metrics used in scene parsing. The current pixel-wise accuracy is a somewhat uninformative measure of the quality of the result. Spotting rare objects is often more important than correctly labeling every boundary pixel of a large region such as the sky. The average per-class accuracy is a step in the right direction, but the authors would prefer a system that correctly spots every object or region, while giving an approximate boundary to a system that produces accurate boundaries for large regions (sky, road, grass, etc), but fails to spot small objects. | ||
Long et al <ref> | |||
Long J, et al . [http://arxiv.org/pdf/1411.4038v2.pdf "Fully Convolutional Networks for Semantic Segmentation"] | |||
</ref> used a fully convolutional networks with extending classification nets to segmentation, and improving the architecture with multi-resolution layer combinations. They compared their algorithm to the Farbet et al approach and improved the pixel accuracy up to six percent. | |||
=References= | |||
<references /> | |||
Latest revision as of 09:46, 30 August 2017
Introduction
This paper considers the problem of scene parsing, in which every pixel in the image is assigned to a category that delineates a distinct object or region. For instance, an image of a cow on a field can be segmented into an image of a cow and an image of a field, with a clear delineation between the two. An example input image and resultant output is shown below to demonstrate this.
Test input: The input into the network was a static image such as the one below:
Training data and desired result: The desired result (which is the same format as the training data given to the network for supervised learning) is an image with large features labelled.
-
Labeled Result
One of the difficulties in solving this problem is that traditional convolutional neural networks (CNNs) only take a small region around each pixel into account which is often not sufficient for labeling it as the correct label is determined by the context on a larger scale. To tackle this problems the authors extend the method of sharing weights between spatial locations as in traditional CNNs to share weights across multiple scales. This is achieved by generating multiple scaled versions of the input image. Furthermore, the weight sharing across scales leads to the learning of scale-invariant features.
A multi-scale convolutional network is trained from raw pixels to extract dense feature vectors that encode regions of multiple sizes centered on each pixel for scene labeling. Also a technique is proposed to automatically retrieve an optimal set of components that best explain the scene from a pool of segmentation components.
Related work
A preliminary work <ref> Grangier, David, Léon Bottou, and Ronan Collobert. "Deep convolutional networks for scene parsing." ICML 2009 Deep Learning Workshop. Vol. 3. 2009. </ref> on using convolutional neural networks for scene parsing showed that CNNs fed with raw pixels could be trained to perform scene parsing with decent accuracy.
Another previous work <ref> Hannes Schulz and Sven Behnke. "Learning Object-Class Segmentation with Convolutional Neural Networks." 11th European Symposium on Artificial Neural Networks (ESANN). Vol. 3. 2012. </ref> also uses convolution neural networks for image segmentation. Pairwise class location filters are used to improve the raw output. The current work uses image gradient instead, which was found to increase accuracy and better respect image boundaries.
Methodology
Below we can see a flow of the overall approach.
This model consists of two parallel components which are two complementary image representations. In the first component, an image patch is seen as a point in [math]\displaystyle{ \mathbb R^P }[/math] and we seek to find a transform [math]\displaystyle{ f:\mathbb R^P \to \mathbb R^Q }[/math] that maps each path into [math]\displaystyle{ \mathbb R^Q }[/math], a space where it can be classified linearly. This stage usually suffers from two main problems with traditional convolutional neural networks: (1) the window considered rarely contains an object that is centred and scaled, (2) integrating a large context involves increasing the grid size and therefore the dimensionality of [math]\displaystyle{ P }[/math] and hence, it is then necessary to enforce some invariance in the function [math]\displaystyle{ f }[/math] itself. This is usually achieved through pooling but this degrades the model to precisely locate and delineate objects. In this paper, [math]\displaystyle{ f }[/math] is implemented by a mutliscale convolutional neural network, which allows integrating large contexts in local decisions while remaining manageable in terms of parameters/dimensionality. In the second component, the image is seen as an edge-weighted graph, on which one or several oversegmentations can be constructed. The components are spatially accurate and naturally delineates objects as this representation conserves pixel-level precision. A classifier is then applied to the aggregated feature grid of each node.
Pre-processing
Before being put into the Convolutional Neural Network (CNN) multiple scaled versions of the image are generated. The set of these scaled images is called a pyramid. There were three different scale outputs of the image created, in a similar manner shown in the picture below
The scaling can be done by different transforms; the paper suggests to use the Laplacian transform. The Laplacian is the sum of partial second derivatives [math]\displaystyle{ \nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} }[/math]. A two-dimensional discrete approximation is given by the matrix [math]\displaystyle{ \left[\begin{array}{ccc}0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0\end{array}\right] }[/math].
Network Architecture
The proposed scene parsing architecture has two main components: Multi-scale convolutional representation and Graph-based classification.
In the first representation, for each scale of the Laplacian pyramid, a typical 3-stage (Each of the first 2 stages is composed of three layers: convolution of kernel with feature map, non-linearity, pooling) CNN architecture was used. The function tanh served as the non-linearity. The kernel being used were 7x7 Toeplitz matrices (matrices with constant values along their diagonals). The pooling operation was performed by the 2x2 max-pool operator. The same CNN was applied to all different sized images. Since the parameters were shared between the networks, the same connection weights were applied to all of the images, thus allowing for the detection of scale-invariant features. The outputs of all CNNs at each scale are upsampled and concatenated to produce a map of feature vectors. The author believe that the more scales used to jointly train the models, the better the representation becomes for all scales.
In the second representation, the image is seen as an edge-weighted graph<ref> Shotton, Jamie, et al."Textonboost: Joint appearance, shape and context modeling for multi-class object recognition and segmentation." Computer Vision–ECCV 2006. Springer Berlin Heidelberg, 2006. 1-15. </ref><ref> Fulkerson, Brian, Andrea Vedaldi, and Stefano Soatto. "Class segmentation and object localization with superpixel neighborhoods." Computer Vision, 2009 IEEE 12th International Conference on. IEEE, 2009. </ref>, on which one or several over-segmentations can be constructed and used to group the feature descriptors. This graph segmentation technique was taken from another paper<ref> Felzenszwalb, Pedro F., and Daniel P. Huttenlocher."Efficient graph-based image segmentation." International Journal of Computer Vision 59.2 (2004): 167-181. </ref>. Three techniques are proposed to produce the final image labelling as discussed below in the Post-Processing section.
Stochastic gradient descent was used for training the filters. To avoid over-fitting the training images were edited via jitter, horizontal flipping, rotations between +8 and -8, and rescaling between 90 and 110%. The objective function was the cross entropy loss function, which is a way to take into account the closeness of a prediction into the error. With respect to the actual training procedure, once the output feature maps for each image in the laplacian pyramid are concatenated to produce the final map of feature vectors, these feature vectors are passed through a linear classifier that produces a probability distribution over class labels for each pixel location [math]\displaystyle{ i }[/math] via the softmax function. In other words, multi-class logistic regression is used to predict class labels for each pixel. Since each pixel in the image has a ground-truth class label, there is target distribution for each pixel that can be compared to the distribution produced by the linear classifier. This comparison allows one to define the cross-entropy loss function that is used to train the filters in the CNN. In short, the derivative of the cross entropy error with respect to the input to each class label unit can be backpropogated through the CNN to iteratively minimize the loss function. Once training is complete, taking the argmax of the predicted class distribution for each pixel gives a labelling to the entire scene. However, this labelling lacks spatial coherence, and hence the post processing techniques described in the next section are used to introduce refinements.
Post-Processing
Unlike previous approaches, the emphasis of this scene-labelling method was to rely on a highly accurate pixel labelling system. So, despite the fact that a variety of approaches were attempted, including SuperPixels, Conditional Random Fields and gPb, the simple approach of super-pixels yielded state of the art results.
SuperPixels are randomly generated chunks of pixels. To label these pixels, a two layer neural network was used. Given inputs from the map of feature vectors produced by the CNN, the 2-layer network produces a distribution over class labels for each pixel in the superpixel. These distributions are averaged, and the argmax of the resulting average is then chosen as the final label for the super pixel. The picture below shows the general approach>
Conditional Random Fields
A standard approach for labelling is training a CRF model on the superpixels. It consists of associating the image to a graph [math]\displaystyle{ (V,E) }[/math] where each vertex [math]\displaystyle{ v \in V }[/math] is a pixel of the image, and the edges [math]\displaystyle{ E = V \times V }[/math] exist for all neighbouring pixels. Let [math]\displaystyle{ l_i }[/math] be the labelling for the [math]\displaystyle{ i }[/math]th pixel. The CRF energy function is used to minimize the difference between the predicted label [math]\displaystyle{ d }[/math], as well as a term that penalizes local changes in labels. The first difference term is [math]\displaystyle{ \Phi(d_i,l_i) }[/math] for all pixels. The second term is motivated by the idea that labels should have broad spatial range in general for good segmentations. As such, a penalty term is applied for each pixel [math]\displaystyle{ v_i }[/math] adjacent to a pixel [math]\displaystyle{ v_j }[/math] having a different label, as [math]\displaystyle{ \Phi(l_i,l_j) }[/math] for each [math]\displaystyle{ e_{ij} \in E }[/math]. Hence the energy function has the form
where [math]\displaystyle{ \Phi(d_i,l_i) = \begin{cases} e^{-\alpha d_i}& (l_i \neq d_i) \\ 0 & \text{else}\\ \end{cases}, }[/math]
and
[math]\displaystyle{ \Psi(l_i,l_j) = \begin{cases} e^{-\beta \|\nabla I\|_i}& (l_i \neq d_i) \\ 0 & \text{else}\\ \end{cases} }[/math]
for constants [math]\displaystyle{ \alpha,\beta,\gamma \gt 0 }[/math].
The entire process of using CRF can be summarized below.
Model
Scale-invariant, Scene-level feature extraction
Given an input image, a multiscale pyramid of images [math]\displaystyle{ \ X_s }[/math], where [math]\displaystyle{ s }[/math] belongs to {1,...,N}, is constructed. The multiscale pyramid is typically pre-processed, so that local neighborhoods have zero mean and unit standard deviation. We denote [math]\displaystyle{ f_s }[/math] as a classical convolutional network with parameter [math]\displaystyle{ \theta_s }[/math], where [math]\displaystyle{ \theta_s }[/math] is shared across [math]\displaystyle{ f_s }[/math].
For a network [math]\displaystyle{ f_s }[/math] with L layers, we have regular convolutional network:
[math]\displaystyle{ \ f_s(X_s; \theta_s)=W_LH_{L-1} }[/math].
[math]\displaystyle{ \ H_L }[/math] is the vector of hidden units at layer L, where:
[math]\displaystyle{ \ H_l=pool(tanh(W_lH_{l-1}+b_l)) }[/math], [math]\displaystyle{ b_l }[/math] is a vector of bias parameter
Finally, the output of N networks are upsampled and concatenated so as to produce F:
[math]\displaystyle{ \ F= [f_1, u(f_2), ... , u(f_N)] }[/math], where [math]\displaystyle{ u }[/math] is an upsampling function.
Learning discriminative scale-invariant features
Ideally a linear classifier should produce the correct categorization for all pixel locations i, from the feature vectors [math]\displaystyle{ F_{i} }[/math]. We train the parameters [math]\displaystyle{ \theta_{s} }[/math] to achieve this goal, using the multiclass cross entropy loss function. Let [math]\displaystyle{ \hat{c_{i}} }[/math] be the normalized prediction vector from the linear classifier for pixel i. We compute normalized predicted probability distributions over classes [math]\displaystyle{ \hat{c}_{i,a} }[/math] using the softmax function:
[math]\displaystyle{ \hat{c}_{i,a} = \frac{e^{w^{T}_{a} F_{i}}}{\sum\nolimits_{b \in classes} e^{w^{T}_{b} F_{i}}} }[/math]
where [math]\displaystyle{ w }[/math] is a temporary weight matrix only used to learn the features. The cross entropy between the predicted class distribution [math]\displaystyle{ \hat{c} }[/math] and the target class distribution [math]\displaystyle{ c }[/math] penalizes their deviation and is measured by
[math]\displaystyle{ L_{cat} = \sum\limits_{i \in pixels} \sum\limits_{a \in classes} c_{i,a} ln(\hat{c}_{i,a}) }[/math]
The true target probability [math]\displaystyle{ c_{i,a} }[/math] of class [math]\displaystyle{ a }[/math] to be present at location [math]\displaystyle{ i }[/math] can either be a distribution of classes at location [math]\displaystyle{ i }[/math], in a given neighborhood or a hard target vector: [math]\displaystyle{ c_{i,a} = 1 }[/math] if pixel [math]\displaystyle{ i }[/math] is labeled [math]\displaystyle{ a }[/math], and [math]\displaystyle{ 0 }[/math] otherwise. For training maximally discriminative features, we use hard target vectors in this first stage. Once the parameters [math]\displaystyle{ \theta s }[/math] are trained, the classifier is discarded, and the feature vectors [math]\displaystyle{ F_{i} }[/math] are used using different strategies, as explained later.
Classification
Having [math]\displaystyle{ \ F }[/math], we now want to classify the superpixels.
[math]\displaystyle{ \ y_i= W_2tanh(W_1F_i+b_1) }[/math],
[math]\displaystyle{ \ W_1 }[/math] and [math]\displaystyle{ \ W_2 }[/math] are trainable parameters of the classifier.
[math]\displaystyle{ \ \hat{d_{i,a}}=\frac{e^{y_{i,a}}}{\sum_{b\in classes}{e^{y_{i,b}}}} }[/math],
[math]\displaystyle{ \hat{d_{i,a}} }[/math] is the predicted class distribution from the linear classifier for pixel [math]\displaystyle{ i }[/math] and class [math]\displaystyle{ a }[/math].
[math]\displaystyle{ \ \hat{d_{k,a}}= \frac{1}{s(k)}\sum_{i\in k}{\hat{d_{i,a}}} }[/math],
where [math]\displaystyle{ \hat{d_k} }[/math] is the pixelwise distribution at superpixel k, [math]\displaystyle{ s(k) }[/math] is the surface of component k.
In this case, the final labeling for each component [math]\displaystyle{ k }[/math] is given by:
[math]\displaystyle{ \ l_k=argmax_{a\in classes}{\hat{d_{k,a}}} }[/math]
Results
The network was tested on the Stanford Background, SIFT Flow and Barcelona datasets.
The Stanford Background dataset shows that super-pixels could achieve state of the art results with minimal processing times.
Since super-pixels were shown to be so effective in the Stanford Dataset, they were the only method of image segmentation used for the SIFT Flow and Barcelona datasets. Instead, exposure of features to the network (whether balanced as super-index 1 or natural as super-index 2) were explored, in conjunction with the aforementioned Graph Based Segmentation method, when combined with the optimal cover algorithm.
From the sift dataset, it can be seen that the Graph Based Segmentation with optimal cover method offers a significant advantage.
In the Barcelona dataset, it can be seen that a dataset with many labels is too difficult for the CNN.
Conclusions
A wide window for contextual information, achieved through the multiscale network, improves the results largely and diminishes the role of the post-processing stage. This allows to replace the computational expensive post-processing with a simpler and faster method (e.g., majority vote) to increase the efficiency without a relevant loss in classification accuracy. The paper has demonstrated that a feed-forward convolutional network, trained end-to-end and fed with raw pixels can produce state of the art performance on scene parsing datasets. The model does not rely on engineered features, and uses purely supervised training from fully-labeled images.
An interesting find in this paper is that even in the absence of any post-processing, by simply labelling each pixel with highest-scoring category produced by he convolutional net for that location, the system yields near sate-of-the-art pixel-wise accuracy.
Future Work
Aside from the usual advances to CNN architecture, such as unsupervised pre-training, rectifying non-linearities and local contrast normalization, there would be a significant benefit, especially in datasets with many variables, to have a semantic understanding of the variables. For example, understanding that a window is often part of a building or a car.
There would also be considerable benefit from improving the metrics used in scene parsing. The current pixel-wise accuracy is a somewhat uninformative measure of the quality of the result. Spotting rare objects is often more important than correctly labeling every boundary pixel of a large region such as the sky. The average per-class accuracy is a step in the right direction, but the authors would prefer a system that correctly spots every object or region, while giving an approximate boundary to a system that produces accurate boundaries for large regions (sky, road, grass, etc), but fails to spot small objects.
Long et al <ref> Long J, et al . "Fully Convolutional Networks for Semantic Segmentation" </ref> used a fully convolutional networks with extending classification nets to segmentation, and improving the architecture with multi-resolution layer combinations. They compared their algorithm to the Farbet et al approach and improved the pixel accuracy up to six percent.
References
<references />