User talk:Dsevern: Difference between revisions
m (Welcome!) |
(`) |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
==Newton-Raphson Method (Lecture: Oct 11, 2011)== | |||
We | Previously we had derivated the log likelihood function for the logistic function. | ||
You | |||
<math>\begin{align} {\ell(\mathbf{\beta\,})} & {} = \sum_{i=1}^n \left(y_i {\mathbf{\beta\,}^T \mathbf{x_i}} - \ln({1+e^{\mathbf{\beta\,}^T \mathbf{x_i}}})\right) \end{align}</math> | |||
Our goal is to find the <math>\beta\,</math> that maximizes <math>{\ell(\mathbf{\beta\,})}</math>. We use calculus to do this ie solve <math>{\frac{\partial \ell}{\partial \mathbf{\beta\,}}}=0</math>. To do this we use the famous numerical method of Newton-Raphson. This is an iterative method were we calculate the first & second derivative at each iteration. | |||
The first derivative is typically called the score vector. | |||
<math>\begin{align} S(\beta\,) {}= {\frac{\partial \ell}{ \partial \mathbf{\beta\,}}}&{} = \sum_{i=1}^n \left(y_i \mathbf{x_i} - \frac{e^{\mathbf{\beta\,}^T \mathbf{x}}}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}} \mathbf{x_i} \right) \\[8pt] \end{align}</math> | |||
The negative of the second derivative is typically called the information matrix. | |||
<math>\begin{align} I(\beta\,) {}= -{\frac{\partial \ell}{\partial \mathbf {\beta\,} \partial \mathbf{\beta\,}^T}}&{} = \sum_{i=1}^n \left(\mathbf{x_i}\mathbf{x_i}^T (\frac{e^{\mathbf{\beta\,}^T \mathbf{x}}}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}})(\frac{1}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}}) \right) \\[8pt] \end{align}</math> | |||
We then use the following update formula to calcalute continually better estimates of the optimal <math>\beta\,</math>. It is not typically important what you use as your initial estimate <math>\beta\,^{(1)}</math> is. | |||
<math> \beta\,^{(r+1)} {}= \beta\,^{(r)} + I^{-1}(\beta\,^{(r)} )S(\beta\,^{(r)} )</math> | |||
===Matrix Notation=== | |||
let <math>\mathbf{y}</math> be a (n x 1) vector of all class labels. This is called the response in other contexts. | |||
let <math>\mathbb{X}</math> be a (n x (d+1)) matrix of all your features. Each row represents a data point. Each column represents a feature/covariate. | |||
let <math>\mathbf{p}^{(r)}</math> be a (n x 1) vector with values <math> P(\mathbf{x_i} |\beta\,^{(r)} ) </math> | |||
let <math>\mathbb{W}^{(r)}</math> be a (n x n) diagonal matrix with <math>\mathbb{W}_{ii}^{(r)} {}= P(\mathbf{x_i} |\beta\,^{(r)} )(1 - P(\mathbf{x_i} |\beta\,^{(r)} ))</math> | |||
we can rewrite our score vector, information matrix & update equation in terms of this new matrix notation. | |||
<math>\begin{align} S(\beta\,^{(r)}) {}= {\frac{\partial \ell}{ \partial \mathbf{\beta\,}}}&{} = \mathbb{X}^T(\mathbf{y} - \mathbf{p}^{(r)})\end{align}</math> | |||
<math>\begin{align} I(\beta\,^{(r)}) {}= -{\frac{\partial \ell}{\partial \mathbf {\beta\,} \partial \mathbf{\beta\,}^T}}&{} = \mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X} \end{align}</math> | |||
<math> \beta\,^{(r+1)} {}= \beta\,^{(r)} + I^{-1}(\beta\,^{(r)} )S(\beta\,^{(r)} ) {}= \beta\,^{(r)} + (\mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X})^{-1}\mathbb{X}^T(\mathbf{y} - \mathbf{p}^{(r)})</math> | |||
=====Iteratively Re-weighted Least Squares===== | |||
If we reorganize this updating formula we can see it is really a iteratively solving a least squares problem each time with a new weighting. | |||
<math>\beta\,^{(r+1)} {}= \beta\,^{(r)} + (\mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X})^{-1}(\mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X}\beta\,^{(r)} + \mathbb{X}^T(\mathbf{y} - \mathbf{p}^{(r)}))</math> | |||
<math>\beta\,^{(r+1)} {}= \beta\,^{(r)} + (\mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X})^{-1}\mathbb{X}^T\mathbb{W}^{(r)}\mathbf(z)^{(r)}</math> | |||
where <math> \mathbf{z}^{(r)} = \mathbb{X}\beta\,^{(r)} + (\mathbb{W}^{(r)})^{-1}(\mathbf{y}-\mathbf{p}^{(r)}) </math> | |||
=====Fisher Scoring Method===== | |||
Fisher Scoring is a method very similiar to Newton-Raphson. It uses the expected Information Matrix as opposed to the observed information matrix. This distinction simplifies the problem and in perticular the computational complexity. To learn more about this method & logistic regression in general you can take Stat431/831 at the University of Waterloo. | |||
==Hidden Markov Models== | |||
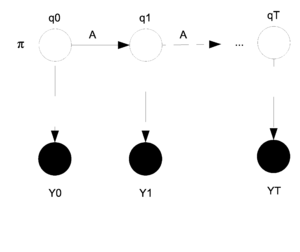
In a Hidden Markov Model (HMM) is a graphical model with a directed graphical model with two layers of nodes. The hidden layer of nodes represents a set of unobserved discrete random variables with supports corresponding to some state space. You the first layer alone as a discrete time Markov Chain. These random variables are sequentially connected and which can often represent a temporal dependancy. In this model we do not observe the states (nodes in layer 1) we instead observe features that may be dependant on the states; this set of features represents the second observed layer of nodes. Thus for each node in layer 1 we have a corresponding dependant node in layer 2 which represents the observed features. Please see the Figure XX for a visual depiction of the graphical structure. | |||
[[File:HMM.png|thumb|right|Fig.XX Hidden Markov Model]] | |||
The nodes in the first and second layers are denoted by <math> {q_0, q_1, ... , q_T} </math> and <math>{y_0, y_1, ... , y_T}</math> respectively. The <math>y_i</math>s are shaded because they have been observed. | |||
The parameters that need to be estimated are <math> \theta = (\pi, A, \eta)</math>. Where <math>\pi</math> represents the starting state for <math>q_0</math>. In general <math>\pi_i</math> represents the state that <math>q_i</math> is in. The matrix <math>A</math> is the transition matrix for the states <math>q_t</math> and <math>q_{t+1}</math> and shows the probability of changing states as we move from one step to the next. Finally, <math>\eta</math> represents the parameter that decides the probability that <math>y_i</math> will produce <math>y^*</math> given that <math>q_i</math> is in state <math>q^*</math>. <br /> | |||
Defining some notation: | |||
Note that we will be using a homogenous descrete time Markov Chain with finite state space for the first layer. | |||
<math> \ q_t^j = \begin{cases} 1 & \text{if } q_t = j \\ 0 & \text{otherwise } \end{cases} | |||
</math> | |||
<math> | |||
\pi_i = P(q_0 = i) = P(q_0^i = 1) | |||
</math> | |||
<math> | |||
a_{ij} = P(q_{t+1} = j | q_t = i) = P(q_{t+1}^j = 1 | q_t^i = 1) | |||
</math> | |||
For the HMM our data comes from the output layer: | |||
<center><math>\ Data = (y_{0i}, y_{1i}, y_{2i}, ... , y_{Ti}) \text{ for } i = 1...n </math></center> | |||
We can use <math>a_{ij}</math> to represent the i,j entry in the matrix A. We can then define: | |||
<center><math> P(q_{t-1}|q_t) = \prod_{i,j=1}^M (a_{ij})^{q_i^t q_j^{t+1}} </math></center> | |||
We can also define: | |||
<center><math> p(q_0) = \prod_{i=1}^M (\pi_i)^{q_0^i} </math></center> | |||
Now, if we take Y to be multinomial we get: | |||
<center><math> P(y_t|q_t) = \prod_{i,j=1}^M (\eta_{ij})^{y_t^i q_t^j} </math> | |||
where <math>n_{ij} = P(y_{t+1} = j | q_t = i) = P(y_{t+1}^j = 1 | q_t^i = 1) </math> | |||
</center> | |||
The random variable Y does not have to be multinomial, this is just an example. | |||
We can write the joint pdf using the structure of the HMM model graphical structure. | |||
<center><math> P(q, y) = p(q_0)\prod_{t=0}^{T-1}P(q_{t-1}|q_t)\prod_{t=0}^{T}P(y_t|q_t) </math></center> | |||
Substituting our representations for the 3 probabilities: | |||
<center><math> P(q, y) = \prod_{i=1}^M (\pi_i)^{q_0^i}\prod_{t=0}^{T-1} \prod_{i,j=1}^M (a_{ij})^{q_i^t q_j^{t+1}} \prod_{t=0}^{T}P(y_t|q_t) </math></center> | |||
We can go on to the E-Step with this new joint pdf. In the E-Step we need to find the expectation of the missing data given the observed data and the initial values of the parameters. Suppose that we only sample once so <math>n=1</math>. Take the log of our pdf and we get: | |||
<center><math> l_c(\theta, q, y) = \sum_{i=1}^M {q_0^i}log(\pi_i)\sum_{t=0}^{T-1} \sum_{i,j=1}^M {q_i^t q_j^{t+1}} log(a_{ij}) \sum_{t=0}^{T}log(P(y_t|q_t)) </math></center> | |||
Then we take the expectation for the E-Step: | |||
<center><math> E[l_c(\theta, q, y)] = \sum_{i=1}^M E[q_0^i]log(\pi_i)\sum_{t=0}^{T-1} \sum_{i,j=1}^M E[q_i^t q_j^{t+1}] log(a_{ij}) \sum_{t=0}^{T}E[log(P(y_t|q_t))] </math></center> | |||
If we continue with our multinomial example then we would get: | |||
<center><math> \sum_{t=0}^{T}E[log(P(y_t|q_t))] = \sum_{t=0}^{T}\sum_{i,j=1}^M E[q_t^j] y_t^i log(\eta_{ij}) </math></center> | |||
So now we need to calculate <math>E[q_0^i]</math> and <math> E[q_i^t q_j^{t+1}] </math> in order to find the expectation of the log likelihood. Let's define some variables to represent each of these quantities. <br /> | |||
Let <math> \gamma_0^i = E[q_0^i] = P(q_0^i=1|y, \theta^{(t)}) </math>. <br /> | |||
Let <math> \xi_{t,t+1}^{ij} = E[q_i^t q_j^{t+1}] = P(q_t^iq_{t+1}^j|y, \theta^{(t)}) </math> .<br /> | |||
We could use the sum product algorithm to calculate these equations but in this case we will introduce a new algorithm that is called the <math>\alpha</math> - <math>\beta</math> Algorithm. | |||
===The <math>\alpha</math> - <math>\beta</math> Algorithm=== | |||
We have from before the expectation: | |||
<center><math> E[l_c(\theta, q, y)] = \sum_{i=1}^M \gamma_0^i log(\pi_i)\sum_{t=0}^{T-1} \sum_{i,j=1}^M \xi_{t,t+1}^{ij} log(a_{ij}) \sum_{t=0}^{T}E[log(P(y_t|q_t))] </math></center> | |||
As usual we take the derivative with respect to <math>\theta</math> and then we set that equal to zero and solve. We obtain the following results (You can check these...) . Note that for <math>\eta</math> we are using a specific <math>y*</math> that is given. | |||
<center><math>\begin{matrix} | |||
\hat \pi_0 & = & \frac{\gamma_0^i}{\sum_{k=1}^M \gamma_0^k} \\ | |||
\hat a_{ij} & = & \frac{\sum_{t=0}^{T-1}\xi_{t,t+1}^{ij}}{\sum_{k=1}^M\sum_{t=0}^{T-1}\xi_{t,t+1}^{ij}} \\ | |||
\hat \eta_i(y^*) & = & \frac{\sum_{t|y_t=y^*}\gamma_t^i}{\sum_{t=0}^T\gamma_t^i} | |||
\end{matrix}</math></center> | |||
For <math>\eta</math> we can think of this intuitively. It represents the proportion of times that state i prodices <math>y^*</math>. For example we can think of the multinomial case for y where: | |||
<center><math> \hat \eta_{ij} = \frac{\sum_{t=0}^T\gamma_t^i y_t^j}{\sum_{t=0}^T\gamma_t^i} </math></center> | |||
Notice here that all of these parameters have been solved in terms of <math>\gamma_t^i</math> and <math>\xi_{t,t+1}^{ij}</math>. If we were to be able to calculate those two parameters then we could calculate everything in this model. This is where the <math>\alpha</math> - <math>\beta</math> Algorithm comes in. | |||
<center><math>\begin{matrix} | |||
\gamma_t^i & = & P(q_t^i = 1|y) \\ | |||
& = & \frac{P(y|q_t)P(q_t)}{P(y)} | |||
\end{matrix}</math></center> | |||
Now due to the Markovian Memoryless property. | |||
<center><math>\begin{matrix} | |||
\gamma_t^i & = & \frac{P(y_0...y_t|q_t)P(y_{t+1}...y_T|q_t)P(q_t)}{P(y)} \\ | |||
& = & \frac{P(y_0...y_t|q_t)P(q_t)P(y_{t+1}...y_T|q_t)}{P(y)} \\ | |||
& = & \frac{P(y_0...y_t, q_t)P(y_{t+1}...y_T|q_t)}{P(y)} | |||
\end{matrix}</math></center> | |||
Define <math>\alpha</math> and <math>\beta</math> as follows: | |||
<center><math> \alpha(q_t) = P(y_0...y_t, q_t) </math></center> | |||
<center><math> \beta(q_t) = P(y_{t+1}...y_T|q_t) </math></center> | |||
Once we have <math>\alpha</math> and <math>\beta</math> then computing <math>P(y)</math> is easy. | |||
<center><math> P(y) = \sum_{q_t}\alpha(q_t)\beta(q_t) </math></center> | |||
To calculate <math>\alpha</math> and <math>\beta</math> themselves we can use:<br /> | |||
For <math>\alpha</math>: | |||
<center><math> \alpha(q_{t+1}) = \sum_{q_t}\alpha(q_t)a_{q_t,q_{t+1}}P(y_{t+1}|q_{t+1}) </math></center> | |||
Where we begin with: | |||
<center><math> \alpha(q_0) = P(y_0, q_0) = P(y_0| q_0)\pi_0 </math></center> | |||
Then for <math>\beta</math>: | |||
<center><math> \beta(q_t) = \sum_{q_t}\beta(q_{t+1})a_{q_t,q_{t+1}}P(y_{t+1}|q_{t+1}) </math></center> | |||
Where we now begin from the other end: | |||
<center><math> \beta(q_T) = (1,1,.....1) = \text{A Vector of Ones} </math></center> | |||
Once both <math>\alpha</math> and <math>\beta</math> have been calculated we can use them to find: | |||
<center><math> \gamma_t^i = \frac{\alpha(q_t)\beta(q_t)}{\sum_{q_t}\alpha(q_t)\beta(q_t)} </math></center> | |||
<center><math> \xi_{t,t+1}^{ij} = \frac{\alpha(q_t)P(y_{t+1}, q_{t+1}) \beta(q_{t+1}) a_{q_t,q_{t+1}}}{P(y)} </math></center> | |||
Latest revision as of 00:48, 4 November 2011
Newton-Raphson Method (Lecture: Oct 11, 2011)
Previously we had derivated the log likelihood function for the logistic function.
[math]\displaystyle{ \begin{align} {\ell(\mathbf{\beta\,})} & {} = \sum_{i=1}^n \left(y_i {\mathbf{\beta\,}^T \mathbf{x_i}} - \ln({1+e^{\mathbf{\beta\,}^T \mathbf{x_i}}})\right) \end{align} }[/math]
Our goal is to find the [math]\displaystyle{ \beta\, }[/math] that maximizes [math]\displaystyle{ {\ell(\mathbf{\beta\,})} }[/math]. We use calculus to do this ie solve [math]\displaystyle{ {\frac{\partial \ell}{\partial \mathbf{\beta\,}}}=0 }[/math]. To do this we use the famous numerical method of Newton-Raphson. This is an iterative method were we calculate the first & second derivative at each iteration.
The first derivative is typically called the score vector.
[math]\displaystyle{ \begin{align} S(\beta\,) {}= {\frac{\partial \ell}{ \partial \mathbf{\beta\,}}}&{} = \sum_{i=1}^n \left(y_i \mathbf{x_i} - \frac{e^{\mathbf{\beta\,}^T \mathbf{x}}}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}} \mathbf{x_i} \right) \\[8pt] \end{align} }[/math]
The negative of the second derivative is typically called the information matrix.
[math]\displaystyle{ \begin{align} I(\beta\,) {}= -{\frac{\partial \ell}{\partial \mathbf {\beta\,} \partial \mathbf{\beta\,}^T}}&{} = \sum_{i=1}^n \left(\mathbf{x_i}\mathbf{x_i}^T (\frac{e^{\mathbf{\beta\,}^T \mathbf{x}}}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}})(\frac{1}{1+e^{\mathbf{\beta\,}^T \mathbf{x}}}) \right) \\[8pt] \end{align} }[/math]
We then use the following update formula to calcalute continually better estimates of the optimal [math]\displaystyle{ \beta\, }[/math]. It is not typically important what you use as your initial estimate [math]\displaystyle{ \beta\,^{(1)} }[/math] is.
[math]\displaystyle{ \beta\,^{(r+1)} {}= \beta\,^{(r)} + I^{-1}(\beta\,^{(r)} )S(\beta\,^{(r)} ) }[/math]
Matrix Notation
let [math]\displaystyle{ \mathbf{y} }[/math] be a (n x 1) vector of all class labels. This is called the response in other contexts.
let [math]\displaystyle{ \mathbb{X} }[/math] be a (n x (d+1)) matrix of all your features. Each row represents a data point. Each column represents a feature/covariate.
let [math]\displaystyle{ \mathbf{p}^{(r)} }[/math] be a (n x 1) vector with values [math]\displaystyle{ P(\mathbf{x_i} |\beta\,^{(r)} ) }[/math]
let [math]\displaystyle{ \mathbb{W}^{(r)} }[/math] be a (n x n) diagonal matrix with [math]\displaystyle{ \mathbb{W}_{ii}^{(r)} {}= P(\mathbf{x_i} |\beta\,^{(r)} )(1 - P(\mathbf{x_i} |\beta\,^{(r)} )) }[/math]
we can rewrite our score vector, information matrix & update equation in terms of this new matrix notation.
[math]\displaystyle{ \begin{align} S(\beta\,^{(r)}) {}= {\frac{\partial \ell}{ \partial \mathbf{\beta\,}}}&{} = \mathbb{X}^T(\mathbf{y} - \mathbf{p}^{(r)})\end{align} }[/math]
[math]\displaystyle{ \begin{align} I(\beta\,^{(r)}) {}= -{\frac{\partial \ell}{\partial \mathbf {\beta\,} \partial \mathbf{\beta\,}^T}}&{} = \mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X} \end{align} }[/math]
[math]\displaystyle{ \beta\,^{(r+1)} {}= \beta\,^{(r)} + I^{-1}(\beta\,^{(r)} )S(\beta\,^{(r)} ) {}= \beta\,^{(r)} + (\mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X})^{-1}\mathbb{X}^T(\mathbf{y} - \mathbf{p}^{(r)}) }[/math]
Iteratively Re-weighted Least Squares
If we reorganize this updating formula we can see it is really a iteratively solving a least squares problem each time with a new weighting.
[math]\displaystyle{ \beta\,^{(r+1)} {}= \beta\,^{(r)} + (\mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X})^{-1}(\mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X}\beta\,^{(r)} + \mathbb{X}^T(\mathbf{y} - \mathbf{p}^{(r)})) }[/math]
[math]\displaystyle{ \beta\,^{(r+1)} {}= \beta\,^{(r)} + (\mathbb{X}^T\mathbb{W}^{(r)}\mathbb{X})^{-1}\mathbb{X}^T\mathbb{W}^{(r)}\mathbf(z)^{(r)} }[/math]
where [math]\displaystyle{ \mathbf{z}^{(r)} = \mathbb{X}\beta\,^{(r)} + (\mathbb{W}^{(r)})^{-1}(\mathbf{y}-\mathbf{p}^{(r)}) }[/math]
Fisher Scoring Method
Fisher Scoring is a method very similiar to Newton-Raphson. It uses the expected Information Matrix as opposed to the observed information matrix. This distinction simplifies the problem and in perticular the computational complexity. To learn more about this method & logistic regression in general you can take Stat431/831 at the University of Waterloo.
Hidden Markov Models
In a Hidden Markov Model (HMM) is a graphical model with a directed graphical model with two layers of nodes. The hidden layer of nodes represents a set of unobserved discrete random variables with supports corresponding to some state space. You the first layer alone as a discrete time Markov Chain. These random variables are sequentially connected and which can often represent a temporal dependancy. In this model we do not observe the states (nodes in layer 1) we instead observe features that may be dependant on the states; this set of features represents the second observed layer of nodes. Thus for each node in layer 1 we have a corresponding dependant node in layer 2 which represents the observed features. Please see the Figure XX for a visual depiction of the graphical structure.
The nodes in the first and second layers are denoted by [math]\displaystyle{ {q_0, q_1, ... , q_T} }[/math] and [math]\displaystyle{ {y_0, y_1, ... , y_T} }[/math] respectively. The [math]\displaystyle{ y_i }[/math]s are shaded because they have been observed.
The parameters that need to be estimated are [math]\displaystyle{ \theta = (\pi, A, \eta) }[/math]. Where [math]\displaystyle{ \pi }[/math] represents the starting state for [math]\displaystyle{ q_0 }[/math]. In general [math]\displaystyle{ \pi_i }[/math] represents the state that [math]\displaystyle{ q_i }[/math] is in. The matrix [math]\displaystyle{ A }[/math] is the transition matrix for the states [math]\displaystyle{ q_t }[/math] and [math]\displaystyle{ q_{t+1} }[/math] and shows the probability of changing states as we move from one step to the next. Finally, [math]\displaystyle{ \eta }[/math] represents the parameter that decides the probability that [math]\displaystyle{ y_i }[/math] will produce [math]\displaystyle{ y^* }[/math] given that [math]\displaystyle{ q_i }[/math] is in state [math]\displaystyle{ q^* }[/math].
Defining some notation:
Note that we will be using a homogenous descrete time Markov Chain with finite state space for the first layer. [math]\displaystyle{ \ q_t^j = \begin{cases} 1 & \text{if } q_t = j \\ 0 & \text{otherwise } \end{cases} }[/math]
[math]\displaystyle{ \pi_i = P(q_0 = i) = P(q_0^i = 1) }[/math]
[math]\displaystyle{ a_{ij} = P(q_{t+1} = j | q_t = i) = P(q_{t+1}^j = 1 | q_t^i = 1) }[/math]
For the HMM our data comes from the output layer:
We can use [math]\displaystyle{ a_{ij} }[/math] to represent the i,j entry in the matrix A. We can then define:
We can also define:
Now, if we take Y to be multinomial we get:
where [math]\displaystyle{ n_{ij} = P(y_{t+1} = j | q_t = i) = P(y_{t+1}^j = 1 | q_t^i = 1) }[/math]
The random variable Y does not have to be multinomial, this is just an example.
We can write the joint pdf using the structure of the HMM model graphical structure.
Substituting our representations for the 3 probabilities:
We can go on to the E-Step with this new joint pdf. In the E-Step we need to find the expectation of the missing data given the observed data and the initial values of the parameters. Suppose that we only sample once so [math]\displaystyle{ n=1 }[/math]. Take the log of our pdf and we get:
Then we take the expectation for the E-Step:
If we continue with our multinomial example then we would get:
So now we need to calculate [math]\displaystyle{ E[q_0^i] }[/math] and [math]\displaystyle{ E[q_i^t q_j^{t+1}] }[/math] in order to find the expectation of the log likelihood. Let's define some variables to represent each of these quantities.
Let [math]\displaystyle{ \gamma_0^i = E[q_0^i] = P(q_0^i=1|y, \theta^{(t)}) }[/math].
Let [math]\displaystyle{ \xi_{t,t+1}^{ij} = E[q_i^t q_j^{t+1}] = P(q_t^iq_{t+1}^j|y, \theta^{(t)}) }[/math] .
We could use the sum product algorithm to calculate these equations but in this case we will introduce a new algorithm that is called the [math]\displaystyle{ \alpha }[/math] - [math]\displaystyle{ \beta }[/math] Algorithm.
The [math]\displaystyle{ \alpha }[/math] - [math]\displaystyle{ \beta }[/math] Algorithm
We have from before the expectation:
As usual we take the derivative with respect to [math]\displaystyle{ \theta }[/math] and then we set that equal to zero and solve. We obtain the following results (You can check these...) . Note that for [math]\displaystyle{ \eta }[/math] we are using a specific [math]\displaystyle{ y* }[/math] that is given.
For [math]\displaystyle{ \eta }[/math] we can think of this intuitively. It represents the proportion of times that state i prodices [math]\displaystyle{ y^* }[/math]. For example we can think of the multinomial case for y where:
Notice here that all of these parameters have been solved in terms of [math]\displaystyle{ \gamma_t^i }[/math] and [math]\displaystyle{ \xi_{t,t+1}^{ij} }[/math]. If we were to be able to calculate those two parameters then we could calculate everything in this model. This is where the [math]\displaystyle{ \alpha }[/math] - [math]\displaystyle{ \beta }[/math] Algorithm comes in.
Now due to the Markovian Memoryless property.
Define [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] as follows:
Once we have [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] then computing [math]\displaystyle{ P(y) }[/math] is easy.
To calculate [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] themselves we can use:
For [math]\displaystyle{ \alpha }[/math]:
Where we begin with:
Then for [math]\displaystyle{ \beta }[/math]:
Where we now begin from the other end:
Once both [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] have been calculated we can use them to find: