Don't Just Blame Over-parametrization: Difference between revisions
mNo edit summary |
|||
| (26 intermediate revisions by 2 users not shown) | |||
| Line 25: | Line 25: | ||
There is a typical question that why such over-confidence happens for vanilla trained models. One common understanding is that over-confidence is a result of over-parametrization, such as deep neural networks in (Mukhoti et al., 20'). However, so far it is unclear whether over-parametrization is the only reason, or whether there are other intrinsic reasons leading to over-confidence. In this paper, the conclusion is that over-confidence is not just a result of over-parametrization and is more inherent. | There is a typical question that why such over-confidence happens for vanilla trained models. One common understanding is that over-confidence is a result of over-parametrization, such as deep neural networks in (Mukhoti et al., 20'). However, so far it is unclear whether over-parametrization is the only reason, or whether there are other intrinsic reasons leading to over-confidence. In this paper, the conclusion is that over-confidence is not just a result of over-parametrization and is more inherent. | ||
== Model Architecture == | == Model Architecture == | ||
'''Data distribution''': Consider <math>\textbf{X} \sim N(0, I_d)</math> and <math>P(Y = 1|\textbf{X} = x) = \sigma(\textbf{w}_*^Tx)</math>, where <math>\textbf{w}_*\in \mathbb{R} </math> is the ground truth coefficient vector. | |||
'''Model''': with the above data input, minimize the binary cross-entropy loss : <center><math> | |||
\hat{\textbf{w}} = \text{argmin}_{\textbf{w}} L(\textbf{w}) = \frac{1}{n}\sum^n_{i=1}[log(1+exp(\textbf{w}^T\textbf{x}_i)) - y_i\textbf{w}^T\textbf{x}_i],</math></center> | |||
given that <math>\sigma(z) = \frac{1}{1+e^{-z}}</math>. | |||
"Logistic regression is well-specified when data comes from itself. With <math>\{y_i\}</math> generated from a logistic model with coefficient <math>\textbf{w}_*</math>, we always have <math>\text{argmin}_{\textbf{w}} L(\textbf{w}) = \textbf{w}_*</math>. (see [Hastie et al., '09]) | |||
== Experiments == | == Experiments == | ||
| Line 35: | Line 43: | ||
[[File:simulation.png|700px|thumb|center]] | [[File:simulation.png|700px|thumb|center]] | ||
The figure above shows four main results: First, the logistic regression is over-confident at all <math> | The figure above shows four main results: First, the logistic regression is over-confident at all <math>d/n</math>. Second, over-confidence is more severe when <math>d/n</math> increases, suggests the conclusion of the theory holds more broadly than its assumptions. Third, <math>\sigma_{underconf}</math> leads to under-confidence for <math>p \in (0.5, 0.51)</math>. Finally, theoretical prediction closely matches the simulation, further confirms the theory. | ||
The generality of the theory beyond the Gaussian input assumption and the binary classification setting was further tested using dataset CIFAR10 by running multi-class logistic regression on the first five classes on it. The author performed logistic regression on two kinds of labels: true label and pseudo-label generated from the multi-class logistic (softmax) model. | The generality of the theory beyond the Gaussian input assumption and the binary classification setting was further tested using dataset CIFAR10 by running multi-class logistic regression on the first five classes on it. The author performed logistic regression on two kinds of labels: true label and pseudo-label generated from the multi-class logistic (softmax) model. | ||
| Line 44: | Line 52: | ||
==Conclusion == | ==Conclusion == | ||
1. The well-specified logistic regression is inherently over-confident: Conditioned on the model predicting <math> p > 0.5</math>, the actual probability of the label being one is lower by an amount of <math> \Theta (d/n)</math>, in the limit of <math> n,d\to ∞</math> proportionally and <math> n/d </math> is large. In other words, the calibration error is always in the over-confident direction. Also, the overall Calibration Error (CE) of the logistic model is <math> \Theta (d/n)</math> in this limiting regime. | 1. '''The well-specified logistic regression is inherently over-confident''': | ||
Conditioned on the model predicting <math> p > 0.5</math>, the actual probability of the label being one is lower by an amount of <math> \Theta (d/n)</math>, in the limit of <math> n,d\to ∞</math> proportionally and <math> n/d </math> is large. In other words, the calibration error is always in the over-confident direction. Also, the overall Calibration Error (CE) of the logistic model is <math> \Theta (d/n)</math> in this limiting regime. | |||
2. The authors identify '''sufficient conditions for over-and under-confidence in general binary classification problems''', where the data is generated from an arbitrary nonlinear activation, and they solve a well-specified empirical risk minimization (ERM) problem with a suitable loss function. Their conditions imply that any symmetric, monotone activation <math> \sigma: R→[0,1]</math> that is concave at all <math> z >0 </math> will yield a classifier that is over-confident at any confidence level. | |||
3. Another perhaps surprising implication is that '''over-confidence is not universal''': | |||
They prove that there exists an activation function for which under-confidence can happen for a certain range of confidence levels. | |||
== Critiques == | == Critiques == | ||
This paper provides a precise theoretical study of the calibration error of logistic regression and a class of general binary classification problems. They show that logistic regression is inherently over-confident by <math> \Theta (d/n) </math> as <math>n /d </math> is large,and establish sufficient conditions for the over-or under-confidence of unregularized ERM for general binary classification. Their results reveal that | |||
(1) Over-confidence is not just a result of over-parametrization; | |||
(2) Over-confidence is a common mode but not universal. | |||
Their work opens up a number of future questions, such as the interplay between calibration and model training (or regularization), or theoretical studies of calibration on nonlinear models. | |||
==References== | ==References== | ||
* <sup>[https://ieeexplore.ieee.org/document/8683376 [1]]</sup>''A Large Scale Analysis of Logistic Regression: Asymptotic Performance and New Insights'', Xiaoyi Mai, Zhenyu Liao, R. Couillet. Published 1 May 2019. Computer Science, Mathematics. ICASSP 2019 - 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). | |||
Latest revision as of 19:11, 15 November 2021
Presented by
Jared Feng, Xipeng Huang, Mingwei Xu, Tingzhou Yu
Introduction
Don't Just Blame Over-parametrization for Over-confidence: Theoretical Analysis of Calibration in Binary Classification is a paper from ICML 2021 written by Yu Bai, Song Mei, Huan Wang, Caiming Xiong.
Machine learning models such as deep neural networks have high accuracy. However, the predicted top probability (confidence) does not reflect the actual accuracy of the model, which tends to be over-confident. For example, a WideResNet 32 on CIFAR100 has on average a predicted top probability of 87%, while the actual test accuracy is only 72% in (Guo et al., 17'). To address this issue, more and more researchers work on improving the calibration of models, which can reduce the over-confidence and preserve (or even improve) the accuracy in (Ovadia et al., 19').
Previous Work
1. Algorithms for model calibration
Practitioners have observed and dealt with the over-confidence of logistic regression long ago. Recalibration algorithms fix this by adjusting the output of a well-trained model and dates back to the classical methods of Platt scaling (Platt et al., 1999), histogram binning (Zadrozny & Elkan), and isotonic regression (Zadrozny & Elkan, 2002). Platt et al. (1999) also use a particular kind of label smoothing as a way of mitigating the over-confidence in logistic regression. Guo et al. (2017)show that temperature scaling, a simple method that learns a rescaling factor for the logits, is a competitive method for calibrating neural networks. A number of recent recalibration methods further improve the performances over these approaches (Kull et al., 2017; 2019; Ding et al., 2020;Rahimi et al., 2020; Zhang et al., 2020)
Another line of work improves calibration by aggregating the probabilistic predictions over multiple models, using either an ensemble of models (Lakshminarayanan et al.,2016; Malinin et al., 2019; Wen et al., 2020; Tran et al.,2020) or randomized predictions such as Bayesian neural networks (Gal & Ghahramani, 2016; Gal et al., 2017; Mad-dox et al., 2019; Dusenberry et al., 2020). Finally, there are techniques for improving the calibration of a single neural network during training (Thulasidasan et al., 2019; Mukhotiet al., 2020; Liu et al., 2020).
2. Theoretical analysis of calibration
Kumar et al. (2019) show that continuous rescaling methods such as temperature scaling is less calibrated than reported, and proposed a method that combines temperature scaling and histogram binning. Gupta et al. (2020) study the relationship between calibration and other notions of uncertainty such as confidence intervals. Shabat et al. (2020); Jung et al. (2020) study the sample complexity of estimating the multicalibration error (group calibration). A related theoretical result to ours is (Liu et al., 2019) which shows that the calibration error of any classifier is upper bounded by its square root excess logistic loss over the Bayes classifier. This result can be translated to a [math]\displaystyle{ O(\sqrt{d/n}) }[/math] upper bound for well-specified logistic regression, whereas our main result implies [math]\displaystyle{ \Theta(d/n) }[/math] calibration error in our high-dimensional limiting regime(with input distribution assumptions).
3. High-dimensional behaviors of empirical risk minimization
There is a rapidly growing literature on limiting characterizations of convex optimization-based estimators in the [math]\displaystyle{ n\propto d }[/math] regime (Donoho et al., 2009; Bayati & Montanari,2011; El Karoui et al., 2013; Karoui, 2013; Stojnic, 2013;Thrampoulidis et al., 2015; 2018; Mai et al., 2019; Sur &Cand`es, 2019; Cand`es et al., 2020). This paper analysis builds on the characterization for unregularized convex risk minimization problems (including logistic regression) derived in Sur& Cand`es (2019).
Motivation
There is a typical question that why such over-confidence happens for vanilla trained models. One common understanding is that over-confidence is a result of over-parametrization, such as deep neural networks in (Mukhoti et al., 20'). However, so far it is unclear whether over-parametrization is the only reason, or whether there are other intrinsic reasons leading to over-confidence. In this paper, the conclusion is that over-confidence is not just a result of over-parametrization and is more inherent.
Model Architecture
Data distribution: Consider [math]\displaystyle{ \textbf{X} \sim N(0, I_d) }[/math] and [math]\displaystyle{ P(Y = 1|\textbf{X} = x) = \sigma(\textbf{w}_*^Tx) }[/math], where [math]\displaystyle{ \textbf{w}_*\in \mathbb{R} }[/math] is the ground truth coefficient vector.
Model: with the above data input, minimize the binary cross-entropy loss :
given that [math]\displaystyle{ \sigma(z) = \frac{1}{1+e^{-z}} }[/math].
"Logistic regression is well-specified when data comes from itself. With [math]\displaystyle{ \{y_i\} }[/math] generated from a logistic model with coefficient [math]\displaystyle{ \textbf{w}_* }[/math], we always have [math]\displaystyle{ \text{argmin}_{\textbf{w}} L(\textbf{w}) = \textbf{w}_* }[/math]. (see [Hastie et al., '09])
Experiments
The authors conducted two experiments to test the theories: the first was based on simulation, and the second used the data CIFAR10.
There are two activations used in the simulation: well-specified under-parametrized logistic regression as well as general convex ERM with the under-confident activation [math]\displaystyle{ \sigma_{underconf} }[/math]. The “calibration curves” were plotted for both activations: the x-axis is p, the y-axis is the average probability given the prediction.
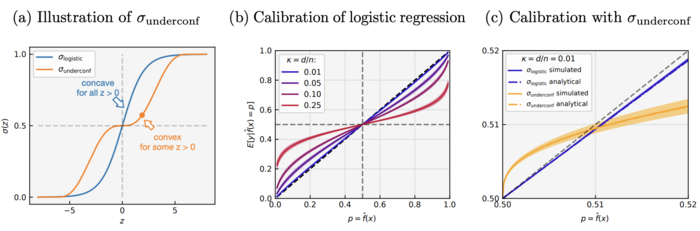
The figure above shows four main results: First, the logistic regression is over-confident at all [math]\displaystyle{ d/n }[/math]. Second, over-confidence is more severe when [math]\displaystyle{ d/n }[/math] increases, suggests the conclusion of the theory holds more broadly than its assumptions. Third, [math]\displaystyle{ \sigma_{underconf} }[/math] leads to under-confidence for [math]\displaystyle{ p \in (0.5, 0.51) }[/math]. Finally, theoretical prediction closely matches the simulation, further confirms the theory.
The generality of the theory beyond the Gaussian input assumption and the binary classification setting was further tested using dataset CIFAR10 by running multi-class logistic regression on the first five classes on it. The author performed logistic regression on two kinds of labels: true label and pseudo-label generated from the multi-class logistic (softmax) model.
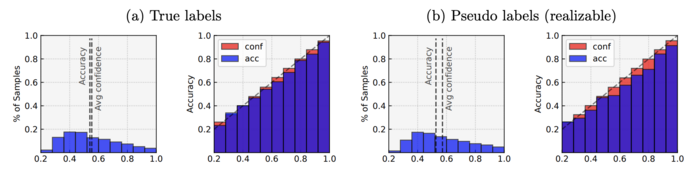
The figure above indicates that the logistic regression is over-confident on both labels, where the over-confidence is more severe on the pseudo-labels than the true labels. This suggests the result that logistic regression is inherently over-confident may hold more broadly for other under-parametrized problems without strong assumptions on the input distribution, or even when the labels are not necessarily realizable by the model.
Conclusion
1. The well-specified logistic regression is inherently over-confident:
Conditioned on the model predicting [math]\displaystyle{ p \gt 0.5 }[/math], the actual probability of the label being one is lower by an amount of [math]\displaystyle{ \Theta (d/n) }[/math], in the limit of [math]\displaystyle{ n,d\to ∞ }[/math] proportionally and [math]\displaystyle{ n/d }[/math] is large. In other words, the calibration error is always in the over-confident direction. Also, the overall Calibration Error (CE) of the logistic model is [math]\displaystyle{ \Theta (d/n) }[/math] in this limiting regime.
2. The authors identify sufficient conditions for over-and under-confidence in general binary classification problems, where the data is generated from an arbitrary nonlinear activation, and they solve a well-specified empirical risk minimization (ERM) problem with a suitable loss function. Their conditions imply that any symmetric, monotone activation [math]\displaystyle{ \sigma: R→[0,1] }[/math] that is concave at all [math]\displaystyle{ z \gt 0 }[/math] will yield a classifier that is over-confident at any confidence level.
3. Another perhaps surprising implication is that over-confidence is not universal:
They prove that there exists an activation function for which under-confidence can happen for a certain range of confidence levels.
Critiques
This paper provides a precise theoretical study of the calibration error of logistic regression and a class of general binary classification problems. They show that logistic regression is inherently over-confident by [math]\displaystyle{ \Theta (d/n) }[/math] as [math]\displaystyle{ n /d }[/math] is large,and establish sufficient conditions for the over-or under-confidence of unregularized ERM for general binary classification. Their results reveal that
(1) Over-confidence is not just a result of over-parametrization;
(2) Over-confidence is a common mode but not universal.
Their work opens up a number of future questions, such as the interplay between calibration and model training (or regularization), or theoretical studies of calibration on nonlinear models.
References
- [1]A Large Scale Analysis of Logistic Regression: Asymptotic Performance and New Insights, Xiaoyi Mai, Zhenyu Liao, R. Couillet. Published 1 May 2019. Computer Science, Mathematics. ICASSP 2019 - 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP).