Self-Supervised Learning of Pretext-Invariant Representations: Difference between revisions

From statwiki
Jump to navigation Jump to search
No edit summary
No edit summary
 
(120 intermediate revisions by 13 users not shown)
Line 1: Line 1:
==Authors==
Ishan Misra, Laurens van der Maaten


== Presented by ==  
== Presented by ==  
Line 5: Line 8:
== Introduction ==  
== Introduction ==  


Modern image recognition and object detection systems find image representations using a large number data using semantic annotation. Some examples of these annotations are class labels and bonding boxes as shown in Figure 1. For finding representations using semantic annotation there is need for large number of labeled data which is not the case in all scenarios. Also, representations usually learn features that are specific for a particular type of class and not semantically meaningful feature that can help to generalize to other domains and classes. '''In other words, pre-defined semantic annotations scale poorly to the long scale of visual concepts.''' Therefore, there has been a big interest in the community to find image representations that more visually meaningful and can help in several tasks such as image recognition and object detection. One of the fast growing areas of research that tries to address this problem is '''Self-Supervised Learning'''. Self-Supervised Learning tries to learn deep models that find image representations from the pixels themselves rather than using sematic annotated data. As we will show there is no need for using class labels or bounding boxes in self-supervised learning.  
Modern image recognition and object detection systems find image representations by using a large number of data points with pre-defined semantic annotations. Examples of these annotations include class labels [1] and bounding boxes [2], as shown in Figure 1. There is a need for a large amount of labeled data, which is often very difficult to obtain. Also, these systems usually learn specific features for a particular type of class and not necessarily semantically meaningful features that can help generalize to other domains and classes. In other words, '''pre-defined semantic annotations scale poorly to the long tail of visual concepts'''[3]. Therefore, there has been a big interest in the community for learning image representations that are more visually meaningful and can help in a variety of tasks, such as image recognition and object detection. One of the fast-growing areas of research that tries to address this problem is '''self-supervised Learning'''. Self-Supervised Learning tries to learn meaningful semantics by just using the inputs themselves rather than using pre-defined semantic annotated data. As will show, the self-supervised learning paradigm removes the need for using human-provided class labels or bounding boxes for classification and object detection tasks, respectively.
 
[[File: SSL_1.JPG | 800px | center]]
<div align="center">'''Figure 1:''' Semantic Annotations used for finding image representations: a) Class labels and b) Bounding Boxes </div>
 
Self-Supervised Learning is often done using a set of tasks called '''pretext tasks'''. During these tasks, a transformation  <math> \tau </math> is applied to unlabeled images <math> I </math> to obtain a set of transformed images, <math> I^{t} </math>. Then, a deep neural network, <math> \phi(\theta) </math>, is trained to predict some characteristic of the transformation from the transformed image. Several pretext tasks exist based on the type of transformation used. For example, if a neural network can accurately determine if an image is upside down or not, then perhaps it has learned some semantically meaningful representation of the image. This pre-empts the need for human-provided labels. Two of the most common pretext tasks used are rotations and jigsaw puzzle [4,5,6]. As shown in Figure 2, in the rotation task, unlabeled images, <math> </math> are rotated by random degrees (0,90,180,270) and the deep network learns to predict the rotation degree. The jigsaw task is more complicated than the rotation prediction task; first unlabeled images are cropped into 9 patches, then the image is perturbed by randomly permuting the nine patches. The unlabeled original image is referred to as the anchor data point (Figure 3-a), the reshuffled image that we get by permuting patches will be our positive sample (Figure 3-b) and the rest of the images in the dataset will be considered as negative samples. Each permutation falls into one of the 35 classes according to a formula given by the authors. A deep network is then trained to predict the class of the permutation of the patches in the perturbed image. Some other tasks include colorization, where the model tries to revert the colors of a colored image turned to grayscale, and image reconstruction where a square chunk of the image is deleted and the model tries to reconstruct that part.           
 
[[File: SSL_2.JPG |1000px | center]]
<div align="center">'''Figure 2:''' Self-Supervised Learning using Rotation and Jigsaw Pretext Tasks </div>
 
[[File:figure3.jpg |600px | center]]
<div align="center">'''Figure 3:''' Jigsaw puzzle used as a pretext task in unsupervised representation learning. (a) Original image (b) augmented image </div>
Although the proposed pretext tasks have achieved promising results, they have the disadvantage of being covariant to the applied transformation. In other words, as deep networks are trained to predict transformation characteristics, they will also learn representations that will vary based on the applied transformation. By intuition, we would like to obtain representations that are common between the original images and the transformed ones. This idea is supported by the fact that humans can recognize these transformed images. For example, a human can identify a permuted image of a tiger (as in figure 3) as a "permuted tiger" as well as the original image as a "tiger". Thus, the "tiger" aspect of the representations human learn is invariant to the transform, which cannot be taken for granted in standard self-supervision. The paper tries to address this problem by introducing '''Pretext Invariant Representation Learning''' (PIRL) that obtains representations which are transformation invariant and therefore more semantically meaningful. The performance of the proposed method is evaluated on several self-supervision learning benchmarks. The results show that the PIRL introduces a new state-of-the-art method in self-supervised Learning by learning transformation invariant representations.
 
== Problem Formulation and Methodology ==
 
[[File: SSL_3.JPG | 800px | center]]
<div align="center">'''Figure 3:''' Overview of Standard Pretext Learning and Pretext-Invariant Representation Learning (PIRL). </div>


Self-Supervised Learning is often done using a set of tasks called '''Pretext tasks'''. During these tasks a transformation is applied to unlabeled data, for example, the image is rotated by 90 degrees. Then, a deep neural network is trained to predict the transformation characteristic, in our case, the rotation degree.       


Big data and deep learning have been merged to create the great success of artificial intelligence which increases the burden on the network's speed, computational complexity, and storage in many applications. The image Classification task is one of the most important computer vision tasks which has shown a high dependency on Deep Neural Networks to improve their performance in many applications. Recently, they tend to use different image classification models on the cloud just to share the computational power between the different users as mentioned in this paper (e.g., SenseTime, Baidu Vision and Google Vision, etc.). Most of the researchers in the literature work to improve the structure and increase the depth of DNNs to achieve better performance from the point of how the features are represented and crafted using Conventional Neural Networks (CNNs). As the most well-known image classification datasets (e.g. ImageNet) are compressed using JPEG and this compression technique is optimized for Human Visual System (HVS) but not the machines (i.e. DNNs), so to be aligned with HVS the authors have to reconfigure the JPEG while maintaining the same classification accuracy.
An overview of the proposed method and a comparison with Pretext Tasks are shown in Figure 3. For a given image , <math>I</math>, in the dataset of unlabeled images, <math> D=\{{I_1,I_2,...,I_{|D|}}\} </math>, a transformation <math> \tau </math> is applied:


'''Why is image compression important?'''
\begin{align} \tag{1} \label{eqn:1}
I^t=\tau(I)
\end{align}


Image compression is crucial in deep learning because we want the image data to take up less disk space and can be loaded faster. Compared to the lossless compression PNG, which preserves the original image data, JPEG is a lossy form of compression meaning some information will be lost though for the benefit of an improved compression ratio. Therefore, it is important to develop deep learning model-based image compression methods which reduce data size without jeopardizing classification accuracy. Some examples of this type of image compression includes the LSTM-based approach proposed by Google [9], the transformation-based method from New York University [10], the autoencoder-based approach by Twitter [11], etc.
Where <math>I^t</math> is the transformed image. We would like to train a convolutional neural network, <math>\phi(\theta)</math>, that constructs image representations <math>v_{I}=\phi_{\theta}(I)</math>. Pretext Task based methods learn to predict transformation characteristics, <math>z(t)</math>, by minimizing a transformation covariant loss function in the form of:


== Methodology ==
\begin{align} \tag{2} \label{eqn:2}
l_{\text{cov}}(\theta,D)=\frac{1}{|D|} \sum_{I \in {D}}^{} L(v_I,z(t))
\end{align}


[[File: ada-fig2.PNG | 400px | center]]
As it can be seen, the loss function covaries with the applied transformation and therefore, the obtained representations may not be semantically meaningful. PIRL tries to solve for this problem as shown in Figure 3. The original and transformed images are passed through two parallel convolutional neural networks to obtain two sets of representations, <math>v(I)</math> and <math>v(I^t)</math>. Then, a contrastive loss function is defined to ensure that the representations of the original and transformed images are similar to each other. The transformation invariant loss function can be defined as:
<div align="center">'''Figure 1:''' Comparing to the conventional solution, the authors [1] solution can update the compression strategy based on the backend model feedback </div>


One of the major parameters that can be changed in the JPEG pipeline is the quantization table, which is the main source of artifacts added in the image to make it lossless compression as shown in [1, 4]. The authors got motivated to change the JPEG configuration to optimize the uploading rate of different cloud computer vision without considering pre-knowledge of the original model and dataset. In contrast to the authors in [2, 3, 5] where they adjust the JPEG configuration by retraining the parameters or according to the structure of the model. They considered the lack of undefined quantization level which decreases the image rate and quality but the deep learning model can still recognize it as shown in [4]. The authors in [1] used Deep Reinforcement learning (DRL) in an online manner to choose the quantization level to upload an image to the cloud for the computer vision model and this is the only approach to design an adaptive JPEG based on ''RL mechanism''.
\begin{align} \tag{3} \label{eqn:3}
l_{\text{inv}}(\theta,D)=\frac{1}{|D|} \sum_{I \in {D}}^{} L(v_I,v_{I^t})
\end{align}


The approach is designed based on an interactive training environment which represents any computer vision cloud services, then they needed a tool to evaluate and predict the performance of quantization level on an uploaded image, so they used a deep Q neural network agent. They feed the agent with a reward function which considers two optimization parameters, accuracy and image size. It works as iterative behavior interacting with the environment. The environment is exposed to different images with different virtual redundant information that needs an adaptive solution for each image to select the suitable compression level for the model. Thus, they designed an explore-exploit mechanism to train the agent on different scenery which is designed in deep Q agent as an inference-estimate-retain mechanism to restart the training procedure for each image. The authors verify their approach by providing some analysis and insight using Grad-Cam [8] by showing some patterns of how a compression level is chosen for each image with its own corresponding quality factor. Each image shows a different response when shown to a deep learning model. In general, images are more sensitive to compression if they have large smooth areas, while those with complex textures are more robust to compression.
Where L is a contrastive loss based on Noise Contrastive Estimators (NCE). The NCE function can be shown as below:   


'''What is a quantization table?'''
\begin{align} \tag{4} \label{eqn:4}
h(v_I,v_{I^t})=\frac{\exp \biggl( \frac{s(v_I,v_{I^t})}{\tau} \biggr)}{\exp \biggl(\frac{s(v_I,v_{I^t})}{\tau} \biggr) + \sum_{I^{'} \in D_N}^{} \exp \biggl( \frac{s(v_{I^t},v_{I^{'}})}{\tau} \biggr)}
\end{align}


Before getting to the quantization table first look at the basic architecture of JPEG's baseline system. This has 4 blocks, which are FDCT (Fast Discrete Cosine Transformation), quantizer, statistical model, and entropy encoder. The FCDT block takes an input image separated into <math> n \times n </math> blocks and applies a discrete cosine transformation creating DCT terms. These DCT terms are values from a relatively large discrete set that will be then mapped through the process of quantization to a smaller discrete set. This is accomplished with a quantization table at the quantizer block, which is designed to preserve low-frequency information at the cost of the high-frequency information. This preference for low frequency information is made because losing high frequency information isn't as impactful to the image when perceived by a humans visual system.
where <math>s(.,.)</math> is the cosine similarity function and <math>\tau</math> is the temperature parameter that is usually set to 0.07. Also, a set of N images are chosen randomly from the dataset where <math>I^{'}\neq I</math>. These images are used in the loss in order to ensure their representation dissimilarity with transformed image representations. Also, during model implementation, two heads (few additional deep layers), <math>f</math> and <math>g</math>, are applied on top of <math>v(I)</math> and <math>v(I^t)</math>. Using the NCE formulation, the contrastive loss can be written as:


== Problem Formulation  ==
\begin{align} \tag{5} \label{eqn:5}
L_{\text{NCE}}(I,I^{t})=-\text{log}[h(f(v_I),g(v_{I^t}))]-\sum_{I^{'}\in D_N}^{} \text{log}[1-h(g(v_{I^t}),f(v_{I^{'}}))]
\end{align}


The authors formulate the problem by referring to the cloud deep learning service as <math> \vec{y}_i = M(x_i)</math> to predict results list <math> \vec{y}_i </math> for an input image <math> x_i </math>, and for reference input  <math> x \in X_{\rm ref} </math> the output is <math> \vec{y}_{\rm ref} = M(x_{\rm ref}) </math>. It is referred <math> \vec{y}_{\rm ref} </math> as the ground truth label and also <math> \vec{y}_c = M(x_c) </math> for compressed image <math> x_{c} </math> with quality factor <math> c </math>.
[[File: SSL_4.JPG | 800px | center]]
<div align="center">'''Figure 4:''' Proposed PIRL </div>


Although the formulation looks complicated, the take-away here is that by minimizing the NCE based loss function, the similarity between the original and transformed image representations, <math>v(I)</math> and <math>v(I^t)</math>, increases and at the same time the dissimilarity between <math>v(I^t)</math> and negative images representations, <math>v(I^{'})</math>, is increased. According to the previous work, an infeasibly large batch size is needed to obtain a large number of negatives. To tackle this problem, a memory bank [9], <math>M</math>, is used during training which contains feature representation <math>m_I</math> for each image in the dataset including the negative images. The proposed PIRL model is shown in Figure 4. Finally, the contrastive loss in equation \eqref{eqn:5} does not take into account the dissimilarity between the original image representations, <math>v(I)</math>, and the negative image representations, <math>v(I^{'})</math>. By taking this into account and using the memory bank, the final contrastive loss function is obtained as:


\begin{align} \tag{1} \label{eq:accuracy}
\begin{align} \tag{6} \label{eqn:6}
\mathcal{A} =& \sum_{k}\min_jd(l_j, g_k) \\
L(I,I^{t})=\lambda L_{\text{NCE}}(m_I,g(v_{I^t})) + (1-\lambda)L_{\text{NCE}}(m_I,f(v_{I}))
& l_j \in \vec{y}_c, \quad j=1,...,5 \nonumber \\
& g_k \in \vec{y}_{\rm ref}, \quad k=1, ..., {\rm length}(\vec{y}_{\rm ref}) \nonumber \\
& d(x, y) = 1 \ \text{if} \ x=y  \ \text{else} \ 0 \nonumber
\end{align}
\end{align}
where <math>\lambda</math> is a hyperparameter that determines the weight of each of NCE losses. The default value for this parameter is 0.5. In the next section, experimental results are shown using the proposed PIRL model.


The authors divided the used datasets according to their contextual group <math> X </math> according to [6] and they compare their results using compression ratio <math> \Delta s = \frac{s_c}{s_{\rm ref}} </math>, where <math>s_{c}</math> is the compressed size and <math>s_{\rm ref}</math> is the original size, and accuracy metric <math> \mathcal{A}_c </math> which is calculated based on the hamming distance of Top-5 of the output of softmax probabilities for both original and compressed images as shown in Eq. \eqref{eq:accuracy}. In the RL designing stage, continuous numerical vectors are represented as the input features to the DRL agent which is Deep Q Network (DQN). The challenges of using this approach are:
==Experimental Results ==
(1) The state space of RL is too large to cover, so the neural network is typically constructed with more layers and nodes, which makes the DRL agent hard to converge and the training time-consuming;
(2) The DRL always starts with a random initial state, but it needs to find a higher reward before starting the training of the DQN. However, the sparse reward feedback resulted from a random initialization makes learning difficult.
The authors solve this problem by using a pre-trained small model called MobileNetV2 as a feature extractor <math> \mathcal{E} </math>  for its ability in lightweight and image classification, and it is fixed during training the  Q Network <math> \phi </math>. The last convolution layer of <math> \mathcal{E} </math> is connected as an input to the Q Network <math>\phi </math>, so by optimizing the parameters of Q network <math> \phi </math>, the RL agent's policy is updated.


==Reinforcement learning framework==
For the experiments in this section, PIRL is implemented using jigsaw transformations. The combination of PIRL with other types of transformations is shown in the last section of the summary. The quality of image representations obtained from PIRL Self-Supervised Learning is evaluated by comparing its performance to other Self-Supervised Learning methods on image recognition and object detection tasks. For the experiments, a ResNet50 model is trained using PIRL and other methods by using 1.28M randomly sampled images from the ImageNet dataset. Also, the number of negative images used for PIRL is N=32000.


This paper [1] described the reinforcement learning problem as <math> \{\mathcal{X}, M\} </math> to be ''emulator environment'', where <math> \mathcal{X} </math> is defining the contextual information created as an input from the user <math> x </math> and <math> M </math> is the backend cloud model. Each RL frame must be defined by ''action and state'', the action is known by 10 discrete quality levels ranging from 5 to 95 by step size of 10 and the state is feature extractor's output <math> \mathcal{E}(J(\mathcal{X}, c)) </math>, where <math> J(\cdot) </math> is the JPEG output at specific quantization level <math> c </math>. They found the optimal quantization level at time <math> t </math> is  <math> c_t = {\rm argmax}_cQ(\phi(\mathcal{E}(f_t)), c; \theta) </math>, where <math> Q(\phi(\mathcal{E}(f_t)), c; \theta) </math> is  action-value function, <math> \theta </math> indicates the parameters of Q network <math> \phi </math>. In the training stage of RL, the goal is to minimize a loss function <math> L_i(\theta_i) = \mathbb{E}_{s, c \sim \rho (\cdot)}\Big[\big(y_i - Q(s, c; \theta_i)\big)^2 \Big] </math> that changes at each iteration <math> i </math> where <math> s = \mathcal{E}(f_t) </math> and <math>f_t</math> is the output of the JPEG, and <math> y_i = \mathbb{E}_{s' \sim \{\mathcal{X}, M\}} \big[ r + \gamma \max_{c'} Q(s', c'; \theta_{i-1}) \mid s, c \big] </math> is the target that has a probability distribution <math> \rho(s, c) </math> over sequences <math> s </math> and quality level <math> c </math> at iteration <math> i </math>, and <math> r </math> is the feedback reward.
===Object Detection===


The framework get more accurate estimation from a selected action when the distance of the target and the action-value function's output <math> Q(\cdot)</math> is minimized. As a results, no feedback signal can tell that an episode has finished a condition value <math>T</math> that satisfies <math> t \geq T_{\rm start} </math> to guarantee to store enough transitions in the memory buffer <math> D </math> to train on. To create this transitions for the RL agent, random trials are collected to observe environment reaction. After fetching some trials from the environment with their corresponding rewards, this randomness is decreased as the agent is trained to minimize the loss function <math> L </math> as shown in the Algorithm below. Thus, it optimizes its actions on a minibatch from <math> \mathcal{D} </math> to be based on historical optimal experience to train the compression level predictor <math> \phi </math>. When this trained predictor <math> \phi </math> is deployed, the RL agent will drive the compression engine with the adaptive quality factor <math> c </math> corresponding to the input image <math> x_{i} </math>.  
A Faster R-CNN model with a ResNet-50 backbone, pre-trained using PIRL and other Self-Supervised methods, is employed for the object detection task. Then, the pre-trained model weights are used as initial weights for the Faster-RCNN model backbone during training on the VOC07+12 dataset. The result of object detection using PIRL is shown in Figure (5) and it is compared to other methods. It can be seen that PIRL not only outperforms other Self-Supervised-based methods, '''for the first time it outperforms Supervised Pre-training on object detection'''. They emphasize that PIRL achieves this result using the same backbone model, the same number of finetuning epochs, and the exact same pre-training data (but without the labels). This result is a substantial improvement over prior self-supervised approaches that obtain worse performance than fully supervised baselines despite using orders of magnitude more curated training data or much larger backbone models.  


The interaction between the agent and environment <math> \{\mathcal{X}, M\} </math> is evaluated using the reward function, which is formulated, by selecting an appropriate action of quality factor <math> c </math>, to be directly proportional to the accuracy metric <math> \mathcal{A}_c </math>, and inversely proportional to the compression rate <math> \Delta s = \frac{s_c}{s_{\rm ref}} </math>. As a result, the reward function is given by <math> R(\Delta s, \mathcal{A}) = \alpha \mathcal{A} - \Delta s + \beta</math>, where <math> \alpha </math> and <math> \beta </math> to form a linear combination.
[[File: SSL_5.PNG | 800px | center]]
<div align="center">'''Figure 5:''' Object detection on VOC07+12 using Faster R-CNN and comparing the Average Precision (AP) of detected bounding boxes. (The values for the blank spaces are not mentioned in the corresponding paper.) </div>


[[File:Alg2.PNG|500px|center|fig: running-retrain]]
===Image Classification with linear models===
<div align="center">'''Algroithim :''' Training RL agent <math> \phi </math> in environment <math> \{\mathcal{X}, M\} </math> </div>


== Inference-Estimate-Retrain Mechanism ==
In the next experiment, the performance of the PIRL is evaluated on image classification using four different datasets. For this experiment, the pre-trained ResNet-50 model is utilized as an image feature extractor. Then, a linear classifier is trained on fixed image representations. The results are shown in Figure (6). The results demonstrate that while PIRL substantially outperforms other Self-Supervised Learning methods, it still falls behind Supervised Pre-trained Learning.      
The system diagram, AdaCompress,  is shown in figure 3 in contrast to the existing modules. When the AdaCompress is deployed, the input images scenery context <math> \mathcal{X} </math> may change, in this case the RL agent’s compression selection strategy may cause the overall accuracy to decrease. So, in order to solve this issue, the estimator will be invoked with probability <math>p_{\rm est} </math>. This will be done by generating a random value <math>  \xi  \in (0,1) </math> and the estimator will be invoked if <math>\xi \leq p_{\rm est}</math>. Then AdaCompress will upload both the original image and the compressed image to fetch their labels. The accuracy will then be calculated and the transition, which also includes the accuracy in this step, will be stored in the memory buffer. Comparing recent  the n steps' average accuracy with earliest average accuracy, the estimator will then invoke the RL training kernel to retrain if the recent average accuracy is much lower than the initial average accuracy.


[[File: diagfig.png|500px|center]]
[[File: SSL_6.PNG | 800px | center]]
<div align="center">'''Figure 6:''' Image classification with linear models. (The values for the blank spaces are not mentioned in the corresponding paper.) </div>


The authors solved the change in the scenery at the inference phase that might cause learning to diverge by introducing '''running-estimate-retain mechanism'''. They introduced estimator with probability <math> p_{\rm est} </math> that changes in an adaptive way and it is compared a generated random value <math> \xi \in (0,1) </math>. As shown in Figure 2, Adacompression is switching between three states in an adaptive way as will be shown in the following sections.
Overall, from Figure6, we can observe that PIRL has the best performance among different Self-Supervised Learning methods. Moreover, PIRL can even perform better than the Supervised Learning Pretrained model on object detection. This is because PIRL learns representations that are invariant to the applied transformations which results in more semantically meaningful and richer visual features. In the next section, some analysis on PIRL is presented.


[[File:fig3.PNG|500px|center|fig: running-retrain]]
==Analysis==
<div align="center">'''Figure 2:''' State Switching Policy </div>


=== Inference State ===
===Does PIRL learn invariant representations?===
The '''inference state''' is running most of the time at which the deployed RL agent is trained and used to predict the compression level <math> c </math> to be uploaded to the cloud with minimum uploading traffic load. The agent will eventually switch to the estimator stage with probability <math> p_{\rm est} </math> so it will be robust to any change in the scenery to have a stable accuracy. The <math> p_{\rm est} </math> is fixed at the inference stage but changes in an adaptive way as a function of accuracy gradient in the next stage. In '''estimator state''', there will be a trade off between the objective of reducing upload traffic and the risk of changing the scenery, an accuracy-aware dynamic <math> p'_{\rm est} </math> is designed to calculate the average accuracy <math> \mathcal{A}_n </math> after running for defined <math> N </math> steps according to Eq. \ref{eqn:accuracy_n}.
 
\begin{align} \tag{2} \label{eqn:accuracy_n}
In order to show that the image representations obtained using PIRL are invariant, several images are chosen from the ImageNet dataset, and representations of the chosen images and their transformed version are obtained using one-time PIRL and another time the jigsaw pretext task which is the transformation covariant version of PIRL. Then, for each method, the L2 norm between the original and transformed image representations are computed and their distributions are plotted in Figure (7). It can be seen that PIRL results in more similarity between the original and transformed image representations. Therefore, PIRL learns invariant representations.   
\bar{\mathcal{A}_n} &=
\begin{cases}
\frac{1}{n}\sum_{i=N-n}^{N} \mathcal{A}_i & \text{ if } N \geq n \\
\frac{1}{n}\sum_{i=1}^{n} \mathcal{A}_i & \text{ if } N < n
\end{cases}
\end{align}
===Estimator State===
The '''estimator state''' is executed when <math> \xi \leq p_{\rm est} </math> is satisfied , where the uploaded traffic is increased as the both the reference image <math> x_{ref} </math> and compressed image <math> x_{i} </math> are uploaded to the cloud to calculate <math> \mathcal{A}_i </math> based on <math> \vec{y}_{\rm ref} </math> and <math> \vec{y}_i </math>. It will be stored in the memory buffer <math> \mathcal{D} </math> as a transition <math> (\phi_i, c_i, r_i, \mathcal{A}_i) </math> of trial <math>i</math>. The estimator will not be anymore suitable for the latest <math>n</math> step when the average accuracy <math> \bar{\mathcal{A}}_n </math> is lower than the earliest <math>n</math> steps of the average <math> \mathcal{A}_0 </math> in the memory buffer <math> \mathcal{D} </math>. Consequently, <math> p_{\rm est} </math> should be changed to higher value to make the estimate stage frequently happened.It is obviously should be a function in the gradient of the average accuracy <math> \bar{\mathcal{A}}_n </math> in such a way to fell the buffer memory <math> \mathcal{D} </math> with some transitions to retrain the agent at a lower average accuracy <math> \bar{\mathcal{A}}_n </math>. The authors formulate <math> p'_{\rm est} = p_{\rm est} + \omega \nabla \bar{\mathcal{A}} </math> and <math> \omega </math> is a scaling factor. Initially the estimated probability <math> p_0 </math> will be a function of <math> p_{\rm est} </math>  in the general form of <math>p_{\rm est} = p_0 + \omega \sum_{i=0}^{N} \nabla \bar{\mathcal{A}_i} </math>.


===Retrain State===
[[File: SSL_7.PNG | 800px | center]]
In '''retrain state''', the RL agent is trained to adapt on the change of the input scenery on the stored transitions in the buffer memory <math> \mathcal{D} </math>. The retain stage is finished at the recent <math> n </math> steps when the average reward <math> \bar{r}_n </math> is higher than a defined <math> r_{th}</math> by the user. Afterward, a new retraining stage should be prepared by saving new next transitions after flushing the old buffer memory <math> \mathcal{D}</math>. The authors supported their compression choice for different cloud application environments by providing some insights by introducing a visualization algorithm [8] to some images with their corresponding quality factor <math> c </math>. The visualization shows that the agent chooses a certain quantization level <math> c </math> based on the visual textures in the image at the different regions. For an instant, a low-quality factor is selected for the rough central region so there is a smooth area surrounded it but for the surrounding smooth region, the agent chooses a relatively higher quality rather than the central region.
<div align="center">'''Figure 7:''' Invariance of PIRL representations. </div>


===Which layer produces the best representation?===
Figure 12 studies the quality of representations in earlier layers of the convolutional networks. The figure reveals that the quality of Jigsaw representations improves from the conv1 to the res4 layer but that their quality sharply decreases in the res5 layer. By contrast, PIRL representations are invariant to image transformations and the best image representations are extracted from the res5 layer of PIRL-trained networks.


[[File: Paper29_SSL.PNG | 800px | center]]
<div align="center">'''Figure 12:'''Quality of PIRL representations per layer. </div>


==Insight of RL agent’s behavior==
===What is the effect of <math>\lambda</math> in the PIRL loss function?===
In the inference state, the  RL agent predicts a proper compression level based on the features of the input image. In the next subsection, we will see that this compression level varies for different image sets and backend cloud services. Also, by taking a look at the attention maps for some of the images, we will figure out why the agent has chosen this compression level.
===Compression level choice variation===
In Figure 5, for Face++ and Amazon Rekognition, the agent’s choices are mostly around compression level = 15, but for Baidu Vision, the agent’s choices are distributed more evenly. Therefore, the backend strategy really affects the choice for the optimal compression level.


[[File:comp-level1.PNG|500px|center|fig: running-retrain]]
In order to investigate the effect of <math>\lambda</math> on PIRL representations, the authors obtained the accuracy of image recognition on ImageNet dataset using different values for <math>\lambda</math> in PIRL. As shown in Figure 8, the results show that the value of <math>\lambda</math> affects the performance of PIRL and the optimum value for <math>\lambda</math> is 0.5.
In figure 6, we will see how the agent's behaviour in selecting the optimal compression level changes for different datasets. The two datasets, ImageNet and DNIM present different contextual sceneries. The images mostly taken at daytime were randomly selected from ImageNet and the images mostly taken at the night time were selected from DNIM. The figure 6 shows that for DNiM images, the agent's choices are mostly concentrated in relatively high compression levels, whereas for ImageNet dataset, the agent's choices are distributed more evenly.  


[[File:comp-level2.PNG|500px|center|fig: running-retrain]]
[[File: SSL_8.PNG | 800px | center]]
<div align="center">'''Figure 8:''' Effect of varying the parameter <math>\lambda</math> </div>


===What is the effect of the number of images transforms?===


As another experiment, the authors investigated the number of image transforms and their effect on PIRL performance. There is a limitation on the number of transformations that can be applied using the jigsaw pretext method as this method has to predict the permutation of the patches and the number of the parameters in the classification layer grows linearly with the number of used transformations. However, PIRL can use all number of image transformations which is equal to <math>9! \approx 3.6\times 10^5</math>. Figure (9) shows the effect of changing the number of patch permutations on PIRL and jigsaw. The results show that increasing the number of permutations increases the mean Average Precision (mAP) of PIRL on image classification using the VOCC07 dataset.   


[[File: SSL_9.PNG | 800px | center]]
<div align="center">'''Figure 9:''' Effect of varying the number of patch permutations </div>


===What is the effect of the number of negative samples?===


In order to investigate the effect of negative samples number, N, on PIRL's performance, the image classification accuracy is obtained using ImageNet dataset for a variety of values for N. As it is shown in Figure 10, increasing the number of negative sample results in richer image representations and higher classification accuracy.   


== Results ==
[[File: SSL_10.PNG | 800px | center]]
The authors reported in Figure 3, 3 different cloud services compared to the benchmark images. It is shown that more than the half of the upload size while roughly preserving the top-5 accuracy calculated by using A with an average of 7% proving the efficiency of the design. In Figure 4, it shows the ''' inference-estimate-retain ''' mechanism as the x-axis indicates steps, while <math> \Delta </math> mark on <math>x</math>-axis is reveal as a change in the scenery. In Figure 4, the estimating probability <math> p_{\rm est} </math> and the accuracy are inversely proportion as the accuracy drops below the initial value the <math> p_{\rm est} </math> increase adaptive as it considers the accuracy metric <math> \mathcal{A}_c </math> each action <math> c </math> making the average accuracy to decrease in the next estimations. At the red vertical line, the scenery started to change and  <math>Q</math> Network start to retrain to adapt the the agent on the current scenery. At retrain stage, the output result is always use from the reference image's prediction label <math> \vec{y}_{\rm ref} </math>.
<div align="center">'''Figure 10:''' Effect of varying the number of negative samples </div>
Also, they plotted the scaled uploading data size of the proposed algorithm and the overhead data size for the benchmark is shown in the inference stage. After the average accuracy became stable and high, the transmission is reduced by decreasing the <math> p_{\rm est} </math> value. As a result,  <math> p_{\rm est} </math> and <math> \mathcal{A} </math>  will be always equal to 1. During this stage, the uploaded file is more than the conventional benchmark. In the inference stage, the uploaded size is halved as shown in both Figures 3, 4.


[[File:ada-fig9.PNG|500px|center|fig: running-retrain]]
==Generalizing PIRL to Other Pretext Tasks==
<div align="center">'''Figure 3:''' Different cloud services compared relative to average size and accuracy </div>


The used PIRL model in this paper used jigsaw permutations as the applied transformation to the original image. However, PIRL is generalizable to other Pretext Tasks. To show this, first, PIRL is used with rotation transformations and the performance of rotation-based PIRL is compared to the covariant rotation Pretext Task. The results in Figure (11) show that using PIRL substantially increases the classification accuracy on four datasets in comparison with the rotation Pretext Task. Next, both jigsaw and rotation transformations are used with PIRL to obtain image representations. The results show that combining multiple transformations with PIRL can further improve the accuracy of the image classification task.   


[[File:ada-fig10.PNG|500px|center|fig: running-retrain]]
[[File: SSL_11.PNG | 800px | center]]
<div align="center">'''Figure 4:''' Scenery change response from AdaCompress Algorithm </div>
<div align="center">'''Figure 11:''' Using PIRL with (combinations of) different pretext tasks </div>


==Conclusion==
==Conclusion==


Most of the research focused on modifying the deep learning model instead of dealing with the currently available approaches. The authors succeed in defining the compression level for each uploaded image to decrease the size and maintain the top-5 accuracy in a robust manner even the scenery is changed.
In this paper, a new state-of-the-art Self-Supervised learning method, PIRL, was presented. The proposed model learns to obtain features that are common between the original and transformed images, resulting in a set of transformation invariant and more semantically meaningful features. This is done by defining a contrastive loss function between the original images, transformed images, and a set of negative images. The results show that PIRL image representation is richer than previously proposed methods, resulting in higher accuracy and precision on image classification and object detection tasks.
In my opinion, Eq. \eqref{eq:accuracy} is not defined well as I found it does not really affect the reward function. Also, they did not use the whole validation set from ImageNet which raises the question of what is the higher file size that they considered from in the mention current set. In addition, if they considered the whole data set, should we expect the same performance for the mechanism.
 
==Critiques==


== Critiques ==
The paper proposes a very nice method for obtaining transformation invariant image representations. However, the authors can extend their work with a richer set of transformations. Also, it would be a good idea to investigate the combination of PIRL with clustering-based methods [7,8]. One of the clustering-based methods is '''DeepCluster''' [7], where each previous version of its representation is used by bootstrapping to produce a target for the next representation.  They built a new representation through clustering data points using the prior representation and then classify the target by using the clustered index of each sample. That may result in better image representations. This will avoid the use of negative pairs but it might also cause collapsing to trivial solutions which create a trade-off.


The authors used a pre-trained model as a feature extractor to select a Quality Factor (QF) for the JPEG. I think what would be missing that they did not report the distribution of each of their span of QFs as it is important to understand which one is expected to contribute more. In my video, I have done one experiment using Inception-V3 to understand if it is possible to get better accuracy. I found that it is possible by using the inception model as a pre-trained model to choose a lower QF, but as well known that the mobile models are shallower than the inception models which make it less complex to run on edge devices. I think it is possible to achieve at least the same accuracy or even more if we replaced the mobile model with the inception. Another point, the authors did not run their approach on a complete database like ImageNet, they only included a part of two different datasets. I know they might have limitations in the available datasets to test like CIFARs, as they are not totally comparable from the resolution perspective for the real online computer vision services work with higher resolutions.
It could be better if they could visualize their network weights and compare them to the other supervised methods for the deeper layers that extract high-level information.


== Source Code ==
== Source Code ==
https://paperswithcode.com/paper/self-supervised-learning-of-pretext-invariant


== References ==
== References ==


[1]
[1] Olga Russakovsky, Jia Deng, Hao Su, Jonathan Krause, Sanjeev Satheesh, Sean Ma, Zhiheng Huang, Andrej Karpathy, Aditya Khosla, Michael Bernstein, Alexander C. Berg, and Li Fei-Fei. ImageNet Large Scale Visual Recognition Challenge. IJCV, 2015.
 
[2] M. Everingham, S. M. A. Eslami, L. Van Gool, C. K. I. Williams, J. Winn, and A. Zisserman. The pascal visual object classes challenge: A retrospective. IJCV, 2015.
 
[3] Grant Van Horn and Pietro Perona. The devil is in the tails: Fine-grained classification in the wild. arXiv preprint, 2017
 
[4] Spyros Gidaris, Praveer Singh, and Nikos Komodakis. Unsupervised representation learning by predicting image rotations. arXiv preprint arXiv:1803.07728, 2018.
 
[5] Mehdi Noroozi and Paolo Favaro. Unsupervised learning of visual representations by solving jigsaw puzzles. In ECCV, 2016.
[6] Jong-Chyi Su, Subhransu Maji, Bharath Hariharan. When does self-supervision improve few-shot learning? European Conference on Computer Vision, 2020.
 
[7] Mathilde Caron, Piotr Bojanowski, Armand Joulin, and Matthijs Douze. Deep clustering for unsupervised learning of visual features. In ECCV, 2018.
 
[8] Mathilde Caron, Piotr Bojanowski, Julien Mairal, and Armand Joulin. Unsupervised pre-training of image features on non-curated data. In ICCV, 2019.
 
[9] Zhirong Wu, Yuanjun Xiong, Stella X Yu, and Dahua Lin. Unsupervised feature learning via non-parametric instance discrimination. In CVPR, 2018.

Latest revision as of 22:02, 12 December 2020

Authors

Ishan Misra, Laurens van der Maaten

Presented by

Sina Farsangi

Introduction

Modern image recognition and object detection systems find image representations by using a large number of data points with pre-defined semantic annotations. Examples of these annotations include class labels [1] and bounding boxes [2], as shown in Figure 1. There is a need for a large amount of labeled data, which is often very difficult to obtain. Also, these systems usually learn specific features for a particular type of class and not necessarily semantically meaningful features that can help generalize to other domains and classes. In other words, pre-defined semantic annotations scale poorly to the long tail of visual concepts[3]. Therefore, there has been a big interest in the community for learning image representations that are more visually meaningful and can help in a variety of tasks, such as image recognition and object detection. One of the fast-growing areas of research that tries to address this problem is self-supervised Learning. Self-Supervised Learning tries to learn meaningful semantics by just using the inputs themselves rather than using pre-defined semantic annotated data. As will show, the self-supervised learning paradigm removes the need for using human-provided class labels or bounding boxes for classification and object detection tasks, respectively.

Figure 1: Semantic Annotations used for finding image representations: a) Class labels and b) Bounding Boxes

Self-Supervised Learning is often done using a set of tasks called pretext tasks. During these tasks, a transformation [math]\displaystyle{ \tau }[/math] is applied to unlabeled images [math]\displaystyle{ I }[/math] to obtain a set of transformed images, [math]\displaystyle{ I^{t} }[/math]. Then, a deep neural network, [math]\displaystyle{ \phi(\theta) }[/math], is trained to predict some characteristic of the transformation from the transformed image. Several pretext tasks exist based on the type of transformation used. For example, if a neural network can accurately determine if an image is upside down or not, then perhaps it has learned some semantically meaningful representation of the image. This pre-empts the need for human-provided labels. Two of the most common pretext tasks used are rotations and jigsaw puzzle [4,5,6]. As shown in Figure 2, in the rotation task, unlabeled images, [math]\displaystyle{ }[/math] are rotated by random degrees (0,90,180,270) and the deep network learns to predict the rotation degree. The jigsaw task is more complicated than the rotation prediction task; first unlabeled images are cropped into 9 patches, then the image is perturbed by randomly permuting the nine patches. The unlabeled original image is referred to as the anchor data point (Figure 3-a), the reshuffled image that we get by permuting patches will be our positive sample (Figure 3-b) and the rest of the images in the dataset will be considered as negative samples. Each permutation falls into one of the 35 classes according to a formula given by the authors. A deep network is then trained to predict the class of the permutation of the patches in the perturbed image. Some other tasks include colorization, where the model tries to revert the colors of a colored image turned to grayscale, and image reconstruction where a square chunk of the image is deleted and the model tries to reconstruct that part.

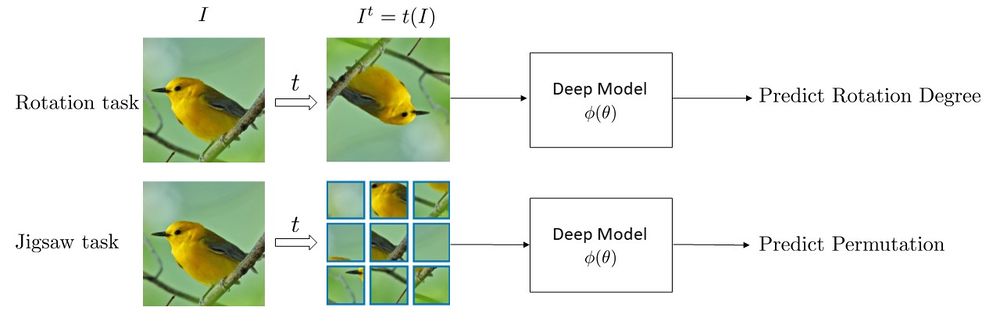
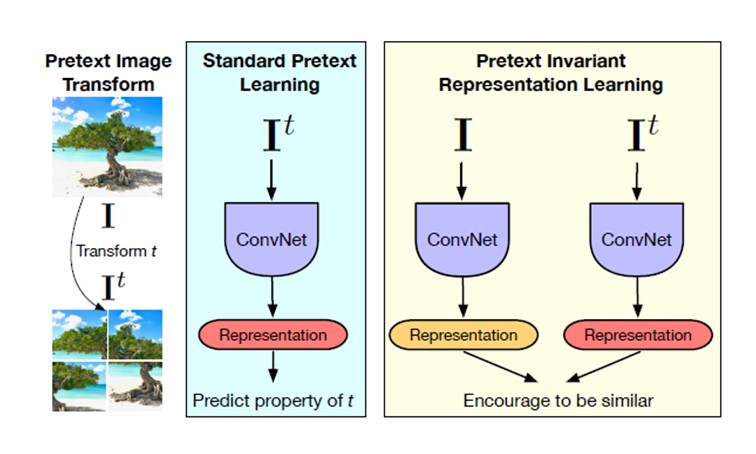
Figure 2: Self-Supervised Learning using Rotation and Jigsaw Pretext Tasks
Figure 3: Jigsaw puzzle used as a pretext task in unsupervised representation learning. (a) Original image (b) augmented image

Although the proposed pretext tasks have achieved promising results, they have the disadvantage of being covariant to the applied transformation. In other words, as deep networks are trained to predict transformation characteristics, they will also learn representations that will vary based on the applied transformation. By intuition, we would like to obtain representations that are common between the original images and the transformed ones. This idea is supported by the fact that humans can recognize these transformed images. For example, a human can identify a permuted image of a tiger (as in figure 3) as a "permuted tiger" as well as the original image as a "tiger". Thus, the "tiger" aspect of the representations human learn is invariant to the transform, which cannot be taken for granted in standard self-supervision. The paper tries to address this problem by introducing Pretext Invariant Representation Learning (PIRL) that obtains representations which are transformation invariant and therefore more semantically meaningful. The performance of the proposed method is evaluated on several self-supervision learning benchmarks. The results show that the PIRL introduces a new state-of-the-art method in self-supervised Learning by learning transformation invariant representations.

Problem Formulation and Methodology

Figure 3: Overview of Standard Pretext Learning and Pretext-Invariant Representation Learning (PIRL).


An overview of the proposed method and a comparison with Pretext Tasks are shown in Figure 3. For a given image , [math]\displaystyle{ I }[/math], in the dataset of unlabeled images, [math]\displaystyle{ D=\{{I_1,I_2,...,I_{|D|}}\} }[/math], a transformation [math]\displaystyle{ \tau }[/math] is applied:

\begin{align} \tag{1} \label{eqn:1} I^t=\tau(I) \end{align}

Where [math]\displaystyle{ I^t }[/math] is the transformed image. We would like to train a convolutional neural network, [math]\displaystyle{ \phi(\theta) }[/math], that constructs image representations [math]\displaystyle{ v_{I}=\phi_{\theta}(I) }[/math]. Pretext Task based methods learn to predict transformation characteristics, [math]\displaystyle{ z(t) }[/math], by minimizing a transformation covariant loss function in the form of:

\begin{align} \tag{2} \label{eqn:2} l_{\text{cov}}(\theta,D)=\frac{1}{|D|} \sum_{I \in {D}}^{} L(v_I,z(t)) \end{align}

As it can be seen, the loss function covaries with the applied transformation and therefore, the obtained representations may not be semantically meaningful. PIRL tries to solve for this problem as shown in Figure 3. The original and transformed images are passed through two parallel convolutional neural networks to obtain two sets of representations, [math]\displaystyle{ v(I) }[/math] and [math]\displaystyle{ v(I^t) }[/math]. Then, a contrastive loss function is defined to ensure that the representations of the original and transformed images are similar to each other. The transformation invariant loss function can be defined as:

\begin{align} \tag{3} \label{eqn:3} l_{\text{inv}}(\theta,D)=\frac{1}{|D|} \sum_{I \in {D}}^{} L(v_I,v_{I^t}) \end{align}

Where L is a contrastive loss based on Noise Contrastive Estimators (NCE). The NCE function can be shown as below:

\begin{align} \tag{4} \label{eqn:4} h(v_I,v_{I^t})=\frac{\exp \biggl( \frac{s(v_I,v_{I^t})}{\tau} \biggr)}{\exp \biggl(\frac{s(v_I,v_{I^t})}{\tau} \biggr) + \sum_{I^{'} \in D_N}^{} \exp \biggl( \frac{s(v_{I^t},v_{I^{'}})}{\tau} \biggr)} \end{align}

where [math]\displaystyle{ s(.,.) }[/math] is the cosine similarity function and [math]\displaystyle{ \tau }[/math] is the temperature parameter that is usually set to 0.07. Also, a set of N images are chosen randomly from the dataset where [math]\displaystyle{ I^{'}\neq I }[/math]. These images are used in the loss in order to ensure their representation dissimilarity with transformed image representations. Also, during model implementation, two heads (few additional deep layers), [math]\displaystyle{ f }[/math] and [math]\displaystyle{ g }[/math], are applied on top of [math]\displaystyle{ v(I) }[/math] and [math]\displaystyle{ v(I^t) }[/math]. Using the NCE formulation, the contrastive loss can be written as:

\begin{align} \tag{5} \label{eqn:5} L_{\text{NCE}}(I,I^{t})=-\text{log}[h(f(v_I),g(v_{I^t}))]-\sum_{I^{'}\in D_N}^{} \text{log}[1-h(g(v_{I^t}),f(v_{I^{'}}))] \end{align}

Figure 4: Proposed PIRL

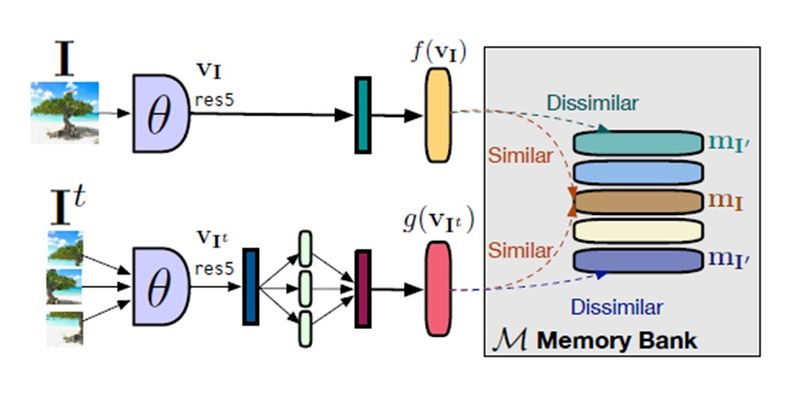
Although the formulation looks complicated, the take-away here is that by minimizing the NCE based loss function, the similarity between the original and transformed image representations, [math]\displaystyle{ v(I) }[/math] and [math]\displaystyle{ v(I^t) }[/math], increases and at the same time the dissimilarity between [math]\displaystyle{ v(I^t) }[/math] and negative images representations, [math]\displaystyle{ v(I^{'}) }[/math], is increased. According to the previous work, an infeasibly large batch size is needed to obtain a large number of negatives. To tackle this problem, a memory bank [9], [math]\displaystyle{ M }[/math], is used during training which contains feature representation [math]\displaystyle{ m_I }[/math] for each image in the dataset including the negative images. The proposed PIRL model is shown in Figure 4. Finally, the contrastive loss in equation \eqref{eqn:5} does not take into account the dissimilarity between the original image representations, [math]\displaystyle{ v(I) }[/math], and the negative image representations, [math]\displaystyle{ v(I^{'}) }[/math]. By taking this into account and using the memory bank, the final contrastive loss function is obtained as:

\begin{align} \tag{6} \label{eqn:6} L(I,I^{t})=\lambda L_{\text{NCE}}(m_I,g(v_{I^t})) + (1-\lambda)L_{\text{NCE}}(m_I,f(v_{I})) \end{align} where [math]\displaystyle{ \lambda }[/math] is a hyperparameter that determines the weight of each of NCE losses. The default value for this parameter is 0.5. In the next section, experimental results are shown using the proposed PIRL model.

Experimental Results

For the experiments in this section, PIRL is implemented using jigsaw transformations. The combination of PIRL with other types of transformations is shown in the last section of the summary. The quality of image representations obtained from PIRL Self-Supervised Learning is evaluated by comparing its performance to other Self-Supervised Learning methods on image recognition and object detection tasks. For the experiments, a ResNet50 model is trained using PIRL and other methods by using 1.28M randomly sampled images from the ImageNet dataset. Also, the number of negative images used for PIRL is N=32000.

Object Detection

A Faster R-CNN model with a ResNet-50 backbone, pre-trained using PIRL and other Self-Supervised methods, is employed for the object detection task. Then, the pre-trained model weights are used as initial weights for the Faster-RCNN model backbone during training on the VOC07+12 dataset. The result of object detection using PIRL is shown in Figure (5) and it is compared to other methods. It can be seen that PIRL not only outperforms other Self-Supervised-based methods, for the first time it outperforms Supervised Pre-training on object detection. They emphasize that PIRL achieves this result using the same backbone model, the same number of finetuning epochs, and the exact same pre-training data (but without the labels). This result is a substantial improvement over prior self-supervised approaches that obtain worse performance than fully supervised baselines despite using orders of magnitude more curated training data or much larger backbone models.

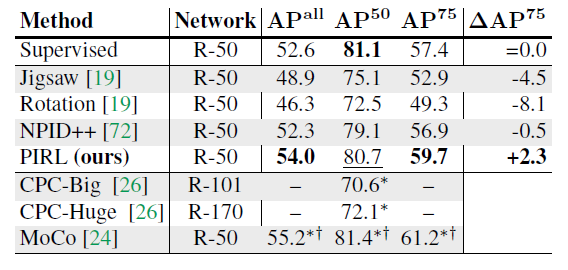
Figure 5: Object detection on VOC07+12 using Faster R-CNN and comparing the Average Precision (AP) of detected bounding boxes. (The values for the blank spaces are not mentioned in the corresponding paper.)

Image Classification with linear models

In the next experiment, the performance of the PIRL is evaluated on image classification using four different datasets. For this experiment, the pre-trained ResNet-50 model is utilized as an image feature extractor. Then, a linear classifier is trained on fixed image representations. The results are shown in Figure (6). The results demonstrate that while PIRL substantially outperforms other Self-Supervised Learning methods, it still falls behind Supervised Pre-trained Learning.

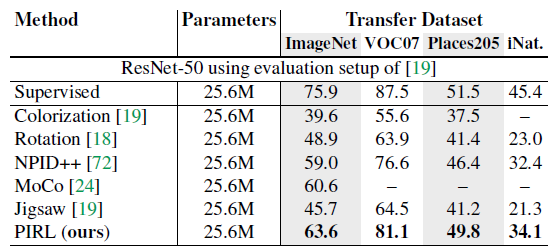
Figure 6: Image classification with linear models. (The values for the blank spaces are not mentioned in the corresponding paper.)

Overall, from Figure6, we can observe that PIRL has the best performance among different Self-Supervised Learning methods. Moreover, PIRL can even perform better than the Supervised Learning Pretrained model on object detection. This is because PIRL learns representations that are invariant to the applied transformations which results in more semantically meaningful and richer visual features. In the next section, some analysis on PIRL is presented.

Analysis

Does PIRL learn invariant representations?

In order to show that the image representations obtained using PIRL are invariant, several images are chosen from the ImageNet dataset, and representations of the chosen images and their transformed version are obtained using one-time PIRL and another time the jigsaw pretext task which is the transformation covariant version of PIRL. Then, for each method, the L2 norm between the original and transformed image representations are computed and their distributions are plotted in Figure (7). It can be seen that PIRL results in more similarity between the original and transformed image representations. Therefore, PIRL learns invariant representations.

Figure 7: Invariance of PIRL representations.

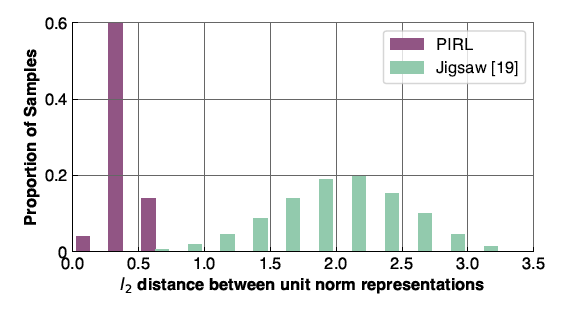
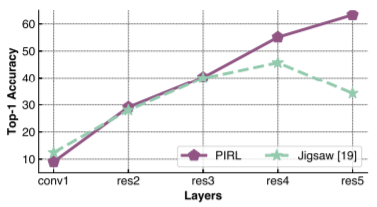
Which layer produces the best representation?

Figure 12 studies the quality of representations in earlier layers of the convolutional networks. The figure reveals that the quality of Jigsaw representations improves from the conv1 to the res4 layer but that their quality sharply decreases in the res5 layer. By contrast, PIRL representations are invariant to image transformations and the best image representations are extracted from the res5 layer of PIRL-trained networks.

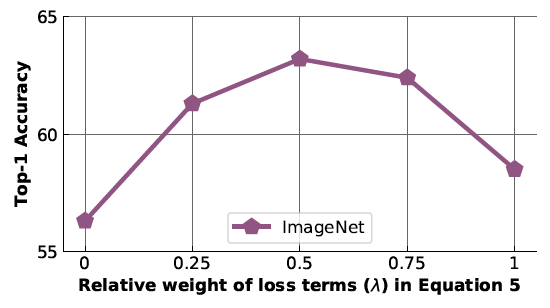
Figure 12:Quality of PIRL representations per layer.

What is the effect of [math]\displaystyle{ \lambda }[/math] in the PIRL loss function?

In order to investigate the effect of [math]\displaystyle{ \lambda }[/math] on PIRL representations, the authors obtained the accuracy of image recognition on ImageNet dataset using different values for [math]\displaystyle{ \lambda }[/math] in PIRL. As shown in Figure 8, the results show that the value of [math]\displaystyle{ \lambda }[/math] affects the performance of PIRL and the optimum value for [math]\displaystyle{ \lambda }[/math] is 0.5.

Figure 8: Effect of varying the parameter [math]\displaystyle{ \lambda }[/math]

What is the effect of the number of images transforms?

As another experiment, the authors investigated the number of image transforms and their effect on PIRL performance. There is a limitation on the number of transformations that can be applied using the jigsaw pretext method as this method has to predict the permutation of the patches and the number of the parameters in the classification layer grows linearly with the number of used transformations. However, PIRL can use all number of image transformations which is equal to [math]\displaystyle{ 9! \approx 3.6\times 10^5 }[/math]. Figure (9) shows the effect of changing the number of patch permutations on PIRL and jigsaw. The results show that increasing the number of permutations increases the mean Average Precision (mAP) of PIRL on image classification using the VOCC07 dataset.

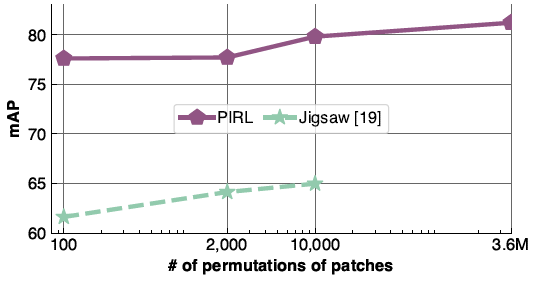
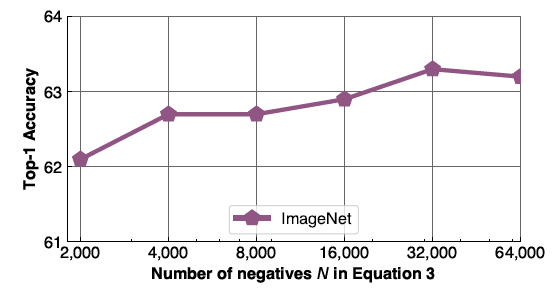
Figure 9: Effect of varying the number of patch permutations

What is the effect of the number of negative samples?

In order to investigate the effect of negative samples number, N, on PIRL's performance, the image classification accuracy is obtained using ImageNet dataset for a variety of values for N. As it is shown in Figure 10, increasing the number of negative sample results in richer image representations and higher classification accuracy.

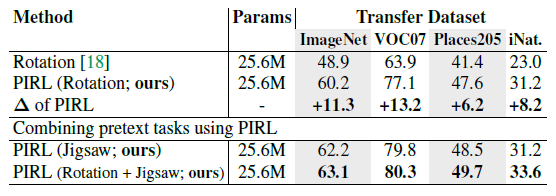
Figure 10: Effect of varying the number of negative samples

Generalizing PIRL to Other Pretext Tasks

The used PIRL model in this paper used jigsaw permutations as the applied transformation to the original image. However, PIRL is generalizable to other Pretext Tasks. To show this, first, PIRL is used with rotation transformations and the performance of rotation-based PIRL is compared to the covariant rotation Pretext Task. The results in Figure (11) show that using PIRL substantially increases the classification accuracy on four datasets in comparison with the rotation Pretext Task. Next, both jigsaw and rotation transformations are used with PIRL to obtain image representations. The results show that combining multiple transformations with PIRL can further improve the accuracy of the image classification task.

Figure 11: Using PIRL with (combinations of) different pretext tasks

Conclusion

In this paper, a new state-of-the-art Self-Supervised learning method, PIRL, was presented. The proposed model learns to obtain features that are common between the original and transformed images, resulting in a set of transformation invariant and more semantically meaningful features. This is done by defining a contrastive loss function between the original images, transformed images, and a set of negative images. The results show that PIRL image representation is richer than previously proposed methods, resulting in higher accuracy and precision on image classification and object detection tasks.

Critiques

The paper proposes a very nice method for obtaining transformation invariant image representations. However, the authors can extend their work with a richer set of transformations. Also, it would be a good idea to investigate the combination of PIRL with clustering-based methods [7,8]. One of the clustering-based methods is DeepCluster [7], where each previous version of its representation is used by bootstrapping to produce a target for the next representation. They built a new representation through clustering data points using the prior representation and then classify the target by using the clustered index of each sample. That may result in better image representations. This will avoid the use of negative pairs but it might also cause collapsing to trivial solutions which create a trade-off.

It could be better if they could visualize their network weights and compare them to the other supervised methods for the deeper layers that extract high-level information.

Source Code

https://paperswithcode.com/paper/self-supervised-learning-of-pretext-invariant

References

[1] Olga Russakovsky, Jia Deng, Hao Su, Jonathan Krause, Sanjeev Satheesh, Sean Ma, Zhiheng Huang, Andrej Karpathy, Aditya Khosla, Michael Bernstein, Alexander C. Berg, and Li Fei-Fei. ImageNet Large Scale Visual Recognition Challenge. IJCV, 2015.

[2] M. Everingham, S. M. A. Eslami, L. Van Gool, C. K. I. Williams, J. Winn, and A. Zisserman. The pascal visual object classes challenge: A retrospective. IJCV, 2015.

[3] Grant Van Horn and Pietro Perona. The devil is in the tails: Fine-grained classification in the wild. arXiv preprint, 2017

[4] Spyros Gidaris, Praveer Singh, and Nikos Komodakis. Unsupervised representation learning by predicting image rotations. arXiv preprint arXiv:1803.07728, 2018.

[5] Mehdi Noroozi and Paolo Favaro. Unsupervised learning of visual representations by solving jigsaw puzzles. In ECCV, 2016.

[6] Jong-Chyi Su, Subhransu Maji, Bharath Hariharan. When does self-supervision improve few-shot learning? European Conference on Computer Vision, 2020.

[7] Mathilde Caron, Piotr Bojanowski, Armand Joulin, and Matthijs Douze. Deep clustering for unsupervised learning of visual features. In ECCV, 2018.

[8] Mathilde Caron, Piotr Bojanowski, Julien Mairal, and Armand Joulin. Unsupervised pre-training of image features on non-curated data. In ICCV, 2019.

[9] Zhirong Wu, Yuanjun Xiong, Stella X Yu, and Dahua Lin. Unsupervised feature learning via non-parametric instance discrimination. In CVPR, 2018.

Retrieved from "http://wiki.math.uwaterloo.ca/statwiki/index.php?title=Self-Supervised_Learning_of_Pretext-Invariant_Representations&oldid=49868"