Graph Structure of Neural Networks: Difference between revisions
| (145 intermediate revisions by 41 users not shown) | |||
| Line 5: | Line 5: | ||
= Introduction = | = Introduction = | ||
A deep neural network is composed of neurons organized into layers and the connections between them. Neural network architecture can be captured by its "computational graph," where neurons are represented as nodes that perform mathematical computations and directed edges that link neurons in different layers. This graphical representation demonstrates how the network transmits and transforms information through its input neurons through the hidden layers and ultimately to the output neurons. | |||
key insight is to focus on message exchange, rather than | |||
just on directed data flow. | However, few researchers have focused on the relationship between neural networks and their predictive performance, which is the main focus of this paper. The aim is to help explain how the addition or deletion of layers, their links, and the number of nodes can impact the performance of the network. | ||
channel and | |||
In Neural Network research, it is often important to build a relation between a neural network’s accuracy and its underlying graph structure. It would contribute to building more efficient and more accurate neural network architectures. A natural choice is to use a computational graph representation. Doing so, however, has many limitations, including: | |||
exchange between the two nodes | |||
(1) Lack of generality: Computational graphs have to follow allowed graph properties, which limits the use of the rich tools developed for general graphs. | |||
(2) Disconnection with biology/neuroscience: Biological neural networks have a much more complicated and less standardized structure. For example, there might be information exchanges in brain networks. It isn't easy to represent these models with directed acyclic graphs. This disconnection between biology/neuroscience makes knowledge less transferable and interdisciplinary research more difficult. | |||
Thus, the authors developed a new way of representing a neural network as a graph, called a relational graph. The new representation's key insight is to focus on message exchange, rather than just on directed data flow. For example, for a fixed-width fully-connected layer, an input channel and output channel pair can be represented as a single node, while an edge in the relational graph can represent the message exchange between the two nodes. Under this formulation, using the appropriate message exchange definition, it can be shown that the relational graph can represent many types of neural network layers. | |||
WS-flex is a graph generator that allows systematically exploring the design space of neural networks. Neural networks are characterized by the clustering coefficient and average path length of their relational graphs under neuroscience insights. Based on the insights from neuroscience, the authors characterize neural networks by the clustering coefficient and average path lengths of their relational graphs. | |||
= Neural Network as Relational Graph = | = Neural Network as Relational Graph = | ||
The author proposes the concept of relational graphs to study the graphical structure of neural network. Each relational graph is based on an undirected graph <math>G =(V; E)</math>, where <math>V =\{v_1,...,v_n\}</math> is the set of all the nodes, and <math>E \subseteq \{(v_i,v_j)|v_i,v_j\in V\}</math> is the set of all edges that connect nodes. Note that for the graph used here, all nodes have self edges, that is <math>(v_i,v_i)\in E</math>. Graphically, a self edge connects an edge to itself, which forms a loop. | |||
To build a relational graph that captures the message exchange between neurons in the network, we associate various mathematical quantities to the graph <math>G</math>. First, a feature quantity <math>x_v</math> is associated with each node. The quantity <math>x_v</math> might be a scalar, vector or tensor depending on what type of neural network it is (see the Table at the end of the section). Then a message function <math>f_{uv}(·)</math> is associated with every edge in the graph. A message function specifically takes a node’s feature as the input and then outputs a message. An aggregation function <math>{\rm AGG}_v(·)</math> then takes a set of messages (the outputs of the message function) and outputs the updated node feature. | |||
A relational graph is a graph <math>G</math> associated with several message exchange rounds, which transform the feature quantity <math>x_v</math> with the message function <math>f_{uv}(·)</math> and the aggregation function <math>{\rm AGG}_v(·)</math>. At each round of message exchange, each node sends messages to its neighbors and aggregates incoming messages from its neighbors. Each message is transformed at each edge through the message function, then they are aggregated at each node via the aggregation function. Suppose we have already conducted <math>r-1</math> rounds of message exchange, then the <math>r^{th}</math> round of message exchange for a node <math>v</math> can be described as | |||
<div style="text-align:center;"><math>\mathbf{x}_v^{(r+1)}= {\rm AGG}^{(r)}(\{f_v^{(r)}(\textbf{x}_u^{(r)}), \forall u\in N(v)\})</math></div> | |||
where <math>\mathbf{x}^{(r+1)}</math> is the feature of the <math>v</math> node in the relational graph after the <math>r^{th}</math> round of update. <math>u,v</math> are nodes in Graph <math>G</math>. <math>N(u)=\{u|(u,v)\in E\}</math> is the set of all the neighbor nodes of <math>u</math> in graph <math>G</math>. | |||
To further illustrate the above, we use the basic Multilayer Perceptron (MLP) as an example. An MLP consists of layers of neurons, where each neuron performs a weighted sum over scalar inputs and outputs, followed by some non-linearity. Suppose the <math>r^{th}</math> layer of an MLP takes <math>x^{(r)}</math> as input and <math>x^{(r+1)}</math> as output, then a neuron computes | |||
<div style="text-align:center;"><math>x_i^{(r+1)}= \sigma(\Sigma_jw_{ij}^{(r)}x_j^{(r)})</math>.</div> | |||
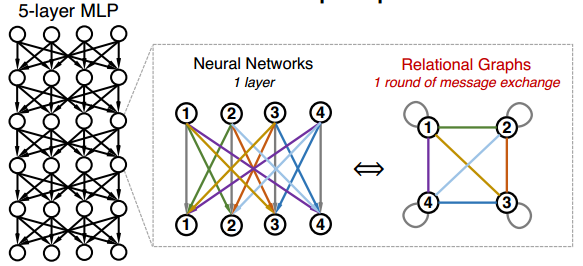
where <math>w_{ij}^{(r)}</math> is the trainable weight and <math>\sigma</math> is the non-linearity function. Let's first consider the special case where the input and output of all the layers <math>x^{(r)}</math>, <math>1 \leq r \leq R </math> have the same feature dimensions <math>d</math>. In this scenario, we can have <math>d</math> nodes in the Graph <math>G</math> with each node representing a neuron in MLP. Each layer of neural network will correspond with a round of message exchange, so there will be <math>R</math> rounds of message exchange in total. The aggregation function here will be the summation with non-linearity transform <math>\sigma(\Sigma)</math>, while the message function is simply the scalar multipication with weight. A fully-connected, fixed-width MLP layer can then be expressed with a complete relational graph, where each node <math>x_v</math> connects to all the other nodes in <math>G</math>, that is neighborhood set <math>N(v) = V</math> for each node <math>v</math>. The figure below shows the correspondence between the complete relation graph with a 5-layer 4-dimension fully-connected MLP. | |||
<div style="text-align:center;">[[File:fully_connnected_MLP.png]]</div> | |||
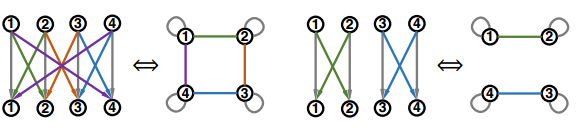
In fact, a fixed-width fully-connected MLP is only a special case under a much more general model family, where the message function, aggregation function, and most importantly, the relation graph structure can vary. The different relational graph will represent the different topological structure and information exchange pattern of the network, which is the property that the paper wants to examine. The plot below shows two examples of non-fully connected fixed-width MLP and their corresponding relational graphs. | |||
<div style="text-align:center;">[[File:otherMLP.png]]</div> | |||
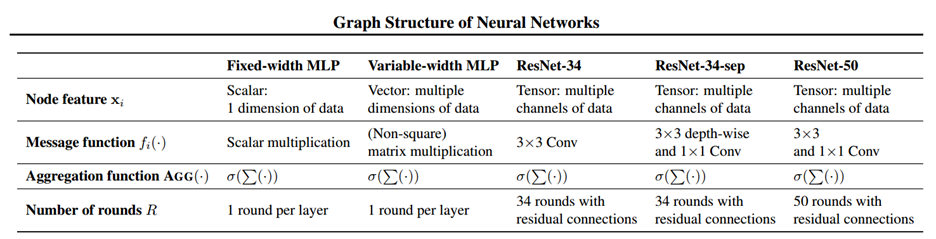
We can generalize the above definitions for fixed-width MLP to Variable-width MLP, Convolutional Neural Network (CNN), and other modern network architecture like Resnet by allowing the node feature quantity <math>\textbf{x}_j^{(r)}</math> to be a vector or tensor respectively. In this case, each node in the relational graph will represent multiple neurons in the network, and the number of neurons contained in each node at each round of message exchange does not need to be the same, which gives us a flexible representation of different neural network architecture. The message function will then change from the simple scalar multiplication to either matrix/tensor multiplication or convolution. And the weight matrix will change to the convolutional filter. The representation of these more complicated networks are described in details in the paper, and the correspondence between different networks and their relational graph properties is summarized in the table below. | |||
<div style="text-align:center;">[[File:relational_specification.png]]</div> | |||
Overall, relational graphs provide a general representation for neural networks. With proper definitions of node features and message exchange, relational graphs can represent diverse neural architectures, thereby allowing us to study the performance of different graph structures. | |||
= Exploring and Generating Relational Graphs= | |||
We will deal with the design and how to explore the space of relational graphs in this section. There are three parts we need to consider: | |||
(1) '''Graph measures''' that characterize graph structural properties: | |||
We will use one global graph measure, average path length, and one local graph measure, clustering coefficient. | |||
To explain clearly, average path length measures the average shortest path distance between any pair of nodes. The clustering coefficient measures the proportion of edges between the nodes within a given node’s neighborhood, divided by the number of edges that could possibly exist between them, averaged over all nodes. | |||
(2) '''Graph generators''' that can generate the diverse graph: | |||
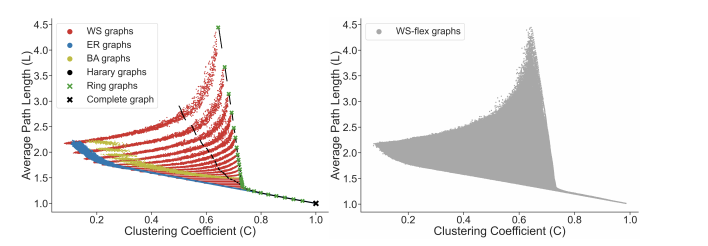
With selected graph measures, we use a graph generator to generate diverse graphs to cover a large span of graph measures. To figure out the limitation of the graph generator and find out the best, we investigate some generators including ER, WS, BA, Harary, Ring, Complete graph and results are shown below: | |||
= | <div style="text-align:center;">[[File:3.2 graph generator.png]]</div> | ||
Thus, from the picture, we could obtain the WS-flex graph generator that can generate graphs with a wide coverage of graph measures. Notably, WS-flex graphs almost encompass all the graphs generated by classic random generators mentioned above. | |||
(3) '''Computational Budget''' that we need to control so that the differences in performance of different neural networks are due to their diverse relational graph structures. | |||
It is important to ensure that all networks have approximately the same complexities so that the differences in performance are due to their relational graph structures when comparing neutral work by their diverse graph. | |||
We use floating point operations (FLOPS) which measures the number of multiply-adds as the metric. We first compute the FLOPS of our baseline network instantiations (i.e. complete relational graph) and use them as the reference complexity in each experiment. From the description in section 2, a relational graph structure can be instantiated as a neural network with variable width. Therefore, we can adjust the width of a neural network to match the reference complexity without changing the relational graph structures. | |||
= Experimental Setup = | |||
The author studied the performance of 3942 sampled relational graphs (generated by WS-flex from the last section) of 64 nodes with two experiments: | |||
== | (1) CIFAR-10 dataset: 10 classes, 50K training images, and 10K validation images | ||
Relational Graph: all 3942 sampled relational graphs of 64 nodes | |||
Studied Network: 5-layer MLP with 512 hidden units | |||
The model was trained for 200 epochs with batch size 128, using cosine learning rate schedule with an initial learning rate of 0.1 | |||
(2) ImageNet classification: 1K image classes, 1.28M training images and 50K validation images | |||
Relational Graph: Due to high computational cost, 52 graphs are uniformly sampled from the 3942 available graphs. | |||
Studied Network: | |||
*ResNet-34, which only consists of basic blocks of 3×3 convolutions (He et al., 2016) | |||
*ResNet-34-sep, a variant where we replace all 3×3 dense convolutions in ResNet-34 with 3×3 separable convolutions (Chollet, 2017) | |||
*ResNet-50, which consists of bottleneck blocks (He et al., 2016) of 1×1, 3×3, 1×1 convolutions | |||
*EfficientNet-B0 architecture (Tan & Le, 2019) | |||
*8-layer CNN with 3×3 convolution | |||
= Results and Discussions = | |||
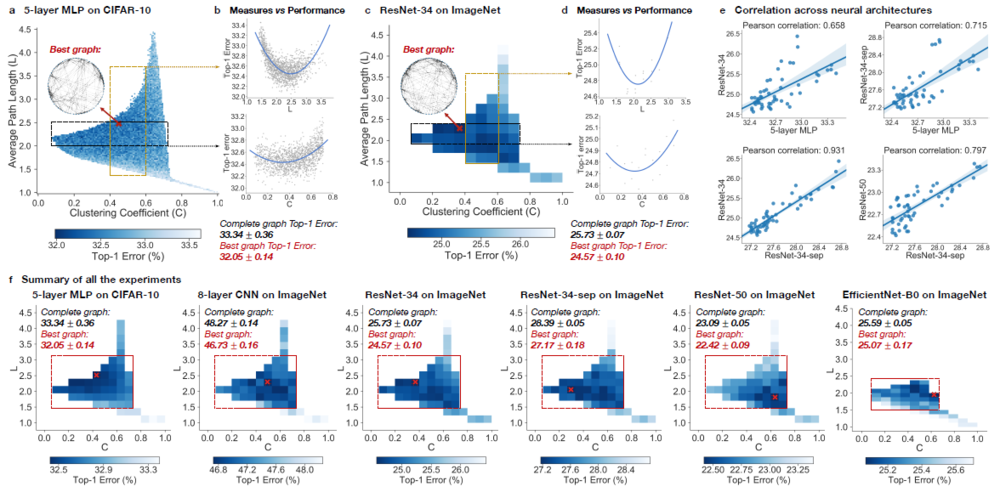
The paper summarizes the result of the experiment among multiple different relational graphs through sampling and analyzing and list six important observations during the experiments, These are: | |||
* There always exists a graph structure that has higher predictive accuracy under Top-1 error compared to the complete graph | |||
* There is a sweet spot such that the graph structure near the sweet spot usually outperforms the base graph | |||
* The predictive accuracy under top-1 error can be represented by a smooth function of Average Path Length <math> (L) </math> and Clustering Coefficient <math> (C) </math> | |||
* The Experiments are consistent across multiple datasets and multiple graph structures with similar Average Path Length and Clustering Coefficient. | |||
* The best graph structure can be identified easily. | |||
* There are similarities between the best artificial neurons and biological neurons. | |||
[[File:Result2_441_2020Group16.png |1000px]] | |||
$$\text{Figure - Results from Experiments}$$ | |||
'''Neural networks performance depends on its structure''' | |||
During the experiment, Top-1 errors for all sampled relational graph among multiple tasks and graph structures are recorded. The parameters of the models are average path length and clustering coefficient. Heat maps were created to illustrate the difference in predictive performance among possible average path length and clustering coefficient. In '''Figure - Results from Experiments (a)(c)(f)''', The darker area represents a smaller top-1 error which indicates the model performs better than the light area. | |||
Compared to the complete graph which has parameter <math> L = 1 </math> and <math> C = 1 </math>, the best performing relational graph can outperform the complete graph baseline by 1.4% top-1 error for MLP on CIFAR-10, and 0.5% to 1.2% for models on ImageNet. Hence it is an indicator that the predictive performance of the neural networks highly depends on the graph structure, or equivalently that the completed graph does not always have the best performance. | |||
'''Sweet spot where performance is significantly improved''' | |||
It had been recognized that training noises often results in inconsistent predictive results. In the paper, the 3942 graphs in the sample had been grouped into 52 bins, each bin had been colored based on the average performance of graphs that fall into the bin. By taking the average, the training noises had been significantly reduced. Based on the heat map '''Figure - Results from Experiments (f)''', the well-performing graphs tend to cluster into a special spot that the paper called “sweet spot” shown in the red rectangle, the rectangle is approximately included clustering coefficient in the range <math>[0.1,0.7]</math> and average path length within <math>[1.5,3]</math>. | |||
'''Relationship between neural network’s performance and parameters''' | |||
When we visualize the heat map, we can see that there is no significant jump of performance that occurred as a small change of clustering coefficient and average path length ('''Figure - Results from Experiments (a)(c)(f)'''). In addition, if one of the variables is fixed in a small range, it is observed that a second-degree polynomial can be used to fit and approximate the data sufficiently well ('''Figure - Results from Experiments (b)(d)'''). Therefore, both the clustering coefficient and average path length are highly related to neural network performance by a convex U-shape. | |||
'''Consistency among many different tasks and datasets''' | |||
They observe that relational graphs with certain graph measures may consistently perform well regardless of how they are instantiated. The paper presents consistency uses two perspectives, one is qualitative consistency and another one is quantitative consistency. | |||
(1) '''Qualitative Consistency''' | |||
It is observed that the results are consistent from different points of view. Among multiple architecture dataset, it is observed that the clustering coefficient within <math>[0.1,0.7]</math> and average path length within <math>[1.5,3]</math> consistently outperform the baseline complete graph. | |||
(2) '''Quantitative Consistency''' | |||
Among different dataset with the network that has similar clustering coefficient and average path length, the results are correlated, The paper mentioned that ResNet-34 is much more complex than 5-layer MLP but a fixed set relational graph would perform similarly in both settings, with Pearson correlation of <math>0.658</math>, the p-value for the Null hypothesis is less than <math>10^{-8}</math>. | |||
'''Top architectures can be identified efficiently''' | |||
The computation cost of finding top architectures can be significantly reduced without training the entire data set for a large value of epoch or a relatively large sample. To achieve the top architectures, the number of graphs and training epochs need to be identified. For the number of graphs, a heatmap is a great tool to demonstrate the result. In the 5-layer MLP on CIFAR-10 example, taking a sample of the data around 52 graphs would have a correlation of 0.9, which indicates that fewer samples are needed for a similar analysis in practice. When determining the number of epochs, correlation can help to show the result. In ResNet34 on ImageNet example, the correlation between the variables is already high enough for future computation within 3 epochs. This means that good relational graphs perform well even at the | |||
initial training epochs. | |||
'''Well-performing neural networks have graph structure surprisingly similar to those of real biological neural networks''' | |||
The way we define relational graphs and average length in the graph is similar to the way information is exchanged in network science. The biological neural network also has a similar relational graph representation and graph measure with the best-performing relational graph. | The way we define relational graphs and average length in the graph is similar to the way information is exchanged in network science. The biological neural network also has a similar relational graph representation and graph measure with the best-performing relational graph. | ||
While there is some organizational similarity between a computational neural network and a biological neural network, we should refrain from saying that both these networks share many similarities or are essentially the same with just different substrates. The biological neurons are still quite poorly understood and it may take a while before their mechanisms are better understood. | |||
= Conclusions= | |||
Our works provided a new viewpoint about combining the fields of graph neural networks (GNNs) and general architecture design by establishing graph structures. The authors believe that the model helps to capture the diverse neural network architectures under a unified framework. In particular, GNNs are instances of general neural architectures where graph structures are seen as input rather than part of the architecture, and message functions are shared across all edges of the graph. We have proved that other scientific disciplines, such as network science, neuroscience, etc., provide graphics techniques and methods to help understand and design deep neural networks. This could provide effective help and inspiration for the study of neural networks. | |||
= Critique = | = Critique = | ||
1. The experiment is only measuring on a single data set which might | |||
2. When we are fitting the model, training data should be | 1. The experiment is only measuring on a single data set which might not be representative enough. As we can see in the whole paper, the "sweet spot" we talked about might be a special feature for the given data set only which is the CIFAR-10 data set. If we change the data set to another imaging data set like CK+, whether we are going to get a similar result is not shown by the paper. Hence, the result that is being concluded from the paper might not be representative enough. | ||
2. When we are fitting the model in practice, we will fit the model with more than one epoch. The order of the model fitting should be randomized since we should create more random jumps to avoid staying inside a local minimum. With the same order within each epoch, the data might be grouped by different classes or levels, the model might result in a better performance with certain classes and worse performance with other classes. In this particular example, without randomization of the training data, the conclusion might not be precise enough. | |||
3. This study shows empirical justification for choosing well-performing models from graphs differing only by average path length and clustering coefficient. An equally important question is whether there is a theoretical justification for why these graph properties may (or may not) contribute to the performance of a general classifier - for example, is there a combination of these properties that is sufficient to recover the universality theorem for MLP's? | |||
4. It might be worth looking into how to identify the "sweet spot" for different datasets. | |||
5. What would be considered a "best graph structure " in the discussion and conclusion part? It seems that the intermediate result of getting an accurate result was by binning graphs into smaller bins, what should we do if the graphs can not be binned into significantly smaller bins in order to proceed with the methodologies mentioned in the paper. Both CIFAR - 10 and ImageNet seem too trivial considering the amount of variation and categories in the dataset. What would the generalizability be to other presentations of images? | |||
6. There is an interesting insight that the idea of the relational graph is similar to applying causal graphs in neuro networks, which is also closer to biology and neuroscience because human beings learning things based on causality. This new approach may lead to higher prediction accuracy but it needs more assumptions, such as correct relations and causalities. | |||
7. This is an interesting topic that uses the knowledge in graph theory to introduce this new structure of Neural Networks. Using more data sets to discuss this approach might be more interesting, such as the MNIST dataset. We think it is interesting to discuss whether this structure will provide a better performance compare to the "traditional" structure of NN in any type of Neural Networks. | |||
8. The key idea is to treat a neural network as a relational graph and investigate the messages exchange over the graphs. It will be interesting to discuss how much improvement a sweet spot can bring to the network. | |||
9. It is interesting to see how figure "b" in the plots showing the experiment results has a U-shape. This shows a correlation between message exchange efficiency and capability of learning distributed representations, giving an idea about the tradeoff between them, as indicated in the paper. | |||
10. From Results and Discussion part, we can find learning at a very abstract level of artificial neurons and biological neurons is similar. But the learning method is different. Artificial neural networks use gradient descent to minimize the loss function and reach the global minimum. Biological neural networks have another learning method. | |||
11. It would be interesting to see if the insights from this paper can be used to create new kinds of neural network architectures which were previously unknown, or to create a method of deciding which neural network to use for a given situation or data set. It may be interesting to compare the performance of neural networks by a property of their graph (like average path length as described in this paper) versus a property of the data (such as noisiness). | |||
12. It would be attractive if the paper dig more into the “sweet pot” and give us a brief introduction of it rather than just slightly mention it. It would be a little bit confused if this technical term shows up and without any previous mention or introduction | |||
13. The paper shows graphical results how well performing graphs cluster into ‘sweet spots’. And the ‘sweet spot’ leads to significant performance improvement of the graph. It would be interesting if the author could provide more justification for the experimental setup chosen and also explore if known graph theorems have any relation to this improved performance. | |||
14. GNN is really interesting, one application I can think of is it can be used for recommending system like Linkedin and Facebook. Since people who knows each other is really easy represented as graph. | |||
15. At the end of the paper, it could also talk about the applications of relational graph, the developed graph-based representation of neural networks. For example, structural scenarios that data has relational structure like atoms and molecules, and non-structural scenarios that data doesn’t have relational structure like images and texts. | |||
Latest revision as of 17:06, 7 December 2020
Presented By
Xiaolan Xu, Robin Wen, Yue Weng, Beizhen Chang
Introduction
A deep neural network is composed of neurons organized into layers and the connections between them. Neural network architecture can be captured by its "computational graph," where neurons are represented as nodes that perform mathematical computations and directed edges that link neurons in different layers. This graphical representation demonstrates how the network transmits and transforms information through its input neurons through the hidden layers and ultimately to the output neurons.
However, few researchers have focused on the relationship between neural networks and their predictive performance, which is the main focus of this paper. The aim is to help explain how the addition or deletion of layers, their links, and the number of nodes can impact the performance of the network.
In Neural Network research, it is often important to build a relation between a neural network’s accuracy and its underlying graph structure. It would contribute to building more efficient and more accurate neural network architectures. A natural choice is to use a computational graph representation. Doing so, however, has many limitations, including:
(1) Lack of generality: Computational graphs have to follow allowed graph properties, which limits the use of the rich tools developed for general graphs.
(2) Disconnection with biology/neuroscience: Biological neural networks have a much more complicated and less standardized structure. For example, there might be information exchanges in brain networks. It isn't easy to represent these models with directed acyclic graphs. This disconnection between biology/neuroscience makes knowledge less transferable and interdisciplinary research more difficult.
Thus, the authors developed a new way of representing a neural network as a graph, called a relational graph. The new representation's key insight is to focus on message exchange, rather than just on directed data flow. For example, for a fixed-width fully-connected layer, an input channel and output channel pair can be represented as a single node, while an edge in the relational graph can represent the message exchange between the two nodes. Under this formulation, using the appropriate message exchange definition, it can be shown that the relational graph can represent many types of neural network layers.
WS-flex is a graph generator that allows systematically exploring the design space of neural networks. Neural networks are characterized by the clustering coefficient and average path length of their relational graphs under neuroscience insights. Based on the insights from neuroscience, the authors characterize neural networks by the clustering coefficient and average path lengths of their relational graphs.
Neural Network as Relational Graph
The author proposes the concept of relational graphs to study the graphical structure of neural network. Each relational graph is based on an undirected graph [math]\displaystyle{ G =(V; E) }[/math], where [math]\displaystyle{ V =\{v_1,...,v_n\} }[/math] is the set of all the nodes, and [math]\displaystyle{ E \subseteq \{(v_i,v_j)|v_i,v_j\in V\} }[/math] is the set of all edges that connect nodes. Note that for the graph used here, all nodes have self edges, that is [math]\displaystyle{ (v_i,v_i)\in E }[/math]. Graphically, a self edge connects an edge to itself, which forms a loop.
To build a relational graph that captures the message exchange between neurons in the network, we associate various mathematical quantities to the graph [math]\displaystyle{ G }[/math]. First, a feature quantity [math]\displaystyle{ x_v }[/math] is associated with each node. The quantity [math]\displaystyle{ x_v }[/math] might be a scalar, vector or tensor depending on what type of neural network it is (see the Table at the end of the section). Then a message function [math]\displaystyle{ f_{uv}(·) }[/math] is associated with every edge in the graph. A message function specifically takes a node’s feature as the input and then outputs a message. An aggregation function [math]\displaystyle{ {\rm AGG}_v(·) }[/math] then takes a set of messages (the outputs of the message function) and outputs the updated node feature.
A relational graph is a graph [math]\displaystyle{ G }[/math] associated with several message exchange rounds, which transform the feature quantity [math]\displaystyle{ x_v }[/math] with the message function [math]\displaystyle{ f_{uv}(·) }[/math] and the aggregation function [math]\displaystyle{ {\rm AGG}_v(·) }[/math]. At each round of message exchange, each node sends messages to its neighbors and aggregates incoming messages from its neighbors. Each message is transformed at each edge through the message function, then they are aggregated at each node via the aggregation function. Suppose we have already conducted [math]\displaystyle{ r-1 }[/math] rounds of message exchange, then the [math]\displaystyle{ r^{th} }[/math] round of message exchange for a node [math]\displaystyle{ v }[/math] can be described as
where [math]\displaystyle{ \mathbf{x}^{(r+1)} }[/math] is the feature of the [math]\displaystyle{ v }[/math] node in the relational graph after the [math]\displaystyle{ r^{th} }[/math] round of update. [math]\displaystyle{ u,v }[/math] are nodes in Graph [math]\displaystyle{ G }[/math]. [math]\displaystyle{ N(u)=\{u|(u,v)\in E\} }[/math] is the set of all the neighbor nodes of [math]\displaystyle{ u }[/math] in graph [math]\displaystyle{ G }[/math].
To further illustrate the above, we use the basic Multilayer Perceptron (MLP) as an example. An MLP consists of layers of neurons, where each neuron performs a weighted sum over scalar inputs and outputs, followed by some non-linearity. Suppose the [math]\displaystyle{ r^{th} }[/math] layer of an MLP takes [math]\displaystyle{ x^{(r)} }[/math] as input and [math]\displaystyle{ x^{(r+1)} }[/math] as output, then a neuron computes
where [math]\displaystyle{ w_{ij}^{(r)} }[/math] is the trainable weight and [math]\displaystyle{ \sigma }[/math] is the non-linearity function. Let's first consider the special case where the input and output of all the layers [math]\displaystyle{ x^{(r)} }[/math], [math]\displaystyle{ 1 \leq r \leq R }[/math] have the same feature dimensions [math]\displaystyle{ d }[/math]. In this scenario, we can have [math]\displaystyle{ d }[/math] nodes in the Graph [math]\displaystyle{ G }[/math] with each node representing a neuron in MLP. Each layer of neural network will correspond with a round of message exchange, so there will be [math]\displaystyle{ R }[/math] rounds of message exchange in total. The aggregation function here will be the summation with non-linearity transform [math]\displaystyle{ \sigma(\Sigma) }[/math], while the message function is simply the scalar multipication with weight. A fully-connected, fixed-width MLP layer can then be expressed with a complete relational graph, where each node [math]\displaystyle{ x_v }[/math] connects to all the other nodes in [math]\displaystyle{ G }[/math], that is neighborhood set [math]\displaystyle{ N(v) = V }[/math] for each node [math]\displaystyle{ v }[/math]. The figure below shows the correspondence between the complete relation graph with a 5-layer 4-dimension fully-connected MLP.
In fact, a fixed-width fully-connected MLP is only a special case under a much more general model family, where the message function, aggregation function, and most importantly, the relation graph structure can vary. The different relational graph will represent the different topological structure and information exchange pattern of the network, which is the property that the paper wants to examine. The plot below shows two examples of non-fully connected fixed-width MLP and their corresponding relational graphs.
We can generalize the above definitions for fixed-width MLP to Variable-width MLP, Convolutional Neural Network (CNN), and other modern network architecture like Resnet by allowing the node feature quantity [math]\displaystyle{ \textbf{x}_j^{(r)} }[/math] to be a vector or tensor respectively. In this case, each node in the relational graph will represent multiple neurons in the network, and the number of neurons contained in each node at each round of message exchange does not need to be the same, which gives us a flexible representation of different neural network architecture. The message function will then change from the simple scalar multiplication to either matrix/tensor multiplication or convolution. And the weight matrix will change to the convolutional filter. The representation of these more complicated networks are described in details in the paper, and the correspondence between different networks and their relational graph properties is summarized in the table below.
Overall, relational graphs provide a general representation for neural networks. With proper definitions of node features and message exchange, relational graphs can represent diverse neural architectures, thereby allowing us to study the performance of different graph structures.
Exploring and Generating Relational Graphs
We will deal with the design and how to explore the space of relational graphs in this section. There are three parts we need to consider:
(1) Graph measures that characterize graph structural properties:
We will use one global graph measure, average path length, and one local graph measure, clustering coefficient. To explain clearly, average path length measures the average shortest path distance between any pair of nodes. The clustering coefficient measures the proportion of edges between the nodes within a given node’s neighborhood, divided by the number of edges that could possibly exist between them, averaged over all nodes.
(2) Graph generators that can generate the diverse graph:
With selected graph measures, we use a graph generator to generate diverse graphs to cover a large span of graph measures. To figure out the limitation of the graph generator and find out the best, we investigate some generators including ER, WS, BA, Harary, Ring, Complete graph and results are shown below:
Thus, from the picture, we could obtain the WS-flex graph generator that can generate graphs with a wide coverage of graph measures. Notably, WS-flex graphs almost encompass all the graphs generated by classic random generators mentioned above.
(3) Computational Budget that we need to control so that the differences in performance of different neural networks are due to their diverse relational graph structures.
It is important to ensure that all networks have approximately the same complexities so that the differences in performance are due to their relational graph structures when comparing neutral work by their diverse graph.
We use floating point operations (FLOPS) which measures the number of multiply-adds as the metric. We first compute the FLOPS of our baseline network instantiations (i.e. complete relational graph) and use them as the reference complexity in each experiment. From the description in section 2, a relational graph structure can be instantiated as a neural network with variable width. Therefore, we can adjust the width of a neural network to match the reference complexity without changing the relational graph structures.
Experimental Setup
The author studied the performance of 3942 sampled relational graphs (generated by WS-flex from the last section) of 64 nodes with two experiments:
(1) CIFAR-10 dataset: 10 classes, 50K training images, and 10K validation images
Relational Graph: all 3942 sampled relational graphs of 64 nodes
Studied Network: 5-layer MLP with 512 hidden units
The model was trained for 200 epochs with batch size 128, using cosine learning rate schedule with an initial learning rate of 0.1
(2) ImageNet classification: 1K image classes, 1.28M training images and 50K validation images
Relational Graph: Due to high computational cost, 52 graphs are uniformly sampled from the 3942 available graphs.
Studied Network:
- ResNet-34, which only consists of basic blocks of 3×3 convolutions (He et al., 2016)
- ResNet-34-sep, a variant where we replace all 3×3 dense convolutions in ResNet-34 with 3×3 separable convolutions (Chollet, 2017)
- ResNet-50, which consists of bottleneck blocks (He et al., 2016) of 1×1, 3×3, 1×1 convolutions
- EfficientNet-B0 architecture (Tan & Le, 2019)
- 8-layer CNN with 3×3 convolution
Results and Discussions
The paper summarizes the result of the experiment among multiple different relational graphs through sampling and analyzing and list six important observations during the experiments, These are:
- There always exists a graph structure that has higher predictive accuracy under Top-1 error compared to the complete graph
- There is a sweet spot such that the graph structure near the sweet spot usually outperforms the base graph
- The predictive accuracy under top-1 error can be represented by a smooth function of Average Path Length [math]\displaystyle{ (L) }[/math] and Clustering Coefficient [math]\displaystyle{ (C) }[/math]
- The Experiments are consistent across multiple datasets and multiple graph structures with similar Average Path Length and Clustering Coefficient.
- The best graph structure can be identified easily.
- There are similarities between the best artificial neurons and biological neurons.
$$\text{Figure - Results from Experiments}$$
Neural networks performance depends on its structure
During the experiment, Top-1 errors for all sampled relational graph among multiple tasks and graph structures are recorded. The parameters of the models are average path length and clustering coefficient. Heat maps were created to illustrate the difference in predictive performance among possible average path length and clustering coefficient. In Figure - Results from Experiments (a)(c)(f), The darker area represents a smaller top-1 error which indicates the model performs better than the light area.
Compared to the complete graph which has parameter [math]\displaystyle{ L = 1 }[/math] and [math]\displaystyle{ C = 1 }[/math], the best performing relational graph can outperform the complete graph baseline by 1.4% top-1 error for MLP on CIFAR-10, and 0.5% to 1.2% for models on ImageNet. Hence it is an indicator that the predictive performance of the neural networks highly depends on the graph structure, or equivalently that the completed graph does not always have the best performance.
Sweet spot where performance is significantly improved
It had been recognized that training noises often results in inconsistent predictive results. In the paper, the 3942 graphs in the sample had been grouped into 52 bins, each bin had been colored based on the average performance of graphs that fall into the bin. By taking the average, the training noises had been significantly reduced. Based on the heat map Figure - Results from Experiments (f), the well-performing graphs tend to cluster into a special spot that the paper called “sweet spot” shown in the red rectangle, the rectangle is approximately included clustering coefficient in the range [math]\displaystyle{ [0.1,0.7] }[/math] and average path length within [math]\displaystyle{ [1.5,3] }[/math].
Relationship between neural network’s performance and parameters
When we visualize the heat map, we can see that there is no significant jump of performance that occurred as a small change of clustering coefficient and average path length (Figure - Results from Experiments (a)(c)(f)). In addition, if one of the variables is fixed in a small range, it is observed that a second-degree polynomial can be used to fit and approximate the data sufficiently well (Figure - Results from Experiments (b)(d)). Therefore, both the clustering coefficient and average path length are highly related to neural network performance by a convex U-shape.
Consistency among many different tasks and datasets
They observe that relational graphs with certain graph measures may consistently perform well regardless of how they are instantiated. The paper presents consistency uses two perspectives, one is qualitative consistency and another one is quantitative consistency.
(1) Qualitative Consistency It is observed that the results are consistent from different points of view. Among multiple architecture dataset, it is observed that the clustering coefficient within [math]\displaystyle{ [0.1,0.7] }[/math] and average path length within [math]\displaystyle{ [1.5,3] }[/math] consistently outperform the baseline complete graph.
(2) Quantitative Consistency Among different dataset with the network that has similar clustering coefficient and average path length, the results are correlated, The paper mentioned that ResNet-34 is much more complex than 5-layer MLP but a fixed set relational graph would perform similarly in both settings, with Pearson correlation of [math]\displaystyle{ 0.658 }[/math], the p-value for the Null hypothesis is less than [math]\displaystyle{ 10^{-8} }[/math].
Top architectures can be identified efficiently
The computation cost of finding top architectures can be significantly reduced without training the entire data set for a large value of epoch or a relatively large sample. To achieve the top architectures, the number of graphs and training epochs need to be identified. For the number of graphs, a heatmap is a great tool to demonstrate the result. In the 5-layer MLP on CIFAR-10 example, taking a sample of the data around 52 graphs would have a correlation of 0.9, which indicates that fewer samples are needed for a similar analysis in practice. When determining the number of epochs, correlation can help to show the result. In ResNet34 on ImageNet example, the correlation between the variables is already high enough for future computation within 3 epochs. This means that good relational graphs perform well even at the initial training epochs.
Well-performing neural networks have graph structure surprisingly similar to those of real biological neural networks
The way we define relational graphs and average length in the graph is similar to the way information is exchanged in network science. The biological neural network also has a similar relational graph representation and graph measure with the best-performing relational graph.
While there is some organizational similarity between a computational neural network and a biological neural network, we should refrain from saying that both these networks share many similarities or are essentially the same with just different substrates. The biological neurons are still quite poorly understood and it may take a while before their mechanisms are better understood.
Conclusions
Our works provided a new viewpoint about combining the fields of graph neural networks (GNNs) and general architecture design by establishing graph structures. The authors believe that the model helps to capture the diverse neural network architectures under a unified framework. In particular, GNNs are instances of general neural architectures where graph structures are seen as input rather than part of the architecture, and message functions are shared across all edges of the graph. We have proved that other scientific disciplines, such as network science, neuroscience, etc., provide graphics techniques and methods to help understand and design deep neural networks. This could provide effective help and inspiration for the study of neural networks.
Critique
1. The experiment is only measuring on a single data set which might not be representative enough. As we can see in the whole paper, the "sweet spot" we talked about might be a special feature for the given data set only which is the CIFAR-10 data set. If we change the data set to another imaging data set like CK+, whether we are going to get a similar result is not shown by the paper. Hence, the result that is being concluded from the paper might not be representative enough.
2. When we are fitting the model in practice, we will fit the model with more than one epoch. The order of the model fitting should be randomized since we should create more random jumps to avoid staying inside a local minimum. With the same order within each epoch, the data might be grouped by different classes or levels, the model might result in a better performance with certain classes and worse performance with other classes. In this particular example, without randomization of the training data, the conclusion might not be precise enough.
3. This study shows empirical justification for choosing well-performing models from graphs differing only by average path length and clustering coefficient. An equally important question is whether there is a theoretical justification for why these graph properties may (or may not) contribute to the performance of a general classifier - for example, is there a combination of these properties that is sufficient to recover the universality theorem for MLP's?
4. It might be worth looking into how to identify the "sweet spot" for different datasets.
5. What would be considered a "best graph structure " in the discussion and conclusion part? It seems that the intermediate result of getting an accurate result was by binning graphs into smaller bins, what should we do if the graphs can not be binned into significantly smaller bins in order to proceed with the methodologies mentioned in the paper. Both CIFAR - 10 and ImageNet seem too trivial considering the amount of variation and categories in the dataset. What would the generalizability be to other presentations of images?
6. There is an interesting insight that the idea of the relational graph is similar to applying causal graphs in neuro networks, which is also closer to biology and neuroscience because human beings learning things based on causality. This new approach may lead to higher prediction accuracy but it needs more assumptions, such as correct relations and causalities.
7. This is an interesting topic that uses the knowledge in graph theory to introduce this new structure of Neural Networks. Using more data sets to discuss this approach might be more interesting, such as the MNIST dataset. We think it is interesting to discuss whether this structure will provide a better performance compare to the "traditional" structure of NN in any type of Neural Networks.
8. The key idea is to treat a neural network as a relational graph and investigate the messages exchange over the graphs. It will be interesting to discuss how much improvement a sweet spot can bring to the network.
9. It is interesting to see how figure "b" in the plots showing the experiment results has a U-shape. This shows a correlation between message exchange efficiency and capability of learning distributed representations, giving an idea about the tradeoff between them, as indicated in the paper.
10. From Results and Discussion part, we can find learning at a very abstract level of artificial neurons and biological neurons is similar. But the learning method is different. Artificial neural networks use gradient descent to minimize the loss function and reach the global minimum. Biological neural networks have another learning method.
11. It would be interesting to see if the insights from this paper can be used to create new kinds of neural network architectures which were previously unknown, or to create a method of deciding which neural network to use for a given situation or data set. It may be interesting to compare the performance of neural networks by a property of their graph (like average path length as described in this paper) versus a property of the data (such as noisiness).
12. It would be attractive if the paper dig more into the “sweet pot” and give us a brief introduction of it rather than just slightly mention it. It would be a little bit confused if this technical term shows up and without any previous mention or introduction
13. The paper shows graphical results how well performing graphs cluster into ‘sweet spots’. And the ‘sweet spot’ leads to significant performance improvement of the graph. It would be interesting if the author could provide more justification for the experimental setup chosen and also explore if known graph theorems have any relation to this improved performance.
14. GNN is really interesting, one application I can think of is it can be used for recommending system like Linkedin and Facebook. Since people who knows each other is really easy represented as graph.
15. At the end of the paper, it could also talk about the applications of relational graph, the developed graph-based representation of neural networks. For example, structural scenarios that data has relational structure like atoms and molecules, and non-structural scenarios that data doesn’t have relational structure like images and texts.