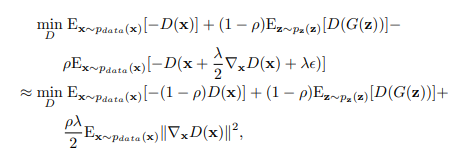Adversarial Fisher Vectors for Unsupervised Representation Learning: Difference between revisions
| (41 intermediate revisions by 11 users not shown) | |||
| Line 1: | Line 1: | ||
== Presented by == | |||
Sobhan Hemati | |||
== Introduction == | == Introduction == | ||
Generative adversarial networks (GANs) are | Generative adversarial networks (GANs) are among the most important generative models, where discriminators and generators compete with each other to solve a minimax game. Based on the original GAN paper, when the training is finished and Nash Equilibrium is reached, the discriminator is nothing but a constant function that assigns a score of 0.5 everywhere. This means that in this setting discriminator is nothing more than a tool to train the generator. Furthermore, the generator in traditional GAN models the data density in an implicit manner, while in some applications we need to have an explicit generative model of data. Recently, it has been shown that training an energy-based model (EBM) with a parameterised variational distribution is also a minimax game similar to the one in GAN. Although they are similar, an advantage of this EBM view is that unlike the original GAN formulation, the discriminator itself is an explicit density model of the data. | ||
Considering some remarks, authors in this paper show that an energy-based model can be trained using similar | Considering some remarks, the authors in this paper show that an energy-based model can be trained using a similar minimax formulation in GANs. After training the energy-based model, they use Fisher Score and Fisher Information (which are calculated based on derivative of the generative models w.r.t its parameters) to evaluate the power of discriminator in modeling the data distribution. More precisely, they calculate normalised Fisher Vectors and Fisher Distance measure using the discriminator's derivative to estimate similarities both between individual data samples and between sets of samples. They name these derived representations Adversarial Fisher Vectors (AFVs). In fact, Fisher vector is a powerful representation that can be calculated using EBMs thanks to the fact that in this EBM model, the discriminator itself is an explicit density model of the data. Fisher vector can be used for setting representation problems which is a challenging task. In fact, as we will see, we can use the Fisher kernel to calculate the distance between two sets of images which is not a trivial task. The authors find several applications and attractive characteristics for AFV as pre-trained features such as: | ||
to estimate similarities both between individual data samples and between sets of samples. They name these derived representations Adversarial Fisher Vectors (AFVs). In fact | |||
* State-of-the-art performance for unsupervised feature extraction and linear classification tasks. | * State-of-the-art performance for unsupervised feature extraction and linear classification tasks. | ||
* Using the similarity function induced by the learned density model | * Using the similarity function induced by the learned density model as a perceptual metric that correlates well with human judgments. | ||
* | * Improved training of GANs through monitoring (AFV metrics) and stability (MCMC updates) which is a difficult task in general. | ||
* Using AFV to estimate distance between sets which | * Using AFV to estimate the distance between sets which allows monitoring the training process. More precisely, the Fisher Distance between the set of validation examples and generated examples can effectively capture the existence of overfitting. | ||
== Background == | == Background == | ||
===Generative Adversarial Networks=== | ===Generative Adversarial Networks=== | ||
The weights of generator and discriminator are updated by solving the following | GANs are a clever way of training a generative model by framing the problem as a supervised learning problem with two sub-models: the generator model that we train to generate new examples, and the discriminator model that tries to classify examples as either real (from the domain) or fake (generated). The weights of generator and discriminator are updated by solving the following optimisation problem: | ||
\begin{equation} | \begin{equation} | ||
\underset{G}{\text{max}} \ \underset{D}{\text{min}} \ E_{\mathbf{x} \sim p_{data(\mathbf{x})}}[-\log D(\mathbf{x})]- E_{\mathbf{z} \sim p_{\mathbf{z}}(\mathbf{z})}[-\log (1-D(G(\mathbf{z})))] | \underset{G}{\text{max}} \ \underset{D}{\text{min}} \ E_{\mathbf{x} \sim p_{data(\mathbf{x})}}[-\log D(\mathbf{x})]- E_{\mathbf{z} \sim p_{\mathbf{z}}(\mathbf{z})}[-\log (1-D(G(\mathbf{z})))] | ||
| Line 20: | Line 22: | ||
\end{equation} | \end{equation} | ||
Where <math> p_{data(\mathbf{x})} </math>, <math> D(x) </math>, and <math> G(x) </math> are distribution of data, discriminator, and generator respectively. To | Where <math> p_{data(\mathbf{x})} </math>, <math> D(x) </math>, and <math> G(x) </math> are distribution of data, discriminator, and generator respectively. To optimise the above problem, in the inner loop <math> D </math> is trained until convergence given <math> G </math>, and in the outer loop <math> G </math>, is updated one step given <math> D </math>. | ||
===GANs as variational training of deep EBMs=== | ===GANs as variational training of deep EBMs=== | ||
An energy-based model (EBM) is a form of generative model (GM) that learns the characteristics of a target dataset and generates a similar but larger dataset. EBMs detect the latent variables of a dataset and generate new datasets with a similar distribution. Let an energy-based model define a density function <math> p_{E}(\mathbf{x}) </math> as <math> \frac{e^{-E(\mathbf{x})}}{ \int_{\mathbf{x}} e^{-E(\mathbf{x})} \,d\mathbf{x} } </math>. Then, the negative log likelihood (NLL) of the <math> p_{E}(\mathbf{x}) </math> can be written as | |||
\begin{equation} | \begin{equation} | ||
| Line 33: | Line 35: | ||
\end{equation} | \end{equation} | ||
where <math> q(x) </math> is an auxiliary distribution which is called | where <math> q(x) </math> is an auxiliary distribution which is called the variational distribution and <math>H(q) </math> defines its entropy. Here Jensen’s inequality was used to obtain the variational lower bound on the NLL given <math>H(q) </math>. This bound is tight if <math> q(x) \propto e^{-E(\mathbf{x})} \ \forall \mathbf{x}, </math> which means <math> q(x) = p_{E}(\mathbf{x}) </math>. In this case, if we put <math> D(\mathbf{x})= -E(\mathbf{x}) </math> and also <math> q(x)= p_{G}(\mathbf{x}) </math>, Eq.\ref{2} turns to the following problem: | ||
| Line 44: | Line 46: | ||
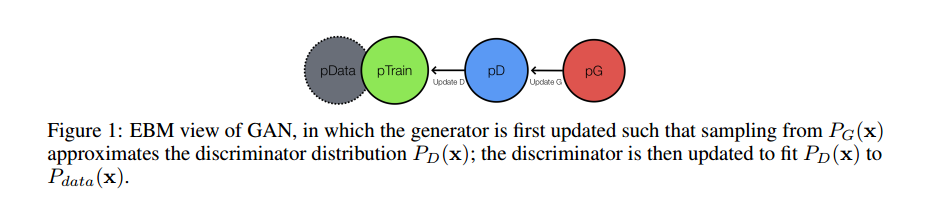
where in the problem, the variational lower bound is | where in the problem, the variational lower bound is maximised w.r.t. <math> p_{G}</math>; the energy model then is updated one step to decrease the NLL with the optimal <math> p_{G}</math> (see Figure1). [[File:Fig1.png|centre]] | ||
Equations \ref{3} and \ref{1} are similar in the sense that both taking the form of a minimax game between <math> D </math> and <math> G </math>. However, there are 3 major differences: | Equations \ref{3} and \ref{1} are similar in the sense that both taking the form of a minimax game between <math> D </math> and <math> G </math>. However, there are 3 major differences: | ||
*The entropy | *The entropy regularisation term <math> H(p_{G})</math> in Eq. \ref{3} prevents the generator from collapsing (although in practice, it is difficult to come up with a differentiable approximation to the entropy term <math> H(p_{G})</math> and instead heuristic regularisation methods such as batch normalisation are used). | ||
* | * The order of optimising <math> D </math> and <math> G </math> is different. | ||
* More importantly, <math> D </math> is a density model for the data distribution and <math> G </math> learns to sample from <math> D </math>. | * More importantly, <math> D </math> is a density model for the data distribution and <math> G </math> learns to sample from <math> D </math>. | ||
== Methodology== | == Methodology== | ||
===Adversarial Fisher Vectors=== | ===Adversarial Fisher Vectors=== | ||
As it was mentioned, one the most important | As it was mentioned, one of the most important advantages of an EBM GAN compared with traditional ones is that discriminator is a dual form of the generator. This means that the discriminator can define a distribution that matches the training data. Generally, there is a straightforward way to evaluate the quality of the generator and inspect the quality of produced samples. However, when it comes to discriminator, this is not clear how to evaluate or use a discriminator trained in minimax scheme. To evaluate and also employ discriminator of the GAN, the authors in this paper propose to employ the theory of Fisher Information. This theory was proposed with the motivation of making connections between two different types of models used in machine learning i.e, generative and discriminator models. Given a density model <math> p_{\theta}(\mathbf{x})</math> where <math> \mathbf{x} \in R^d </math> and <math> \theta </math> are input and model parameters, the fisher score of an example <math> \mathbf{x} </math> is defined as <math> U_\mathbf{x}=\nabla_{\theta} \log p_{\theta}(\mathbf{x}) </math>. This gradient maps an example <math> \mathbf{x} </math> into a feature vector that is a point in the gradient space of the manifold. Intuitively, This gradient <math> U_\mathbf{x} </math> can be used to define the direction of steepest ascent in <math> \log p(\mathbf{x}|\theta) </math> for the example <math> \mathbf{x} </math> along the manifold. In other words, The Fisher | ||
Score encodes the desired change of model parameters to better fit the example <math> \mathbf{x} </math>. The authors define the Fisher Information as <math> I=E_{\mathbf{x} \sim} p_{\theta}(\mathbf{x}) [U_\mathbf{x} U_\mathbf{x}^T]</math>. Having Fisher Information and Fisher Score, one can then map an example <math> \mathbf{x} </math> from feature space to the model space, and measure the proximity between two examples <math> \mathbf{x} </math>; <math> \mathbf{y} </math> by <math> U_\mathbf{x}^T I^{-1} U_\mathbf{y}</math>. The metric distance based on this proximity is defined as <math> (U_\mathbf{x}-U_\mathbf{y})^T I^{-1} (U_\mathbf{x}-U_\mathbf{y})</math>. This metric distance is called Fisher distance and easily can be | Score encodes the desired change of model parameters to better fit the example <math> \mathbf{x} </math>. The authors define the Fisher Information as <math> I=E_{\mathbf{x} \sim} p_{\theta}(\mathbf{x}) [U_\mathbf{x} U_\mathbf{x}^T]</math>. Having Fisher Information and Fisher Score, one can then map an example <math> \mathbf{x} </math> from feature space to the model space, and measure the proximity between two examples <math> \mathbf{x} </math>; <math> \mathbf{y} </math> by <math> U_\mathbf{x}^T I^{-1} U_\mathbf{y}</math>. The metric distance based on this proximity is defined as <math> (U_\mathbf{x}-U_\mathbf{y})^T I^{-1} (U_\mathbf{x}-U_\mathbf{y})</math>. This metric distance is called Fisher distance and easily can be generalised to measure distance between two sets. Finally, The adversarial Fisher Distance (AFV) is defined as | ||
| Line 62: | Line 64: | ||
\end{equation} | \end{equation} | ||
As | As a result, Fisher Distance is equivalent to the Euclidean distance with AFVs. The fisher vector theory has been using simple generative models like gmms. | ||
In the domain of the EBMs, where the density model is | In the domain of the EBMs, where the density model is parameterised as <math> p_\theta(\mathbf{x})= \frac{e^{-D(\mathbf{x},\theta)}}{\int_{\mathbf{x}} e^{-D(\mathbf{x},\theta)} \,d\mathbf{x}} </math> and <math> \theta </math> are parameters of <math> D</math>, the fisher score is derived as | ||
| Line 90: | Line 92: | ||
\end{equation} | \end{equation} | ||
Remember that by using Fisher Score, we transform data from feature space to the parameter space which means that the dimensionality of the | Remember that by using Fisher Score, we transform data from feature space to the parameter space which means that the dimensionality of the vectors can easily be up to millions. As a result, replacing <math> I </math> with <math>\mbox{diag}(I) </math> is an attempt to reduce the computational load of calculating final AFV. | ||
=== On the Fisher metric === | |||
The Fisher metric between two points <math>x,y \in \mathbb{R}^d</math> is defined as <math> d(x,y) = (U_x - Y_y)^T \mathcal{I}^{-1} (U_x - U_y) </math>; being a quadratic form, it is elementary to see that this distance is equivalent to the usual norm in <math>\mathbb{R}^d</math>. | |||
A notion of a Fisher distance between finite subsets <math>X,Y \subset \mathbb{R}^d</math> is: | |||
\begin{align} | |||
dist(X,Y) = \left( \frac{1}{|X|} \sum_{x \in X} U_x - \frac{1}{|Y|} \right)^T \mathcal{I}^{-1} \left( \frac{1}{|X|} \sum_{x \in X} U_x - \frac{1}{|Y|} \right) | |||
\end{align} | |||
Note, however, that this is not a metric. An alternative to extending the Fisher distance to compact subsets of <math>\mathbb{R}^d</math> is to use the Hausdorff metric from elementary real analysis. A discussion of the Hausdorff metric can be found on page 5 of Ken Davidson's Real Analysis notes: http://www.math.uwaterloo.ca/~krdavids/PM351/PMath351Notes.pdf. For completeness, given two compact subsets <math>K, L \subset \mathbb{R}^d</math> the Hausdorff metric induced by the Fisher distance is given by: | |||
\begin{align} | |||
d_H(K,L) = \max \left\lbrace \sup_{a \in K} d(a, L), \sup_{b \in L} d(b,K) \right\rbrace | |||
\end{align} | |||
It is readily seen that this is a complete metric on the metric space of compact subsets of <math>\mathbb{R}^d</math>. The analysis performed in the paper might be able to be extended to the choice of this metric. | |||
===Generator update as stochastic gradient MCMC=== | |||
The use of a generator provides an efficient way of drawing samples from the EBM. However, in practice, great care needs to be taken to make sure that G is well conditioned to produce examples that cover enough modes of D. There is also a related issue where the parameters of G will occasionally undergo sudden changes, generating samples drastically different from iteration to iteration, which contributes to training instability and lower model quality. | |||
In light of these issues, they provide a different treatment of G, borrowing inspirations from the Markov chain Monte Carlo (MCMC) literature. MCMC variants have been widely studied in the context of EBM's, which can be used to sample from an unnormalised density and approximate the partition function. Stochastic gradient MCMC is of particular interest as it uses the gradient of the log probability w.r.t. the input, and performs gradient ascent to incrementally update the samples(while adding noise to the gradients). See for a recent application of this technique to deepEBMs. We speculate that it is possible to train G to mimic the stochastic gradient MCMC update rule, such that the samples produced by G will approximate the true model distribution. | |||
== Related Work == | |||
There are many variants of GAN method that use a discriminator as a critic to differentiate given distributions. Examples of such variants are Wasserstein GAN, f-GAN and MMD-GAN. There is a resemblance between the training procedure of GAN and deep EBM (with variational inference) but the work present in the paper is different as its discriminator directly learns the target distribution. The implementation of EBM presented in the paper directly learns the parametrised sampler. In some works, regularisation (by noise addition, penalising gradients, spectral normalisation) has been introduced to make GAN more stable. But these additions do not have any formal justification. This paper connects the MCMC based G update rule with the gradient penalty line of work. The following equation show how this method does not always sample from the generator but a small proportion (with probability p) of the samples come from real examples. | |||
<div align="center">[[File:related_work_equations.png]]</div> | |||
Early works showed incorporation of Fisher Information to measure similarity and this was extended to use Fisher Vector representations in case of images. Recently, Fisher Information has been used for meta learning as well. This paper explores the possibility of using Fisher Information in deep learning generative models. By using the generator as a sampler, Fisher Information can be computed even from an unnormalised density model. | |||
== Experiments == | == Experiments == | ||
===Evaluating AFV representations=== | ===Evaluating AFV representations=== | ||
As it was pointed out, the main advantage of the EBM GANs is their powerful discriminator which | As it was pointed out, the main advantage of the EBM GANs is their powerful discriminator, which can learn a density function that characterises the data manifold of the training data. To evaluate how good the discriminator learns the data distribution, authors proposed to use Fisher Information theory. To do this, authors trained some models under different models and employed the discriminator to extract AFVs and then use these vectors for unsupervised pretraining classification task. | ||
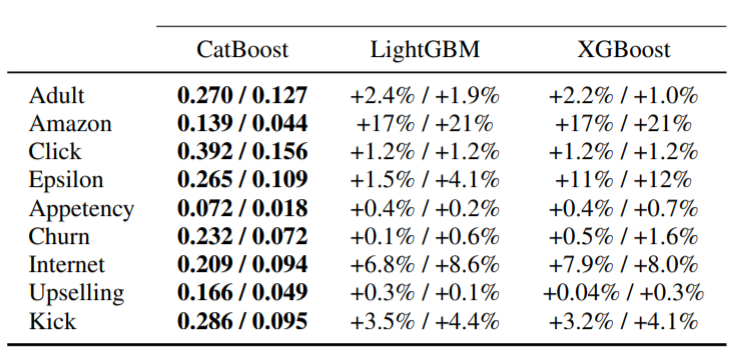
Results in Table 1 suggest that AFVs achieve state-of-art performance in unsupervised pretraining classification | Results in Table 1 suggest that AFVs achieve state-of-art performance in unsupervised pretraining classification tasks and comparable with the supervised learning. | ||
[[File:Table1.png]] | [[File:Table1.png||center]] | ||
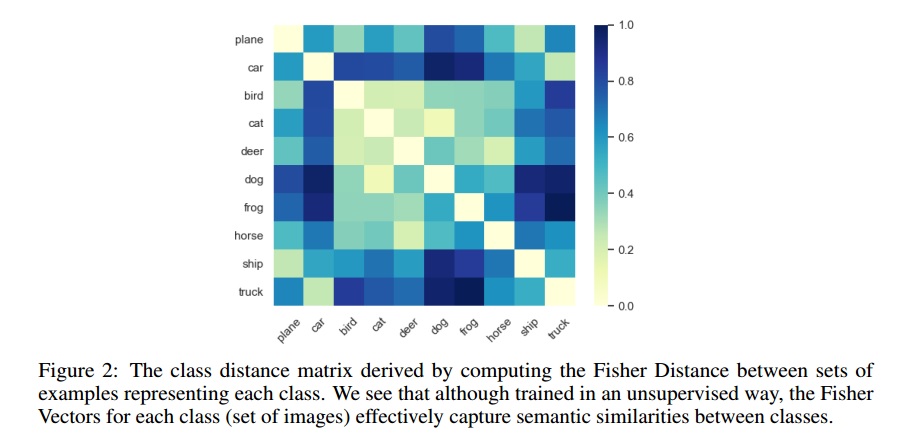
AFVs can also be used to measure distance between a set of data points. Authors took advantage of this point and calculate the semantic distance between classes (all data points of every class) in CIFAR 10. As | AFVs can also be used to measure distance between a set of data points. Authors took advantage of this point and calculate the semantic distance between classes (all data points of every class) in CIFAR 10. As shown in Figure 2, although the training has been unsupervised, the semantic relation between classes is well estimated. For example, in Figure 2 cars are similar to trucks, dogs are similar to cats. | ||
[[File:Sobhan_Fig2.jpg]] | [[File:Sobhan_Fig2.jpg||center]] | ||
| Line 108: | Line 136: | ||
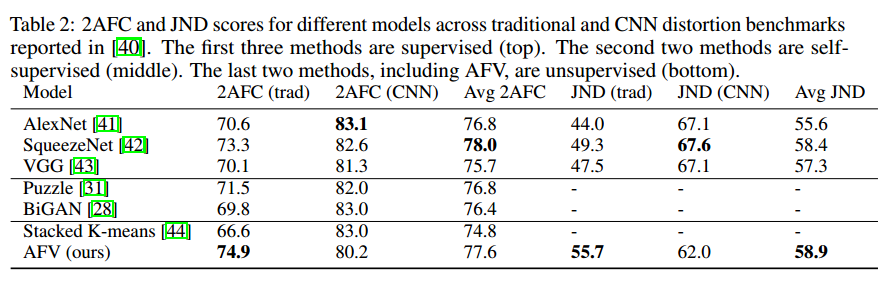
Table 2 shows the performance of AFV along with a variety of existing benchmarks. Clearly, AFV exceeds the reported unsupervised and self-supervised methods and is competitive with supervised methods trained on ImageNet. | Table 2 shows the performance of AFV along with a variety of existing benchmarks. Clearly, AFV exceeds the reported unsupervised and self-supervised methods and is competitive with supervised methods trained on ImageNet. | ||
[[File:Sobhan_Table2.png]] | [[File:Sobhan_Table2.png||center]] | ||
An interesting point about AFVs is their robustness to overfitting. AFVs are 3 orders of magnitude higher than those of the existing methods, which would typically bring a higher propensity to overfitting. However, AFVs still show great | An interesting point about AFVs is their robustness to overfitting. AFVs are 3 orders of magnitude higher than those of the existing methods, which would typically bring a higher propensity to overfitting. However, AFVs still show great generalisation ability, demonstrating that they are indeed encoding a meaningful low dimensional subspace of original data. Figure 6 shows the nearest neighbours. | ||
[[File:Sobhan_Fig_6.png]] | [[File:Sobhan_Fig_6.png||center]] | ||
===Using the Fisher Distance to monitor training=== | ===Using the Fisher Distance to monitor training=== | ||
Training GANs has been a challenging task which is | Training GANs has been a challenging task which is partly because of the lack of reliable metrics. Although recently some domain specific metrics such as Inception Scores and Fréchet Inception Distance have been proposed, they are mainly relied on a discriminative model trained on ImageNet, and thus have limited | ||
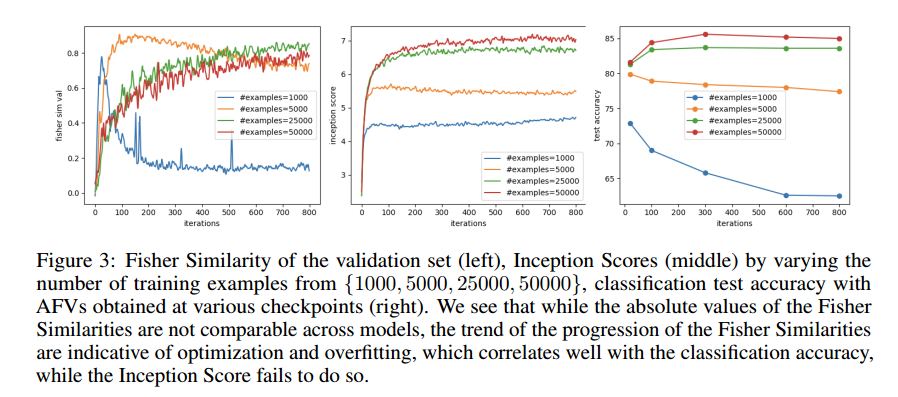
applicability to datasets that are drastically different. In this paper, authors the Fisher Distance between the set of real and generated examples to monitor and diagnose the training process. To do this, conducted a set of experiments on CIFAR10 by varying the number of training examples from the set {1000; 5000; 25000; 50000}. Figure 3 shows batch-wise estimate of Inception Score and the "Fisher Similarity". This is clear that for higher number of training examples, the validation Fisher Similarity steadily increases, in the similar trend to the Inception Score. On the other hand, when the number of training examples is small, the validation Fisher Similarity starts decreasing at some point. | applicability to datasets that are drastically different. In this paper, authors the Fisher Distance between the set of real and generated examples to monitor and diagnose the training process. To do this, conducted a set of experiments on CIFAR10 by varying the number of training examples from the set {1000; 5000; 25000; 50000}. Figure 3 shows batch-wise estimate of Inception Score and the "Fisher Similarity". This is clear that for higher number of training examples, the validation Fisher Similarity steadily increases, in the similar trend to the Inception Score. On the other hand, when the number of training examples is small, the validation Fisher Similarity starts decreasing at some point. | ||
[[File:Sobhan_Fig_3.png]] | [[File:Sobhan_Fig_3.png||center]] | ||
===Interpreting G update as parameterised MCMC=== | |||
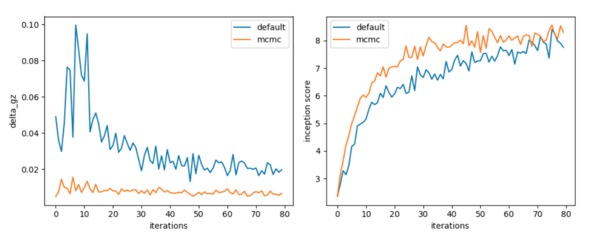
AFC can only be applied if a generator approximates EBM during the training process. Model is trained on Imagenet with 64X64 along with modification of default architecture with the addition of residual blocks to discriminator and generator. Following figure shows training stats over 80,000 iterations. | |||
[[File:training 80K.png|600px|center]] | |||
<div align="center">Left: default generator objective. Right: corresponding Inception scores.</div> | |||
== Conclusion == | == Conclusion == | ||
In this paper, authors demonstrated that GANs can be reinterpreted in order to learn representations across a diverse set of tasks without requiring domain knowledge or | In this paper, the authors demonstrated that GANs can be reinterpreted in order to learn representations across a diverse set of tasks without requiring domain knowledge or annotated data. Authors also showed that in an EBM GAN, discriminator can explicitly learn data distribution and capture the intrinsic manifold of data with low error rate. This is especially different from regular GANs where the discriminator is reduced to a constant function once the Nash Equilibrium is reached. To evaluate how well the discriminator estimates data distribution, the authors took advantage of Fisher Information theory. First, they showed that AFVs are a reliable indicator of whether GAN | ||
training is well behaved, and that we can use this monitoring to select good model checkpoints. Second they | training is well behaved, and that we can use this monitoring to select good model checkpoints. Second, they illustrated that AFVs are a useful feature representation for linear and nearest neighbour classification, achieving state-of-the-art among unsupervised feature representations and competitive with supervised results on CIFAR-10. | ||
Finally, | Finally, they showed that a well-trained GAN discriminator does contain useful information for fine-grained perceptual similarity suggesting that AFVs are good candidates for image search. All in all, the conducted experiments show the effectiveness of the EBM GANs coupled with the Fisher Information framework for extracting useful representational features from GANs. | ||
As future work, authors propose to improve the scalability of the AFV method by compressing the Fisher Vector representation, using methods like product quantisation. | |||
== Source Code == | |||
The code for this paper is freely available at [https://github.com/apple/ml-afv link Adversarial Fisher Vectors]. | |||
== Critique == | |||
This paper has an excellent contribution in feature representation exploiting information theory and GANs. Although it lacked intuitive explanation of the defined formula and how this representation is performing well in classification tasks. Therefore, an "Analysis" section would help the paper to be more readable and understandable. | |||
== References== | == References== | ||
Latest revision as of 16:50, 6 December 2020
Presented by
Sobhan Hemati
Introduction
Generative adversarial networks (GANs) are among the most important generative models, where discriminators and generators compete with each other to solve a minimax game. Based on the original GAN paper, when the training is finished and Nash Equilibrium is reached, the discriminator is nothing but a constant function that assigns a score of 0.5 everywhere. This means that in this setting discriminator is nothing more than a tool to train the generator. Furthermore, the generator in traditional GAN models the data density in an implicit manner, while in some applications we need to have an explicit generative model of data. Recently, it has been shown that training an energy-based model (EBM) with a parameterised variational distribution is also a minimax game similar to the one in GAN. Although they are similar, an advantage of this EBM view is that unlike the original GAN formulation, the discriminator itself is an explicit density model of the data.
Considering some remarks, the authors in this paper show that an energy-based model can be trained using a similar minimax formulation in GANs. After training the energy-based model, they use Fisher Score and Fisher Information (which are calculated based on derivative of the generative models w.r.t its parameters) to evaluate the power of discriminator in modeling the data distribution. More precisely, they calculate normalised Fisher Vectors and Fisher Distance measure using the discriminator's derivative to estimate similarities both between individual data samples and between sets of samples. They name these derived representations Adversarial Fisher Vectors (AFVs). In fact, Fisher vector is a powerful representation that can be calculated using EBMs thanks to the fact that in this EBM model, the discriminator itself is an explicit density model of the data. Fisher vector can be used for setting representation problems which is a challenging task. In fact, as we will see, we can use the Fisher kernel to calculate the distance between two sets of images which is not a trivial task. The authors find several applications and attractive characteristics for AFV as pre-trained features such as:
- State-of-the-art performance for unsupervised feature extraction and linear classification tasks.
- Using the similarity function induced by the learned density model as a perceptual metric that correlates well with human judgments.
- Improved training of GANs through monitoring (AFV metrics) and stability (MCMC updates) which is a difficult task in general.
- Using AFV to estimate the distance between sets which allows monitoring the training process. More precisely, the Fisher Distance between the set of validation examples and generated examples can effectively capture the existence of overfitting.
Background
Generative Adversarial Networks
GANs are a clever way of training a generative model by framing the problem as a supervised learning problem with two sub-models: the generator model that we train to generate new examples, and the discriminator model that tries to classify examples as either real (from the domain) or fake (generated). The weights of generator and discriminator are updated by solving the following optimisation problem: \begin{equation} \underset{G}{\text{max}} \ \underset{D}{\text{min}} \ E_{\mathbf{x} \sim p_{data(\mathbf{x})}}[-\log D(\mathbf{x})]- E_{\mathbf{z} \sim p_{\mathbf{z}}(\mathbf{z})}[-\log (1-D(G(\mathbf{z})))] \tag{1} \label{1} \end{equation}
Where [math]\displaystyle{ p_{data(\mathbf{x})} }[/math], [math]\displaystyle{ D(x) }[/math], and [math]\displaystyle{ G(x) }[/math] are distribution of data, discriminator, and generator respectively. To optimise the above problem, in the inner loop [math]\displaystyle{ D }[/math] is trained until convergence given [math]\displaystyle{ G }[/math], and in the outer loop [math]\displaystyle{ G }[/math], is updated one step given [math]\displaystyle{ D }[/math].
GANs as variational training of deep EBMs
An energy-based model (EBM) is a form of generative model (GM) that learns the characteristics of a target dataset and generates a similar but larger dataset. EBMs detect the latent variables of a dataset and generate new datasets with a similar distribution. Let an energy-based model define a density function [math]\displaystyle{ p_{E}(\mathbf{x}) }[/math] as [math]\displaystyle{ \frac{e^{-E(\mathbf{x})}}{ \int_{\mathbf{x}} e^{-E(\mathbf{x})} \,d\mathbf{x} } }[/math]. Then, the negative log likelihood (NLL) of the [math]\displaystyle{ p_{E}(\mathbf{x}) }[/math] can be written as
\begin{equation} E_{\mathbf{x} \sim p_{data(\mathbf{x})}}[E(\mathbf{x})]+ \log \int_{\mathbf{x}} q(\mathbf{x}) \frac{e^{-E(\mathbf{x})}} {q(\mathbf{x})}\,d\mathbf{x} = E_{\mathbf{x} \sim p_{data(\mathbf{x})}}[E(\mathbf{x})]+ \log E_{\mathbf{x} \sim q(\mathbf{x})}[\frac{e^{-E(\mathbf{x})}} {q(\mathbf{x})}] \geq \\ E_{\mathbf{x} \sim p_{data(\mathbf{x})}}[E(\mathbf{x})]+ E_{\mathbf{x} \sim q(\mathbf{x})}[\log \frac{e^{-E(\mathbf{x})}} {q(\mathbf{x})}]= E_{\mathbf{x} \sim p_{data(\mathbf{x})}}[E(\mathbf{x})]- E_{\mathbf{x} \sim q(\mathbf{x})}[E(\mathbf{x})] + H(q) \tag{2} \label{2} \end{equation}
where [math]\displaystyle{ q(x) }[/math] is an auxiliary distribution which is called the variational distribution and [math]\displaystyle{ H(q) }[/math] defines its entropy. Here Jensen’s inequality was used to obtain the variational lower bound on the NLL given [math]\displaystyle{ H(q) }[/math]. This bound is tight if [math]\displaystyle{ q(x) \propto e^{-E(\mathbf{x})} \ \forall \mathbf{x}, }[/math] which means [math]\displaystyle{ q(x) = p_{E}(\mathbf{x}) }[/math]. In this case, if we put [math]\displaystyle{ D(\mathbf{x})= -E(\mathbf{x}) }[/math] and also [math]\displaystyle{ q(x)= p_{G}(\mathbf{x}) }[/math], Eq.\ref{2} turns to the following problem:
\begin{equation} \underset{D}{\text{min}} \ \underset{G}{\text{max}} \ E_{\mathbf{x} \sim p_{data(\mathbf{x})}}[-\log D(\mathbf{x})]+ E_{\mathbf{z} \sim p_{\mathbf{z}}(\mathbf{z})}[\log (D(G(\mathbf{z})))] +H(p_{G}) \tag{3} \label{3} \end{equation}
where in the problem, the variational lower bound is maximised w.r.t. [math]\displaystyle{ p_{G} }[/math]; the energy model then is updated one step to decrease the NLL with the optimal [math]\displaystyle{ p_{G} }[/math] (see Figure1).
Equations \ref{3} and \ref{1} are similar in the sense that both taking the form of a minimax game between [math]\displaystyle{ D }[/math] and [math]\displaystyle{ G }[/math]. However, there are 3 major differences:
- The entropy regularisation term [math]\displaystyle{ H(p_{G}) }[/math] in Eq. \ref{3} prevents the generator from collapsing (although in practice, it is difficult to come up with a differentiable approximation to the entropy term [math]\displaystyle{ H(p_{G}) }[/math] and instead heuristic regularisation methods such as batch normalisation are used).
- The order of optimising [math]\displaystyle{ D }[/math] and [math]\displaystyle{ G }[/math] is different.
- More importantly, [math]\displaystyle{ D }[/math] is a density model for the data distribution and [math]\displaystyle{ G }[/math] learns to sample from [math]\displaystyle{ D }[/math].
Methodology
Adversarial Fisher Vectors
As it was mentioned, one of the most important advantages of an EBM GAN compared with traditional ones is that discriminator is a dual form of the generator. This means that the discriminator can define a distribution that matches the training data. Generally, there is a straightforward way to evaluate the quality of the generator and inspect the quality of produced samples. However, when it comes to discriminator, this is not clear how to evaluate or use a discriminator trained in minimax scheme. To evaluate and also employ discriminator of the GAN, the authors in this paper propose to employ the theory of Fisher Information. This theory was proposed with the motivation of making connections between two different types of models used in machine learning i.e, generative and discriminator models. Given a density model [math]\displaystyle{ p_{\theta}(\mathbf{x}) }[/math] where [math]\displaystyle{ \mathbf{x} \in R^d }[/math] and [math]\displaystyle{ \theta }[/math] are input and model parameters, the fisher score of an example [math]\displaystyle{ \mathbf{x} }[/math] is defined as [math]\displaystyle{ U_\mathbf{x}=\nabla_{\theta} \log p_{\theta}(\mathbf{x}) }[/math]. This gradient maps an example [math]\displaystyle{ \mathbf{x} }[/math] into a feature vector that is a point in the gradient space of the manifold. Intuitively, This gradient [math]\displaystyle{ U_\mathbf{x} }[/math] can be used to define the direction of steepest ascent in [math]\displaystyle{ \log p(\mathbf{x}|\theta) }[/math] for the example [math]\displaystyle{ \mathbf{x} }[/math] along the manifold. In other words, The Fisher Score encodes the desired change of model parameters to better fit the example [math]\displaystyle{ \mathbf{x} }[/math]. The authors define the Fisher Information as [math]\displaystyle{ I=E_{\mathbf{x} \sim} p_{\theta}(\mathbf{x}) [U_\mathbf{x} U_\mathbf{x}^T] }[/math]. Having Fisher Information and Fisher Score, one can then map an example [math]\displaystyle{ \mathbf{x} }[/math] from feature space to the model space, and measure the proximity between two examples [math]\displaystyle{ \mathbf{x} }[/math]; [math]\displaystyle{ \mathbf{y} }[/math] by [math]\displaystyle{ U_\mathbf{x}^T I^{-1} U_\mathbf{y} }[/math]. The metric distance based on this proximity is defined as [math]\displaystyle{ (U_\mathbf{x}-U_\mathbf{y})^T I^{-1} (U_\mathbf{x}-U_\mathbf{y}) }[/math]. This metric distance is called Fisher distance and easily can be generalised to measure distance between two sets. Finally, The adversarial Fisher Distance (AFV) is defined as
\begin{equation}
V_\mathbf{x}=I^{-\frac{1}{2}}U_\mathbf{x}
\end{equation}
As a result, Fisher Distance is equivalent to the Euclidean distance with AFVs. The fisher vector theory has been using simple generative models like gmms. In the domain of the EBMs, where the density model is parameterised as [math]\displaystyle{ p_\theta(\mathbf{x})= \frac{e^{-D(\mathbf{x},\theta)}}{\int_{\mathbf{x}} e^{-D(\mathbf{x},\theta)} \,d\mathbf{x}} }[/math] and [math]\displaystyle{ \theta }[/math] are parameters of [math]\displaystyle{ D }[/math], the fisher score is derived as
\begin{equation}
U_\mathbf{x}=\nabla_{\theta} D(\mathbf{x};\theta) - \nabla_{\theta} \log \int_{\mathbf{x}} e^{D(\mathbf{x},\theta)} \,d\mathbf{x}= \nabla_{\theta} D(\mathbf{x};\theta) - E_{\mathbf{x} \sim p_\theta(\mathbf{x})} \nabla_{\theta} D(\mathbf{x};\theta).
\tag{4}
\label{4}
\end{equation}
As we know, in an EBM GAN, the generator is updated during the training to match the distribution of [math]\displaystyle{ p_G(\mathbf{x}) }[/math] to [math]\displaystyle{ p_\theta(\mathbf{x}) }[/math]. This allows us to approximate the second term in Eq.\ref{4} by sampling form generator's distribution which let us to compute the Fisher Information and Fisher Score in EBM GAN as follow:
\begin{equation} U_\mathbf{x}=\nabla_{\theta} D(\mathbf{x};\theta) - E_{\mathbf{z} \sim p(\mathbf{z})} \nabla_{\theta} D(G(\mathbf{z});\theta), \quad I= E_{\mathbf{z} \sim p(\mathbf{z})}[U_{G(\mathbf{z})} U^T_{G(\mathbf{z})}] \tag{5} \label{5} \end{equation}
Finally, having Fisher Score and Fisher Information, we use the following approximation to calculate AFV:
\begin{equation}
V_\mathbf{x}=\mbox{diag}(I)^{-\frac{1}{2}}U_\mathbf{x}
\tag{6}
\label{6}
\end{equation}
Remember that by using Fisher Score, we transform data from feature space to the parameter space which means that the dimensionality of the vectors can easily be up to millions. As a result, replacing [math]\displaystyle{ I }[/math] with [math]\displaystyle{ \mbox{diag}(I) }[/math] is an attempt to reduce the computational load of calculating final AFV.
On the Fisher metric
The Fisher metric between two points [math]\displaystyle{ x,y \in \mathbb{R}^d }[/math] is defined as [math]\displaystyle{ d(x,y) = (U_x - Y_y)^T \mathcal{I}^{-1} (U_x - U_y) }[/math]; being a quadratic form, it is elementary to see that this distance is equivalent to the usual norm in [math]\displaystyle{ \mathbb{R}^d }[/math]. A notion of a Fisher distance between finite subsets [math]\displaystyle{ X,Y \subset \mathbb{R}^d }[/math] is: \begin{align} dist(X,Y) = \left( \frac{1}{|X|} \sum_{x \in X} U_x - \frac{1}{|Y|} \right)^T \mathcal{I}^{-1} \left( \frac{1}{|X|} \sum_{x \in X} U_x - \frac{1}{|Y|} \right) \end{align}
Note, however, that this is not a metric. An alternative to extending the Fisher distance to compact subsets of [math]\displaystyle{ \mathbb{R}^d }[/math] is to use the Hausdorff metric from elementary real analysis. A discussion of the Hausdorff metric can be found on page 5 of Ken Davidson's Real Analysis notes: http://www.math.uwaterloo.ca/~krdavids/PM351/PMath351Notes.pdf. For completeness, given two compact subsets [math]\displaystyle{ K, L \subset \mathbb{R}^d }[/math] the Hausdorff metric induced by the Fisher distance is given by: \begin{align} d_H(K,L) = \max \left\lbrace \sup_{a \in K} d(a, L), \sup_{b \in L} d(b,K) \right\rbrace \end{align}
It is readily seen that this is a complete metric on the metric space of compact subsets of [math]\displaystyle{ \mathbb{R}^d }[/math]. The analysis performed in the paper might be able to be extended to the choice of this metric.
Generator update as stochastic gradient MCMC
The use of a generator provides an efficient way of drawing samples from the EBM. However, in practice, great care needs to be taken to make sure that G is well conditioned to produce examples that cover enough modes of D. There is also a related issue where the parameters of G will occasionally undergo sudden changes, generating samples drastically different from iteration to iteration, which contributes to training instability and lower model quality.
In light of these issues, they provide a different treatment of G, borrowing inspirations from the Markov chain Monte Carlo (MCMC) literature. MCMC variants have been widely studied in the context of EBM's, which can be used to sample from an unnormalised density and approximate the partition function. Stochastic gradient MCMC is of particular interest as it uses the gradient of the log probability w.r.t. the input, and performs gradient ascent to incrementally update the samples(while adding noise to the gradients). See for a recent application of this technique to deepEBMs. We speculate that it is possible to train G to mimic the stochastic gradient MCMC update rule, such that the samples produced by G will approximate the true model distribution.
Related Work
There are many variants of GAN method that use a discriminator as a critic to differentiate given distributions. Examples of such variants are Wasserstein GAN, f-GAN and MMD-GAN. There is a resemblance between the training procedure of GAN and deep EBM (with variational inference) but the work present in the paper is different as its discriminator directly learns the target distribution. The implementation of EBM presented in the paper directly learns the parametrised sampler. In some works, regularisation (by noise addition, penalising gradients, spectral normalisation) has been introduced to make GAN more stable. But these additions do not have any formal justification. This paper connects the MCMC based G update rule with the gradient penalty line of work. The following equation show how this method does not always sample from the generator but a small proportion (with probability p) of the samples come from real examples.
Early works showed incorporation of Fisher Information to measure similarity and this was extended to use Fisher Vector representations in case of images. Recently, Fisher Information has been used for meta learning as well. This paper explores the possibility of using Fisher Information in deep learning generative models. By using the generator as a sampler, Fisher Information can be computed even from an unnormalised density model.
Experiments
Evaluating AFV representations
As it was pointed out, the main advantage of the EBM GANs is their powerful discriminator, which can learn a density function that characterises the data manifold of the training data. To evaluate how good the discriminator learns the data distribution, authors proposed to use Fisher Information theory. To do this, authors trained some models under different models and employed the discriminator to extract AFVs and then use these vectors for unsupervised pretraining classification task. Results in Table 1 suggest that AFVs achieve state-of-art performance in unsupervised pretraining classification tasks and comparable with the supervised learning.
AFVs can also be used to measure distance between a set of data points. Authors took advantage of this point and calculate the semantic distance between classes (all data points of every class) in CIFAR 10. As shown in Figure 2, although the training has been unsupervised, the semantic relation between classes is well estimated. For example, in Figure 2 cars are similar to trucks, dogs are similar to cats.
As AFVs transform data from feature space to the parameter space of the generative model and as a result carry information about the data manifold, they are also expected to carry additional fine-grained perceptual information. To evaluate this, authors ran experiments to examine the usefulness of AFVs as a perceptual similarity metric consistent with human judgments. They use the AFV representation to calculate distances between image patches and compare with current methods on the Berkeley-Adobe Perceptual Patch Similarity (BAPPS) dataset on 2AFC and Just Noticeable Difference (JND) metrics. They trained a GAN on ImageNet and then calculate AFVs on the BAPPS evaluation set.
Table 2 shows the performance of AFV along with a variety of existing benchmarks. Clearly, AFV exceeds the reported unsupervised and self-supervised methods and is competitive with supervised methods trained on ImageNet.
An interesting point about AFVs is their robustness to overfitting. AFVs are 3 orders of magnitude higher than those of the existing methods, which would typically bring a higher propensity to overfitting. However, AFVs still show great generalisation ability, demonstrating that they are indeed encoding a meaningful low dimensional subspace of original data. Figure 6 shows the nearest neighbours.

Using the Fisher Distance to monitor training
Training GANs has been a challenging task which is partly because of the lack of reliable metrics. Although recently some domain specific metrics such as Inception Scores and Fréchet Inception Distance have been proposed, they are mainly relied on a discriminative model trained on ImageNet, and thus have limited applicability to datasets that are drastically different. In this paper, authors the Fisher Distance between the set of real and generated examples to monitor and diagnose the training process. To do this, conducted a set of experiments on CIFAR10 by varying the number of training examples from the set {1000; 5000; 25000; 50000}. Figure 3 shows batch-wise estimate of Inception Score and the "Fisher Similarity". This is clear that for higher number of training examples, the validation Fisher Similarity steadily increases, in the similar trend to the Inception Score. On the other hand, when the number of training examples is small, the validation Fisher Similarity starts decreasing at some point.
Interpreting G update as parameterised MCMC
AFC can only be applied if a generator approximates EBM during the training process. Model is trained on Imagenet with 64X64 along with modification of default architecture with the addition of residual blocks to discriminator and generator. Following figure shows training stats over 80,000 iterations.
Conclusion
In this paper, the authors demonstrated that GANs can be reinterpreted in order to learn representations across a diverse set of tasks without requiring domain knowledge or annotated data. Authors also showed that in an EBM GAN, discriminator can explicitly learn data distribution and capture the intrinsic manifold of data with low error rate. This is especially different from regular GANs where the discriminator is reduced to a constant function once the Nash Equilibrium is reached. To evaluate how well the discriminator estimates data distribution, the authors took advantage of Fisher Information theory. First, they showed that AFVs are a reliable indicator of whether GAN training is well behaved, and that we can use this monitoring to select good model checkpoints. Second, they illustrated that AFVs are a useful feature representation for linear and nearest neighbour classification, achieving state-of-the-art among unsupervised feature representations and competitive with supervised results on CIFAR-10. Finally, they showed that a well-trained GAN discriminator does contain useful information for fine-grained perceptual similarity suggesting that AFVs are good candidates for image search. All in all, the conducted experiments show the effectiveness of the EBM GANs coupled with the Fisher Information framework for extracting useful representational features from GANs. As future work, authors propose to improve the scalability of the AFV method by compressing the Fisher Vector representation, using methods like product quantisation.
Source Code
The code for this paper is freely available at link Adversarial Fisher Vectors.
Critique
This paper has an excellent contribution in feature representation exploiting information theory and GANs. Although it lacked intuitive explanation of the defined formula and how this representation is performing well in classification tasks. Therefore, an "Analysis" section would help the paper to be more readable and understandable.
References
Jaakkola, Tommi, and David Haussler. "Exploiting generative models in discriminative classifiers." Advances in neural information processing systems. 1999.
Zhai, Shuangfei, et al. "Adversarial Fisher Vectors for Unsupervised Representation Learning." Advances in Neural Information Processing Systems. 2019.
Perronnin, Florent, and Christopher Dance. "Fisher kernels on visual vocabularies for image categorization." 2007 IEEE conference on computer vision and pattern recognition. IEEE, 2007.
Sánchez, Jorge, et al. "Image classification with the fisher vector: Theory and practice." International journal of computer vision 105.3 (2013): 222-245.