User:Msikarou: Difference between revisions
| (46 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
== Previous Work == | == Previous Work == | ||
Originated from model-agnostic meta-learning (MAML), episodic training has been vastly leveraged for addressing domain generalization [ | Originated from model-agnostic meta-learning (MAML), episodic training has been vastly leveraged for addressing domain generalization [3, 4, 5, 7, 8, 6, 9, 10, 11]. The method of MLDG [4] closely follows MAML in terms of back-propagating the gradients from an ordinary task loss on meta-test data, but it has its own limitation as the use of the task objective might be sub-optimal since it only uses class probabilities. Most of the works [3,7] in the literature lack notable guidance from the semantics of feature space, which contains crucial domain-independent ‘general knowledge’ that can be useful for domain generalization. The authors claim that their method is orthogonal to previous works. | ||
| Line 22: | Line 22: | ||
<math> F_{\psi}: X \rightarrow Z</math> where <math> Z </math> is a feature space | <math> F_{\psi}: X \rightarrow Z</math> where <math> Z </math> is a feature space | ||
<math> T_{\theta}: X \rightarrow \mathbf {R}^{C}</math> where <math> C </math> is the number of classes in <math> Y </math> | <math> T_{\theta}: X \rightarrow \mathbf {R}^{C}</math> where <math> C </math> is the number of classes in <math> Y </math> | ||
Assume that <math>\hat{y}= softmax(T_{\theta}(F_{\psi}(x))) </math>. The parameters <math> (\psi, \theta) </math> are optimized with minimizing a cross-entropy loss namely <math> \mathbf{L}_{task} </math> formulated as <math> l_{task}(y, \hat{y} = - \sum_{c}1[y=C]log(\hat{y}_{c})) </math> | Assume that <math>\hat{y}= softmax(T_{\theta}(F_{\psi}(x))) </math>. The parameters <math> (\psi, \theta) </math> are optimized with minimizing a cross-entropy loss namely <math> \mathbf{L}_{task} </math> formulated as: | ||
<div style="text-align: center;"> | |||
<math> l_{task}(y, \hat{y} = - \sum_{c}1[y=C]log(\hat{y}_{c})) </math> | |||
</div> | |||
Although the task loss is a decent predictor nothing prevents the model from overfitting to the source domains and suffering from degradation on unseen test domains. So the other loss terms are responsible for this aim. | Although the task loss is a decent predictor nothing prevents the model from overfitting to the source domains and suffering from degradation on unseen test domains. So the other loss terms are responsible for this aim. | ||
=== Global class alignment === | === Global class alignment === | ||
Since <math> L_{task} </math> focuses only on the dominant hard label prediction the inter-class alignment across domains is disregarded. Hence, minimising symmetrized Kullback–Leibler (KL) divergence across domains, averaged over all <math> C </math> classes has been used: | Since <math> L_{task} </math> focuses only on the dominant hard label prediction the inter-class alignment across domains is disregarded. Hence, minimising symmetrized Kullback–Leibler (KL) divergence across domains, averaged over all <math> C </math> classes has been used: | ||
<div style="text-align: center;"> | |||
<math> l_{global}(D_{i}, D{j}; \psi^{'}, \theta^{'}) = 1/C \sum_{c=1}^{C} 1/2[D_{KL}(s_{c}^{(i)}||s_{c}^{(j)}) + D_{KL}(s_{c}^{(j)}||s_{c}^{(i)})], </math> | <math> l_{global}(D_{i}, D{j}; \psi^{'}, \theta^{'}) = 1/C \sum_{c=1}^{C} 1/2[D_{KL}(s_{c}^{(i)}||s_{c}^{(j)}) + D_{KL}(s_{c}^{(j)}||s_{c}^{(i)})], </math> | ||
</div> | |||
The authors stated that symmetric divergences such as Jensen–Shannon (JS) showed no significant difference with KL over symm. | The authors stated that symmetric divergences such as Jensen–Shannon (JS) showed no significant difference with KL over symm. | ||
| Line 38: | Line 44: | ||
</math> | </math> | ||
</div> | </div> | ||
== Model agnostic learning of semantic features == | |||
These losses are used in an episodic training scheme showed in the below figure: | |||
[[File:algo2.PNG|700px|center]] | |||
== Experiments == | == Experiments == | ||
The usefulness of the proposed method has been demonstrated using two common benchmark datasets for domain generalization, i.e. VLCS and PACS, alongside a real-world MRI medical imaging segmentation task. In all of their experiments, the AlexNet with ImageNet pre-trained weights has been utilized. | |||
=== VLCS === | |||
VLCS[12] is an aggregation of images from four other datasets: PASCAL VOC2007 (V) [13], LabelMe (L) [14], Caltech (C) [15], and SUN09 (S) [16] | |||
leave-one-domain-out validation with randomly dividing each domain into 70% training and 30% test. | |||
<gallery> | |||
File:p6.PNG|VLCS dataset | |||
</gallery> | |||
Notably, MASF outperforms MLDG[4], in the table below on this dataset, indicating that semantic properties would provide superior performance with respect to purely highly-abstracted task loss on meta-test. "DeepAll" in the table is the case in which there is no domain generalization. In DeepAll case the class labels have been used only, regardless of the domain each sample would lie in. | |||
[[File:table1_masf.PNG|600px|center]] | |||
The | === PACS === | ||
The more challenging domain generalization benchmark with a significant domain shift is the PACS dataset. It contains art painting, cartoon, photo, sketch domains with objects from seven classes: dog, elephant, giraffe, guitar, house, horse, person. | |||
<gallery> | |||
File:p7_masf.jpg|PACS dataset sample | |||
</gallery> | |||
As you can see in the table below, MASF outperforms state of the art JiGen[17], MLDG[4], MetaReg[3], significantly. In addition, the best improvement has achieved (6.20%) when the unseen domain is "sketch", which requires more general knowledge about semantic concepts since it is different from other domains significantly. | |||
[[File:table2_masf.PNG|600px|center]] | |||
[[File: | === Ablation study over PACS=== | ||
The ablation study over the PACS dataset shows the effectiveness of each loss term. | |||
[[File:table3_masf.PNG|600px|center]] | |||
=== Multi-site Brain MRI image segmentation === | |||
The effectiveness of the MASF has been also demonstrated using a segmentation task of MRI images gathering from four different clinical centers denoted as (Set-A, Set-B, Set-C, and Set-D). The domain shift, in this case, would occur due to differences in hardware, acquisition protocols, and many other factors, hindering translating learning-based methods to real clinical practice. | |||
<gallery> | |||
File:p8_masf.PNG|MRI dataset | |||
</gallery> | |||
The results showed the effectiveness of the MASF in comparison to not use domain generalization. | |||
[[File:table5_masf.PNG|300px|center]] | |||
== Conclusion == | |||
A new domain generalization technique by taking the advantage of incorporating global and local constraints for learning semantic feature spaces presented which outperforms the state-of-the-art. The effectiveness of this method has been demonstrated using two domain generalization benchmarks, and a real clinical dataset (MRI image segmentation). | |||
== References == | |||
[ | [1]: Koch, Gregory, Richard Zemel, and Ruslan Salakhutdinov. "Siamese neural networks for one-shot image recognition." ICML deep learning workshop. Vol. 2. 2015. | ||
[2]: Hoffer, Elad, and Nir Ailon. "Deep metric learning using triplet network." International Workshop on Similarity-Based Pattern Recognition. Springer, Cham, 2015. | |||
[3]: Balaji, Yogesh, Swami Sankaranarayanan, and Rama Chellappa. "Metareg: Towards domain generalization using meta-regularization." Advances in Neural Information Processing Systems. 2018. | |||
[4]: Li, Da, et al. "Learning to generalize: Meta-learning for domain generalization." arXiv preprint arXiv:1710.03463 (2017). | |||
[ | [5]: Li, Da, et al. "Episodic training for domain generalization." Proceedings of the IEEE International Conference on Computer Vision. 2019. | ||
[6]: Li, Haoliang, et al. "Domain generalization with adversarial feature learning." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018. | |||
[7]: Li, Yiying, et al. "Feature-critic networks for heterogeneous domain generalization." arXiv preprint arXiv:1901.11448 (2019). | |||
[8]: Ghifary, Muhammad, et al. "Domain generalization for object recognition with multi-task autoencoders." Proceedings of the IEEE international conference on computer vision. 2015. | |||
[9]: Li, Ya, et al. "Deep domain generalization via conditional invariant adversarial networks." Proceedings of the European Conference on Computer Vision (ECCV). 2018 | |||
[10]: Motiian, Saeid, et al. "Unified deep supervised domain adaptation and generalization." Proceedings of the IEEE International Conference on Computer Vision. 2017. | |||
[ | [11]: Muandet, Krikamol, David Balduzzi, and Bernhard Schölkopf. "Domain generalization via invariant feature representation." International Conference on Machine Learning. 2013. | ||
[ | [12]: Fang, Chen, Ye Xu, and Daniel N. Rockmore. "Unbiased metric learning: On the utilization of multiple datasets and web images for softening bias." Proceedings of the IEEE International Conference on Computer Vision. 2013. | ||
[ | [13]: Everingham, Mark, et al. "The pascal visual object classes (voc) challenge." International journal of computer vision 88.2 (2010): 303-338. | ||
[ | [14]: Russell, Bryan C., et al. "LabelMe: a database and web-based tool for image annotation." International journal of computer vision 77.1-3 (2008): 157-173. | ||
[ | [15]: Fei-Fei, Li. "Learning generative visual models from few training examples." Workshop on Generative-Model Based Vision, IEEE Proc. CVPR, 2004. 2004. | ||
[ | [16]: Chopra, Sumit, Raia Hadsell, and Yann LeCun. "Learning a similarity metric discriminatively, with application to face verification." 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05). Vol. 1. IEEE, 2005. | ||
[ | [17]: Carlucci, Fabio M., et al. "Domain generalization by solving jigsaw puzzles." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019. | ||
Latest revision as of 17:52, 15 November 2020
Presented by
Milad Sikaroudi
Introduction
Transfer learning is a line of research in machine learning which focuses on storing knowledge from one domain (source domain) to solve a similar problem in another domain (target domain). In addition to regular transfer learning, one can use "transfer metric learning" in which through utilizing similarity relationship between samples [1], [2] a more robust and discriminative data representation is formed. However, both of these kinds of techniques work insofar as the domain shift, between source and target domains, is negligible. Domain shift is defined as the deviation in the distribution of the source domain and the target domain and it would cause the DNN model to completely fail. The multi-domain learning is the solution when the assumption of "source domain and target domain comes from an almost same distribution" may not hold. There are two variants of MDL in the literature that can be confused, i.e. domain generalization, and domain adaptation; however in domain adaptation, we have access to the target domain data somehow, while that is not the case in domain generalization. This paper introduces a technique for domain generalization based on two complementary losses that regularize the semantic structure of the feature space through an episodic training scheme originally inspired by the model-agnostic meta-learning.
Previous Work
Originated from model-agnostic meta-learning (MAML), episodic training has been vastly leveraged for addressing domain generalization [3, 4, 5, 7, 8, 6, 9, 10, 11]. The method of MLDG [4] closely follows MAML in terms of back-propagating the gradients from an ordinary task loss on meta-test data, but it has its own limitation as the use of the task objective might be sub-optimal since it only uses class probabilities. Most of the works [3,7] in the literature lack notable guidance from the semantics of feature space, which contains crucial domain-independent ‘general knowledge’ that can be useful for domain generalization. The authors claim that their method is orthogonal to previous works.
Model Agnostic Meta Learning
a.k.a learning to learn is a learning paradigm in which optimal initial weights are found incrementally (episodic training) by minimizing a loss function over some similar tasks (meta-train, meta-test sets). Imagine a 4-shot 2-class image classification task as below:
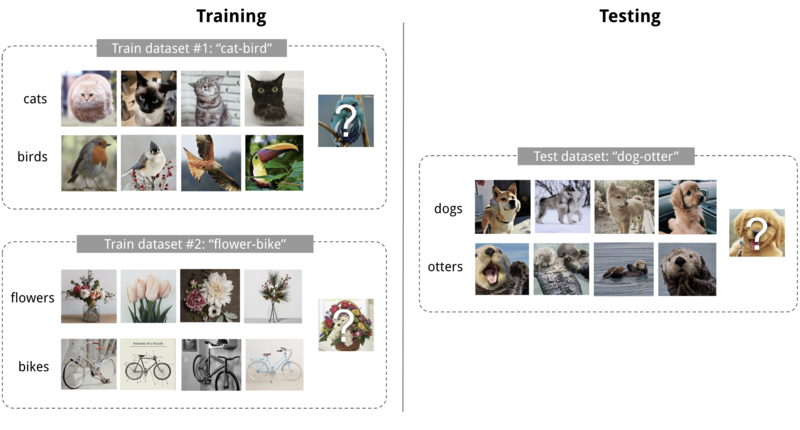
Each of the training tasks provides an optimal initial weight for the next round of the training. By considering all of these sets of updates and meta-test set, the updated weights are calculated using the below algorithm.

Method
In domain generalization, we assume that there are some domain-invariant patterns in the inputs (e.g. semantic features). These features can be extracted to learn a predictor that performs well across seen and unseen domains. This paper assumes that there are inter-class relationships across domains. In total, the MASF is composed of a task loss, global class alignment term and a local sample clustering term.
Task loss
[math]\displaystyle{ F_{\psi}: X \rightarrow Z }[/math] where [math]\displaystyle{ Z }[/math] is a feature space [math]\displaystyle{ T_{\theta}: X \rightarrow \mathbf {R}^{C} }[/math] where [math]\displaystyle{ C }[/math] is the number of classes in [math]\displaystyle{ Y }[/math] Assume that [math]\displaystyle{ \hat{y}= softmax(T_{\theta}(F_{\psi}(x))) }[/math]. The parameters [math]\displaystyle{ (\psi, \theta) }[/math] are optimized with minimizing a cross-entropy loss namely [math]\displaystyle{ \mathbf{L}_{task} }[/math] formulated as:
[math]\displaystyle{ l_{task}(y, \hat{y} = - \sum_{c}1[y=C]log(\hat{y}_{c})) }[/math]
Although the task loss is a decent predictor nothing prevents the model from overfitting to the source domains and suffering from degradation on unseen test domains. So the other loss terms are responsible for this aim.
Global class alignment
Since [math]\displaystyle{ L_{task} }[/math] focuses only on the dominant hard label prediction the inter-class alignment across domains is disregarded. Hence, minimising symmetrized Kullback–Leibler (KL) divergence across domains, averaged over all [math]\displaystyle{ C }[/math] classes has been used:
[math]\displaystyle{ l_{global}(D_{i}, D{j}; \psi^{'}, \theta^{'}) = 1/C \sum_{c=1}^{C} 1/2[D_{KL}(s_{c}^{(i)}||s_{c}^{(j)}) + D_{KL}(s_{c}^{(j)}||s_{c}^{(i)})], }[/math]
The authors stated that symmetric divergences such as Jensen–Shannon (JS) showed no significant difference with KL over symm.
Local cluster sampling
Explicit metric learning, i.e. contrastive or triplet losses, have been used to ensure that the semantic features, locally cluster according to only class labels, regardless of the domain.
[math]\displaystyle{ l_{triplet}^{a,p,n} = \sum_{i=1}^{b} \sum_{k=1}^{c-1} \sum_{\ell=1}^{c-1}\! [m\!+\!\|x_{i}\!- \!x_{k}\|_2^2 \!-\! \|x_{i}\!-\!x_{\ell}\|_2^2 ]_+, }[/math]
Model agnostic learning of semantic features
These losses are used in an episodic training scheme showed in the below figure:

Experiments
The usefulness of the proposed method has been demonstrated using two common benchmark datasets for domain generalization, i.e. VLCS and PACS, alongside a real-world MRI medical imaging segmentation task. In all of their experiments, the AlexNet with ImageNet pre-trained weights has been utilized.
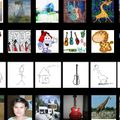
VLCS
VLCS[12] is an aggregation of images from four other datasets: PASCAL VOC2007 (V) [13], LabelMe (L) [14], Caltech (C) [15], and SUN09 (S) [16] leave-one-domain-out validation with randomly dividing each domain into 70% training and 30% test.
-
VLCS dataset
Notably, MASF outperforms MLDG[4], in the table below on this dataset, indicating that semantic properties would provide superior performance with respect to purely highly-abstracted task loss on meta-test. "DeepAll" in the table is the case in which there is no domain generalization. In DeepAll case the class labels have been used only, regardless of the domain each sample would lie in.

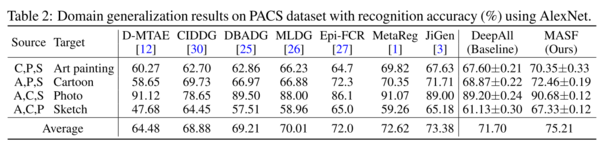
PACS
The more challenging domain generalization benchmark with a significant domain shift is the PACS dataset. It contains art painting, cartoon, photo, sketch domains with objects from seven classes: dog, elephant, giraffe, guitar, house, horse, person.
-
PACS dataset sample
As you can see in the table below, MASF outperforms state of the art JiGen[17], MLDG[4], MetaReg[3], significantly. In addition, the best improvement has achieved (6.20%) when the unseen domain is "sketch", which requires more general knowledge about semantic concepts since it is different from other domains significantly.
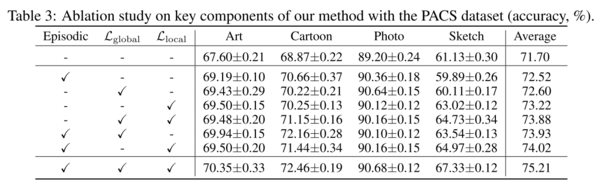
Ablation study over PACS
The ablation study over the PACS dataset shows the effectiveness of each loss term.
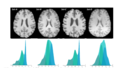
Multi-site Brain MRI image segmentation
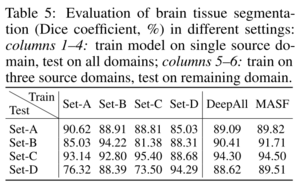
The effectiveness of the MASF has been also demonstrated using a segmentation task of MRI images gathering from four different clinical centers denoted as (Set-A, Set-B, Set-C, and Set-D). The domain shift, in this case, would occur due to differences in hardware, acquisition protocols, and many other factors, hindering translating learning-based methods to real clinical practice.
-
MRI dataset
The results showed the effectiveness of the MASF in comparison to not use domain generalization.
Conclusion
A new domain generalization technique by taking the advantage of incorporating global and local constraints for learning semantic feature spaces presented which outperforms the state-of-the-art. The effectiveness of this method has been demonstrated using two domain generalization benchmarks, and a real clinical dataset (MRI image segmentation).
References
[1]: Koch, Gregory, Richard Zemel, and Ruslan Salakhutdinov. "Siamese neural networks for one-shot image recognition." ICML deep learning workshop. Vol. 2. 2015.
[2]: Hoffer, Elad, and Nir Ailon. "Deep metric learning using triplet network." International Workshop on Similarity-Based Pattern Recognition. Springer, Cham, 2015.
[3]: Balaji, Yogesh, Swami Sankaranarayanan, and Rama Chellappa. "Metareg: Towards domain generalization using meta-regularization." Advances in Neural Information Processing Systems. 2018.
[4]: Li, Da, et al. "Learning to generalize: Meta-learning for domain generalization." arXiv preprint arXiv:1710.03463 (2017).
[5]: Li, Da, et al. "Episodic training for domain generalization." Proceedings of the IEEE International Conference on Computer Vision. 2019.
[6]: Li, Haoliang, et al. "Domain generalization with adversarial feature learning." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018.
[7]: Li, Yiying, et al. "Feature-critic networks for heterogeneous domain generalization." arXiv preprint arXiv:1901.11448 (2019).
[8]: Ghifary, Muhammad, et al. "Domain generalization for object recognition with multi-task autoencoders." Proceedings of the IEEE international conference on computer vision. 2015.
[9]: Li, Ya, et al. "Deep domain generalization via conditional invariant adversarial networks." Proceedings of the European Conference on Computer Vision (ECCV). 2018
[10]: Motiian, Saeid, et al. "Unified deep supervised domain adaptation and generalization." Proceedings of the IEEE International Conference on Computer Vision. 2017.
[11]: Muandet, Krikamol, David Balduzzi, and Bernhard Schölkopf. "Domain generalization via invariant feature representation." International Conference on Machine Learning. 2013.
[12]: Fang, Chen, Ye Xu, and Daniel N. Rockmore. "Unbiased metric learning: On the utilization of multiple datasets and web images for softening bias." Proceedings of the IEEE International Conference on Computer Vision. 2013.
[13]: Everingham, Mark, et al. "The pascal visual object classes (voc) challenge." International journal of computer vision 88.2 (2010): 303-338.
[14]: Russell, Bryan C., et al. "LabelMe: a database and web-based tool for image annotation." International journal of computer vision 77.1-3 (2008): 157-173.
[15]: Fei-Fei, Li. "Learning generative visual models from few training examples." Workshop on Generative-Model Based Vision, IEEE Proc. CVPR, 2004. 2004.
[16]: Chopra, Sumit, Raia Hadsell, and Yann LeCun. "Learning a similarity metric discriminatively, with application to face verification." 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05). Vol. 1. IEEE, 2005.
[17]: Carlucci, Fabio M., et al. "Domain generalization by solving jigsaw puzzles." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019.