stat946w18/Tensorized LSTMs: Difference between revisions
No edit summary |
|||
| (104 intermediate revisions by 18 users not shown) | |||
| Line 5: | Line 5: | ||
= Introduction = | = Introduction = | ||
Long Short-Term Memory (LSTM) is a popular approach to boosting the ability of Recurrent Neural Networks to store longer term temporal information. The capacity of an LSTM network can be increased by widening and adding layers ( | Long Short-Term Memory (LSTM) is a popular approach to boosting the ability of Recurrent Neural Networks to store longer term temporal information. The capacity of an LSTM network can be increased by widening and adding layers. Increasing the width (increasing the number of units in a hidden layer) causes the number of parameters to increase quadratically which in turn increases the time required for model training and evaluation. While increasing the depth by stacking multiple LSTMs increases runtime by a proportional amount. As an alternative He et. al (2017) in ''Wider and Deeper, Cheaper and Faster: Tensorized LSTMs for Sequence Learning'' have proposed a model based on LSTM called the '''Tensorized LSTM''' in which the hidden states are represented by '''tensors''' and updated via a '''cross-layer convolution'''. | ||
* By increasing the tensor size, the network can be widened efficiently without additional parameters since the parameters are shared across different locations in the tensor | * By increasing the tensor size, the network can be widened efficiently without additional parameters since the parameters are shared across different locations in the tensor | ||
* By delaying the output, the network can be deepened implicitly with little additional | * By delaying the output, the network can be deepened implicitly with little additional run-time since deep computations for each time step are merged into temporal computations of the sequence. | ||
Also, the paper | Also, the paper presents experiments that were conducted on five challenging sequence learning tasks to show the potential of the proposed model. | ||
= A Quick Introduction to RNN and LSTM = | = A Quick Introduction to RNN and LSTM = | ||
We consider the time-series prediction task of producing a desired output <math>y_t</math> at each time-step t∈ {1, ..., T} given an observed input sequence <math> | We consider the time-series prediction task of producing a desired output <math>y_t</math> at each time-step t∈ {1, ..., T} given an observed input sequence <math>x_{1:t} = {x_1,x_2, ···, x_t}</math>, where <math>x_t∈R^R</math> and <math>y_t∈R^S</math> are vectors. RNNs learn how to use a hidden state vector <math>h_t ∈ R^M</math> to encapsulate the relevant features of the entire input history x1:t (indicates all inputs from the initial time-step to the final step before predication - illustration given below) up to time-step t. | ||
\begin{align} | \begin{align} | ||
| Line 26: | Line 23: | ||
Where <math>h_{t-1}^{cat} ∈R^{R+M}</math> is the concatenation of the current input <math>x_t</math> and the previous hidden state <math>h_{t−1}</math>, which expands the dimensionality of intermediate information. | Where <math>h_{t-1}^{cat} ∈R^{R+M}</math> is the concatenation of the current input <math>x_t</math> and the previous hidden state <math>h_{t−1}</math>, which expands the dimensionality of intermediate information. | ||
The update of the hidden state | The update of the hidden state h_t is defined as: | ||
\begin{align} | \begin{align} | ||
| Line 38: | Line 35: | ||
\end{align} | \end{align} | ||
<math>W^h∈R^(R+M) | <math>W^h∈R^{(R+M)\times M} </math> guarantees each hidden state provided by the previous step is of dimension M. <math> a_t ∈R^M </math> is the hidden activation, and φ(·) is the element-wise hyperbolic tangent. Finally, the output <math> y_t </math> at time-step t is generated by: | ||
\begin{align} | \begin{align} | ||
| Line 44: | Line 41: | ||
\end{align} | \end{align} | ||
where <math>W^y∈R^{M×S}</math> and <math>b^y∈R^S</math>, and <math>\varphi(·)</math> can be any differentiable function | where <math>W^y∈R^{M×S}</math> and <math>b^y∈R^S</math>, and <math>\varphi(·)</math> can be any differentiable function. Note that the <math>\phi</math> is a non-linear, element-wise function which generates hidden output, while <math>\varphi</math> generates the final network output. | ||
[[File:StdRNN.png|650px|center||Figure 1: Recurrent Neural Network]] | [[File:StdRNN.png|650px|center||Figure 1: Recurrent Neural Network]] | ||
One shortfall of RNN is the problem of vanishing/exploding gradients. This shortfall is significant, especially when modeling long-range dependencies. One alternative is to instead use LSTM (Long Short-Term Memory), which alleviates these problems by employing several gates to selectively modulate the information flow across each neuron. Since LSTMs have been successfully used in sequence models, it is natural to consider them for accommodating more complex analytical needs. | |||
[[File:LSTM_Gated.png|650px|center||Figure 2: LSTM]] | [[File:LSTM_Gated.png|650px|center||Figure 2: LSTM]] | ||
| Line 65: | Line 62: | ||
= Method = | = Method = | ||
== Part 1: Tensorize RNN hidden State vectors == | == Part 1: Tensorize RNN hidden State vectors == | ||
| Line 79: | Line 74: | ||
'''Effects:''' This '''widens''' the network since the hidden state vectors are in fact broadcast to interact with the tensorized parameters. | '''Effects:''' This '''widens''' the network since the hidden state vectors are in fact broadcast to interact with the tensorized parameters. | ||
We adopt parameter sharing to cutdown the parameter number for RNNs, since compared with factorization, it has the following advantages: | We adopt parameter sharing to cutdown the parameter number for RNNs, since compared with factorization, it has the following advantages: | ||
(i) | (i) '''Scalability,''' the number of shared parameters can be set independent of the hidden state size | ||
(ii) | (ii) '''Separability,''' the information flow can be carefully managed by controlling the receptive field, allowing one to shift RNN deep computations to the temporal domain | ||
| Line 90: | Line 87: | ||
We also explicitly tensorize the RNN hidden state vectors, since compared with vectors, tensors have a better: | We also explicitly tensorize the RNN hidden state vectors, since compared with vectors, tensors have a better: | ||
(i) | (i) '''Flexibility,''' one can specify which dimensions to share parameters and then can just increase the size of those dimensions without introducing additional parameters | ||
(ii) '''Efficiency,''' with higher-dimensional tensors, the network can be widened faster w.r.t. its depth when fixing the parameter number (explained later). | |||
'''Illustration:''' For ease of exposition, we first consider 2D tensors (matrices): we tensorize the hidden state <math>h_t∈R^{M}</math> to become <math>Ht∈R^{P×M}</math>, '''where P is the tensor size,''' and '''M the channel size'''. We locally-connect the first dimension of <math>H_t</math> (which is P - the tensor size) in order to share parameters, and fully-connect the second dimension of <math>H_t</math> (which is M - the channel size) to allow global interactions. This is analogous to the CNN which fully-connects one dimension (e.g., the RGB channel for input images) to globally fuse different feature planes. Also, if one compares <math>H_t</math> to the hidden state of a Stacked RNN (sRNN) (see Figure Blow). | |||
[[File:Screen_Shot_2018-03-26_at_11.28.37_AM.png|160px|center||Figure 4: Stacked RNN]] | |||
[[File:ind.png|60px|center||Figure 4: Stacked RNN]] | |||
Then P is akin to the number of stacked hidden layers (vertical length in the graph), and M the size of each hidden layer (each white node in the graph). We start to describe our model based on 2D tensors, and finally show how to strengthen the model with higher-dimensional tensors. | |||
== Part 2: Merging Deep Computations == | |||
Since an RNN is already deep in its temporal direction, we can deepen an input-to-output computation by associating the input <math>x_t</math> with a (delayed) future output. In doing this, we need to ensure that the output <math>y_t</math> is separable, i.e., not influenced by any future input <math>x_{t^{'}}</math> <math>(t^{'}>t)</math>. Thus, we concatenate the projection of <math>x_t</math> to the top of the previous hidden state <math>H_{t−1}</math>, then gradually shift the input information down when the temporal computation proceeds, and finally generate <math>y_t</math> from the bottom of <math>H_{t+L−1}</math>, where L−1 is the number of delayed time-steps for computations of depth L. | |||
An example with L= 3 is shown in Figure. | |||
[[File:tRNN.png|160px|center||Figure 5: skewed sRNN]] | |||
[[File:ind.png|60px|center||Figure 5: skewed sRNN]] | |||
This is in fact a skewed sRNN (or tRNN without feedback). However, the method does not need to change the network structure and also allows different kinds of interactions as long as the output is separable; for example, one can increase the local connections and '''use feedback''' (shown in figure below), which can be beneficial for sRNNs (or tRNN). | |||
[[File:tRNN_wF.png|160px|center||Figure 5: skewed sRNN with F]] | |||
[[File:ind.png|60px|center||Figure 5: skewed sRNN with F]] | |||
'''In order to share parameters, we update <math>H_t</math> using a convolution with a learnable kernel.''' In this manner we increase the complexity of the input-to-output mapping (by delaying outputs) and limit parameter growth (by sharing transition parameters using convolutions). | |||
To examine the resulting model mathematically, let <math>H^{cat}_{t−1}∈R^{(P+1)×M}</math> be the concatenated hidden state, and <math>p∈Z_+</math> the location at a tensor. The channel vector <math>h^{cat}_{t−1, p }∈R^M</math> at location p of <math>H^{cat}_{t−1}</math> (the p-th channel of H) is defined as: | |||
\begin{align} | |||
h^{cat}_{t-1, p} = x_t W^x + b^x \hspace{1cm} if p = 1 \hspace{1cm} (5) | |||
\end{align} | |||
\begin{align} | |||
h^{cat}_{t-1, p} = h_{t-1, p-1} \hspace{1cm} if p > 1 \hspace{1cm} (6) | |||
\end{align} | |||
where <math>W^x ∈ R^{R×M}</math> and <math>b^x ∈ R^M</math> (recall the dimension of input x is R). Then, the update of tensor <math>H_t</math> is implemented via a convolution: | |||
\begin{align} | |||
A_t = H^{cat}_{t-1} \circledast \{W^h, b^h \} \hspace{2cm} (7) | |||
\end{align} | |||
\begin{align} | |||
H_t = \Phi{A_t} \hspace{2cm} (8) | |||
\end{align} | |||
where <math>W^h∈R^{K×M^i×M^o}</math> is the kernel weight of size K, with <math>M^i =M</math> input channels and <math>M^o =M</math> output channels, <math>b^h ∈ R^{M^o}</math> is the kernel bias, <math>A_t ∈ R^{P×M^o}</math> is the hidden activation, and <math>\circledast</math> is the convolution operator. Since the kernel convolves across different hidden layers, we call it the cross-layer convolution. The kernel enables interaction, both bottom-up and top-down across layers. Finally, we generate <math>y_t</math> from the channel vector <math>h_{t+L−1,P}∈R^M</math> which is located at the bottom of <math>H_{t+L−1}</math>: | |||
\begin{align} | |||
y_t = \varphi(h_{t+L−1}, _PW^y + b^y) \hspace{2cm} (9) | |||
\end{align} | |||
Where <math>W^y ∈R^{M×S}</math> and <math>b^y ∈R^S</math>. To guarantee that the receptive field of <math>y_t</math> only covers the current and previous inputs x1:t. (Check the Skewed sRNN again below): | |||
[[File:tRNN_wF.png|160px|center||Figure 5: skewed sRNN with F]] | |||
[[File:ind.png|60px|center||Figure 5: skewed sRNN with F]] | |||
=== Quick Summary of Set of Parameters === | |||
'''1. <math> W^x</math> and <math>b_x</math>''' connect input to the first hidden node | |||
'''2. <math> W^h</math> and <math>b_h</math>''' convolute between layers | |||
'''3. <math> W^y</math> and <math>b_y</math>''' produce output of each stages | |||
== Part 3: Extending to LSTMs== | |||
Similar to standard RNN, to allow the tRNN (skewed sRNN) to capture long-range temporal dependencies, one can straightforwardly extend it | |||
to a tLSTM by replacing the tRNN tensors: | |||
\begin{align} | |||
[A^g_t, A^i_t, A^f_t, A^o_t] = H^{cat}_{t-1} \circledast \{W^h, b^h \} \hspace{2cm} (10) | |||
\end{align} | |||
\begin{align} | |||
[G_t, I_t, F_t, O_t]= [\Phi{(A^g_t)}, σ(A^i_t), σ(A^f_t), σ(A^o_t)] \hspace{2cm} (11) | |||
\end{align} | |||
Which are pretty similar to tRNN case, the main differences can be observes for memory cells of tLSTM (Ct): | |||
\begin{align} | |||
C_t= G_t \odot I_t + C_{t-1} \odot F_t \hspace{2cm} (12) | |||
\end{align} | |||
\begin{align} | |||
H_t= \Phi{(C_t )} \odot O_t \hspace{2cm} (13) | |||
\end{align} | |||
Note that since the previous memory cell <math>C_{t-1}</math> is only gated along the temporal direction, increasing the tensor size ''P'' might result in the loss of long-range dependencies from the input to the output. | |||
Summary of the terms: | |||
1. '''<math>\{W^h, b^h \}</math>:''' Kernel of size K | |||
2. '''<math>A^g_t, A^i_t, A^f_t, A^o_t \in \mathbb{R}^{P\times M}</math>:''' Activations for the new content <math>G_t</math> | |||
3. '''<math>I_t</math>:''' Input gate | |||
4. '''<math>F_t</math>:''' Forget gate | |||
5. '''<math>O_t</math>:''' Output gate | |||
6. '''<math>C_t \in \mathbb{R}^{P\times M}</math>:''' Memory cell | |||
Then, see graph below for illustration: | |||
[[File:tLSTM_wo_MC.png |160px|center||Figure 5: tLSTM wo MC]] | |||
[[File:ind.png|60px|center||Figure 5: tLSTM wo MC]] | |||
To further evolve tLSTM, we invoke the '''Memory Cell Convolution''' to capture long-range dependencies from multiple directions, we additionally introduce a novel memory cell convolution, by which the memory cells can have a larger receptive field (figure provided below). | |||
[[File:tLSTM_w_MC.png |160px|center||Figure 5: tLSTM w MC]] | |||
[[File:ind.png|60px|center||Figure 5: tLSTM w MC]] | |||
One can also dynamically generate this convolution kernel so that it is both time - and location-dependent, allowing for flexible control over long-range dependencies from different directions. Mathematically, it can be represented in with the following formulas: | |||
\begin{align} | |||
[A^g_t, A^i_t, A^f_t, A^o_t, A^q_t] = H^{cat}_{t-1} \circledast \{W^h, b^h \} \hspace{2cm} (14) | |||
\end{align} | |||
\begin{align} | |||
[G_t, I_t, F_t, O_t, Q_t]= [\Phi{(A^g_t)}, σ(A^i_t), σ(A^f_t), σ(A^o_t), ς(A^q_t)] \hspace{2cm} (15) | |||
\end{align} | |||
\begin{align} | |||
W_t^c(p) = reshape(q_{t,p}, [K, 1, 1]) \hspace{2cm} (16) | |||
\end{align} | |||
\begin{align} | |||
C_{t-1}^{conv}= C_{t-1} \circledast W_t^c(p) \hspace{2cm} (17) | |||
\end{align} | |||
\begin{align} | |||
C_t= G_t \odot I_t + C_{t-1}^{conv} \odot F_t \hspace{2cm} (18) | |||
\end{align} | |||
\begin{align} | |||
H_t= \Phi{(C_t )} \odot O_t \hspace{2cm} (19) | |||
\end{align} | |||
where the kernel <math>{W^h, b^h}</math> has additional <K> output channels to generate the activation <math>A^q_t ∈ R^{P×<K>}</math> for the dynamic kernel bank <math>Q_t∈R^{P × <K>}</math>, <math>q_{t,p}∈R^{<K>}</math> is the vectorized adaptive kernel at the location p of <math>Q_t</math>, and <math>W^c_t(p) ∈ R^{K×1×1}</math> is the dynamic kernel of size K with a single input/output channel, which is reshaped from <math>q_{t,p}</math>. Each channel of the previous memory cell <math>C_{t-1}</math> is convolved with <math>W_t^c(p)</math> whose values vary with <math>p</math>, to form a memory cell convolution, which produces a convolved memory cell <math>C_{t-1}^{conv} \in \mathbb{R}^{P\times M}</math>. This convolution is defined by: | |||
\begin{align} | |||
C_{t-1,p,m}^{conv} = \sum\limits_{k=1}^K C_{t-1,p-\frac{K-1}{2}+k,m} · W_{t,k,1,1}^c(p) \hspace{2cm} (30) | |||
\end{align} | |||
where <math>C_{t-1}</math> is padded with the boundary values to retain the stored information. | |||
Note the paper also employed a softmax function ς(·) to normalize the channel dimension of <math>Q_t</math>. which can also stabilize the value of memory cells and help to prevent the vanishing/exploding gradients. An illustration is provided below to better illustrate the process: | |||
[[File:MCC.png |240px|center||Figure 5: MCC]] | |||
Theorem 17-18 of Leifert et al. [3] proves the prevention of vanishing/exploding gradients for the lambda gate, which is very similar to the proposed memory cell convolution kernel. The only major differences between the two are the use of softmax for normalization and the sharing the of the kernal for all channels. Since these changes to not affect the assertions made in Theorem 17-18, it can be established that the prevention of vanishing/exploding gradients is a feature of the memory cell convolution kernel as well. | |||
To improve training, the authors introduced a new normalization technique for ''t''LSTM termed channel normalization (adapted from layer normalization), in which the channel vector are normalized at different locations with their own statistics. Note that layer normalization does not work well with ''t''LSTM, because lower level information is near the input and higher level information is near the output. Channel normalization (CN) is defined as: | |||
\begin{align} | |||
\mathrm{CN}(\mathbf{Z}; \mathbf{\Gamma}, \mathbf{B}) = \mathbf{\hat{Z}} \odot \mathbf{\Gamma} + \mathbf{B} \hspace{2cm} (20) | |||
\end{align} | |||
where <math>\mathbf{Z}</math>, <math>\mathbf{\hat{Z}}</math>, <math>\mathbf{\Gamma}</math>, <math>\mathbf{B} \in \mathbb{R}^{P \times M^z}</math> are the original tensor, normalized tensor, gain parameter and bias parameter. The <math>m^z</math>-th channel of <math>\mathbf{Z}</math> is normalized element-wisely: | |||
\begin{align} | |||
\hat{z_{m^z}} = (z_{m^z} - z^\mu)/z^{\sigma} \hspace{2cm} (21) | |||
\end{align} | |||
where <math>z^{\mu}</math>, <math>z^{\sigma} \in \mathbb{R}^P</math> are the mean and standard deviation along the channel dimension of <math>\mathbf{Z}</math>, and <math>\hat{z_{m^z}} \in \mathbb{R}^P</math> is the <math>m^z</math>-th channel <math>\mathbf{\hat{Z}}</math>. Channel normalization introduces very few additional parameters compared to the number of other parameters in the model. | |||
= Results and Evaluation = | |||
Summary of list of models tLSTM family (may be useful later): | |||
(a) sLSTM (baseline): the implementation of sLSTM with parameters shared across all layers. | |||
(b) 2D tLSTM: the standard 2D tLSTM. | |||
(c) 2D tLSTM–M: removing memory (M) cell convolutions from (b). | |||
(d) 2D tLSTM–F: removing (–) feedback (F) connections from (b). | |||
(e) 3D tLSTM: tensorizing (b) into 3D tLSTM. | |||
(f) 3D tLSTM+LN: applying (+) Layer Normalization. | |||
(g) 3D tLSTM+CN: applying (+) Channel Normalization. | |||
=== Efficiency Analysis === | |||
'''Fundaments:''' For each configuration, fix the parameter number and increase the tensor size to see if the performance of tLSTM can be boosted without increasing the parameter number. Can also investigate how the runtime is affected by the depth, where the runtime is measured by the average GPU milliseconds spent by a forward and backward pass over one timestep of a single example. | |||
'''Dataset:''' The Hutter Prize Wikipedia dataset consists of 100 million characters taken from 205 different characters including alphabets, XML markups and special symbols. We model the dataset at the character-level, and try to predict the next character of the input sequence. | |||
All configurations are evaluated with depths L = 1, 2, 3, 4. Bits-per-character(BPC) is used to measure the model performance and the results are shown in the figure below. | |||
[[File:wiki.png |280px|center||Figure 5: WifiPerf]] | |||
[[File:Wiki_Performance.png |480px|center||Figure 5: WifiPerf]] | |||
=== Accuracy Analysis === | |||
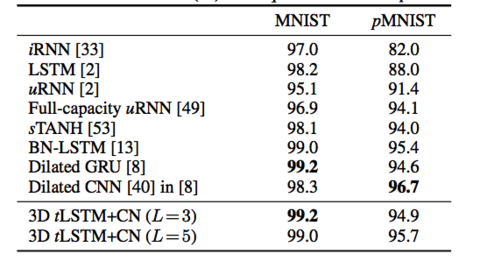
The MNIST dataset [35] consists of 50000/10000/10000 handwritten digit images of size 28×28 for training/validation/test. Two tasks are used for evaluation on this dataset: | |||
(a) '''Sequential MNIST:''' The goal is to classify the digit after sequentially reading the pixels in a scan-line order. It is therefore a 784 time-step sequence learning task where a single output is produced at the last time-step; the task requires very long range dependencies in the sequence. | |||
(b) '''Sequential Permuted MNIST:''' We permute the original image pixels in a fixed random order, resulting in a permuted MNIST (pMNIST) problem that has even longer range dependencies across pixels and is harder. | |||
In both tasks, all configurations are evaluated with M = 100 and L= 1, 3, 5. The model performance is measured by the classification accuracy and results are shown in the figure below. | |||
[[File:MNISTperf.png |480px|center]] | |||
[[File:Acc_res.png |480px|center||Figure 5: MNIST]] | |||
[[File:33_mnist.PNG|center|thumb|800px| This figure displays a visualization of the means of the diagonal channels of the tLSTM memory cells per task. The columns indicate the time steps and the rows indicate the diagonal locations. The values are normalized between 0 and 1.]] | |||
It can be seen in the above figure that tLSTM behaves differently with different tasks: | |||
- Wikipedia: the input can be carried to the output location with less modification if it is sufficient to determine the next character, and vice versa | |||
- addition: the first integer is gradually encoded into memories and then interacts (performs addition) with the second integer, producing the sum | |||
- memorization: the network behaves like a shift register that continues to move the input symbol to the output location at the correct timestep | |||
- sequential MNIST: the network is more sensitive to the pixel value change (representing the contour, or topology of the digit) and can gradually accumulate evidence for the final prediction | |||
- sequential pMNIST: the network is sensitive to high value pixels (representing the foreground digit), and we conjecture that this is because the permutation destroys the topology of the digit, making each high value pixel potentially important. | |||
From the figure above it can can also be observe some common phenomena in all tasks: | |||
# it is clear that wider (larger) tensors can encode more information by observing that at each timestep, the values at different tensor locations are markedly different | |||
# from the input to the output, the values become increasingly distinct and are shifted by time, revealing that deep computations are indeed performed together with temporal computations, with long-range dependencies carried by memory cells. | |||
= Related work = | |||
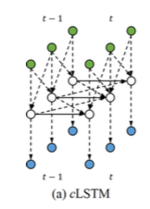
=== Convolutional LSTMs === | |||
Convolutional LSTMs are proposed to parallelize the computation of LSTMs when the input at each timestep is structured | |||
[[File:clstm.png|150px|center||Figure 1: Example of Convolutional LSTMs]] | |||
=== Deep LSTMs === | |||
Deep LSTMs. Deep LSTMs (dLSTMs) extend sLSTMs by making them deeper (see Fig. 7(b)-(d)). | |||
To keep the parameter number small and ease training, Graves [22], Kalchbrenner et al. [30], Mujika | |||
et al. [38], Zilly et al. [54] apply another RNN/LSTM along the depth direction of dLSTMs, which, | |||
however, multiplies the runtime. Though there are implementations to accelerate the deep computation | |||
[1, 16], they generally aim at simple architectures such sLSTMs. Compared with dLSTMs, tLSTM | |||
performs the deep computation with little additional runtime, and employs a cross-layer convolution to | |||
enable the feedback mechanism. Moreover, the capacity of tLSTM can be increased more efficiently | |||
by using higher-dimensional tensors, whereas in dLSTM all hidden layers as a whole only equal to a | |||
2D tensor (i.e., a stack of hidden vectors), the dimensionality of which is fixed. | |||
= Conclusions = | |||
The paper introduced the Tensorized LSTM, which employs tensors to share parameters and utilizes the temporal computation to perform the deep computation for sequential tasks. Then validated the model | |||
on a variety of tasks, showing its potential over other popular approaches. The paper shows a method to widen and deepen the LSTM network at the same time and the following 3 points list their main contributions: | |||
* The RNNs are now tensorized into higher dimensional tensors which are more flexible. | |||
* RNNs' deep computation is merged into the temporal computation, referred to as the tensorizedRNN. | |||
* tRNN is extended to a LSTM architecture and a new architecture is studied: tensorizedLSTM | |||
= Critique(to be edited) = | |||
* Using tensor as hidden layer indeed increasing the capability of the network, but authors never mentioned the trade-off in terms of extra computation cost and training time. | |||
= References = | |||
#Zhen He, Shaobing Gao, Liang Xiao, Daxue Liu, Hangen He, and David Barber. <Wider and Deeper, Cheaper and Faster: Tensorized LSTMs for Sequence Learning> (2017) | |||
#Ali Ghodsi, <Deep Learning: STAT 946 - Winter 2018> | |||
#Gundram Leifert, Tobias Strauß, Tobias Grüning, Welf Wustlich, and Roger Labahn. Cells in multidimensional recurrent neural networks. JMLR, 17(1):3313–3349, 2016. | |||
Latest revision as of 22:50, 20 April 2018
Presented by
Chen, Weishi(Edward)
Introduction
Long Short-Term Memory (LSTM) is a popular approach to boosting the ability of Recurrent Neural Networks to store longer term temporal information. The capacity of an LSTM network can be increased by widening and adding layers. Increasing the width (increasing the number of units in a hidden layer) causes the number of parameters to increase quadratically which in turn increases the time required for model training and evaluation. While increasing the depth by stacking multiple LSTMs increases runtime by a proportional amount. As an alternative He et. al (2017) in Wider and Deeper, Cheaper and Faster: Tensorized LSTMs for Sequence Learning have proposed a model based on LSTM called the Tensorized LSTM in which the hidden states are represented by tensors and updated via a cross-layer convolution.
- By increasing the tensor size, the network can be widened efficiently without additional parameters since the parameters are shared across different locations in the tensor
- By delaying the output, the network can be deepened implicitly with little additional run-time since deep computations for each time step are merged into temporal computations of the sequence.
Also, the paper presents experiments that were conducted on five challenging sequence learning tasks to show the potential of the proposed model.
A Quick Introduction to RNN and LSTM
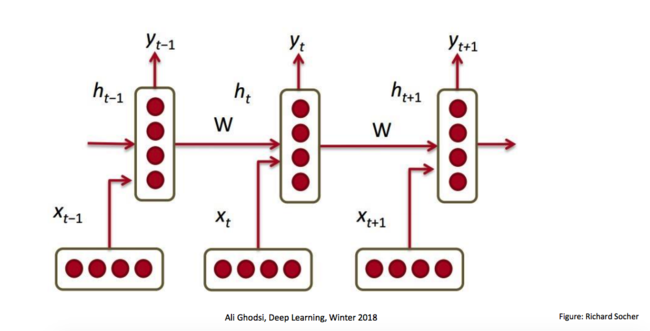
We consider the time-series prediction task of producing a desired output [math]\displaystyle{ y_t }[/math] at each time-step t∈ {1, ..., T} given an observed input sequence [math]\displaystyle{ x_{1:t} = {x_1,x_2, ···, x_t} }[/math], where [math]\displaystyle{ x_t∈R^R }[/math] and [math]\displaystyle{ y_t∈R^S }[/math] are vectors. RNNs learn how to use a hidden state vector [math]\displaystyle{ h_t ∈ R^M }[/math] to encapsulate the relevant features of the entire input history x1:t (indicates all inputs from the initial time-step to the final step before predication - illustration given below) up to time-step t.
\begin{align} h_{t-1}^{cat} = [x_t, h_{t-1}] \hspace{2cm} (1) \end{align}
Where [math]\displaystyle{ h_{t-1}^{cat} ∈R^{R+M} }[/math] is the concatenation of the current input [math]\displaystyle{ x_t }[/math] and the previous hidden state [math]\displaystyle{ h_{t−1} }[/math], which expands the dimensionality of intermediate information.
The update of the hidden state h_t is defined as:
\begin{align} a_{t} =h_{t-1}^{cat} W^h + b^h \hspace{2cm} (2) \end{align}
and
\begin{align} h_t = \Phi(a_t) \hspace{2cm} (3) \end{align}
[math]\displaystyle{ W^h∈R^{(R+M)\times M} }[/math] guarantees each hidden state provided by the previous step is of dimension M. [math]\displaystyle{ a_t ∈R^M }[/math] is the hidden activation, and φ(·) is the element-wise hyperbolic tangent. Finally, the output [math]\displaystyle{ y_t }[/math] at time-step t is generated by:
\begin{align} y_t = \varphi(h_{t}^{cat} W^y + b^y) \hspace{2cm} (4) \end{align}
where [math]\displaystyle{ W^y∈R^{M×S} }[/math] and [math]\displaystyle{ b^y∈R^S }[/math], and [math]\displaystyle{ \varphi(·) }[/math] can be any differentiable function. Note that the [math]\displaystyle{ \phi }[/math] is a non-linear, element-wise function which generates hidden output, while [math]\displaystyle{ \varphi }[/math] generates the final network output.
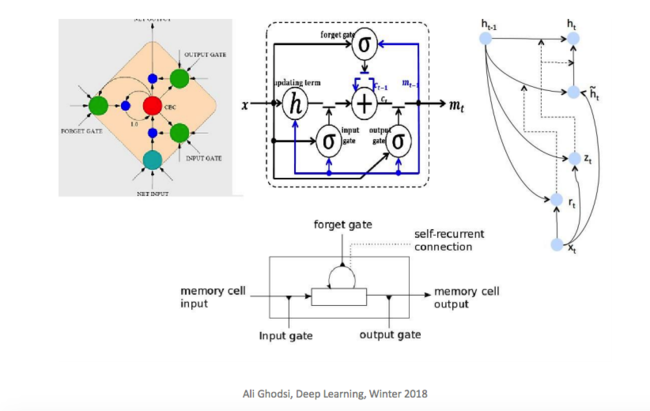
One shortfall of RNN is the problem of vanishing/exploding gradients. This shortfall is significant, especially when modeling long-range dependencies. One alternative is to instead use LSTM (Long Short-Term Memory), which alleviates these problems by employing several gates to selectively modulate the information flow across each neuron. Since LSTMs have been successfully used in sequence models, it is natural to consider them for accommodating more complex analytical needs.
Structural Measurement of Sequential Model
We can consider the capacity of a network consists of two components: the width (the amount of information handled in parallel) and the depth (the number of computation steps).
A way to widen the LSTM is to increase the number of units in a hidden layer; however, the parameter number scales quadratically with the number of units. To deepen the LSTM, the popular Stacked LSTM (sLSTM) stacks multiple LSTM layers. The drawback of sLSTM, however, is that runtime is proportional to the number of layers and information from the input is potentially lost (due to gradient vanishing/explosion) as it propagates vertically through the layers. This paper introduced a way to both widen and deepen the LSTM whilst keeping the parameter number and runtime largely unchanged. In summary, we make the following contributions:
(a) Tensorize RNN hidden state vectors into higher-dimensional tensors, to enable more flexible parameter sharing and can be widened more efficiently without additional parameters.
(b) Based on (a), merge RNN deep computations into its temporal computations so that the network can be deepened with little additional runtime, resulting in a Tensorized RNN (tRNN).
(c) We extend the tRNN to an LSTM, namely the Tensorized LSTM (tLSTM), which integrates a novel memory cell convolution to help to prevent the vanishing/exploding gradients.
Method
Definition: Tensorization is defined as the transformation or mapping of lower-order data to higher-order data. For example, the low-order data can be a vector, and the tensorized result is a matrix, a third-order tensor or a higher-order tensor. The ‘low-order’ data can also be a matrix or a third-order tensor, for example. In the latter case, tensorization can take place along one or multiple modes.
Optimization Methodology Part 1: It can be seen that in an RNN, the parameter number scales quadratically with the size of the hidden state. A popular way to limit the parameter number when widening the network is to organize parameters as higher-dimensional tensors which can be factorized into lower-rank sub-tensors that contain significantly fewer elements, which is is known as tensor factorization.
Optimization Methodology Part 2: Another common way to reduce the parameter number is to share a small set of parameters across different locations in the hidden state, similar to Convolutional Neural Networks (CNNs).
Effects: This widens the network since the hidden state vectors are in fact broadcast to interact with the tensorized parameters.
We adopt parameter sharing to cutdown the parameter number for RNNs, since compared with factorization, it has the following advantages:
(i) Scalability, the number of shared parameters can be set independent of the hidden state size
(ii) Separability, the information flow can be carefully managed by controlling the receptive field, allowing one to shift RNN deep computations to the temporal domain
We also explicitly tensorize the RNN hidden state vectors, since compared with vectors, tensors have a better:
(i) Flexibility, one can specify which dimensions to share parameters and then can just increase the size of those dimensions without introducing additional parameters
(ii) Efficiency, with higher-dimensional tensors, the network can be widened faster w.r.t. its depth when fixing the parameter number (explained later).
Illustration: For ease of exposition, we first consider 2D tensors (matrices): we tensorize the hidden state [math]\displaystyle{ h_t∈R^{M} }[/math] to become [math]\displaystyle{ Ht∈R^{P×M} }[/math], where P is the tensor size, and M the channel size. We locally-connect the first dimension of [math]\displaystyle{ H_t }[/math] (which is P - the tensor size) in order to share parameters, and fully-connect the second dimension of [math]\displaystyle{ H_t }[/math] (which is M - the channel size) to allow global interactions. This is analogous to the CNN which fully-connects one dimension (e.g., the RGB channel for input images) to globally fuse different feature planes. Also, if one compares [math]\displaystyle{ H_t }[/math] to the hidden state of a Stacked RNN (sRNN) (see Figure Blow).
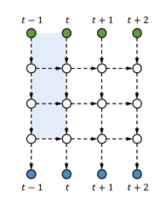

Then P is akin to the number of stacked hidden layers (vertical length in the graph), and M the size of each hidden layer (each white node in the graph). We start to describe our model based on 2D tensors, and finally show how to strengthen the model with higher-dimensional tensors.
Part 2: Merging Deep Computations
Since an RNN is already deep in its temporal direction, we can deepen an input-to-output computation by associating the input [math]\displaystyle{ x_t }[/math] with a (delayed) future output. In doing this, we need to ensure that the output [math]\displaystyle{ y_t }[/math] is separable, i.e., not influenced by any future input [math]\displaystyle{ x_{t^{'}} }[/math] [math]\displaystyle{ (t^{'}\gt t) }[/math]. Thus, we concatenate the projection of [math]\displaystyle{ x_t }[/math] to the top of the previous hidden state [math]\displaystyle{ H_{t−1} }[/math], then gradually shift the input information down when the temporal computation proceeds, and finally generate [math]\displaystyle{ y_t }[/math] from the bottom of [math]\displaystyle{ H_{t+L−1} }[/math], where L−1 is the number of delayed time-steps for computations of depth L.
An example with L= 3 is shown in Figure.
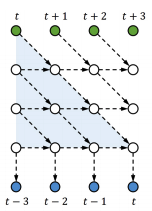

This is in fact a skewed sRNN (or tRNN without feedback). However, the method does not need to change the network structure and also allows different kinds of interactions as long as the output is separable; for example, one can increase the local connections and use feedback (shown in figure below), which can be beneficial for sRNNs (or tRNN).
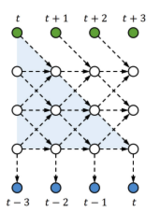

In order to share parameters, we update [math]\displaystyle{ H_t }[/math] using a convolution with a learnable kernel. In this manner we increase the complexity of the input-to-output mapping (by delaying outputs) and limit parameter growth (by sharing transition parameters using convolutions).
To examine the resulting model mathematically, let [math]\displaystyle{ H^{cat}_{t−1}∈R^{(P+1)×M} }[/math] be the concatenated hidden state, and [math]\displaystyle{ p∈Z_+ }[/math] the location at a tensor. The channel vector [math]\displaystyle{ h^{cat}_{t−1, p }∈R^M }[/math] at location p of [math]\displaystyle{ H^{cat}_{t−1} }[/math] (the p-th channel of H) is defined as:
\begin{align} h^{cat}_{t-1, p} = x_t W^x + b^x \hspace{1cm} if p = 1 \hspace{1cm} (5) \end{align}
\begin{align} h^{cat}_{t-1, p} = h_{t-1, p-1} \hspace{1cm} if p > 1 \hspace{1cm} (6) \end{align}
where [math]\displaystyle{ W^x ∈ R^{R×M} }[/math] and [math]\displaystyle{ b^x ∈ R^M }[/math] (recall the dimension of input x is R). Then, the update of tensor [math]\displaystyle{ H_t }[/math] is implemented via a convolution:
\begin{align} A_t = H^{cat}_{t-1} \circledast \{W^h, b^h \} \hspace{2cm} (7) \end{align}
\begin{align} H_t = \Phi{A_t} \hspace{2cm} (8) \end{align}
where [math]\displaystyle{ W^h∈R^{K×M^i×M^o} }[/math] is the kernel weight of size K, with [math]\displaystyle{ M^i =M }[/math] input channels and [math]\displaystyle{ M^o =M }[/math] output channels, [math]\displaystyle{ b^h ∈ R^{M^o} }[/math] is the kernel bias, [math]\displaystyle{ A_t ∈ R^{P×M^o} }[/math] is the hidden activation, and [math]\displaystyle{ \circledast }[/math] is the convolution operator. Since the kernel convolves across different hidden layers, we call it the cross-layer convolution. The kernel enables interaction, both bottom-up and top-down across layers. Finally, we generate [math]\displaystyle{ y_t }[/math] from the channel vector [math]\displaystyle{ h_{t+L−1,P}∈R^M }[/math] which is located at the bottom of [math]\displaystyle{ H_{t+L−1} }[/math]:
\begin{align} y_t = \varphi(h_{t+L−1}, _PW^y + b^y) \hspace{2cm} (9) \end{align}
Where [math]\displaystyle{ W^y ∈R^{M×S} }[/math] and [math]\displaystyle{ b^y ∈R^S }[/math]. To guarantee that the receptive field of [math]\displaystyle{ y_t }[/math] only covers the current and previous inputs x1:t. (Check the Skewed sRNN again below):


Quick Summary of Set of Parameters
1. [math]\displaystyle{ W^x }[/math] and [math]\displaystyle{ b_x }[/math] connect input to the first hidden node
2. [math]\displaystyle{ W^h }[/math] and [math]\displaystyle{ b_h }[/math] convolute between layers
3. [math]\displaystyle{ W^y }[/math] and [math]\displaystyle{ b_y }[/math] produce output of each stages
Part 3: Extending to LSTMs
Similar to standard RNN, to allow the tRNN (skewed sRNN) to capture long-range temporal dependencies, one can straightforwardly extend it to a tLSTM by replacing the tRNN tensors:
\begin{align} [A^g_t, A^i_t, A^f_t, A^o_t] = H^{cat}_{t-1} \circledast \{W^h, b^h \} \hspace{2cm} (10) \end{align}
\begin{align} [G_t, I_t, F_t, O_t]= [\Phi{(A^g_t)}, σ(A^i_t), σ(A^f_t), σ(A^o_t)] \hspace{2cm} (11) \end{align}
Which are pretty similar to tRNN case, the main differences can be observes for memory cells of tLSTM (Ct):
\begin{align} C_t= G_t \odot I_t + C_{t-1} \odot F_t \hspace{2cm} (12) \end{align}
\begin{align} H_t= \Phi{(C_t )} \odot O_t \hspace{2cm} (13) \end{align}
Note that since the previous memory cell [math]\displaystyle{ C_{t-1} }[/math] is only gated along the temporal direction, increasing the tensor size P might result in the loss of long-range dependencies from the input to the output.
Summary of the terms:
1. [math]\displaystyle{ \{W^h, b^h \} }[/math]: Kernel of size K
2. [math]\displaystyle{ A^g_t, A^i_t, A^f_t, A^o_t \in \mathbb{R}^{P\times M} }[/math]: Activations for the new content [math]\displaystyle{ G_t }[/math]
3. [math]\displaystyle{ I_t }[/math]: Input gate
4. [math]\displaystyle{ F_t }[/math]: Forget gate
5. [math]\displaystyle{ O_t }[/math]: Output gate
6. [math]\displaystyle{ C_t \in \mathbb{R}^{P\times M} }[/math]: Memory cell
Then, see graph below for illustration:
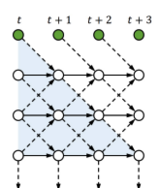

To further evolve tLSTM, we invoke the Memory Cell Convolution to capture long-range dependencies from multiple directions, we additionally introduce a novel memory cell convolution, by which the memory cells can have a larger receptive field (figure provided below).
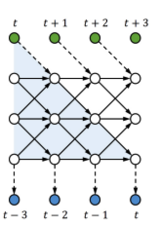

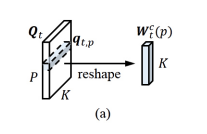
One can also dynamically generate this convolution kernel so that it is both time - and location-dependent, allowing for flexible control over long-range dependencies from different directions. Mathematically, it can be represented in with the following formulas:
\begin{align} [A^g_t, A^i_t, A^f_t, A^o_t, A^q_t] = H^{cat}_{t-1} \circledast \{W^h, b^h \} \hspace{2cm} (14) \end{align}
\begin{align} [G_t, I_t, F_t, O_t, Q_t]= [\Phi{(A^g_t)}, σ(A^i_t), σ(A^f_t), σ(A^o_t), ς(A^q_t)] \hspace{2cm} (15) \end{align}
\begin{align} W_t^c(p) = reshape(q_{t,p}, [K, 1, 1]) \hspace{2cm} (16) \end{align}
\begin{align} C_{t-1}^{conv}= C_{t-1} \circledast W_t^c(p) \hspace{2cm} (17) \end{align}
\begin{align} C_t= G_t \odot I_t + C_{t-1}^{conv} \odot F_t \hspace{2cm} (18) \end{align}
\begin{align} H_t= \Phi{(C_t )} \odot O_t \hspace{2cm} (19) \end{align}
where the kernel [math]\displaystyle{ {W^h, b^h} }[/math] has additional <K> output channels to generate the activation [math]\displaystyle{ A^q_t ∈ R^{P×\lt K\gt } }[/math] for the dynamic kernel bank [math]\displaystyle{ Q_t∈R^{P × \lt K\gt } }[/math], [math]\displaystyle{ q_{t,p}∈R^{\lt K\gt } }[/math] is the vectorized adaptive kernel at the location p of [math]\displaystyle{ Q_t }[/math], and [math]\displaystyle{ W^c_t(p) ∈ R^{K×1×1} }[/math] is the dynamic kernel of size K with a single input/output channel, which is reshaped from [math]\displaystyle{ q_{t,p} }[/math]. Each channel of the previous memory cell [math]\displaystyle{ C_{t-1} }[/math] is convolved with [math]\displaystyle{ W_t^c(p) }[/math] whose values vary with [math]\displaystyle{ p }[/math], to form a memory cell convolution, which produces a convolved memory cell [math]\displaystyle{ C_{t-1}^{conv} \in \mathbb{R}^{P\times M} }[/math]. This convolution is defined by:
\begin{align} C_{t-1,p,m}^{conv} = \sum\limits_{k=1}^K C_{t-1,p-\frac{K-1}{2}+k,m} · W_{t,k,1,1}^c(p) \hspace{2cm} (30) \end{align}
where [math]\displaystyle{ C_{t-1} }[/math] is padded with the boundary values to retain the stored information.
Note the paper also employed a softmax function ς(·) to normalize the channel dimension of [math]\displaystyle{ Q_t }[/math]. which can also stabilize the value of memory cells and help to prevent the vanishing/exploding gradients. An illustration is provided below to better illustrate the process:
Theorem 17-18 of Leifert et al. [3] proves the prevention of vanishing/exploding gradients for the lambda gate, which is very similar to the proposed memory cell convolution kernel. The only major differences between the two are the use of softmax for normalization and the sharing the of the kernal for all channels. Since these changes to not affect the assertions made in Theorem 17-18, it can be established that the prevention of vanishing/exploding gradients is a feature of the memory cell convolution kernel as well.
To improve training, the authors introduced a new normalization technique for tLSTM termed channel normalization (adapted from layer normalization), in which the channel vector are normalized at different locations with their own statistics. Note that layer normalization does not work well with tLSTM, because lower level information is near the input and higher level information is near the output. Channel normalization (CN) is defined as:
\begin{align} \mathrm{CN}(\mathbf{Z}; \mathbf{\Gamma}, \mathbf{B}) = \mathbf{\hat{Z}} \odot \mathbf{\Gamma} + \mathbf{B} \hspace{2cm} (20) \end{align}
where [math]\displaystyle{ \mathbf{Z} }[/math], [math]\displaystyle{ \mathbf{\hat{Z}} }[/math], [math]\displaystyle{ \mathbf{\Gamma} }[/math], [math]\displaystyle{ \mathbf{B} \in \mathbb{R}^{P \times M^z} }[/math] are the original tensor, normalized tensor, gain parameter and bias parameter. The [math]\displaystyle{ m^z }[/math]-th channel of [math]\displaystyle{ \mathbf{Z} }[/math] is normalized element-wisely:
\begin{align} \hat{z_{m^z}} = (z_{m^z} - z^\mu)/z^{\sigma} \hspace{2cm} (21) \end{align}
where [math]\displaystyle{ z^{\mu} }[/math], [math]\displaystyle{ z^{\sigma} \in \mathbb{R}^P }[/math] are the mean and standard deviation along the channel dimension of [math]\displaystyle{ \mathbf{Z} }[/math], and [math]\displaystyle{ \hat{z_{m^z}} \in \mathbb{R}^P }[/math] is the [math]\displaystyle{ m^z }[/math]-th channel [math]\displaystyle{ \mathbf{\hat{Z}} }[/math]. Channel normalization introduces very few additional parameters compared to the number of other parameters in the model.
Results and Evaluation
Summary of list of models tLSTM family (may be useful later):
(a) sLSTM (baseline): the implementation of sLSTM with parameters shared across all layers.
(b) 2D tLSTM: the standard 2D tLSTM.
(c) 2D tLSTM–M: removing memory (M) cell convolutions from (b).
(d) 2D tLSTM–F: removing (–) feedback (F) connections from (b).
(e) 3D tLSTM: tensorizing (b) into 3D tLSTM.
(f) 3D tLSTM+LN: applying (+) Layer Normalization.
(g) 3D tLSTM+CN: applying (+) Channel Normalization.
Efficiency Analysis
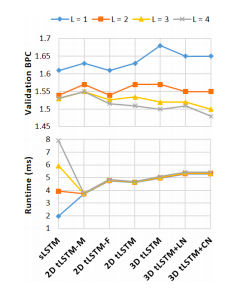
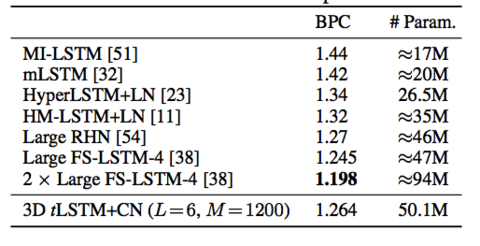
Fundaments: For each configuration, fix the parameter number and increase the tensor size to see if the performance of tLSTM can be boosted without increasing the parameter number. Can also investigate how the runtime is affected by the depth, where the runtime is measured by the average GPU milliseconds spent by a forward and backward pass over one timestep of a single example.
Dataset: The Hutter Prize Wikipedia dataset consists of 100 million characters taken from 205 different characters including alphabets, XML markups and special symbols. We model the dataset at the character-level, and try to predict the next character of the input sequence.
All configurations are evaluated with depths L = 1, 2, 3, 4. Bits-per-character(BPC) is used to measure the model performance and the results are shown in the figure below.
Accuracy Analysis
The MNIST dataset [35] consists of 50000/10000/10000 handwritten digit images of size 28×28 for training/validation/test. Two tasks are used for evaluation on this dataset:
(a) Sequential MNIST: The goal is to classify the digit after sequentially reading the pixels in a scan-line order. It is therefore a 784 time-step sequence learning task where a single output is produced at the last time-step; the task requires very long range dependencies in the sequence.
(b) Sequential Permuted MNIST: We permute the original image pixels in a fixed random order, resulting in a permuted MNIST (pMNIST) problem that has even longer range dependencies across pixels and is harder.
In both tasks, all configurations are evaluated with M = 100 and L= 1, 3, 5. The model performance is measured by the classification accuracy and results are shown in the figure below.
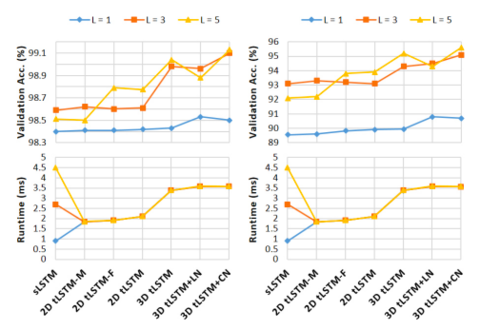
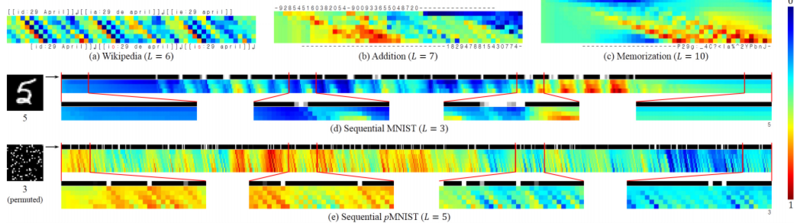
It can be seen in the above figure that tLSTM behaves differently with different tasks:
- Wikipedia: the input can be carried to the output location with less modification if it is sufficient to determine the next character, and vice versa
- addition: the first integer is gradually encoded into memories and then interacts (performs addition) with the second integer, producing the sum
- memorization: the network behaves like a shift register that continues to move the input symbol to the output location at the correct timestep
- sequential MNIST: the network is more sensitive to the pixel value change (representing the contour, or topology of the digit) and can gradually accumulate evidence for the final prediction
- sequential pMNIST: the network is sensitive to high value pixels (representing the foreground digit), and we conjecture that this is because the permutation destroys the topology of the digit, making each high value pixel potentially important.
From the figure above it can can also be observe some common phenomena in all tasks:
- it is clear that wider (larger) tensors can encode more information by observing that at each timestep, the values at different tensor locations are markedly different
- from the input to the output, the values become increasingly distinct and are shifted by time, revealing that deep computations are indeed performed together with temporal computations, with long-range dependencies carried by memory cells.
Related work
Convolutional LSTMs
Convolutional LSTMs are proposed to parallelize the computation of LSTMs when the input at each timestep is structured
Deep LSTMs
Deep LSTMs. Deep LSTMs (dLSTMs) extend sLSTMs by making them deeper (see Fig. 7(b)-(d)). To keep the parameter number small and ease training, Graves [22], Kalchbrenner et al. [30], Mujika et al. [38], Zilly et al. [54] apply another RNN/LSTM along the depth direction of dLSTMs, which, however, multiplies the runtime. Though there are implementations to accelerate the deep computation [1, 16], they generally aim at simple architectures such sLSTMs. Compared with dLSTMs, tLSTM performs the deep computation with little additional runtime, and employs a cross-layer convolution to enable the feedback mechanism. Moreover, the capacity of tLSTM can be increased more efficiently by using higher-dimensional tensors, whereas in dLSTM all hidden layers as a whole only equal to a 2D tensor (i.e., a stack of hidden vectors), the dimensionality of which is fixed.
Conclusions
The paper introduced the Tensorized LSTM, which employs tensors to share parameters and utilizes the temporal computation to perform the deep computation for sequential tasks. Then validated the model on a variety of tasks, showing its potential over other popular approaches. The paper shows a method to widen and deepen the LSTM network at the same time and the following 3 points list their main contributions:
- The RNNs are now tensorized into higher dimensional tensors which are more flexible.
- RNNs' deep computation is merged into the temporal computation, referred to as the tensorizedRNN.
- tRNN is extended to a LSTM architecture and a new architecture is studied: tensorizedLSTM
Critique(to be edited)
- Using tensor as hidden layer indeed increasing the capability of the network, but authors never mentioned the trade-off in terms of extra computation cost and training time.
References
- Zhen He, Shaobing Gao, Liang Xiao, Daxue Liu, Hangen He, and David Barber. <Wider and Deeper, Cheaper and Faster: Tensorized LSTMs for Sequence Learning> (2017)
- Ali Ghodsi, <Deep Learning: STAT 946 - Winter 2018>
- Gundram Leifert, Tobias Strauß, Tobias Grüning, Welf Wustlich, and Roger Labahn. Cells in multidimensional recurrent neural networks. JMLR, 17(1):3313–3349, 2016.