stat441w18/summary 1: Difference between revisions
| (25 intermediate revisions by the same user not shown) | |||
| Line 33: | Line 33: | ||
In the first part of this paper on random features, it is based on the Fourier transform of the kernel. The authors made use of the fact that for any kernel that is positive definite, its corresponding Fourier transform is also positive definite as well. For any shift-invariant kernel k(x-y), we can build a low-dimension randomized function z so that <math> \forall x, y </math> <math> k(x,y) = <\phi(x), \phi(y) > \approx Z(x)^TZ(y) </math> where the last term approximated represents the dot product of the featurized inputs. | In the first part of this paper on random features, it is based on the Fourier transform of the kernel. The authors made use of the fact that for any kernel that is positive definite, its corresponding Fourier transform is also positive definite as well. For any shift-invariant kernel k(x-y), we can build a low-dimension randomized function z so that <math> \forall x, y </math> <math> k(x,y) = <\phi(x), \phi(y) > \approx Z(x)^TZ(y) </math> where the last term approximated represents the dot product of the featurized inputs. | ||
<math> k(x - y) = \int _{\Omega} p(\omega) e ^{ | If <math> k(x - y) = \int _{\Omega} p(\omega) e ^{i\omega'(x-y) } d\omega </math> then we can approximate k(x-y) by | ||
<math> \approx \sum_j e^{i\omega_j^Tx}e^{i\omega_j^Tx}</math> randomly sampling <math>\omega \text{ from its Fourier transform } p(\omega)</math>. | |||
Bochner's theorem[2] guarantees that <math> p(\omega) </math> is a proper distribution with <math> E_\omega [Z_\omega(x)' Z_\omega(y)] = k(x,y) </math>. For a given <math> \omega </math>, the random features are bounded between -1 and 1 and which guarantees fast convergence. | |||
===Random Binning Features === | ===Random Binning Features === | ||
The second random map uses randomly shifted grids at randomly chosen resolutions and assigns points the bit string z(x) linked to the assigned bin. This arose from the fact that shift-invariant kernels can be written as combinations of hat kernels. | |||
<math> </math> | |||
== Results == | == Results == | ||
| Line 52: | Line 57: | ||
=== Experiments === | === Experiments === | ||
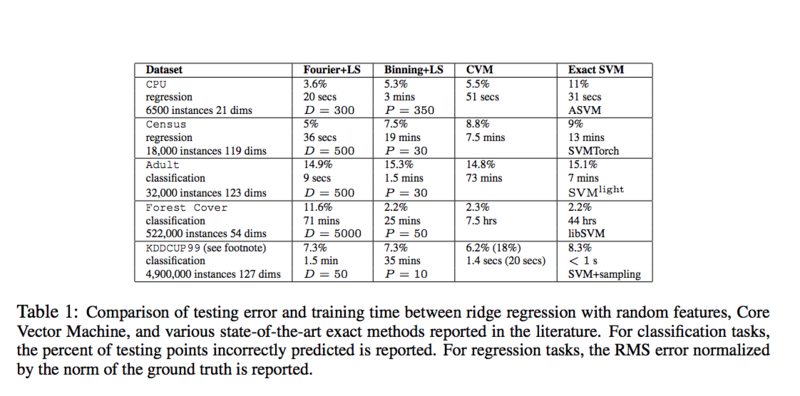
Authors presented ridge regression with random features to approximate training using supervised kernel machines in Table 1. | Authors presented ridge regression with random features to approximate training using supervised kernel machines in Table 1 and Figure 3 of the paper. | ||
Recall that ridge regression is of the form : | Recall that ridge regression is of the form : | ||
<math> \text{min}_w || Z'w - y||_2^2 + \lambda ||w||_2^2</math> where the second term is a penalization term. | <math> \text{min}_w || Z'w - y||_2^2 + \lambda ||w||_2^2</math> where the second term is a penalization term. The experiments were conducted on large scale datasets and methods compared are Fourier features, binning features, core vector machine and exact support vector machine. | ||
[[File:Image_Table3.png|800px]] | |||
== Conclusion == | == Conclusion == | ||
Latest revision as of 12:51, 7 March 2018
Random features for large scale kernel machines
Group members
Faith Lee
Jacov Lisulov
Shiwei Gong
Introduction and problem motivation
In classification problems, kernel methods are used for pattern analysis and require only user-specified kernel. Kernel methods can be thought of as instance-based methods where they learn the i-th training examples are "remembered" to learn for corresponding weights. Prediction on untrained examples are then treated with a similarity function, k (also called a kernel between this untrained example and each of the training inputs. A similarity function measures similarity between two objects. By conventional notation, we have that
[math]\displaystyle{ f(x; \alpha) = \sum_{i = 1}^{N} \alpha_i k(x, x_i) }[/math] where k is a kernel function, [math]\displaystyle{ k(x, x') \approx \sum_{j = i}^{D} Z(X; W_j)Z(X'; W_j) }[/math]
and [math]\displaystyle{ \alpha }[/math] are the corresponding weights.
An example of a kernel method is the support vector machine. Kernel methods provides a means of approximating a non-linear function or decision boundary. However, the problem of using kernel methods are that:
1) It scales poorly with the size of the dataset
2) Computationally expensive (kernel machines result in large matrices with entries of kernels operated on training points)
In this paper, the authors propose mapping of input data to a randomized low-dimensional feature space and then apply existing linear methods. The main goal is to reduce the bottleneck of kernel-based inference methods.
Methods
Random Fourier Features
The Fourier transform of a function is given by definition as [math]\displaystyle{ \int_{-\infty}^{\infty} exp^{-2\pi i x \epsilon} dx }[/math]. In the first part of this paper on random features, it is based on the Fourier transform of the kernel. The authors made use of the fact that for any kernel that is positive definite, its corresponding Fourier transform is also positive definite as well. For any shift-invariant kernel k(x-y), we can build a low-dimension randomized function z so that [math]\displaystyle{ \forall x, y }[/math] [math]\displaystyle{ k(x,y) = \lt \phi(x), \phi(y) \gt \approx Z(x)^TZ(y) }[/math] where the last term approximated represents the dot product of the featurized inputs.
If [math]\displaystyle{ k(x - y) = \int _{\Omega} p(\omega) e ^{i\omega'(x-y) } d\omega }[/math] then we can approximate k(x-y) by [math]\displaystyle{ \approx \sum_j e^{i\omega_j^Tx}e^{i\omega_j^Tx} }[/math] randomly sampling [math]\displaystyle{ \omega \text{ from its Fourier transform } p(\omega) }[/math]. Bochner's theorem[2] guarantees that [math]\displaystyle{ p(\omega) }[/math] is a proper distribution with [math]\displaystyle{ E_\omega [Z_\omega(x)' Z_\omega(y)] = k(x,y) }[/math]. For a given [math]\displaystyle{ \omega }[/math], the random features are bounded between -1 and 1 and which guarantees fast convergence.
Random Binning Features
The second random map uses randomly shifted grids at randomly chosen resolutions and assigns points the bit string z(x) linked to the assigned bin. This arose from the fact that shift-invariant kernels can be written as combinations of hat kernels. [math]\displaystyle{ }[/math]
Results
The authors advertise their methodology can train large datasets in very few lines of code: To illustrate the use of random feature to approximate the Gaussian kernel in MatLab,
w = randn(D, size(X,1));
Z = exp(i*w*X);
alpha = (eye(size(X,1))*lambda+Z*Z')\(Z*y(:));
ztest = alpha(:)'*exp(i*w*xtest(:));
Experiments
Authors presented ridge regression with random features to approximate training using supervised kernel machines in Table 1 and Figure 3 of the paper. Recall that ridge regression is of the form : [math]\displaystyle{ \text{min}_w || Z'w - y||_2^2 + \lambda ||w||_2^2 }[/math] where the second term is a penalization term. The experiments were conducted on large scale datasets and methods compared are Fourier features, binning features, core vector machine and exact support vector machine.
Conclusion
In this paper, the authors presented a method where randomized features can be used to approximate popular kernels. Empirically shown in their results, plugging in these features in standard linear learning algorithms showed results that are competent in terms of accuracy and training time compared to the conventional kernel methods. While the tasks at hand here focused on regression and classification, computational speed-up can also be achieved in the semi-supervised and unsupervised learning cases.
In short the framework for this paper :
[math]\displaystyle{ \text{Big data} \rightarrow \text{Random Featurization} \rightarrow \text{Linear machine learning training methods} \rightarrow \text{Classifier} }[/math] in comparison to the conventional
[math]\displaystyle{ \text{Big data} \rightarrow \text{Kernel Machine Training} \rightarrow \text{Classifier} }[/math]