learning Fast Approximations of Sparse Coding: Difference between revisions
m (Conversion script moved page Learning Fast Approximations of Sparse Coding to learning Fast Approximations of Sparse Coding: Converting page titles to lowercase) |
|||
| (76 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
= | = Background = | ||
In contrast to a dimensionality-reduction approach to feature-extraction, sparse coding is an unsupervised method which attempts to construct a novel representation of the data by mapping it linearly into a higher-dimensional space. This transformation is performed with the objective of obtaining a new feature space in which, for each vector, we can find a smaller subset of features that largely reconstruct it. Essentially, this allows us to perform case-specific feature-extraction, as for a given input, we seek a smaller subset of features to which we will assign the majority of the weight for its representation, with the remainder being negligibly small. This provides us with a procedure which attempts to flexibly represent unseen instances of the input space. | In contrast to a dimensionality-reduction approach to feature-extraction, sparse coding is an unsupervised method which attempts to construct a novel representation of the data by mapping it linearly into a higher-dimensional space. This transformation is performed with the objective of obtaining a new feature space in which, for each vector, we can find a smaller subset of features that largely reconstruct it. Essentially, this allows us to perform case-specific feature-extraction, as for a given input, we seek a smaller subset of features to which we will assign the majority of the weight for its representation, with the remainder being negligibly small. This provides us with a procedure which attempts to flexibly represent unseen instances of the input space. | ||
The introduction of a larger set of spanning vectors is a consequence of the | The introduction of a larger set of spanning vectors is a consequence of the desire to produce accurate reconstructions across a broad range of possible input from the original space. However, the algebra of linear transformations tells us that input vectors will no longer have a unique representation in the higher-dimensional feature space. This short-coming is alleviated by the fact that we would like to assign the majority of influence to only a subset of the new features. We implement this goal using the notion of sparsity; namely, we will penalize large weight values. | ||
Unfortunately, there are some implementation issues which prevent the use of sparse coding in certain contexts. The fact that we must find a representation for each new case the system is provided with often renders the procedure infeasible for online processing tasks, as new data must be handled in real-time. Several approximation algorithms have been proposed to address issues in processing speed. However, these methods suffer from deficiencies in their ability to take into account some relevant conditional-independence structures in the data. To resolve these limitations, the authors introduce a feed-forward architecture which | Unfortunately, there are some implementation issues which prevent the use of sparse coding in certain contexts. The fact that we must find a representation for each new case the system is provided with often renders the procedure infeasible for online processing tasks, as new data must be handled in real-time. Several approximation algorithms have been proposed to address issues in processing speed. However, these methods suffer from deficiencies in their ability to take into account some relevant conditional-independence structures in the data. To resolve these limitations, the authors introduce a feed-forward architecture which utilizes these approximation schemes, giving a new procedure which is demonstrated to be ~10 times more efficient than the previous state-of-the-art approximation, in empirical testing.The main contribution of this paper is a highly efficient learning-based method that computes good approximations of optimal sparse codes in a fixed amount of time. | ||
= Review of Sparse Coding = | = Review of Sparse Coding = | ||
For an input <math> X \epsilon \mathbb{R}^n </math>, we seek a new representation <math> Z \epsilon \mathbb{R}^m </math> which satisfies the previously-stated objective. In order to find an optimal code <math> Z </math> of <math> X </math>, we also require a dictionary <math> W_d \epsilon \mathbb{R}^{m x n} </math>, the matrix of normalized vectors that the coordinates of <math> Z </math> are defined in relation to. Given a training set, we will estimate the optimal sparse codes for each training case, in pursuit of the dictionary matrix to be used in coding novel input. | For an input <math> X \epsilon \mathbb{R}^n </math>, we seek a new representation <math> Z \epsilon \mathbb{R}^m </math> which satisfies the previously-stated objective. In order to find an optimal code <math> \, Z </math> of <math> \, X </math>, we also require a dictionary <math> W_d \epsilon \mathbb{R}^{m x n} </math>, the matrix of normalized vectors that the coordinates of <math> \, Z </math> are defined in relation to. Given a training set, we will estimate the optimal sparse codes for each training case, in pursuit of the dictionary matrix to be used in coding novel input. | ||
These solutions will be found based on a loss function taking into account the squared reconstruction error and the complexity of the code: | These solutions will be found based on a loss function taking into account the squared reconstruction error and the complexity of the code: | ||
:: <math> E_{W_d}(X, Z) = \frac{1}{2}\|X - W_dZ\|_2^2 + \alpha \|Z\|_1 </math>, | :: <math> E_{W_d}(X, Z) = \frac{1}{2}\|X - W_dZ\|_2^2 + \alpha \|Z\|_1 </math>, | ||
Using this, the optimal code for input <math> X </math> is naturally defined as <math> Z^* = argmin_Z E(X, Z) </math>. | where <math> \, \alpha </math> is the specified sparsity penalty. Using this, the optimal code for input <math> X </math> is naturally defined as <math> \, Z^* = argmin_Z E(X, Z) </math>. | ||
From here, the dictionary is learned in an unsupervised manner, typically through the application of stochastic gradient descent to the minimization of the average loss <math> E_{W_d}(X, Z^*) </math> across a subset of the training cases. The dictionary to be applied to new cases is learned prior to the execution of the approximation proposed here. | From here, the dictionary is learned in an unsupervised manner, typically through the application of stochastic gradient descent to the minimization of the average loss <math> E_{W_d}(X, Z^*) </math> across a subset of the training cases. The dictionary to be applied to new cases is learned prior to the execution of the approximation proposed here. | ||
| Line 21: | Line 21: | ||
=Pre-existing Approximations: Iterative Shrinkage Algorithms= | =Pre-existing Approximations: Iterative Shrinkage Algorithms= | ||
Here baseline iterative shrinkage algorithms for finding sparse codes are introduced and explained. The ISTA and FISTA methods update the whole code vector in parallel, while the more efficient Coordinate Descent method (CoD) updates the components one at a time and carefully selects which component to update at each step. | |||
Both methods refine the initial guess through a form of mutual inhibition between code component, and component-wise shrinkage. | |||
==Iterative Shrinkage & Thresholding (ISTA)== | |||
The Iterative Shrinkage & Thresholding Algorithm (ISTA) and its sped-up variant Fast ISTA approximate the optimal code vector of an input by updating all the code components in parallel. The idea is that, at each iteration, we should shift our current code in the direction of greatest reconstruction error, and then apply a component-wise shrinkage function to enforce sparsity. Initializing <math> \, Z^{(0)} = 0 </math>, we have the recursive update rule: | |||
Depending on a few possible choices to be made in implementing this scheme, the time complexity in using ISTA to construct a code for a new input will be <math> O(m^2) </math>, <math> O(nm) </math>, or <math> O(km) </math>, with <math> k </math> being the average sparsity across samples and iterations. | :: <math> Z^{(k + 1)} = h_{\theta}(Z^{(k)} - \frac{1}{L}W_d^T(W_dZ^{(k)} - X)) = h_{\theta}(W_eX + SZ^{(k)}) </math> (**), | ||
:: where <math> W_e = \frac{1}{L}W_d^T </math> is the filter matrix, and <math> S = I - \frac{1}{L}W_d^TW_d </math> is the mutual-inhibition matrix. | |||
Here, <math> \, L </math> is an upper-bound on the size of the eigenvalues of <math> W_d^TW_d </math>, and <math>\, h_{\theta}( ) </math> is the shrinkage function with components <math> \, h_{\theta}(V)_i = sign(V_i) </math> <math> \, max(|V_i| - \theta_i, </math> <math> \, 0) </math>, where <math> \theta \epsilon \mathbb{R}^m </math> consists of the sparsity thresholds for the components of the code. Thresholds are typically set to <math> \theta_i =\frac{\alpha}{L} </math>. | |||
=== Fast ISTA === | |||
Depending on a few possible choices to be made in implementing this scheme, the per-iteration time complexity in using ISTA to construct a code for a new input will be <math> \, O(m^2) </math>, <math> \, O(nm) </math>, or <math> \, O(km) </math>, with <math> \, k </math> being the average sparsity across samples and iterations. | |||
Fast ISTA is a modification of this approximation which ensures faster convergence through the addition of a momentum term. Here, our update rule becomes: | |||
:: <math> Z^{(k + 1)} = h_{\theta}(Z^{(k)}) + \lambda (h_{\theta}^{(k-1)} - h_{\theta}^{(k - 2)}) </math> | |||
In other words, the updated code is the shrinkage function applied to the current code, plus a multiple of the difference of the outputs of the shrinkage function for the preceding two iterations. This second term the rate at which the approximated code is changing. | |||
== Coordinate Descent == | |||
Instead of automatically updating all the entries of the code in parallel, we might consider strategically selecting a single component to be updated each iteration. Coordinate Descent (CoD) adopts this mentality, and resultantly yields a superior approximation to the parallel ISTA methods in the same order of time. In fact, Coordinate Descent was widely believed to be the most efficient algorithm available for approximating sparse codes. | |||
The CoD algorithm is presented below: | |||
<blockquote> | |||
<math>\textbf{function} \, \textbf{CoD}\left(X, Z, W_d, S, \alpha\right)</math> | |||
: <math>\textbf{Require:} \,S = I - W_d^T W_d</math> | |||
: <math>\textbf{Initialize:} \,Z = 0; B = W_d^TX</math> | |||
: <math> \textbf{repeat}</math> | |||
:: <math>\bar{Z} = h_{\alpha}\left(B\right)</math> | |||
:: <math> \,k = \mbox{ index of largest component of} \left|Z - \bar{Z}\right|</math> | |||
:: <math> \forall j \in \left[1, m\right]: B_j = B_j + S_{jk}\left(\bar{Z}_k - Z_k\right)</math> | |||
:: <math> Z_k = \bar{Z}_k</math> | |||
: <math>\textbf{until}\,\text{change in}\,Z\,\text{is below a threshold}</math> | |||
: <math> Z = h_{\alpha}\left(B\right)</math> | |||
<math> \textbf{end} \, \textbf{function} </math> | |||
</blockquote> | |||
In each iteration of the procedure, we search for the entry of the current code which, if updated so as to minimize the corresponding loss while holding the other components constant, results in the largest change in comparison to the current code. This search step takes <math> \, O(m) </math> operations, and, so in also accounting for each component-wise optimization performed (which follows a similar process to that of the parallel case), each iteration requires <math> \, O(m^2) </math> steps. Alternatively, we could repeat the update process <math> \, O(n) </math> times instead, to achieve a per-iteration complexity of <math> \, O(nm) </math>, which is again comparable to ISTA. This algorithm has a similar feedback concept to ISTA, but can it can expressed as a linear feedback operation with a very sparse matrix (since only one component is updated at a time). Either way, it turns out that, deploying both for an approximately equal amount of time, Coordinate Descent will out-perform the ISTA methods in its approximation to an optimal code. | |||
= Encoders for Sparse Code Approximation = | |||
In seeking an approach to further improve upon the efficiency of Coordinate Descent, the authors present the use of feed-forward networks for real-time sparse code inference. Essentially, for the training phase, we will perform learning for a neural network which takes our original input <math> \, X \epsilon \mathbb{R}^n </math> and generates a prediction of its optimal code with respect to the previously-estimated dictionary. The training set will consist of the original <math> \, X </math> as our input, and their sparse codes estimated via Coordinate Descent as the target values. In learning the network weights, we use stochastic gradient descent to minimize the average squared-error between the network's predictions and these estimated sparse codes. The size of the network will be chosen with consideration of its feasibility in applying it to online processing. | |||
==A Simplistic Architecture and its Limitations== | |||
The most straight-forward approach to this task would be to use a single-layer feed-forward network. However, since we have the additional requirement that the network output is to be sparse, special consideration of the activation function must be made. The authors consider three such candidates: double tanh, a learned non-linearity, and the shrinkage function <math> \, h_{\theta}( ) </math> used for ISTA. The three approaches perform comparably in the authors' empirical testing, and so they opt to use <math> \, h_{\theta}( ) </math> to maintain a strong basis for comparison with the previous methods. | |||
Despite the appeal of its simplicity, this network configuration is unable to learn "explaining-away" phenomena, a conditional-independence structure relevant to this task. Essentially, this means that if the learned weight matrix happens to contain two highly similar rows, the network will uniformly represent two components of the code as nearly-equal. However, this inability to select only one of the components and suppress the other redundant one is clearly indicative of a limitation of the network's ability to produce sparse encodings. Consequently, a more sophisticated architecture is proposed. | |||
== Learned ISTA & Learned Coordinate Descent == | |||
To address explaining-away phenomena, interaction terms between components are introduced. To implement these terms controlling redundancy amongst the components, the authors design a sequence of feed-forward networks structured so as to be analogous to executing some number of steps of ISTA or a pre-determined number of steps of Coordinate Descent. The use of ISTA versus Coordinate Descent corresponds to two distinct encoders, both of which can be viewed as a "time-unfolded" recurrent network. | |||
Before understanding the rationale behind this approach, we must recognize a few relevant values which are inherently fixed in the process of executing ISTA or Coordinate Descent. The recursive equations iterated over in these procedures can both be re-expressed in terms parameters including a threshold vector <math> \, \theta </math>, a filter matrix <math> \, W_e </math>, and a mutual-inhibition matrix <math> \, S </math>, where these terms are defined differently for the two procedures. Now, instead of using these fully-determined parameter forms and iterating the procedure until it converges, this encoder-driven approach purposes to learn <math> \, \theta </math>, <math> \, W_e </math>, <math> \, S </math>, and then execute only a fixed number of steps of one of these procedures, in order to reduce the total computational cost. Using the available data to adaptively set these parameters allows the corresponding network to handle the issues pertaining to explaining-away. | |||
In Learned ISTA (LISTA), the encoder structure takes the form defined by the recursive update for ISTA (**), iterated for a fixed number of times ''T''. We learn the parameters <math> \, W_e </math>, <math> \, \theta </math>, and <math> \, S </math> by using stochastic gradient descent to minimize the previously-described squared-error loss for sparse code prediction. From its definition, we can see that <math> \, S </math> is shared across the <math> T </math> time steps, and so we use back-propagation through time to compute the error gradient for gradient descent. | |||
Similarly, in Learned Coordinate Descent (LCoD), the network architecture is defined by the recursive update for Coordinate Descent (omitted for brevity) iterated for a fixed number of time steps. The parameters <math> \, W_e </math>, <math> \, \theta </math>, and ''S'' are learned analogous to the procedure for LISTA, except for the technicality that sub-gradients are propagated, resulting from the fact that we search for the component inducing the largest update in the code ''Z''. | |||
The algorithm for LCoD can be summarized as | |||
[[File:Q12.png]] | |||
A main advantage of the system proposed in this paper is speed, so it is necessary to take note of the asymptotic complexity of the above algorithm: only <math>\, O(m)</math> operations are required for each step of the bprop procedure, and each iteration only requires <math>\, O(m)</math> space; as almost all of the stored variables are scalar, with the exception of <math>\, B(T)</math>. (Recall that m refers to the number of dimensions in the new feature space with the sparse representations.) | |||
= Empirical Performance = | |||
Two sets of experiments were undertaken: | |||
* The procedures were compared in their performance on exact sparse code inference, using the Berkeley image database. | |||
* The MNIST digits dataset was used in assessing whether improved error-rates in code-prediction yields superior performance in recognition tasks. | |||
Overall, the results indicate that this proposal to construct encoders from a set of iterations of ISTA or Coordinate Descent yields a significantly-reduced runtime when compared to the pre-existing procedures, at a pre-specified error-rate. | |||
== Berkeley Image Database == | |||
From this database, 10x10-pixel image patches were randomly drawn to compare (Fast) ISTA with LISTA, and Coordinate Descent with LCoD, in sparse code prediction. Performance was tested on dictionaries of sizes ''m'' = 100 and ''m'' = 400, using a sparsity penalty of <math> \alpha = 0.5 </math>, and the squared-error loss for the distance between the estimate and the optimal code, as computed by Coordinate Descent. | |||
Figure 1 suggests that, LISTA notably out-performs FISTA here. Furthermore, 18 iterations of FISTA are required to achieve the error-rate produced by 1 iteration of LISTA when ''m'' = 100, and 35 iterations when ''m'' = 400. This leads the authors to conclude that LISTA is ~20 times faster than FISTA. | |||
<center> | |||
[[File:LISTA2.png |frame | center |Figure 1: Comparison of LISTA and FISTA. Squared-error in code prediction plotted against number of iterations. In the legend, "1x" denotes ''m'' = 100, and "4x" for ''m'' = 400 ]] | |||
</center> | |||
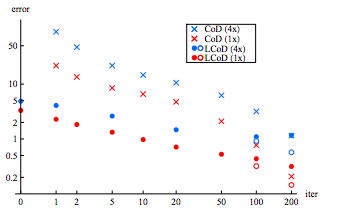
Figure 2 indicates that, for a moderately-large number of iterations, LCoD has superior accuracy to Coordinate Descent. When the number of iterations is larger, Coordinate Descent out-performs LCoD, but this can be reversed by initializing matrices with their CoD values prior to training. | |||
<center> | |||
[[File:LCOD.png |frame | center |Figure 2: Comparison of LCoD and Coordinate Descent. Squared-error in code prediction plotted against number of iterations. In the legend, "1x" denotes ''m'' = 100, and "4x" for ''m'' = 400. Open Circles indicate that matrices have been initialized with their CoD values prior to training ]] | |||
</center> | |||
== MNIST Digits == | |||
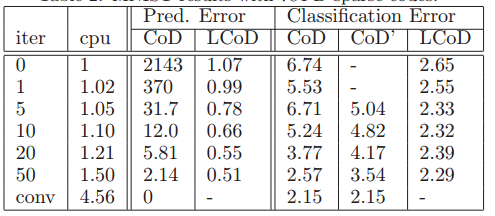
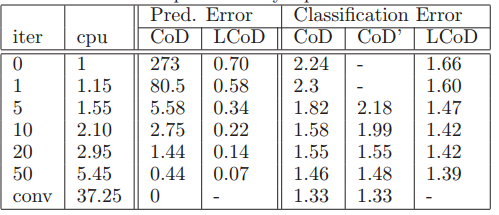
Here, the authors examined whether these coding approximations could be effectively applied in classification tasks. Evaluation was conducted using both the entire 28x28-pixel images to create 784-dimensional codes, as well as extracted 16x16-pixel patches for codes with 256 components. In addition to the finding that increasing the number of iterations reduced classification error across all procedures, it was observed that Learned Coordinate Descent approached the optimal error rate after only 10 iterations. | |||
A complete feature vector consisted of 25 concatenated such vectors, extracted | |||
from all 16 × 16 patches shifted by 3 pixels on the input. | |||
The features were extracted for all digits using | |||
CoD with exact inference, CoD with a fixed number of | |||
iterations, and LCoD. Additionally a version of CoD | |||
(denoted CoD’) used inference with a fixed number | |||
of iterations during training of the filters, and used | |||
the same number of iterations during test (same complexity | |||
as LCoD). A logistic regression classifier was | |||
trained on the features thereby obtained. | |||
Classification errors on the test set are shown in the following figures . While the error rate decreases with the | |||
number of iterations for all methods, the error rate | |||
of LCoD with 10 iterations is very close to the optimal | |||
(differences in error rates of less than 0.1% are | |||
insignificant on MNIST) | |||
[[File:T1.png]] | |||
MNIST results with 784-D sparse codes | |||
MNIST results with 25 256-D sparse codes extracted | |||
from 16 × 16 patches every 3 pixels | |||
[[File:T2.png]] | |||
= Conclusions = | |||
The idea of time unfolding an inference algorithm in order to construct a fixed-depth network in application to sparse coding is introduced in this paper. In sparse coding, inference algorithms are iterative and converge to a fixed point. In this paper it is proposed to unroll an inference algorithm for a fixed number of iterations in order to define an approximator network.The main result of this paper is the demonstration that the number of iterations required to reach a given code prediction error can be heavily reduced - by a factor of about 20 - when learning the filters and mutual inhibition matrices FISTA and CoD, when truncated. In other words, not much data-specific mutual inhibition is required to handle the phenomenon of "explaining away" superfluous parts of the code vector. | |||
= References = | |||
References | |||
Beck, A. and Teboulle, M. A fast iterative shrinkagethresholding | |||
algorithm with application to waveletbased | |||
image deblurring. ICASSP’09, pp. 693–696, 2009. | |||
Chen, S.S., Donoho, D.L., and Saunders, M.A. Atomic | |||
decomposition by basis pursuit. SIAM review, 43(1): | |||
129–159, 2001. | |||
Daubechies, I, Defrise, M., and De Mol, C. An iterative | |||
thresholding algorithm for linear inverse problems with a | |||
sparsity constraint. Comm. on Pure and Applied Mathematics, | |||
57:1413–1457, 2004. | |||
Donoho, D.L. and Elad, M. Optimally sparse representation | |||
in general (nonorthogonal) dictionaries via ℓ | |||
1 minimization. | |||
PNAS, 100(5):2197–2202, 2003. | |||
Elad, M. and Aharon, M. Image denoising via learned dictionaries | |||
and sparse representation. In CVPR’06, 2006. | |||
Hale, E.T., Yin, W., and Zhang, Y. Fixed-point continuation | |||
for l1-minimization: Methodology and convergence. | |||
SIAM J. on Optimization, 19:1107, 2008. | |||
Hoyer, P. O. Non-negative matrix factorization with | |||
sparseness constraints. JMLR, 5:1457–1469, 2004. | |||
Jarrett, K., Kavukcuoglu, K., Ranzato, M., and LeCun, | |||
Y. What is the best multi-stage architecture for object | |||
recognition? In ICCV’09. IEEE, 2009. | |||
Kavukcuoglu, Koray, Ranzato, Marc’Aurelio, and LeCun, | |||
Yann. Fast inference in sparse coding algorithms | |||
with applications to object recognition. Technical Report | |||
CBLL-TR-2008-12-01, Computational and Biological | |||
Learning Lab, Courant Institute, NYU, 2008. | |||
Lee, H., Battle, A., Raina, R., and Ng, A.Y. Efficient | |||
sparse coding algorithms. In NIPS’06, 2006. | |||
Lee, H., Chaitanya, E., and Ng, A. Y. Sparse deep belief | |||
net model for visual area v2. In Advances in Neural | |||
Information Processing Systems, 2007. | |||
Lee, H., Grosse, R., Ranganath, R., and Ng, A.Y. Convolutional | |||
deep belief networks for scalable unsupervised | |||
learning of hierarchical representations. In International | |||
Conference on Machine Learning. ACM New York, 2009. | |||
Li, Y. and Osher, S. Coordinate descent optimization for | |||
l1 minimization with application to compressed sensing; | |||
a greedy algorithm. Inverse Problems and Imaging, 3 | |||
(3):487–503, 2009. | |||
Mairal, J., Elad, M., and Sapiro, G. Sparse representation | |||
for color image restoration. IEEE T. Image Processing, | |||
17(1):53–69, January 2008. | |||
Mairal, J., Bach, F., Ponce, J., and Sapiro, G. Online | |||
dictionary learning for sparse coding. In ICML’09, 2009. | |||
Olshausen, B.A. and Field, D. Emergence of simple-cell | |||
receptive field properties by learning a sparse code for | |||
natural images. Nature, 381(6583):607–609, 1996. | |||
Ranzato, M., Huang, F.-J., Boureau, Y.-L., and LeCun, | |||
Y. Unsupervised learning of invariant feature hierarchies | |||
with applications to object recognition. In CVPR’07. | |||
IEEE, 2007a. | |||
Ranzato, M.-A., Boureau, Y.-L., Chopra, S., and LeCun, | |||
Y. A unified energy-based framework for unsupervised | |||
learning. In AI-Stats’07, 2007b. | |||
Rozell, C.J., Johnson, D.H, Baraniuk, R.G., and Olshausen, | |||
B.A. Sparse coding via thresholding and local | |||
competition in neural circuits. Neural Computation, 20: | |||
2526–2563, 2008. | |||
Vonesch, C. and Unser, M. A fast iterative thresholding algorithm | |||
for wavelet-regularized deconvolution. In IEEE | |||
ISBI, 2007. | |||
Wu, T.T. and Lange, K. Coordinate descent algorithms | |||
for lasso penalized regression. Ann. Appl. Stat, 2(1): | |||
224–244, 2008. | |||
Yang, Jianchao, Yu, Kai, Gong, Yihong, and Huang, | |||
Thomas. Linear spatial pyramid matching using sparse | |||
coding for image classification. In CVPR’09, 2009. | |||
Yu, Kai, Zhang, Tong, and Gong, Yihong. Nonlinear learning | |||
using local coordinate coding. In NIPS’09, 2009. | |||
Latest revision as of 09:46, 30 August 2017
Background
In contrast to a dimensionality-reduction approach to feature-extraction, sparse coding is an unsupervised method which attempts to construct a novel representation of the data by mapping it linearly into a higher-dimensional space. This transformation is performed with the objective of obtaining a new feature space in which, for each vector, we can find a smaller subset of features that largely reconstruct it. Essentially, this allows us to perform case-specific feature-extraction, as for a given input, we seek a smaller subset of features to which we will assign the majority of the weight for its representation, with the remainder being negligibly small. This provides us with a procedure which attempts to flexibly represent unseen instances of the input space.
The introduction of a larger set of spanning vectors is a consequence of the desire to produce accurate reconstructions across a broad range of possible input from the original space. However, the algebra of linear transformations tells us that input vectors will no longer have a unique representation in the higher-dimensional feature space. This short-coming is alleviated by the fact that we would like to assign the majority of influence to only a subset of the new features. We implement this goal using the notion of sparsity; namely, we will penalize large weight values.
Unfortunately, there are some implementation issues which prevent the use of sparse coding in certain contexts. The fact that we must find a representation for each new case the system is provided with often renders the procedure infeasible for online processing tasks, as new data must be handled in real-time. Several approximation algorithms have been proposed to address issues in processing speed. However, these methods suffer from deficiencies in their ability to take into account some relevant conditional-independence structures in the data. To resolve these limitations, the authors introduce a feed-forward architecture which utilizes these approximation schemes, giving a new procedure which is demonstrated to be ~10 times more efficient than the previous state-of-the-art approximation, in empirical testing.The main contribution of this paper is a highly efficient learning-based method that computes good approximations of optimal sparse codes in a fixed amount of time.
Review of Sparse Coding
For an input [math]\displaystyle{ X \epsilon \mathbb{R}^n }[/math], we seek a new representation [math]\displaystyle{ Z \epsilon \mathbb{R}^m }[/math] which satisfies the previously-stated objective. In order to find an optimal code [math]\displaystyle{ \, Z }[/math] of [math]\displaystyle{ \, X }[/math], we also require a dictionary [math]\displaystyle{ W_d \epsilon \mathbb{R}^{m x n} }[/math], the matrix of normalized vectors that the coordinates of [math]\displaystyle{ \, Z }[/math] are defined in relation to. Given a training set, we will estimate the optimal sparse codes for each training case, in pursuit of the dictionary matrix to be used in coding novel input.
These solutions will be found based on a loss function taking into account the squared reconstruction error and the complexity of the code:
- [math]\displaystyle{ E_{W_d}(X, Z) = \frac{1}{2}\|X - W_dZ\|_2^2 + \alpha \|Z\|_1 }[/math],
where [math]\displaystyle{ \, \alpha }[/math] is the specified sparsity penalty. Using this, the optimal code for input [math]\displaystyle{ X }[/math] is naturally defined as [math]\displaystyle{ \, Z^* = argmin_Z E(X, Z) }[/math].
From here, the dictionary is learned in an unsupervised manner, typically through the application of stochastic gradient descent to the minimization of the average loss [math]\displaystyle{ E_{W_d}(X, Z^*) }[/math] across a subset of the training cases. The dictionary to be applied to new cases is learned prior to the execution of the approximation proposed here.
Pre-existing Approximations: Iterative Shrinkage Algorithms
Here baseline iterative shrinkage algorithms for finding sparse codes are introduced and explained. The ISTA and FISTA methods update the whole code vector in parallel, while the more efficient Coordinate Descent method (CoD) updates the components one at a time and carefully selects which component to update at each step. Both methods refine the initial guess through a form of mutual inhibition between code component, and component-wise shrinkage.
Iterative Shrinkage & Thresholding (ISTA)
The Iterative Shrinkage & Thresholding Algorithm (ISTA) and its sped-up variant Fast ISTA approximate the optimal code vector of an input by updating all the code components in parallel. The idea is that, at each iteration, we should shift our current code in the direction of greatest reconstruction error, and then apply a component-wise shrinkage function to enforce sparsity. Initializing [math]\displaystyle{ \, Z^{(0)} = 0 }[/math], we have the recursive update rule:
- [math]\displaystyle{ Z^{(k + 1)} = h_{\theta}(Z^{(k)} - \frac{1}{L}W_d^T(W_dZ^{(k)} - X)) = h_{\theta}(W_eX + SZ^{(k)}) }[/math] (**),
- where [math]\displaystyle{ W_e = \frac{1}{L}W_d^T }[/math] is the filter matrix, and [math]\displaystyle{ S = I - \frac{1}{L}W_d^TW_d }[/math] is the mutual-inhibition matrix.
Here, [math]\displaystyle{ \, L }[/math] is an upper-bound on the size of the eigenvalues of [math]\displaystyle{ W_d^TW_d }[/math], and [math]\displaystyle{ \, h_{\theta}( ) }[/math] is the shrinkage function with components [math]\displaystyle{ \, h_{\theta}(V)_i = sign(V_i) }[/math] [math]\displaystyle{ \, max(|V_i| - \theta_i, }[/math] [math]\displaystyle{ \, 0) }[/math], where [math]\displaystyle{ \theta \epsilon \mathbb{R}^m }[/math] consists of the sparsity thresholds for the components of the code. Thresholds are typically set to [math]\displaystyle{ \theta_i =\frac{\alpha}{L} }[/math].
Fast ISTA
Depending on a few possible choices to be made in implementing this scheme, the per-iteration time complexity in using ISTA to construct a code for a new input will be [math]\displaystyle{ \, O(m^2) }[/math], [math]\displaystyle{ \, O(nm) }[/math], or [math]\displaystyle{ \, O(km) }[/math], with [math]\displaystyle{ \, k }[/math] being the average sparsity across samples and iterations.
Fast ISTA is a modification of this approximation which ensures faster convergence through the addition of a momentum term. Here, our update rule becomes:
- [math]\displaystyle{ Z^{(k + 1)} = h_{\theta}(Z^{(k)}) + \lambda (h_{\theta}^{(k-1)} - h_{\theta}^{(k - 2)}) }[/math]
In other words, the updated code is the shrinkage function applied to the current code, plus a multiple of the difference of the outputs of the shrinkage function for the preceding two iterations. This second term the rate at which the approximated code is changing.
Coordinate Descent
Instead of automatically updating all the entries of the code in parallel, we might consider strategically selecting a single component to be updated each iteration. Coordinate Descent (CoD) adopts this mentality, and resultantly yields a superior approximation to the parallel ISTA methods in the same order of time. In fact, Coordinate Descent was widely believed to be the most efficient algorithm available for approximating sparse codes.
The CoD algorithm is presented below:
[math]\displaystyle{ \textbf{function} \, \textbf{CoD}\left(X, Z, W_d, S, \alpha\right) }[/math]
- [math]\displaystyle{ \textbf{Require:} \,S = I - W_d^T W_d }[/math]
- [math]\displaystyle{ \textbf{Initialize:} \,Z = 0; B = W_d^TX }[/math]
- [math]\displaystyle{ \textbf{repeat} }[/math]
- [math]\displaystyle{ \bar{Z} = h_{\alpha}\left(B\right) }[/math]
- [math]\displaystyle{ \,k = \mbox{ index of largest component of} \left|Z - \bar{Z}\right| }[/math]
- [math]\displaystyle{ \forall j \in \left[1, m\right]: B_j = B_j + S_{jk}\left(\bar{Z}_k - Z_k\right) }[/math]
- [math]\displaystyle{ Z_k = \bar{Z}_k }[/math]
- [math]\displaystyle{ \textbf{until}\,\text{change in}\,Z\,\text{is below a threshold} }[/math]
- [math]\displaystyle{ Z = h_{\alpha}\left(B\right) }[/math]
[math]\displaystyle{ \textbf{end} \, \textbf{function} }[/math]
In each iteration of the procedure, we search for the entry of the current code which, if updated so as to minimize the corresponding loss while holding the other components constant, results in the largest change in comparison to the current code. This search step takes [math]\displaystyle{ \, O(m) }[/math] operations, and, so in also accounting for each component-wise optimization performed (which follows a similar process to that of the parallel case), each iteration requires [math]\displaystyle{ \, O(m^2) }[/math] steps. Alternatively, we could repeat the update process [math]\displaystyle{ \, O(n) }[/math] times instead, to achieve a per-iteration complexity of [math]\displaystyle{ \, O(nm) }[/math], which is again comparable to ISTA. This algorithm has a similar feedback concept to ISTA, but can it can expressed as a linear feedback operation with a very sparse matrix (since only one component is updated at a time). Either way, it turns out that, deploying both for an approximately equal amount of time, Coordinate Descent will out-perform the ISTA methods in its approximation to an optimal code.
Encoders for Sparse Code Approximation
In seeking an approach to further improve upon the efficiency of Coordinate Descent, the authors present the use of feed-forward networks for real-time sparse code inference. Essentially, for the training phase, we will perform learning for a neural network which takes our original input [math]\displaystyle{ \, X \epsilon \mathbb{R}^n }[/math] and generates a prediction of its optimal code with respect to the previously-estimated dictionary. The training set will consist of the original [math]\displaystyle{ \, X }[/math] as our input, and their sparse codes estimated via Coordinate Descent as the target values. In learning the network weights, we use stochastic gradient descent to minimize the average squared-error between the network's predictions and these estimated sparse codes. The size of the network will be chosen with consideration of its feasibility in applying it to online processing.
A Simplistic Architecture and its Limitations
The most straight-forward approach to this task would be to use a single-layer feed-forward network. However, since we have the additional requirement that the network output is to be sparse, special consideration of the activation function must be made. The authors consider three such candidates: double tanh, a learned non-linearity, and the shrinkage function [math]\displaystyle{ \, h_{\theta}( ) }[/math] used for ISTA. The three approaches perform comparably in the authors' empirical testing, and so they opt to use [math]\displaystyle{ \, h_{\theta}( ) }[/math] to maintain a strong basis for comparison with the previous methods.
Despite the appeal of its simplicity, this network configuration is unable to learn "explaining-away" phenomena, a conditional-independence structure relevant to this task. Essentially, this means that if the learned weight matrix happens to contain two highly similar rows, the network will uniformly represent two components of the code as nearly-equal. However, this inability to select only one of the components and suppress the other redundant one is clearly indicative of a limitation of the network's ability to produce sparse encodings. Consequently, a more sophisticated architecture is proposed.
Learned ISTA & Learned Coordinate Descent
To address explaining-away phenomena, interaction terms between components are introduced. To implement these terms controlling redundancy amongst the components, the authors design a sequence of feed-forward networks structured so as to be analogous to executing some number of steps of ISTA or a pre-determined number of steps of Coordinate Descent. The use of ISTA versus Coordinate Descent corresponds to two distinct encoders, both of which can be viewed as a "time-unfolded" recurrent network.
Before understanding the rationale behind this approach, we must recognize a few relevant values which are inherently fixed in the process of executing ISTA or Coordinate Descent. The recursive equations iterated over in these procedures can both be re-expressed in terms parameters including a threshold vector [math]\displaystyle{ \, \theta }[/math], a filter matrix [math]\displaystyle{ \, W_e }[/math], and a mutual-inhibition matrix [math]\displaystyle{ \, S }[/math], where these terms are defined differently for the two procedures. Now, instead of using these fully-determined parameter forms and iterating the procedure until it converges, this encoder-driven approach purposes to learn [math]\displaystyle{ \, \theta }[/math], [math]\displaystyle{ \, W_e }[/math], [math]\displaystyle{ \, S }[/math], and then execute only a fixed number of steps of one of these procedures, in order to reduce the total computational cost. Using the available data to adaptively set these parameters allows the corresponding network to handle the issues pertaining to explaining-away.
In Learned ISTA (LISTA), the encoder structure takes the form defined by the recursive update for ISTA (**), iterated for a fixed number of times T. We learn the parameters [math]\displaystyle{ \, W_e }[/math], [math]\displaystyle{ \, \theta }[/math], and [math]\displaystyle{ \, S }[/math] by using stochastic gradient descent to minimize the previously-described squared-error loss for sparse code prediction. From its definition, we can see that [math]\displaystyle{ \, S }[/math] is shared across the [math]\displaystyle{ T }[/math] time steps, and so we use back-propagation through time to compute the error gradient for gradient descent.
Similarly, in Learned Coordinate Descent (LCoD), the network architecture is defined by the recursive update for Coordinate Descent (omitted for brevity) iterated for a fixed number of time steps. The parameters [math]\displaystyle{ \, W_e }[/math], [math]\displaystyle{ \, \theta }[/math], and S are learned analogous to the procedure for LISTA, except for the technicality that sub-gradients are propagated, resulting from the fact that we search for the component inducing the largest update in the code Z.
The algorithm for LCoD can be summarized as
A main advantage of the system proposed in this paper is speed, so it is necessary to take note of the asymptotic complexity of the above algorithm: only [math]\displaystyle{ \, O(m) }[/math] operations are required for each step of the bprop procedure, and each iteration only requires [math]\displaystyle{ \, O(m) }[/math] space; as almost all of the stored variables are scalar, with the exception of [math]\displaystyle{ \, B(T) }[/math]. (Recall that m refers to the number of dimensions in the new feature space with the sparse representations.)
Empirical Performance
Two sets of experiments were undertaken:
- The procedures were compared in their performance on exact sparse code inference, using the Berkeley image database.
- The MNIST digits dataset was used in assessing whether improved error-rates in code-prediction yields superior performance in recognition tasks.
Overall, the results indicate that this proposal to construct encoders from a set of iterations of ISTA or Coordinate Descent yields a significantly-reduced runtime when compared to the pre-existing procedures, at a pre-specified error-rate.
Berkeley Image Database
From this database, 10x10-pixel image patches were randomly drawn to compare (Fast) ISTA with LISTA, and Coordinate Descent with LCoD, in sparse code prediction. Performance was tested on dictionaries of sizes m = 100 and m = 400, using a sparsity penalty of [math]\displaystyle{ \alpha = 0.5 }[/math], and the squared-error loss for the distance between the estimate and the optimal code, as computed by Coordinate Descent.
Figure 1 suggests that, LISTA notably out-performs FISTA here. Furthermore, 18 iterations of FISTA are required to achieve the error-rate produced by 1 iteration of LISTA when m = 100, and 35 iterations when m = 400. This leads the authors to conclude that LISTA is ~20 times faster than FISTA.
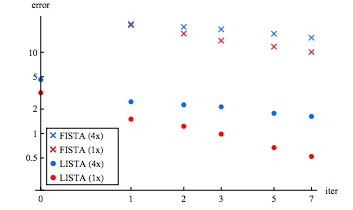
Figure 2 indicates that, for a moderately-large number of iterations, LCoD has superior accuracy to Coordinate Descent. When the number of iterations is larger, Coordinate Descent out-performs LCoD, but this can be reversed by initializing matrices with their CoD values prior to training.
MNIST Digits
Here, the authors examined whether these coding approximations could be effectively applied in classification tasks. Evaluation was conducted using both the entire 28x28-pixel images to create 784-dimensional codes, as well as extracted 16x16-pixel patches for codes with 256 components. In addition to the finding that increasing the number of iterations reduced classification error across all procedures, it was observed that Learned Coordinate Descent approached the optimal error rate after only 10 iterations.
A complete feature vector consisted of 25 concatenated such vectors, extracted from all 16 × 16 patches shifted by 3 pixels on the input. The features were extracted for all digits using CoD with exact inference, CoD with a fixed number of iterations, and LCoD. Additionally a version of CoD (denoted CoD’) used inference with a fixed number of iterations during training of the filters, and used the same number of iterations during test (same complexity as LCoD). A logistic regression classifier was trained on the features thereby obtained.
Classification errors on the test set are shown in the following figures . While the error rate decreases with the number of iterations for all methods, the error rate of LCoD with 10 iterations is very close to the optimal (differences in error rates of less than 0.1% are insignificant on MNIST)
MNIST results with 784-D sparse codes
MNIST results with 25 256-D sparse codes extracted from 16 × 16 patches every 3 pixels
Conclusions
The idea of time unfolding an inference algorithm in order to construct a fixed-depth network in application to sparse coding is introduced in this paper. In sparse coding, inference algorithms are iterative and converge to a fixed point. In this paper it is proposed to unroll an inference algorithm for a fixed number of iterations in order to define an approximator network.The main result of this paper is the demonstration that the number of iterations required to reach a given code prediction error can be heavily reduced - by a factor of about 20 - when learning the filters and mutual inhibition matrices FISTA and CoD, when truncated. In other words, not much data-specific mutual inhibition is required to handle the phenomenon of "explaining away" superfluous parts of the code vector.
References
References Beck, A. and Teboulle, M. A fast iterative shrinkagethresholding algorithm with application to waveletbased image deblurring. ICASSP’09, pp. 693–696, 2009. Chen, S.S., Donoho, D.L., and Saunders, M.A. Atomic decomposition by basis pursuit. SIAM review, 43(1): 129–159, 2001.
Daubechies, I, Defrise, M., and De Mol, C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Comm. on Pure and Applied Mathematics, 57:1413–1457, 2004.
Donoho, D.L. and Elad, M. Optimally sparse representation in general (nonorthogonal) dictionaries via ℓ 1 minimization. PNAS, 100(5):2197–2202, 2003.
Elad, M. and Aharon, M. Image denoising via learned dictionaries and sparse representation. In CVPR’06, 2006. Hale, E.T., Yin, W., and Zhang, Y. Fixed-point continuation for l1-minimization: Methodology and convergence. SIAM J. on Optimization, 19:1107, 2008. Hoyer, P. O. Non-negative matrix factorization with sparseness constraints. JMLR, 5:1457–1469, 2004. Jarrett, K., Kavukcuoglu, K., Ranzato, M., and LeCun, Y. What is the best multi-stage architecture for object recognition? In ICCV’09. IEEE, 2009.
Kavukcuoglu, Koray, Ranzato, Marc’Aurelio, and LeCun, Yann. Fast inference in sparse coding algorithms with applications to object recognition. Technical Report CBLL-TR-2008-12-01, Computational and Biological Learning Lab, Courant Institute, NYU, 2008.
Lee, H., Battle, A., Raina, R., and Ng, A.Y. Efficient sparse coding algorithms. In NIPS’06, 2006.
Lee, H., Chaitanya, E., and Ng, A. Y. Sparse deep belief net model for visual area v2. In Advances in Neural Information Processing Systems, 2007.
Lee, H., Grosse, R., Ranganath, R., and Ng, A.Y. Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations. In International Conference on Machine Learning. ACM New York, 2009. Li, Y. and Osher, S. Coordinate descent optimization for l1 minimization with application to compressed sensing; a greedy algorithm. Inverse Problems and Imaging, 3 (3):487–503, 2009.
Mairal, J., Elad, M., and Sapiro, G. Sparse representation for color image restoration. IEEE T. Image Processing, 17(1):53–69, January 2008.
Mairal, J., Bach, F., Ponce, J., and Sapiro, G. Online dictionary learning for sparse coding. In ICML’09, 2009. Olshausen, B.A. and Field, D. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature, 381(6583):607–609, 1996.
Ranzato, M., Huang, F.-J., Boureau, Y.-L., and LeCun, Y. Unsupervised learning of invariant feature hierarchies with applications to object recognition. In CVPR’07. IEEE, 2007a.
Ranzato, M.-A., Boureau, Y.-L., Chopra, S., and LeCun, Y. A unified energy-based framework for unsupervised learning. In AI-Stats’07, 2007b.
Rozell, C.J., Johnson, D.H, Baraniuk, R.G., and Olshausen, B.A. Sparse coding via thresholding and local competition in neural circuits. Neural Computation, 20: 2526–2563, 2008.
Vonesch, C. and Unser, M. A fast iterative thresholding algorithm for wavelet-regularized deconvolution. In IEEE ISBI, 2007.
Wu, T.T. and Lange, K. Coordinate descent algorithms for lasso penalized regression. Ann. Appl. Stat, 2(1): 224–244, 2008.
Yang, Jianchao, Yu, Kai, Gong, Yihong, and Huang, Thomas. Linear spatial pyramid matching using sparse coding for image classification. In CVPR’09, 2009. Yu, Kai, Zhang, Tong, and Gong, Yihong. Nonlinear learning using local coordinate coding. In NIPS’09, 2009.