The Stochastic Pendulum with red noise

This script is a tutorial script for stochastic integration and visualization using red noise realized using the method of Bartosch.

Contents

The governing ODEs of the damped pendulum are

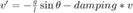
is taken to vary as 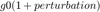where the perturbation is red noise this means no Ito calculus comes in.

This section is all the book keeping for initialization

Initialize the random number generator and seed it.

rng('shuffle');

Specify the global parameters for the pendulum.

length=1;
g0=9.81;
damp=1e-1;

Specify the time step and stochastic parameters.

numsteps=10; % sets how many time steps between saves.
numouts=500; % sets the number of outputs.
dt=1e-3; % sets the time step.  Stochastic methods are low order so small time steps are required.
numens=1000; % sets the number of ensemble members.

The parameters for the red noise as realized by Bartosch's algorithm

memt=0.1; % sets the memory of the noise.  Need at least ten time steps in memt.
rho=exp(-dt/memt); rhoc=sqrt(1-rho*rho); % parameters for Bartosch's method.
mysig=0.35; % set the standard deviation of the noise.
prevrand=zeros(numens,1); % start g at g0.

Initial conditions

%theta=2*pi*rand(numens,1); %initially assume random angles.
theta=(1-1e-4)*pi*ones(numens,1); % start near the unstable state.
%theta=1e-4*pi*ones(numens,1); % start near the stable state.
v=zeros(numens,1); % initially assume zero velocity.
t=0;

Set up arrays for storage and store initial state

thetas=zeros(numouts+1,numens);
vs=zeros(numouts+1,numens);
ts=zeros(numouts+1,1);
thetas(1,:)=theta;
vs(1,:)=v;
ts(1)=t;

The main work horse loops. The double loop can be used view to intermediate results

for ii=1:numouts
    for jj=1:numsteps
        nowrand=randn(numens,1)*mysig; % generate a new bunch of random numbers.
        pertnow=(nowrand*rhoc+rho*prevrand); prevrand=pertnow; % use Bartosch's memory to get the right "memory".
        g=g0*(1+pertnow); % define g.
        % now define the RHS for the DE
        rhth=v;
        rhv=-(g/length).*sin(theta)-damp*v;
        % Step the DE forward. If g had a white noise component this would
        % get trickier to account for the sqrt(dt) in Ito's calculus.
        theta=theta+dt*rhth;
        v=v+dt*rhv;
        t=t+dt;
    end
    thetas(ii+1,:)=theta;
    vs(ii+1,:)=v;
    ts(ii+1)=t;
end
plot(thetas)

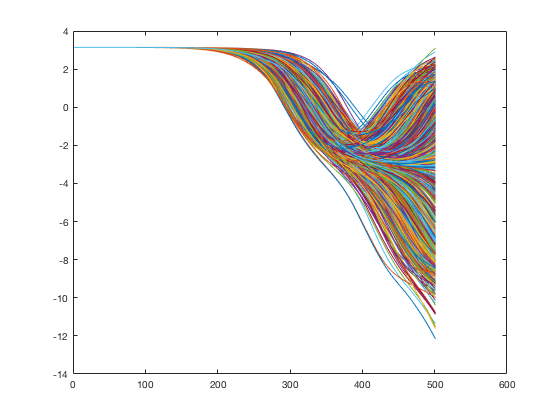
Now that we have the data we can make a variety of pictures

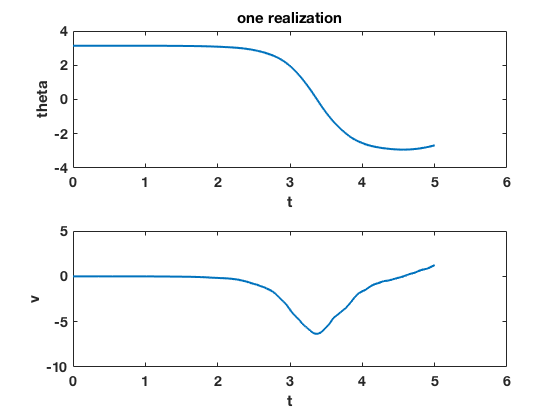
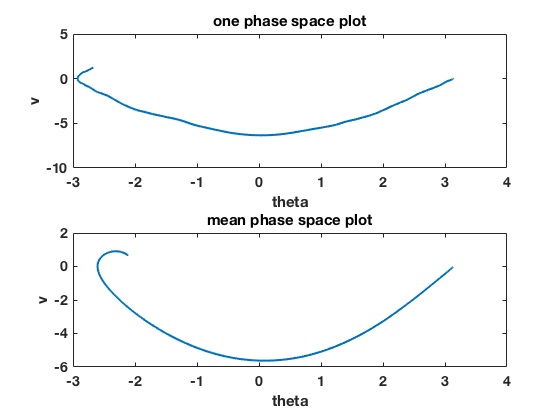
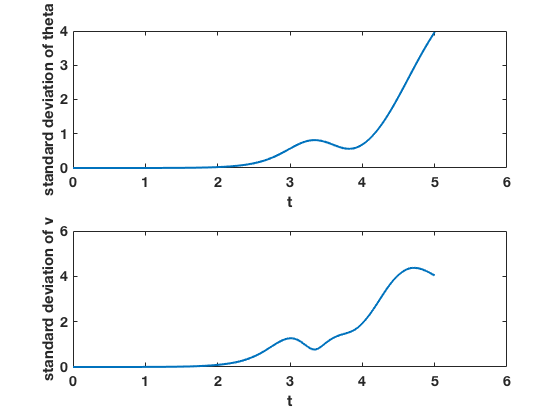
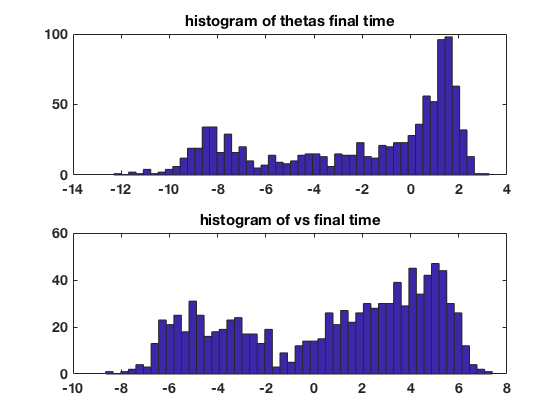
figure(1)
clf
set(gcf,'DefaultLineLineWidth',2,'DefaultTextFontSize',14,...
        'DefaultTextFontWeight','bold','DefaultAxesFontSize',14,...
          'DefaultAxesFontWeight','bold');
      subplot(2,1,1)
      plot(ts,thetas(:,1))
      xlabel('t')
      ylabel('theta')
      title('one realization')
      subplot(2,1,2)
      plot(ts,vs(:,1))
      xlabel('t')
      ylabel('v')

      figure(2)
clf
set(gcf,'DefaultLineLineWidth',2,'DefaultTextFontSize',14,...
        'DefaultTextFontWeight','bold','DefaultAxesFontSize',14,...
          'DefaultAxesFontWeight','bold');
      subplot(2,1,1)
      plot(thetas(:,1),vs(:,1))
      ylabel('v')
      xlabel('theta')
      title('one phase space plot')
      subplot(2,1,2)
      plot(mean(thetas,2),mean(vs,2))
      ylabel('v')
      xlabel('theta')
      title('mean phase space plot')

      figure(3)
clf
set(gcf,'DefaultLineLineWidth',2,'DefaultTextFontSize',14,...
        'DefaultTextFontWeight','bold','DefaultAxesFontSize',14,...
          'DefaultAxesFontWeight','bold');
      subplot(2,1,1)
      plot(ts,std(thetas,[],2))
      ylabel('standard deviation of theta')
      xlabel('t')
      subplot(2,1,2)
      plot(ts,std(vs,[],2))
      ylabel('standard deviation of v')
      xlabel('t')

      figure(4)
clf
set(gcf,'DefaultLineLineWidth',2,'DefaultTextFontSize',14,...
        'DefaultTextFontWeight','bold','DefaultAxesFontSize',14,...
          'DefaultAxesFontWeight','bold');
      subplot(2,1,1)
      mnth=min(thetas(end,:));
      mxth=max(thetas(end,:));
      bins=linspace(mnth,mxth,floor(numens/20)+1);
      hist(thetas(end,:),bins)
      title('histogram of thetas final time')
      subplot(2,1,2)
      mnv=min(vs(end,:));
      mxv=max(vs(end,:));
      bins=linspace(mnv,mxv,floor(numens/20)+1);
      hist(vs(end,:),bins)
      title('histogram of vs final time')

Published with MATLAB® R2017a