Convergence of Ito scheme

This script is an implementation of a really simple stochastic ODE to test the Euler Maruyama scheme.

Contents

clear all, close all

Begin defining various parameters and setting initializations

Initialize the random number generator and seed it.

rng('shuffle');

Specify the global parameters.

mysig=0.3;
myper=3e-2;

Specify the time step and stochastic parameters.

Sets how many time steps between saves.

numsteps=10;

Sets the number of outputs.

numouts=1000;

Sets the time step. Stochastic methods are low order so small time steps tend to be required.

dt=1e-5;

For white noise this is needed.

dtrt=sqrt(dt);
dtb=dt*numsteps;
dtbrt=sqrt(dtb);

Sets the number of ensemble members.

numens=4000;

Set up arrays for storage and store initial state.

noise=randn(numsteps*numouts,numens);
t=0;
xs=zeros(numouts+1,numens);
xs2=zeros(numouts+1,numens);
xbs=zeros(numouts+1,numens);
x0=ones(1,numens);
xs(1,:)=x0;
xbs(1,:)=x0;
xd=x0(1);x=x0;x2=x0;
ts(1)=t;
cntr=0;
xs(1,:)=x;
xds(1)=xd;
ts(1)=t;

Primary Loop

for ii=1:numouts
    oldt=t;
    oldnoise=noise(cntr+1,:);
    for jj=1:numsteps
        cntr=cntr+1;
        xd=xd+dt*sin(2*pi*t/myper);
        x=x+dt*sin(2*pi*t/myper)+dtrt*mysig*noise(cntr,:);
        t=t+dt;
    end
    xbs(ii+1,:)=xbs(ii,:)+dtb*sin(2*pi*oldt/myper)+dtbrt*mysig*oldnoise;
    xs(ii+1,:)=x;
    xds(ii+1)=xd;
    ts(ii+1)=t;
end

Plot

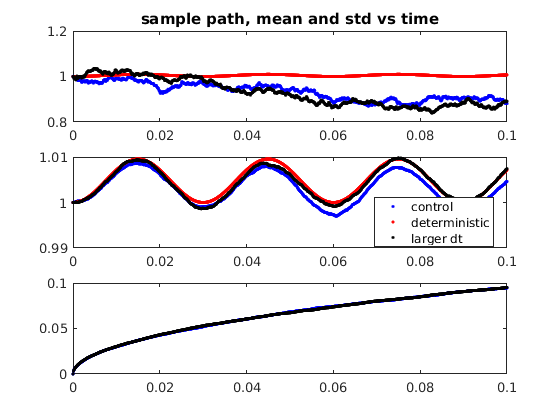
Plot one path, mean and standard deviation.

figure(1)
clf
subplot(3,1,1)
plot(ts,xs(:,1),'b.',ts,xds,'r.',ts,xbs(:,1),'k.')
title('sample path, mean and std vs time')
subplot(3,1,2)
plot(ts,mean(xs,2),'b.',ts,xds,'r.',ts,mean(xbs,2),'k.')
legend('control','deterministic','larger dt','Location','best')
subplot(3,1,3)
plot(ts,std(xs,[],2),'b.',ts,std(xbs,[],2),'k.')

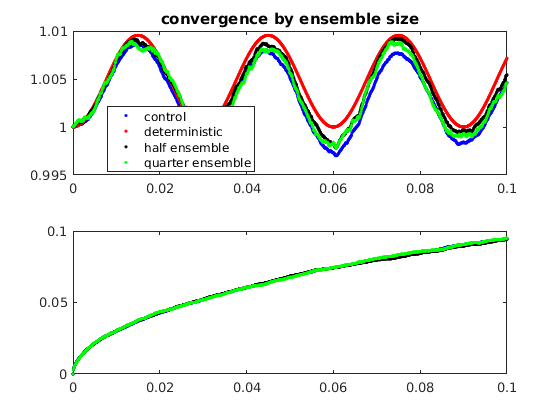
Plot statistics by ensemble size.

figure(2)
clf
subplot(2,1,1)
plot(ts,mean(xs,2),'b.',ts,xds,'r.',ts,mean(xs(:,1:numens/2),2),'k.',ts,mean(xs(:,1:numens/4),2),'g.')
title('convergence by ensemble size')
legend('control','deterministic','half ensemble','quarter ensemble','Location','best')
subplot(2,1,2)
plot(ts,std(xs,[],2),'b.',ts,std(xs(:,1:numens/2),[],2),'k.',ts,std(xs(:,1:numens/4),[],2),'g.')

Published with MATLAB® R2016b