Stochastic Hunter-Prey model in 2D
This script is a model of two species, one hunter and one prey. The prey can reproduce and die naturally, and both the hunter and prey occupy a physical location in 2D. Both the hunter and prey move according to Browninan motion and if the hunter occupies the same space as the prey it is considered to have 'eaten' them. The prey are an example of branching diffusion. The hunter is an example of a diffusion with lingering effects so that if the hunter eats, it slows down to "look around". There is also a background current to mimic a passing internal wave.
Contents
clear all,close all
The maximum humber of particles.
numparts=1000;
Number of particles to start with.
numactive=500;
Parameters for domain size
L=20; H=10;
Brownian motion parameters
dt=1e-3; dtrt=sqrt(dt); sigx=1e-2*H; sigz=1e-2*H;
Birth process parameters
Uniform random number larger than this gives birth.
birth_thresh=0.975;
Uniform random number larger than this gives death.
death_thresh=0.97575;
Hunter parameters
hunter_rad=0.05*min(L,H); hunter_sigx0=2e-1*H; hunter_sigz0=2e-1*H; hunter_sigx=hunter_sigx0; hunter_sigz=hunter_sigz0; xhunter=0.25*L; zhunter=0.5*H;
How many did I have to eat to slow down and eat more.
eattostop=10;
The number of time steps to slowdown for.
lengthstop=200;
whatiate=0; eating=0;
Deterministic motion parameters
Mode number.
modenum=1;
Wave number.
k=2*pi/L;
Vertical wave number.
m=modenum*pi/H;
Buoyancy frequency.
N0=2e-2;
Buoyancy frequency squared.
N02=N0^2;
Frequency.
sigma=(N0*k*H)/sqrt(modenum^2*pi^2+k*H*k*H);
Period.
myper=2*pi/sigma;
Wave amplitude.
amp=0.025*100;
Flow solution to Internal Wave problem.
psi=@(x,z,t) amp*cos(k*x).*sin(m*z)*cos(sigma*t); u=@(x,z,t) amp*cos(k*x).*cos(m*z)*m*cos(sigma*t); w=@(x,z,t) amp*k*sin(k*x).*sin(m*z)*cos(sigma*t);
Time stepping parameters
numsteps=20; numouts=20;
Allocate and Initialize
Allocate arrays particles.
x=-1e4*ones(numparts,1); z=-1e4*ones(numparts,1); alive=zeros(numparts,1);
Initialize particles.
x(1:numactive,1)=L*rand(numactive,1); z(1:numactive,1)=H*rand(numactive,1); alive(1:numactive)=1;
Grid for velocity field pictures.
myxs=linspace(0,1*L,1000); myzs=linspace(0,H,100); [xx ,zz]=meshgrid(myxs,myzs);
t=0; totdead=zeros(numouts); totborn=zeros(numouts); toteaten=zeros(numouts);
Primary Loop
for ii=1:numouts
totdead(ii)=0;
totborn(ii)=0;
toteaten(ii)=0;
for jj=1:numsteps
Advect and diffuse the active particles.
pertx=sigx*randn(numactive,1);
pertz=sigz*randn(numactive,1);
x(1:numactive,1)=mod(x(1:numactive,1)+alive(1:numactive).*(dt*u(x(1:numactive,1),z(1:numactive,1),t)+dtrt*pertx),L);
z(1:numactive,1)=z(1:numactive,1)+alive(1:numactive).*(dt*w(x(1:numactive,1),z(1:numactive,1),t)+dtrt*pertz);
z(1:numactive,1)=H-abs(z(1:numactive,1)-H);
perthunterx=hunter_sigx*randn(1,1);
perthunterz=hunter_sigz*randn(1,1);
xhunter=mod(xhunter+dt*u(xhunter,zhunter,t)+dtrt*perthunterx,L);
zhunter=zhunter+dt*w(xhunter,zhunter,t)+dtrt*perthunterz;
zhunter=H-abs(zhunter-H);
t=t+dt;
Natural death, do this first so you're not always killing the newborns.
deathpert=rand(numactive,1);
deathcheck=(deathpert>death_thresh);
numdead=sum(deathcheck);
numactive=numactive-numdead;
totdead(ii)=totdead(ii)+numdead;
Birth new particles.
birthpert=rand(numactive,1);
birthcheck=(birthpert>birth_thresh);
numborn=sum(birthcheck);
totborn(ii)=totborn(ii)+numborn;
Get born next to parent where parents are automatically at the end Put the newborns at the front of the queue so they are not the first to die.
dummyx=x(1:numactive);
dummyz=z(1:numactive);
x(1:numborn)=x(numactive-numborn+1:numactive);
z(1:numborn)=z(numactive-numborn+1:numactive);
x(numborn+1:numactive+numborn)=dummyx;
z(numborn+1:numactive+numborn)=dummyz;
numactive=numactive+numborn;
alive=zeros(numparts,1);
alive(1:numactive)=1;
Can you eat it?
huntdist=sqrt((x(1:numactive,1)-xhunter*ones(numactive,1)).^2+(z(1:numactive,1)-zhunter*ones(numactive,1)).^2);
eaten=find(huntdist<hunter_rad);
toteaten(ii)=toteaten(ii)+length(eaten);
alive(eaten)=0;
x(eaten,1)=-1e10;
z(eaten,1)=-1e10;
deadind=find(alive==0);
didIeat=length(eaten);
whatiate=whatiate+didIeat;
eating=eating*(didIeat<eattostop+1)+lengthstop*(didIeat>eattostop);
sigfactor=0.01*(eating>0)+1*(eating==0);
If the hunter has just eaten it will stop to look around. This is achieved by lowering its standard deviation.
hunter_sigx=hunter_sigx0*sigfactor;
hunter_sigz=hunter_sigz0*sigfactor;
eating=max(eating-1,0);
end
Plot
figure(1)
set(gcf,'DefaultLineLineWidth',1,'DefaultTextFontSize',14,...
'DefaultAxesFontSize',14);
clf
diagfact=1/sqrt(2);
pcolor(xx,zz,psi(xx,zz,t)/amp),shading flat
hold on
plot(x(1:numactive,1),z(1:numactive,1),'k.','Markersize',4)
plot(xhunter,zhunter,'ko','Markersize',8)
plot(mod(xhunter+hunter_rad,L),(zhunter),'ko','Markersize',4)
plot(mod(xhunter-hunter_rad,L),(zhunter),'ko','Markersize',4)
plot(mod(xhunter,L),(zhunter+hunter_rad),'ko','Markersize',4)
plot(mod(xhunter,L),(zhunter-hunter_rad),'ko','Markersize',4)
plot(mod(xhunter+diagfact*hunter_rad,L),(zhunter-diagfact*hunter_rad),'ko','Markersize',4)
plot(mod(xhunter-diagfact*hunter_rad,L),(zhunter-diagfact*hunter_rad),'ko','Markersize',4)
plot(mod(xhunter-diagfact*hunter_rad,L),(zhunter+diagfact*hunter_rad),'ko','Markersize',4)
plot(mod(xhunter+diagfact*hunter_rad,L),(zhunter+diagfact*hunter_rad),'ko','Markersize',4)
myindalive=(alive(1:numactive)==1);
title(['Number of active prey ' int2str(sum(myindalive))])
drawnow
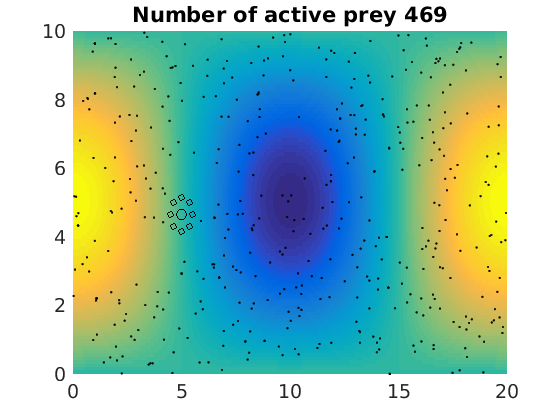
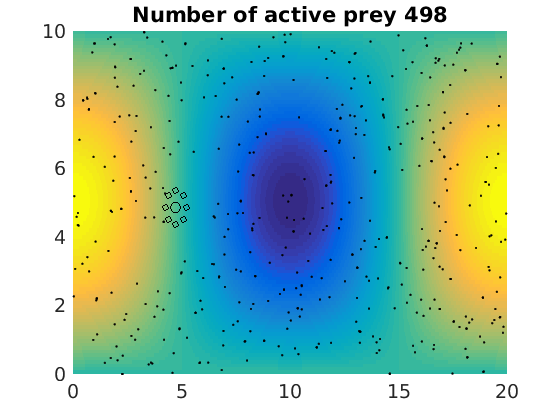
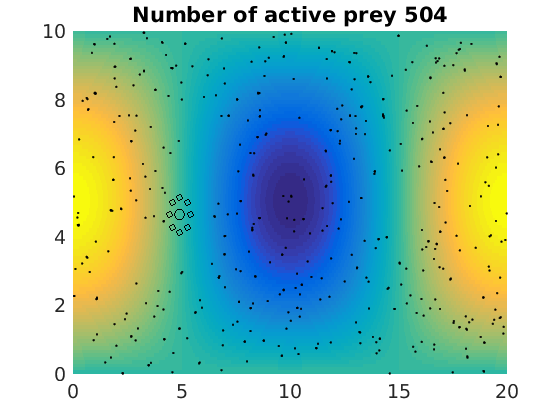
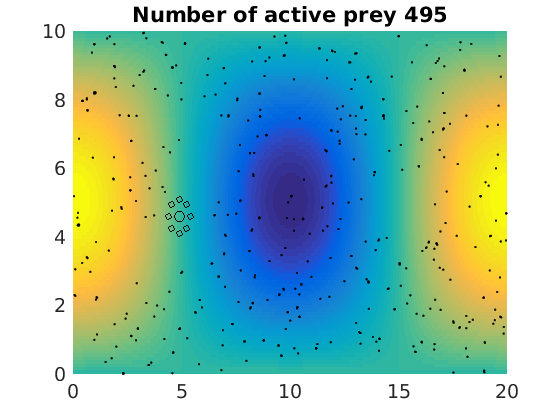
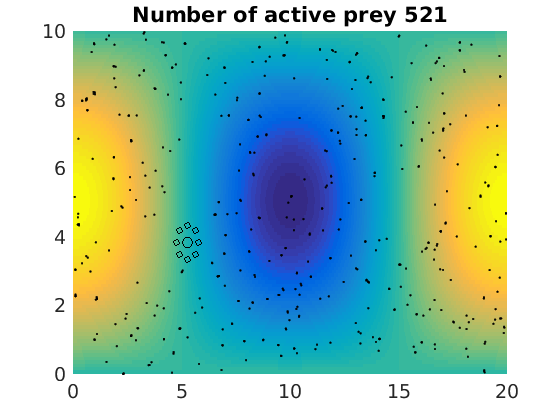
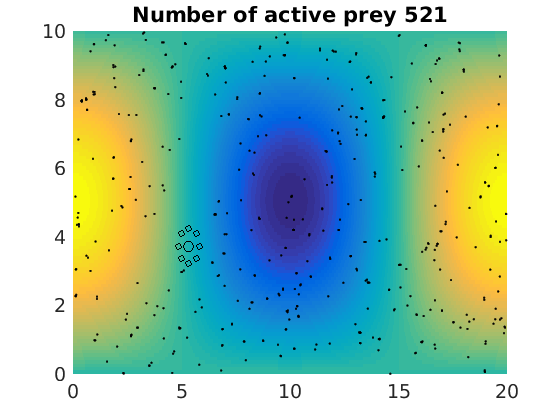
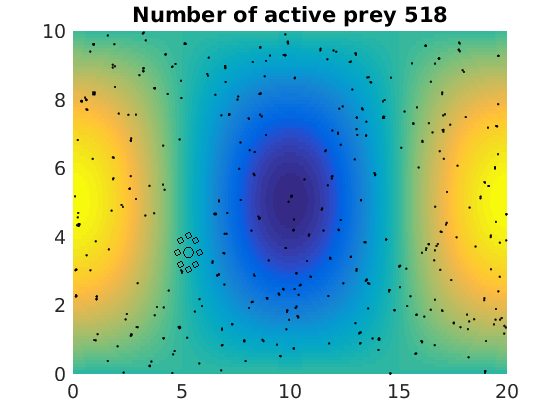
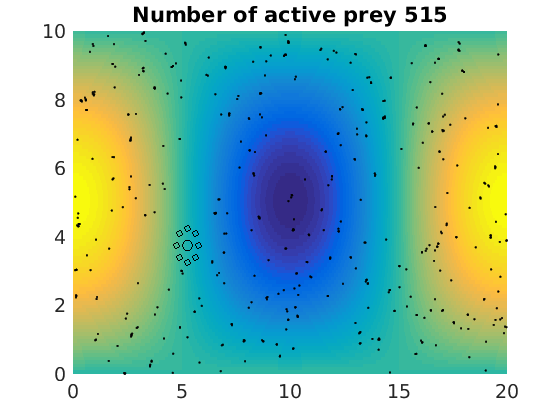
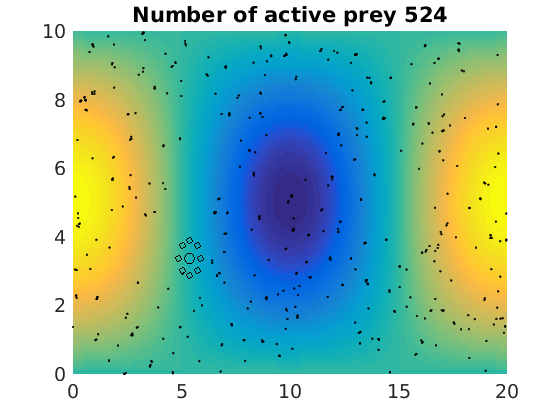
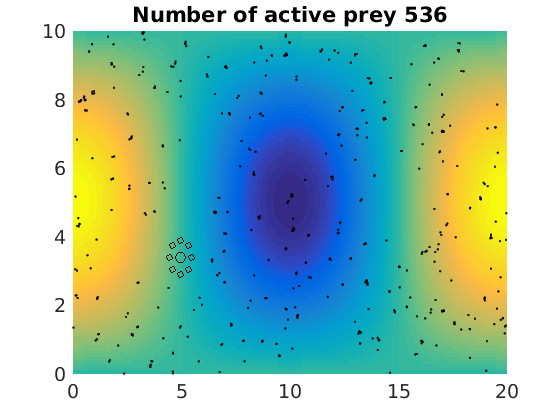
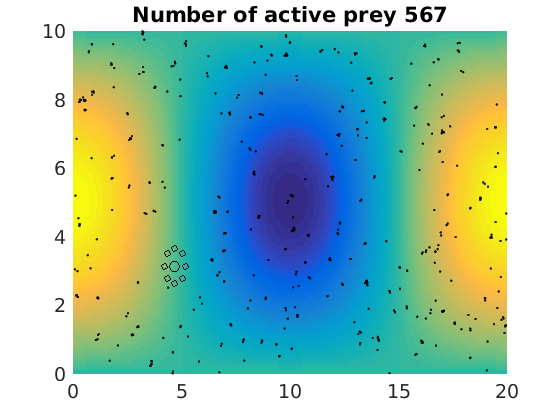
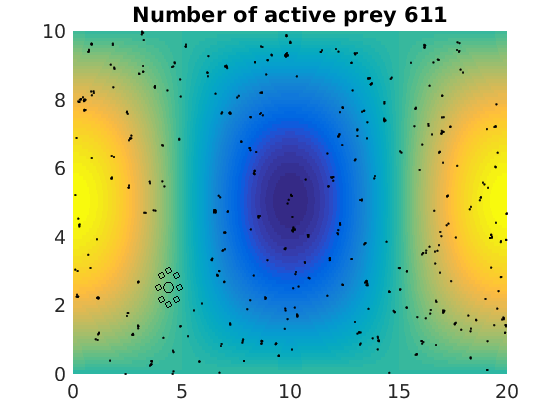
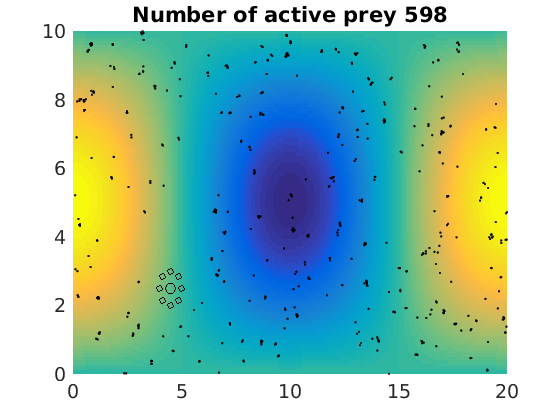
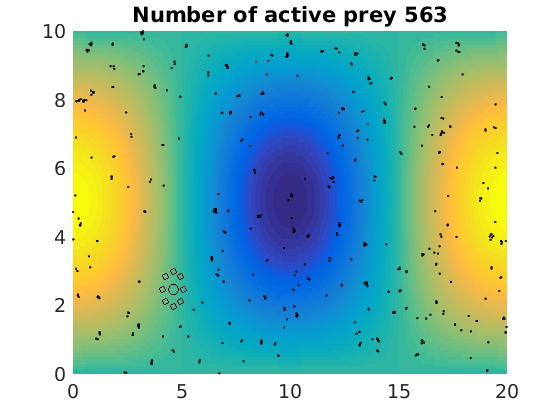
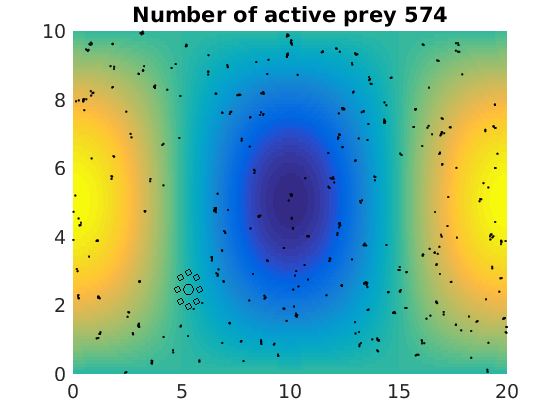
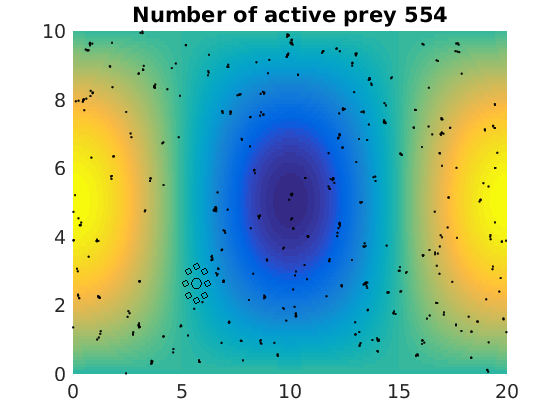
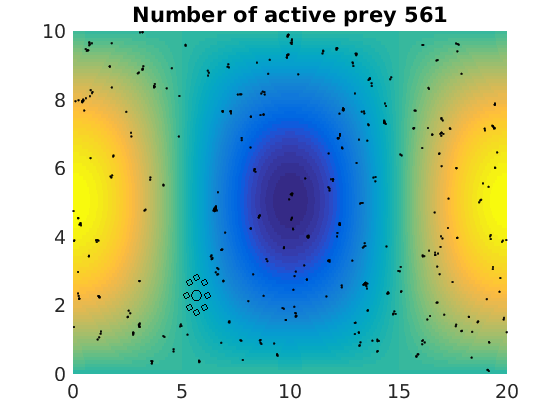
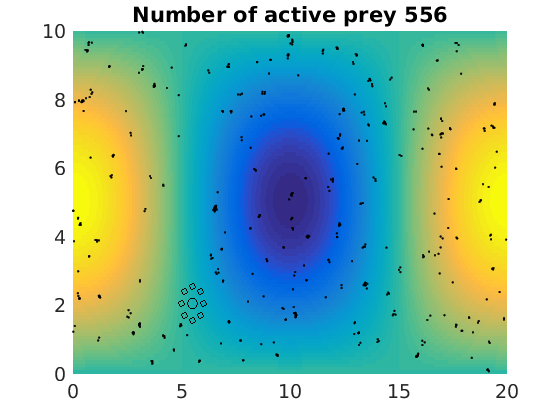
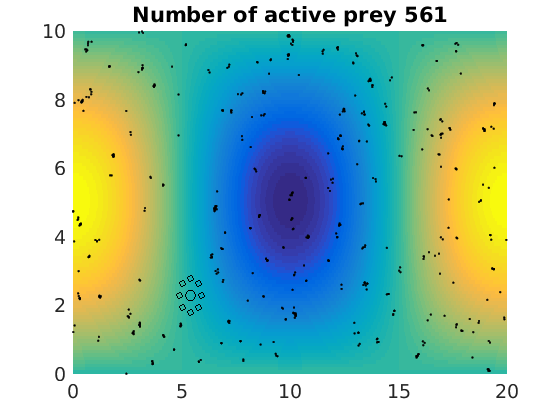
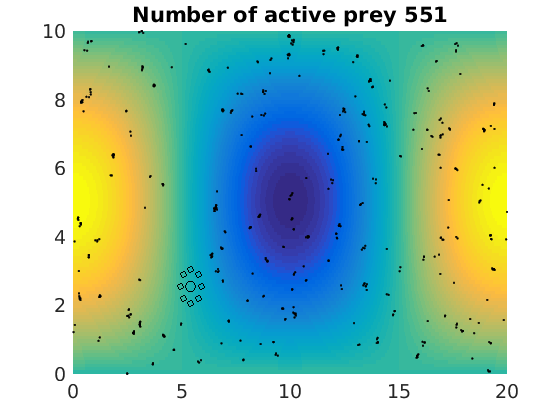
Update
Now remove the eaten particles.
livingind=find(alive==1);
dummyx=x(livingind);
dummyz=z(livingind);
numactive=length(dummyx);
Allocate arrays particles.
x=-1e4*ones(numparts,1);
z=-1e4*ones(numparts,1);
alive=zeros(numparts,1);
alive(1:numactive)=1;
x(1:numactive)=dummyx;
z(1:numactive)=dummyz;
end