Wavelet Coherence examples
This script presents multiple examples of the wavelet coherence of various simple functions to get a better understanding of how to interpret the results.
Contents
close all;clear;
t = linspace(0,10,1000); dt = seconds(t(2)-t(1));
Various sines
The base case is a sine wave with a period of one.
sin1 = sin(2*pi*t);
We shift by pi/2 backwards.
sin2 = sin(2*pi*t+pi/2);
Shift pi/4 forwards.
sin3 = sin(2*pi*t-pi/4);
Shift pi forwards.
sin4 = sin(2*pi*t-pi);
Shift pi backwards
sin5 = sin(2*pi*t+pi);
Increase the amplitude by five.
sin6 = 5*sin(2*pi*t);
Add some noise throughout the signal.
sin7 = sin(2*pi*t)+rand(1,1000);
Shift by pi/2 and add some noise.
sin8 = sin(2*pi*t+pi/2)+rand(1,1000);
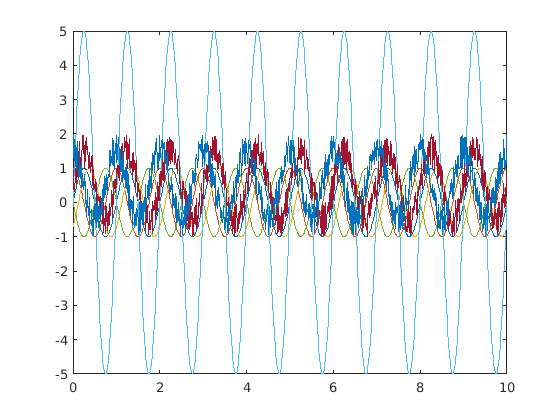
A comparison of the various waves.
figure(1) clf plot(t,sin1) hold plot(t,sin2) plot(t,sin3) plot(t,sin4) plot(t,sin5) plot(t,sin6) plot(t,sin7) plot(t,sin8)
Current plot held
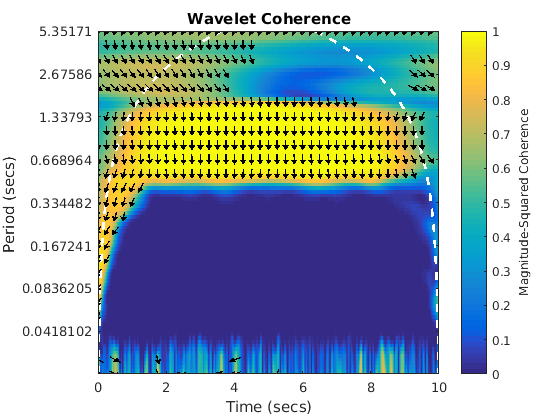
Sine and phase shift pi/2. We can see the phase shift as the arrows pointing downwards. Most areas are coherent, especially along the band of a one second period.
figure(2) wcoherence(sin1,sin2,dt)
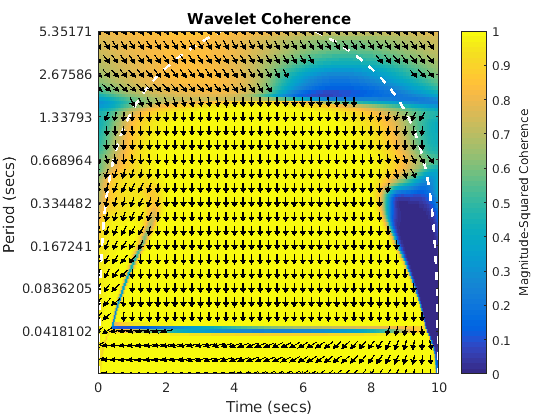
Sine and phase shift -pi/4. The arrows are shifted to point at 45 degrees as is expected. Similar to the previous figure in that there are some odd areas which are not coherent, but the important band is visible.
figure(3) wcoherence(sin1,sin3,dt)
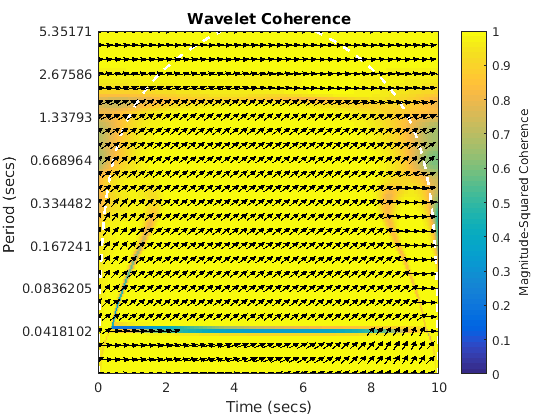
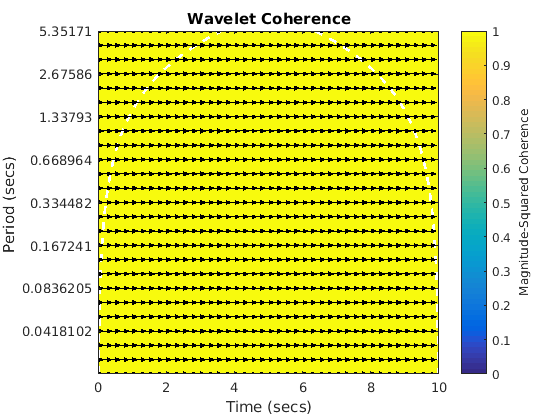
Sine and phase shift pi. Arrows point to the left and appears coherent everywhere.
figure(4) wcoherence(sin1,sin4,dt)
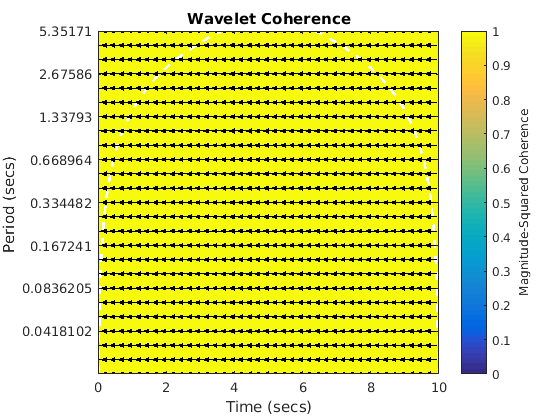
Sine and phase shift -pi. Same as the pervious figure, this indicates that you can get some aliasing effect with the arrows.
figure(5) wcoherence(sin1,sin5,dt)
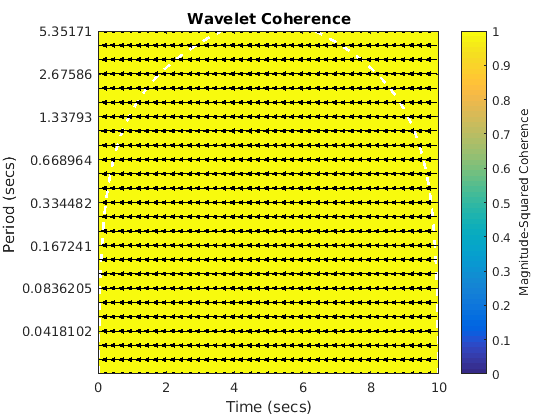
Sine and amplitude increase. As would be expected the amplitude has no effect on the wavelet coherence.
figure(6) wcoherence(sin1,sin6,dt)
Aine and noisy sine. The primary effect of the noise appears to be making the low period (high frequency) areas no longer coherent. This logically makes sense as the noise is random and should be correlated to a smooth curve. We can also see that the primary period (one) is clearly visible as a band of coherence.
figure(7) wcoherence(sin1,sin7,dt)
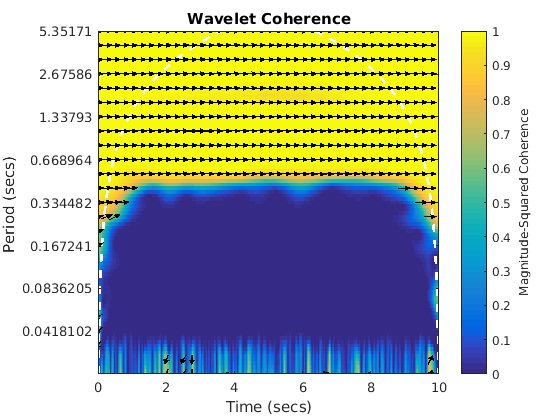
Sine and noisy sine with a phase shift pi/2. We see that as expected we have a combination of the effects we have seen. The noise takes out the coherence at the lower periods and the band is seen with the arrows pointing in the shifted direction. Interestingly we also appear to have lost coherence at large periods.
figure(8) wcoherence(sin1,sin8,dt)