Sparse Matrices

This M-file considers full and sparse matrices It looks at their construction, manipulation and visualization.

A sparse matrix is a matrix where the majority of the entries are zero, in Matlab a special type of matrix is used which "squeezes" out the zero entries (it saves memory).

This is a random matrix:

N=5;
M=rand(N);
M2=M*M; % This is its matrix square.
Mp2=M.*M; % This is its point-wise square.

This is an identity matrix and a sparse identity matrix:

myI=eye(N)
myspI=speye(N)

myI =

     1     0     0     0     0
     0     1     0     0     0
     0     0     1     0     0
     0     0     0     1     0
     0     0     0     0     1


myspI =

   (1,1)        1
   (2,2)        1
   (3,3)        1
   (4,4)        1
   (5,5)        1

I can check if a matrix is sparse like this:

issparse(myI)
issparse(myspI)

ans =

  logical

   0


ans =

  logical

   1

I can force a matrix to be sparse:

mysamp=3*myI; mysamp(2,3)=-2;
mysamp=sparse(mysamp);

This looks dumb but can be quite effective especially if we want to use the sparse matrix many times later.

This is an example of a sparse matrix build in action. It builds a second order differentiation matrix.

Define a spatial grid:

xmin = 0;
xmax = 50;
N = 2^7;
x = linspace(xmin,xmax,N+1);
dx=x(2)-x(1); dx2=dx*dx;

Now build a vector of ones,

e=ones(N+1,1);

Next use spdiags to drop the correct vectors into the correct diagonals.

Dxx = spdiags([e -2*e e], -1:1, N+1, N+1);
% finally scale
Dxx=(1/dx2)*Dxx;

This is how you visualize a matrix structure. Filled entries are in blue while empty ones are white.

figure(1)
clf
spy(Dxx);

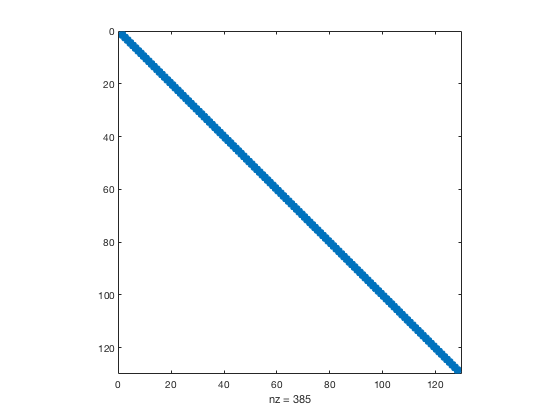
Sparsity can be very helpful when carrying out matrix solves since it offers immense speed up especially for very large matrices.

Dxxf=full(Dxx); % This converts Dxx to a full matrix.
myrhs=sin(8*pi*x/(xmax-xmin))';
tic,mysols=Dxx\myrhs; toc
tic,mysolsf=Dxxf\myrhs; toc
max(abs(mysols-mysolsf))

Elapsed time is 0.000244 seconds.
Elapsed time is 0.028909 seconds.

ans =

   3.6027e-14