Basic Matlab definitions and operations
This tutorial script shows the basic ways that Matlab can be used and some built-in operations.
Contents
A Calculator
From the start Matlab can be used as a basic calculator, for example:
5+2342 2354.3452*45345.23 234/23
ans =
2347
ans =
1.0676e+08
ans =
10.1739
Column and Row vectors
Matlab's basic data structure is an array with the mathematical properties of a vector or matrix (an individual number is a scalar, or vector of length one). A vector can be created by using the "[]" symbols with spaces in between:
A=[ 1 2 3 4 5]
A =
1 2 3 4 5
The default is to make a row vector. To make a column vector use the ";" symbol to separate:
B=[ 1; 2; 3; 4; 5]
B =
1
2
3
4
5
Matrix operations
For another example, I define the number of rows and columns then I use the rand command to make up random vectors and matrices. Next I give examples of standard operations, including special Matlab operations.
numrows=5; numcols=5; myrowvec=rand(numrows,1); mycolvec=rand(1,numcols); mymatrix=rand(numrows,numcols);
Matrix multiplication right.
ans1=mymatrix*myrowvec
ans1 =
1.4788
1.8762
2.2505
1.8595
1.8251
Matrix multiplication left.
ans2=mycolvec*mymatrix
ans2 =
2.0461 2.3164 2.0875 1.2882 0.3671
Dot product method 1.
ans3=dot(myrowvec,mycolvec)
ans3 =
1.8859
Dot product method 2.
ans3b=mycolvec*myrowvec
ans3b =
1.8859
Outer product.
ans4=myrowvec*mycolvec
ans4 =
0.0795 0.2269 0.4456 0.7801 0.7861
0.0884 0.2523 0.4954 0.8673 0.8740
0.0124 0.0354 0.0694 0.1216 0.1225
0.0891 0.2544 0.4995 0.8746 0.8813
0.0617 0.1761 0.3458 0.6055 0.6102
Transpose.
ans5=mymatrix' myrowvec ans6=myrowvec'
ans5 =
0.1576 0.9706 0.9572 0.4854 0.8003
0.1419 0.4218 0.9157 0.7922 0.9595
0.6557 0.0357 0.8491 0.9340 0.6787
0.7577 0.7431 0.3922 0.6555 0.1712
0.7060 0.0318 0.2769 0.0462 0.0971
myrowvec =
0.8147
0.9058
0.1270
0.9134
0.6324
ans6 =
0.8147 0.9058 0.1270 0.9134 0.6324
Entry by entry multiplication.
ans7=myrowvec.*(2*ones(size(myrowvec))) ans8=myrowvec.*mycolvec'
ans7 =
1.6294
1.8116
0.2540
1.8268
1.2647
ans8 =
0.0795
0.2523
0.0694
0.8746
0.6102
Searching vectors
Consider trying to find all the entries in a vector with a value larger than 0.5.
myrowvec2=rand(50000,1);
Time how long it takes.
tic myind=zeros(size(myrowvec2)); for ii=1:50000 if myrowvec2(ii)>0.5 myind(ii)=1; end end time1=toc
time1 =
0.0025
But Matlab is a vectorized language so for large vectors a much faster way to do this is to use the logical operations.
tic myind2=(myrowvec2>0.5); time2=toc
time2 = 5.7922e-04
and it would be easy to have multiple ifs, say finding values between 0.5 and 0.75.
tic myind3=((myrowvec2>0.5)&(myrowvec2<0.75)); time3=toc
time3 = 7.8635e-04
The savings from vectorization become evident for large matrices. There is another related command that is sometimes useful.
myind=find(myrowvec2<0.5); % finds the indices of the entries in myrowvec2 that are less than a half.
IMPORTANT: IN GENERAL TRY TO AVOID FOR LOOPS IN MATLAB
Function definition
While Matlab has the means to create complex software structures involving functions I tend to prefer flat codes and for these inline function definitions are very useful. If you define your parameters before the function definition the functions will just use them all the time. This example is a traveling internal wave in a channel.
H=20; % total depth. L=2*1e1; % wavelength. k=2*pi/L; % wave number. modenum=1; % mode number. m=modenum*pi/H; % vertical wave number. N0=2e-2; N02=N0^2; % buoyancy frequency and buoyancy frequency squared. sigma=(N0*k*H)/sqrt(modenum^2*pi^2+k*H*k*H); % frequency. myper=2*pi/sigma; % period. amp=0.1; % wave amplitude.
You use the th '@' symbol to define an anonymous function. Basically put @(variables) function_definition.
myf=@(x,z,t) amp*cos(k*x-sigma*t).*sin(m*z);
% To call the function we would just say:
wavenow=myf(0,H/2,0)
wavenow =
0.1000
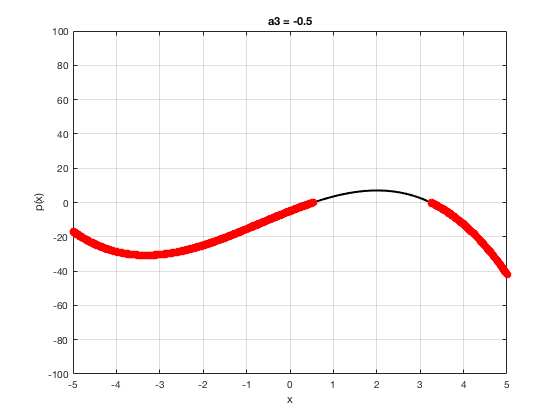
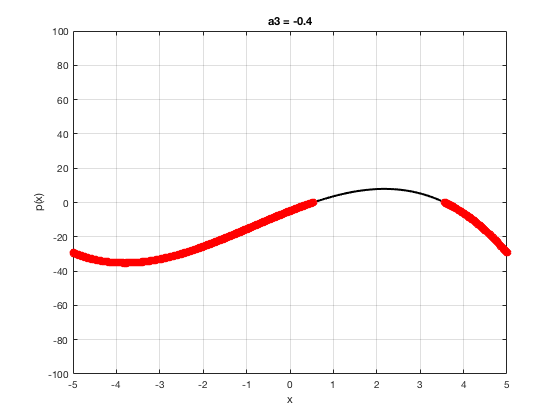
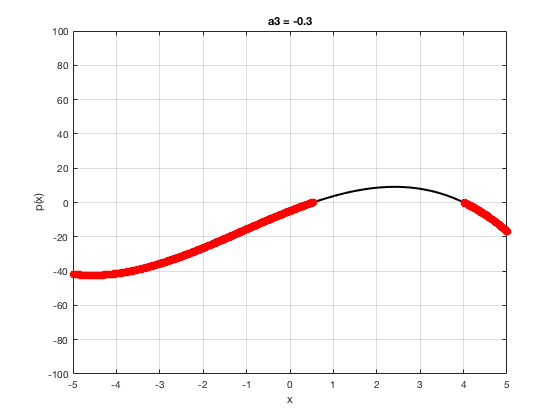
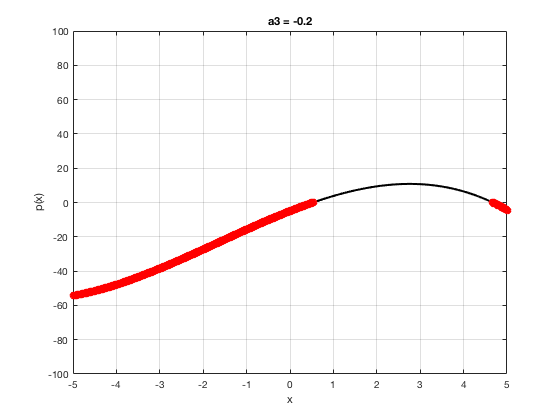
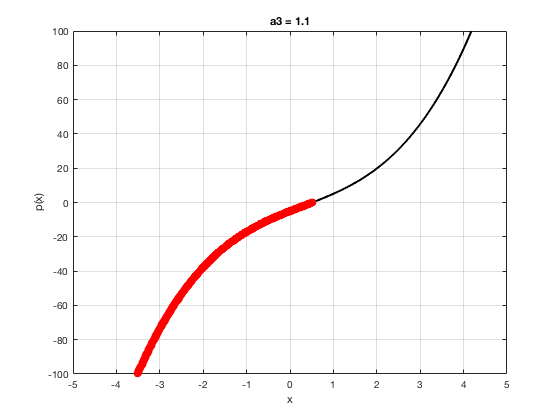
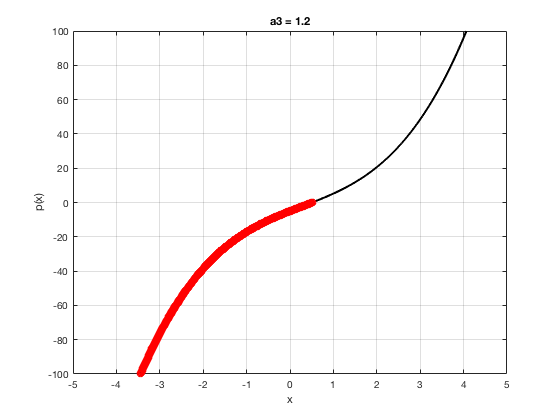
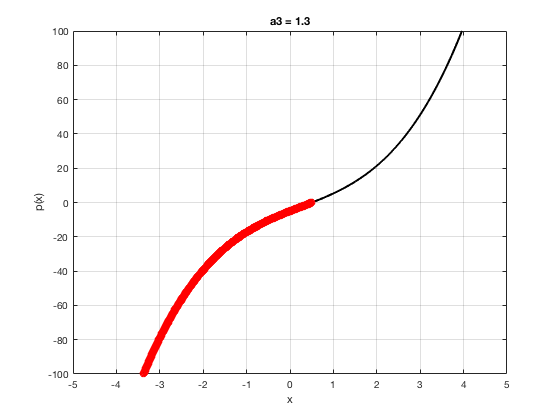
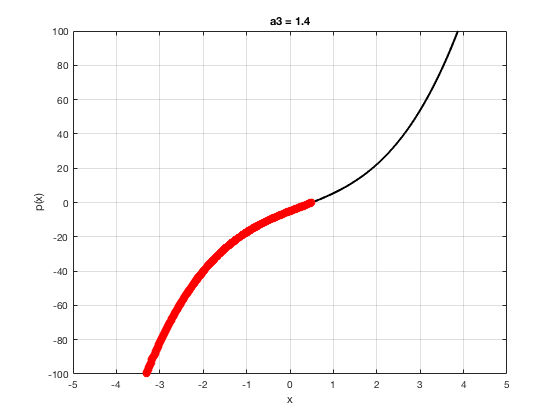
OK let's use all that to do something cool This loop makes a movie of the graph of a polynomial as the coefficient of the cubic term changes and marks the negative regions.
xg=linspace(-5,5,1001); % define a grid. figure(1),clf % open a figure and clear it. for a3=-2:0.1:2 % loop over the coefficient of x^3.
myp=@(x) 0.001*x.^4+a3.*x.^3-x.^2+10*x-5; pg=myp(xg); myind=find(pg<0); clf plot(xg,pg,'k',xg(myind),pg(myind),'ro','linewidth',2)
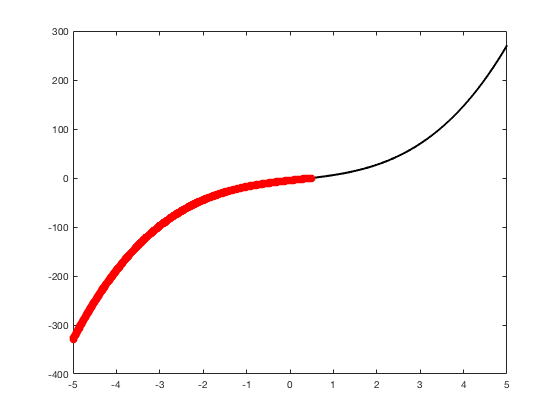
xlabel('x') % label ylabel('p(x)') % label title(['a3 = ' num2str(a3,4)]) % title axis([-5 5 -100 100]) % fix the axis, [x_min x_max y_min y_max] grid on drawnow
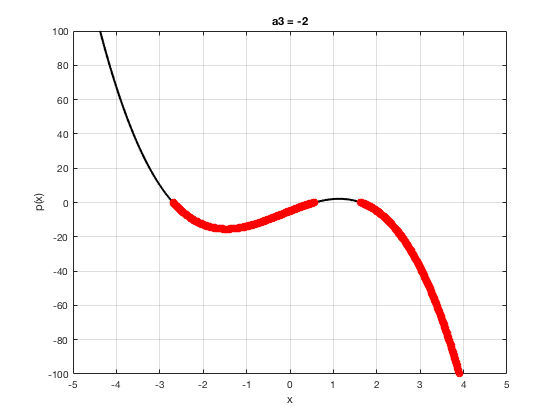
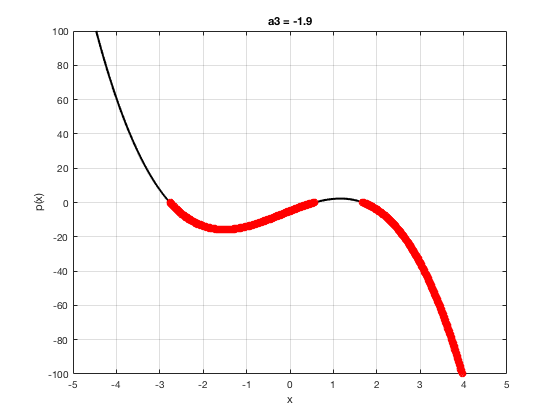
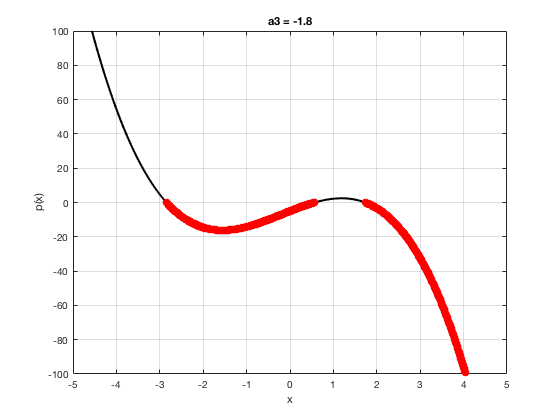
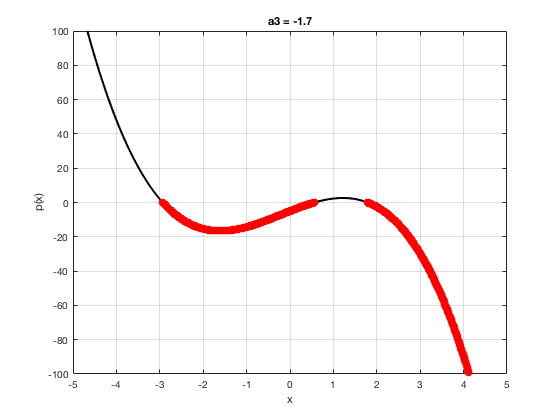
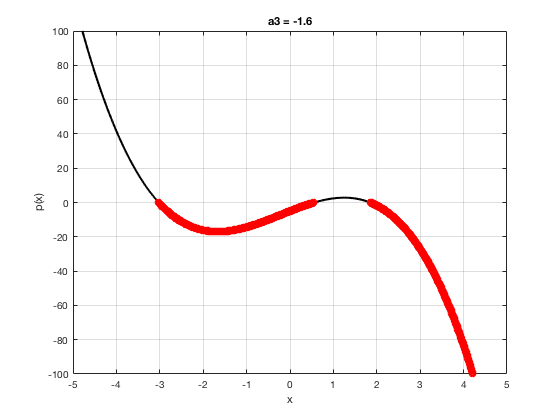
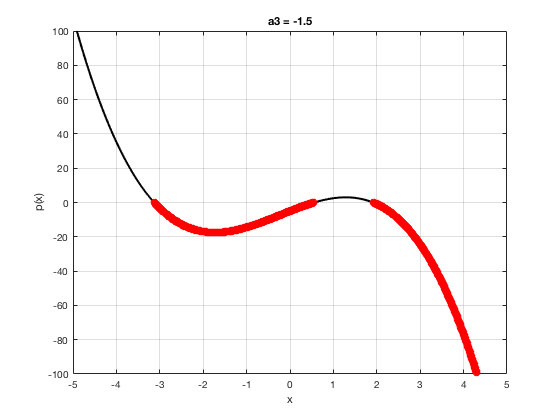
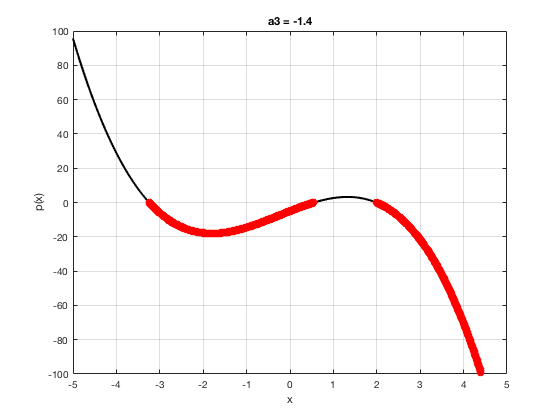
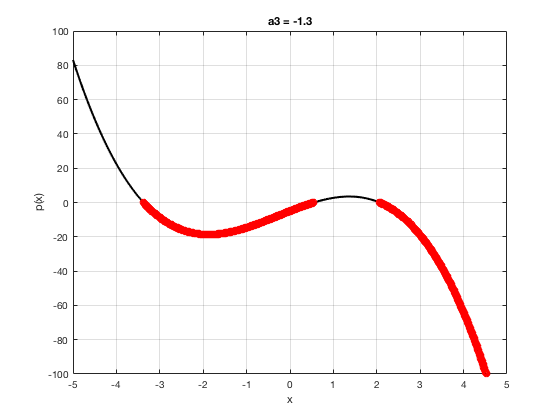
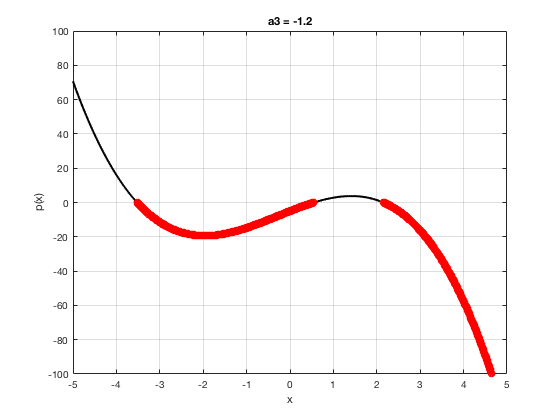
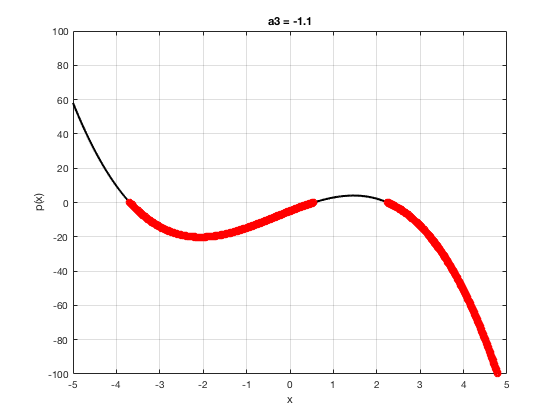
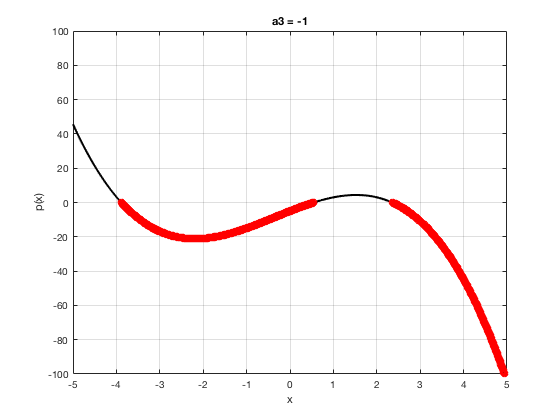
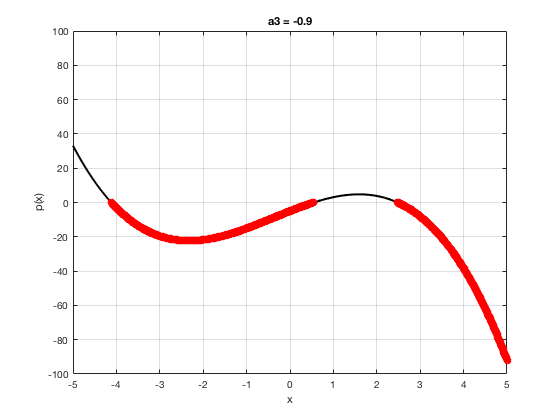
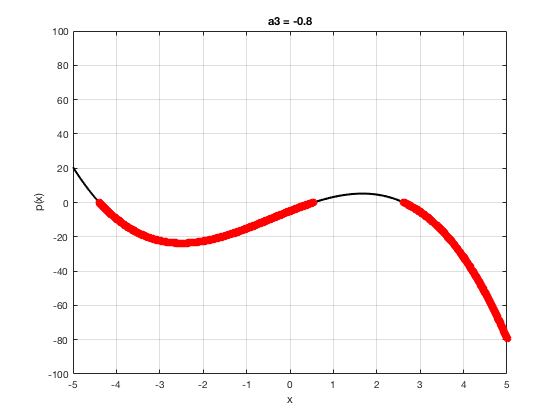
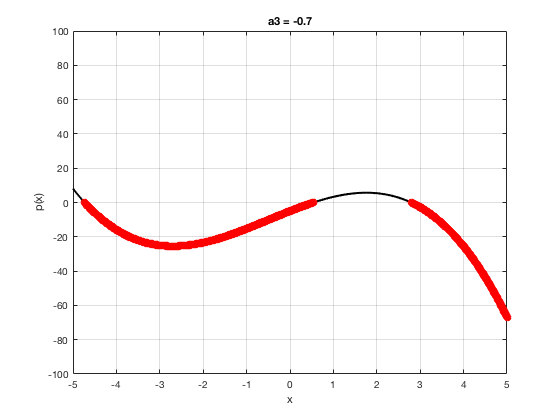
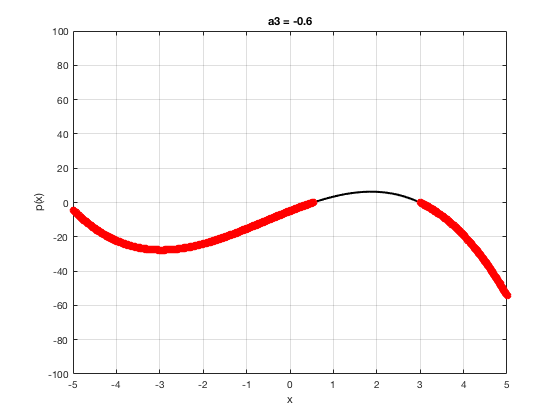
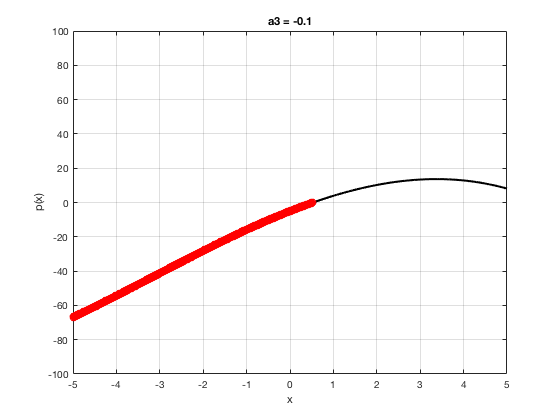
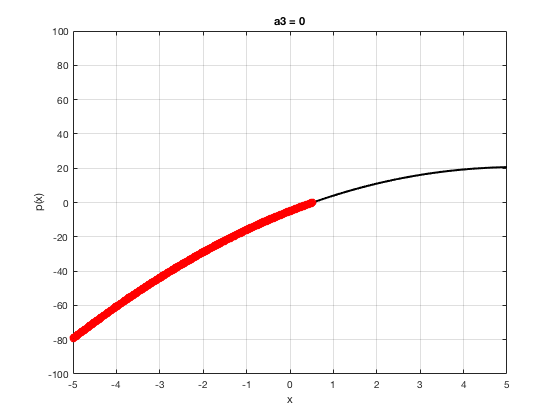
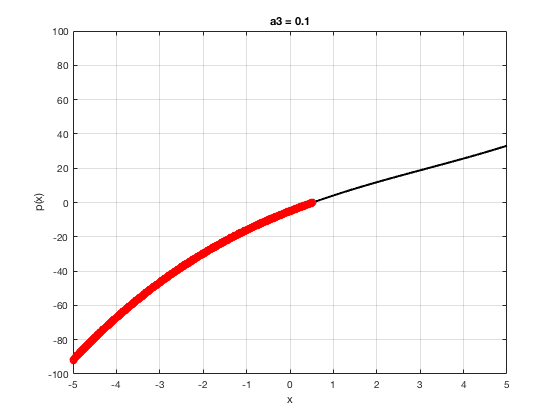
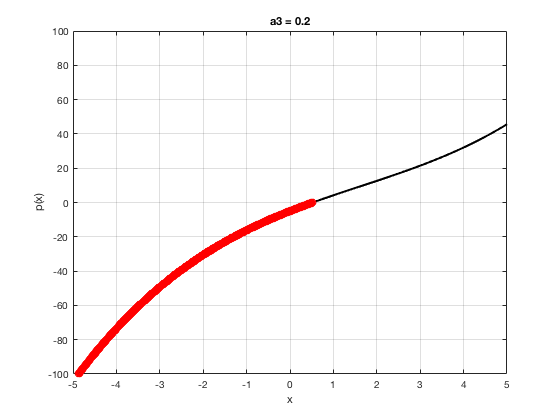
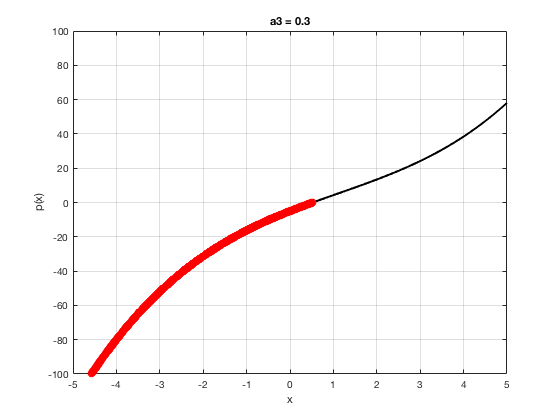
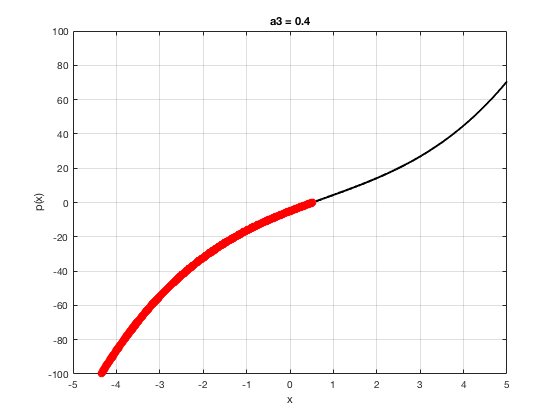
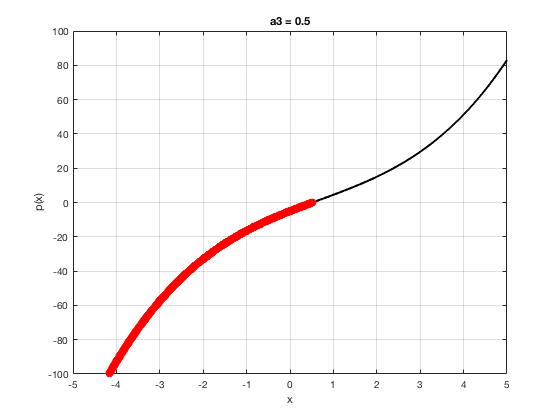
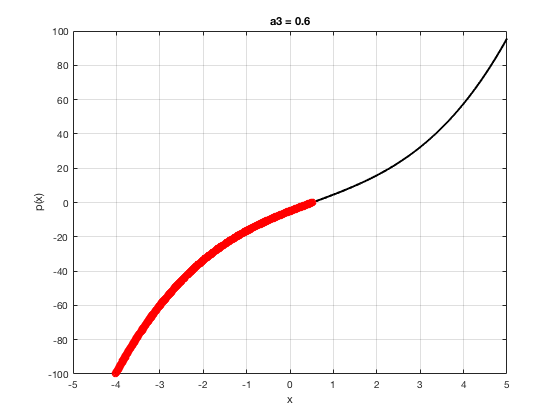
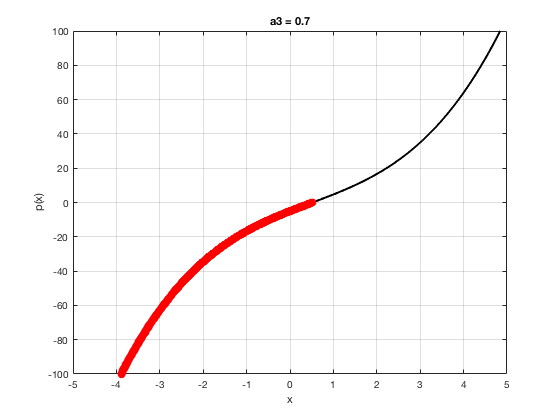
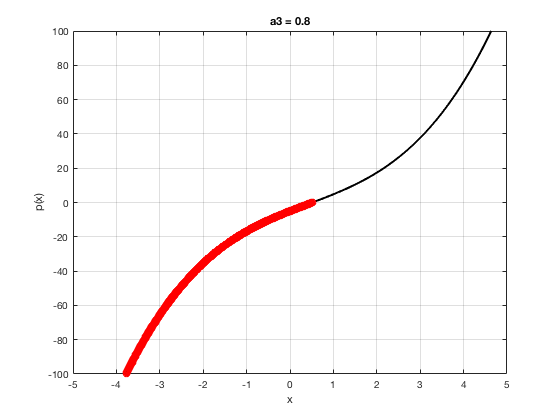
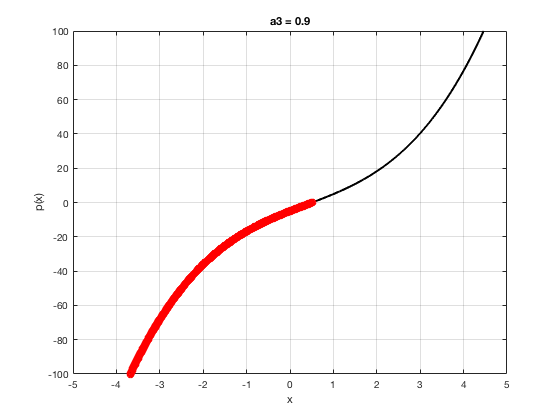
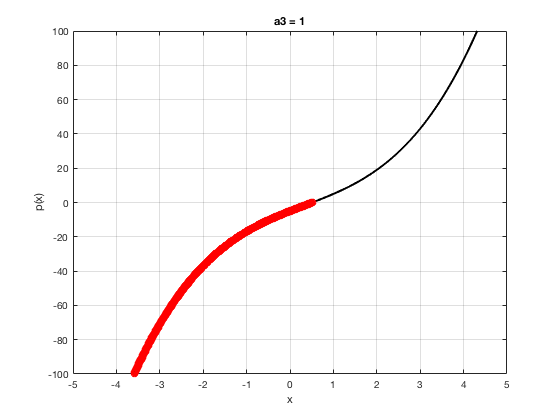
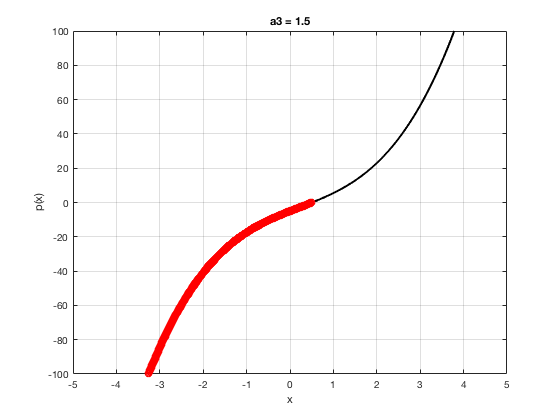
end