Solving a two box Lotka-Volterra system

The previous script was extremely simple and not particularly very useful. An extension of the original idea is that we have two predator-prey systems that are connected. An example of this could be two islands which are for the most part separate except for a small land bridge whereby some of the populations can interchange. In this case we would have the equations:

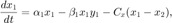
$$\frac{dx_1}{dt} = \alpha_1 x_1-\beta_1 x_1y_1-C_x(x_1-x_2) ,\\$$

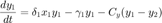
$$\frac{dy_1}{dt} = \delta_1 x_1y_1 - \gamma_1 y_1-C_y(y_1-y_2)$$

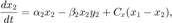
$$\frac{dx_2}{dt} = \alpha_2 x_2-\beta_2 x_2y_2+C_x(x_1-x_2) ,\\$$

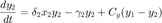
$$\frac{dy_2}{dt} = \delta_2 x_2y_2 - \gamma_2 y_2+C_y(y_1-y_2)$$

Please note that this script defines functions at the end, which is only supported by MATLAB 2016b or later.

Contents

close all;clear

Initialization

We now have different parameters for each box.

alpha = [2 2];
beta = [1/2 1];
delta = [1 2/3];
gamma = [4/3 1];

Correlation constants

New correlation constants for how the populations interchange.

First consider no interaction.

C_x = 0;
C_y = 0;

We define the ICs for both systems.

prey01 = 5;
pred01 = 10;
prey02 = 5;
pred02 = 1;
N0 = [prey01 pred01 prey02 pred02];

Use ODE45

Same form as the previous script, only with more parameters and a different function.

tic
[ts, Ns] = ode45(@(t,N) func_lotkavolterra2(t,N,alpha,beta,delta,gamma,C_x,C_y),[0 100],N0);
toc

Plot

Results for the uncoupled case.

figure(1)
clf
plot(ts,Ns)
figure(2)
clf
plot(Ns(:,1),Ns(:,2),'-ob')
hold
plot(Ns(:,3),Ns(:,4),'-or')

Current plot held

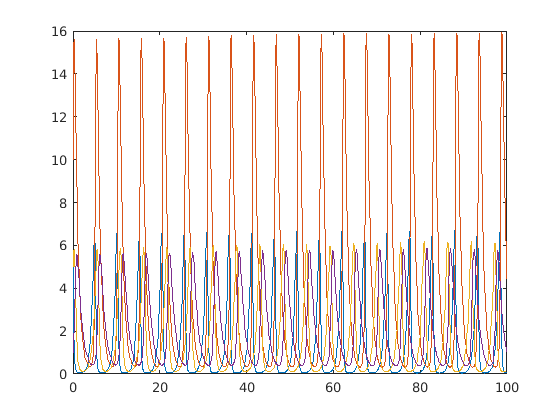
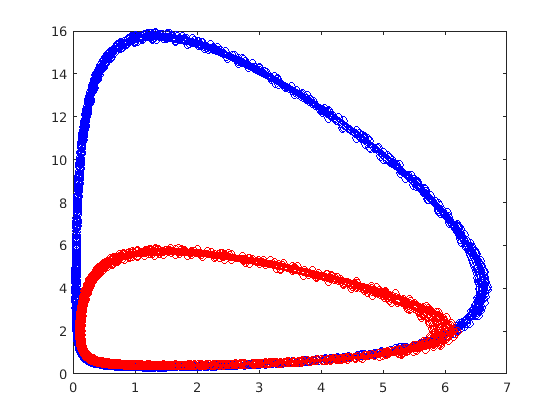
Correlated case

Now consider a case where we allow for movement between the two boxes.

C_x = 1;
C_y = 1;

tic
[ts, Ns] = ode45(@(t,N) func_lotkavolterra2(t,N,alpha,beta,delta,gamma,C_x,C_y),[0 100],N0);
toc

Elapsed time is 57.687436 seconds.

Plot

Results for the uncoupled case.

figure(1)
clf
plot(ts,Ns)
figure(2)
clf
plot(Ns(:,1),Ns(:,2),'-ob')
hold
plot(Ns(:,3),Ns(:,4),'-or')

Current plot held

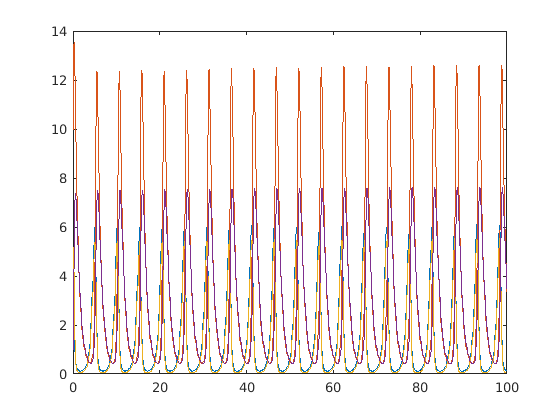
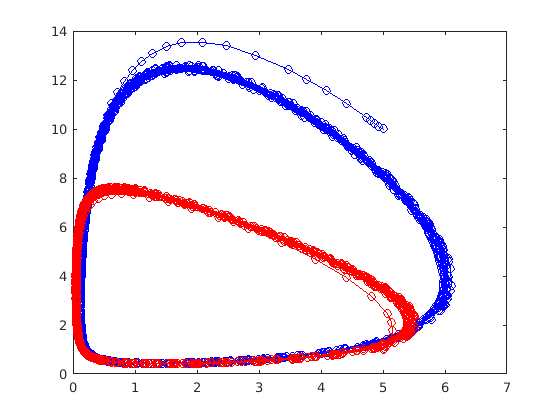
This system will still form limit cycles, however the final state for each box is modified by the correlation values. Try testing different parameter values, especially when one box begins at a steady state.

The two box Lotka-Volterra equations

Two Lotka-Volterra boxes connected by a correlation term.

function  dNdt  = func_lotkavolterra2(t, N,alpha,beta,delta,gamma,C_x,C_y)

The ODE equations

The difference between this model and the single box model is the addition of the correlation terms which transfer population from the high population box to the low population one. The different parameters also allow for the boxes to have different steady states if there were no connection. The order of the populations is box 1: prey, predator, and box 2: prey predator.

dNdt(1) = alpha(1)*N(1)-beta(1)*N(1)*N(2)-C_x*(N(1)-N(3));
dNdt(2) = delta(1)*N(1)*N(2) - gamma(1)*N(2)-C_y*(N(2)-N(4));
dNdt(3) = alpha(2)*N(3)-beta(2)*N(3)*N(4)+C_x*(N(1)-N(3));
dNdt(4) = delta(2)*N(3)*N(4) - gamma(2)*N(4)+C_y*(N(2)-N(4));
dNdt = dNdt(:);

end

Elapsed time is 59.053217 seconds.


Published with MATLAB® R2016b