Solving the Lotka-Volterra equations

This script solves the simple predator-prey equations using the built in Matlab functions. Please note that this script defines functions at the end, which is only supported by MATLAB 2016b or later. The Lotka-Volterra equations are:

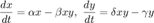
$\frac{dx}{dt} = \alpha x-\beta xy ,\\$$ $$\frac{dy}{dt} = \delta xy - \gamma y$

Initialization
Use ODE45
Zero population
The Lotka-Volterra equations
The ODE equations

close all; clear

Initialization

alpha = 2/3;
beta = 4/3;
delta = 1;
gamma = 1;

We define the ICs.

prey0 = 1;
pred0 = 2;
N0 = [prey0 pred0];

Use ODE45

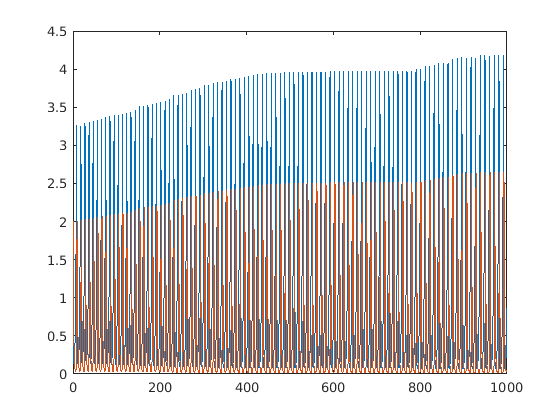
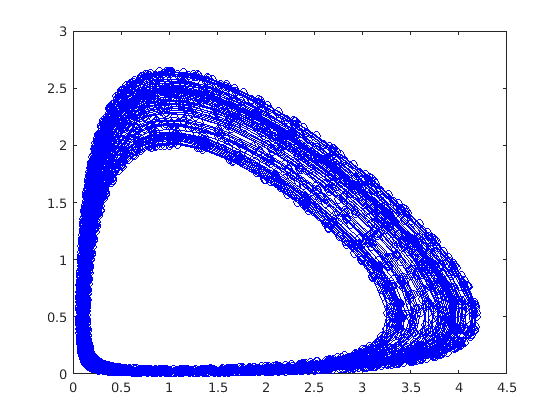
tic
% To pass additional parameters to the DE function, use the anonymous
% function @(t,N) so that the first parameter of ode45 "only" takes in two
% parameters.
[ts, Ns] = ode45(@(t,N) func_lotkavolterra(t,N,alpha,beta,delta,gamma),[0 1000],N0);
toc
figure(1)
clf
plot(ts,Ns)
figure(2)
clf
plot(Ns(:,1),Ns(:,2),'-ob')

Zero population

Now consider if one of the populations is zero.

prey0 = 0;
pred0 = 2;
N0 = [prey0 pred0];
[ts, Ns] = ode45(@(t,N) func_lotkavolterra(t,N,alpha,beta,delta,gamma),[0 1000],N0);
toc
figure(1)
clf
plot(ts,Ns)
figure(2)
clf
plot(Ns(:,1),Ns(:,2),'-ob')

This system forms a limit cycle around the fixed point (gamma/delta,alpha/beta). There is also another fixed point at (0,0).

You can try varying the parameters or move to the intro_ODE_LV2 tutorial to consider a more complicated system.

The Lotka-Volterra equations

The simplest form of the L-V equations. Takes in time, the current populations, and the model parameters alpha, beta, delta and gamma. It returns the time derivative of the populations.

function  dNdt  = func_lotkavolterra(t, N,alpha,beta,delta,gamma)

The ODE equations

The first entry of the population numbers is the prey while the second is the predator. alpha*N(1) represents the natural exponential growth of the prey population while the beta*N(1)*N(2) term represents the rate of predation. The delta*N(1)*N(2) term is the growth of the predator population which is similar to the previous term but the constant may be different. The gamma*N(2) term is the natural decline of the predator population without a food source.

dNdt(1) = alpha*N(1)-beta*N(1)*N(2);
dNdt(2) = delta*N(1)*N(2) - gamma*N(2);
dNdt = dNdt(:);

end