Boundary conditions with diffusion operator
A tutorial version of Script 36 from Spectral Methods in Matlab by Trefethen. This solves the variables coefficient diffusion equation on a box with non-trivial boundary conditions. We also have the "\" matlab operator explain its logic when solving the problem. There is no time dependence. Please note that this script defines functions at the end, which is only supported by MATLAB 2016b or later. NOTE: IF YOU WOULD LIKE THIS SCRIPT TO WORK WITH OLDER VERSIONS OF MATLAB REMOVE THE FUNCTION FROM THE END AND GIVE IT ITS OWN .m FILE.
Contents
clear,close all
Set up grid and 2D Laplacian, boundary points included:
Notice the low number of points.
N = 64;
Use the cheb function to get the Chebyshev points.
[D,x] = cheb(N); y = x;
Create the 2D grid.
[xx,yy] = meshgrid(x,y); [xxx,yyy] = meshgrid(-1:.04:1,-1:.04:1);
Create the differentiation matrices
Make them sparse to save space.
D2 = sparse(D^2);
I = speye(N+1);
% Use the outer product to create the matrices.
Dy=kron(I,D);
Dx=kron(D,I);
Dyy=kron(I,D2);
Dxx=kron(D2,I);
Create variable diffusion constant
r=sqrt((xx-0.5).^2+(yy+0.75).^2); kappa0=1e-2; kappa=kappa0*(1+0.5*sech((r/0.5).^2)); kappav=kappa(:); mykappax=Dx*kappa(:); mykappay=Dy*kappa(:); kappaxv=mykappax(:); kappayv=mykappay(:); kappavmat=sparse(diag(kappav)); kappaxmat=sparse(diag(kappaxv)); kappaymat=sparse(diag(kappayv));
Create the Laplacian operator
Combine the last two parts and build the Laplacian operator.
L = kappavmat*(Dxx+Dyy)+kappaxmat*Dx+kappaymat*Dy;
Boundary Conditions
Impose boundary conditions by replacing appropriate rows of L:
bxp1 = find(xx==1); %rows of the big matrix at which x=1 bxn1 = find(xx==-1); %rows of the big matrix at which x=-1 byp1 = find(yy==1); %rows of the big matrix at which y=1 byn1 = find(yy==-1); %rows of the big matrix at which y=-1 rhs = zeros((N+1)^2,1); L(bxp1,:) = zeros(N+1,(N+1)^2); L(bxp1,bxp1) = eye(N+1); rhs(bxp1)=-yy(bxp1); %Dirichlet BC at x=-1 notice how RHS is modified for ii=1:length(byp1) L(byp1(ii),:) = Dy(byp1(ii),:); rhs(byp1)=2.5;% set L=Dy at y=1, notice RHS is set to zero above L(bxn1(ii),:) = Dx(bxn1(ii),:); rhs(bxn1)=sin(pi*(1+yy(bxn1))); % set L=Dy at x=-1, notice RHS modified end L(byn1,:) = zeros(N+1,(N+1)^2); L(byn1,byn1) = eye(N+1); rhs(byn1)=-cos(3*pi*xx(byn1));
Solve the equation
Use spparms to show the logic used by Matlab to solve the linear system with the "\" command.
spparms('spumoni',2)
Just solve the equations with nothing extra.
tic u1 = L\rhs; uu1 = reshape(u1,N+1,N+1); justsolve=toc
sp\: bandwidth = 4160+1+4095.
sp\: is A diagonal? no.
sp\: is band density (0.0291729) > bandden (0.5) to try banded solver? no.
sp\: is A triangular? no.
sp\: is A morally triangular? no.
sp\: is A a candidate for Cholesky (symmetric, real positive diagonal)? no.
sp\: use Unsymmetric MultiFrontal PACKagewith automatic reordering.
UMFPACK V5.4.0 (May 20, 2009), Control:
Matrix entry defined as: double
Int (generic integer) defined as: UF_long
0: print level: 2
1: dense row parameter: 0.2
"dense" rows have > max (16, (0.2)*16*sqrt(n_col) entries)
2: dense column parameter: 0.2
"dense" columns have > max (16, (0.2)*16*sqrt(n_row) entries)
3: pivot tolerance: 0.1
4: block size for dense matrix kernels: 32
5: strategy: 0 (auto)
6: initial allocation ratio: 0.7
7: max iterative refinement steps: 2
12: 2-by-2 pivot tolerance: 0.01
13: Q fixed during numerical factorization: 0 (auto)
14: AMD dense row/col parameter: 10
"dense" rows/columns have > max (16, (10)*sqrt(n)) entries
Only used if the AMD ordering is used.
15: diagonal pivot tolerance: 0.001
Only used if diagonal pivoting is attempted.
16: scaling: 1 (divide each row by sum of abs. values in each row)
17: frontal matrix allocation ratio: 0.5
18: drop tolerance: 0
19: AMD and COLAMD aggressive absorption: 1 (yes)
The following options can only be changed at compile-time:
8: BLAS library used: Fortran BLAS. size of BLAS integer: 8
9: compiled for MATLAB
10: CPU timer is POSIX times ( ) routine.
11: compiled for normal operation (debugging disabled)
computer/operating system: Linux
size of int: 4 UF_long: 8 Int: 8 pointer: 8 double: 8 Entry: 8 (in bytes)
sp\: UMFPACK's factorization was successful.
sp\: UMFPACK's solve was successful.
UMFPACK V5.4.0 (May 20, 2009), Info:
matrix entry defined as: double
Int (generic integer) defined as: UF_long
BLAS library used: Fortran BLAS. size of BLAS integer: 8
MATLAB: yes.
CPU timer: POSIX times ( ) routine.
number of rows in matrix A: 4225
number of columns in matrix A: 4225
entries in matrix A: 520449
memory usage reported in: 16-byte Units
size of int: 4 bytes
size of UF_long: 8 bytes
size of pointer: 8 bytes
size of numerical entry: 8 bytes
strategy used: symmetric
ordering used: amd on A+A'
modify Q during factorization: no
prefer diagonal pivoting: yes
pivots with zero Markowitz cost: 130
submatrix S after removing zero-cost pivots:
number of "dense" rows: 0
number of "dense" columns: 0
number of empty rows: 0
number of empty columns 0
submatrix S square and diagonal preserved
pattern of square submatrix S:
number rows and columns 4095
symmetry of nonzero pattern: 1.000000
nz in S+S' (excl. diagonal): 508032
nz on diagonal of matrix S: 4095
fraction of nz on diagonal: 1.000000
AMD statistics, for strict diagonal pivoting:
est. flops for LU factorization: 1.79750e+10
est. nz in L+U (incl. diagonal): 10523205
est. largest front (# entries): 6230016
est. max nz in any column of L: 2496
number of "dense" rows/columns in S+S': 0
symbolic factorization defragmentations: 0
symbolic memory usage (Units): 1195977
symbolic memory usage (MBytes): 18.2
Symbolic size (Units): 10846
Symbolic size (MBytes): 0
symbolic factorization CPU time (sec): 0.05
symbolic factorization wallclock time(sec): 0.05
matrix scaled: yes (divided each row by sum of abs values in each row)
minimum sum (abs (rows of A)): 1.00000e+00
maximum sum (abs (rows of A)): 4.30892e+04
symbolic/numeric factorization: upper bound actual %
variable-sized part of Numeric object:
initial size (Units) 1089912 1085688 100%
peak size (Units) 15802496 11432659 72%
final size (Units) 8154726 5295040 65%
Numeric final size (Units) 8177995 5316197 65%
Numeric final size (MBytes) 124.8 81.1 65%
peak memory usage (Units) 15872229 11502392 72%
peak memory usage (MBytes) 242.2 175.5 72%
numeric factorization flops 3.65049e+10 1.79750e+10 49%
nz in L (incl diagonal) 7186015 5271844 73%
nz in U (incl diagonal) 8386756 5263908 63%
nz in L+U (incl diagonal) 15568546 10531527 68%
largest front (# entries) 12892006 6230016 48%
largest # rows in front 3149 2496 79%
largest # columns in front 4094 2496 61%
initial allocation ratio used: 0.851
# of forced updates due to frontal growth: 0
number of off-diagonal pivots: 0
nz in L (incl diagonal), if none dropped 5271844
nz in U (incl diagonal), if none dropped 5263908
number of small entries dropped 0
nonzeros on diagonal of U: 4225
min abs. value on diagonal of U: 5.11e-03
max abs. value on diagonal of U: 1.00e+00
estimate of reciprocal of condition number: 5.11e-03
indices in compressed pattern: 50236
numerical values stored in Numeric object: 10523335
numeric factorization defragmentations: 1
numeric factorization reallocations: 1
costly numeric factorization reallocations: 1
numeric factorization CPU time (sec): 11.67
numeric factorization wallclock time (sec): 3.23
numeric factorization mflops (CPU time): 1540.28
numeric factorization mflops (wallclock): 5565.02
symbolic + numeric CPU time (sec): 11.72
symbolic + numeric mflops (CPU time): 1533.71
symbolic + numeric wall clock time (sec): 3.28
symbolic + numeric mflops (wall clock): 5480.19
solve flops: 7.05811e+07
iterative refinement steps taken: 1
iterative refinement steps attempted: 2
sparse backward error omega1: 2.35e-16
sparse backward error omega2: 0.00e+00
solve CPU time (sec): 0.12
solve wall clock time (sec): 0.10
solve mflops (CPU time): 588.18
solve mflops (wall clock time): 705.81
total symbolic + numeric + solve flops: 1.80456e+10
total symbolic + numeric + solve CPU time: 11.84
total symbolic + numeric + solve mflops (CPU): 1524.12
total symbolic+numeric+solve wall clock time: 3.40
total symbolic+numeric+solve mflops(wallclock) 5307.53
justsolve =
3.3830
Solve the equations with factoring.
tic [ll,uu,pp,qq]= lu(L); factortime=toc tic u2 = qq*(uu\(ll\(pp*rhs))); uu2 = reshape(u2,N+1,N+1); factorsolve=toc
UMFPACK V5.4.0 (May 20, 2009), Control:
Matrix entry defined as: double
Int (generic integer) defined as: UF_long
0: print level: 2
1: dense row parameter: 0.2
"dense" rows have > max (16, (0.2)*16*sqrt(n_col) entries)
2: dense column parameter: 0.2
"dense" columns have > max (16, (0.2)*16*sqrt(n_row) entries)
3: pivot tolerance: 0.1
4: block size for dense matrix kernels: 32
5: strategy: 0 (auto)
6: initial allocation ratio: 0.7
7: max iterative refinement steps: 2
12: 2-by-2 pivot tolerance: 0.01
13: Q fixed during numerical factorization: 0 (auto)
14: AMD dense row/col parameter: 10
"dense" rows/columns have > max (16, (10)*sqrt(n)) entries
Only used if the AMD ordering is used.
15: diagonal pivot tolerance: 0.001
Only used if diagonal pivoting is attempted.
16: scaling: 0 (no)
17: frontal matrix allocation ratio: 0.5
18: drop tolerance: 0
19: AMD and COLAMD aggressive absorption: 1 (yes)
The following options can only be changed at compile-time:
8: BLAS library used: Fortran BLAS. size of BLAS integer: 8
9: compiled for MATLAB
10: CPU timer is POSIX times ( ) routine.
11: compiled for normal operation (debugging disabled)
computer/operating system: Linux
size of int: 4 UF_long: 8 Int: 8 pointer: 8 double: 8 Entry: 8 (in bytes)
UMFPACK V5.4.0 (May 20, 2009), Info:
matrix entry defined as: double
Int (generic integer) defined as: UF_long
BLAS library used: Fortran BLAS. size of BLAS integer: 8
MATLAB: yes.
CPU timer: POSIX times ( ) routine.
number of rows in matrix A: 4225
number of columns in matrix A: 4225
entries in matrix A: 520449
memory usage reported in: 16-byte Units
size of int: 4 bytes
size of UF_long: 8 bytes
size of pointer: 8 bytes
size of numerical entry: 8 bytes
strategy used: symmetric
ordering used: amd on A+A'
modify Q during factorization: no
prefer diagonal pivoting: yes
pivots with zero Markowitz cost: 130
submatrix S after removing zero-cost pivots:
number of "dense" rows: 0
number of "dense" columns: 0
number of empty rows: 0
number of empty columns 0
submatrix S square and diagonal preserved
pattern of square submatrix S:
number rows and columns 4095
symmetry of nonzero pattern: 1.000000
nz in S+S' (excl. diagonal): 508032
nz on diagonal of matrix S: 4095
fraction of nz on diagonal: 1.000000
AMD statistics, for strict diagonal pivoting:
est. flops for LU factorization: 1.79750e+10
est. nz in L+U (incl. diagonal): 10523205
est. largest front (# entries): 6230016
est. max nz in any column of L: 2496
number of "dense" rows/columns in S+S': 0
symbolic factorization defragmentations: 0
symbolic memory usage (Units): 1195977
symbolic memory usage (MBytes): 18.2
Symbolic size (Units): 10846
Symbolic size (MBytes): 0
symbolic factorization CPU time (sec): 0.05
symbolic factorization wallclock time(sec): 0.05
matrix scaled: no
symbolic/numeric factorization: upper bound actual %
variable-sized part of Numeric object:
initial size (Units) 1089912 1085688 100%
peak size (Units) 15802496 11432659 72%
final size (Units) 8154726 5295040 65%
Numeric final size (Units) 8177995 5314084 65%
Numeric final size (MBytes) 124.8 81.1 65%
peak memory usage (Units) 15872229 11500279 72%
peak memory usage (MBytes) 242.2 175.5 72%
numeric factorization flops 3.65049e+10 1.79750e+10 49%
nz in L (incl diagonal) 7186015 5271844 73%
nz in U (incl diagonal) 8386756 5263908 63%
nz in L+U (incl diagonal) 15568546 10531527 68%
largest front (# entries) 12892006 6230016 48%
largest # rows in front 3149 2496 79%
largest # columns in front 4094 2496 61%
initial allocation ratio used: 0.851
# of forced updates due to frontal growth: 0
number of off-diagonal pivots: 0
nz in L (incl diagonal), if none dropped 5271844
nz in U (incl diagonal), if none dropped 5263908
number of small entries dropped 0
nonzeros on diagonal of U: 4225
min abs. value on diagonal of U: 1.00e+00
max abs. value on diagonal of U: 1.87e+04
estimate of reciprocal of condition number: 5.34e-05
indices in compressed pattern: 50236
numerical values stored in Numeric object: 10523335
numeric factorization defragmentations: 1
numeric factorization reallocations: 1
costly numeric factorization reallocations: 1
numeric factorization CPU time (sec): 10.11
numeric factorization wallclock time (sec): 2.88
numeric factorization mflops (CPU time): 1777.94
numeric factorization mflops (wallclock): 6241.33
symbolic + numeric CPU time (sec): 10.16
symbolic + numeric mflops (CPU time): 1769.20
symbolic + numeric wall clock time (sec): 2.93
symbolic + numeric mflops (wall clock): 6134.82
factortime =
3.5751
sp\: bandwidth = 4195+1+0.
sp\: is A diagonal? no.
sp\: is A triangular? yes.
sp\: do a triangular solve.
sp\: bandwidth = 0+1+4067.
sp\: is A diagonal? no.
sp\: is A triangular? yes.
sp\: do a triangular solve.
factorsolve =
0.0234
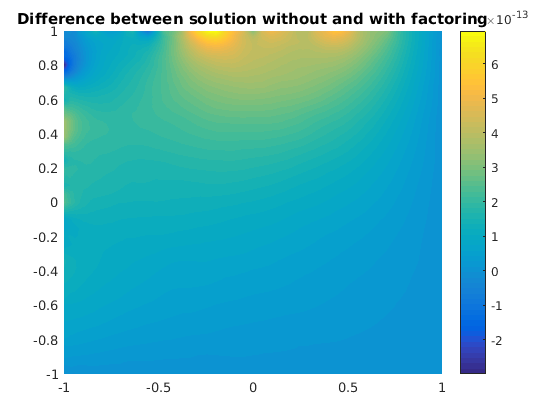
The difference between the solutions.
figure(1) clf pcolor(xx,yy,uu1-uu2),shading interp,colorbar title('Difference between solution without and with factoring')
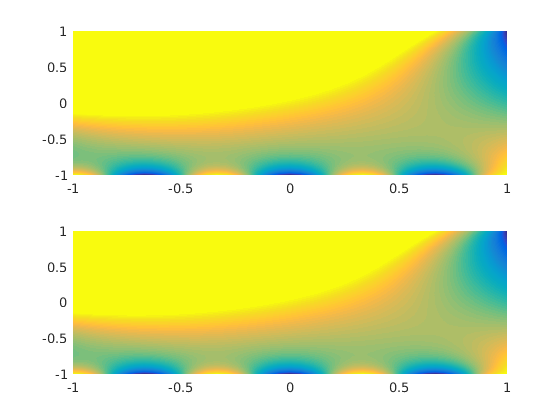
The individual solutions.
figure(2) clf subplot(2,1,1) pcolor(xx,yy,uu1),shading interp,caxis([-1 1]) subplot(2,1,2) pcolor(xx,yy,uu2),shading interp,caxis([-1 1])
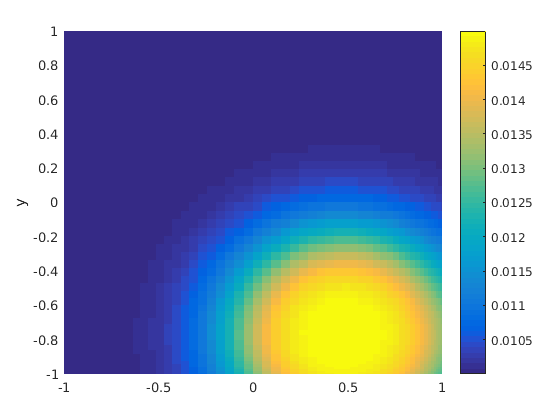
The diffusivity.
figure(3) clf pcolor(xx,yy,kappa),shading flat,colorbar ylabel('y')
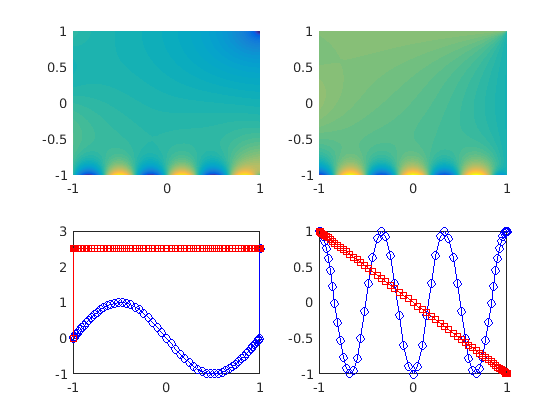
Create the derivatives.
u1y=Dy*u1; u1x=Dx*u1; uy=reshape(u1y,N+1,N+1); ux=reshape(u1x,N+1,N+1);
figure(4) clf % Plot the derivatives. subplot(2,2,1) pcolor(xx,yy,ux),shading interp,caxis([-10 10]) subplot(2,2,2) pcolor(xx,yy,uy),shading interp,caxis([-10 10]) subplot(2,2,3) % Plot the derivatives at the boundaries. plot(yy(bxn1),ux(bxn1),'bo-',xx(byp1),uy(byp1),'rs-') subplot(2,2,4) plot(xx(byn1),u1(byn1),'bo-',yy(bxp1),u1(bxp1),'rs-')
Chebyshev function
CHEB compute D = differentiation matrix, x = Chebyshev grid
function [D,x] = cheb(N) if N==0, D=0; x=1; return, end x = cos(pi*(0:N)/N)'; c = [2; ones(N-1,1); 2].*(-1).^(0:N)'; X = repmat(x,1,N+1); dX = X-X'; D = (c*(1./c)')./(dX+(eye(N+1))); % off-diagonal entries D = D - diag(sum(D')); % diagonal entries end