Using spectral methods to solve the Helmholtz problem

This code is a tutorial code for solving the Helmholtz (Poisson) problem in a doubly periodic domain. Since the diffusivity is constant, once we compute the Fourier transforms, solving for 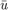$\bar{u}$ is trivial.

Construct grid
FFT related material
Diffusivity
Solve the problem via multiplication in spectral space
Plot the Results

close all;clear

Construct grid

Define the various grid parameters.

Nx = 256; % uonal resolution
Ny = 256; % meridional resolution
Lx=3e3;
Ly=3e3;
dx=Lx/Nx;
dy=Ly/Ny;
x=dx*(1:Nx)';
y=dy*(1:Ny)';
dx2o2 = dx^2/2;
dy2o2 = dy^2/2;
[xx,yy] = meshgrid(x,y);

FFT related material

For this problem we will be solving the PDE using spectral methods. We transform the problem using Fourier transforms so that the derivatives become multiplication.

Build the wavenumbers and create the variable diffusivity.

dk = 2*pi/Lx; % Nyquist wavenumbers
dl = 2*pi/Ly;

k=[0:Nx/2-1 Nx/2 -Nx/2+1:-1]'*dk;
l=[0:Ny/2-1 Ny/2 -Ny/2+1:-1]'*dl;
[kk,ll]=meshgrid(k,l);

l2 = l.^2; % 1D meridional wavenumber arrays for splitting up the 1D problems
il = 1i*l;

k2 = k.^2; % 1D uonal wavenumber arrays for differentiating within a sub problem
ik = 1i*k;

ll2 = ll.^2; % 2D meridional wavenumber arrays for differentiation purposes
ill = 1i*ll;

kk2 = kk.^2; % 2D uonal wavenumber arrays for general differentiation purposes
ikk = 1i*kk;

Diffusivity

The diffusivity is constant here. In another script we will explore what happens when it is non-constant.

kappa = 100;

Solve the problem via multiplication in spectral space

We solve for u by taking the Fourier transform of our RHS and multiplying it by 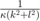$\frac{1}{\kappa (k^2+l^2)}$ . We then invert the transform to return to physical space.

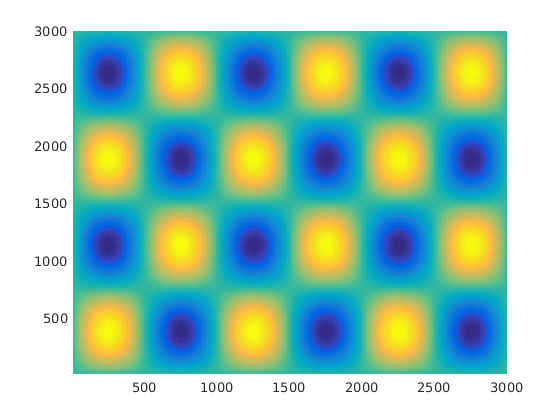
RHS = sin(6*pi*xx/Lx).*sin(4*pi*yy/Ly);
ftRHS = fft2(RHS);
multfac = 1./(kappa*(kk2+ll2));
ftu = multfac.*ftRHS;
ftu(1,1)=ftRHS(1,1);
u = real(ifft2(ftu));

Plot the Results