Reaction Diffusion model leading to pattern formtaion

This model is usually referred to as the Scott-Grey model in the literature. Here I use a Crank-Nicolson scheme for the diffusion and RK4 along with Strang Splitting for the reaction. The RK4 is homemade and is not the built in Matlab version. For more information look for Reaction-Diffusion models.

Contents

Parameters

Grid and constants.

N=256
z=linspace(-1,1,N+1);
z=z(1:end-1);
L=2.5;
[x,y]=meshgrid(L*z,L*z);
t=0;
f=0.038;
kpar=0.06;
ru=2e-5;
rv=1e-5;

N =

   256

RK4 functions.

f1=@(u,v) -u.*v.*v+f*(1-u);
f2=@(u,v) u.*v.*v-(f+kpar)*v;

Initial conditions.

r2=x.*x+y.*y;
u0=ones(size(x)); v0=zeros(size(x));
u0=u0-(0.5).*exp(-(r2.^8)/((0.25*L)^8))+0.02*(rand(size(r2))-0.5);
v0=v0+(0.254).*exp(-(r2.^8)/((0.25*L)^8))+0.02*(rand(size(r2))-0.5);
u=u0;
v=v0;

Spectral parameters.

dk=pi/L;
ksvec(1)=0;
for ii=2:(N/2)
    ksvec(ii)=ii-1;
    ksvec(N/2+ii)=-N/2 + ii -1;
end
ksvec=ksvec*dk;
[k2,l2]=meshgrid(ksvec.^2,ksvec.^2);
ksvec(N/2+1)=0;
[k,l]=meshgrid(ksvec,ksvec);
k2=k.*k; l2=l.*l;
lapu=-ru*(k2+l2);
lapv=-rv*(k2+l2);

Time and output parameters.

dt=0.2;
dto2=dt/2;
dt2=dt*dt;
numsteps=500;
numouts=5;

Plot ICs

figure(1)
clf
set(gcf,'DefaultLineLineWidth',3,'DefaultTextFontSize',12,...
    'DefaultTextFontWeight','bold','DefaultAxesFontSize',12,...
    'DefaultAxesFontWeight','bold');
subplot(2,1,1)
pcolor(x,y,u); shading interp
xlabel('x','fontweight','bold','fontsize',12);
ylabel('y','fontweight','bold','fontsize',12);
colorbar
mystr=['time = ' num2str(t)];
title(mystr);
subplot(2,1,2)
pcolor(x,y,v); shading interp
xlabel('x','fontweight','bold','fontsize',12);
ylabel('y','fontweight','bold','fontsize',12);
colorbar
drawnow

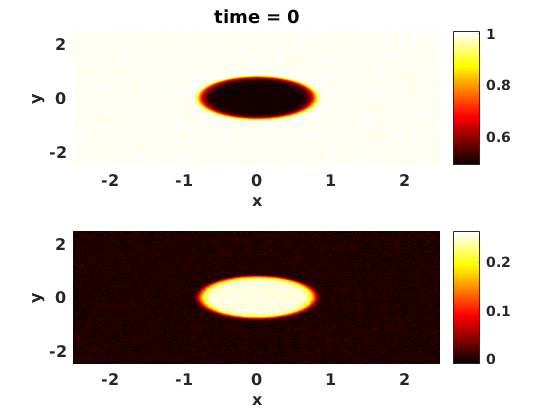
Set up Strang splitting.

myfactue=dt*lapu;
myfactve=dt*lapv;
myfactu=(1+dto2*lapu)./(1-dto2*lapu);
myfactv=(1+dto2*lapv)./(1-dto2*lapv);

Main Loop

for ii=1:numouts

    for jj=1:numsteps

        t=t+dt;

Strang split two steps at a time reversing order.

        u=ifft2(myfactu.*fft2(u));
        v=ifft2(myfactv.*fft2(v));

RK4.

        rkk1=f1(u,v);
        rkl1=f2(u,v);
        rkk2=f1(u+0.5*dt*rkk1,v+0.5*dt*rkl1);
        rkl2=f2(u+0.5*dt*rkk1,v+0.5*dt*rkl1);
        rkk3=f1(u+0.5*dt*rkk2,v+0.5*dt*rkl2);
        rkl3=f2(u+0.5*dt*rkk2,v+0.5*dt*rkl2);
        rkk4=f1(u+dt*rkk3,v+0.5*dt*rkl3);
        rkl4=f2(u+dt*rkk3,v+0.5*dt*rkl3);
        kforrk=(dt/6)*(rkk1+2*rkk2+2*rkk3+rkk4);
        lforrk=(dt/6)*(rkl1+2*rkl2+2*rkl3+rkl4);

First part.

        u=u+kforrk;
        v=v+lforrk;

Second step in reverse order now.

        t=t+dt;
        % RK4
        rkk1=f1(u,v);
        rkl1=f2(u,v);
        rkk2=f1(u+0.5*dt*rkk1,v+0.5*dt*rkl1);
        rkl2=f2(u+0.5*dt*rkk1,v+0.5*dt*rkl1);
        rkk3=f1(u+0.5*dt*rkk2,v+0.5*dt*rkl2);
        rkl3=f2(u+0.5*dt*rkk2,v+0.5*dt*rkl2);
        rkk4=f1(u+dt*rkk3,v+0.5*dt*rkl3);
        rkl4=f2(u+dt*rkk3,v+0.5*dt*rkl3);
        kforrk=(dt/6)*(rkk1+2*rkk2+2*rkk3+rkk4);
        lforrk=(dt/6)*(rkl1+2*rkl2+2*rkl3+rkl4);

Second part.

        u=u+kforrk;
        v=v+lforrk;

Diffusion.

        u=ifft2(myfactu.*fft2(u));
        v=ifft2(myfactv.*fft2(v));

    end

Plot

    figure(1)
    clf
    set(gcf,'DefaultLineLineWidth',3,'DefaultTextFontSize',12,...
        'DefaultTextFontWeight','bold','DefaultAxesFontSize',12,...
        'DefaultAxesFontWeight','bold');
    subplot(2,1,1)
    pcolor(x,y,u); shading interp
    xlabel('x','fontweight','bold','fontsize',12);
    ylabel('y','fontweight','bold','fontsize',12);
    colorbar
    mystr=['time = ' num2str(t)];
    title(mystr);
    subplot(2,1,2)
    pcolor(x,y,v); shading interp
    xlabel('x','fontweight','bold','fontsize',12);
    ylabel('y','fontweight','bold','fontsize',12);
    colorbar
    drawnow

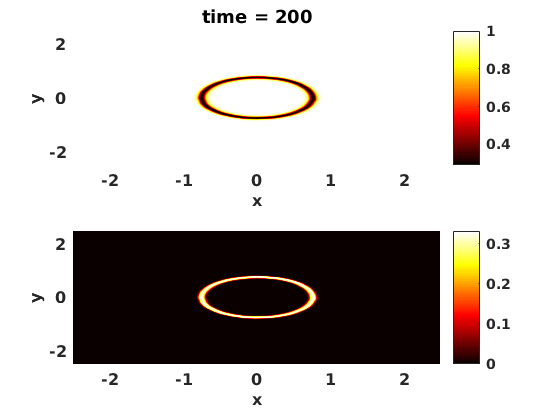
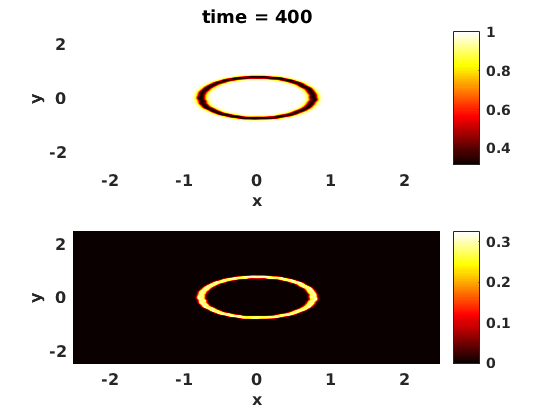
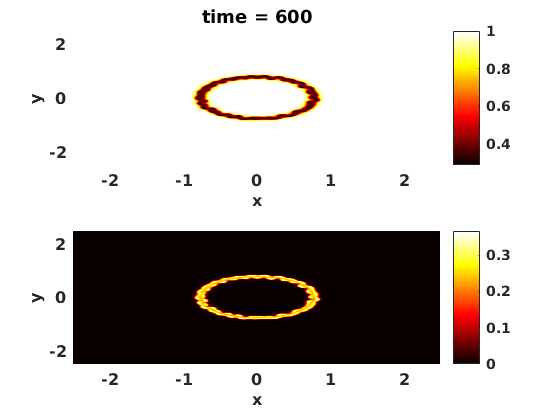
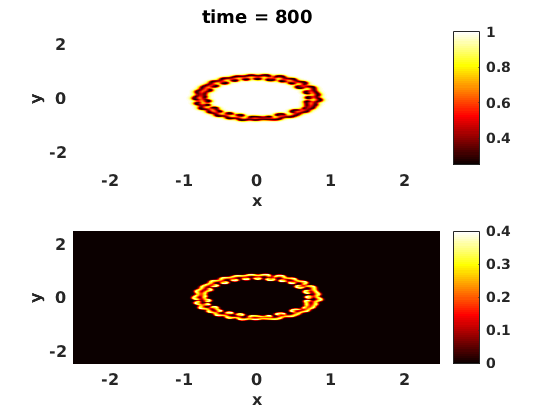
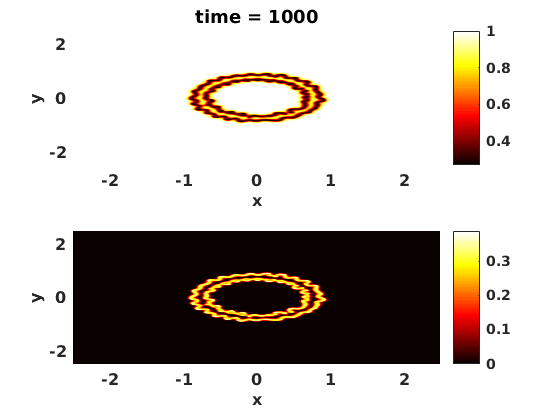
end

Published with MATLAB® R2016b