Internal Wave: Difference between revisions
| Line 25: | Line 25: | ||
== Waves in a channel == | == Waves in a channel == | ||
Consider two-dimensional flow between boundaries at <math> z=0</math> and <math> z=H</math>. The boundary conditions are <math> w=0</math> at <math> z=0,H</math>. Since <math> w= -\psi_x</math> by the definition of the stream-function, the boundary condition becomes <math> \psi_x = 0 \text{ at } z=0,H</math>. The equation of motion is | |||
:<math> | |||
\begin{equation} | |||
(\nabla^2 \psi)_{tt} = - N^2(z) \psi_{xx} | |||
\end{equation} </math> (1) | |||
Suppose a rightward propagating wave exists within this waveguide, | |||
:<math> \psi (x,z) = \phi(z) \exp{\left(i(k x - \omega t)\right)}</math>, | |||
then equation 1 becomes | |||
:<math> \phi_{zz} + \left( \frac{N^2 k^2}{\omega^2} - k^2 \right) \phi =0 </math>. (2) | |||
This is an eigenvalue problem which only has a simple solution when the stratification is linear (ie. <math> N^2(z) = N^2_0</math>). Equation (2) is then simplified to | |||
:<math> \phi_{zz} + m^2 \phi =0 </math>. | |||
The solutions that satisfies both boundary conditions is | |||
:<math> \phi(z) = \sin(mz) </math> | |||
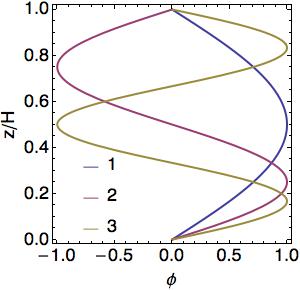
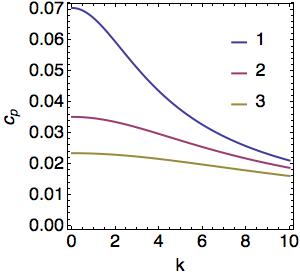
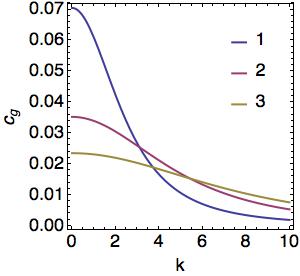
where <math> m = n \pi/H </math>. The vertical wavenumber, <math> m </math>, is now quantized and only wave of a particular vertical structure exist. The vertical structure function, <math> \phi </math>, phase speed, <math> c_p </math>, and group speed, <math> c_g </math> for the first three modes are plotted below | |||
[[File:VertStruct.jpg|bottom|<!-- Caption here -->]][[File:cp.jpg|bottom|<!-- Caption here -->]][[File:cg.jpg|bottom|<!-- Caption here -->]] | |||
Revision as of 15:55, 23 June 2015
Phase speed is perpendicular to group speed
Let us assume that a fluid is inviscid, linear, non-diffusive, Boussinesq, and consists of motion independent of the coordinate. The Navier-Stokes equations can therefore be written using the stream-function, , as
- .
Making the wave ansatz, , where and , the dispersion relation is
- Failed to parse (unknown function "\lvert"): {\displaystyle \omega = \frac{N k_x}{\lvert\vec{k}\rvert} }
where Failed to parse (unknown function "\lvert"): {\displaystyle \lvert\vec{k}\rvert = \sqrt{k_x^2 + k_z^2} } .
The phase speed is thus
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{c}_p = \frac{\omega}{\lvert\vec{k}\rvert} \hat{k} = \frac{\omega}{\lvert\vec{k}\rvert^2} \vec{k} = \frac{Nk_x}{\lvert\vec{k}\rvert^3}\vec{k} = \frac{Nk_x}{\lvert\vec{k}\rvert^3}\left( k_x, k_z \right)} .
The group speed is
- Failed to parse (unknown function "\lvert"): {\displaystyle \begin{align} \vec{c}_g &= \left( \frac{\partial\omega}{\partial k_x}, \frac{\partial\omega}{\partial k_z} \right)\\ &= \left( \frac{N}{\lvert\vec{k}\rvert} - \frac{N k_x^2}{\lvert\vec{k}\rvert^3}, - \frac{N k_x k_z}{\lvert\vec{k}\rvert^3} \right)\\ &= \left( \frac{N\left( k_x^2 + k_z^2\right)}{\lvert\vec{k}\rvert^3} - \frac{N k_x^2}{\lvert\vec{k}\rvert^3}, - \frac{N k_x k_z}{\lvert\vec{k}\rvert^3} \right)\\ &= \frac{N k_z}{\lvert\vec{k}\rvert^3}\left( k_z, - k_x \right)\\ \end{align}}
Therefore we find that the group velocity is perpendicular to the phase velocity!
- Failed to parse (unknown function "\lvert"): {\displaystyle \vec{c}_p \cdot \vec{c}_g = \frac{N^2 k_x k_z}{\lvert\vec{k}\rvert^6}\left( k_x, k_z \right) \cdot \left( k_z, -k_x \right) = 0}
This is completely counterintuitive from our experiences with surface waves, sound waves, and in fact most other waves, where the energy propagates in the same direction as the phase. The Saint Andrew's Cross experiment is the classic example demonstrating this. See Kundu for pictures and further elaboration.
Waves in a channel
Consider two-dimensional flow between boundaries at and . The boundary conditions are at . Since by the definition of the stream-function, the boundary condition becomes . The equation of motion is
- Failed to parse (unknown function "\begin{equation}"): {\displaystyle \begin{equation} (\nabla^2 \psi)_{tt} = - N^2(z) \psi_{xx} \end{equation} } (1)
Suppose a rightward propagating wave exists within this waveguide,
- ,
then equation 1 becomes
- . (2)
This is an eigenvalue problem which only has a simple solution when the stratification is linear (ie. ). Equation (2) is then simplified to
- .
The solutions that satisfies both boundary conditions is
where . The vertical wavenumber, , is now quantized and only wave of a particular vertical structure exist. The vertical structure function, , phase speed, , and group speed, for the first three modes are plotted below