Buoyancy Frequency: Difference between revisions
(Created page with "thumb|400px|right|Forces on a fluid parcel raised by <math> z </math> from it's rest state at <math> z_0 </math>. Here we demonstrate that a fluid parce...") |
mNo edit summary |
||
| Line 5: | Line 5: | ||
Consider a stable, motionless stratification, <math> \rho(z) </math>. A fluid parcel of volume <math> V </math> at depth <math> z_0 </math> will therefore have a mass of <math> \rho(z_0) V </math>. If that parcel of fluid is adiabatically lifted by a infinitesimal amount to a depth of <math> z_0 + z </math> then the fluid will experience a net downward force due to it being heavier than the surrounding fluid. | Consider a stable, motionless stratification, <math> \rho(z) </math>. A fluid parcel of volume <math> V </math> at depth <math> z_0 </math> will therefore have a mass of <math> \rho(z_0) V </math>. If that parcel of fluid is adiabatically lifted by a infinitesimal amount to a depth of <math> z_0 + z </math> then the fluid will experience a net downward force due to it being heavier than the surrounding fluid. | ||
By Archimedes' principle the buoyancy force is | By Archimedes' principle, the magnitude of the buoyancy force is equivalent to the weight of the fluid displaced by the fluid parcel. Therefore, the net force at a depth of <math> z_0 + z </math> is | ||
:<math> \begin{align} | :<math> \begin{align} | ||
F &= B-F_g\\ | F &= B-F_g\\ | ||
| Line 21: | Line 21: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
where <math> N^2(z) = -\frac{g}{\rho(z)} \frac{d\rho(z)}{dz} </math>. The negative sign | where <math> N^2(z) = -\frac{g}{\rho(z)} \frac{d\rho(z)}{dz} </math>. This is simply an undamped harmonic oscillator which vibrates at a frequency of <math> N </math>. The negative sign in <math> N </math> is necessary to ensure that the buoyancy frequency is real for stable stratification. | ||
Revision as of 22:55, 24 June 2015
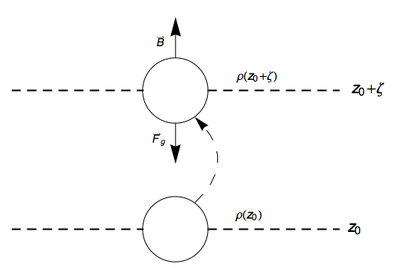
Here we demonstrate that a fluid parcel oscillates around it's rest state at the buoyancy frequency. Vallis (2006) has similar derivation to the following.
Consider a stable, motionless stratification, . A fluid parcel of volume at depth will therefore have a mass of . If that parcel of fluid is adiabatically lifted by a infinitesimal amount to a depth of then the fluid will experience a net downward force due to it being heavier than the surrounding fluid.
By Archimedes' principle, the magnitude of the buoyancy force is equivalent to the weight of the fluid displaced by the fluid parcel. Therefore, the net force at a depth of is
By Newton's second law,
where . This is simply an undamped harmonic oscillator which vibrates at a frequency of . The negative sign in is necessary to ensure that the buoyancy frequency is real for stable stratification.









