Wave Envelope: Difference between revisions
mNo edit summary |
|||
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:wave_envelope2.gif|thumb|left]] | [[File:wave_envelope2.gif|thumb|left|Stationary wave crests, propagating envelope.]] | ||
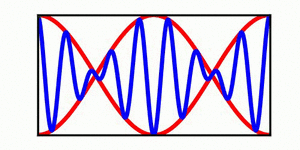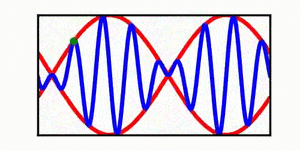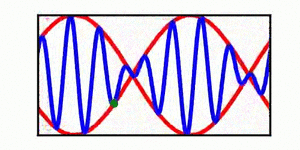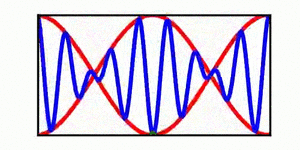
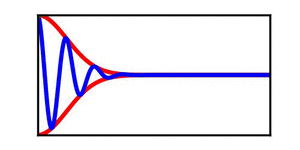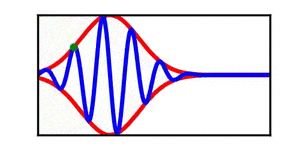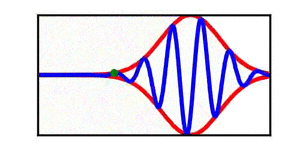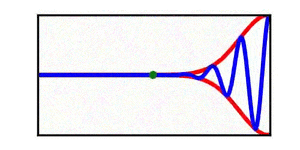
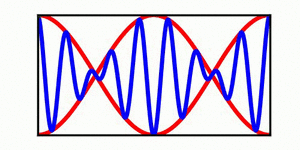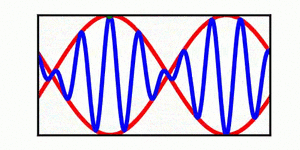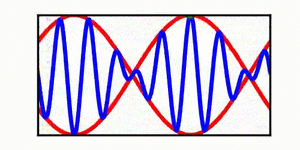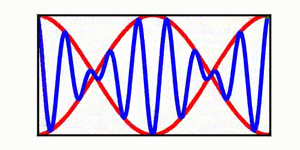
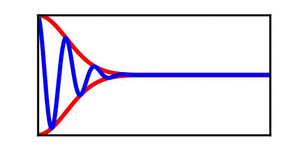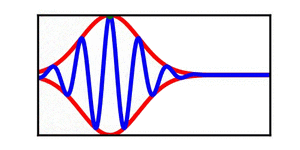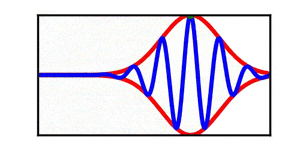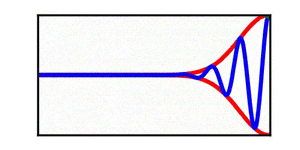
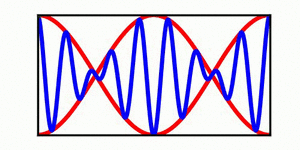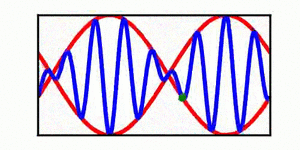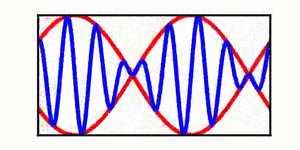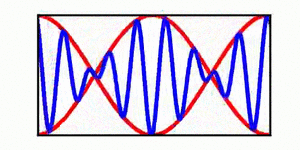
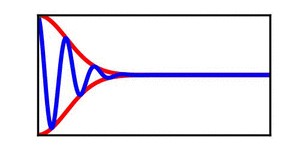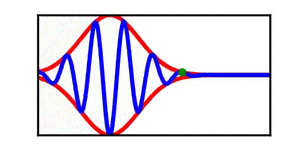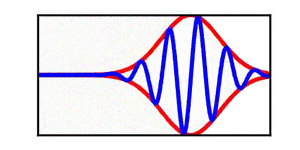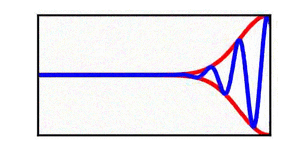
The image on the left provides a simple demonstration of the distinction between a wave envelope and individual wave crests. The red curves depict the wave envelope, while the blue curve indicates the individual wave crests (in the context of a surface wave, the blue curve can be viewed as the water surface). | |||
The blue curve is not propagating while the red curve is steadily propagating to the right, highlighting the distinction between the propagation of an individual wave crest. | The blue curve is not propagating while the red curve is steadily propagating to the right, highlighting the distinction between the propagation of an individual wave crest and the propagation of the overlaying envelope. | ||
A table is included | A brief discussion of envelope propagation is presented from the perspective of the [[KdV equation]], and table is included that demonstrates three different cases: envelope propagation faster than crest propagation, envelope propagation equal to crest propagation, and envelope propagation slower than crest propagation. Both a continuous wave train and a single wave packet are shown. | ||
=== Derivation using KdV === | === Derivation using KdV === | ||
The linear KdV equation is <math>\frac{\partial}{\partial t}\eta+c\frac{\partial}{\partial x}\eta + \beta\frac{\partial^3}{\partial x^3}\eta = 0</math>. Using the method of multiple scales, suppose that the wave envelope evolves on slower temporal and spatial scales than the wave crests. Denote the slower scales by <math>(\tau,\chi)=(\epsilon t,\epsilon x)</math>, for <math>0<\epsilon\ll1</math>, and separate using <math>\eta=A(\tau,\chi)\phi(x,t)</math>. After substituting into the KdV equation, the equation becomes: | The linear [[KdV equation]] is <math>\frac{\partial}{\partial t}\eta+c\frac{\partial}{\partial x}\eta + \beta\frac{\partial^3}{\partial x^3}\eta = 0</math>. Using the method of multiple scales, suppose that the wave envelope evolves on slower temporal and spatial scales than the wave crests. Denote the slower scales by <math>(\tau,\chi)=(\epsilon t,\epsilon x)</math>, for <math>0<\epsilon\ll1</math>, and separate using <math>\eta=A(\tau,\chi)\phi(x,t)</math>. After substituting into the KdV equation, the equation becomes: | ||
<math>A\phi_t + \epsilon A_{\tau}\phi + cA\phi_x + \epsilon cA_{\chi}\phi + \beta\left(A\phi_{xxx} + 3\epsilon A_{\chi}\phi_{xx} + 3\epsilon^2 A_{\chi\chi}\phi_{x} + \epsilon^3 A_{\chi\chi\chi}\phi \right) = 0</math>, where subscripts denote derivatives. | :<math>A\phi_t + \epsilon A_{\tau}\phi + cA\phi_x + \epsilon cA_{\chi}\phi + \beta\left(A\phi_{xxx} + 3\epsilon A_{\chi}\phi_{xx} + 3\epsilon^2 A_{\chi\chi}\phi_{x} + \epsilon^3 A_{\chi\chi\chi}\phi \right) = 0</math>, | ||
where subscripts denote partial derivatives. | |||
===== <math>\mathcal{O}(1)</math> Problem: ===== | ===== <math>\mathcal{O}(1)</math> Problem: ===== | ||
| Line 17: | Line 18: | ||
===== <math>\mathcal{O}(\epsilon)</math> Problem: ===== | ===== <math>\mathcal{O}(\epsilon)</math> Problem: ===== | ||
Again assuming that <math>\phi=e^{i\left(kx-\omega t \right)}</math>, the first order problem is found to be <math>\left[\frac{\partial}{\partial \tau}+ \left(c-3\beta k^2\right)\frac{\partial}{\partial \chi}\right] A=0 </math>. | Again assuming that <math>\phi=e^{i\left(kx-\omega t \right)}</math>, the first order problem is found to be <math>\left[\frac{\partial}{\partial \tau}+ \left(c-3\beta k^2\right)\frac{\partial}{\partial \chi}\right] A=0 </math>. Writing <math>c_g = c-3\beta k^2</math>, the problem reduces to <math>\left[\frac{\partial}{\partial \tau}+ c_g\frac{\partial}{\partial \chi}\right] A=0</math>, and so <math>A(\tau,\chi)=A(\chi-c_g\tau)</math>, showing that the propagation speed of the wave envelope is given by <math>c_g</math>. In particular, <math>c_g=\frac{\partial}{\partial k}\omega</math>. | ||
== More Examples == | == More Examples == | ||
In each animation, the red curves denote the envelope, the blue curves denote the individual waves, and the green dots track a single wave crest for illustrative purposes. | |||
{| class="wikitable" | {| class="wikitable" | ||
Latest revision as of 14:14, 24 July 2020
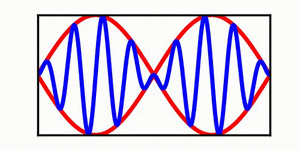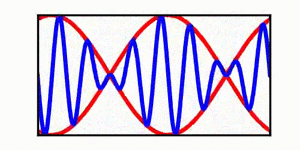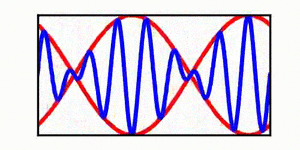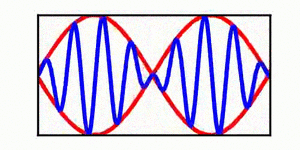
The image on the left provides a simple demonstration of the distinction between a wave envelope and individual wave crests. The red curves depict the wave envelope, while the blue curve indicates the individual wave crests (in the context of a surface wave, the blue curve can be viewed as the water surface). The blue curve is not propagating while the red curve is steadily propagating to the right, highlighting the distinction between the propagation of an individual wave crest and the propagation of the overlaying envelope.
A brief discussion of envelope propagation is presented from the perspective of the KdV equation, and table is included that demonstrates three different cases: envelope propagation faster than crest propagation, envelope propagation equal to crest propagation, and envelope propagation slower than crest propagation. Both a continuous wave train and a single wave packet are shown.
Derivation using KdV
The linear KdV equation is . Using the method of multiple scales, suppose that the wave envelope evolves on slower temporal and spatial scales than the wave crests. Denote the slower scales by , for , and separate using . After substituting into the KdV equation, the equation becomes:
- ,
where subscripts denote partial derivatives.
Problem:
Assuming that , the first order problem is found to be . If a plane-wave solution of is taken, then the problem reduces to . This gives the dispersion relation for the linear problem.
Problem:
Again assuming that , the first order problem is found to be . Writing , the problem reduces to , and so , showing that the propagation speed of the wave envelope is given by . In particular, .
More Examples
In each animation, the red curves denote the envelope, the blue curves denote the individual waves, and the green dots track a single wave crest for illustrative purposes.







![{\displaystyle \left[{\frac {\partial }{\partial t}}+c{\frac {\partial }{\partial x}}+\beta {\frac {\partial ^{3}}{\partial x^{3}}}\right]\phi =0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b892792ea15656ff512d07c737dbe4af5494fd7b)



![{\displaystyle \left[{\frac {\partial }{\partial \tau }}+\left(c-3\beta k^{2}\right){\frac {\partial }{\partial \chi }}\right]A=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/248727a65df7455190008d053c6893cc488df328)

![{\displaystyle \left[{\frac {\partial }{\partial \tau }}+c_{g}{\frac {\partial }{\partial \chi }}\right]A=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/677fcf5109d97dd696c7b13a2d2341d6bb09b27a)