Internal Wave: Difference between revisions
m (Fixed the parse errors.) |
|||
| (One intermediate revision by one other user not shown) | |||
| Line 4: | Line 4: | ||
:<math> (\nabla^2 \psi)_{tt} = - N^2(z) \psi_{xx} </math>. | :<math> (\nabla^2 \psi)_{tt} = - N^2(z) \psi_{xx} </math>. | ||
Making the wave ansatz, <math> \psi = \exp{\left(i(\vec{k}\cdot\vec{x} - \omega t)\right)} </math>, where <math> \vec{k}=(k_x,k_z)</math> and <math> \vec{x}=(x,z)</math>, the dispersion relation is | Making the wave ansatz, <math> \psi = \exp{\left(i(\vec{k}\cdot\vec{x} - \omega t)\right)} </math>, where <math> \vec{k}=(k_x,k_z)</math> and <math> \vec{x}=(x,z)</math>, the dispersion relation is | ||
:<math> \omega = \frac{N k_x}{\ | :<math> \omega = \frac{N k_x}{\left|\vec{k}\right|} </math> | ||
where <math> \ | where <math> \left|\vec{k}\right| = \sqrt{k_x^2 + k_z^2} </math>. | ||
The phase speed is thus | The phase speed is thus | ||
:<math> \vec{c}_p = \frac{\omega}{\ | :<math> \vec{c}_p = \frac{\omega}{\left|\vec{k}\right|} \hat{k} = \frac{\omega}{\left|\vec{k}\right|^2} \vec{k} = \frac{Nk_x}{\left|\vec{k}\right|^3}\vec{k} = \frac{Nk_x}{\left|\vec{k}\right|^3}\left( k_x, k_z \right)</math>. | ||
The group speed is | The group speed is | ||
:<math>\begin{align} | :<math>\begin{align} | ||
\vec{c}_g &= \left( \frac{\partial\omega}{\partial k_x}, \frac{\partial\omega}{\partial k_z} \right)\\ | \vec{c}_g &= \left( \frac{\partial\omega}{\partial k_x}, \frac{\partial\omega}{\partial k_z} \right)\\ | ||
&= \left( \frac{N}{\ | &= \left( \frac{N}{\left|\vec{k}\right|} - \frac{N k_x^2}{\left|\vec{k}\right|^3}, - \frac{N k_x k_z}{\left|\vec{k}\right|^3} \right)\\ | ||
&= \left( \frac{N\left( k_x^2 + k_z^2\right)}{\ | &= \left( \frac{N\left( k_x^2 + k_z^2\right)}{\left|\vec{k}\right|^3} - \frac{N k_x^2}{\left|\vec{k}\right|^3}, - \frac{N k_x k_z}{\left|\vec{k}\right|^3} \right)\\ | ||
&= \frac{N k_z}{\ | &= \frac{N k_z}{\left|\vec{k}\right|^3}\left( k_z, - k_x \right)\\ | ||
\end{align}</math> | \end{align}</math> | ||
Therefore we find that the group velocity is perpendicular to the phase velocity! | Therefore we find that the group velocity is perpendicular to the phase velocity! | ||
:<math> \vec{c}_p \cdot \vec{c}_g = \frac{N^2 k_x k_z}{\ | :<math> \vec{c}_p \cdot \vec{c}_g = \frac{N^2 k_x k_z}{\left|\vec{k}\right|^6}\left( k_x, k_z \right) \cdot \left( k_z, -k_x \right) = 0</math> | ||
This is completely counterintuitive from our experiences with surface waves, sound waves, and in fact most other waves, where the energy propagates in the same direction as the phase. The Saint Andrew's Cross experiment is the classic example demonstrating this. See Kundu for pictures and further elaboration. | This is completely counterintuitive from our experiences with surface waves, sound waves, and in fact most other waves, where the energy propagates in the same direction as the phase. The Saint Andrew's Cross experiment is the classic example demonstrating this. See Kundu for pictures and further elaboration. | ||
== Waves in a channel == | == Waves in a channel == | ||
Consider two-dimensional flow between boundaries at <math> z=0</math> and <math> z=H</math>. The boundary conditions are <math> w=0</math> at <math> z=0,H</math>. Since <math> w= -\psi_x</math> by the definition of the stream-function, the boundary condition becomes <math> \psi_x = 0 \text{ at } z=0,H</math>. The equation of motion is | |||
:<math> (\nabla^2 \psi)_{tt} = - N^2(z) \psi_{xx} </math> (1) | |||
Suppose a rightward propagating wave exists within this waveguide, | |||
:<math> \psi (x,z) = \phi(z) \exp{\left(i(k x - \omega t)\right)}</math>, | |||
then equation 1 becomes | |||
:<math> \phi_{zz} + \left( \frac{N^2 k^2}{\omega^2} - k^2 \right) \phi =0 </math>. (2) | |||
This is an eigenvalue problem which only has a simple solution when the stratification is linear (ie. <math> N^2(z) = N^2_0</math>). Equation (2) is then simplified to | |||
:<math> \phi_{zz} + m^2 \phi =0 </math>. | |||
The solutions that satisfies both boundary conditions is | |||
:<math> \phi(z) = \sin(mz) </math> | |||
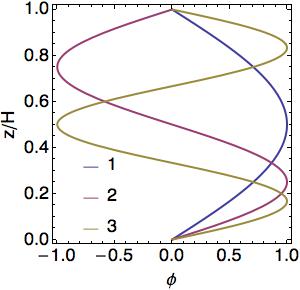
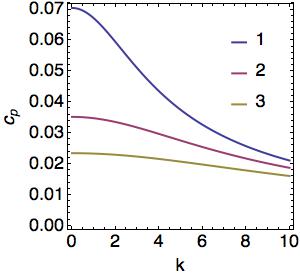
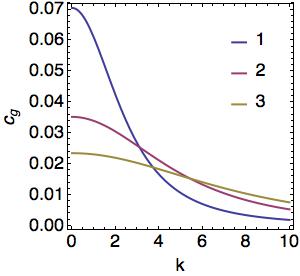
where <math> m = n \pi/H </math>. The vertical wavenumber, <math> m </math>, is now quantized and only wave of a particular vertical structure exist. The vertical structure function, <math> \phi </math>, phase speed, <math> c_p </math>, and group speed, <math> c_g </math> for the first three modes are plotted below | |||
[[File:VertStruct.jpg|bottom|<!-- Caption here -->]][[File:cp.jpg|bottom|<!-- Caption here -->]][[File:cg.jpg|bottom|<!-- Caption here -->]] | |||
Latest revision as of 17:51, 3 March 2017
Phase speed is perpendicular to group speed
Let us assume that a fluid is inviscid, linear, non-diffusive, Boussinesq, and consists of motion independent of the coordinate. The Navier-Stokes equations can therefore be written using the stream-function, , as
- .
Making the wave ansatz, , where and , the dispersion relation is
where .
The phase speed is thus
- .
The group speed is
Therefore we find that the group velocity is perpendicular to the phase velocity!
This is completely counterintuitive from our experiences with surface waves, sound waves, and in fact most other waves, where the energy propagates in the same direction as the phase. The Saint Andrew's Cross experiment is the classic example demonstrating this. See Kundu for pictures and further elaboration.
Waves in a channel
Consider two-dimensional flow between boundaries at and . The boundary conditions are at . Since by the definition of the stream-function, the boundary condition becomes . The equation of motion is
- (1)
Suppose a rightward propagating wave exists within this waveguide,
- ,
then equation 1 becomes
- . (2)
This is an eigenvalue problem which only has a simple solution when the stratification is linear (ie. ). Equation (2) is then simplified to
- .
The solutions that satisfies both boundary conditions is
where . The vertical wavenumber, , is now quantized and only wave of a particular vertical structure exist. The vertical structure function, , phase speed, , and group speed, for the first three modes are plotted below