a Direct Formulation For Sparse PCA Using Semidefinite Programming
Introduction
Principle Component Analysis is a popular technique of dimensionality reduction. It has been effectively and widely used in the areas of data analysis, data compression, and data visualization, and it has also been found to be applicable to problems throughout science and engineering. For a given set of data points, PCA finds a linear combination of a subset of the variables that are uncorrelated with each other; these variables are called principal components, and they correspond to the directions of maximal variance in the data. The Principal components can be representative of the whole data with minimum information loss. PCA commonly uses singular value decomposition (SVD) to obtain the principal components of a data set. Not only is PCA useful as a tool for dimensionality reduction, it also makes subsequent interpretations and analysis of the resulting data much simpler to do, because the variables (principal components) in the resulting data are all uncorrelated with each other. Though PCA has been found to be a very useful technique in many areas, it has a major disadvantage in that each principal component is usually a linear combination of every variable in the data, i.e. usually every weight (loading) in each principal component's linear combination of variables is non-zero. This disadvantage makes PCA difficult to work with in certain areas. In one type of such areas, each variable (axis) has a physical meaning. One such area is gene analysis, where each variable (axis) might represent a specific gene. When PCA is applied to these areas, the interpretation of the principal components can be made to be much easier to understand if each principal component's linear combination of variables contains only a few non-zero weights (loading or coordinates). Furthermore, this disadvantage of PCA makes it inefficient in the area of financial asset trading in that, for financial asset trading strategies that are based on principal component techniques, fewer non-zero loadings would directly lead to fewer transaction costs. This disadvantage of PCA is what led to the formulation of sparse PCA, whose aim is to find the sparse principal components. Sparse principal components, like principal components, are vectors that span a lower-dimensional space that explain most of variance in the original data. However, in order to find the sparse principal components using sparse PCA, it is necessary to make some sacrifices such as:
- There is a reduction in the explained variance in the original data captured by the sparse principal components as compared to PCA.
- There is a reduction in the orthogonality (independence or uncorrelation) between the resulting variables (sparse principal components) as compared to PCA.
In sparse PCA, the embedded variables are linear combination of the input variables subject to the constraint that the number of non-zero elements in this combination is limited. Sparse PCA decomposition interpretation is facilitated since the number of non-zero elements are not all variables if the coordinate axes have a physical meaning. It is also helpful in expressing a space of a set of low-dimensional vectors with minimum loss of information.
Semidefinite programs<ref name="VB1996">L. Vandenberghe and S. Boyd, Semidefinite programming, SIAM Review, 38 (1996), pp. 49–
95.</ref> are convex optimization. They optimize a linear function by constraining it to an affine combination of symmetric matrices which are positive semidefinite. Semidefinite programs can be solved in polynomial time by interior-point solvers like SEDUMI or SDPT3. Unfortunately, they are not viable and practical for high dimensional data sets.
This paper suggests a direct approach to convex formulation of the sparse PCA via semidefinite programming. Since interior-point solvers cannot handle large data sets, Nesterov’s smoothing technique <ref name='N2004'>Smoothing technique and its application in semidefinite optimization, CORE Discussion Paper No. 2004/73, (2004).</ref> is used efficiently to help solving large dimensional problems. First order methods require less memory which is an important issue in interior-point solvers. On the other hand, their convergence is slower but it is not a major concern in certain cases. So, the optimal first-order minimization algorithm is going to be applied for solving the optimization problem.
The content of the paper could be summarized as below:
First, they tried to maximize the variance projection by limiting the number of non-zero elements via semidefinite programming. Then, they show how this method could be used for decomposing a matrix in to limited number of variables. As their problem size is large and can not be solved by common techniques which are used for solving the convex optimization problems, they show that Nesterov's smoothing method <ref name="N2004"/> helps achieving the solution.
Semidefinite relaxation
Sparse variance maximization
Let [math]\displaystyle{ \textbf{S}^n }[/math] be the set of symmetric matrices of size [math]\displaystyle{ \, n }[/math]. Let [math]\displaystyle{ A \in \textbf{S}^n }[/math], then WLOG, assume [math]\displaystyle{ \,A }[/math] is a covariance matrix. We are going to maximize the variance of the vector [math]\displaystyle{ x \in \textbf{R}^n }[/math] while constraining it to be sparse. Let [math]\displaystyle{ \, k }[/math] be an integer where [math]\displaystyle{ 1 \leq k \leq n }[/math] then the problem can be written formally as
[math]\displaystyle{ \textrm{ subject } \; \textrm{ to }\;\|x\|_2=1 }[/math]
This problem is hard, because of the cardinality constraint. Therefore, we should look for a convex relaxation.
Semidefinite relaxation
Rewriting the above formulas, we get:
[math]\displaystyle{ \textrm{ subject } \; \textrm{ to } \; \textbf{Tr}({X})=1 }[/math],
[math]\displaystyle{ \textbf{Card}({X})\leq k^2, }[/math]
[math]\displaystyle{ {X}\succeq 0, }[/math]
where [math]\displaystyle{ X \in \textbf{S}^n }[/math].
[math]\displaystyle{ X }[/math] is a solution to the above problem and the last two constraints imply that [math]\displaystyle{ X=xx^T }[/math]. Finally, by replacing the only non-convex constraint, [math]\displaystyle{ \textbf{Card}({X})\leq k^2 }[/math], to a weaker but convex one, we come to a semidefinite relaxation of the sparse PCA for square matrices.
maximize [math]\displaystyle{ \textbf{Tr}({A}{X}) }[/math]
subject to [math]\displaystyle{ \textbf{Tr}({X})=1 }[/math],
[math]\displaystyle{ \textbf{1}^{T}|{X}|\textbf{1}\leq k }[/math],
[math]\displaystyle{ {X}\geq 0 }[/math]
The above formula can be extended to case of non-square matrices. The sparse variance maximization problem can be written as followed:
maximize [math]\displaystyle{ u^{T}{A}v }[/math]
subject to [math]\displaystyle{ \|u\|_{2}=\|v\|_{2}=1 }[/math],
[math]\displaystyle{ \textbf{Card}(u)\leq k_{1},\textbf{Card}(v)\leq k_{2} }[/math],
Changing the constraint to the convex one, in the same way as we did for square cases, the following formulas will be achieved:
maximize [math]\displaystyle{ \textbf{Tr}({A}^{T}{X}^{12}) }[/math]
subject to [math]\displaystyle{ {X}\leq0, \textbf{Tr}({X}^{ii})=1 }[/math],
[math]\displaystyle{ \textbf{1}^{T}|{X}^{ii}|\textbf{1}\leq k_{i}, i=1,2 }[/math],
[math]\displaystyle{ \textbf{1}^{T}|{X}^{12}|\textbf{1}\leq \sqrt{k_1k_2} }[/math]
Sparse decomposition
Here, we are going to apply our formula for obtaining component of sparse PCA. Given matrix [math]\displaystyle{ A_1 \in \textbf{S}^n }[/math], our goal is to decompose it to components which are sparse.
maximize [math]\displaystyle{ \textbf{Tr}({A}_1{X}) }[/math]
subject to [math]\displaystyle{ \textbf{Tr}({X})=1 }[/math],
[math]\displaystyle{ \textbf{1}^{T}|{X}|\textbf{1}\leq k }[/math],
[math]\displaystyle{ {X}\geq 0 }[/math]
[math]\displaystyle{ X_1 }[/math] will be truncated as below and the only first eigenvector [math]\displaystyle{ x_1 }[/math] which corresponds to the largest eigenvalue will be kept.
[math]\displaystyle{ {A}_2={A}_1-(x_{1}^{T}{A}_1x_1)x_1x_1^T }[/math]
And repeat the algorithm to obtain more components. But the issue is when should we stop?
When the values in [math]\displaystyle{ A_i }[/math] are all less than a constant [math]\displaystyle{ \rho }[/math], we must stop. [math]\displaystyle{ \rho }[/math] acn be interpreted as noise level and when the matrix can not be distinguished from noise, we will terminate the iterations.
Algorithm
SEDUMI and SDPT3 are used for small size problems of semidefinite programming. But for larger problems, those methods are not practical because it is impossible to store any second order information of size [math]\displaystyle{ n }[/math], which is necessary in interior-pointSDP solvers. So, the first order methods would be popular. These methods need a smaller size memory cost per iteration but their convergence time is [math]\displaystyle{ O(1/\epsilon) }[/math] while interior-point method will converge in [math]\displaystyle{ O(log(1/\epsilon)) }[/math]. Fortunately, convergence time is not important in our application.
Smoothing technique
There are two important issue for large scale semidefinite programming. One is the memory difficulty and for solving this problem we 'll look forward first-order techniques. The other one is smoothness. As [math]\displaystyle{ X\geq 0 }[/math] is not smooth, as a result the number of iteration using first-order methods to an accuracy of [math]\displaystyle{ \epsilon }[/math] is given by [math]\displaystyle{ O(1/\epsilon ^2) }[/math]. this bound is tight without any further information about the structure. since we have available information this complexity will be brought to [math]\displaystyle{ O(1/\epsilon) }[/math].
As we have in the previous sections the function is:
maximize [math]\displaystyle{ x^{T}{A}x }[/math]
subject to [math]\displaystyle{ \|x\|_2=1 }[/math]
[math]\displaystyle{ \textbf{Card}(x)\leq k }[/math]
We can replace the constraint and penalize the cardinality and solve:
maximize [math]\displaystyle{ x^{T}{A}x-\textbf{Card}^{2}(x) \rho }[/math]
subject to [math]\displaystyle{ \|x\|_2=1 }[/math]
which is equal to:
maximize [math]\displaystyle{ \textbf{Tr}({A}{X})-\textbf{Card}({X})\rho }[/math]
subject to [math]\displaystyle{ \textbf{Tr}({X})=1 }[/math]
[math]\displaystyle{ {X}\geq 0 }[/math]
[math]\displaystyle{ \textbf{Rank}({X})=1 }[/math]
By changing the formula to a semidefinite programming problem we 'll have:
maximize [math]\displaystyle{ \textbf{Tr}({A}{X})-\rho\textbf{1}^{T}|{X}|\textbf{1} }[/math]
subject to [math]\displaystyle{ \textbf{Tr}({X})=1 }[/math],
[math]\displaystyle{ {X}\geq 0 }[/math]
we can rewrite this problem as:
[math]\displaystyle{ max _{{X}\geq 0, \textbf{Tr}({X})=1} min _{|{U}_{ij}\leq \rho|}\textbf{Tr}({X}({A}+{U})) }[/math]
which can be written as a saddle-function format:
[math]\displaystyle{ f(x)=\hat{f}(x)+max_{u}\{\lt \textbf{T}x,u\gt -\hat{\phi}(u) : u \in \textbf{Q}_2\} }[/math]
Where [math]\displaystyle{ f }[/math] is defined over [math]\displaystyle{ Q_1 }[/math] which is a convex and differentiable and [math]\displaystyle{ \hat{\phi} (U) }[/math] is a continuous convex function over [math]\displaystyle{ Q_2 }[/math]. When a function can be written as a saddle-function format, using smoothing techniques will help us to reduce the complexity of solving
[math]\displaystyle{ min _{x\in \textbf{Q}_1}f(x) }[/math]
from [math]\displaystyle{ O(1/\epsilon ^2) }[/math] to [math]\displaystyle{ O(1/\epsilon) }[/math].
These process can be done in two steps.
1-Regularization :Regularization adds a strongly convex penalty to the saddle function and then estimate its [math]\displaystyle{ \epsilon- }[/math]approximation of [math]\displaystyle{ f }[/math] with Lipschitz continuous gradient
2-Optimal first-order minimization:It applies the optimal first-order scheme for Lipschitz continuous function.
Application of sparse PCA
We consider the problem which is discussed in previous sections as below:
maximize [math]\displaystyle{ \textbf{Tr}({A}{X})-\textbf{1}^{T}|{X}|\textbf{1} }[/math]
subject to [math]\displaystyle{ \textbf{Tr}({X})=1 }[/math],
[math]\displaystyle{ {X}\geq 0 }[/math]
[math]\displaystyle{ \rho }[/math] is assumed to be one without loss of generality. Duality allows us to rewrite this in saddle-function format:
[math]\displaystyle{ min_{{U}\in{Q}_1}f({U}) }[/math]
where
[math]\displaystyle{ {Q}_1=\{{U}\in \textbf{S}^{n}:|{U}_{ij}|\leq 1,i,j=1,...,n\},{Q}_2=\{{X}\in\textbf{S}^n:\textbf{Tr} X=1,X\geq0\} }[/math]
and
[math]\displaystyle{ f(U):=max_{X \in Q_2}\lt TU,X\gt -\hat{\phi}(X) }[/math] with [math]\displaystyle{ T=I_{n^2}, \hat{\phi}(X)=-\textbf{Tr}(AX) }[/math]
The same as what Nesterov <ref name='N2004'/> applied in his paper in 2003, we define Frobenius norm and prox-functions as following:
[math]\displaystyle{ d_1(U)=\frac{1}{2}U^T U }[/math]
where [math]\displaystyle{ U \in Q_1 }[/math] and ,[math]\displaystyle{ U_0 }[/math] is the center of it and satisfies [math]\displaystyle{ d_1(U_0)=0 }[/math].
[math]\displaystyle{ U_0:=arg min_{U\in Q_{1}}d_1(U) }[/math].
In addition we have:
[math]\displaystyle{ D_1:=max_{U \in Q_1}d_1(U)=n^2/2 }[/math]
The following could be concluded for [math]\displaystyle{ Q_2 }[/math] as well:
[math]\displaystyle{ d_2(X)=\textbf{Tr}(XlogX)+log(n) }[/math]
[math]\displaystyle{ max_{X\in Q_2}d_2(X)\leq log n:=D_2 }[/math]
Next we estimate the norm [math]\displaystyle{ (1,2) }[/math] norm of operator [math]\displaystyle{ T }[/math], which is defined as:
[math]\displaystyle{ \| T\| _{1,2}:= max_{X,U}\lt TX,U\gt :\| X\| _{F}=1,\|U\|^*_2=1 }[/math]
[math]\displaystyle{ =max_X\|X\|_2:\|X\|_F\leq 1 }[/math]
[math]\displaystyle{ =1 }[/math]
So the parameter are set to the following values:
[math]\displaystyle{ D_1=n^2/2,\sigma _1=1,D_2=log(n),\sigma_2=1/2,\|T\|_{1,2}=1 }[/math]
Regularization
As we discussed earlier and in Nesterov <ref name="N2004"/> paper, by regularization parameter which is [math]\displaystyle{ \mu }[/math]
[math]\displaystyle{ \mu:=\frac{\epsilon}{2D_2} }[/math]
the non-smooth function [math]\displaystyle{ f(X) }[/math] of the original problem is changed with
[math]\displaystyle{ min_{U \in Q_1}f_{\mu}(U) }[/math]
where it is penalized function with prox-function [math]\displaystyle{ d_2 }[/math]:
[math]\displaystyle{ f_{\mu}(U):=max_{X \in Q_2}\lt TU,X\gt -\hat{\phi}(X)-\mu d_2(X) }[/math]
Now the [math]\displaystyle{ f_\mu }[/math] is a smooth approximation of [math]\displaystyle{ f }[/math] on [math]\displaystyle{ Q_2 }[/math] and also [math]\displaystyle{ f_\mu }[/math] is Lipschitz-continuous function with constant [math]\displaystyle{ L }[/math] which is:
[math]\displaystyle{ L:=\frac{D_2\|T\|_{1,2}^2}{\epsilon 2\sigma_2} }[/math]
In our problem, the function can be computed explicitly as:
[math]\displaystyle{ f_\mu(U)=\mu log(\textbf{Tr}exp((A+U)/\mu))-\mu log n }[/math]
First order minimization
The input of this section is the smooth convex function [math]\displaystyle{ f_\mu }[/math] which is defined and computed in the previous section.Now the algorithm proceeds as follows <ref name="book2003">Introductory Lectures on Convex Optimization, Springer, 2003.</ref>:
Repeat
- Compute [math]\displaystyle{ f_\mu(U_k) }[/math] and [math]\displaystyle{ \nabla f_\mu (U_k) }[/math]
- Find [math]\displaystyle{ Y_k=argmin_{Y\in Q_1}\lt \nabla f_\mu (U), Y\gt +\frac{1}{2}L\|U-Y\|_F^2 }[/math]
- Find [math]\displaystyle{ Z_k=argmin_X\{\frac{L}{\sigma _1}d_1 (U)+\sum_{i=0}^{k}\frac{i+1}{2}\lt \nabla f_\mu (U_i), U-U_i\gt : U \in Q_1\} }[/math]
- set [math]\displaystyle{ U_k= \frac{2}{k+3}Z_k+\frac{k+1}{k+3}Y_k }[/math]
Until [math]\displaystyle{ gap \leq \epsilon }[/math]
The first step calculate the smooth function and its gradient. The second step estimate the gradient mapping and in the third and forth steps the sequence of [math]\displaystyle{ f_\mu }[/math] whose minimum could be calculated explicitly will be updated. for more detail about these steps you can see <ref name='N1983'>Y. Nesterov, A method of solving a convex programming problem with convergence rate O(1/k2), Soviet Mathematics Doklady, 27 (1983), pp. 372–376</ref> and <ref name="N2003">Smoothing technique and its application in semidefinite optimization, CORE Discussion Paper No. 2004/73, (2004).</ref>.
An Experiment Comparing SPCA To PCA
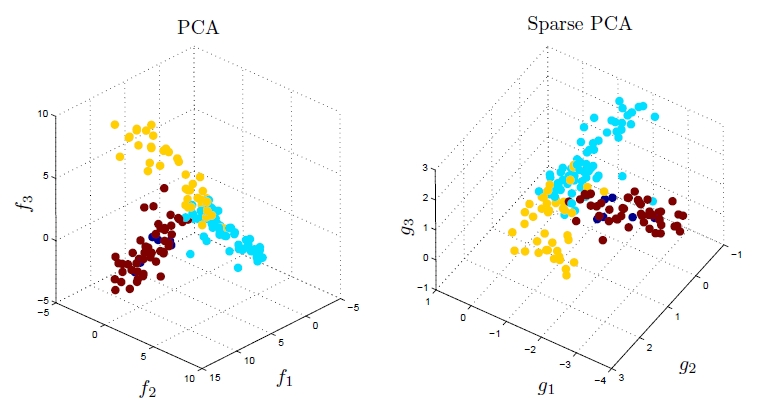
As mentioned in the Introduction section, in the area of gene expression analysis, PCA does not appear to be very suitable because the weights (loadings) of the resulting principal components are dense, i.e. the vast majority of them are non-zero; this makes subsequent interpretation and analysis difficult, because one could hardly tell which genes are highly expressed and which are not. The authors of the original paper of sparse PCA (a link to which can be found here) conducted an experiment by comparing what they referred to as DSPCA (Direct Approach Sparse PCA) to PCA on gene expression data. Using both PCA and DSPCA, the authors reduced the dimensionality of the gene data to only three, and then they looked for distinct clusters in the resulting low-dimensionality data using a simple assignment of color coding to each labeled data point that represents its known class. As expected by the authors, the sparsity in the weights (loadings) of the sparse principal components found by DSPCA made interpretation of the lower-dimensional gene expression data much easier as compared to PCA. According to the authors, there were only 14 nonzero gene coefficients (weights or loadings of the sparse principal components) in the case where DSPCA was used, whereas the nonzero gene coefficients (weights or loadings of the principal components) in the case where PCA was used were dense and they numbered about 1,500.
Fig. 1 (taken from [6]) illustrates the results of this experiment.
Code
The numerical codes used in this paper are provided by A. d'Aspremont and can be found here.
References
<references />
6. Alexandre d’Aspremont, Laurent El Ghaoui, Michael I. Jordan, and Gert R. G. Lanckriet. A Direct Formulation For Sparse PCA Using Semidefinite Programming.