Deep Residual Learning for Image Recognition Summary

ImageNet Classification

The authors used the ImageNet classification dataset to measure accuracy on different models.

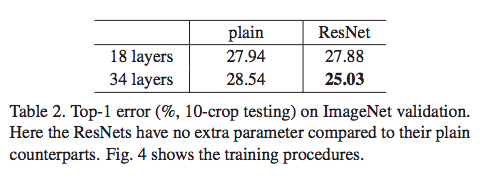
They first compare plain nets to ResNets with 18 and 34 layers. The ResNets are identical save for the identity shortcuts joining each two layer stack (A). Note that in order to change dimensions, they use zero-padded shortcuts. The 34-layer plain net gives a higher training error than its 18-layer counterpart (the degradation problem; shown above in Table 2). This discrepancy is attributed to exponentially low convergence rates since BN is used which should prevent vanishing gradients. The 34 layer ResNet performs better on the train set than its 18-layer counterpart and performs better than the 34-layer plain net. So, the degradation problem is addressed.

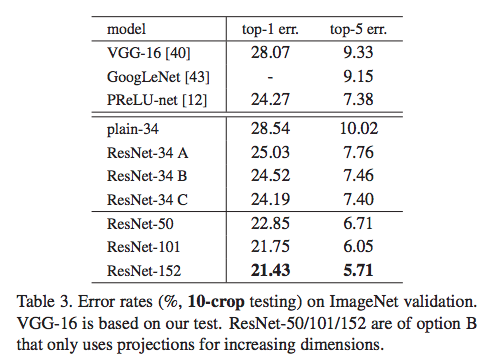
The authors also consider the use of projection shortcuts where: (B) projection shortcuts are only used for changing dimensions and (C) all shortcuts are projections. The use of projections improves accuracy since additional residual learning is added. However, this improvement is not practical when compared to the added time complexity.

To train deeper nets, they used the identity shortcut and modified the structure to a bottleneck design. The bottleneck design uses a stack of three layers instead of two in each residual function (shortcut) and cuts the time complexity in half. When applied to 50-layer, 101-layer, and 152-layer ResNets, accuracy improves (Table 3). The 152-layer model won 1st place in ILSVRC 2015.

CIFAR-10 and Analysis

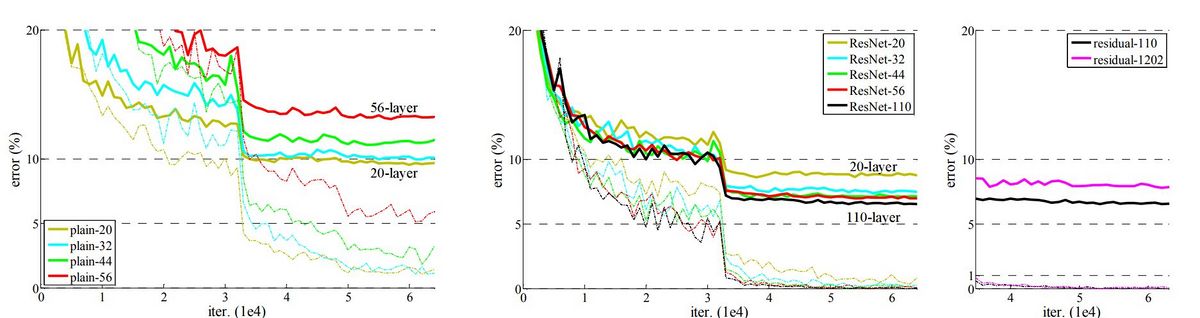
Using the CIFAR-10 dataset, which consists of 50k training images and 10k testing images in 10 classes, the following shows the results of experiments trained on the training set and evaluated on the test set. The aim is to compare the behaviours of extremely deep networks using plain architectures and residual networks. A higher training error is observed when going deeper for deep plain nets. This phenomenon is similar to what was observed with the ImageNet dataset, suggesting that such an optimization difficulty is a fundamental problem. However, similar to the ImageNet case, the proposed architecture manages to overcome the optimization difficulty and reach accuracy gains as the depth increases. The training and testing errors are shown in the following graphs: