Synthesizing Programs for Images usingReinforced Adversarial Learning
Synthesizing Programs for Images usingReinforced Adversarial Learning: Summary of the ICML 2018 paper http://proceedings.mlr.press/v80/ganin18a.html
Presented by
1. Nekoei, Hadi [Quest ID: 20727088]
Motivation
Conventional neural generative models have major problems.
- Firstly, it is not clear how to inject knowledge to the model about the data.
- Secondly, latent space is not easily interpretable.
The provided solution in this paper is to generate programs to incorporate tools, e.g. graphics editors, illustration software, CAD. and creating more meaningful API(sequence of complex actions vs raw pixels).
Introduction
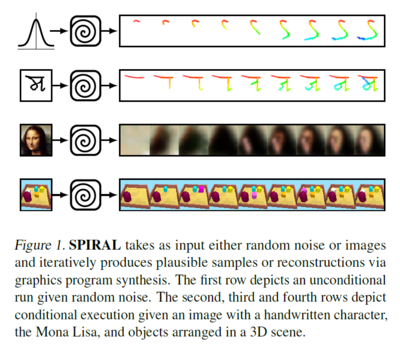
Humans, frequently, use the ability to recover structured representation from raw sensation to understand their environment. Decomposing a picture of a hand-written character into strokes or understanding the layout of a building can be exploited to learn how actually our brain works. To address these problems, a new approach is presented for interpreting and generating images using Deep Reinforced Adversarial Learning in order to solve the need for a large amount of supervision and scalability to larger real-world datasets. In this approach, an adversarially trained agent (SPIRAL) generates a program which is executed by a graphics engine to generate images, either conditioned on data or unconditionally. The agent is rewarded by fooling a discriminator network and is trained with distributed reinforcement learning without any extra supervision. The discriminator network itself is trained to distinguish between generated and real images.
Related Work
Related works in this filed is summarized as follows:
- There has been a huge amount of studies on inverting simulators to interpret images (Nair et al., 2008; Paysan et al., 2009; Mansinghka et al., 2013; Loper & Black, 2014; Kulkarni et al., 2015a; Jampani et al., 2015)
- Inferring motor programs for reconstruction of MNIST digits (Nair & Hinton, 2006)
- Visual program induction in the context of hand-written characters on the OMNIGLOT dataset (Lake et al., 2015)
- inferring and learning feed-forward or recurrent procedures for image generation (LeCun et al., 2015; Hinton & Salakhutdinov, 2006; Goodfellow et al., 2014; Ackley et al., 1987; Kingma & Welling, 2013; Oord et al., 2016; Kulkarni et al., 2015b; Eslami et al., 2016; Reed et al., 2017; Gregor et al., 2015).
However, all of these methods have limitations such as:
- Scaling to larger real-world datasets
- Requiring hand-crafted parses and supervision in the form of sketches and corresponding images
- Lack the ability to infer structured representations of images
The SPIRAL Agent
Overview
The paper aims to construct a generative model [math]\displaystyle{ \mathbf{G} }[/math] to take samples from a distribution [math]\displaystyle{ p_{d} }[/math]. The generative model consists of a recurrent network $\pi$ (called policy network or agent) and an external rendering simulator R that accepts a sequence of commands from the agent and maps them into the domain of interest, e.g. R could be a CAD program rendering descriptions of primitives into 3D scenes. In order to train policy network $\pi$, the paper has exploited generative adversarial network. In this framework, generator tries to fool a discriminator network which is trained to distinguish between real and fake samples. Thus, the distribution generated by [math]\displaystyle{ \mathbf{G} }[/math] approaches [math]\displaystyle{ pd }[/math].
Objectives
The authors give training objective for [math]\displaystyle{ \mathbf{G} }[/math] and [math]\displaystyle{ \mathbf{D} }[/math] as follows.
Discriminator:
Following (Gulrajani et al., 2017), the objective for [math]\displaystyle{ \mathbf{D} }[/math] is defined as:
[math]\displaystyle{ \mathcal{L}_D = -\mathbb{E}_{x\sim p_d}[D(x)] + \mathbb{E}_{x\sim p_g}[D(x)] + R }[/math]
where [math]\displaystyle{ \mathbf{R} }[/math] is a regularization term softly constraining [math]\displaystyle{ \mathbf{D} }[/math] to stay in the set of Lipschitz continuous functions (for some fixed Lipschitz constant).
Generator:
To define the objective for [math]\displaystyle{ \mathbf{G} }[/math], a variant of the REINFORCE (Williams, 1992) algorithm, advantage actor-critic (A2C) is employed:
[math]\displaystyle{ \mathcal{L}_G = -\sum_{t} log\pi(a_t|s_t;\theta)[R_t - V^{\pi}(s_t)] }[/math]
where [math]\displaystyle{ V^{\pi} }[/math] is an approximation to the value function which is considered to be independent of theta, and [math]\displaystyle{ R_{t} = \sum_{t}^{N}r_{t} }[/math] is a 1-sample Monte-Carlo estimate of the return. Rewards are set to: [math]\displaystyle{ r_t = \left\{ \begin{array}{@{} l c @{}} 0 \text{ t N} \\ D(\mathbb{R}(a_1, a_2, ..., a_N)) & \text{ t = N} \end{array}\right. \label{eq4} }[/math]
One interesting aspect of this new formulation is that we
can also bias the search by introducing intermediate rewards
which may depend not only on the output of R but also on
commands used to generate that output.
Conditional generation:
In some cases such as producing a given image [math]\displaystyle{ x_{target} }[/math], conditioning the model on auxiliary inputs is useful. That can be done by feeding [math]\displaystyle{ x_{target} }[/math] to both policy and discriminator networks as: [math]\displaystyle{ p_g = -\matcal{R}(p_a(a|x_{target})) }[/math] While [math]\displaystyle{ p_{d} }[/math] becomes a dirac function centered at [math]\displaystyle{ x_{target} }[/math]. It can be proven that for this particular setting of [math]\displaystyle{ p_{g} }[/math] and [math]\displaystyle{ p_{d} }[/math], the [math]\displaystyle{ l2 }[/math]-distance is an optimal discriminator.
Distributed Learning:
Our training pipeline is outlined in Figure 2b. It is an extension of the recently proposed IMPALA architecture (Espeholt et al., 2018). For training, we define three kinds of workers:
- Actors are responsible for generating the training trajectories through interaction between the policy network and the rendering simulator. Each trajectory contains a sequence $((\pi_{t}; a_{t}) | 1 \leq t \leq N)$ as well as all intermediate
renderings produced by R.
- A policy learner receives trajectories from the actors, combines them into a batch and updates $\pi$ by performingan SGD step on $\mathcal{L}_G$ (2). Following common practice (Mnih et al., 2016), we augment $\mathcal{L}_G$ with an entropy penalty encouraging exploration.
- In contrast to the base IMPALA setup, we define an additional discriminator learner. This worker consumes
random examples from pd, as well as generated data (final renders) coming from the actor workers, and optimizes $\mathcal{L}_D$ (1).
Note: We do not omit any trajectories in the policy learner. Instead, we decouple the D updates from the $D$ updates by introducing a replay buffer that serves as a communication layer between the actors and the discriminator learner. That allows the latter to optimize D at a higher rate than the training of the policy network due to the difference in network sizes ($D$ is a multi-step RNN, while $D$ is a plain $CNN$). We note that even though sampling from a replay buffer inevitably leads to smoothing of pg, we found this setup to work well in practice.