probabilistic Matrix Factorization
Introduction and Motivation (Netflix Dataset)
The problem provides an approach to collaborative filtering that scales linearly and, thus, can handle large datasets. The methods are discussed in the context of the Netflix dataset. A very popular way to do collaborative filtering is to train low-dimensional factor models. This approach is based on the idea that the attitudes or preferences of a user can be determined by a small number of unobserved factors.
This dataset is an [math]\displaystyle{ N \times M }[/math] matrix where each row corresponds to a user, each column to a movie and the entries to a rating. Ratings take on values [math]\displaystyle{ \,1,...,K }[/math]. The difficulty in this problem arises from the fact that each user has only rated a subset of movies. If there is some latent rank-[math]\displaystyle{ \,D }[/math] structure underlying these ratings (that is, underlying variables that determine how much a user enjoys a movie) then to find these variables we could factor the matrix.
Formally, given a preference matrix [math]\displaystyle{ R\, }[/math] which is [math]\displaystyle{ N \times M }[/math], we wish to find an [math]\displaystyle{ N \times D }[/math] matrix [math]\displaystyle{ \,U^T }[/math] and an [math]\displaystyle{ D \times M }[/math] matrix [math]\displaystyle{ \,V }[/math] such that [math]\displaystyle{ \,R = U^TV }[/math]. [math]\displaystyle{ \,V }[/math] is a factor matrix (i.e. for the [math]\displaystyle{ \,D }[/math] latent variables, it gives the value for each movie) and [math]\displaystyle{ \,U^T }[/math] gives coefficients of these factors for each user. The actual "Prize" dataset has [math]\displaystyle{ \,N=480,189, M = 17,770 }[/math] with over 100 million of these entries having values. To train a low-dimensional factor model for this dataset, one must, under a given loss function, find the best rank-[math]\displaystyle{ \,D }[/math] approximation [math]\displaystyle{ \,\hat{R} = U^T V }[/math] for the observed [math]\displaystyle{ N \times M }[/math] target matrix [math]\displaystyle{ \,R }[/math].
Recently, researchers have proposed a variety of probabilistic factor-based models that can be described as graphical models in which hidden factor variables have directed connections to variables that represent user ratings. However, for these models, the exact inference is intractable.
Another difficulty that arises with this dataset is that it is unbalanced. There is a lot of variance in user activity; thus, some rows are much sparser than others. In fact, over 10% of users have fewer than 20 ratings.
There are several existing ways to solve this problem but they often require approximations that are slow and, at times, inaccurate. Another instinctive approach might be to use SVD. However, since there is a lot of missing data in this case, the optimization problem that needs to be solved is not convex. Thus, existing methods do not scale well and often have lower accuracy in cases where a row is sparse.
Instead of constraining the rank of [math]\displaystyle{ \,\hat{R} }[/math], i.e. the number of factors, researchers have proposed penalizing the norms of [math]\displaystyle{ \,U }[/math] and [math]\displaystyle{ \,V }[/math]. However, to learn this model, one needs to solve a sparse semi-definite program, and so it is infeasible to use this approach for very large datasets such as this one that has millions of observations.
The proposed solution is to use a probabilistic model - probabilistic matrix factorization<ref name="PMF">R. Salakhutdinov and A.Mnih. "Probabilistic Matrix Factorization".</ref>. Unlike all of the above-mentioned approaches with the exception of the matrix-factorization-based ones, PMF scales well to large datasets. Furthermore, unlike most of the existing algorithms, which have trouble making accurate predictions for users who have very few ratings, PMF performs well on very sparse and imbalanced datasets, such as the Netflix dataset.
Probabilistic Matrix Factorization
Given the preference matrix described above with entries [math]\displaystyle{ \,R_{ij} }[/math], the aim is to find a factorization that minimizes the root mean squared error(RMSE) on the test set. An initial attempt is to use a linear model where we assume that there is Gaussian noise in the data. Define [math]\displaystyle{ \,I_{ij} }[/math] to be 1 if [math]\displaystyle{ \,R_{ij} }[/math] is known (i.e. user [math]\displaystyle{ \,i }[/math] has rated movie [math]\displaystyle{ \,j }[/math]) and 0 otherwise. Further, let [math]\displaystyle{ \,\mathcal N(x|\mu,\sigma^2) = f_X(x) }[/math] with [math]\displaystyle{ X \sim \mathcal N(\mu,\sigma^2) }[/math]. Then, we can define a conditional probability of the ratings with hyperparameter [math]\displaystyle{ \,\sigma^2 }[/math]
[math]\displaystyle{ p(R|U,V,\sigma^2) = \prod_{i=1}^N \prod_{j=1}^M \left[ \mathcal N(R_{ij}|U_i^TV_j,\sigma^2)\right]^{I_{ij}}\,\,\,\,\,\,\,\,(1) }[/math]
and priors on [math]\displaystyle{ \,U }[/math] and [math]\displaystyle{ \,V }[/math] with hyperparameters [math]\displaystyle{ \sigma^2_U, \sigma^2_V }[/math]
[math]\displaystyle{ p(U|\sigma^2_U) = \prod_{i=1}^N \mathcal N(U_i|0,\sigma^2_U\textbf{I})\,\,\,\,\textrm{and}\,\,\,\,p(V|\sigma^2_V) = \prod_{i=1}^M \mathcal N(V_i|0,\sigma^2_V\textbf{I}).\,\,\,\,\,\,\,\,(2) }[/math]
Then we aim to maximize the log posterior over [math]\displaystyle{ \,U }[/math] and [math]\displaystyle{ \,V }[/math] (to derive this, simply substitute the definition of [math]\displaystyle{ \mathcal{N} }[/math] and take the log):
[math]\displaystyle{ \ln p(U,V,\sigma^2,\sigma^2_V,\sigma^2_U) = - \frac{1}{2\sigma^2}\sum_{i=1}^N\sum_{j=1}^M I_{ij}(R_{ij} - U_i^TV_j)^2 - \frac{1}{2\sigma^2_U} \sum_{i=1}^N U_i^TU_i - \frac{1}{2\sigma^2_V} \sum_{i=1}^N V_i^TV_i }[/math][math]\displaystyle{ - \frac{1}{2}\left(\kappa\ln\sigma^2 + ND\ln\sigma^2_U + MD\ln\sigma^2_V\right) + C\,\,\,\,\,\,\,\,(3) }[/math]
where [math]\displaystyle{ \,\kappa }[/math] is the number of known entries and [math]\displaystyle{ \,C }[/math] is a constant independent of the parameters. We can fix the three variance hyperparameters as constants which reduces the optimization to the first three terms. Then defining [math]\displaystyle{ \lambda_M = \sigma^2/\sigma^2_M }[/math] for [math]\displaystyle{ \,M=U,V }[/math] and multiplying by [math]\displaystyle{ \,-\sigma^2\lt 0 }[/math] results in a the following objective function
[math]\displaystyle{ E = \frac{1}{2}\left(\sum_{i=1}^N\sum_{j=1}^M I_{ij}(R_{ij} - U_i^TV_j)^2 + \lambda_U \sum_{i=1}^N \|U_i \|^2_F + \lambda_V \sum_{i=1}^M \| V_i \|^2_F \right)\,\,\,\,\,\,\,(4) }[/math]
where [math]\displaystyle{ \|A \|^2_F = \sum_{i=1}^m\sum_{j=1}^n |a_{ij}|^2 }[/math] is the Frobenius norm. Note that if all values are known (i.e. [math]\displaystyle{ I_{ij} = 1 \,\, \forall(i,j) }[/math] ) then as [math]\displaystyle{ \sigma^2_U, \sigma^2_V \rightarrow \infty }[/math], [math]\displaystyle{ \, E }[/math] reduces to the SVD objective function.
The objective function, (4), can be minimized using the method of steepest descent which is linear in the number of observations.
The following figure (taken from the authors' paper listed in the Reference section) shows the graphical model for Probabilistic Matrix Factorization (PMF):
In this paper, the dot product between user- and movie-specific feature vectors is passed through the logistic function [math]\displaystyle{ \,g(x) = 1/(1+exp(−x)) }[/math], which bounds the range of predictions, since using a simple linear-Gaussian model makes predictions outside of the range of valid rating values. As well, the ratings from 1 to [math]\displaystyle{ K }[/math] are mapped to the [math]\displaystyle{ [0,1] }[/math] interval using the function [math]\displaystyle{ \,t(x) = (x-1)/(K-1) }[/math]. This ensures that the range of valid rating values matches the range of predictions made by the model. Thus,
Automatic Complexity Control for PMF Models
In order for PMF models to generalize well to new data, it is essential to apply good capacity control. Given sufficiently many factors, a PMF model can approximate any given matrix arbitrarily well.
The simplest way to control a PMF model's capacity is to change the dimensionality of feature vectors. However, this approach is not suitable if the dataset is unbalanced, because any single number of feature dimensions will be too high for some feature vectors and at the same time be too low for other feature vectors.
The use of regularization parameters such as [math]\displaystyle{ \,\lambda_U }[/math] and [math]\displaystyle{ \,\lambda_V }[/math] defined above is a more flexible approach to regularization. Cross-validation is usually the simplest way for finding suitable values for these parameters; however, this approach is usually very computationally expensive.
A method proposed by Nowlan and Hinton <ref name = "NH1992">S.J. Nowlan and G. E. Hinton. Simplifying neural networks by soft weight-sharing. Neural Computation, 4:473-493, 1992.</ref>, which was originally applied to neural networks, can be used to determine suitable values for a PMF model's regularization parameters automatically and at the same time without significantly affecting the model's training time.
The problem of approximating a matrix in the [math]\displaystyle{ \,L_2 }[/math] sense by a product of two low-rank matrices, where the low-rank matrices are regularized by penalizing their Frobenius norms, can be expressed as a MAP estimation (described in detail in Jaakkola's lecture slides) in a probabilistic model that has spherical Gaussian priors(also described in detail in the same lecture slides) on the rows of the low-rank matrices. The complexity of the PMF model is controlled by the hyperparameters, which consist of the noise variance ([math]\displaystyle{ \,\sigma^2 }[/math]) and the parameters of the priors ([math]\displaystyle{ \,\sigma_U^2 }[/math] and [math]\displaystyle{ \,\sigma_V^2 }[/math]).
As suggested in <ref name = "NH1992"/>, by introducing priors for the hyperparameters and maximizing the PMF model's log-posterior (more details can be found in Nychka's slides) over both the parameters and the hyperparameters, one can use the training data to automatically control the PMF model's complexity. Thus, for the NetFlix data, by using spherical priors for the user feature vectors and the movie feature vectors, one obtains the standard form of PMF whose values for
[math]\displaystyle{ \,\lambda_U }[/math] and [math]\displaystyle{ \,\lambda_V }[/math] are automatically selected. In summary, to
control the PMF model's capacity automatically and efficiently, we estimate the parameters and hyperparameters by maximizing the log posterior given by
[math]\displaystyle{ \,ln \; p(U,V,\sigma^2,\Theta_U,\Theta_V|R) = ln \; p(R|U,V,\sigma^2) + ln \; p(U|\Theta_U) + ln \; p(V|\Theta_V) + ln \; p(\Theta_U) + ln \; p(\Theta_V) + C, }[/math]
where [math]\displaystyle{ \,\Theta_U }[/math] and [math]\displaystyle{ \,\Theta_V }[/math] are the hyperparameters for the priors over the user feature vectors and the priors over the movie feature vectors, respectively, and [math]\displaystyle{ \,C }[/math] is a constant that does not depend on the parameters or hyperparameters.
When the prior distribution is Gaussian and the movie and user feature vectors are kept fixed, the optimal hyperparameters can be expressed in closed form. Thus to simplify learning we alternate between optimizing the hyperparameters and updating the feature vectors using steepest ascent with the values of hyperparameters fixed. When the prior is a mixture of Gaussians, the hyperparameters can be updated by performing a single step of EM. Usually the authors use improper priors for the hyperparameters, but it is easy to extend the closed form updates to handle conjugate priors for the hyperparameters.
Constrained Probabilistic Matrix Factorization
In the above PMF approach, if a row is very sparse (i.e., a user has rated very few movies) then the estimated values will be approximately equal to the mean rating by other users. Thus, we need a way remedy this. This is done by introducing a constraint and modifying PMF to create a constrained PMF algorithm.
First, we define an [math]\displaystyle{ N \times M }[/math] indicator matrix [math]\displaystyle{ \,I }[/math] whose [math]\displaystyle{ \,(i,j) \;th }[/math] element is [math]\displaystyle{ \,1 }[/math] if user [math]\displaystyle{ \,i }[/math] has rated movie [math]\displaystyle{ \,j }[/math] and is [math]\displaystyle{ \,0 }[/math] if otherwise. Recall that [math]\displaystyle{ \,D }[/math] is the estimated number of latent factors. Let [math]\displaystyle{ \,W }[/math] be the [math]\displaystyle{ D \times M }[/math] latent similarity constraint matrix whose entries measure similarities between the movies and the latent variables.
Then for each user [math]\displaystyle{ \,i }[/math], [math]\displaystyle{ \,i = 1,\dots,N }[/math], we can define [math]\displaystyle{ U_i = Y_i + \frac{\sum_{k=1}^M I_{ik}W_k}{\sum_{k=1}^MI_{ik}}. }[/math]
This means that users with similar sets of watched movies will have similar priors for [math]\displaystyle{ \,U_i }[/math].
Constrained PMF differs from PMF in the second term, so that [math]\displaystyle{ U_i \neq Y_i }[/math]; in contrast, in the unconstrained PMF model, [math]\displaystyle{ \,U_i }[/math] and [math]\displaystyle{ \,Y_i }[/math] are equal, because the prior mean is fixed at a value of [math]\displaystyle{ \,0 }[/math]. So, replacing [math]\displaystyle{ \,U_i }[/math] in [math]\displaystyle{ \,(5) }[/math] gives
[math]\displaystyle{ p(R|Y,V,W,\sigma^2) = \prod_{i=1}^N \prod_{j=1}^M \left[ \mathcal N(R_{ij}|g\left(\left[Y_i + \frac{\sum_{k=1}^M I_{ik}W_k}{I_{ik}}\right]^TV_j\right),\sigma^2)\right]^{I_{ij}},\,\,\,\,\,\,\,\,(6) }[/math]
where, again, [math]\displaystyle{ \,g }[/math] is the logistic function.
[math]\displaystyle{ \,W }[/math] is regularized by placing a zero-mean spherical Gaussian prior on it; this prior is [math]\displaystyle{ \,p(W|\sigma_W) = \prod_{k=1}^M \; \mathcal N(W_k|0,\sigma_W^2I) }[/math].
Again, we can transform this maximization into a minimization like with [math]\displaystyle{ \,(4) }[/math] and use gradient descent (linear in number of observations). There is a significant improvement in performance.
The following figure (taken from the authors' paper listed in the Reference section) shows the graphical model for the constrained Probabilistic Matrix Factorization (PMF) model:
Experimental Results
Consider a subset of the Netflix data set with 50,000 users and 1,850 movies, with 1,082,982 known values. In this dataset, more than half of the rows are sparse (less than 10 entries), which will help to show the improvement offered by constrained PMF.
A factorization was created with [math]\displaystyle{ \,D = 30 }[/math] using SVD, PMF and constrained PMF. The parameters [math]\displaystyle{ \,\lambda_K = 0.002 }[/math] for [math]\displaystyle{ \,K = U,V,W,Y }[/math]. The results are shown in the figures below<ref name="PMF"/>. On the left, RMSE is plotted against the number of passes through the data. On the right, the RMSE is plotted against the sparsity of the rows.
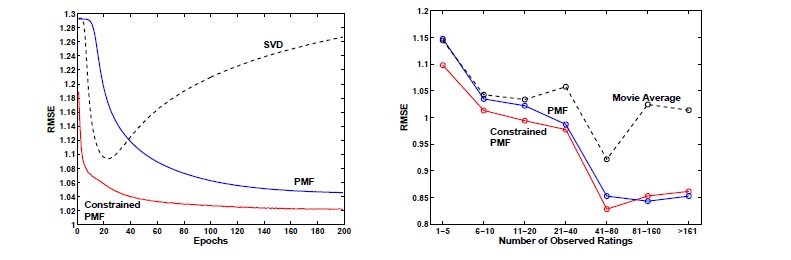
Both PMF models outperform SVD and, further, constrained PMF beats PMF. An interesting, but expected, result is that constrained PMF is clearly the best method in the case of sparse rows, but is indistinguishable from PMF when there are many known entries. They both do much better than a simple average of the movie ratings as the amount of information increases.
Another test was done looking at matrix in which the only known data is whether a movie has been rated. Tests show that PMF can use this information to provide better estimates than a simple average.
Results of similar tests on the full Netflix dataset provide comparable results.
Conclusion
The main problem is to factor a matrix that has many missing values, including many sparse rows, with hopes of using the known values to provide information about the missing values.
PMF provides a probabilistic approach using Gaussian assumptions on the known data and the factor matrices. We can further constrain priors to improve the algorithm, especially in the case of sparse rows.
Experimental results show that PMF and constrained PMF perform quite well.
The next steps might be a completely Bayesian approach which would involve a computationally expensive MCMC step but has shown improvement in preliminary experiments.
References
<references />