deflation Methods for Sparse PCA

Introduction

Principal component analysis (PCA) is a popular change of variables technique used in dimension reduction and visualization. The goal of PCA is to extract several principal components, linear combinations of input variables that together best account for the variance in a data set. Often, PCA is formulated as an eigenvalue decomposition problem: each eigenvector of the sample covariance matrix of a data set corresponds to the loadings or coefficients of a principal component. A common approach to solving this partial eigenvalue decomposition is to iteratively alternate between two subproblems: rank-one variance maximization and matrix deflation.

A primary drawback of PCA is its lack of sparsity. Each principal component is a linear combination of all variables, and the loadings are typically non-zero. Sparsity is desirable as it often leads to more interpretable results, reduced computation time, and improved generalization. In analogy to the PCA setting, many authors attempt to solve the sparse PCA problem by iteratively alternating between two subtasks: cardinality-constrained rank-one variance maximization and matrix deflation. The former is a hard problem, and a variety of relaxations and approximate solutions have been developed in the literature. The latter subtask has received relatively little attention and is typically borrowed without justification from the PCA context. In this paper, author demonstrates that the standard PCA deflation procedure is seldom appropriate for the sparse PCA setting. To rectify the situation, he first develops several heuristic deflation alternatives with more desirable properties, then reformulate the sparse PCA optimization problem to explicitly reflect the maximum additional variance objective on each round. The result is a generalized deflation procedure that typically outperforms more standard techniques on real-world datasets.

Notation

[math]\displaystyle{ I }[/math] is the identity matrix. [math]\displaystyle{ \mathbb{S}^{p}_{+} }[/math] is the set set of all symmetric, positive semidefinite matrices in [math]\displaystyle{ \mathbb{R}^{p\times p} }[/math]. [math]\displaystyle{ \textbf{Card}(x) }[/math] represents the cardinality of or number of non-zero entries in the vector [math]\displaystyle{ x }[/math].

Deflation methods

A matrix deflation modifies a matrix to eliminate the influence of a given eigenvector, typically by setting the associated eigenvalue to zero.

Hotelling's deflation and PCA

In the PCA setting, the goal is to extract the [math]\displaystyle{ r }[/math] leading eigenvectors of the sample covariance matrix, [math]\displaystyle{ A_0 \in\mathbb{S}^{p}_{+} }[/math], as its eigenvectors are equivalent to the loadings of the first [math]\displaystyle{ r }[/math] principal components. Hotelling’s deflation method is a simple and popular technique for sequentially extracting these eigenvectors. On the [math]\displaystyle{ t }[/math]-th iteration of the deflation method, we first extract the leading eigenvector of [math]\displaystyle{ A_{t -1} }[/math],

[math]\displaystyle{ x_t = argmax_{x:x^Tx=1}x^TA_{t-1}x }[/math]

and we then use Hotelling's deflation to annihilate [math]\displaystyle{ x_t }[/math]:

[math]\displaystyle{ A_{t}=A_{t-1}-x_tx^T_tA_{t-1}x_tx^T_t }[/math]

The deflation step ensures that the [math]\displaystyle{ t }[/math]+1-st leading eigenvector of A0 is the leading eigenvector of [math]\displaystyle{ A_{t} }[/math]. The following proposition explains why.

Proposition

If [math]\displaystyle{ \lambda _{1}\ge ...\ge \lambda _{p} }[/math]are the eigenvalues of [math]\displaystyle{ A\in\mathbb{S}_{+}^{p},x_{1}...x_{p} }[/math]are the corresponding eigenvectors, and [math]\displaystyle{ \hat{A}=A-x_{j}x_{j}^{T}Ax_{j}x_{j}^{T} }[/math]for some [math]\displaystyle{ j\in 1,...p }[/math],then [math]\displaystyle{ \hat{A} }[/math] has eigenvectors [math]\displaystyle{ x_{1},...x_{p} }[/math]with corresponding eigenvalues [math]\displaystyle{ \lambda _{1},...\lambda _{j-1},0,\lambda _{j+1},\lambda _{p} }[/math].

Hotelling's deflation and sparse PCA

In the sparse PCA setting, we seek [math]\displaystyle{ r }[/math]sparse loadings which together capture the maximum amount of variance in the data. To find the first such "pseudo-eigenvector" equation, we can consider cardinality-constrained version of equation:

[math]\displaystyle{ x_1=argmax_{x:x^Tx=1\textbf{Card}(x)\leq k_1}x^TA_0x. }[/math]

Typically, Hotelling’s deflation is utilized by substituting an extracted pseudo-eigenvector for a true eigenvector in the deflation step of [math]\displaystyle{ A_{t}=A_{t-1}-x_tx^T_tA_{t-1}x_tx^T_t }[/math]. This substitution, however, is seldom justified, for the properties of Hotelling’s deflation, depend crucially on the use of a true eigenvector.

Alternative deflation techniques

Rectifying the failings of pseudo-eigenvector Hotelling's deflation by considering several alternative deflation techniques better suited to the sparse PCA setting.

Projection deflation

Given a data matrix [math]\displaystyle{ Y \in \mathbb{R}^{n\times p} }[/math] and an arbitrary unit vector in [math]\displaystyle{ x\in \mathbb{R} }[/math], an intuitive way to remove the contribution of [math]\displaystyle{ x }[/math] from [math]\displaystyle{ Y }[/math] is to project [math]\displaystyle{ Y }[/math] onto the orthocomplement of the space spanned by [math]\displaystyle{ x:\hat{Y} = Y(I-xx^T) }[/math]. If [math]\displaystyle{ A }[/math] is the sample covariance matrix of [math]\displaystyle{ Y }[/math] , then the sample covariance of [math]\displaystyle{ \hat{Y} }[/math] is given by[math]\displaystyle{ \hat{A}=(I-xx^T)A(I-xx^T) }[/math], which leads to our formulation for projection deflation:

[math]\displaystyle{ A_t=A_{t-1}-x_tx_t^TA_{t-1}-A_{t-1}x_tx_t^T+x_tx_t^TA_{t-1}x_tx_t^T=(I-x_tx_t^T)A_{t-1}(I-x_tx_t^T) }[/math]

- When [math]\displaystyle{ x_t }[/math]is a true eigenvector of [math]\displaystyle{ A_{t-1} }[/math]with eigenvalue [math]\displaystyle{ \lambda_t }[/math],projection deflation reduces to Hotelling;s deflation.

[math]\displaystyle{ A_t=A_{t-1}-x_tx_t^TA_{t-1}-A_{t-1}x_tx_t^T+x_tx_t^TA_{t-1}x_tx_t^T }[/math]

[math]\displaystyle{ =A_{t-1}-\lambda_tx_tx_t^T-\lambda_tx_tx_t^T+\lambda_tx_tx_t^T }[/math]

[math]\displaystyle{ =A_{t-1}-x_tx^T_tA_{t-1}x_tx^T_t }[/math]

- When [math]\displaystyle{ x_t }[/math]is not a true eigenvector,projection deflation maintains the desirable properties that were lost to Hotelling's deflation.

Schur complement deflation

Let [math]\displaystyle{ x\in\mathbb{R}^p }[/math]be a unit vector and [math]\displaystyle{ W\in\mathbb{R}^p }[/math]be a Gaussian random vector, representing the joint distribution of the data variables. If [math]\displaystyle{ W }[/math]has covariance matrix [math]\displaystyle{ \sigma }[/math], then ([math]\displaystyle{ W,Wx }[/math])has covariance matrix[math]\displaystyle{ V=\left( \begin{matrix} \Sigma & \Sigma x_{{}} \\ x^{T}\Sigma & x^{T}\Sigma x \\\end{matrix} \right) }[/math], and [math]\displaystyle{ Var(W|Wx)=\Sigma -\frac{\Sigma xx^{T}\Sigma }{x^{T}\Sigma x} }[/math]whenever[math]\displaystyle{ x^{T}\Sigma x\ne 0 }[/math]. That is, the conditional variance is the Schur complement of the vector variance [math]\displaystyle{ x^T \sigma x }[/math]in the full covariance matrix [math]\displaystyle{ V }[/math]. Substituting sample covariance matrices for their population counterparts, Schur complement deflation is:

[math]\displaystyle{ A_{t}=A_{t-1}-\frac{A_{t-1}x_{t}x_{t}^{T}A_{t-1}}{x_{t}^{T}A_{t-1}x_{t}} }[/math]

Like projection deflation, it preserves positive-semi-definiteness.

-when [math]\displaystyle{ x_t }[/math] is an eigenvector of [math]\displaystyle{ A-{t-1} }[/math] with eigenvalue [math]\displaystyle{ \lambda_t ne 0 }[/math], it reduces to Hotelling's deflation.

[math]\displaystyle{ A_{t}=A_{t-1}-\frac{A_{t-1}x_{t}x_{t}^{T}A_{t-1}}{x_{t}^{T}A_{t-1}x_{t}} }[/math]

[math]\displaystyle{ =A_{t-1}-\frac{\lambda+t x_tx_t^T\lambda_t}{\lambda_t} }[/math]

[math]\displaystyle{ =A_{t-1}-x_tx^T_tA_{t-1}x_tx^T_t }[/math]

Orthogonalized deflation

Whenever we deal with a sequence of non-orthogonal vectors, we must take care to distinguish between the variance explained by a vector and the additional variance explained, given all previous vectors.The additional variance explained by the [math]\displaystyle{ t }[/math]-th pseudo-eigenvector, [math]\displaystyle{ x_t }[/math], is equivalent to the variance explained by the component of [math]\displaystyle{ x_t }[/math] orthogonal to the space spanned by all previous pseudo-eigenvectors, [math]\displaystyle{ q_t=x_t-P_{t-1}x_t }[/math]is the orthogonal projection onto the space spanned by [math]\displaystyle{ x_1,...,x_{t-1} }[/math]. On each deflation step, therefore, we only want to eliminate the variance associated with [math]\displaystyle{ q_t }[/math].

-when deflation procedure is equivalent to Hotelling's deflation for [math]\displaystyle{ t }[/math]=1:

[math]\displaystyle{ A_{t}=A_{t-1}-x_tx^T_tA_{t-1}x_tx^T_t }[/math]

-when [math]\displaystyle{ t }[/math]>1, it can be expressed in terms of a running Gram-Schmidt decomposition:

[math]\displaystyle{ q_{t}=\frac{(I-Q_{t-1}Q_{t-1}^{T})x_{t}}{\left\| (I-Q_{t-1}Q_{t-1}^{T})x{}_{t} \right\|} }[/math]

[math]\displaystyle{ A_{t}=A_{t-1}-q_{t}q_{t}^{T}A_{t-1}q_{t}q_{t}^{T} }[/math]

where[math]\displaystyle{ q_t }[/math]=[math]\displaystyle{ x_1 }[/math], and [math]\displaystyle{ q_1,...,q_{t-1} }[/math]from the the columns of [math]\displaystyle{ Q_{t-1} }[/math].Since [math]\displaystyle{ q_1,...,q_{t-1} }[/math]from an orthonormal basis for the space spanned by [math]\displaystyle{ x_1,...,x_{t-1} }[/math],we have [math]\displaystyle{ Q_{t-1}Q_{t-1}^T=P_{t-1} }[/math], the aforementioned orthogonal projection.

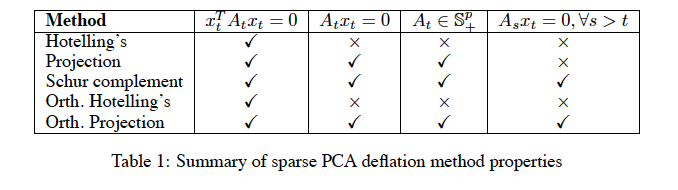
Summary of sparse PCA deflation method properties

Proposition

Orthogonalized Schur complement deflation is equivalent to Schur complement deflation.

The following table compares properties of the various deflation techniques studied above.

Reformulating sparse PCA

Recall that the goal of sparse PCA is to find [math]\displaystyle{ r }[/math] cardinality-constrained pseudo-eigenvectors which together explain the most variance in the data. If we additionally constrain the sparse loadings to be generated sequentially, as in the PCA setting and the previous section, then a greedy approach of maximizing the additional variance of each new vector naturally suggests itself. On round [math]\displaystyle{ t }[/math], the additional variance of a vector [math]\displaystyle{ x }[/math] is given by [math]\displaystyle{ \frac{q_{t}A_{0}q}{q^{T}q} }[/math] where [math]\displaystyle{ A_{0} }[/math]is the data covariance matrix[math]\displaystyle{ q=(I-P_{t-1})x\lt .math\gt , and \lt math\gt P_{t-1} }[/math] is the projection onto the space spanned by previous pseudo-eigenvectors [math]\displaystyle{ x_{1},...,x_{t-1} }[/math]. As [math]\displaystyle{ q^{T}q=x^{T}(I-P_{t-1})(I-P_{t-1})x=x^{T}(I-P_{t-1})x }[/math], maximizing additional variance is equivalent to solving a cardinality-constrained maximum generalized eigenvalue problem,

[math]\displaystyle{ \underset{x}{\mathop{\max }}\,x^{T}(I-P_{t-1})A_{0}(I-P_{t-1})x }[/math]

subject to [math]\displaystyle{ x^{T}(I-P_{t-1})x=1 }[/math]

[math]\displaystyle{ \textbf{Card}(x)\leq k_t }[/math]

If we let [math]\displaystyle{ q_{s}=(I-P_{t-1})x_{s},\forall s\le t-1 }[/math],then[math]\displaystyle{ q_1,...,q_{t-1} }[/math]from an orthonormal basis for the space spanned by [math]\displaystyle{ x_1,...,x_{t-1} }[/math]. Writing[math]\displaystyle{ I-P_{t-1}=I-\sum\limits_{s=1}^{t-1}{q_{s}q_{s}^{T}=\prod\limits_{s=1}^{t-1}{(I-q_{s}q_{s}^{T})}} }[/math]suggests a generalized deflation techniques that leads to the solution on each round.

Algorithm 1

Generalized deflation method for sparse PCA: Given[math]\displaystyle{ \lt math\gt A_{0}\in S_{+}^{p},r\in N,\{k_{1},...,k_{r}\}\subset N }[/math],

Execute:

1.[math]\displaystyle{ B_{0}\leftarrow I }[/math]

2.For [math]\displaystyle{ t:=1,...r }[/math]

[math]\displaystyle{ \bullet x_{t}\leftarrow \underset{x:x^{T}B_{t-1}x=1,\text{Card}(x)\le k_{t}}{\mathop{\arg \max }}\,x^{T}A_{t-1}x }[/math]

[math]\displaystyle{ \bullet q_{t}\leftarrow B_{t-1}x_{t} }[/math]

[math]\displaystyle{ \bullet A_{t}\leftarrow (I-q_{t}q_{t}^{T})A_{t-1}(I-q_{t}q_{t}^{T}) }[/math]

[math]\displaystyle{ \bullet B_{t}\leftarrow B_{t-1}(I-q_{t}q_{t}^{T}) }[/math]

[math]\displaystyle{ \bullet x_{t}\leftarrow x_{t}/\left\| x_{t} \right\| }[/math]

Return: [math]\displaystyle{ \{x_{1},...x_{r}\} }[/math]

Experiment

Gene expression data

The Berkeley Drosophila Transcription Network Project (BDTNP) 3D gene expression data contains gene expression levels measured in each nucleus of developing Drosophila embryos and averaged across many embryos and developmental stages. An aggregate VirtualEmbryo contains 21 genes and 5759 example nuclei.Run GSLDA for eight iterations with cardinality pattern 9,7,6,5,3,2,2,2 and report the results in following table.

It shows a clear hierarchy among the deflation method and the generalized deflation method performs best.

Conclusion

The utility of above Hotelling's deflation procedures is not limited to the sparse PCA setting. Indeed, the methods presented can be applied to any of a number of constrained eigendecomposition-based problems, including sparse canonical correlation analysis and linear discriminant analysis.