Adversarial Attacks on Copyright Detection Systems

Presented by

Luwen Chang, Qingyang Yu, Tao Kong, Tianrong Sun

Introduction

Copyright detection system is one of the most commonly used machine learning systems; however, the hardiness of copyright detection and content control systems to adversarial attacks, inputs intentionally designed by people to cause the model to make a mistake, has not been widely addressed by public. Copyright detection systems are vulnerable to attacks for three reasons.

1. Unlike physical-world attacks where adversarial samples need to survive under different conditions like resolutions and viewing angles, any digital files can be uploaded directly to the web without going through a camera or microphone.

2. The detection system is open which means the uploaded files may not correspond to an existing class. In this case, it will prevent people from uploading unprotected audio/video whereas most of the uploaded files nowadays are not protected.

3. The detection system needs to handle a vast majority of content which have different labels but similar features. For example, in the ImageNet classification task, the system is easily attacked when there are two cats/dogs/birds with high similarities but from different classes.

In this paper, different types of copyright detection systems will be introduced. A widely used detection model from Shazam, a popular app used for recognizing music, will be discussed. Next, the paper talks about how to generate audio fingerprints using convolutional neural network and formulates the adversarial loss function using standard gradient methods. An example of remixing music is given to show how adversarial examples can be created. Then the adversarial attacks are applied onto industrial systems like AudioTag and YouTube Content ID to evaluate the effectiveness of the systems, and the conclusion is made at the end.

Types of copyright detection systems

Fingerprinting algorithm is to extract the features of the source file as a hash and then compare that to the materials protected by copyright in the database. If enough matches are found between the source and existing data, the copyright detection system is able to reject the copyright declaration of the source. Most audio, image and video fingerprinting algorithms work by training a neural network to output features or extracting hand-crafted features.

In terms of video fingerprinting, a useful algorithm is to detect the entering/leaving time of the objects in the video (Saviaga & Toxtli, 2018). The final hash consists of the entering/leaving of different objects and a unique relationship of the objects. However, most of these video fingerprinting algorithms only train their neural networks by using simple distortions such as adding noise or flipping the video rather than adversarial perturbations. This leads to that these algorithms are strong against pre-defined distortions but not adversarial attacks.

Moreover, some plagiarism detection systems also depend on neural networks to generate a fingerprint of the input document. Though using deep feature representations as a fingerprinting is efficient in detecting plagiarism, it still might be weak to adversarial attacks.

Audio fingerprinting may perform better than the algorithms above since most of time, the hash is generated by extracting hand-crafted features rather than training a neural network. But it still is easy to attack.

Case study: evading audio fingerprinting

Audio Fingerprinting Model

The audio fingerprinting model plays an important role in copyright detection. It is useful for quickly locating or finding similar samples inside an audio database. Shazam is a popular music recognization application, which uses one of the most well-known fingerprinting models. With three principles: temporally localized, translation invariant, and robustness, the Shazam algorithm is treated as a good fingerprint algorithm. It shows strong robustness even in presence of noise by using local maximum in spectrogram to form hashes.

Interpreting the fingerprint extractor as a CNN

The intention of this section is to build a differentiable neural network whose function resembles that of an audio fingerprinting algorithm, which is well-known for its ability to identify the meta-data, i.e. song names, artists and albums, while independent of audio format (Group et al., 2005). The generic neural network will then be used as an example of implementing black-box attacks on many popular real-world systems, in this case, YouTube and AudioTag.

The generic neural network model consists of two convolutional layers and a max-pooling layer, which is used for dimension reduction. This is depicted in the figure below. As mentioned above, the convolutional neural network is well-known for its properties of temporarily localized and transformational invariant. The purpose of this network is to generate audio fingerprinting signals that extract features that uniquely identify a signal, regardless of the starting and ending time of the inputs.

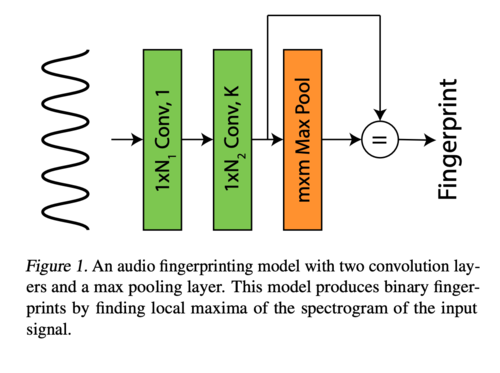
While an audio sample enters the neural network, it is first transformed by the initial network layer, which can be described as a normalized Hann function. The form of the function is shown below, with N being the width of the Kernel.

$$ f_{1}(n)=\frac {sin^2(\frac{\pi n} {N})} {\sum sin^2(\frac{\pi n}{N})} $$

The intention of the normalized Hann function is to smooth the adversarial perturbation of the input audio signal, which removes the discontinuity as well as the bad spectral properties. This transformation enhances the efficiency of black-box attacks that is later implemented.

The next convolutional layer applies a Short Term Fourier Transformation to the input signal by computing the spectrogram of the waveform and converts the input into a feature representation. Once the input signal enters this network layer, it is being transformed by the convolutional function below.

$$f_{2}(k,n)=e^{-i 2 \pi k n / N} $$ where k [math]\displaystyle{ {\in} }[/math] 0,1,...,N-1 (output channel index) and n [math]\displaystyle{ {\in} }[/math] 0,1,...,N-1 (index of filter coefficient)

The output of this layer is described as φ(x) (x being the input signal), a feature representation of the audio signal sample. However, this representation is flawed due to its vulnerability to noise and perturbation, as well as its difficulty to store and inspect. Therefore, a maximum pooling layer is being implemented to φ(x), in which the network computes a local maximum using a max-pooling function. This network layer outputs a binary fingerprint ψ (x) (x being the input signal) that will be used later to search for a signal against a database of previously processed signals.

Formulating the adversarial loss function

In the previous section, local maxima of spectrogram are used to generate fingerprints by CNN, but a loss has not been quantified to compare how similar two fingerprints are. After the loss is found, standard gradient methods can be used to find a perturbation [math]\displaystyle{ {\delta} }[/math], which can be added to a signal so that the copyright detection system will be tricked. Also, a bound is set to make sure the generated fingerprints are close enough to the original audio signal. $$\text{bound:}\ ||\delta||_p\le\epsilon$$

where [math]\displaystyle{ {||\delta||_p\le\epsilon} }[/math] is the [math]\displaystyle{ {l_p} }[/math]-norm of the perturbation and [math]\displaystyle{ {\epsilon} }[/math] is the bound of the difference between the original file and the adversarial example.

To compare how similar two binary fingerprints are, Hamming distance is employed. Hamming distance between two strings is the number of digits that are different (Hamming distance, 2020). For example, the Hamming distance between 101100 and 100110 is 2.

Let [math]\displaystyle{ {\psi(x)} }[/math] and [math]\displaystyle{ {\psi(y)} }[/math] be two binary fingerprints outputted from the model, the number of peaks shared by [math]\displaystyle{ {x} }[/math] and [math]\displaystyle{ {y} }[/math] can be found through [math]\displaystyle{ {|\psi(x)\cdot\psi(y)|} }[/math]. Now, to get a differentiable loss function, the equation is found to be

$$J(x,y)=|\phi(x)\cdot\psi(x)\cdot\psi(y)|$$

This is effective for white-box attacks with knowing the fingerprinting system. However, the loss can be easily minimized by modifying the location of the peaks by one pixel, which would not be reliable to transfer to black-box industrial systems. To make it more transferable, a new loss function which involves more movements of the local maxima of the spectrogram is proposed. The idea is to move the locations of peaks in [math]\displaystyle{ {\psi(x)} }[/math] outside of neighborhood of the peaks of [math]\displaystyle{ {\psi(y)} }[/math]. In order to implement the model more efficiently, two max-pooling layers are used. One of the layers has a bigger width [math]\displaystyle{ {w_1} }[/math] while the other one has a smaller width [math]\displaystyle{ {w_2} }[/math]. For any location, if the output of [math]\displaystyle{ {w_1} }[/math] pooling is strictly greater than the output of [math]\displaystyle{ {w_2} }[/math] pooling, then it can be concluded that no peak is in that location with radius [math]\displaystyle{ {w_2} }[/math].

The loss function is as the following:

$$J(x,y) = \sum_i\bigg(ReLU\bigg(c-\bigg(\underset{|j| \leq w_1}{\max}\phi(i+j;x)-\underset{|j| \leq w_2}{\max}\phi(i+j;x)\bigg)\bigg)\cdot\psi(i;y)\bigg)$$ The equation above penalizes the peaks of [math]\displaystyle{ {x} }[/math] which are in neighborhood of peaks of [math]\displaystyle{ {y} }[/math] with radius of [math]\displaystyle{ {w_2} }[/math]. The activation function uses [math]\displaystyle{ {ReLU} }[/math]. [math]\displaystyle{ {c} }[/math] is the difference between the outputs of two max-pooling layers.

Lastly, instead of the maximum operator, smoothed max function is used here: $$S_\alpha(x_1,x_2,...,x_n) = \frac{\sum_{i=1}^{n}x_ie^{\alpha x_i}}{\sum_{i=1}^{n}e^{\alpha x_i}}$$ where [math]\displaystyle{ {\alpha} }[/math] is a smoothing hyper parameter. When [math]\displaystyle{ {\alpha} }[/math] approaches positive infinity, [math]\displaystyle{ {S_\alpha} }[/math] is closer to the actual max function.

To summarize, the optimization problem can be formulated as the following:

$$ \underset{\delta}{\min}J(x+\delta,x)\\ s.t.||\delta||_{\infty}\le\epsilon $$ where [math]\displaystyle{ {x} }[/math] is the input signal, [math]\displaystyle{ {J} }[/math] is the loss function with the smoothed max function.

Remix adversarial examples

While solving the optimization problem, the resulted example would be able to fool the copyright detection system. But it could sound unnatural with the perturbations.

Instead, the fingerprinting could be made in a more natural way (i.e., a different audio signal).

By modifying the loss function, which switches the order of the max-pooling layers in the smooth maximum components in the loss function, this remix loss function is to make two signal x and y look as similar as possible.

$$J_{remix}(x,y) = \sum_i\bigg(ReLU\bigg(c-\bigg(\underset{|j| \leq w_2}{\max}\phi(i+j;x)-\underset{|j| \leq w_1}{\max}\phi(i+j;x)\bigg)\bigg)\cdot\psi(i;y)\bigg)$$

By adding this new loss function, a new optimization problem could be defined.

$$ \underset{\delta}{\min}J(x+\delta,x) + \lambda J_{remix}(x+\delta,y)\\ s.t.||\delta||_{p}\le\epsilon $$

where [math]\displaystyle{ {\lambda} }[/math] is a scalar parameter that controls the similarity of [math]\displaystyle{ {x+\delta} }[/math] and [math]\displaystyle{ {y} }[/math].

This optimization problem is able to generate an adversarial example from the selected source, and also enforce the adversarial example to be similar to another signal. The resulting adversarial example is called Remix adversarial example because it gets the references to its source signal and another signal.

Evaluating transfer attacks on industrial systems

The effectiveness of default and remix adversarial examples is tested through white-box attacks on the proposed model and black-box attacks on two real-world audio copyright detection systems - AudioTag and YouTube “Content ID” system. [math]\displaystyle{ {l_{\infty}} }[/math] norm and [math]\displaystyle{ {l_{2}} }[/math] norm of perturbations are two measures of modification. Both of them are calculated after normalizing the signals so that the samples could lie between 0 and 1.

Before evaluating black-box attacks against real-world systems, white-box attacks against our own proposed model is used to provide the baseline of adversarial examples’ effectiveness. Loss function [math]\displaystyle{ {J(x,y)=|\phi(x)\cdot\psi(x)\cdot\psi(y)|} }[/math] is used to generate white-box attacks. The unnoticeable fingerprints of the audio with the noise can be changed or removed by optimizing the loss function.

Table 1: Norms of the perturbations for white-box attacks

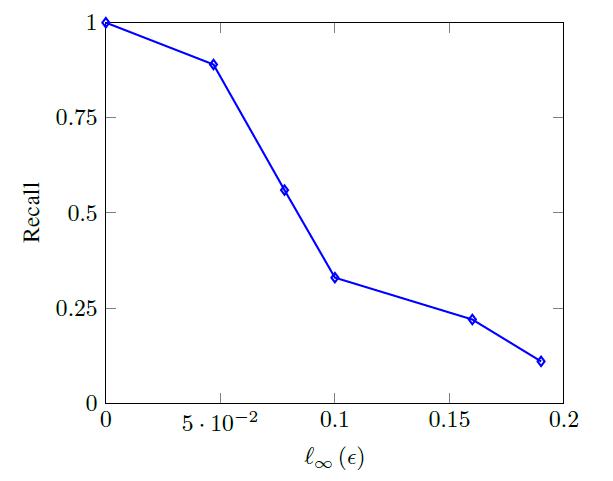
In black-box attacks, the AudioTag system is found to be relatively sensitive to the attacks since it can detect the songs with a benign signal while it failed to detect both default and remix adversarial examples. The architecture of the AudioTag fingerprint model and surrogate CNN model is guessed to be similar based on the experimental observations.

Similar to AudioTag, the YouTube “Content ID” system also got the result with successful identification of benign songs but failure to detect adversarial examples. However, to fool the YouTube Content ID system, a larger value of the parameter [math]\displaystyle{ {\epsilon} }[/math] is required. YouTube Content ID system has a more robust fingerprint model.

Table 2: Norms of the perturbations for black-box attacks

Figure 2: YouTube’s copyright detection recall against the magnitude of noise

Conclusion

In conclusion, many industrial copyright detection systems used in the popular video and music website such as YouTube and AudioTag are significantly vulnerable to adversarial attacks established in the existing literature. By building a simple music identification system resembling that of Shazam using neural network and attack it by the well-known gradient method, this paper firmly proved the lack of robustness of the current online detector. The intention of this paper is to raise the awareness of the vulnerability of the current online system to adversarial attacks and to emphasize the significance of enhancing our copyright detection system. More approach, such as adversarial training needs to be developed and examined, in order to protect us against the threat of adversarial copyright attack.

Critiques

- The experiments in this paper appear like to be a proof-of-concept rather than a serious evaluation of a model. One problem is that the norm is used to evaluate the perturbation. Unlike the norm in image domains which can be visualized and easily understood, the perturbations in the audio domain are a more difficult to comprehend. A cognitive study or something like a user study might need be conducted in order to understand this. Another question related to this is that if the random noise is 2x bigger or 3x bigger in terms of norm, does this make huge difference when listening to it? Are these two perturbations both very obvious or both unnoticeable? In addition, it seems that a dataset is built but the stats are missing. Third, no baseline methods are being compared to in this paper, not even an ablation study. The proposed two methods (default and remix) seem to perform similarly.

References

Group, P., Cano, P., Group, M., Group, E., Batlle, E., Ton Kalker Philips Research Laboratories Eindhoven, . . . Authors: Pedro Cano Music Technology Group. (2005, November 01). A Review of Audio Fingerprinting. Retrieved November 13, 2020, from https://dl.acm.org/doi/10.1007/s11265-005-4151-3

Hamming distance. (2020, November 1). In Wikipedia. https://en.wikipedia.org/wiki/Hamming_distance

Jovanovic. (2015, February 2). How does Shazam work? Music Recognition Algorithms, Fingerprinting, and Processing. Toptal Engineering Blog. https://www.toptal.com/algorithms/shazam-it-music-processing-fingerprinting-and-recognition

Saadatpanah, P., Shafahi, A., & Goldstein, T. (2019, June 17). Adversarial attacks on copyright detection systems. Retrieved November 13, 2020, from https://arxiv.org/abs/1906.07153.

Saviaga, C. and Toxtli, C. Deepiracy: Video piracy detection system by using longest common subsequence and deep learning, 2018. https://medium.com/hciwvu/piracy-detection-using-longestcommon-subsequence-and-neuralnetworks-a6f689a541a6

Wang, A. et al. An industrial strength audio search algorithm. In Ismir, volume 2003, pp. 7–13. Washington, DC, 2003.